- Research Article
- Open access
- Published:
An Entropy-Based Propagation Speed Estimation Method for Near-Field Subsurface Radar Imaging
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 636458 (2010)
Abstract
During the last forty years, Subsurface Radar (SR) has been used in an increasing number of noninvasive/nondestructive imaging applications, ranging from landmine detection to breast imaging. To properly assess the dimensions and locations of the targets within the scan area, SR data sets have to be reconstructed. This process usually requires the knowledge of the propagation speed in the medium, which is usually obtained by performing an offline measurement from a representative sample of the materials that form the scan region. Nevertheless, in some novel near-field SR scenarios, such as Microwave Wood Inspection (MWI) and Breast Microwave Radar (BMR), the extraction of a representative sample is not an option due to the noninvasive requirements of the application. A novel technique to determine the propagation speed of the medium based on the use of an information theory metric is proposed in this paper. The proposed method uses the Shannon entropy of the reconstructed images as the focal quality metric to generate an estimate of the propagation speed in a given scan region. The performance of the proposed algorithm was assessed using data sets collected from experimental setups that mimic the dielectric contrast found in BMI and MWI scenarios. The proposed method yielded accurate results and exhibited an execution time in the order of seconds.
1. Introduction
Subsurface Radar (SR) is a reliable technology that is currently used for an increasing number of nondestructive inspection applications [1–5]. SR techniques are used to image and detect inclusions present in a given scan region by processing the reflections produced when the area is irradiated using electromagnetic waves. Some advantages of SR technology are the use of nonionizing radiation and a highly automated and/or portable operation [1]. Targets present nonlinear signatures in raw SR data that difficult the proper determination of the correct dimensions and locations of the inclusions inside the scan region [6, 7]. This phenomenon is caused by the different signal travel times along the scan geometry and the wide beam width exhibited by antennas that operate in the Ultra Wide Band (UWB) frequency range. To properly detect and visualize the inclusion responses, SR datasets must be properly reconstructed.
Several reconstruction techniques have been proposed to form SR images [2, 5–8]. These approaches transfer the recorded responses from the spatiotemporal domain where they were collected to the spatial domain where the data will be displayed. Since SR image formation methods use either the time of arrival of the recorded responses or the wavenumber of the radiated waveforms, the wave speed in the propagation medium is required to accurately map the target reflections to their original spatial locations. This value can be obtained from offline measurements using a representative sample of the materials forming the scan area or by using an estimation technique. Any errors in the estimate will cause shifts in the location of the reconstructed responses and the formation of artifacts.
To determine the propagation speed in SR scenarios, a wide variety of estimation techniques have been proposed. These approaches can be divided into two main categories, focal quality measurement techniques and wave modeling approaches. Focal quality measurement techniques reconstruct the collected datasets using different propagation speed values and calculate a focal quality metric that is used to determine a suitable estimate [9–11]. Wave modeling, also called tomographic, techniques perform a minimization process by solving iteratively Maxwell's equations for a set of possible scan scenarios until the difference between the measured data and the analytical solution satisfies a stop criterion [12–15]. Techniques in both categories have been validated on experimental data, yielding accurate results in far-field SR imaging settings.
In the last decade, SR has been used for a series of novel near-field imaging scenarios, such as Breast Microwave Radar (BMR) and Microwave Wood Inspection (MWI). The targets in these applications have sizes in the order of millimetres making necessary the use of large bandwidth waveforms (>5 GHz) to achieve spatial resolution values within this order of magnitude. To the best of the authors' knowledge, only a few propagation speed estimation techniques for this SR imaging setting have been proposed [16–18]. Nevertheless, these methods have some limitations that can potentially limit their use in realistic scenarios. The parametric search proposed in [16] requires a large number of datasets from the scan region to generate accurate estimates. The wave modeling approaches presented in [17, 18] rely on computationally intensive procedures that result in processing times that can range from several minutes to a couple of days [17, 18], resulting in low data throughput rates. Additionally, the method proposed in [17] has limited use when the radiated waveform has a bandwidth over 3 GHz, which is quite common in BMR and MWI scenarios.
This paper proposes a novel technique to accurately determine the propagation speed in near-field SR scenarios. This technique reconstructs a given dataset using different propagation speed values and calculates the Shannon entropy to measure their focal quality. The value used to form the minimum entropy image is then processed to estimate the propagation speed in the scan region. Entropy metrics have been used for airborne radar to estimate the motion parameters of a given target and in SR to eliminate artifacts in reconstructed images arising from a random air-soil interface [19, 20]. The entropy of a radar image is an indicator of its focal quality. As the image is blurred, the uncertainty in the location and dimensions of a target increases. On the other hand, as the focal quality increases, the uncertainty in the position and size of each inclusion decreases. Therefore, the best focal quality is achieved when the entropy of the reconstructed SR image is minimized [21]. The proposed technique exhibits a number of improvements over standard propagation speed estimation methods for near-field imaging, including lower execution time and the ability to generate accurate results using a single data set. This paper is organized as follows. The signal model is described in Section 2. In Section 3 the proposed approach is explained. In Section 4, the performance of the proposed technique is assessed using experimental data sets. Finally, concluding remarks can be found in Section 5.
2. SR Imaging in Homogeneous Media
2.1. Signal Model
Consider a linear scan geometry formed by  scan locations in the (
scan locations in the ( ) plane. The problem domain contains
) plane. The problem domain contains  targets over the intervals [
targets over the intervals [ ] on the
] on the  axis and [
axis and [ ] on the
] on the  axis and is assumed to have a constant propagation speed
axis and is assumed to have a constant propagation speed  . The distance between the scan location and the
. The distance between the scan location and the  th target is given by
th target is given by  , where (
, where ( ) and (
) and ( ) are the antenna and the
) are the antenna and the  th target coordinates, respectively. In this scan geometry, the antenna element(s) face downwards.
th target coordinates, respectively. In this scan geometry, the antenna element(s) face downwards.
At ( ), a waveform
), a waveform  is radiated, and the reflections from the targets inside the scan region are recorded at the same scan location. The remaining scan locations are inactive during this process. This process is repeated for each scan location. The responses recorded at this scan location can be expressed by
is radiated, and the reflections from the targets inside the scan region are recorded at the same scan location. The remaining scan locations are inactive during this process. This process is repeated for each scan location. The responses recorded at this scan location can be expressed by

where  is the reflectivity of the
is the reflectivity of the  th target. Now consider the responses from the
th target. Now consider the responses from the  th target
th target  . The Fourier transform of
. The Fourier transform of  along the
along the  direction is given by
direction is given by

where  , and it is known as the wave number. Equation (2) is known as the spherical phase function of the scan geometry.
, and it is known as the wave number. Equation (2) is known as the spherical phase function of the scan geometry.
Since the targets are located at near-field distances, the differences between travel times at adjacent scan locations are not negligible. These differences lead to the formation of hyperbolic signatures, which make it difficult to properly assess the dimension and location of the targets inside the scan region [1]. To properly visualize the dimensions and locations of these inclusions, the collected data must be reconstructed. One of the most effective image formation algorithms for near-field SR imaging is the frequency-wavenumber migration algorithm [6, 8]. This technique has been used in seismic applications for more than three decades, and it is extensively used in subsurface radar imaging. This method can be summarized as follows. First the Fourier transform of  is calculated in the
is calculated in the  direction yielding
direction yielding

In order to transfer the data contained in  to the rectangular frequency space (
to the rectangular frequency space ( ), a mapping
), a mapping  is performed. The resulting spectrum is given by
is performed. The resulting spectrum is given by

Finally, the reconstructed image,  , is obtained by calculating the inverse 2D fast Fourier transform of
, is obtained by calculating the inverse 2D fast Fourier transform of  .
.
2.2. Propagation Speed Uncertainty Effects
In the majority of the SR scenarios, it is assumed that the medium propagation speed is known a priori. This consideration can have several negative effects on the reconstructed images if there is a difference between the value used in the reconstruction process and the propagation speed of the scan region. Let us denote the propagation speed estimate  and the scan region propagation speed
and the scan region propagation speed  . Their corresponding wavenumbers are
. Their corresponding wavenumbers are  and
and  , and the wavenumber difference is given by
, and the wavenumber difference is given by  . If
. If  is reconstructed using
is reconstructed using  , the mapping function would have the form
, the mapping function would have the form

where the value of  will introduce a nonlinear error in the frequency mapping process. Depending on the magnitude, two cases can occur. If
will introduce a nonlinear error in the frequency mapping process. Depending on the magnitude, two cases can occur. If  , then
, then  and
and

The resulting spectrum has a frequency shift on the  axis that decreases as the
axis that decreases as the  value increases. Since
value increases. Since  determines the
determines the  spatial frequency of the reconstructed data, the mapping error will produce a nonlinear displacement on the
spatial frequency of the reconstructed data, the mapping error will produce a nonlinear displacement on the  axis. Given that the error varies along the
axis. Given that the error varies along the  axis, the targets in the reconstructed images will have concave signatures. Alternatively, if
axis, the targets in the reconstructed images will have concave signatures. Alternatively, if  , then
, then  and
and

then the error introduced by the mapping process would produce convex signatures in the spatial domain. Although the length of these target signatures will not be as large as they would have been had  been left unprocessed (due to the subtraction of the
been left unprocessed (due to the subtraction of the  term in the mapping process), the target signatures still present augmented sizes and nonlinear behaviour.
term in the mapping process), the target signatures still present augmented sizes and nonlinear behaviour.
In both cases, the defocusing caused by propagation speed error can be quantified by using the histogram of the reconstructed image magnitude values. Let us consider the case where  . In this case, the histogram would contain a series of components corresponding to the different
. In this case, the histogram would contain a series of components corresponding to the different  values. As the wavenumber error increases, the length of the nonlinear signatures grows as well. The defocusing caused the target responses to spread among a larger number of magnitude levels in the image. This will result in an increased number of modes in the histogram compared to the image reconstructed using
values. As the wavenumber error increases, the length of the nonlinear signatures grows as well. The defocusing caused the target responses to spread among a larger number of magnitude levels in the image. This will result in an increased number of modes in the histogram compared to the image reconstructed using  . Therefore, the image sharpness decreases as the magnitude of
. Therefore, the image sharpness decreases as the magnitude of  increases.
increases.
To illustrate this effect, a simulated data set,  , was generated using an SR simulator developed by the authors [22]. This data set contained three point scatters located at (0.1, 0.15)m, (0.35, 0.24)m, and (0.8, 0.22)m. The irradiated signal was a Stepped Frequency Continuous Wave (SFCW) with a bandwidth of 11 GHz and a center frequency of 6.5 GHz. The propagation speed in the scan region was
, was generated using an SR simulator developed by the authors [22]. This data set contained three point scatters located at (0.1, 0.15)m, (0.35, 0.24)m, and (0.8, 0.22)m. The irradiated signal was a Stepped Frequency Continuous Wave (SFCW) with a bandwidth of 11 GHz and a center frequency of 6.5 GHz. The propagation speed in the scan region was  m/s. The unprocessed data set is shown in Figure 1. The image obtained by reconstructing
m/s. The unprocessed data set is shown in Figure 1. The image obtained by reconstructing  using
using  and its corresponding histogram is shown in Figures 2(a) and 2(b), respectively. To evaluate the effects in the image when
and its corresponding histogram is shown in Figures 2(a) and 2(b), respectively. To evaluate the effects in the image when  ,
,  was also reconstructed using propagation speed values of 1.5
was also reconstructed using propagation speed values of 1.5 and 1.2
and 1.2 . The resulting images are shown in Figures 3(a) and 4(a), respectively. The histograms of the reconstructed images are given in Figures 3(b) and 4(b). Notice how the target signatures exhibit a concave shape that becomes more elongated as the wavenumber error increases. The number of modes in the histogram grows as the magnitude of
. The resulting images are shown in Figures 3(a) and 4(a), respectively. The histograms of the reconstructed images are given in Figures 3(b) and 4(b). Notice how the target signatures exhibit a concave shape that becomes more elongated as the wavenumber error increases. The number of modes in the histogram grows as the magnitude of  increases as well. It can also be appreciated how the location of the targets is shifted upwards as a result of the wavenumber error.
increases as well. It can also be appreciated how the location of the targets is shifted upwards as a result of the wavenumber error.
The effects on the reconstruction process when  were analyzed by processing
were analyzed by processing  using propagation speed values of 0.5
using propagation speed values of 0.5 and 0.8
and 0.8 . The resulting images are shown in Figures 5(a) and 6(a), respectively. Their corresponding histograms are given in Figures 5(b) and 6(b). Although the signature size in these images is smaller than in the unprocessed data set, they still have a convex shape. Similarly to when
. The resulting images are shown in Figures 5(a) and 6(a), respectively. Their corresponding histograms are given in Figures 5(b) and 6(b). Although the signature size in these images is smaller than in the unprocessed data set, they still have a convex shape. Similarly to when  was reconstructed using propagation speed values greater than
was reconstructed using propagation speed values greater than  , the spread in the target signatures causes an increase in the image energy levels. This is reflected in the additional modes in Figures 4(b) and 5(b), compared to Figure 2(a).
, the spread in the target signatures causes an increase in the image energy levels. This is reflected in the additional modes in Figures 4(b) and 5(b), compared to Figure 2(a).
2.3. Entropy As a Focal Quality Metric
The focal quality of the image  depends on the value of
depends on the value of  used during the reconstruction process. Therefore, in order to determine the fitness of
used during the reconstruction process. Therefore, in order to determine the fitness of  as an accurate propagation speed estimate, the focal quality of the reconstructed data can be used as a metric. An efficient way of determining the focal quality of a radar image is by calculating its entropy. This metric measures the level of uncertainty in a random variable. Let
as an accurate propagation speed estimate, the focal quality of the reconstructed data can be used as a metric. An efficient way of determining the focal quality of a radar image is by calculating its entropy. This metric measures the level of uncertainty in a random variable. Let  be a discrete random variable with a probability density function
be a discrete random variable with a probability density function  . According to Shannon's definition [23], the entropy of
. According to Shannon's definition [23], the entropy of  is given by
is given by

Pun [24] defined the entropy of a digital image with  intensity levels as
intensity levels as

where  are the pixels corresponding to the
are the pixels corresponding to the  th intensity level on the image and
th intensity level on the image and  is the total number of pixels in the image. It can be seen in (9) that the entropy value of an image depends on the pixel intensity distribution. To illustrate the performance of entropy as a focal quality metric,
is the total number of pixels in the image. It can be seen in (9) that the entropy value of an image depends on the pixel intensity distribution. To illustrate the performance of entropy as a focal quality metric,  was reconstructed using a set of one hundred different
was reconstructed using a set of one hundred different  values in the interval
values in the interval  ; see Figure 7. The plot of the different entropy values is shown in Figure 8. Note that the minimum entropy value is located at
; see Figure 7. The plot of the different entropy values is shown in Figure 8. Note that the minimum entropy value is located at  .
.
3. Methodology
3.1. Radar Imaging in a Two-Layer Scenario
Most near-field SR scenarios have a layer formed by air or a homogeneous matching material between the scan geometry and the scan region [20, 25, 26]. This can be modeled as an observation domain  composed of two regions, denoted a
composed of two regions, denoted a  and
and  , with different propagation speeds, denoted a
, with different propagation speeds, denoted a  and
and  , respectively. Since the dielectric properties of
, respectively. Since the dielectric properties of  are usually known a priori or can be calculated offline, determining
are usually known a priori or can be calculated offline, determining  is a trivial process. On the other hand,
is a trivial process. On the other hand,  ,
,  , where
, where  and
and  are the minimum and maximum propagation speed values that are physically feasible for this scan region. Using the signal model illustrated in (1), the recorded signal from a single target in this scenario would have the form
are the minimum and maximum propagation speed values that are physically feasible for this scan region. Using the signal model illustrated in (1), the recorded signal from a single target in this scenario would have the form

where  and
and  and
and  are the signal travel distance and propagation speed corresponding to the
are the signal travel distance and propagation speed corresponding to the  th region, respectively. A diagram for this generic scan geometry can be seen in Figure 8.
th region, respectively. A diagram for this generic scan geometry can be seen in Figure 8.
By dividing the total travel distance by the signal travel time, the average propagation speed is given by

or alternatively

To reconstruct the recorded data using a wavefront reconstruction approach, the stationary point in the following expression must be determined:

Obtaining a closed form expression for  from (13) can be difficult. A feasible approach is to perform the reconstruction process using a constant propagation value estimate,
from (13) can be difficult. A feasible approach is to perform the reconstruction process using a constant propagation value estimate,  , for the whole scan area. In this case the best focal quality will be achieved for the
, for the whole scan area. In this case the best focal quality will be achieved for the  value that has the smallest error for all the recorded reflections in the data set, which can be expressed as
value that has the smallest error for all the recorded reflections in the data set, which can be expressed as

By taking the first derivative of the right hand of (14) and equating it to zero, we obtain

By algebraically manipulating (15), we obtain

which is equivalent to averaging  along the
along the  direction. This approach can also be used to determine the
direction. This approach can also be used to determine the  value in a multitarget scenario as follows:
value in a multitarget scenario as follows:

By following a similar approach to the one used in the single-target scenario, the result is

which can also be written as

where

where  is the average location of the reflections from the scan region surface,
is the average location of the reflections from the scan region surface,  . Note that this estimate takes into account the effects of
. Note that this estimate takes into account the effects of  in the signal travel time.
in the signal travel time.
3.2. Propagation Speed Estimation Algorithm
Based on the previous discussion, we can now formulate a propagation speed estimation method. To detect the surface responses and estimate the average location of the targets in the dataset, the datasets were processed using the approach presented by the authors in [27]. This method uses wavelet multiscale products to eliminate the noise components in the dataset and preserve the target responses. The surface responses are characterized using the method proposed in [28]. The denoised dataset will be reconstructed using a set of feasible propagation speed values, defined as

The proposed estimation method can be described as follows.
-
(1)
Calculate the wavelet multiscale products of the range profile
 , in the recorded data. The result of this operation is denoted as
, in the recorded data. The result of this operation is denoted as 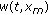 .
. -
(2)
Determine the range bin
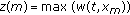 which corresponds to the location the surface.
which corresponds to the location the surface. -
(3)
Obtain the denoised range profile,
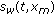 , using the method proposed by the authors in [28].
, using the method proposed by the authors in [28]. -
(4)
Repeat for
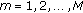 .
. -
(5)
Reconstruct
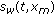 using the
using the  th value in the set
th value in the set  , yielding
, yielding 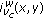 .
. -
(6)
Calculate the discrete probability density function of the energy levels on the reconstructed image.
-
(7)
Determine the entropy value of
 ,
, 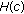 , using (10).
, using (10). -
(8)
Repeat steps (6) through (8) for each element in
 .
. -
(9)
Determine the value,
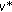 , in which the minimum entropy value is achieved.
, in which the minimum entropy value is achieved. -
(10)
Next, the image components in
 are segmented and labelled. Then
are segmented and labelled. Then 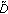 is estimated using the following operation:
is estimated using the following operation: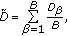 (22)
(22)where
 is the range location of the
is the range location of the 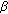 th target centroid, and the
th target centroid, and the  is the number of segmented objects in
is the number of segmented objects in  .
. -
(11)
The area of
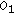 is calculated as follows:
is calculated as follows: (23)
(23) -
(12)
Finally, by algebraically manipulating (22), the value of
 can be determined using the following operation:
can be determined using the following operation: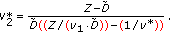 (24)
(24)By using the proportion of
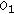 over the extension of
over the extension of 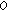 , it is possible to estimate the value of
, it is possible to estimate the value of 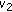 by determining the propagation speed that yields the reconstructed image with the best focal quality. A block diagram of the proposed method is shown in Figure 9.
by determining the propagation speed that yields the reconstructed image with the best focal quality. A block diagram of the proposed method is shown in Figure 9.
3.3. Refraction Effects and Lossy Medium Considerations
Compared to ray tracing approaches, wave front reconstruction methods only consider the phase behavior of the recorded responses to focus the collected data. As shown in [29], the refraction produced as the radiated wavefronts penetrate into  will affect the spectral support band,
will affect the spectral support band,  , of the target responses along the scan direction. The spectral support band in a radar system is closely related to the size of its point spread function [7]. In a single medium scenario, the support band size is given by
, of the target responses along the scan direction. The spectral support band in a radar system is closely related to the size of its point spread function [7]. In a single medium scenario, the support band size is given by

where  ,
,  is the size of the antenna radiation footprint, and
is the size of the antenna radiation footprint, and  is the range extension of the scan region. The refraction caused by the interface between the two mediums will change the emergence angle of the wavefronts [29], affecting the beam width coverage in
is the range extension of the scan region. The refraction caused by the interface between the two mediums will change the emergence angle of the wavefronts [29], affecting the beam width coverage in  . By using the approach proposed in [7] and the Huygens-Fresnel principle, the resulting spatial bandwidth is given by
. By using the approach proposed in [7] and the Huygens-Fresnel principle, the resulting spatial bandwidth is given by

where  ,
,  ,
,  is the antenna divergence angle, and
is the antenna divergence angle, and  is the extension of
is the extension of  . To satisfy the Nyquist-Shannon criterion along the scan trajectory, the separation between adjacent scan location must satisfy the following rule:
. To satisfy the Nyquist-Shannon criterion along the scan trajectory, the separation between adjacent scan location must satisfy the following rule:

where  is the wavelength corresponding to the maximum frequency component in
is the wavelength corresponding to the maximum frequency component in  .
.
The previous analysis can also be used to be extended to deal with lossy media, by modeling the wavenumber as

where  accounts for the attenuation in the medium. By performing the search process over a 2D search space where
accounts for the attenuation in the medium. By performing the search process over a 2D search space where  and
and  and evaluating the focal quality of the resulting images, an estimate of the attenuation factor in
and evaluating the focal quality of the resulting images, an estimate of the attenuation factor in  can be obtained. A similar approach was used in [20] to enhance near-field GPR images.
can be obtained. A similar approach was used in [20] to enhance near-field GPR images.
4. Results
In order to test the proposed method, a SFCW radar system was used. The system consists of a 360B Wiltron Network Analyzer and an AEL H Horn Antenna which has a length of 19 cm. A bandwidth of 11 GHz (1–12 GHz) was used in all the experiments. The system was characterized by recording the antenna responses inside an anechoic chamber. This reference signal was subtracted from the experiment data in order to eliminate distortions introduced by the components of the system. The data acquisition setup was surrounded by absorbing material in order to reduce undesirable environment reflections. The data was reconstructed using a 3 GHz PC with 1 GB RAM.
The proposed estimation algorithm was tested using experimental data acquired from a 3 × 1 × 13 m rectangular deposit filled with dry sand. The walls of this deposit were covered with electromagnetic wave absorbing material to eliminate their responses. The targets were buried within a region of 20 cms beneath the sand surface. Different distances between the antenna and the sand surface were used in each experiment to assess the effect of the air layer in the estimation method. In the first three experiments the box was filled with silica sand which has a propagation speed of  m/s [30]. The dielectric contrast between the scan region layers in this scenario is similar to the one present in BMI and MWI [31, 32] scenarios. The propagation speeds of the materials used in the experimental setups are shown in Table 1. The
m/s [30]. The dielectric contrast between the scan region layers in this scenario is similar to the one present in BMI and MWI [31, 32] scenarios. The propagation speeds of the materials used in the experimental setups are shown in Table 1. The  values of materials commonly found in BMI and MWI scan scenarios are summarized in Table 2. To demonstrate the robustness of the proposed approach, the search process is performed over the interval [1 × 108 m/s, 3 × 108 m/s] which is significantly larger than the range of values reported in the literature for dry sand ([1.37 × 108 m/s, 2.12 × 108 m/s]) [33]. A total of 200 equidistant values were defined in the search interval. In the experimental setup, the antenna was mounted on a horizontal rail that was 1.2 meters above the bottom of the box. The antenna motion was controlled by a stepper motor that was connected to a custom control interface controlled by a 2 GHz PC with 1 GB RAM. In all the experiments, the step size in the
values of materials commonly found in BMI and MWI scan scenarios are summarized in Table 2. To demonstrate the robustness of the proposed approach, the search process is performed over the interval [1 × 108 m/s, 3 × 108 m/s] which is significantly larger than the range of values reported in the literature for dry sand ([1.37 × 108 m/s, 2.12 × 108 m/s]) [33]. A total of 200 equidistant values were defined in the search interval. In the experimental setup, the antenna was mounted on a horizontal rail that was 1.2 meters above the bottom of the box. The antenna motion was controlled by a stepper motor that was connected to a custom control interface controlled by a 2 GHz PC with 1 GB RAM. In all the experiments, the step size in the  direction was 1 cm. The limit of the near-field region,
direction was 1 cm. The limit of the near-field region,  , on this imaging system is given by
, on this imaging system is given by

where  is the largest dimension of the antenna at its phase center. Since the maximum distance between the antenna and the sandbox bottom is 1.2 m, the targets in all the experiments were at near-field distances.
is the largest dimension of the antenna at its phase center. Since the maximum distance between the antenna and the sandbox bottom is 1.2 m, the targets in all the experiments were at near-field distances.
The first experimental data set is shown in Figure 10(a). In this experiment, two aluminum pipes with a diameter of 3 cm and two steel pieces with a length of 2 cm and a thickness of 5 mm were used. The average separation between the antenna and the sand surface was 10 cms. Figure 10(b) shows the energy of the denoised data. Note that the target signatures are easier to visualize in this image. The clutter in the image corresponds to stationary waves caused by multiple reflections between the surface and the antenna. Nevertheless, the magnitude of these responses is less than half of the magnitude of the target signatures. Figure 10(c) shows the resulting entropy values for the images formed using the values in the search interval. For this experiment, the minimum value is located at  m/s. The difference between this value and
m/s. The difference between this value and  is caused by higher propagation speed of the air layer (3 × 108 m/s). From the mathematical model of
is caused by higher propagation speed of the air layer (3 × 108 m/s). From the mathematical model of  described in (22), an increase in the value of
described in (22), an increase in the value of  will result in an increased
will result in an increased  . Substituting the values of
. Substituting the values of  ,
,  , and
, and  in (24) yields a value of
in (24) yields a value of  m/s, which has a 12% error compared to
m/s, which has a 12% error compared to  . The reconstructed image using
. The reconstructed image using  is shown in Figure 10(d).
is shown in Figure 10(d).
Figure 11(a) shows data collected from the second experimental setup. In this case, the targets were two aluminum pipes with a diameter of 1 cm and a steel plate with a length of 7 cms and a thickness of 1 cm. The average separation between the antenna and the sand surface was 7 cm. It can be seen that the sand surface in this experiment is closer to the antenna, which according to the modeling performed in Section 3 will result in a lower composite propagation speed estimate. Figure 11(b) shows the corresponding denoised image. The entropy values for the search interval are shown in Figure 11(c). The minimum entropy value was located at 2.04 × 108 m/s, and the corresponding propagation speed estimate was 1.63 × 108 m/s. Similarly to the last dataset, the dataset was reconstructed using  . The resulting image is shown in Figure 12(d). Notice increased focal quality of these images compared to the previous dataset. These results are consistent with the simulations presented in Section 3. As the error between propagation speed the medium and the estimate decreases, the focal quality of the image improves.
. The resulting image is shown in Figure 12(d). Notice increased focal quality of these images compared to the previous dataset. These results are consistent with the simulations presented in Section 3. As the error between propagation speed the medium and the estimate decreases, the focal quality of the image improves.
The recorded data from a third experimental setup is shown in Figure 12(a). In this setup, the same targets than in the previous experiment were used. The steel plate target was moved 7 cm deeper to observe the effect on the propagation speed estimate. The average separation between the sand surface and the antenna was 7 cm. The denoised data can be seen in Figure 12(b). The entropy values for the search interval are shown in Figure 12(c). The minimum entropy value was located at 2.17 × 108 m/s, and the corresponding propagation speed estimate was 1.743 × 108 m/s. The reconstructed image using  is shown in Figure 12(d).
is shown in Figure 12(d).
In order to test the proposed method in a different propagation medium, four targets were buried in desert sand ( m/s) [34]. In this case, the targets were aluminum pipes with a diameter of 1 cm. The average distance between the antenna and the sand surface was 6 cm. The recorded data set is shown in Figure 13(a). The result of the denoising process can be seen in Figure 13(b). The search was conducted also in the interval [1 × 108 m/s, 3 × 108 m/s]. The calculated entropy values are displayed in Figure 13(c). The location of the minimum value (2.3 × 108 m/s) was shifted towards the right. This is consistent with the model presented in Section 3, as the wave propagates faster in this medium than in silica sand. The estimated value of for this data set was 1.9 × 108 m/s. The reconstructed image using
m/s) [34]. In this case, the targets were aluminum pipes with a diameter of 1 cm. The average distance between the antenna and the sand surface was 6 cm. The recorded data set is shown in Figure 13(a). The result of the denoising process can be seen in Figure 13(b). The search was conducted also in the interval [1 × 108 m/s, 3 × 108 m/s]. The calculated entropy values are displayed in Figure 13(c). The location of the minimum value (2.3 × 108 m/s) was shifted towards the right. This is consistent with the model presented in Section 3, as the wave propagates faster in this medium than in silica sand. The estimated value of for this data set was 1.9 × 108 m/s. The reconstructed image using  is shown in Figure 13(d).
is shown in Figure 13(d).
The performance of the proposed technique was compared to the algorithm described in [16] which is based on the use of the Hough Transform (HT). This technique offers a good balance between execution time and estimation accuracy. The results of this comparison are shown in Table 3. The HT technique has a higher error and a larger execution time than the proposed approach.
5. Conclusions
A novel technique for propagation speed estimation in near-field SR scenarios is presented in this paper. The proposed algorithm focuses the data using initial estimates of the propagation speed on the media followed by the calculation of the focal quality of the reconstructed images using Shannon's entropy as a metric. A clutter removal process is performed on the data in order to allow a more accurate estimation. A search process is performed on the resulting entropy measurements in order to find the propagation speed value associated with the minimum entropy value. The proposed method yielded accurate propagation speed estimates (with an error less that 13%) and has an execution time in the order of seconds. Finally, the proposed algorithm exhibits both lower execution times and estimation errors compared to current noninvasive estimation techniques based on the use of the HT.
References
Daniels D: Ground Penetrating Radar. IEE Press, London, UK; 2004.
Pettinelli E, Di Matteo A, Mattei E, Crocco L, Soldovieri F, Redman JD, Annan AP: GPR response from buried pipes: measurement on field site and tomographic reconstructions. IEEE Transactions on Geoscience and Remote Sensing 2009, 47(8):2639-2645.
Travassos XL, Vieira DAG, Ida N, Vollaire C, Nicolas A: Inverse algorithms for the GPR assessment of concrete structures. IEEE Transactions on Magnetics 2008, 44(6):994-997.
Frigui H, Gader P: Detection and discrimination of land mines in ground-penetrating radar based on edge histogram descriptors and a possibilistic K-nearest neighbor classifier. IEEE Transactions on Fuzzy Systems 2009, 17(1):185-199.
Fear EC, Stuchly MA: Microwave detection of breast cancer. IEEE Transactions on Microwave Theory and Techniques 2000, 48(1):1854-1863. 10.1109/22.883862
Milman AS: SAR imaging by ω -k migration. International Journal of Remote Sensing 1993, 14(10):1965-1979. 10.1080/01431169308954015
Soumekh M: Synthetic Aperture Radar Signal Processing with MATLAB Algorithms. Wiley-Interscience, New York, NY, USA; 1999.
Stolt RH: Migration by Fourier transform. Geophysics 1978, 43(1):23-48. 10.1190/1.1440826
Ahmad F, Amin MG, Mandapati G: Autofocusing of through-the-wall radar imagery under unknown wall characteristics. IEEE Transactions on Image Processing 2007, 16(7):1785-1795.
Li L, Zhang W, Li F: A novel autofocusing approach for real-time through-wall imaging under unknown wall characteristics. IEEE Transactions on Geoscience and Remote Sensing 2010, 48(1):423-431.
Capineri L, Daniels DJ, Falorni P, Lopera OL, Windsor CG: Estimation of relative permittivity of shallow soils by using the ground penetrating radar response from different buried targets. Progress in Electromagnetics Research Letters 2008, 2: 63-71.
Lambot S, Slob EC, van den Bosch I, Stockbroeckx B, Scheers B, Vanclooster M: Estimating soil electric properties from monostatic ground-penetrating radar signal inversion in the frequency domain. Water Resources Research 2004, 40(4):W042051-W0420512.
Lambot S, Slob EC, van den Bosch I, Stockbroeckx B, Scheers B, Vanclooster M: GPR design and modeling for identifying the shallow subsurface dielectric properties. Proceedings of the 2nd International Workshop Advanced Ground Penetrating Radar, 2003, Delft, The Netherlands 1: 130-135.
Soldovieri F, Prisco G, Persico R: A strategy for the determination of the dielectric permittivity of a lossy soil exploiting GPR surface measurements and a cooperative target. Journal of Applied Geophysics 2009, 67(4):288-295. 10.1016/j.jappgeo.2008.09.007
Lambot S, Slob EC, van den Bosch I, Stockbroeckx B, Vanclooster M: Modeling of ground-penetrating radar for accurate characterization of subsurface electric properties. IEEE Transactions on Geoscience and Remote Sensing 2004, 42(11):2555-2568.
Milisavljevic N, Yarovoy AG: An effective algorithm for subsurface SAR imaging. Proceedings of the IEEE Antennas and Propagation Society International Symposium, June 2002, San Antonio, Tex, USA 4: 314-317.
Gentili GG, Spagnolini U: Electromagnetic inversion in monostatic ground penetrating radar: TEM horn calibration and application. IEEE Transactions on Geoscience and Remote Sensing 2000, 38(4):1936-1946. 10.1109/36.851775
Winters DW, Bond EJ, Van Veen BD, Hagness SC: Estimation of the frequency-dependent average dielectric properties of breast tissue using a time-domain inverse scattering technique. IEEE Transactions on Antennas and Propagation 2006, 54(11):3517-3528.
Flores BC, Martinez A, Hammer J: Optimization of high-resolution-radar motion compensation via entropy-like functions. Proceedings of the IEEE International Symposium Digest of Antennas and Propagation, July 1993, Ann Arbor, Mich, USA 3: 1906-1909.
Xu X, Miller EL, Rappaport CM: Minimum entropy regularization in frequency-wavenumber migration to localize subsurface objects. IEEE Transactions on Geoscience and Remote Sensing 2003, 41(8):1804-1812. 10.1109/TGRS.2003.813497
Sok-Son J, Thomas G, Flores BC: Range-Doppler Radar Imaging and Motion Compensation. Artech House, Norwood, Mass, USA; 2001.
Flores-Tapia D, Thomas G, Sabouni A, Noghanian S, Pistorius S: Breast tumor microwave simulator based on a radar signal model. Proceedings of the 6th IEEE International Symposium on Signal Processing and Information Technology (ISSPIT '07), 2007, Vancouver, Canada 17-22.
Cover T, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Pun T: A new method for grey-level picture thresholding using the entropy of the histogram. Signal Processing 1980, 2(3):223-237. 10.1016/0165-1684(80)90020-1
Leuschen CJ, Plumb RG: A matched-filter-based reverse-time migration algorithm for ground-penetrating radar data. IEEE Transactions on Geoscience and Remote Sensing 2001, 39(5):929-936. 10.1109/36.921410
Lopera O, Slob EC, Milisavljević N, Lambot S: Filtering soil surface and antenna effects from GPR data to enhance landmine detection. IEEE Transactions on Geoscience and Remote Sensing 2007, 45(3):707-717.
Flores-Tapia D, Thomas G, Phelan MC: Clutter reduction of GPR images using multiscale products. Proceedings of IASTED International Conference on Antennas, Radar and Wave Propagation (ARP '04), 2004, Banff, Canada 1:
Flores-Tapia D, Thomas G, Pistorius S: Skin surface removal on breast microwave imagery using wavelet multiscale products. Medical Imaging: Physiology, Function, and Structure from Medical Images, February 2006, Proceedings of SPIE 6143:
Margrave GF: Seismic acquisition parameter considerations for a linear velocity medium. Proceedings of the 67th Annual International Meetings of the Society of Exporation Geophycists, 1997, Dallas, Tex, USA 1: paper ACQ2.6
Fratticcioli E, Dionigi M, Sorrentino R: A new permittivity model for the microwave moisture measurement of wet sand. Proceedings of the 33rd European Microwave Conference, 2003 539-542.
Sill JM, Fear EC: Tissue sensing adaptive radar for breast cancer detection-experimental investigation of simple tumor models. IEEE Transactions on Microwave Theory and Techniques 2005, 53(11):3312-3319.
Daian G, Taube A, Birnboim A, Daian M, Shramkov Y: Modeling the dielectric properties of wood. Wood Science and Technology 2006, 40(3):237-246. 10.1007/s00226-005-0060-7
Davis JL, Annan AP: Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophysical Prospecting 1989, 37(5):531-551. 10.1111/j.1365-2478.1989.tb02221.x
Mätzler C: microwave permittivity of dry sand. IEEE Transactions on Geoscience and Remote Sensing 1998, 36(1):317-319. 10.1109/36.655342
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Flores-Tapia, D., Pistorius, S. An Entropy-Based Propagation Speed Estimation Method for Near-Field Subsurface Radar Imaging. EURASIP J. Adv. Signal Process. 2010, 636458 (2010). https://doi.org/10.1155/2010/636458
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/636458


 . (b) Image histogram.
. (b) Image histogram.
 . (b) Image histogram.
. (b) Image histogram.
 . (b) Image histogram.
. (b) Image histogram.
 . (b) Image histogram.
. (b) Image histogram.
 . (b) Image histogram.
. (b) Image histogram.
 ].
].
 , in the recorded data. The result of this operation is denoted as
, in the recorded data. The result of this operation is denoted as 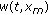 .
.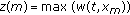 which corresponds to the location the surface.
which corresponds to the location the surface.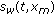 , using the method proposed by the authors in [
, using the method proposed by the authors in [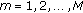 .
.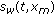 using the
using the  th value in the set
th value in the set  , yielding
, yielding 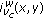 .
. ,
, 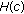 , using (10).
, using (10). .
.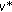 , in which the minimum entropy value is achieved.
, in which the minimum entropy value is achieved. are segmented and labelled. Then
are segmented and labelled. Then 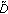 is estimated using the following operation:
is estimated using the following operation: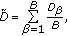
 is the range location of the
is the range location of the 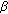 th target centroid, and the
th target centroid, and the  is the number of segmented objects in
is the number of segmented objects in  .
.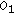 is calculated as follows:
is calculated as follows:
 can be determined using the following operation:
can be determined using the following operation: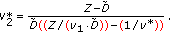
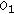 over the extension of
over the extension of 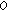 , it is possible to estimate the value of
, it is possible to estimate the value of 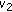 by determining the propagation speed that yields the reconstructed image with the best focal quality. A block diagram of the proposed method is shown in Figure
by determining the propagation speed that yields the reconstructed image with the best focal quality. A block diagram of the proposed method is shown in Figure 

 .
.
 .
.
 .
.
 .
.