- Research Article
- Open access
- Published:
Optical Flow and Principal Component Analysis-Based Motion Detection in Outdoor Videos
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 680623 (2010)
Abstract
We propose a joint optical flow and principal component analysis (PCA) method for motion detection. PCA is used to analyze optical flows so that major optical flows corresponding to moving objects in a local window can be better extracted. This joint approach can efficiently detect moving objects and more successfully suppress small turbulence. It is particularly useful for motion detection from outdoor videos with low quality. It can also effectively delineate moving objects in both static and dynamic background. Experimental results demonstrate that this approach outperforms other existing methods by extracting the moving objects more completely with lower false alarms.
1. Introduction
The detection of moving objects is critical in many defense and security applications, where motion detection is usually performed in a preprocessing step, a key to the success in the following target tracking and recognition. Many videos used in defense and security applications are outdoor videos whose quality may be degraded by various noisy sources, such as atmospheric turbulence, and sensor platform scintillation. Meanwhile, moving objects may be very small occupying a few pixels only, which makes motion detection very challenging. Under this circumstance, existing approaches may generate significant amount of false alarms.
Motion detection has been extensively investigated [1–3]. Many research works are conducted for indoor videos with large objects. As one of the major techniques, optical flow-based approaches have been widely used for motion detection. There are two classic methods of optical flow computation in computer vision: Horn-Schunck (HS) method and Lucas-Kanade (LK) method [4–7]. Both of them are based on the two-frame differential algorithms. LK method may not perform well in dense flow field; on the other hand, HS method can detect minor motion of objects and provide a 100% flow field [7]. Thus, we focus on HS method for optical flow computation in our research. Considering outdoor videos with low quality, special care needs to be taken in order to better extract features related to moving objects from optical flows while suppressing false alarms.
Principal component analysis (PCA) is a typical approach in multivariate analysis [8]. It is also named the discrete Karhunen-Loève transform (KLT) or the Hotelling transform [9]. PCA includes the eigen-decomposition of a data covariance matrix or singular value decomposition of a data matrix, usually after mean centering. It projects the original data onto an orthogonal subspace, where each direction is mutually decorrelated and major data information is present in the first several principal components (PCs). For optical flows in a local window, moving objects have consistent flows while pixels with only turbulence have random flows. Thus, if PCA is applied to the two-dimensional (2D) data of optical flows, the difference between desired motion pixels and random motion pixels may be magnified because their contributions to the two eigenvalues are very different; the contribution from random motion pixels can be very small, even to the second eigenvalue. Experimental results show that this approach actually is an effective way of analyzing outdoor videos; it can reduce false alarms for videos with either static or dynamic background, and it is also useful to delineate the size of moving objects.
This paper is organized as follows. Section 2 explains the proposed method based on optical flow and PCA. Section 3 presents experiments using ground-based and airborne videos. Section 4 draws the conclusion.
2. Proposed Method
HS method is a special approach of using global constraint of smoothness to express a brightness variation in certain areas of the frames in a video sequence. It is also a specially defined framework to lay out the smoothness of the flow field. Let  represent the brightness of a pixel at
represent the brightness of a pixel at  coordinates and the
coordinates and the  frame. According to [4], the image constraint at
frame. According to [4], the image constraint at  with Taylor series can be expressed as
with Taylor series can be expressed as

which results in

where  and
and  are the
are the  and
and  components of the velocity or optical flow of
components of the velocity or optical flow of  respectively, and
respectively, and  and
and  are the derivatives of the image at
are the derivatives of the image at  in the corresponding directions. A constrained minimization problem can be formulated to calculate optical flow vector
in the corresponding directions. A constrained minimization problem can be formulated to calculate optical flow vector  for the
for the  th frame:
th frame:

where  and
and  are the estimated local average optical flow velocities, and
are the estimated local average optical flow velocities, and  is a weighting factor. A larger value of
is a weighting factor. A larger value of  results in a smoother flow; in our experiments using 8-bit videos, it is empirically set to be 30000. Based on the norm of an optical flow vector, one can determine if the motion exists or not, while the direction of this vector provides the motion orientation.
results in a smoother flow; in our experiments using 8-bit videos, it is empirically set to be 30000. Based on the norm of an optical flow vector, one can determine if the motion exists or not, while the direction of this vector provides the motion orientation.
Two optical flow images can be constructed by pixel optical flow vector  A mask of size
A mask of size  slides through these
slides through these  and
and  images. At location
images. At location  a two-dimensional (2D) data matrix X can be constructed, which includes all the 2D vectors covered by the mask. The covariance matrix can be calculated as
a two-dimensional (2D) data matrix X can be constructed, which includes all the 2D vectors covered by the mask. The covariance matrix can be calculated as

where  is the optical flow matrix after mean removal. After eigen-decomposition, two eigenvalues
is the optical flow matrix after mean removal. After eigen-decomposition, two eigenvalues  are assigned to the central pixel of the mask. Motion detection is accomplished by analyzing or thresholding the eignenvalue (s). Since
are assigned to the central pixel of the mask. Motion detection is accomplished by analyzing or thresholding the eignenvalue (s). Since  is the major flow component and
is the major flow component and  is the minor flow component, it may be more effective to considering
is the minor flow component, it may be more effective to considering  than the values in the original
than the values in the original  space.
space.
Intuitively, only  needs to be considered because it corresponds to the major flow component and
needs to be considered because it corresponds to the major flow component and  corresponds to the minor flow component or even turbulence. An appropriate threshold can be determined by using the Ostu's method on the
corresponds to the minor flow component or even turbulence. An appropriate threshold can be determined by using the Ostu's method on the  histogram [10]. However, in practice,
histogram [10]. However, in practice,  should be considered as well since pixels inside object boundaries usually have quite large
should be considered as well since pixels inside object boundaries usually have quite large  but not
but not  Thus, thresholding may need to be taken on the
Thus, thresholding may need to be taken on the  histogram; a pixel is claimed to have motion if either
histogram; a pixel is claimed to have motion if either  or
or  are above the corresponding thresholds.
are above the corresponding thresholds.
Thus, the motion detection algorithm can be described as follows.
-
(1)
Calculate optical flows between two adjacent frames (after registration as needed).
-
(2)
For each pixel in the 2D optical flow data, perform PCA for a local mask (of size
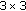 in the experiment), and two eigenvalues are assigned to the central pixel.
in the experiment), and two eigenvalues are assigned to the central pixel. -
(3)
Apply the Ostu's thresholding to the eigenvalues of all the pixels (
 in the experiment).
in the experiment).
Figure 1 illustrates the framework of the proposed method with a  mask and resulting
mask and resulting  data matrices.
data matrices.
It is noteworthy that some variants exist when implementing the proposed method differently.
-
(1)
In Step
 we may use the optical flow data from multiple frames. For instance, optical flow data from Frames 1 and 2 can be combined with optical flow data from Frames 2 and 3; this may help to emphasize the desired optical flows of moving objects and to emphasize the randomness of turbulence.
we may use the optical flow data from multiple frames. For instance, optical flow data from Frames 1 and 2 can be combined with optical flow data from Frames 2 and 3; this may help to emphasize the desired optical flows of moving objects and to emphasize the randomness of turbulence. -
(2)
In Step
 masks with different sizes can be used. Intuitively, for a large moving object, mask size should be large.
masks with different sizes can be used. Intuitively, for a large moving object, mask size should be large. -
(3)
In Step
 thresholding can take place on either
thresholding can take place on either 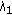 or
or  depending upon the object size and the features of turbulence.
depending upon the object size and the features of turbulence.
In the experiments, we use two adjacent frames, a  mask, and only
mask, and only  for thresholding. It is to show that such simplest implementation is sufficient to provide better performance than other widely used techniques.
for thresholding. It is to show that such simplest implementation is sufficient to provide better performance than other widely used techniques.
3. Experiments
In the experiments, videos with both static and dynamic backgrounds were analyzed. They were taken by a commercial Sony Camcorder. We compared our proposed method with the original optical flow method, the motion detection methods based on Kalman filtering [11], background modeling using Gaussian mixture model [12], difference-based spatial temporal entropy image (DSTEI) [13], and forward-backward motion history images (MHI) [14]. They were chosen for comparison because they are either typical methods or designed specifically for more complicated videos (e.g., those with dynamic background).
3.1. Experiment 1: Ground-Based Video with Relatively Large Object
In this experiment, a video with static background in a small regional airport was studied, which was taken when the camcorder was mounted on a tripod. As shown in Figure 2, a Hughes Cayuse helicopter was the moving object. Since the video was taken during a humid summer afternoon, there were significant atmospheric turbulence effects, which were visible around the vehicle, runway, and tree profiles.
Figure 3 shows the detection result using optical flow only, where detected pixels were highlighted in red. It contained many false alarm pixels in runway and tree profiles. Figures 4, 5, 6, and 7 are the detection results using Kalman filtering, background modeling, DSTEI, and MHI methods, respectively. We can see that they all could detect the helicopter but with some regions missing and a few false alarm background pixels. The background modeling method could detect the largest areas of the helicopter; however, there were erroneously detected pixels scattered in the scene (even in the sky area). This method relies on an accurate background model, generally requiring complicated computations.
Figure 8 is the result of the proposed method, where almost all the false alarm pixels were removed (only two pixels in the vehicles were left) and major regions in the helicopter were detected. Compared to Figure 3, introducing PCA can significantly improve the performance of optical flow-based detection. Compared to the results in Figures 4–7, the proposed method can reduce false alarm while detecting larger regions in the moving object.
3.2. Experiment 2: Airborne Videos with Small Objects
The second experiment used an airborne video with low quality. It was taken by the camcorder mounted on the helicopter in the video shown in Experiment 1. In addition to atmospheric turbulence, scintillation from the airborne platform (i.e., the small helicopter) further degraded the video quality. As shown in Figure 9, there were three moving vehicles on the highway, highlighted in yellow circles. They consisted of only a few pixels. The two frames were pre-registered using the method in [15].
Figure 10 shows the detection result using optical flow only, where three vehicles on the highway were completely detected and the shape of the vehicles were outlined compactly. Figures 11, 12, 13, and 14 are the results for comparison, where the three vehicles were detected but not well delineated. For instance, the detected vehicle sizes were too small when using Kalman filtering and background modeling, and too big when using DSTEI and MHI. More false alarm pixels were contained in these results. Figure 15 is the result using optical flow and PCA, which could further reduce false alarm and the vehicle sizes seemed to be more reasonable. Although the proposed method provided the best result, there were still several false alarmed pixels, mainly located around the edges of buildings.
We found out that such false alarms in airborne videos with small moving objects can be better removed by corner-based detection [16]. Harris corners were detected from two difference images, and many false alarm pixels around buildings could be removed; false alarms were further reduced through local tracking of detected corners in several consecutive frames. The drawback is that the detected result contains only object corners. In conjunction with the proposed method, the complete regions of moving objects can be segmented for the corner-based detection while the false alarm can be reduced in the proposed method. As shown in Figure 16(a), the corner-based method can accurately detect the three vehicles without false alarms; however, it detects only a corner corresponding to an object as detailed in Figure 16(b). Figure 16(c) shows the extracted vehicles using the MHI method, where the object sizes were slightly magnified. Figure 16(d) is the extracted vehicles using the proposed method, where the object sizes were reasonably reduced and pruned.
The result using another airborne video is shown in Figure 17, which further demonstrated that our method can better extract object sizes.
4. Conclusion
In this paper, we propose a joint optical flow and PCA approach for motion detection. Instead of considering the original optical flow, the two eigenvalues of the covariance matrix of local optical flows are analyzed. Since the first eigenvalue represents the major motion component and the second eigenvalue represents the minor motion component or turbulence, they are more useful to detect true motions while more successfully suppressing false alarms. The proposed method is also effective in extracting the actual size of moving objects.
The computational complexity involved in PCA includes the calculation of covariance matrix of local optical flow and its eigen-decomposition. For a mask of size  the number of multiplications in calculating the covariance matrix of size
the number of multiplications in calculating the covariance matrix of size  is
is  and complexity of eigen-decomposition is generally
and complexity of eigen-decomposition is generally  For an image frame with m pixels, the total computational complexity is
For an image frame with m pixels, the total computational complexity is  It can be reduced to
It can be reduced to  if using iterative PCA (IPCA) as discussed in [17], where
if using iterative PCA (IPCA) as discussed in [17], where  is a small integer. As the future work, we will investigate the performance when using IPCA to expedite motion detection.
is a small integer. As the future work, we will investigate the performance when using IPCA to expedite motion detection.
References
Mitiche A, Bouthemy P: Computation and analysis of image motion: a synopsis of current problems and methods. International Journal of Computer Vision 1996, 19(1):29-55. 10.1007/BF00131147
Hu W, Tan T, Wang L, Maybank S: A survey on visual surveillance of object motion and behaviors. IEEE Transactions on Systems, Man and Cybernetics Part C 2004, 34(3):334-352. 10.1109/TSMCC.2004.829274
Yilmaz A, Javed O, Shah M: Object tracking: a survey. ACM Computing Surveys 2006, 38(4):1-45.
Horn BKP, Schunck BG: Determining optical flow. Artificial Intelligence 1981, 17(1–3):185-203.
Horn BKP, Schunck BG: Determining optical flow. Artificial Intelligence 1993, 59(1-2):81-87. 10.1016/0004-3702(93)90173-9
Lucas BD, Kanade T: An iterative image registration technique with an application to stereo vision. Proceedings of the 7th International Joint Conference on Artificial Intelligence, 1981 2: 674-679.
Bruhn A, Weickert J, Schnorr C: Lucas/Kanade meets Horn/Schunck: combining local and global optic flow methods. International Journal of Computer Vision 2005, 61(3):211-231.
Pearson K: On lines and planes of closest fit to systems of points in space. Philosophical Magazine 1901, 2(6):559-572.
Hotelling H: Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology 1933, 24(6):417-441.
Otsu N: A threshold selection method from gray-level histograms. IEEE Transactions on Systems, Man, and Cybernetics 1979, 9(1):62-66.
Karmann K-P, Brandt AV: Moving object recognition using an adaptive background memory. In Time-Varing Image Processing and Moving Object Recognition. Volume 2. Edited by: Cappellini V. Elsevier, Amsterdam, The Netherlands; 1990:297-307.
Kaewtrakulpong P, Bowden R: An improved adaptive background mixture model for real-time tracking with shadow detection. Proceedings of 2nd European Workshop on Advanced Video-Based Surveillance Systems(AVBS '01), September 2001
Jing G, Siong CE, Rajan D: Foreground motion detection by difference-based spatial temporal entropy image. Proceedings of IEEE TENCON Conference, 2004 A379-A382.
Yin Z, Collins R: Moving object localization in thermal imagery by forward-backward MHI. Proceedings of IEEE Computer Vision and Pattern Recognition Workshops (CVPRW '06), 2006
Bergen JR, Anandan P, Hanna KJ, Hingorani R: Hierarchical model-based motion estimation. In Proceedings of the 2nd European Conference on Computer Vision, 1992. Volume 588. Springer; 237-252.
Yang H, Ma B, Du Q: Very small moving object detection from airborne videos using corners in differential images. Proceedings of IEEE International Conference on Image Processing, 2010
Du Q, Fowler JE: Low-complexity principal component analysis for hyperspectral image compression. International Journal of High Performance Computing Applications 2008, 22(4):438-448. 10.1177/1094342007088380
Acknowledgment
This research was supported by National Geospatial-Intelligence Agency of the United States.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, K., Du, Q., Yang, H. et al. Optical Flow and Principal Component Analysis-Based Motion Detection in Outdoor Videos. EURASIP J. Adv. Signal Process. 2010, 680623 (2010). https://doi.org/10.1155/2010/680623
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/680623
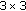 in the experiment), and two eigenvalues are assigned to the central pixel.
in the experiment), and two eigenvalues are assigned to the central pixel. in the experiment).
in the experiment).
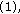 we may use the optical flow data from multiple frames. For instance, optical flow data from Frames 1 and 2 can be combined with optical flow data from Frames 2 and 3; this may help to emphasize the desired optical flows of moving objects and to emphasize the randomness of turbulence.
we may use the optical flow data from multiple frames. For instance, optical flow data from Frames 1 and 2 can be combined with optical flow data from Frames 2 and 3; this may help to emphasize the desired optical flows of moving objects and to emphasize the randomness of turbulence.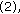 masks with different sizes can be used. Intuitively, for a large moving object, mask size should be large.
masks with different sizes can be used. Intuitively, for a large moving object, mask size should be large. thresholding can take place on either
thresholding can take place on either 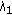 or
or  depending upon the object size and the features of turbulence.
depending upon the object size and the features of turbulence.














