- Research Article
- Open access
- Published:
The Alamouti Scheme with CDMA-OFDM/OQAM
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 703513 (2010)
Abstract
This paper deals with the combination of OFDM/OQAM with the Alamouti scheme. After a brief presentation of the OFDM/OQAM modulation scheme, we introduce the fact that the well-known Alamouti decoding scheme cannot be simply applied to this modulation. Indeed, the Alamouti coding scheme requires a complex orthogonality property; whereas OFDM/OQAM only provides real orthogonality. However, as we have recently shown, under some conditions, a transmission scheme combining CDMA and OFDM/OQAM can satisfy the complex orthogonality condition. Adding a CDMA component can thus be seen as a solution to apply the Alamouti scheme in combination with OFDM/OQAM. However, our analysis shows that the CDMA-OFDM/OQAM combination has to be built taking into account particular features of the transmission channel. Our simulation results illustrate the  Alamouti coding scheme for which CDMA-OFDM/OQAM and CP-OFDM are compared in two different scenarios: (i) CDMA is performed in the frequency domain, (ii) CDMA is performed in time domain.
Alamouti coding scheme for which CDMA-OFDM/OQAM and CP-OFDM are compared in two different scenarios: (i) CDMA is performed in the frequency domain, (ii) CDMA is performed in time domain.
1. Introduction
Increasing the transmission rate and/or providing robustness to channel conditions are nowadays two of the main research topics for wireless communications. Indeed, much effort is done in the area of multiantennas, where Space Time Codes (STCs) enable to exploit the spatial diversity when using several antennas either at the transmitting side or at the receiving side. One of the most known and used STC technique is Alamouti code [1]. Alamouti code has the nice property to be simple to implement while providing the maximum channel diversity. On the other hand, multicarrier modulation (MCM) is becoming, mainly with the popular Orthogonal Frequency Division Multiplexing (OFDM) scheme, the appropriate modulation for transmission over frequency selective channels. Furthermore, when appending the OFDM symbols with a Cyclic Prefix (CP) longer than the maximum delay spread of the channel to preserve the orthogonality, CP-OFDM has the capacity to transform a frequency selective channel into a bunch of flat fading channels which naturally leads to various efficient combinations of the STC and CP-OFDM schemes. However, the insertion of the CP yields spectral efficiency loss. In addition, the conventional OFDM modulation is based on a rectangular windowing in the time domain which leads to a poor ( ) behavior in the frequency domain. Thus CP-OFDM gives rise to two drawbacks: loss of spectral efficiency and sensitivity to frequency dispersion, for example, Doppler spread.
) behavior in the frequency domain. Thus CP-OFDM gives rise to two drawbacks: loss of spectral efficiency and sensitivity to frequency dispersion, for example, Doppler spread.
These two strong limitations may be overcome by some other OFDM variants that also use the exponential base of functions. But then, in any case, as it can be deduced from the Balian-Low theorem, see, for example, [2], it is not possible to get at the same time (i) Complex orthogonality; (ii) Maximum spectral efficiency; (iii) A well-localized pulse shape in time and frequency. With CP-OFDM conditions (ii) and (iii) are not satisfied, while there are two main alternatives that satisfy two of these three requirements and can be implemented as filter bank-based multicarrier (FBMC) modulations. Relaxing condition (ii) we get a modulation scheme named Filtered MultiTone (FMT) [3], also named oversampled OFDM in [4], where the authors show that the baseband implementation scheme can be seen as the dual of an oversampled filter bank. But if one really wants to avoid the two drawbacks of CP-OFDM the only solution is to relax the complex orthogonality constraint. The transmission system proposed in [5] is a pioneering work that illustrates this possibility. Later on an efficient Discrete Fourier Transform (DFT) implementation of the Saltzberg system [5], named Orthogonally Quadrature Amplitude Modulation (O-QAM), has been proposed by Hirosaki [6]. To the best of our knowledge, the acronym OFDM/OQAM, where OQAM now corresponds to Offset QAM, appeared for the first time in [7]. In [7] the authors also present an invention of Alard, named Isotropic Orthogonal Transform Algorithm (IOTA), and explicitly use a real inner product to prove the orthogonality of the OFDM/OQAM-IOTA modem. A formal link between these continuous-time modulation models and a precise filter bank implementation, the Modified Discrete Fourier Transform (MDFT) [8], is established in [9].
It is now recognized in a large number of applications, with cognitive radio being the most recent and important one [10], that appropriate OFDM/OQAM pulse shapes which satisfy conditions (ii) and (iii) can be designed, and these can lead to some advantages over the CP-OFDM. However, most of these publications are related to a single user case and to Single-Input-Single-Output (SISO) systems. On the contrary, only a few results are available concerning more general requirements being related either to multiaccess techniques or multiantenna, that is, of Multiple Input Multiple Output (MIMO) type. In a recent publication [11], we have shown that, under certain conditions, a combination of Coded Division Multiple Access (CDMA) with OFDM/OQAM could be used to provide the complex orthogonal property. On the other hand, it has also been shown in [12] that spatial multiplexing MIMO could be directly applied to OFDM/OQAM. However, in the MIMO case there is still a problem which has not yet found a fully favorable issue: It concerns the combined use of the popular STBC Alamouti code together with OFDM/OQAM. Basically the problem is related to the fact that OFDM/OQAM by construction produces an imaginary interference term. Unfortunately, the processing that can be used in the SISO case, for cancelling it at the transmitter side (TX) [13] or estimating it at the receiver side (RX) [14], cannot be successfully extended to the Alamouti coding/decoding scheme. Indeed, the solutions proposed so far are not fully satisfactory. The Alamouti-like scheme for OFDM/OQAM proposed in [15] complicates the RX and introduces a processing delay. The pseudo-Alamouti scheme recently introduced in [16] is less complex but requires the appending of a CP to the OFDM/OQAM signal which means that condition (ii) is no longer satisfied.
The aim of this paper is to take advantage of the orthogonality property resulting from the CDMA-OFDM/OQAM combination introduced in [11] to get a new MIMO Alamouti scheme with OFDM/OQAM. The contents of our paper is as follows. In Section 2, after some general descriptions of the OFDM/OQAM modulation in Section 2.1 and the MIMO Alamouti scheme in Section 2.2, we will combine both techniques. However, as we will see in Section 2.3, the MIMO decoding process is very difficult because of the orthogonality mismatch between Alamouti and OFDM/OQAM. In Section 3, we propose to combine Alamouti and CDMA-OFDM/OQAM in order to solve the problem. Indeed, in [11], we have shown that the combination of CDMA and OFDM/OQAM (CDMA-OFDM/OQAM) can provide the complex orthogonality property; this interesting property is first recalled in Section 3.1. Then, two different approaches with Alamouti coding are proposed, by considering either a spreading in the frequency (in Section 3.2) or in the time domain (in Section 4.2). When spreading in time is considered, 2 strategies of implementing the Alamouti coding are proposed. Some simulation results finally show that, using particular channel assumptions, the Alamouti CDMA-OFDM/OQAM technique achieves similar performance to the Alamouti CP-OFDM system.
2. OFDM/OQAM and Alamouti
2.1. The OFDM/OQAM Transmultiplexer
The baseband equivalent of a continuous-time multicarrier OFDM/OQAM signal can be expressed as follows [7]:

with  the set of integers,
the set of integers,  an even number of subcarriers,
an even number of subcarriers,  the subcarrier spacing,
the subcarrier spacing,  the prototype function assumed here to be a real-valued and even function of time, and
the prototype function assumed here to be a real-valued and even function of time, and  an additional phase term such that
an additional phase term such that  where
where  can be chosen arbitrarily. The transmitted data symbols
can be chosen arbitrarily. The transmitted data symbols  are real-valued. They are obtained from a
are real-valued. They are obtained from a  -QAM constellation, taking the real and imaginary parts of these complex-valued symbols of duration
-QAM constellation, taking the real and imaginary parts of these complex-valued symbols of duration  , where
, where  denotes the time offset between the two parts [2, 6, 7, 9].
denotes the time offset between the two parts [2, 6, 7, 9].
Assuming a distortion-free channel, the Perfect Reconstruction (PR) of the real data symbols is obtained owing to the following real orthogonality condition:

where  denotes conjugation,
denotes conjugation,  denotes the inner product, and
denotes the inner product, and  if
if  and
and  if
if  . Otherwise said, for
. Otherwise said, for  ,
,  is a pure imaginary number. For the sake of brevity, we set
is a pure imaginary number. For the sake of brevity, we set  . The orthogonality condition for the prototype filter can also be conveniently expressed using its ambiguity function
. The orthogonality condition for the prototype filter can also be conveniently expressed using its ambiguity function

It is well-known [7] that to satisfy the orthogonality condition (2), the prototype filter should be chosen such that  if
if  and
and  .
.
In practical implementations, the baseband signal is directly generated in discrete time, using the continuous-time signal samples at the critical frequency, that is, with  . Then, based on [9], the discrete-time baseband signal taking the causality constraint into account, is expressed as
. Then, based on [9], the discrete-time baseband signal taking the causality constraint into account, is expressed as

The parallel between (1) and (4) shows that the overlapping of duration  corresponds to
corresponds to  discrete-time samples. For the sake of simplicity, we will assume that the prototype filter length, denoted
discrete-time samples. For the sake of simplicity, we will assume that the prototype filter length, denoted  , is such that
, is such that  , with
, with  being a positive integer. With the discrete time formulation, the real orthogonality condition can also be expressed as:
being a positive integer. With the discrete time formulation, the real orthogonality condition can also be expressed as:

As shown in [9], the OFDM/OQAM modem can be realized using the dual structure of the MDFT filter bank. A simplified description is provided in Figure 1, where it has to be noted that the premodulation corresponds to a single multiplication by an exponential whose argument depends on the phase term  and on the prototype length. Note also that in this scheme, to transmit QAM symbols of a given duration, denoted
and on the prototype length. Note also that in this scheme, to transmit QAM symbols of a given duration, denoted  , the IFFT block has to be run twice faster than for CP-OFDM. The polyphase block contains the polyphase components of the prototype filter
, the IFFT block has to be run twice faster than for CP-OFDM. The polyphase block contains the polyphase components of the prototype filter  . At the RX side, the dual operations are carried out.
. At the RX side, the dual operations are carried out.
The prototype filter has to be PR, or nearly PR. In this paper, we use a nearly PR prototype filter, with length  , resulting from the discretization of the continuous time function named Isotropic Orthogonal Transform Algorithm (IOTA) in [7].
, resulting from the discretization of the continuous time function named Isotropic Orthogonal Transform Algorithm (IOTA) in [7].
Before being transmitted through a channel the baseband signal is converted to continuous-time. Thus, in the rest of this paper, we present an OFDM/OQAM modulator that delivers a signal denoted  , but keeping in mind that this modulator corresponds to an FBMC modulator as shown in Figure 1.
, but keeping in mind that this modulator corresponds to an FBMC modulator as shown in Figure 1.
The block diagram in Figure 2 illustrates our OFDM/OQAM transmission scheme. Note that compared to Figure 1, here a channel breaks the real orthogonality condition thus an equalization must be performed at the receiver side to restore this orthogonality.
Let us consider a time-varying channel, with maximum delay spread equal to  . We denote it by
. We denote it by  in time, and it can also be represented by a complex-valued number
in time, and it can also be represented by a complex-valued number  for subcarrier
for subcarrier  at symbol time
at symbol time  . At the receiver side, the received signal is the summation of the
. At the receiver side, the received signal is the summation of the  signal convolved with the channel impulse response and a noise component
signal convolved with the channel impulse response and a noise component  . For a locally invariant channel, we can define a neighborhood, denoted
. For a locally invariant channel, we can define a neighborhood, denoted  , around the
, around the  position, with
position, with

and we also define  .
.
Note also that  and
and  are chosen according to the time and bandwidth coherence of the channel, respectively. Then, assuming
are chosen according to the time and bandwidth coherence of the channel, respectively. Then, assuming  , for all
, for all  , the demodulated signal can be expressed as [13, 14, 17]
, the demodulated signal can be expressed as [13, 14, 17]

with  the noise component,
the noise component,  , the interference created by the neighbor symbols, given by
, the interference created by the neighbor symbols, given by

and  the interference created by the data symbols outside
the interference created by the data symbols outside  .
.
It can be shown that, even for small size neighborhoods, if the prototype function  is well localized in time and frequency,
is well localized in time and frequency,  becomes negligible when compared to the noise term
becomes negligible when compared to the noise term  . Indeed a good time-frequency localization [7] means that the ambiguity function of
. Indeed a good time-frequency localization [7] means that the ambiguity function of  , which is directly related to the
, which is directly related to the  terms, is concentrated around its origin in the time-frequency plane, that is, only takes small values outside the
terms, is concentrated around its origin in the time-frequency plane, that is, only takes small values outside the  region. Thus, the received signal can be approximated by
region. Thus, the received signal can be approximated by

For the rest of our study, we consider (9) as the expression of the signal at the output of the OFDM/OQAM demodulator.
2.2. Alamouti Scheme: General Case
In order to describe the Alamouti scheme [1], let us consider the one-tap channel model described as

where, at time instant  ,
,  is the channel gain between the transmit antenna
is the channel gain between the transmit antenna  and the receive antenna and
and the receive antenna and  is an additive noise. We assume that
is an additive noise. We assume that  is a complex-valued Gaussian random process with unitary variance. One transmit antenna and one receive antenna are generally referred as SISO model. We consider coherent detection, that is, we assume that the receiver has a perfect knowledge of
is a complex-valued Gaussian random process with unitary variance. One transmit antenna and one receive antenna are generally referred as SISO model. We consider coherent detection, that is, we assume that the receiver has a perfect knowledge of  .
.
The Alamouti scheme is implemented with 2 transmit and one receive antennas. Let us consider  and
and  to be the two symbols to transmit at time (time and frequency axis can be permuted in multicarrier modulation.) instants
to be the two symbols to transmit at time (time and frequency axis can be permuted in multicarrier modulation.) instants  and
and  , respectively. At time instant
, respectively. At time instant  , the antenna
, the antenna  transmits
transmits  whereas the antenna
whereas the antenna  transmits
transmits  . At time instant
. At time instant  , the antenna
, the antenna  transmits
transmits  whereas the antenna
whereas the antenna  transmits
transmits  . The
. The  factor is added to normalize the total transmitted power. The received signal samples at time instants
factor is added to normalize the total transmitted power. The received signal samples at time instants  and
and  are given by
are given by

Assuming the channel to be constant between the time instants  and
and  , we get
, we get

Note that  is an orthogonal matrix with
is an orthogonal matrix with  , where
, where  is the identity matrix of size
is the identity matrix of size  and
and  stands for the transpose conjugate operation. Thus, using the Maximum Ratio Combining (MRC) equalization, the estimates
stands for the transpose conjugate operation. Thus, using the Maximum Ratio Combining (MRC) equalization, the estimates  and
and  are obtained as
are obtained as

where,

Since the noise components  and
and  are uncorrelated,
are uncorrelated,  , where
, where  denotes the monolateral noise density. Thus, assuming a QPSK modulation, based on [18], the bit error probability, denoted
denotes the monolateral noise density. Thus, assuming a QPSK modulation, based on [18], the bit error probability, denoted  , is given by
, is given by

where  denotes the Signal-to-Noise Ratio (SNR) at the transmitter side. When the two channel coefficients are uncorrelated, we will have a diversity gain of two [18].
denotes the Signal-to-Noise Ratio (SNR) at the transmitter side. When the two channel coefficients are uncorrelated, we will have a diversity gain of two [18].
2.3. OFDM/OQAM with Alamouti Scheme
Equation (9) indicates that we can consider the transmission of OFDM/OQAM on each subcarrier as a flat fading transmission. Moreover, recalling that in OFDM/OQAM each complex data symbol,  , is divided into two real symbols,
, is divided into two real symbols,  and
and  , transmitted at successive time instants, transmission of a pair of data symbols, according to Alamouti scheme, is organized as follows:
, transmitted at successive time instants, transmission of a pair of data symbols, according to Alamouti scheme, is organized as follows:

We also assume that in OFDM/OQAM the channel gain is a constant between the time instants  and
and  . Let us denote the channel gain between the transmit antenna
. Let us denote the channel gain between the transmit antenna  and the receive antenna at subcarrier
and the receive antenna at subcarrier  and time instant
and time instant  by
by  . Therefore, at the single receive antenna we have
. Therefore, at the single receive antenna we have

Setting

and using (16), we obtain

where,

This results in

We note that  is an orthogonal matrix which is similar to the one found in (12) for the conventional
is an orthogonal matrix which is similar to the one found in (12) for the conventional  Alamouti scheme. However, the
Alamouti scheme. However, the  term appears, which is an interference term due to the fact that OFDM/OQAM has only a real orthogonality. Therefore, even without noise and assuming a distortion-free channel, we cannot achieve a good error probability since
term appears, which is an interference term due to the fact that OFDM/OQAM has only a real orthogonality. Therefore, even without noise and assuming a distortion-free channel, we cannot achieve a good error probability since  is an inherent "noise interference" component that, differently from the one expressed in (9), cannot be easily removed. (in a particular case, where
is an inherent "noise interference" component that, differently from the one expressed in (9), cannot be easily removed. (in a particular case, where  , one can nevertheless get rid of the interference terms.)
, one can nevertheless get rid of the interference terms.)
To tackle this drawback some research studies are being carried out. However, as mentioned in the introduction, the first one [15] significantly increases the RX complexity, while the second one [16] fails to reach the objective of theoretical maximum spectral efficiency, that is, does not satisfy condition (ii). The one we propose hereafter is based on a combination of CDMA with OFDM/OQAM and avoids these two shortcomings.
3. CDMA-OFDM/OQAM and Alamouti
3.1. CDMA-OFDM/OQAM
In this section we summarize the results obtained, assuming a distortion-free channel, in [19] and [11] for CDMA-OFDM/OQAM schemes transmitting real and complex data symbols, respectively. Then, we show how this latter scheme can be used for transmission over a realistic channel model in conjunction with Alamouti coding.
3.1.1. Transmission of Real Data Symbols
We denote by  the length of the CDMA code used and assume that
the length of the CDMA code used and assume that  is an integer number. Let us denote by
is an integer number. Let us denote by  , where
, where  stands for the transpose operation, the code used by the
stands for the transpose operation, the code used by the  th user. When applying spreading in the frequency domain such as in pure MC-CDMA (Multi-Carrier-CDMA) [20], for a user
th user. When applying spreading in the frequency domain such as in pure MC-CDMA (Multi-Carrier-CDMA) [20], for a user  at a given time
at a given time  ,
,  different data are transmitted denoted by:
different data are transmitted denoted by:  . Then by spreading with the
. Then by spreading with the  codes, we get the real symbol
codes, we get the real symbol  transmitted at frequency
transmitted at frequency  and time
and time  by
by

where  is the number of users, / the modulo operator, and
is the number of users, / the modulo operator, and  the floor operator. From the
the floor operator. From the  term, the reconstruction of
term, the reconstruction of  (for
(for  ) is insured thanks to the orthogonality of the code, that is,
) is insured thanks to the orthogonality of the code, that is,  ; see [21] for more details. Therefore, noise taken apart, the despreading operator leads to
; see [21] for more details. Therefore, noise taken apart, the despreading operator leads to

In [19], it is shown that, since no CP is inserted, the transmission of these spread real data ( ) can be insured at a symbol rate which is more than twice the one used for transmitting complex MC-CDMA data. Figure 3 depicts the real CDMA-OFDM/OQAM transmission scheme for real data and a maximum spreading length (limited by the number of subcarriers), where after the despreading operation, only the real part of the symbol is kept whereas the imaginary component
) can be insured at a symbol rate which is more than twice the one used for transmitting complex MC-CDMA data. Figure 3 depicts the real CDMA-OFDM/OQAM transmission scheme for real data and a maximum spreading length (limited by the number of subcarriers), where after the despreading operation, only the real part of the symbol is kept whereas the imaginary component  is not detected. This scheme satisfies a real orthogonality condition and can work for a number of users up to
is not detected. This scheme satisfies a real orthogonality condition and can work for a number of users up to  .
.
3.1.2. Interference Cancellation
A closer examination of the interference term is proposed in [11] assuming that the CDMA codes are Walsh-Hadamard (W-H) codes of length  , with
, with  an integer. The prototype filter being of length
an integer. The prototype filter being of length  , its duration is also given by the indicating function
, its duration is also given by the indicating function  , equal to 1 if
, equal to 1 if  and
and  elsewhere. Then, the scalar product of the base functions can be expressed as
elsewhere. Then, the scalar product of the base functions can be expressed as

where  is given by
is given by

For a maximum spreading length, that is,  , based on [11, Equation (18)], the interference term when transmitting real data can be expressed as
, based on [11, Equation (18)], the interference term when transmitting real data can be expressed as

It is shown in [11] that if  spreading codes are properly selected then the
spreading codes are properly selected then the  interference is cancelled. The W-H matrix being of size
interference is cancelled. The W-H matrix being of size  can be divided into two subsets of column indices,
can be divided into two subsets of column indices,  and
and  , with cardinal equal to
, with cardinal equal to  making a partition of all the index set. To guarantee the absence of interference between users, the construction rule for theses two subsets is as follows.
making a partition of all the index set. To guarantee the absence of interference between users, the construction rule for theses two subsets is as follows.
For  , each subset is initialized by setting:
, each subset is initialized by setting:  and
and  .
.
Let us now assume that, for a given integer  , the two subsets contain the following list of indices:
, the two subsets contain the following list of indices:

These subsets are used to build two new subsets of identical size such that

Then, we get the subsets of higher size,  , as follows:
, as follows:

Applying this rule one can check that for  , as an example, we get
, as an example, we get

Hence, for a given user and at a given time, we get  and
and  and these equalities hold for a number of
and these equalities hold for a number of  users up to
users up to  . The complete proof given in [11] takes advantage of three properties of W-H codes.
. The complete proof given in [11] takes advantage of three properties of W-H codes.
3.1.3. Transmission of Complex Data Symbols
As the imaginary component can be cancelled when transmitting real data through a distortion-free channel when using CDMA-OFDM/OQAM, one can imagine to extend this scheme to the transmission of complex data. Indeed, the transmission system being linear, real and imaginary parts will not interfere if the previous rule is satisfied.
Then, denoting by  the complex data to transmit, the OFDM/OQAM symbols transmitted at time
the complex data to transmit, the OFDM/OQAM symbols transmitted at time  over the carrier
over the carrier  and for the code
and for the code  are complex numbers, that is,
are complex numbers, that is,  are complex symbols. The corresponding complex CDMA-OQAM transmission scheme is depicted in Figure 4. The baseband equivalent of the transmitted signal, with a spreading in frequency, can be written as
are complex symbols. The corresponding complex CDMA-OQAM transmission scheme is depicted in Figure 4. The baseband equivalent of the transmitted signal, with a spreading in frequency, can be written as

In this expression, as in [11], we assume that the phase term is  , that is,
, that is,  . Then, if the
. Then, if the  codes are all in
codes are all in  , or
, or  , the interference terms are cancelled and we get
, the interference terms are cancelled and we get

Otherwise said, this CDMA-OFDM/OQAM scheme satisfies a complex orthogonality condition, that is, the back-to-back transmultiplexer is a PR system for the transmission of complex data. Note also that, differently from what we saw for the transmission of real data symbols, as explained in Section 3.1.2, here the maximum number of users is  instead of
instead of  . In both cases the overall data rate is therefore the same.
. In both cases the overall data rate is therefore the same.
In the presence of a channel, an equalization must be performed before the despreading since the signal at the output of the equalization block is supposed to be free from any channel distortion or attenuation. Then, the signal at the equalizer output is somewhat equivalent to the one obtained with a distortion-free channel. Then, despreading operation will recover the complex orthogonality.
Now, the question is: "Can we use this complex orthogonality for combining Alamouti coding scheme and CDMA-OFDM/OQAM?''. Let us analyze this problem assuming a one-tap equalization.
3.2. Alamouti with CDMA-OFDM/OQAM with Spreading in the Frequency Domain
In a realistic transmission scheme the channel is no longer distortion-free. So, we assume now that we are in the case of a wireless Down-Link (DL) transmission and perfectly synchronized.
3.2.1. Problem Statement
Before trying to apply Alamouti scheme to CDMA-OFDM/OQAM, one must notice that the channel equalization process is replaced by the Alamouti decoding. When adapting Alamouti scheme to CDMA-OFDM/OQAM, the equalizer component, depicted in Figure 4, must be replaced by the Alamouti decoding process and the despreading operation must be carried out just after the OFDM/OQAM modulator. Then, contrary to the DL conventional MC-CDMA case, the despreading operation must be performed before the Alamouti decoding. Indeed, with OFDM/OQAM, we can only recover a complex orthogonality property at the output of the despreading block. This point is critical since it rises the question: does complex orthogonality hold in CDMA-OFDM/OQAM if we perform despreading operation before equalization? and if yes, at which cost? The first point leads to the following problem: let us consider complex quantities  ,
,  ,
,  . Does it sound possible to obtain
. Does it sound possible to obtain  (equalization + despreading) from
(equalization + despreading) from  (despreading)? Here, equalization is materialized by
(despreading)? Here, equalization is materialized by  and the despreading operation by
and the despreading operation by  . The answer is in general (obviously) NO, except if all the
. The answer is in general (obviously) NO, except if all the  are the same, that is,
are the same, that is,  . That is the case if we are in the presence of a constant channel over frequencies. Indeed, only in this case the order of the equalization and despreading operations can be exchanged without impairing the transmission performance. Conversely, applying despreading before equalization should have an impact in terms of performance for a channel being nonconstant in frequency. So, let us consider at first a flat channel. Then the subset of subcarriers where a given spreading code is applied will be affected by the same channel coefficient.
. That is the case if we are in the presence of a constant channel over frequencies. Indeed, only in this case the order of the equalization and despreading operations can be exchanged without impairing the transmission performance. Conversely, applying despreading before equalization should have an impact in terms of performance for a channel being nonconstant in frequency. So, let us consider at first a flat channel. Then the subset of subcarriers where a given spreading code is applied will be affected by the same channel coefficient.
3.2.2. Implementation Scheme
In a SISO configuration, if we denote by  the single channel coefficient between the transmit antenna
the single channel coefficient between the transmit antenna  and the single receive antenna at time instant
and the single receive antenna at time instant  , the despreaded signal is given by:
, the despreaded signal is given by:

where  is the complex data of user
is the complex data of user  being transmitted at time instant
being transmitted at time instant  by antenna
by antenna  . Now, if we consider a system with 2 antennas with indexes 0 and 1, respectively, and if we apply Alamouti coding scheme to every user
. Now, if we consider a system with 2 antennas with indexes 0 and 1, respectively, and if we apply Alamouti coding scheme to every user  data, denoting by
data, denoting by  the main stream of complex data for user
the main stream of complex data for user  , we have
, we have

For a flat fading channel, ignoring noise, the despreaded signal for user  is given by
is given by

Hence,

This is the same decoding equation as in the Alamouti scheme presented in Section 2.2. Hence, the decoding could be performed in the same way. Figures 5 and 6 present the Alamouti CDMA-OFDM/OQAM transmitter and receiver, respectively.
3.2.3. Performance Evaluation
We compare the proposed Alamouti CDMA-OFDM/OQAM scheme with the Alamouti OFDM using the following parameters:
-
(i)
QPSK modulation
-
(ii)
 subcarriers
subcarriers -
(iii)
maximum spreading length, implying that the W-H spreading codes are of length
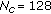 ,
, -
(iv)
flat fading channel (one single Rayleigh coefficient for all 128 subcarriers);
-
(v)
the IOTA prototype filter with length 512,
-
(vi)
zero forcing one tap equalization for both transmission schemes,
-
(vii)
no channel coding.
Figure 7 gives the performance results. As expected, both systems perform the same.
4. Alamouti and CDMA-OFDM/OQAM with Time Domain Spreading
In this section, we keep the same assumptions as the ones used for the transmission of complex data with a spreading in frequency. Firstly, we again suppose that the prototype function is a real-valued symmetric function and also that the W-H codes are selected using the procedure recalled in Section 3.1.2.
4.1. CDMA-OFDM/OQAM with Spreading in the Time Domain
Let us first consider a CDMA-OFDM/OQAM system carrying out a spreading in the time domain, that is, on each subcarrier  the data are spread over the time duration frame length. Let us consider
the data are spread over the time duration frame length. Let us consider  the length of the frame, that is, the frame is made of
the length of the frame, that is, the frame is made of  data in the frequency domain and
data in the frequency domain and  data in time domain.
data in time domain.  is the length of the spreading code. We assume that
is the length of the spreading code. We assume that  is an integer number. Let us denote by:
is an integer number. Let us denote by:  the code used by the
the code used by the  th user. Then, for a user
th user. Then, for a user  at a given frequency
at a given frequency  ,
,  different data are transmitted denoted by:
different data are transmitted denoted by:  . By spreading with the
. By spreading with the  codes, we get the real symbol
codes, we get the real symbol  transmitted at frequency
transmitted at frequency  and time
and time  by
by

where  is the number of users. From the
is the number of users. From the  term, the reconstruction of
term, the reconstruction of  (for
(for  ) is insured thanks to the orthogonality of the code, that is,
) is insured thanks to the orthogonality of the code, that is,  , see [21] for more details. Therefore, the despreading operator leads to
, see [21] for more details. Therefore, the despreading operator leads to

We now propose to consider the transmission of complex data, denoted  , using
, using  well chosen W-H codes. In order to establish the theoretical features of this complex CDMA-OFDM/OQAM scheme, we suppose that the transmission channel is free of any type of distortion. Also, for the sake of simplicity, we now assume a maximum spreading length (in time domain,
well chosen W-H codes. In order to establish the theoretical features of this complex CDMA-OFDM/OQAM scheme, we suppose that the transmission channel is free of any type of distortion. Also, for the sake of simplicity, we now assume a maximum spreading length (in time domain,  ). We denote by
). We denote by  the complex data and by
the complex data and by  the complex symbol transmitted at time
the complex symbol transmitted at time  over the carrier
over the carrier  and for the code
and for the code  . As usual, the length of the W-H codes are supposed to be a power of 2, that is,
. As usual, the length of the W-H codes are supposed to be a power of 2, that is,  with
with  an integer.
an integer.
The block diagram of the transmitter is depicted in Figure 8. For a frame containing  OFDM/OQAM data symbols, the baseband signal spread in time, can be written as
OFDM/OQAM data symbols, the baseband signal spread in time, can be written as

In (39), we assume that the phase term is  as in [7]. Let us also recall that the prototype function
as in [7]. Let us also recall that the prototype function  satisfies the real orthogonality condition (2) and is real-valued and symmetric, that is,
satisfies the real orthogonality condition (2) and is real-valued and symmetric, that is,  . To express the complex inner product of the base functions
. To express the complex inner product of the base functions  , using a similar procedure that led to (24), we get
, using a similar procedure that led to (24), we get

where  is given by
is given by

As the channel is distortion-free, the received signal is  and the demodulated symbols are obtained as follows:
and the demodulated symbols are obtained as follows:

In this configuration, the demodulation operation only takes place when the whole frame is received. Then, the despreading operation gives us the despreaded data for the code  as
as

Replacing  and
and  by their expression given in (39) and (40), respectively, we get:
by their expression given in (39) and (40), respectively, we get:

Splitting the summation over  in two parts, with
in two parts, with  equal to
equal to  or not to
or not to  , (44) can be rewritten as:
, (44) can be rewritten as:

Considering the W-H codes, we obtain

In [11], for W-H codes of length  , we have shown that for
, we have shown that for  ,
,

where  is given by
is given by

To prove the result given in (47), we had the following requirements:
-
(i)
W-H codes satisfy the set of mathematical properties that are proved in [11].
-
(ii)
Since
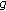 is a real-valued function,
is a real-valued function,  is real valued and the ambiguity function of the prototype function
is real valued and the ambiguity function of the prototype function 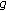 also satisfies the identities
also satisfies the identities  and
and 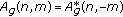 .
.
Using these results, (47) can be proved straighforwardly.
It is worth mentioning that the above requirements are independent of the phase term and thus are satisfied in the case of the CDMA-OFDM/OQAM system with spreading in time. It can also be shown that the modification of the phase term  leads to the substitutions
leads to the substitutions  and
and  , in obtaining (48) from (41). Accordingly the second term on the right hand side of (46) vanishes and we obtain
, in obtaining (48) from (41). Accordingly the second term on the right hand side of (46) vanishes and we obtain

4.2. Alamouti with CDMA-OFDM/OQAM with Spreading in Time
Now, if we consider the CDMA-OFDM/OQAM with spreading in time, contrary to the case of a spreading in frequency domain, as long as the channel is constant during the spreading time duration, we can perform despreading before equalization. At the equalizer output we will have a complex orthogonality. Indeed, considering at first a SISO case, if we denote by  the channel coefficient between a single transmit antenna
the channel coefficient between a single transmit antenna  and the receive antenna at subcarrier
and the receive antenna at subcarrier  , the despreaded signal is given by
, the despreaded signal is given by

where  is the complex data of user
is the complex data of user  being transmitted at subcarrier
being transmitted at subcarrier  by antenna
by antenna  . Thus, we can easily apply the Alamouti decoding scheme knowing the channel is constant for each antenna at each frequency. Otherwise said, the method becomes applicable for a frequency selective channel. Actually two strategies can be envisioned.
. Thus, we can easily apply the Alamouti decoding scheme knowing the channel is constant for each antenna at each frequency. Otherwise said, the method becomes applicable for a frequency selective channel. Actually two strategies can be envisioned.
(1) Strategy 1. Alamouti performed over pairs of frequencies. If we consider a system with 2 transmit antennas, 0 and 1, and if we apply the Alamouti coding scheme to every user  data, that is, if we denote by
data, that is, if we denote by  the main stream of complex data for user
the main stream of complex data for user  , then we have the following at subcarrier
, then we have the following at subcarrier  :
:

and at subcarrier  ,
,

Then, considering a flat fading channel, the despreaded signal for user  is given by
is given by

Therefore, we get

That means, when assuming the channel to be flat over two consecutive subcarriers, that is,  for all
for all  , we have exactly the same decoding equation as the Alamouti scheme presented in Section 3.2, by permuting the frequency and time axis. Then, the decoding is performed in the same way.
, we have exactly the same decoding equation as the Alamouti scheme presented in Section 3.2, by permuting the frequency and time axis. Then, the decoding is performed in the same way.
(2) Strategy 2. Alamouti performed over pairs of spreading codes. In this second strategy, we apply the Alamouti scheme on pairs of codes, that is, we divide the  codes in two groups (assuming
codes in two groups (assuming  to be even). That is, we process the codes by pair
to be even). That is, we process the codes by pair  . We denote by
. We denote by  the main stream of complex data for user pair
the main stream of complex data for user pair  . At subcarrier
. At subcarrier  , antennas 0 and 1 transmit
, antennas 0 and 1 transmit

At the receiver side we get,

Then, we do not need to consider the channel constant over two consecutive subcarriers. We have exactly the same decoding equation as the Alamouti scheme presented in Section 3.2. Hence, the decoding is performed in the same way.
We have tested two different channels considering each time the same channel profile, but with different realizations, between the 2 transmit antennas and one receive antenna. The Guard Interval (GI) is adjusted to take into account the delay spread profiles corresponding to a 4-path and to a 7-path channel. The 4-path channel is characterized by the following parameters:
-
(i)
power profile (in dB): 0, -6, -9, -12,
-
(ii)
delay profile (in samples): 0, 1, 2, 3,
-
(iii)
GI for CP-OFDM: 5 samples,
and the 7-path by
-
(i)
power profile (in dB): 0, -6, -9, -12, -16, -20, -22,
-
(ii)
delay profile (in samples): 0, 1, 2, 3, 5, 7, 8,
-
(iii)
GI for CP-OFDM: 9 samples;
We also consider the following system parameters:
-
(i)
QPSK modulation,
-
(ii)
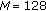 subcarriers,
subcarriers, -
(iii)
time invariant channel (no Doppler),
-
(iv)
the IOTA prototype filter of length 512,
-
(v)
spreading codes of length 32, corresponding to the frame duration (32 complex OQAM symbols),
-
(vi)
number of CDMA W-H codes equals to 16 in complex OFDM/OQAM, with symbol duration
 and this corresponds to 32 codes in OFDM, with symbol duration
and this corresponds to 32 codes in OFDM, with symbol duration 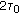 , leading to the same spectral efficiency
, leading to the same spectral efficiency -
(vii)
zero forcing, one tap equalization,
-
(viii)
no channel coding.
In Figures 9 and 10, the BER results of the Alamouti CDMA-OFDM/OQAM technique for the two proposed strategies are presented.
The two strategies perform the same until a BER of  or
or  for the 4 and 7-path channel, respectively. For lower BER the strategy 2 performs better than the strategy 1. This could be explained by the fact that strategy 1 makes the approximation that the channel is constant over two consecutive subcarriers. This approximation leads to a degradation of the performance whereas the strategy 2 does not consider this approximation. If we compare the performance of Alamouti CDMA-OFDM/OQAM strategy 2 with the Alamouti CP-OFDM, we see that both system perform approximately the same. It is worth mentioning that however the corresponding throughput is higher for the OFDM/OQAM solutions (no CP). Indeed, it is increased by approximately 4 and 7% for the 4 and 7-path channels, respectively.
for the 4 and 7-path channel, respectively. For lower BER the strategy 2 performs better than the strategy 1. This could be explained by the fact that strategy 1 makes the approximation that the channel is constant over two consecutive subcarriers. This approximation leads to a degradation of the performance whereas the strategy 2 does not consider this approximation. If we compare the performance of Alamouti CDMA-OFDM/OQAM strategy 2 with the Alamouti CP-OFDM, we see that both system perform approximately the same. It is worth mentioning that however the corresponding throughput is higher for the OFDM/OQAM solutions (no CP). Indeed, it is increased by approximately 4 and 7% for the 4 and 7-path channels, respectively.
5. Conclusion
In this paper, we showed that the well-known Alamouti decoding scheme cannot be directly applied to the OFDM/OQAM modulation. To tackle this problem, we proposed to combine the MIMO Alamouti coding scheme with CDMA-OFDM/OQAM. If the CDMA spreading is carried out in the frequency domain, the Alamouti decoding scheme can only be applied if the channel is assumed to be flat. On the other hand, for a frequency selective channel, the CDMA spreading component has to be applied in the time domain. For the Alamouti scheme with time spreading CDMA-OFDM/OQAM, we elaborate two strategies for implementing the MIMO space-time coding scheme. Strategy 1 implements the Alamouti over pairs of adjacent frequency domain samples whereas the strategy 2 processes the Alamouti coding scheme over pairs of spreading codes from two successive time instants. Strategy 2 appears to be more appropriate since it requires less restrictive assumptions on the channel variations across the frequencies. We also made some performance comparisons with Alamouti CP-OFDM. It was found that, under some channel hypothesis, the combination of Alamouti with complex CDMA-OFDM/OQAM is possible without increasing the complexity of the Alamouti decoding process. Furthermore, in the case of a frequency selective channel, OFDM/OQAM keeps its intrinsic advantage with a SNR gain in direct relation with the CP length. To find a simpler Alamouti scheme, that is, without adding a CDMA component, remains an open problem. Naturally, some other alternative transmit diversity schemes for OFDM/OQAM, as for instance cyclic delay diversity, could also deserve further investigations.
References
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Bölcskei H: Orthogonal frequency division multiplexing based on offset QAM. In Advances in Gabor Analysis. Birkhäuser, Boston, Mass, USA; 2003.
Cherubini G, Eleftheriou E, Ölçer S: Filtered multitone modulation for very high-speed digital subscriber lines. IEEE Journal on Selected Areas in Communications 2002, 20(5):1016-1028. 10.1109/JSAC.2002.1007382
Hleiss R, Duhamel P, Charbit M: Oversampled OFDM systems. Proceedings of the International Conference on Digital Signal Processing (DSP '97), July 1997, Santorini, Greece 1: 329-331.
Saltzberg BR: Performance of an efficient parallel data transmission system. IEEE Transactions on Communication Technology 1967, 15(6):805-811.
Hirosaki B: An orthogonally multiplexed QAM system using the discrete Fourier transform. IEEE Transactions on Communications Systems 1981, 29(7):982-989. 10.1109/TCOM.1981.1095093
Le Floch B, Alard M, Berrou C: Coded orthogonal frequency division multiplex. Proceedings of the IEEE 1995, 83: 982-996. 10.1109/5.387096
Karp T, Fliege NJ: MDFT filter banks with perfect reconstruction. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '95), May 1995, Seattle, Wash, USA 1: 744-747.
Siohan P, Siclet C, Lacaille N: Analysis and design of OFDM/OQAM systems based on filterbank theory. IEEE Transactions on Signal Processing 2002, 50(5):1170-1183. 10.1109/78.995073
Farhang-Boroujeny B, Kempter R: Multicarrier communication techniques for spectrum sensing and communication in cognitive radios. IEEE Communications Magazine 2008, 46(4):80-85.
Lélé C, Siohan P, Legouable R, Bellanger M: CDMA transmission with complex OFDM/OQAM. EURASIP Journal on Wireless Communications and Networking 2008, 2008:-12.
El Tabach M, Javaudin J-P, Hélard M: Spatial data multiplexing over OFDM/OQAM modulations. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, Scotland 4201-4206.
Javaudin J-P, Lacroix D, Rouxel A: Pilot-aided channel estimation for OFDM/OQAM. Proceedings of the IEEE Vehicular Technology Conference (VTC '03), April 2003, Jeju, South Korea 3: 1581-1585.
Lélé C, Javaudin J-P, Legouable R, Skrzypczak A, Siohan P: Channel estimation methods for preamble-based OFDM/OQAM modulations. Proceedings of the 13th European Wireless Conference (EW '07), April 2007, Paris, France
Bellanger M: Transmit diversity in multicarrier transmission using OQAM modulation. Proceedings of the 3rd International Symposium on Wireless Pervasive Computing (ISWPC '08), May 2008, Santorini, Greece 727-730.
Lin H, Lélé C, Siohan P: A pseudo alamouti transceiver design for OFDM/OQAM modulation with cyclic prefix. Proceedings of the IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '09), June 2009, Perugia, Italy 300-304.
Lacroix-Penther D, Javaudin J-P: A new channel estimation method for OFDM/OQAM. Proceedings of the 7th International OFDM Workshop (InOWo '02), September 2002, Hamburg, Germany
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, Mass, USA; 2004.
Lélé C, Siohan P, Legouable R, Bellanger M: OFDM/OQAM for spread spectrum transmission. Proceedings of the International Workshop on Multi-Carrier Spread-Spectrum (MCSS '07), May 2007, Herrsching, Germany
Fazel K, Papke L: On the performance of convolutionnally-coded CDMA/OFDM for mobile communication system. Proceedings of the Symposium on Personnal, Indoor and Mobile Radio Communications (PIMRC '93), September 1993, Yokohama, Japan 468-472.
Dinan EH, Jabbari B: Spreading codes for direct sequence CDMA and wideband CDMA cellular networks. IEEE Communications Magazine 1998, 36(9):48-54. 10.1109/35.714616
Acknowledgments
The authors would like to thank the reviewers and Professor Farhang-Boroujeny for their careful reading of our manuscript and for their helpful suggestions. This work was partially supported by the European ICT-2008-211887 project PHYDYAS.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lélé, C., Siohan, P. & Legouable, R. The Alamouti Scheme with CDMA-OFDM/OQAM. EURASIP J. Adv. Signal Process. 2010, 703513 (2010). https://doi.org/10.1155/2010/703513
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/703513






 subcarriers
subcarriers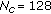 ,
,

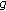 is a real-valued function,
is a real-valued function,  is real valued and the ambiguity function of the prototype function
is real valued and the ambiguity function of the prototype function 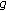 also satisfies the identities
also satisfies the identities  and
and 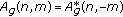 .
.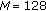 subcarriers,
subcarriers, and this corresponds to 32 codes in OFDM, with symbol duration
and this corresponds to 32 codes in OFDM, with symbol duration 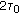 , leading to the same spectral efficiency
, leading to the same spectral efficiency
