- Research Article
- Open access
- Published:
Geometrical Feature Extraction from Ultrasonic Time Frequency Responses: An Application to Nondestructive Testing of Materials
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 706732 (2010)
Abstract
Signal processing is an essential tool in nondestructive material characterization. Pulse-echo inspection with ultrasonic energy provides signals (A-scans) that can be processed in order to obtain parameters which are related to physical properties of inspected materials. Conventional techniques are based on the use of a short-term frequency analysis of the A-scan, obtaining a time-frequency response (TFR), to isolate the evolution of the different frequency-dependent parameters. The application of geometrical estimators to TFRs provides an innovative way to complement conventional techniques based on the one-dimensional evolution of an A-scan extracted parameter (central or centroid frequency, bandwidth, etc.). This technique also provides an alternative method of obtaining similar meaning and less variance estimators. A comparative study of conventional versus new proposed techniques is presented in this paper. The comparative study shows that working with binarized TFRs and the use of shape descriptors provide estimates with lower bias and variance than conventional techniques. Real scattering materials, with different scatterer sizes, have been measured in order to demonstrate the usefulness of the proposed estimators to distinguish among scattering soft tissues. Superior results, using the proposed estimators in real measures, were obtained when classifying according to mean scatterer size.
1. Introduction
Signal processing is an essential tool in nondestructive material characterization. Modern technologies can take benefit of more sophisticated algorithms allowing to classify and characterize materials precisely. One of the techniques that takes advantage of all these advances is the nondestructive testing (NDT) using ultrasounds. Thanks to the advances in signal processing it is now easy to find applications of NDT using ultrasonics in materials, that some years ago was very hard to find [1–3].
The Signal Processing Group (GTS) of the Universidad Politécnica de Valencia published a technique [2] that allows to characterize dispersive materials by means of pulse-echo inspection with ultrasonic energy. The aforementioned technique was based on extracting time of flight-dependent parameters from the ultrasonic A-scan. This technique involves assuming a Linear Time Varying (LTV) model for the ultrasonic inspection of dispersive material. The extracted parameters were affected by the physical properties of the material and automatic classifiers could be used.
In this paper we introduce a novel technique to extract parameters, based on the shape analysis of time frequency responses, that complement or in some situations improve the performance of the previously published methods.
This work is going to be structured as follows. In Section 2 we describe a simple model that demonstrates how physical properties of scattering materials affect the time frequency representation (TFR) of the A-scan. Later, in Section 3, we briefly review the traditional parameter estimators presented in [2]. In Section 4 a new technique based on computing geometrical descriptors from the TFR is introduced. A comparative study of the traditional versus the new proposed technique is presented in Section 5. An example of application to characterize mean scatterer size on soft dispersive materials is also shown in this section. Finally in Section 6, conclusions are presented.
2. Ultrasonic Pulse Modeling in the Frequency Domain
The use of Gaussian envelope pulses is very extended for the modeling of ultrasonic echoes [4, 5]. Ping He [4] demonstrates in his study that a Gaussian pulse propagating in soft tissues could also be modeled as a Gaussian pulse with parameters changing as the pulse propagates deep within tissue. Let us assume that the ultrasonic pulse can be modeled in the frequency domain as,

with  ,
,  , and
, and  , being the pulse amplitude, transducer central pulsation, and transducer bandwidth. When the ultrasonic pulse propagates deep within material (
, being the pulse amplitude, transducer central pulsation, and transducer bandwidth. When the ultrasonic pulse propagates deep within material ( -axis), then, it was demonstrated in [4] that for an attenuation law of the form
-axis), then, it was demonstrated in [4] that for an attenuation law of the form  (with
(with  , or
, or  ), the previous expression can be reformulated as
), the previous expression can be reformulated as

The new parameters  ,
,  , and
, and  are the new amplitude, central pulsation, and bandwidth as the ultrasonic pulse travels deep inside the material. These parameters provide new information about the tissue dependent attenuation parameters (
are the new amplitude, central pulsation, and bandwidth as the ultrasonic pulse travels deep inside the material. These parameters provide new information about the tissue dependent attenuation parameters ( and
and  ). A couple of these parameters are shown in (3) and (4) when
). A couple of these parameters are shown in (3) and (4) when  . For a complete derivation see [4].
. For a complete derivation see [4].


This idea can be extended to most of the attenuation phenomena that suffer an ultrasonic pulse as they travels through a material (absorption, scattering, etc.). If we take into account that most of these phenomena can be modeled by power laws [6], their individual effect can be accumulated and the final envelope of the pulse can be still modeled with a Gaussian expression. We are going to illustrate this idea with the example of attenuation due to Stochastic scattering. Stochastic scattering is frequently modeled by

where  is the attenuation due to Stochastic scattering and
is the attenuation due to Stochastic scattering and  is the mean scatterer size. Without lack of generality and in order not to obtain long equations we will assume that Stochastic scattering is the only source of attenuation of the ultrasonic pulse. Under this assumption and similarly to what happens in (2) the effect of the Stochastic scattering can be obtained using the previous equations for
is the mean scatterer size. Without lack of generality and in order not to obtain long equations we will assume that Stochastic scattering is the only source of attenuation of the ultrasonic pulse. Under this assumption and similarly to what happens in (2) the effect of the Stochastic scattering can be obtained using the previous equations for 

The new parameters  ,
,  , and
, and  that take into account attenuation due to Stochastic scattering can be derived by equations (7), (8), and (9)
that take into account attenuation due to Stochastic scattering can be derived by equations (7), (8), and (9)



Equations (7) and (8) predict a downshift in the central frequency and a pulse narrowing due to Stochastic scattering attenuation. Similarly, and as it was expected, (9) predicts faster attenuation in depth for materials with larger mean grain size. All these behaviors affect the shape of the A-scan TFR and can be used to design algorithms for material classification, based on the amplitude, frequency, or bandwidth profiles. This shape dependence can also be used for scatterer mean size estimation. The TFR of a register obtained in NDT of scattering materials can be modeled using (6). The parameters  ,
,  , and
, and  will affect the shape of the TFR.
will affect the shape of the TFR.
Figure 1 shows the aspect of the TFR as described in (6). This figure was simulated for a  = 500 KHz central frequency ultrasonic pulse with initial fractional bandwidth
= 500 KHz central frequency ultrasonic pulse with initial fractional bandwidth  = 75% that propagates according to the law defined in (6) up to
= 75% that propagates according to the law defined in (6) up to  = 1.5
= 1.5 −3 m for three different mean scatterer size 0.5, 1, and 1.5 mm. Figure 1 also shows the superimposed parameters
−3 m for three different mean scatterer size 0.5, 1, and 1.5 mm. Figure 1 also shows the superimposed parameters  (dashed line) and
(dashed line) and  (solid line).
(solid line).
3. Conventional Parameter Extraction for Material Characterization: The Ultrasonic Signature (US) Concept
As already mentioned, information about the material is included in the A-scan. Among some other possibilities to extract information about the materials [5, 7], the analysis of the variant impulse response (or equivalently the variant frequency response) of the LTV is a feasible alternative. The time-variant characteristic of the model leads naturally to a nonstationary analysis of the recorded signal.
This technique proposes the use of a short-term frequency analysis of the signal to isolate the evolution of the different frequency components. This can be done by means of explicit implementation of a bank of filters or, more usually, by means of some type of linear or nonlinear time-frequency transformation, including nonconstant bandwidth analysis like wavelet transform. From the time-frequency signal we obtain the US which is a one-dimensional signal hopefully encompassing the relevant information needed for every particular purpose. The US [2] is obtained by computing for every time instant, along a finite discrete time interval, a spectral parameter; some possible alternatives are
-
(i)
centroid frequency (normalized first moment):
 (10)
(10)where
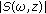 is the magnitude of the time-frequency transformation, and
is the magnitude of the time-frequency transformation, and 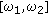 defines the integration band,
defines the integration band, -
(ii)
The fractional bandwidth:
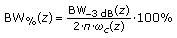 (11)
(11) -
(iii)
the central pulsation:
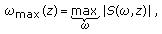 (12)
(12) -
(iv)
many other depth-dependent (
 ) parameters that can be obtained from
) parameters that can be obtained from 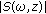 (higher-order statistics, median, etc.).
(higher-order statistics, median, etc.).
4. An Alternative Technique to Conventional Parameter Extraction for Material Characterization
2-D shape analysis can be applied to the TFR of the ultrasonic A-scans for material characterization. The motivation of this idea was based on the observation that the mean scatterer diameter,  , affects TFR shapes (see Figure 1). It is expected that using shape-related parameters applied to the TFR, we will be able to classify materials with different scatterer sizes. Additionally, if a process of binarization of TFR is employed, previous to the extraction of geometrical parameters, the obtained parameters should be less affected by noise.
, affects TFR shapes (see Figure 1). It is expected that using shape-related parameters applied to the TFR, we will be able to classify materials with different scatterer sizes. Additionally, if a process of binarization of TFR is employed, previous to the extraction of geometrical parameters, the obtained parameters should be less affected by noise.
The application of geometrical parameters to TFR diagrams provides an innovative way to complement classical techniques based on one dimensional US and an alternative way of obtaining similar meaning and less variance estimators (as we will show in Section 5).
After computing the TFR of the ultrasonic A-scan, binarization with an adequate threshold is done. If we assume that the ultrasonic signal recorded is contaminated with additive white Gaussian noise (AWGN), the binarized TFR will exhibit some sort of two dimensional "jitter". This jitter will affect the shape of the binarized TFR and, of course, the geometrical parameters derived from it. What we propose in this work is to choose a variable with depth-adaptive threshold located at the maximum slope of the Gaussian pulse for the region of the TFR where Gaussian pulse is higher than AWGN. This will minimize the effect of noise in the binarized shape. In the zone of the TFR where amplitude of the Gaussian pulse is comparable to AWGN power we use a constant threshold. An example of a binarized TFR using the adaptive threshold is shown in Figure 2.
Shape-related parameters are obtained from the binarized TFR matrix. These geometrical parameters depend on physical properties of the inspected material. An example of how this can be mathematically modeled is given as follows. Being Figure 2 the binarized TFR generated with the mixed threshold previously described. Let us call  the binarized TFR of Figure 2. This representation can be mathematically formulated, in a first approximation, as in (13) if the threshold is properly selected. The parameters
the binarized TFR of Figure 2. This representation can be mathematically formulated, in a first approximation, as in (13) if the threshold is properly selected. The parameters  and
and  take into account material-related parameters (
take into account material-related parameters ( ,
,  ,
,  , and
, and  ) as derived by (7) and (8). If we take into account (for simplicity) only the Stochastic scattering, we can obtain that the area of the binarized TFR, up to a given depth (
) as derived by (7) and (8). If we take into account (for simplicity) only the Stochastic scattering, we can obtain that the area of the binarized TFR, up to a given depth ( ), is given by equation (14). Note that to compute the area, the shift term
), is given by equation (14). Note that to compute the area, the shift term  can be omitted
can be omitted

For an arbitrary threshold selection, equality of (13) and (14) does not hold. However, proportionally relationship makes these expressions equally valid for classification purposes. Equation (14) shows that the higher  or
or  are, the lower the final area of the binarized response is. This simple demonstration confirms that basic geometrical descriptors can provide important information to compare material characteristics such us attenuation or mean scatterer size
are, the lower the final area of the binarized response is. This simple demonstration confirms that basic geometrical descriptors can provide important information to compare material characteristics such us attenuation or mean scatterer size

We are going to see in the next section the set of geometrical parameters that allow us to classify materials according to scatterer size.
4.1. Geometrical Descriptors
From  , the binarized TFR generated with the mixed threshold, we can calculate many geometrical descriptors [8, 9]. Our contribution, at this point, is to work with shape or geometrical parameters having a physical meaning related to the expected changes produced in the TFR. It is expected that geometrical descriptors will provide a most intuitive representation of the model in comparison with the classical signal-processing parameters. For example, we can establish visual relations between orientation parameters and physical variations of attenuation or frequency along depth.
, the binarized TFR generated with the mixed threshold, we can calculate many geometrical descriptors [8, 9]. Our contribution, at this point, is to work with shape or geometrical parameters having a physical meaning related to the expected changes produced in the TFR. It is expected that geometrical descriptors will provide a most intuitive representation of the model in comparison with the classical signal-processing parameters. For example, we can establish visual relations between orientation parameters and physical variations of attenuation or frequency along depth.
The most representative geometrical descriptors that have proven to give good classification results are given below.
4.1.1. Area
For a generic discrete function in two variables, the moments are defined as

where  is the binarized TFR, at coordinates
is the binarized TFR, at coordinates  .
.
The area is related to attenuation parameters and mean scatterer size as it was demonstrated in (14). The area can be obtained as the zero-order moment  .
.
If we use the area parameter to distinguish between materials with similar attenuation coefficient but including scatterers with different sizes, it is expected that materials with higher scatterer sizes get lower value of the area descriptor.
4.1.2. Center of Gravity
By using first-order moments, the center of gravity or centroid of a binary representation can be calculated.
Being  and
and  , the center of mass can be defined as
, the center of mass can be defined as  where
where

By dividing the binary representation in smaller regions, along horizontal  -axis, we will be able to study the central frequency evolution with depth. Moreover, the center of gravity is used in the definition of the second-order moments as described in (17), note the invariance with respect to response scaling
-axis, we will be able to study the central frequency evolution with depth. Moreover, the center of gravity is used in the definition of the second-order moments as described in (17), note the invariance with respect to response scaling

4.1.3. Orientation
Object orientation ( ) can be calculated using second-order moments. It is geometrically described as the angle between the major axis of the object and the
) can be calculated using second-order moments. It is geometrically described as the angle between the major axis of the object and the  -axis. By minimizing the function
-axis. By minimizing the function  , we get the next expression for the orientation
, we get the next expression for the orientation

4.1.4. Eccentricity
An important parameter, which is also dependent on TFR shape, is the eccentricity  . The eccentricity allows to estimate how similar to a circle an object is. The value ranges from 0 to 1 (
. The eccentricity allows to estimate how similar to a circle an object is. The value ranges from 0 to 1 ( ). For circular objects
). For circular objects  and for elliptical objects
and for elliptical objects  . To compute the eccentricity we have used the next expression
. To compute the eccentricity we have used the next expression

where  and
and  are, respectively, the maior and minor axis of the object, as it is depicted in Figure 3.
are, respectively, the maior and minor axis of the object, as it is depicted in Figure 3.
We can use the eccentricity parameter to distinguish between materials with similar attenuation coefficient but including scatterers with different sizes. For lower scatterer sizes eccentricity is expected to be higher than for higher scatterer size materials. Seeing TFR diagrams depicted in Figure 1, we can notice how materials with higher value of  have more circular shapes than those having lower
have more circular shapes than those having lower  . So, it is expected that the higher
. So, it is expected that the higher  the lower the eccentricity value is.
the lower the eccentricity value is.
4.1.5. Boundary Signature (BS)
The BS is a 1-D representation of an object boundary. One of the most simple ways to generate the BS of a region is to plot the distance from the center of gravity of the region to the boundary as a function of the angle,  . Figure 3 illustrates this concept. The changes in size of binarized TFR result in changes in the amplitude values of the corresponding BS. It is expected that the higher the value of
. Figure 3 illustrates this concept. The changes in size of binarized TFR result in changes in the amplitude values of the corresponding BS. It is expected that the higher the value of  is, the lower the amplitude of the corresponding BS. Moreover, the BS not only provides information about area changes but also provides the angular direction of such changes. To compute the BS we need to compute for each angle,
is, the lower the amplitude of the corresponding BS. Moreover, the BS not only provides information about area changes but also provides the angular direction of such changes. To compute the BS we need to compute for each angle,  , the Euclidean distance between the center of gravity and the boundary of the region. As will be demonstrated, it is expected that different values of
, the Euclidean distance between the center of gravity and the boundary of the region. As will be demonstrated, it is expected that different values of  , for the model or material under test, will correspond with different BSs for the binarized TFR.
, for the model or material under test, will correspond with different BSs for the binarized TFR.
4.1.6. Frequency-Derived Parameters
Some frequency-derived parameters have been also tested such as centroid frequency, central frequency, or bandwidth.
To compute the central frequency we work with the TFR in gray scale (not binarized). We divide the TFR diagram into small rectangles (see Figure 4) along the  -axis (horizontal), and then we compute the maximum of each rectangle. The final result is the evolution of central frequency along depth.
-axis (horizontal), and then we compute the maximum of each rectangle. The final result is the evolution of central frequency along depth.
To compute the centroid frequency evolution with depth we divide the binzarized TFR into small rectangles along the  -axis and then we compute the center of gravity (described above) for every rectangle, the final result is the evolution of centroid frequency along horizontal direction.
-axis and then we compute the center of gravity (described above) for every rectangle, the final result is the evolution of centroid frequency along horizontal direction.
The process to compute the bandwidth evolution is similar to centroid frequency computation. In the case of bandwidth the width of each rectangle is computed, thus obtaining the evolution of bandwidth with depth.
5. Experiments
5.1. Application of Conventional and Geometrical Descriptors to Simulated Signals
Simulated signals have been generated according to the model presented in Section 2.
Transducer response (ARMA order) was estimated using phantom data based on the final prediction error and residual time series methods [10]. The best results for the employed transducer that will be later used in this section, were achieved with an  model. The LTV system was modeled according to (20) with the expressions for
model. The LTV system was modeled according to (20) with the expressions for  ,
,  and
and  given by (7), (8) and (9), respectively.
given by (7), (8) and (9), respectively.

The block diagram of the simulated signal generator is represented in Figure 5. Several signals (A-scans) were generated using this model. The purpose of these simulations was to compare conventional signal-processing estimators with the geometrical estimators described in Section 4.1. The results are presented in the form of bias/variance graphs for each estimator as the amount of observation noise increases (AWGN). The variance is presented in the graphs with vertical color bars whereas the bias is presented with a convenient marker to distinguish between conventional or geometrical estimators.
Figure 6 was generated using  mm and AWGN variance varying from 0.05 to 0.5. The figure shows the variance (red bars) and bias (marker "*") of conventional estimators: central frequency, centroid frequency, and fractional bandwidth, as described in Section 3. Superimposed, Figure 6, also represents the variance (green bars) and bias (marker "o") of shape analysis operators: central frequency, centroid frequency and fractional bandwidth, as they were described in Section 4.
mm and AWGN variance varying from 0.05 to 0.5. The figure shows the variance (red bars) and bias (marker "*") of conventional estimators: central frequency, centroid frequency, and fractional bandwidth, as described in Section 3. Superimposed, Figure 6, also represents the variance (green bars) and bias (marker "o") of shape analysis operators: central frequency, centroid frequency and fractional bandwidth, as they were described in Section 4.
Figure 7 was generated for  mm and AWGN variance varying from 0.05 to 0.5. It represents the same information that has been described in the above point but changing
mm and AWGN variance varying from 0.05 to 0.5. It represents the same information that has been described in the above point but changing  mm with
mm with  mm.
mm.
From the observation of Figures 6 and 7 we can conclude that both methods are equivalent when estimating the central frequency. This is quite obvious, if we take into account, that the central frequency estimator is computed using the nonbinarized TFR diagram and it computes the maximum of each block along  -axis (2-D shape analysis is not applied). However, the estimator behavior changes when extracting 2-D geometrical parameters from the binarized diagrams (centroid and fractional bandwidth estimators). If we compare the fractional bandwidth estimator computed using the conventional technique with the fractional bandwidth estimator computed over binarized TFR diagrams, it can be appreciated the lower variance (represented by shorter vertical bars) but higher bias (represented by higher value markers). If we compare centroid frequency parameter computed with both presented techniques, we observe that we get lower variance (vertical bars) and bias (markers) when geometrical estimator is employed. For the centroid frequency parameter, superior performance of the geometrical estimator is obtained in high noise conditions.
-axis (2-D shape analysis is not applied). However, the estimator behavior changes when extracting 2-D geometrical parameters from the binarized diagrams (centroid and fractional bandwidth estimators). If we compare the fractional bandwidth estimator computed using the conventional technique with the fractional bandwidth estimator computed over binarized TFR diagrams, it can be appreciated the lower variance (represented by shorter vertical bars) but higher bias (represented by higher value markers). If we compare centroid frequency parameter computed with both presented techniques, we observe that we get lower variance (vertical bars) and bias (markers) when geometrical estimator is employed. For the centroid frequency parameter, superior performance of the geometrical estimator is obtained in high noise conditions.
It is also worth mentioning that if we compare the centroid estimator in Figures 6 and 7, benefits of using the proposed geometrical estimators are as big as the mean scatterer diameter ( ) increases. Note, that the bias increases when
) increases. Note, that the bias increases when  increases for the conventional centroid estimator.
increases for the conventional centroid estimator.
5.2. Application of Conventional and Geometrical Descriptors to Distinguish Variable Size Scatterers in an Agar-Agar Matrix
Real measurements were performed on a set of 8 test pieces. The 8 test pieces were created at the laboratory of the group and were composed of a uniform matrix of Agar-Agar and 3 Armstrong porosity molecular sieves of different sizes. All the pieces were made with the same concentration of molecular sieves and Agar-Agar. With this homogeneous matrix of Agar-Agar and Molecular sieves, we can simulate soft tissues containing scatterers resembling the theoretical model proposed at Section 2. The detailed composition of the test pieces is given in Table 1. Note that, in order to check the repeatability of the process, two test pieces were created for each scatterer size.
The molecular sieves (scatterers) were homogeneously distributed into the uniform Agar-Agar matrix. Figure 8 shows the aspect of a test piece.
The measurement equipment was a PC with an ultrasonic board IPR-100 (Physical Acoustics) working in pulse-echo mode with 400 V of attack voltage, 40 dB in the receiver amplifier, and damping impedance of 2000 Ohms. The transducer frequency was chosen to be 1 MHz (K1SC transducer probe from Krautkramer and Branson). Received signal was acquired with the Tektronix 3000 oscilloscope ( = 50 MSamples/s).
= 50 MSamples/s).
The set of 8 test pieces was separated in two subsets: the odd subset (composed by test pieces 1, 3, 5, and 7) and the even subset (composed by test pieces 2, 4, 6, and 8). Both subsets were measured separately and individual estimators were computed and compared between subsets. The measurement procedure was as follows: uniformly distributed A-scans were obtained around each test piece contour. Individual A-scan TFRs were obtained using the Spectrogram (by means of the Short-Time Fourier Transform). Final TFR for each test piece was obtained averaging individual A-scan TFRs. After thresholding the final TFR, geometrical descriptors presented in Section 4 were calculated for each subset. The parameters and graphs obtained after processing each subset were similar, for that (and for representation purposes) all parameters and graphs presented in this section were averaged for even and odd subsets, thus representing an only value for each parameter for every value of  .
.
Table 2 shows area, orientation, and eccentricity parameters obtained from the test pieces created in the experiment.
The area values obtained in Table 2 agree with the expected behavior described in Section 4. It can be noticed that higher scatterer sizes get lower value of the area descriptor. This trend is coarsely maintained among all scatterer diameter sizes ( ).
).
The orientation parameter values presented in Table 2 also agree with the expected behavior described by (7) since it predicts a downshift in the TFR shape (see Figure 1). Physical explanation is based on the fact that the higher the value of  , the higher the attenuation of the ultrasonic energy at high frequencies. As a result of that, higher
, the higher the attenuation of the ultrasonic energy at high frequencies. As a result of that, higher  values get higher negative slope (with respect to horizontal axis). The orientation parameter allows to distinguish coarsely between small scatterer test pieces (
values get higher negative slope (with respect to horizontal axis). The orientation parameter allows to distinguish coarsely between small scatterer test pieces ( and
and  mm) and large (
mm) and large ( and
and  mm).
mm).
However, there are geometrical parameters that allow a precise classification of test pieces according to  : eccentricity, centroid frequency, and BS are the main ones.
: eccentricity, centroid frequency, and BS are the main ones.
The eccentricity parameter values presented in Table 2 show that the higher  the lower the eccentricity value is. This behavior agrees with theoretical equations and allows to classify all the test pieces.
the lower the eccentricity value is. This behavior agrees with theoretical equations and allows to classify all the test pieces.
Figure 9 represents the centroid frequency evolution with depth (time of flight). The parameter has been estimated using both techniques presented. The left figure was obtained using the conventional estimator (see (10)) and the right figure was obtained using the geometrical estimator (Figure 4). Results were averaged for both subsets (even and odd). Both estimators should give results of the same order of magnitude as it can be verified. However, as the ultrasonic pulse travels deep into the agar-agar matrix (increasing time axes) it suffers from attenuation, whereas the grain noise remains constant. This phenomenon produces that late-time samples estimates requires lower variance estimators to be able to distinguish among categories (grain diameter  ). Figure 9(a) only allows to distinguish among scatterer mean diameter at the very beginning of the centroid frequency (from sample 1000 to 1150). Figure 9(b) allows to distinguish in a wider range (from sample 1000 to 1750 and from sample 3600 to 4400). This experiment confirms once more the superior bias/variance performance predicted by simulations (Figures 6 and 7).
). Figure 9(a) only allows to distinguish among scatterer mean diameter at the very beginning of the centroid frequency (from sample 1000 to 1150). Figure 9(b) allows to distinguish in a wider range (from sample 1000 to 1750 and from sample 3600 to 4400). This experiment confirms once more the superior bias/variance performance predicted by simulations (Figures 6 and 7).
Promising results are also obtained using the BS parameter, see Figure 10. Note that the amplitude of BS increases as the scatterer size decreases. This result is coherent with the eccentricity result, see Table 2 where pieces with lower  have higher eccentricity than pieces with higher
have higher eccentricity than pieces with higher  .
.
To sum up, from Table 2 and Figures 9(b) and 10, it is important to stress that area and orientation parameters can classify test pieces in two categories (large and small scatterer sizes) whereas eccentricity, centroid frequency and BS provide better results since they are able to distinguish among the four different scatterers sizes.
6. Conclusions
In this paper we show that parameters extracted from the TFR of ultrasonic A-scans can be used for material characterization/classification. The novelty of this work is based on the use of TFRs as input information in 2D-shape analysis algorithms, specifically geometrical descriptors. This technique compliments traditional classification parameters (attenuation, longitudinal ultrasonic velocity, etc.) with shape-related parameters. Additionally, for some parameters, the new technique allows to obtain lower variance estimators. When binarized TFRs are processed and 2-D geometrical modeling, inherent in our approach, is used, a new set of estimators can be derived. The proposed geometrical estimators can provide better estimates and moreover, they are less sensitive to noise than conventional estimators. Thanks to this superior performance, in terms of bias and variance, a better classification of scattering materials can be achieved. This behavior has been validated through simulations.
The results were applied to real test pieces created at the laboratory. Traditional estimators could hardly be used to classify according to mean scatterer size. However, estimators based on geometrical descriptors of the binarized A-scan TFR could easily distinguish among the different scattering sizes. Concretely, area and orientation parameters can classify test pieces in two categories (large and small scatterer sizes) while eccentricity, centroid frequency and BS provide better results since they are able to distinguish among the four different scatterers sizes.
References
Edwards M (Ed): Detecting Foreign Bodies in Food. Woodhead, Cambridge, UK; CRC Press, Boca Raton, Fla, USA; 2004.
Vergara L, Gosálbez J, Fuente JV, Miralles R, Bosch I: Measurement of cement porosity by centroid frequency profiles of ultrasonic grain noise. Signal Processing 2004, 84(12):2315-2324. 10.1016/j.sigpro.2004.07.025
Gosálbez J, Salazar A, Bosch I, Miralles R, Vergara L: Application of ultrasonic nondestructive testing to the diagnosis of consolidation of a restored dome. Materials Evaluation 2006, 64(5):492-497.
He P: Simulation of ultrasound pulse propagation in lossy media obeying a frequency power law. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 1998, 45(1):114-125. 10.1109/58.646916
Demirli R, Saniie J: Model-based estimation of ultrasonic echoes—part I: analysis and algorithms. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2001, 48(3):787-802. 10.1109/58.920713
Karaoguz M, Bilgütay N, Onaral B: Modeling of scattering dominated ultrasonic attenuation using power-law function. Proceedings of the IEEE Ultrasonics Symposium, October 2000 1: 793-796.
Vergara L, Gosálbez J, Fuente JV, et al.: Ultrasonic nondestructive testing on marble rock blocks. Materials Evaluation 2004, 62(1):73-78.
Pitas I: Digital Image Processing Algorithms and Applications. 1st edition. Wiley-Interscience, New York, NY, USA; 2000.
Gonzalez RC, Woods RE: Digital Image Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 2007.
Nandi AK: Blind Estimation Using Higher-Order Statistics. Kluwer Academic Publishers, Boston, Mass, USA; 1999.
Acknowledgment
This work was supported by the national R + D program under Grant TEC2008-02975 (Spain), FEDER programme and Generalitat Valenciana PROMETEO 2010/040.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gómez, S., Miralles (EURASIP Member), R., Naranjo, V. et al. Geometrical Feature Extraction from Ultrasonic Time Frequency Responses: An Application to Nondestructive Testing of Materials. EURASIP J. Adv. Signal Process. 2010, 706732 (2010). https://doi.org/10.1155/2010/706732
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/706732

 = 500 KHz, fractional bandwidth
= 500 KHz, fractional bandwidth  = 75%, and mean scatterer size
= 75%, and mean scatterer size  =
=  0.5, 1 and 1.5 mm
0.5, 1 and 1.5 mm . (a)
. (a)  = 0.5 mm, (b)
= 0.5 mm, (b)  = 1 mm, and (c)
= 1 mm, and (c)  = 1.5 mm.
= 1.5 mm.
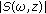 is the magnitude of the time-frequency transformation, and
is the magnitude of the time-frequency transformation, and 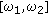 defines the integration band,
defines the integration band,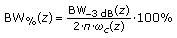
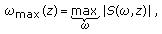
 ) parameters that can be obtained from
) parameters that can be obtained from 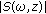 (higher-order statistics, median, etc.).
(higher-order statistics, median, etc.).
 = 500 KHz, AWGN of variance 0.15, and
= 500 KHz, AWGN of variance 0.15, and  = 1.5 mm.
= 1.5 mm.



 mm, AWGN of variance varying from 0.05 to 0.5. Bias (marker "*" or "o"), and variance (vertical bars).
mm, AWGN of variance varying from 0.05 to 0.5. Bias (marker "*" or "o"), and variance (vertical bars).
 mm, AWGN of variance varying from 0.05 to 0.5. Bias (marker "*" or "o"), and variance (vertical bars).
mm, AWGN of variance varying from 0.05 to 0.5. Bias (marker "*" or "o"), and variance (vertical bars).

