- Research Article
- Open access
- Published:
A Baseband Signal Processing Scheme for Joint Data Frame Synchronization and Symbol Decoding for RFID Systems
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 724260 (2010)
Abstract
We proposed a novel Viterbi-based algorithm using jiggling substates for joint data sequence detection, symbol boundary self-calibration, and signal frame synchronization for the EPC-Global Gen-2 system. The proposed algorithm first represents the data-encoded scheme as a trellis diagram, and then, as a consequence; the data sequence estimation can be carried out through the Viterbi algorithm. Moreover, time duration of the symbol waveform is iteratively adjusted to generate two substates in the Viterbi algorithm so as to trace and calibrate the symbol boundary on the fly. Compared with conventional approaches, the proposed Viterbi-based algorithm can significantly improve the system performance in terms of data detection accuracy due to its full exploitation of the baseband signal structure combining with the developed substate technique.
1. Introduction
Radio frequency identification (RFID) technology has become popular as an effective, low-cost solution for tagging and wireless identification. As RFID technology becomes cheaper, it is becoming increasingly prevalent in many applications, including asset tracking, passports, and mobile payment. Figure 1 presents a block diagram of a RFID system. It typically consists of tags (or transponders) and interrogators (or readers), between which information and commands are exchanged under a specific communication protocol. Depending upon the sources of the operating power, tags are generally classified into three categories: passive, semipassive, and active [1, 2].
Recent research on RFID systems mainly focuses on RF circuit design issues such as sensitivity improvement of the tag's antenna [3, 4] and long-range transmitter circuit design [5, 6]. Very few studies are aimed at the design of optimal baseband signal processing algorithms. As both antenna design and transmitter circuit realization pose major challenges in improving power efficiency, baseband signal processing that further boosts RFID system performance with high signal integrity is an interesting topic to explore. Conventional RFID interrogators use either a matched filter or an edge detector [7, 8] to detect encoded data. The matched filter (also known as the correlator) compares the received waveform with the prescribed data-encoded signals by using a set of integral and dump circuits for each symbol duration and then selects the most likely one as its decision output. On the other hand, the edge detector [8] uses the edge transition imposed on each data-encoded baseband signal as its decoding criterion. Assuming perfect symbol period estimation, the matched filter achieves high accuracy on data decoding at the expense of complex hardware implementation whereas the edge detector is vulnerable to noise perturbation due to its simple circuit structure.
However, during the initiation of inventory round, the low cost tag generally uses a rather simple way to estimate the symbol time period of the training signal sent by interrogator, and therefore there is inevitably symbol period bias between interrogator and tag. This bias estimates then accordingly serves as the symbol period for the tag's backscatter waveform. In addition to the over/or under-estimation of data symbol duration, the backscatter waveform may deteriorate further when passing through a multipath wireless fading channel. These two factors limit the application of conventional RFID systems to environments with low throughput and moderate data rate transmission. However, in a high data rate system with a large amount of information being organized into several signal frames, the accumulation of symbol period biases severely degrades system performance in terms of data detection reliability and signal frame synchronization. To overcome this problem, this study proposes a novel Viterbi-based [9–11] algorithm, called the jiggle-Viterbi with substate selection (JVSS) algorithm, which flexibly uses extended substates for joint symbol period compensation, data sequence estimation, and signal frame synchronization.
The proposed JVSS algorithm is applicable to systems that use structured waveforms to represent encoded data. In this paper, the FM0 baseband signal, employed in backscatter communication of the EPC-Global Generation-2 standard [8], is adopted as an example to illustrate the proposed algorithm. By decomposing the FM0 baseband signal on a half-cycle basis, we first represent the data-encoded FM0 baseband signal by a four-state Moore machine, and then the associated data detection in the interrogator can be carried out in a maximum likelihood sequence estimation (MLSE) manner which is practically attainable through the use of the Viterbi-based algorithm with acceptable computational complexity. To cope with the symbol period bias, the duration of the basis waveforms of the FM0 baseband signals is dynamically inflated/deflated by a prescribed step size in the execution of the proposed JVSS algorithm. This makes it possible to trace the symbol boundary on the fly. It is then possible to simultaneously confine the signal frame boundary within a single step size while performing data detection and signal frame synchronization. Compared to conventional approaches, in addition to significantly improving the accuracy of data detection, the proposed JVSS algorithm can effectively perform signal frame synchronization because it fully exploits the structure of the baseband signals of RFID systems. The proposed algorithm is therefore particularly useful in advanced RFID systems that transmit a large amount of information at a high data rate.
The rest of this paper is organized as follows. Section 2 introduces the system model of the backscatter modulation; Section 3 reviews the matched filter and the edge detector for baseband signal detection techniques of conventional RFID interrogators; Section 4 introduces the proposed JVSS algorithm for joint data sequence detection and signal frame synchronization; Section 5 presents computer simulation results to support the validity of the proposed algorithm; Section 6 summarize the paper.
2. System Model
The communication protocol of the EPCglobal system is classified into a physical layer (PL) and a tag identification layer (TIL). The PL includes the employed data coding scheme and modulation waveforms whereas the TIL designates the regulation required to establish the communication link between interrogator and tags. The operation of a RFID system begins with an inventory round in which fundamental parameters for the communication link, such as the symbol period and modulation scheme, are determined. Specifically, tags estimate the symbol period by measuring the temporal support of the training signal sent by the interrogator during the initiation of the inventory round. This training signal also provides the power source required by the circuit on passive tags to backscatter their reply messages via antennas. In this paper, we refer the communication mode from tags to interrogator as the backscatter mode. All information transmitted in the link is first processed by a baseband data-encoded scheme and then modulated by either the amplitude-shift keying (ASK) or the phase-shift keying (PSK). The backscatter mode of the EPCglobal system supports two types of the baseband data-encoding schemes: ( ) The FM0 baseband scheme and (
) The FM0 baseband scheme and ( ) the Miller modulation. Both schemes employ the same baseband basis functions but have different data-encoding rules to represent the output data stream. Since the proposed JVSS algorithm is applicable to both baseband data-encoding schemes, this study uses the FM0 baseband scheme as the study case to describe the proposed JVSS algorithm.
) the Miller modulation. Both schemes employ the same baseband basis functions but have different data-encoding rules to represent the output data stream. Since the proposed JVSS algorithm is applicable to both baseband data-encoding schemes, this study uses the FM0 baseband scheme as the study case to describe the proposed JVSS algorithm.
2.1. The FM0 Baseband Signals
Figure 2(a) depicts the basis functions and the state diagram representing the rule of the FM0 baseband data-encoding scheme. The key feature of the FM0 scheme is that it inverts the baseband signal phase at every symbol boundary. With this feature, during each symbol period estimate  , tags use both
, tags use both  and its inversion
and its inversion  to represent data-1 and both
to represent data-1 and both  and its inversion
and its inversion  to represent data-0. Basically, the phase inversion of the FM0 signal is used to against the possible polarity negation caused by the wireless fading channel. The channel-induced phase ambiguity is thus relieved by using both a basis function and its phase inversion replica to represent a single data in the FM0 scheme. Next, combining the basis functions with phase inversion at symbol boundary, the FM0 baseband scheme can be equivalently represented as a hidden Markov information source, as illustrated by the state diagram of the Moore machine in Figure 2(a)
to represent data-0. Basically, the phase inversion of the FM0 signal is used to against the possible polarity negation caused by the wireless fading channel. The channel-induced phase ambiguity is thus relieved by using both a basis function and its phase inversion replica to represent a single data in the FM0 scheme. Next, combining the basis functions with phase inversion at symbol boundary, the FM0 baseband scheme can be equivalently represented as a hidden Markov information source, as illustrated by the state diagram of the Moore machine in Figure 2(a) This state diagram defines four states,
This state diagram defines four states,  to represent the corresponding baseband signals
to represent the corresponding baseband signals  whereas the directed-links between states denote the transition with the associated triggering data-symbols. Figure 2(b) shows an example of the modulated baseband signals of all possible two-bit data sequences. Complying with the boundary phase inversion, there are two possible baseband signals for each two-bit data sequence. Next, to conveniently illustrate the proposed JVSS algorithm, the state diagram in Figure 2(a) can also be expressed by the trellis diagram in Figure 2(c).
whereas the directed-links between states denote the transition with the associated triggering data-symbols. Figure 2(b) shows an example of the modulated baseband signals of all possible two-bit data sequences. Complying with the boundary phase inversion, there are two possible baseband signals for each two-bit data sequence. Next, to conveniently illustrate the proposed JVSS algorithm, the state diagram in Figure 2(a) can also be expressed by the trellis diagram in Figure 2(c).
2.2. The Received Signal at the Interrogator
In a large space, such as an airport or warehouse, where interrogator and tags are of several to several tens meters apart, electromagnetic waves transmitted between tags and interrogator experience multipath propagation due to the reflection/diffraction caused by the surrounding objects. The response of a wireless multipath channel can be expressed as

where  denotes the fading amplitude of the
denotes the fading amplitude of the  multipath and
multipath and  represents the propagation delay. In the backscatter communication mode, a signal propagating through the wireless multipath channel and received at the interrogator can be represented as
represents the propagation delay. In the backscatter communication mode, a signal propagating through the wireless multipath channel and received at the interrogator can be represented as

where  ,
,  denotes the symbol period estimated at the tag and
denotes the symbol period estimated at the tag and  is the number of data bits in a signal frame. The additive noise
is the number of data bits in a signal frame. The additive noise  is assumed to be a white Gaussian process with zero mean and two-side spectral density
is assumed to be a white Gaussian process with zero mean and two-side spectral density  .
.
With a nominal symbol period  , the interrogator recovers the backscatter data symbols from the receive signal. In this process, there are two key factors that dominate the accuracy of the recovered data. (
, the interrogator recovers the backscatter data symbols from the receive signal. In this process, there are two key factors that dominate the accuracy of the recovered data. ( ) Since precise clock generators are generally not affordable for low-cost tags, and especially passive tags, a symbol period bias
) Since precise clock generators are generally not affordable for low-cost tags, and especially passive tags, a symbol period bias  always exists between tags and the interrogator; (
always exists between tags and the interrogator; ( ) the channel response
) the channel response  will spread the waveform of each data symbol in time if the bandwidth of the channel is less than that of the baseband signal
will spread the waveform of each data symbol in time if the bandwidth of the channel is less than that of the baseband signal  Specifically, the effects of these two factors become obvious in advanced systems where a large amount of data symbols is transmitted at a high data rate
Specifically, the effects of these two factors become obvious in advanced systems where a large amount of data symbols is transmitted at a high data rate Consequently, without handling these two factors well, conventional RFID interrogators limit themselves to scenarios with low data rates and relatively less information being sent. The following subsection briefly reviews two conventional data detection approaches, the matched filter and the edge detector. Both of these approaches are symbol-based algorithms and are widely used in current RFID systems. The subsequent section introduces the proposed sequence-based JVSS algorithm.
Consequently, without handling these two factors well, conventional RFID interrogators limit themselves to scenarios with low data rates and relatively less information being sent. The following subsection briefly reviews two conventional data detection approaches, the matched filter and the edge detector. Both of these approaches are symbol-based algorithms and are widely used in current RFID systems. The subsequent section introduces the proposed sequence-based JVSS algorithm.
3. Conventional Interrogators
The matched filter uses a set of correlators each adopting a delayed basis function as its template to match the received signal over each symbol period. Each correlator consists of a multiplier and an integral and dump circuit. The output signal, denoted as the correlation coefficient of the  correlator, can be expressed as
correlator, can be expressed as

Accordingly, the  data symbol can be decoded as the one mapped to the most likely estimate of basis function with the maximal correlation coefficient,
data symbol can be decoded as the one mapped to the most likely estimate of basis function with the maximal correlation coefficient,

where  denotes the basis function estimate during time interval
denotes the basis function estimate during time interval  . Note that the integration for each correlator is taken over the nominal period
. Note that the integration for each correlator is taken over the nominal period  , which means that the performance of the matched filter is greatly affected by the accumulated symbol period bias
, which means that the performance of the matched filter is greatly affected by the accumulated symbol period bias  ,
,  . In other words, with an
. In other words, with an  , the matched filter can survive only when the size of the signal frame,
, the matched filter can survive only when the size of the signal frame,  , is limited to yield a trivial ASPB.
, is limited to yield a trivial ASPB.
The other existing RFID signal detection approach is the edge detector, which senses the occurrence of the transition edge on  over each symbol time period to carry out data detection. Figure 2(a) shows that the waveform of the data-0 has a transition edge imposed at the middle point of the symbol period whereas the waveform of the data-1 remains constant. Compared to the matched filter, the edge detector is relatively easily implemented since it uses only a single integrator to sense the occurrence of the transition edge. However, the main drawback of the edge detector is its extreme sensitivity to noise perturbation, even if there is no symbol period bias.
over each symbol time period to carry out data detection. Figure 2(a) shows that the waveform of the data-0 has a transition edge imposed at the middle point of the symbol period whereas the waveform of the data-1 remains constant. Compared to the matched filter, the edge detector is relatively easily implemented since it uses only a single integrator to sense the occurrence of the transition edge. However, the main drawback of the edge detector is its extreme sensitivity to noise perturbation, even if there is no symbol period bias.
Apparently, without handling the ASPB or the waveform distortion induced by the wireless channel, both the matched filter and the edge detector are not applicable to advanced RFID systems transmitting a large amount of information at a high data rate. To this end, by fully exploiting the structure of the FM0 basis functions, the following section proposes a maximum likelihood sequence estimation-based (MLSE-based) algorithm for joint data detection, symbol boundary self-calibration, and signal frame synchronization. This algorithm can optimally solve the stringent problems encountered by an RFID interrogator.
4. The Optimum Interrogator
4.1. The Viterbi Algorithm
The Viterbi algorithm [9, 10], with practically acceptable complexity, is used to find the most likely sequence of hidden states that results in a sequence of observed events, especially in the context of Markov information sources. The algorithm makes a number of assumptions. ( ) Both the observed events and hidden events must be in a time sequence; (
) Both the observed events and hidden events must be in a time sequence; ( ) these two sequences must be aligned, and an instance of an observed event must correspond to exactly one instance of a hidden event; (
) these two sequences must be aligned, and an instance of an observed event must correspond to exactly one instance of a hidden event; ( ) computing the most likely hidden sequence up to a certain stage
) computing the most likely hidden sequence up to a certain stage  must depend only on both the observed event at stage
must depend only on both the observed event at stage  and the most likely sequence at the previous stage
and the most likely sequence at the previous stage  . Obviously, all the above conditions are satisfactory to the signal sequences generated by the FM0 data encoding scheme as Figure 2(a) illustrates. The following section briefly reviews the Viterbi algorithm and then presents the JVSS algorithm as an extension of the Viterbi algorithm.
. Obviously, all the above conditions are satisfactory to the signal sequences generated by the FM0 data encoding scheme as Figure 2(a) illustrates. The following section briefly reviews the Viterbi algorithm and then presents the JVSS algorithm as an extension of the Viterbi algorithm.
Given the received signal  in (2) and assuming that equally likely data symbols are transmitted, the MLSE problem can be expressed as optimization of the posteriori probability
in (2) and assuming that equally likely data symbols are transmitted, the MLSE problem can be expressed as optimization of the posteriori probability

where  denotes the signal vector defined as
denotes the signal vector defined as

With white Gaussian noise contamination and a sufficiently broad channel bandwidth, and by taking logarithmic operation, (5) can be rewritten as

where  ,
,  is the receive waveform segment during the
is the receive waveform segment during the  th symbol time period and
th symbol time period and  . Apparently, solving (7) through brute force exhaustive signal sequence searching is impractical due to its formidably high computational complexity, which grows exponentially with the block length
. Apparently, solving (7) through brute force exhaustive signal sequence searching is impractical due to its formidably high computational complexity, which grows exponentially with the block length  . The Viterbi algorithm provides an alternative way to reduce the overall complexity by recursively updating the sequence searching metrics during its execution.
. The Viterbi algorithm provides an alternative way to reduce the overall complexity by recursively updating the sequence searching metrics during its execution.
The Viterbi algorithm can be represented in a finite-state trellis structure with weighted branches connecting the states between time stages of execution. Figure 2(c) shows that each state has two incoming branches from the dedicated initiating state of the previous time stage and two outgoing branches to the destination states of next time stage. For convenience, we define  as the set of initiating states, with state
as the set of initiating states, with state  as their destination. For instance,
as their destination. For instance,  and
and  In each time stage, each state recursively updates the cumulative branch metric (CBM) of its incoming branches and retains the one with the largest CBM as the survival branch. The CBM of the survival branch of state
In each time stage, each state recursively updates the cumulative branch metric (CBM) of its incoming branches and retains the one with the largest CBM as the survival branch. The CBM of the survival branch of state  at time stage
at time stage  is defined as
is defined as

The above process is iteratively repeated until the end of the signal frame. A survival path is then decided by choosing the path contributing the largest CBM,  in the final time stage. Accordingly, the data sequence can be collectively determined by tracing the causes of branches on the survival path.
in the final time stage. Accordingly, the data sequence can be collectively determined by tracing the causes of branches on the survival path.
Although the decoding of the FM0 signal sequences, via the Viterbi algorithm, can be carried out in the sense of the MLSE, which reaps a power gain over the conventional symbol-based approaches such as the matched filter and the edge detector. However, the presence of symbol period bias can not be alleviated by simply applying the traditional Viterbi algorithm. To solve this problem, the next subsection proposes a novel Viterbi-based algorithm that can simultaneously perform MLSE, symbol boundary compensation, and data frame synchronization using the proposed jiggling substate technology.
4.2. The Jiggle-Viterbi Algorithm with Substate Selection (JVSS)
To trace and compensate for the symbol boundaries simultaneously, we propose a state jiggling technique in which each state of the aforementioned Viterbi algorithm is extended to a group of two substates, including a dilated and a shrunk substate, each of which corresponds to a variant FM0 baseband signal. These variant FM0 baseband signals are defined by extending FM0 signals with adjustable dynamic symbol periods  . The DSP of group
. The DSP of group  at time
at time  is denoted by
is denoted by  , which is iteratively adjusted to trace the symbol period bias
, which is iteratively adjusted to trace the symbol period bias Besides the DSP, in every time stage of execution, the JVSS algorithm equips each group with a symbol boundary indicator (SBI), denoted as
Besides the DSP, in every time stage of execution, the JVSS algorithm equips each group with a symbol boundary indicator (SBI), denoted as  for group
for group  In addition to catching the symbol boundary difference, both the DSP and SBI help the JVSS algorithm to restrict the deviation of the data frame boundaries within a single step size
In addition to catching the symbol boundary difference, both the DSP and SBI help the JVSS algorithm to restrict the deviation of the data frame boundaries within a single step size  making it possible to achieve data frame synchronization
making it possible to achieve data frame synchronization Figure 3 illustrates the variant FM0 baseband signals and their corresponding substates. By using an increment step size
Figure 3 illustrates the variant FM0 baseband signals and their corresponding substates. By using an increment step size  , the dilated substate
, the dilated substate  in Figure 3 uses the dilated basis function
in Figure 3 uses the dilated basis function  with period
with period  as its reference for the associated CBM calculation. On the other hand, the shrunk substate
as its reference for the associated CBM calculation. On the other hand, the shrunk substate  in Figure 3 uses
in Figure 3 uses  with period
with period  as the reference basis function. Note that the dynamic symbol period in time
as the reference basis function. Note that the dynamic symbol period in time  is iteratively updated according to its previous value,
is iteratively updated according to its previous value,  with
with  With this arrangement, the temporal support of the basis functions used in this study may vary greatly. This allows the JVSS algorithm to trace the symbol period bias. The basic idea behinds the JVSS algorithm is to take advantage of the substates, in conjunction with the adjustable DSP and the SBI to jointly detect the data sequence and trace the symbol boundaries on the fly.
With this arrangement, the temporal support of the basis functions used in this study may vary greatly. This allows the JVSS algorithm to trace the symbol period bias. The basic idea behinds the JVSS algorithm is to take advantage of the substates, in conjunction with the adjustable DSP and the SBI to jointly detect the data sequence and trace the symbol boundaries on the fly.
The execution of the JVSS algorithm is controlled by ( ) the survival substate determination of each group; (
) the survival substate determination of each group; ( ) the decision of the DSP
) the decision of the DSP  (
( ) the modification of the SBI
) the modification of the SBI  . Figure 4 illustrates the execution using a modified trellis diagram, in which, for easy identification, the substates of each group are enclosed by a dashed rectangular box whereas survival branches being of solid arrows. This figure shows that, starting from the very beginning time stage
. Figure 4 illustrates the execution using a modified trellis diagram, in which, for easy identification, the substates of each group are enclosed by a dashed rectangular box whereas survival branches being of solid arrows. This figure shows that, starting from the very beginning time stage  , we assume the dilated substates
, we assume the dilated substates  are the initial substates and the DSPs and SBIs are initialized to
are the initial substates and the DSPs and SBIs are initialized to  and
and  , for all
, for all  Next, in time stage
Next, in time stage  , each group of substates calculates the CBM using the associated basis functions
, each group of substates calculates the CBM using the associated basis functions

where  represents the CBM of the branch from
represents the CBM of the branch from  to the substate
to the substate  at time stage
at time stage  while
while  represents the CBM of the branch from
represents the CBM of the branch from  to
to  . Notice that the CBMs in (9) are integrated over the adjustable intervals defined by the SBI
. Notice that the CBMs in (9) are integrated over the adjustable intervals defined by the SBI  , the DSP
, the DSP  and the step size
and the step size  . According to these CBMs, within each group of substates, only the survival substate, with the largest CBM, can be retained, and the others are discarded. We denote the largest CBM of group
. According to these CBMs, within each group of substates, only the survival substate, with the largest CBM, can be retained, and the others are discarded. We denote the largest CBM of group  at time stage 1 as
at time stage 1 as

and the corresponding survival substate can be represented as

For instance, with assumed magnitudes of CBMs, Figure 4 shows that  and
and  . Intuitively, instead of using all the substates within a group to take part the execution of the JVSS algorithm, the determination of the survival substate can substantially mitigate the computational complexity via reducing the number of working substates.
. Intuitively, instead of using all the substates within a group to take part the execution of the JVSS algorithm, the determination of the survival substate can substantially mitigate the computational complexity via reducing the number of working substates.
After the survival substate determination, to help specify the symbol boundary of next CBM calculations, according to  the SBI and the DSP in time stage 1 are updated by
the SBI and the DSP in time stage 1 are updated by


Figure 4 also shows some updates of the DSPs and the SBIs as time proceeds. The above processes are repeated until the end of the data frame, where, with the maximal CBM, a survival path is determined, and the data sequence is then detected as in the conventional Viterbi algorithm. The final value of the SBI can then be used as the estimate of the signal frame boundary, achieving signal frame synchronization.
The basic idea behind the proposed algorithm is to fix the accumulative symbol period bias (ASPB) problem by using a basis waveform with adjustable temporal support in the calculation of the CBM. In a low noise contamination scenario, the JVSS algorithm can always correctly update its symbol boundary indicator (SBI) and the dynamic symbol period (DSP) at each time stage. An intuitive way for the determination of the step size is that the accumulated value of the SBI at the final stage of the JVSS algorithm must be greater than the accumulated ASPB value

where  denotes the tolerance of symbol period bias of the JVSS algorithm. Therefore, the step size to generate the basis waveforms of jiggle substates is
denotes the tolerance of symbol period bias of the JVSS algorithm. Therefore, the step size to generate the basis waveforms of jiggle substates is

The overall procedures of the JVSS algorithm are summarized in Algorithm 1.
Algorithm 1: The JVSS algorithm.
( ) Initialization:
) Initialization:
-
(1a)
Let

-
(1b)
Set
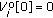 ,
, 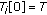 and
and 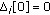 , for all
, for all 
( ) CBM calculation and survival substate determination for time stages
) CBM calculation and survival substate determination for time stages  :
:
-
(2a)
CBM calculation:
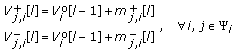
where
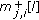 denotes the weight of the branch from
denotes the weight of the branch from  to
to  whereas
whereas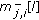 is that of the branch from
is that of the branch from  to
to  ; and are calculated as
; and are calculated as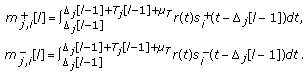
-
(2b)
Survival substate determination:
Determine the largest CBM
 of group
of group  at
attime instance
 and the corresponding survival substate is
and the corresponding survival substate is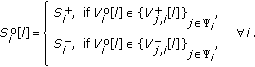
( ) SBI and DSP modification:
) SBI and DSP modification:
Assuming that the corresponding survival branch is initiated from group  , for each
, for each
group the SBI of time instance  is updated by
is updated by

and the DSP is updated by

( ) Joint data sequence estimation and signal frame synchronization:
) Joint data sequence estimation and signal frame synchronization:
Repeat steps 2-3 for each time stage. The survival path is the one with the maximal
final CBM  Data sequence estimation is performed by
Data sequence estimation is performed by
tracing the survival path on the trellis diagram, whereas the final value of the SBI
is used to estimate the signal frame boundary.
Remark 1.
Unlike the conventional Viterbi algorithm, in addition to passing the cumulative branch metrics of the survival path to next time stage, each substate of the JVSS algorithm provides the adapted symbol boundary information via the SBIs,  to increase the accuracy of the succeeding CBM calculation. On the other hand, adjustable DSPs can effectively alleviate the accumulation of symbol period bias.
to increase the accuracy of the succeeding CBM calculation. On the other hand, adjustable DSPs can effectively alleviate the accumulation of symbol period bias.
Remark 2.
The proposed JVSS is a blind algorithm which requires no information about the channel response  . Although the fading effect of the wireless channel may reverse the phase of the transmit signal, the FM0 data encoding scheme, which uses two opposite waveforms to represent a single data symbol, makes itself resistant to the phase reversal.
. Although the fading effect of the wireless channel may reverse the phase of the transmit signal, the FM0 data encoding scheme, which uses two opposite waveforms to represent a single data symbol, makes itself resistant to the phase reversal.
Remark 3.
With the trellis structure shown in Figure 4, the implementation of the JVSS incurs a computational complexity linearly proportional to the product of the number of employed substates and the number of the elapsed time stages. Since in each time stage half number of totally 8 substates being selected by the substate selection scheme, each of the selected substate will execute 4 CBM calculations for the succeeding time stage. Therefore, the computational complexity of the JVSS algorithm is about  CBM calculations
CBM calculations However, the computational complexity can be further reduced if the JVSS algorithm can be fulfilled by using only a portion of the original 4 groups. To do this, note that both
However, the computational complexity can be further reduced if the JVSS algorithm can be fulfilled by using only a portion of the original 4 groups. To do this, note that both  and
and  with phase negation of the FM0 baseband signals represent a data-1, and
with phase negation of the FM0 baseband signals represent a data-1, and  and
and  are
are both corresponding a data-0. This implies that the complexity of the JVSS algorithm can be further reduced to
both corresponding a data-0. This implies that the complexity of the JVSS algorithm can be further reduced to  CBM calculations by only employing the first two groups with substates
CBM calculations by only employing the first two groups with substates  in the JVSS algorithm and simply discarding the other two groups of substates. In doing so, the associated CBM calculations must be modified to the absolute versions as follows
in the JVSS algorithm and simply discarding the other two groups of substates. In doing so, the associated CBM calculations must be modified to the absolute versions as follows

Remark 4.
As an alternative to the data-encoding scheme for the backscatter signals in the EPC-global standard, Miller-modulated subcarrier (or Miller encoding) uses the same basis functions, but with inverted logical meaning, as those of the FM0 scheme. To generate the transmitted waveform, the Miller encoding scheme first generates its baseband data symbols by the transition diagram as shown in Figure 5, and then the transmitted waveform is the product of these baseband data symbols and a square wave at  times the symbol rate. The value
times the symbol rate. The value  is specified in the Query command that initiated the associated inventory round. Since the proposed JVSS algorithm is essentially applicable to any data encoding scheme directed by a transition diagram, the Miller-modulated subcarrier can thus be decoded via the JVSS algorithm by simply replacing the basis functions in the CBM calculations with the corresponding square-wave-modulated ones. The resultant CBM calculations can be represented as
is specified in the Query command that initiated the associated inventory round. Since the proposed JVSS algorithm is essentially applicable to any data encoding scheme directed by a transition diagram, the Miller-modulated subcarrier can thus be decoded via the JVSS algorithm by simply replacing the basis functions in the CBM calculations with the corresponding square-wave-modulated ones. The resultant CBM calculations can be represented as

where  denotes the associated square wave at
denotes the associated square wave at  times the symbol rate.
times the symbol rate.
5. Computer Simulations
This section presents computer simulations to evaluate the performance of the proposed algorithm. Compared with the conventional matched filter and edge detector, two different scenarios, corresponding to a regular and a high data transmission rate, are employed to assess the accuracy of data detection and the signal frame synchronization capability of the JVSS algorithm. Both scenarios employ passive tags which backscatter the continuous waveform sent from the interrogator. All the computer simulations are conducted in their equivalent baseband models with the assumption of zero carrier frequency offset between tags and interrogator due to the use of backscatter communication. The prescribed tolerance of the symbol period bias is set to be  ppm of the nominal symbol time period, that is,
ppm of the nominal symbol time period, that is,  .
.
Example 1 (the regular data rate case).
This example uses a typical value of symbol time period of the EPC-Global Generation 2 standard,  which corresponds to a transmission rate of
which corresponds to a transmission rate of  K bits per second (bps). Consider a wireless channel of two multipaths with delays
K bits per second (bps). Consider a wireless channel of two multipaths with delays  and
and  , and the corresponding fading amplitudes are assumed
, and the corresponding fading amplitudes are assumed  , and
, and  , respectively. The wireless channel is thus equivalent to a low pass filter with an approximate coherent bandwidth of
, respectively. The wireless channel is thus equivalent to a low pass filter with an approximate coherent bandwidth of  KHz
KHz which is significantly greater than that of the signal bandwidth
which is significantly greater than that of the signal bandwidth  KHz
KHz The symbol period bias is assumed
The symbol period bias is assumed  , or equivalently
, or equivalently  ppm. Ten thousands of independent Monte Carlo trials are conducted, each with signal frame size
ppm. Ten thousands of independent Monte Carlo trials are conducted, each with signal frame size  and
and  data symbols, respectively. For both cases, the step size of the JVSS algorithm is chosen as
data symbols, respectively. For both cases, the step size of the JVSS algorithm is chosen as  With the overestimated symbol period bias (i.e.,
With the overestimated symbol period bias (i.e.,  ), shown in Figure 6 is the comparison of the bit error rate (BER) curves of the proposed JVSS algorithm to that of conventional approaches. It is indicated that, with a moderate number of data symbols
), shown in Figure 6 is the comparison of the bit error rate (BER) curves of the proposed JVSS algorithm to that of conventional approaches. It is indicated that, with a moderate number of data symbols  , all three algorithms can work properly since the accumulation of the mismatched symbol duration causes trivial effects on the accuracy of signal detection. Also, the proposed JVSS algorithm possesses about 4-dB power gain over the matched filter. On the contrary, as the number of data symbols increases, for the case of
, all three algorithms can work properly since the accumulation of the mismatched symbol duration causes trivial effects on the accuracy of signal detection. Also, the proposed JVSS algorithm possesses about 4-dB power gain over the matched filter. On the contrary, as the number of data symbols increases, for the case of  the performance of conventional detectors is seriously affected by the accumulation of symbol period biases. On the other hand, the proposed JVSS algorithm, when dealing with large size of signal frame, is the only survivor due to its superior self-calibration capability on tracing symbol boundaries.
the performance of conventional detectors is seriously affected by the accumulation of symbol period biases. On the other hand, the proposed JVSS algorithm, when dealing with large size of signal frame, is the only survivor due to its superior self-calibration capability on tracing symbol boundaries.
Example 2 (the high data rate case).
This example uses almost the same scenario settings as those in Example 1 but adopts a smaller symbol period  which corresponds to a frequency bandwidth of
which corresponds to a frequency bandwidth of  KHz. Apparently, this bandwidth is broader than the coherence bandwidth of the wireless channel. The short channel bandwidth gives rise to channel distortion, which smears the transmitted signals on their temporal supports. Shown in Figure 7 is the comparisons of BERs of the proposed JVSS algorithm, the matched filter and the edge detector, respectively. This figure shows that the proposed JVSS algorithm can not only cope with the ASPB effect but also robust to against the pulse deformation caused by the bandlimited channel. Also as shown in the figure, even in the case of small size of signal frame,
KHz. Apparently, this bandwidth is broader than the coherence bandwidth of the wireless channel. The short channel bandwidth gives rise to channel distortion, which smears the transmitted signals on their temporal supports. Shown in Figure 7 is the comparisons of BERs of the proposed JVSS algorithm, the matched filter and the edge detector, respectively. This figure shows that the proposed JVSS algorithm can not only cope with the ASPB effect but also robust to against the pulse deformation caused by the bandlimited channel. Also as shown in the figure, even in the case of small size of signal frame,  the conventional approaches are seriously degraded by both the ASPB and the channel distortion.
the conventional approaches are seriously degraded by both the ASPB and the channel distortion.
Figure 8 shows the performance evaluation of the JVSS algorithm for signal frame synchronization. As the measure criterion, the mean square error (MSE) of the signal frame boundary is defined as the averaged absolute difference between SBI and its nominal value,  in which
in which  denotes the final value of SBI on the survival path of the
denotes the final value of SBI on the survival path of the  th trial, and
th trial, and  is the total number of Monte Carlo trials. As shown in the figure, for both cases of
is the total number of Monte Carlo trials. As shown in the figure, for both cases of  and
and  , the proposed approach can effectively trace the symbol boundaries and make the symbol frame being synchronized within the scale of step size
, the proposed approach can effectively trace the symbol boundaries and make the symbol frame being synchronized within the scale of step size  . In addition, the synchronization error of the signal frame of the JVSS algorithm can be mitigated with an increased sequence length
. In addition, the synchronization error of the signal frame of the JVSS algorithm can be mitigated with an increased sequence length  Compared to conventional approaches, due to the ASPB, both the matched filter and the edge detector have a synchronization error of
Compared to conventional approaches, due to the ASPB, both the matched filter and the edge detector have a synchronization error of  that remains constant and is therefore not illustrated in Figure 8 for simplification.
that remains constant and is therefore not illustrated in Figure 8 for simplification.
6. Conclusions
This paper proposes a novel MLSE-based algorithm for joint signal frame synchronization and data detection in an RFID system. The proposed algorithm fully exploits the structure of the baseband signal of the EPC-Global Gen-2 standard to develop a trellis representation of the FM0 data encoding scheme which makes the realization of the Viterbi algorithm on the FM0 scheme feasible. In addition, by inflating or deflating the waveform of FM0 baseband signals, the JVSS algorithm can effectively trace the boundaries of data symbols during its execution. Computer simulations show that, compared to conventional approaches, the proposed JVSS algorithm has significantly higher accuracy in data detection, superior capabilities in signal frame synchronization and is robust against bandlimited channel distortion. With these features, we conclude that the proposed algorithm is particularly useful to RFID systems with large amount information to be sent in high transmission data rate.
References
Chawla V, Ha DS: An overview of passive RFID. IEEE Applications and Practice 2007, 45(9):11-17.
Preradovic S, Karmakar NC, Balbin I: RFID transponders. IEEE Microwave Magazine 2008, 9(5):90-103.
Flores JLM, Srikant SS, Sareen B, Vagga A: Performance of rfid tags in near and far field. Proceedings of the 7th IEEE International Conference on Personal Wireless Communications (ICPWC '05), January 2005 353-357.
Aroor SR, Deavours DD: Evaluation of the state of passive UHF RFID: an experimental approach. IEEE System Journal 2007, 1(2):168-176.
Mayordomo I, Berenguer R, Garcia-Alonso A, Fernandez I, Gutierrez Í: Design and implementation of a long-range rfid reader for passive transponders. IEEE Transactions on Microwave Theory and Techniques 2009, 57(5):1283-1290.
Safarian A, Shameli A, Rofougaran A, Rofougaran M, De Flaviis F: RF identification (RFID) reader front ends with active blocker rejection. IEEE Transactions on Microwave Theory and Techniques 2009, 57(5):1320-1329.
Finkenzeller K: RFID Handbook: Fundamentals and Applications in Contactless Smart Cards and Identification. 2nd edition. John Wiley & Sons, New York, NY, USA; 2003.
EPCglobal :
 Radio-Frequency Identity Protocols Class-1 Generation-2 UHF RFID Protocol for Communications at 860 MHz–969 MHz Version 1.1.0. December 2005.
Radio-Frequency Identity Protocols Class-1 Generation-2 UHF RFID Protocol for Communications at 860 MHz–969 MHz Version 1.1.0. December 2005.Viterbi AJ: Convolutional codes and their performance in communication systems. IEEE Transactions on Communications Technology 1971, 19(5):751-772. 10.1109/TCOM.1971.1090700
Lin S, Costello DJ: Error Control Coding: Fundamentals and Applications. Prentice-Hall, Englewood Cliffs, NJ, USA; 1983.
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge, Mass, USA; 2005.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, YY., Chen, JT. A Baseband Signal Processing Scheme for Joint Data Frame Synchronization and Symbol Decoding for RFID Systems. EURASIP J. Adv. Signal Process. 2010, 724260 (2010). https://doi.org/10.1155/2010/724260
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/724260





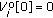 ,
, 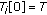 and
and 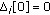 , for all
, for all 
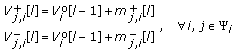
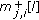 denotes the weight of the branch from
denotes the weight of the branch from  to
to  whereas
whereas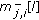 is that of the branch from
is that of the branch from  to
to  ; and are calculated as
; and are calculated as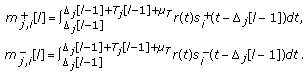
 of group
of group  at
at and the corresponding survival substate is
and the corresponding survival substate is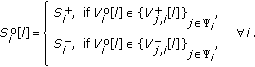




 , respectively.
, respectively.
 Radio-Frequency Identity Protocols Class-1 Generation-2 UHF RFID Protocol for Communications at 860 MHz–969 MHz Version 1.1.0. December 2005.
Radio-Frequency Identity Protocols Class-1 Generation-2 UHF RFID Protocol for Communications at 860 MHz–969 MHz Version 1.1.0. December 2005.