- Research Article
- Open access
- Published:
An MCMC Algorithm for Target Estimation in Real-Time DNA Microarrays
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 736301 (2010)
Abstract
DNA microarrays detect the presence and quantify the amounts of nucleic acid molecules of interest. They rely on a chemical attraction between the target molecules and their Watson-Crick complements, which serve as biological sensing elements (probes). The attraction between these biomolecules leads to binding, in which probes capture target analytes. Recently developed real-time DNA microarrays are capable of observing kinetics of the binding process. They collect noisy measurements of the amount of captured molecules at discrete points in time. Molecular binding is a random process which, in this paper, is modeled by a stochastic differential equation. The target analyte quantification is posed as a parameter estimation problem, and solved using a Markov Chain Monte Carlo technique. In simulation studies where we test the robustness with respect to the measurement noise, the proposed technique significantly outperforms previously proposed methods. Moreover, the proposed approach is tested and verified on experimental data.
1. Introduction
Molecular biosensors [1] are devices that contain a biological sensing element closely coupled with a transducer. They measure interaction of biomolecules of interest (target analytes) with the biological sensing element, and generate signal proportional to the amount of the analyte molecules. Detection in affinity biosensors [2] relies on chemical attraction between target analytes and their molecular complements, which serve as biological sensing elements (probes). The attraction between these biomolecules (their affinity for each other) leads to binding, in which probes capture target analytes. For instance, nucleic acid probes (DNA, RNA, or synthetic oligonucleotides) capture their Watson-Crick complements, antibody probes capture antigens, cell receptor probes capture ligands, and so forth. A transducer then converts the number of complex molecular structures that are formed due to the binding into a signal. Affinity biosensors can be multiplexed, which led to the development of microarrays—arrays of affinity biosensors capable of testing a large number of analytes simultaneously. DNA microarrays [3], in particular, are capable of screening tens or even hundreds of thousands of different gene sequences at the same time, revealing critical information about the functionality of cells, effects of drugs on organisms, and so forth. Microarrays are time- and cost-efficient, and may enable exciting new applications in drug discovery, medicine, defense systems, and environmental monitoring.
Despite their enormous potential, however, microarrays have not fully met the expectations of the research community and industry. Although in principle reliable [4], their performance still leaves something to be desired [5, 6]. Today, the sensitivity, dynamic range, and resolution of DNA microarrays are limited by interference, noise, probe saturation, and other sources of errors in the analyte detection procedure. Several of these limitations stem from the fact that the molecular binding is a stochastic process, which many of the conventional affinity biosensors attempt to characterize based on a single measurement of its equilibrium, that is, by taking one sample from the steady-state distribution of the binding process. On the other hand, real-time DNA microarrays are capable of taking multiple temporal samples of a binding process [7–9]. However, analyte estimation therein is typically performed using only the data collected in the equilibrium, and rarely relies on the kinetics [10].
In [11], analyte targets in real-time DNA microarrays are estimated using the temporally sampled kinetics of the binding process. However, the kinetics process there is described using a deterministic model. In this paper, we propose a comprehensive stochastic model of the binding process and state a Markov Chain Monte Carlo (MCMC) algorithm for the estimation of the target analytes. The performance of the proposed algorithm is tested on both synthetic and experimental data.
The paper is organized as follows. In Section 2, we describe the stochastic differential equation modeling the probe-target binding process. In Section 3, parameter estimation in discretely sampled diffusion processes is described, assuming noiseless data acquisition. An MCMC algorithm for the parameter estimation in the realistic noisy scenario is discussed in Section 4. Section 5 shows simulation results, while the experimental verification is provided in Section 6. Section 7 concludes the paper and outlines future work.
2. Stochastic Model
Let  denote the total number of analyte molecules, and let
denote the total number of analyte molecules, and let  denote the number of those that are bound to their corresponding probes at time
denote the number of those that are bound to their corresponding probes at time  . For simplicity, let us assume that the number of probe molecules,
. For simplicity, let us assume that the number of probe molecules,  , is greater than
, is greater than  . Then the probability that a free analyte molecule becomes captured during the
. Then the probability that a free analyte molecule becomes captured during the  time interval is
time interval is

where  denotes the association rate of the capturing process assuming an unlimited amount of probe molecules, and
denotes the association rate of the capturing process assuming an unlimited amount of probe molecules, and  is the fraction of the probe molecules that are available. Assuming that the binding events are mutually independent and that
is the fraction of the probe molecules that are available. Assuming that the binding events are mutually independent and that  is large, the number of analyte molecules captured during the
is large, the number of analyte molecules captured during the  time interval follows Binomial distribution with mean
time interval follows Binomial distribution with mean  and variance
and variance  . For large
. For large  (which in the biosensor context is certainly the case), this Binomial distribution can be approximated by a Gaussian
(which in the biosensor context is certainly the case), this Binomial distribution can be approximated by a Gaussian

Following a similar argument, it can be shown that the number of analyte molecules which are released during the  time interval is distributed with
time interval is distributed with

where  is the probability of release of a captured analyte molecule, and where
is the probability of release of a captured analyte molecule, and where  denotes the disassociation rate (for more details see, e.g., [12]).
denotes the disassociation rate (for more details see, e.g., [12]).
Now,  is a continuous-time Markov process. Its states are discrete, but under some mild conditions [13] (the transition probabilities do not change abruptly and
is a continuous-time Markov process. Its states are discrete, but under some mild conditions [13] (the transition probabilities do not change abruptly and  is sufficiently large, both of which are readily satisfied in the biosensor context), we can describe the dynamics of
is sufficiently large, both of which are readily satisfied in the biosensor context), we can describe the dynamics of  by the following stochastic differential equation (SDE)
by the following stochastic differential equation (SDE)

where  , the drift
, the drift  and diffusion
and diffusion  coefficients are given by
coefficients are given by

and where  denotes the Wiener process (detailed derivation is in [12]).
denotes the Wiener process (detailed derivation is in [12]).
Real-time DNA microarrays collect noisy observations of the temporally sampled diffusion process (4). Ultimately, we would like to use the collected observations to estimate parameters of the model  (including
(including  , the number of target molecules). A survey of techniques for parameter estimation of discretely observed diffusion processes is given in [14]. These techniques include (i) estimating functions [15]; (ii) indirect inference and efficient method of moments [16]; (iii) Bayesian analysis and Markov Chain Monte Carlo (MCMC) methods [17–20]; (iv) analytical and numerical approximation of the likelihood function [21–23]. For Bayesian analysis and the MCMC methods, the SDE is first discretized in-sync with the measurements, using time increments equal to the sampling period of the measurements. Additional time points are introduced between the samples [24], and the corresponding values of
, the number of target molecules). A survey of techniques for parameter estimation of discretely observed diffusion processes is given in [14]. These techniques include (i) estimating functions [15]; (ii) indirect inference and efficient method of moments [16]; (iii) Bayesian analysis and Markov Chain Monte Carlo (MCMC) methods [17–20]; (iv) analytical and numerical approximation of the likelihood function [21–23]. For Bayesian analysis and the MCMC methods, the SDE is first discretized in-sync with the measurements, using time increments equal to the sampling period of the measurements. Additional time points are introduced between the samples [24], and the corresponding values of  are treated as missing data points. The MCMC techniques [25] are then used to generate the missing data points. We should point out that MCMC techniques may be employed to estimate parameters in fairly general SDE models where the drift and diffusion coefficients are allowed to be nonlinear functions of diffusion process, or where parameters may enter into these coefficients nonlinearly. This is the case for the SDE model of real-time biosensor arrays (4).
are treated as missing data points. The MCMC techniques [25] are then used to generate the missing data points. We should point out that MCMC techniques may be employed to estimate parameters in fairly general SDE models where the drift and diffusion coefficients are allowed to be nonlinear functions of diffusion process, or where parameters may enter into these coefficients nonlinearly. This is the case for the SDE model of real-time biosensor arrays (4).
In this paper, we rely on MCMC techniques to estimate the parameters  of the SDE model (4) observed at discrete points in time and subject to measurement noise. In order to derive suitable proposal densities in the MCMC algorithm, we assume that the drift and diffusion coefficients satisfy the Lipschitz and linear growth conditions
of the SDE model (4) observed at discrete points in time and subject to measurement noise. In order to derive suitable proposal densities in the MCMC algorithm, we assume that the drift and diffusion coefficients satisfy the Lipschitz and linear growth conditions


for some positive constant  (see, e.g., [26]). For the sake of clarity of presentation, in the next section we first consider the noise-free case. Then, in the following section, we turn our attention to the noisy case.
(see, e.g., [26]). For the sake of clarity of presentation, in the next section we first consider the noise-free case. Then, in the following section, we turn our attention to the noisy case.
3. Parameter Estimation in the Noise-Free Case
Denote the set of  observations acquired over
observations acquired over  by
by  =
=  , where
, where  where
where  denotes the sampling (data acquisition) period. In principle, we may try to use the observed data to form the log-likelihood,
denotes the sampling (data acquisition) period. In principle, we may try to use the observed data to form the log-likelihood,

where  , and then find
, and then find  by maximizing
by maximizing  . The challenge, however, is that
. The challenge, however, is that  , a closed form expression for the transitional density between two consecutive discrete observation points is unavailable for the system in (4). Therefore, the likelihood function is often approximated via various numerical techniques [27, 28]. Here we describe the data augmentation procedure.
, a closed form expression for the transitional density between two consecutive discrete observation points is unavailable for the system in (4). Therefore, the likelihood function is often approximated via various numerical techniques [27, 28]. Here we describe the data augmentation procedure.
Consider the SDE (4) over a time interval  , and assume that we uniformly sample
, and assume that we uniformly sample  every
every  . Therefore, we assume that the value
. Therefore, we assume that the value  at the beginning of the time interval
at the beginning of the time interval  is known. For convenience, denote
is known. For convenience, denote  . Finding exact analytical expression for the transition density
. Finding exact analytical expression for the transition density  appears difficult to obtain. However, if
appears difficult to obtain. However, if  is very small, we could approximate it by
is very small, we could approximate it by  , where
, where  denotes the normal distribution with mean
denotes the normal distribution with mean  and variance
and variance  , and where
, and where

On the other hand, the sampling time  used for data acquisition is typically not sufficiently small to justify the approximation above. Therefore, we further discretize the interval
used for data acquisition is typically not sufficiently small to justify the approximation above. Therefore, we further discretize the interval  dividing it into
dividing it into  subintervals, where each subinterval is of the length
subintervals, where each subinterval is of the length  . Following [29], we employ the Euler-Maruyama integration scheme to generate points from a sample path of
. Following [29], we employ the Euler-Maruyama integration scheme to generate points from a sample path of  on
on  . [Note that
. [Note that  .] Denote these points by
.] Denote these points by  ,
,  , where
, where  . We put all these latent values between
. We put all these latent values between  into
into  . The Euler-Maruyama scheme generates
. The Euler-Maruyama scheme generates  by recursively computing
by recursively computing

 , where
, where  , and where
, and where  .
.
Now, we can form the joint distribution of latent values  with
with  given
given  and
and  and then integrate out the missing values to find the transition density.
and then integrate out the missing values to find the transition density.

where  and
and  and we use the Markov property of diffusion process. However, this multidimensional integral is not easy to evaluate. As a standard approach, we can use Monte Carlo integration together with the importance sampler to approximate this integral:
and we use the Markov property of diffusion process. However, this multidimensional integral is not easy to evaluate. As a standard approach, we can use Monte Carlo integration together with the importance sampler to approximate this integral:

In this equations, we are using the fact that  is a Markov process to write the joint distribution as a product of marginal distributions. We are generating
is a Markov process to write the joint distribution as a product of marginal distributions. We are generating  sample paths of the
sample paths of the  on the time interval
on the time interval  to approximate the transition density. Now, we must construct efficient importance samplers to draw the missing samples
to approximate the transition density. Now, we must construct efficient importance samplers to draw the missing samples  .
.
The importance sampler that we consider draws  from the Euler approximation of the SDE ([24]). Then, since the
from the Euler approximation of the SDE ([24]). Then, since the  is also approximated using this discrete model; the first
is also approximated using this discrete model; the first  terms of the target density
terms of the target density  and the density of the importance sampler
and the density of the importance sampler  are identical and cancel each other and the only remaining term is the
are identical and cancel each other and the only remaining term is the  . After this cancelation, we have the following approximate transition density:
. After this cancelation, we have the following approximate transition density:

Therefore, the last point obtained by the scheme (10) is  , which can be regarded as a sample of the process
, which can be regarded as a sample of the process  at
at  . The Euler-Maruyama integration procedure is repeated
. The Euler-Maruyama integration procedure is repeated  times, generating points
times, generating points  . The approximation converges weakly to the desired process as
. The approximation converges weakly to the desired process as  increases (see, e.g., [28] and the references therein). Thus the transition density can be approximated by
increases (see, e.g., [28] and the references therein). Thus the transition density can be approximated by

where

for each 
To summarize, in each time interval  we perform the following steps.
we perform the following steps.
-
(1)
Starting from
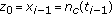 , employ the Euler-Maruyama technique (10) to generate
, employ the Euler-Maruyama technique (10) to generate 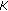 samples of the process
samples of the process 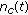 at
at 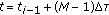 . These samples are denoted by
. These samples are denoted by 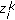 ,
, 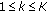 .
. -
(2)
Use
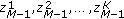 to estimate the transition density according to (14).
to estimate the transition density according to (14).
The approximate transition density converges to the true one as  . We repeat the above procedure to obtain approximate transition densities
. We repeat the above procedure to obtain approximate transition densities  for each
for each  , and form the likelihood function
, and form the likelihood function

Finally,  is maximized over
is maximized over  . For large
. For large  ,
,  , the resulting
, the resulting  approaches the true ML estimate of
approaches the true ML estimate of  .
.
To lower the computational complexity of the approach described in this section, various modifications have been proposed. For instance, alternative importance samplers are employed to accelerate the convergence of the Monte Carlo integration, resulting in significant computational savings (see, e.g., [30] and the references therein). We shall not pursue these alternative importance samplers here. Instead, we switch our attention to the estimation problem in the noisy measurement case.
4. An MCMC Algorithm for Parameter Estimation in Noisy Case
The technique described in the previous section assumes noise-free data. In this section, we focus our attention on the more realistic noisy scenario. We do not explicitly form the likelihood function but instead rely on an MCMC technique which alternates between drawing missing data conditioned on parameters and observations, and the parameters conditioned on the missing data and the observations. Assume that the continuous diffusion (4) is sampled, and denote the obtained noisy observations by  , that is, assume the continuous-discrete model
, that is, assume the continuous-discrete model

where  denotes iid Gaussian noise
denotes iid Gaussian noise  , and where
, and where  is introduced for notational convenience. (Note that for the sake of simplicity we set the transduction coefficient in the measurement equation to
is introduced for notational convenience. (Note that for the sake of simplicity we set the transduction coefficient in the measurement equation to  .) Let
.) Let  denote the set of collected noisy observations,
denote the set of collected noisy observations,  where
where  . Furthermore, we denote
. Furthermore, we denote  and collect the points
and collect the points  into
into 
 . (Note that
. (Note that  is a noisy observation of
is a noisy observation of  .)
.)
Following [19], to enable estimation of the parameters  , we form the joint posterior density of the parameters and simulated missing data
, we form the joint posterior density of the parameters and simulated missing data

where the transition density  and the measurement density
and the measurement density  are given by
are given by

and where  ,
,  . We rely on the Gibbs sampling technique to draw the missing data conditioned on the current state of the parameters and observations, and draw the parameters conditioned on the simulated missing data and observations. This procedure generates a Markov chain whose stationary distribution is (18). Expressed algorithmically, we perform the following steps.
. We rely on the Gibbs sampling technique to draw the missing data conditioned on the current state of the parameters and observations, and draw the parameters conditioned on the simulated missing data and observations. This procedure generates a Markov chain whose stationary distribution is (18). Expressed algorithmically, we perform the following steps.
-
(1)
Initialize parameters and latent values. Use linear interpolation between the measured points in
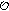 to initialize
to initialize 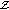 . Set the iteration counter to
. Set the iteration counter to 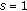 .
. -
(2)
In the iteration
 , draw
, draw  .
. -
(3)
Draw
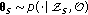 via Gaussian random walk update.
via Gaussian random walk update. -
(4)
Set
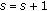 and go to step 2.
and go to step 2.
Finding the analytical expressions of the distributions in steps 2 and 3 appears infeasible. Hence, we employ the Metropolis-Hasting (M-H) algorithm to compute them numerically. In step 2, we generate a single component of  (i.e.,
(i.e.,  ) at a time (the so-called single site update), where there are four different cases depending on the value of the time index
) at a time (the so-called single site update), where there are four different cases depending on the value of the time index  . Case 1 deals with drawing the missing data
. Case 1 deals with drawing the missing data  for which there are no corresponding noisy observations in
for which there are no corresponding noisy observations in  (i.e.,
(i.e.,  is not an integer multiple of
is not an integer multiple of  ). On the other hand, Cases 2–4 deal with drawing the missing data
). On the other hand, Cases 2–4 deal with drawing the missing data  for which we do acquire noisy measurements. Among these, Cases 3 and 4 deal with the missing data at the start and at the end of the binding process, respectively (i.e., the boundary points corresponding to
for which we do acquire noisy measurements. Among these, Cases 3 and 4 deal with the missing data at the start and at the end of the binding process, respectively (i.e., the boundary points corresponding to  and
and  ). Case 2 deals with drawing the remaining missing data
). Case 2 deals with drawing the remaining missing data  (i.e.,
(i.e.,  is an integer multiple of
is an integer multiple of  ,
,  ).
).
Case 1.
 (is not an integer multiple of
(is not an integer multiple of  ). In this case, the conditional distribution is given by
). In this case, the conditional distribution is given by

Direct sampling from this distribution is not feasible. Therefore, we need to employ the M-H algorithm.
Following [17], when the drift and the diffusion coefficients are constant it holds that

However, we need to consider a more general case where drift and diffusion coefficients are functions of parameters  and the diffusion process
and the diffusion process  (clearly, this is the case for our model).
(clearly, this is the case for our model).
Now, drift and diffusion coefficients have bounded growth as stated in (7); moreover, sample paths of the diffusion process (i.e., the molecular binding process) are continuous since the sample paths of the underlying Brownian motion are continuous. This implies that the drift and diffusion coefficients are locally constant. Thus, for small time interval  the previous result stated for constant drift and diffusion coefficients also holds for arbitrary drift and diffusion. The rigorous proof is given in [17]. It follows that a suitable proposal density
the previous result stated for constant drift and diffusion coefficients also holds for arbitrary drift and diffusion. The rigorous proof is given in [17]. It follows that a suitable proposal density  is given by
is given by

It can be shown that

as  . The proposed data point
. The proposed data point

is accepted with probability  , where
, where

Here,  is the value at the iteration
is the value at the iteration  and
and  is the value obtained at iteration
is the value obtained at iteration  of the Gibbs Sampler.
of the Gibbs Sampler.
Case 2 ( is an integer multiple of
is an integer multiple of  ,
,  ,
,  ).
).
In this case, the conditional distribution is

Starting from (22), we can form the joint density of  and
and  conditioned on
conditioned on  and as
and as

From this joint Gaussian density, it is straightforward to obtain the conditional one

where the mean and the variance are given by

The proposed value  is accepted with probability
is accepted with probability  , where
, where

Case 3 ( ).
).
The conditional distribution is given by

Using the Euler approximation, we can write:

Since sample paths of the diffusion process are continuous, and since drift and diffusion coefficients have bounded growth by assumption given in (7),  and
and  are locally constant. Hence, we can approximate
are locally constant. Hence, we can approximate  by
by  and
and  by
by  which leads to
which leads to

Then,

Combining this density with the measurement error density given by

we obtain the joint density of  and
and  conditioned on
conditioned on  and
and  as
as

By applying the relation between the joint Gaussian distribution and its corresponding conditionals, we arrive to a suitable proposal density for the M-H algorithm given by

where the mean and the variance are defined as

The proposed value  is chosen with probability
is chosen with probability  , where
, where

Case 4 ( ).
).
Now the conditional distribution is

By using the Euler transition density  and the measurement error density
and the measurement error density  , we can form the joint density of
, we can form the joint density of  and
and  conditioned on
conditioned on  and
and  as
as

where  . It follows that
. It follows that

where the mean and the variance are given by

In this case, we can directly sample from the above density, so there is no need for the M-H algorithm.
On another note, in step 3 of the Gibbs sampling algorithm we update  as
as  , where
, where  and
and  . (These variances determine the mixing properties of the generated Markov chain.) We again use the M-H algorithm and accept
. (These variances determine the mixing properties of the generated Markov chain.) We again use the M-H algorithm and accept  with probability
with probability  , where
, where

When the noise variance is known,  is independent of the parameters
is independent of the parameters  and thus we can simplify
and thus we can simplify  to
to

5. Simulation Results
We simulate the reaction (4), where the parameters are set to  ,
,  ,
,  , and
, and  . The signal is sampled (
. The signal is sampled ( ), where the samples are perturbed by an additive Gaussian noise (zero-mean, variance
), where the samples are perturbed by an additive Gaussian noise (zero-mean, variance  ). In Figure 1, we compare the square root of the relative mean-square error,
). In Figure 1, we compare the square root of the relative mean-square error,  , of the MCMC algorithm for stochastically modeled real-time microarrays and the least-mean-squares estimation approach for deterministically modeled (by means of ordinary differential equations) real-time microarrays (see [11] for details). (We assume that all parameters other than
, of the MCMC algorithm for stochastically modeled real-time microarrays and the least-mean-squares estimation approach for deterministically modeled (by means of ordinary differential equations) real-time microarrays (see [11] for details). (We assume that all parameters other than  are known.) The error is plotted as a function of the observation noise variance (the error is averaged over
are known.) The error is plotted as a function of the observation noise variance (the error is averaged over  trials). The simulation results indicate that the proposed approach significantly outperforms the least-mean-squares method over the broad range of parameters. The Gibbs Sampler is performed with
trials). The simulation results indicate that the proposed approach significantly outperforms the least-mean-squares method over the broad range of parameters. The Gibbs Sampler is performed with  and
and  . The burn-in period of the algorithm is
. The burn-in period of the algorithm is  iterations, while no more than
iterations, while no more than  -
- iterations are needed for the convergence (see Figure 2).
iterations are needed for the convergence (see Figure 2).
6. Experimental Verification
To verify the proposed approach in experiments, we used the real-time microarray data reported in [11]. In those experiments, cDNA targets were generated from The RNA Spikes, a commercially available set of 8 purified Escherichia Coli RNA transcripts purchased from Ambion Inc. Lengths of the RNA sequences in the set are (750, 752, 1000, 1000, 1034, 1250, 1475, 2000), respectively. The RNA sequences were reverse transcribed to obtain the cDNA targets, which were then labeled with Cy5 dyes. Eight probes (25 mer oligonucleotides) were designed and printed on slides, where each probe was repeated in 6 different spots; hence, the printed slides had 48 spots. We focus on two experiments, one where the concentrations of the targets was 80 ng/50  L, and the other where the concentrations of the targets was 16 ng/50
L, and the other where the concentrations of the targets was 16 ng/50  l.
l.
In order to mitigate the numerical problems caused by large numbers (e.g.,  is on the order of
is on the order of  in the experimental data), we scale down the variables in the SDE (in particular, scaling factor
in the experimental data), we scale down the variables in the SDE (in particular, scaling factor  was chosen). Then, exploiting the linearity of our SDE model, the scaled down continuous-discrete model is given by
was chosen). Then, exploiting the linearity of our SDE model, the scaled down continuous-discrete model is given by

where  ,
,  ,
,  , and
, and

where  and
and  .
.
Moreover, since the noise variance is generally unknown, we add it to the vector of the unknown parameters, that is,  . This requires slight modification in the step 3 of the MCMC algorithm (as described previously).
. This requires slight modification in the step 3 of the MCMC algorithm (as described previously).
We applied the proposed Gibbs Sampler to the estimation of the parameters of the process which generated the described experimental data. We run  iterations of the algorithm with
iterations of the algorithm with  and
and  , and averaged its performance over
, and averaged its performance over  trials. For the first experiment, we obtained
trials. For the first experiment, we obtained  , while in the second experiment
, while in the second experiment  . Figure 3 and 4 show a sample convergence of the parameter estimates as a function of the number of iterations of the Gibbs sampler applied to the second data set. We note that the ratio of the estimated target amounts is
. Figure 3 and 4 show a sample convergence of the parameter estimates as a function of the number of iterations of the Gibbs sampler applied to the second data set. We note that the ratio of the estimated target amounts is  , which is close to the true ratio of
, which is close to the true ratio of  . On the other hand, unable to observe the kinetics of the hybridization process conventional microarrays would simply estimate the ratio of target molecules by the ratio of captured molecules at the end of the experimental run. For the experiments under consideration, this ratio is
. On the other hand, unable to observe the kinetics of the hybridization process conventional microarrays would simply estimate the ratio of target molecules by the ratio of captured molecules at the end of the experimental run. For the experiments under consideration, this ratio is  .
.
7. Summary and Conclusion
In this paper, we considered the problem of estimating the number of target molecules in stochastically modeled biomolecular sensors. We posed it as a parameter estimation problem in systems modeled by stochastic differential equations, where the noise-perturbed data is acquired at discrete points in time. Since the problem is analytically intractable, we employed MCMC techniques to obtain a numerical solution. In particular, we relied on the use of the Gibbs Sampler to alternate between drawing missing data conditioned on parameters and observations, and drawing parameters conditioned on the simulated missing data and the observations. We used the Metropolis-Hastings technique within the Gibbs Sampler to simulate analytically untractable densities. Simulation results indicate that the proposed algorithm significantly outperforms the existing least-mean-squares approach, and that the algorithm is robust with respect to the measurement noise. Moreover, we applied the algorithm to experimental data to verify the validity of the estimation algorithm in a realistic scenario.
There are several possible extensions of the current work. For instance, the MCMC algorithm described in this paper can also be applied to multivariate diffusion processes. Such processes arise in the context of gene regulatory network as well as in real-time biosensor arrays affected by cross-hybridization. For this scenario, one may extend the algorithm so that it handles unobserved parts of a multivariate diffusion process. On another note, a variation of the MCMC algorithm performs (random) block updating (see, e.g., [19, 20]). It is worth pursuing this modification in the context of parameter estimation in real-time biosensors.
References
Cooper J, Cass T (Eds): Biosensors. 2nd edition. Oxford University Press, Oxford, UK; 2004.
Rogers KR, Mulchandani A: Affinity Biosensors. Humana Press, Totowa, NJ, USA; 1998.
M. Schena KR: Microarray Analysis. John Wiley & Sons, New York Ny, USA; 2003.
Shi L, Reid LH, Jones WD, et al.: The MicroArray Quality Control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements. Nature Biotechnology 2006, 24(9):1151-1161. 10.1038/nbt1239
Marshall E: Getting the noise out of gene arrays. Science 2004, 306(5696):630-631. 10.1126/science.306.5696.630
Draghici S, Khatri P, Eklund AC, Szallasi Z: Reliability and reproducibility issues in DNA microarray measurements. Trends in Genetics 2006, 22(2):101-109. 10.1016/j.tig.2005.12.005
Stimpson DI, Hoijer JV, Hsieh W, Jou C, Gordon J, Theriault T, Gamble R, Baldeschwieler JD: Real-time detection of DNA hybridization and melting on oligonucleotide arrays by using optical wave guides. Proceedings of the National Academy of Sciences of the United States of America 1995, 92(14):6379-6383. 10.1073/pnas.92.14.6379
Bishop J, Chagovetz AM, Blair S: Kinetics of multiplex hybridization: mechanisms and implications. Biophysical Journal 2008, 94(5):1726-1734. 10.1529/biophysj.107.121459
Henry MR, Stevens PW, Sun J, Kelso DM: Real-time measurements of DNA hybridization on microparticles with fluorescence resonance energy transfer. Analytical Biochemistry 1999, 276(2):204-214. 10.1006/abio.1999.4344
Mirsky VM: Affinity sensors in non-equilibrium conditions: highly selective chemosensing by means of low selective chemosensors. Sensors 2001, 1(1):13-17. 10.3390/s10100013
Vikalo H, Hassibi B, Hassibi A: Modeling and estimation for real-time microarrays. IEEE Journal on Selected Topics in Signal Processing 2008, 2(3):286-296.
Das S, Vikalo H, Hassibi A: On scaling laws of biosensors: a stochastic approach. Journal of Applied Physics 2009., 105(10):
Allen E: Modeling with Itô Stochastic Differential Equations. Springer, New York, NY, USA; 2007.
Sørensen H: Parametric inference for diffusion processes observed at discrete points in time: a survey. International Statistical Review 2004, 72(3):337-354.
Bibby BM: Estimating functions for discretely sampled diffusion type models. In Handbook of Financial Econometrics. North-Holland, Amsterdam, The Netherlands; 2002.
Gallant AR, Long JR: Estimating stochastic differential equations efficiently by minimum chi-squared. Biometrika 1997, 84(1):125-141. 10.1093/biomet/84.1.125
Eraker B: MCMC analysis of diffusion models with application to finance. Journal of Business and Economic Statistics 2001, 19(2):177-191. 10.1198/073500101316970403
Roberts GO, Stramer O: On inference for partially observed nonlinear diffusion models using the Metropolis-Hastings algorithm. Biometrika 2001, 88(3):603-621. 10.1093/biomet/88.3.603
Golightly A: Bayesian inference for nonlinear multivariate diffusion processes, Ph.D. thesis. Newcastle University, Newcastle, UK; 2006.
Elerian O, Chib S, Shephard N: Likelihood inference for discretely observed nonlinear diffusions. Econometrica 2001, 69(4):959-993. 10.1111/1468-0262.00226
Aït-Sahalia Y: Maximum likelihood estimation of discretely sampled diffusions: a closed-form approximation approach. Econometrica 2002, 70(1):223-262. 10.1111/1468-0262.00274
Lo AW: Maximum likelihood estimation of generalized Ito processes with discretely sampled data. Econometric Theory 1988, 4: 231-247. 10.1017/S0266466600012044
Poulsen R: Approximate maximum likelihood estimation of discretely observed diffusion processes. Centre for Analytical Finance, University of Aarhus; 1999.
Pedersen AR: A new approach to maximum likelihood estimation for stochastic differential equations based on discrete observations. Scandinavian Journal of Statistics 1995, 22: 55-71.
Spall JC: Estimation via Markov chain Monte Carlo. IEEE Control Systems Magazine 2003, 23(2):34-45. 10.1109/MCS.2003.1188770
Oksendal B: Stochastic Differential Equations: An Introduction with Applications. Springer, Berlin, Germany; 2003.
Bishwal JPN: Parameter Estimation in Stochastic Differential Equations. Springer, New York, NY, USA; 2007.
Kloeden P, Platen E: Numeric Solutions of Stochastic Differential Equations. Springer, New York, NY, USA; 1992.
Brandt MW, Santa-Clara P: Simulated likelihood estimation of diffusions with an application to exchange rate dynamics in incomplete markets. Journal of Financial Economics 2002, 63(2):161-210. 10.1016/S0304-405X(01)00093-9
Durham GB, Gallant AR: Numerical techniques for maximum likelihood estimation of continuous-time diffusion processes. Journal of Business and Economic Statistics 2002, 20(3):297-316. 10.1198/073500102288618397
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Vikalo, H., Gokdemir, M. An MCMC Algorithm for Target Estimation in Real-Time DNA Microarrays. EURASIP J. Adv. Signal Process. 2010, 736301 (2010). https://doi.org/10.1155/2010/736301
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/736301
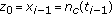 , employ the Euler-Maruyama technique (10) to generate
, employ the Euler-Maruyama technique (10) to generate  samples of the process
samples of the process  at
at 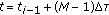 . These samples are denoted by
. These samples are denoted by 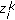 ,
, 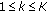 .
.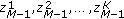 to estimate the transition density according to (14).
to estimate the transition density according to (14). to initialize
to initialize 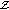 . Set the iteration counter to
. Set the iteration counter to 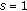 .
. , draw
, draw  .
.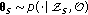 via Gaussian random walk update.
via Gaussian random walk update.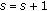 and go to step 2.
and go to step 2.
 , of the Gibbs Sampler and the least-mean-squares estimation approach, as a function of the observation noise variance of 100, 250, 500 and 1000.
, of the Gibbs Sampler and the least-mean-squares estimation approach, as a function of the observation noise variance of 100, 250, 500 and 1000.
 as a function of the number of iterations.
as a function of the number of iterations.

 (d) as a function of the number of iterations of the Gibbs sampler.
(d) as a function of the number of iterations of the Gibbs sampler.
