- Research Article
- Open access
- Published:
Moving Target Indication via RADARSAT-2 Multichannel Synthetic Aperture Radar Processing
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 740130 (2009)
Abstract
With the recent launches of the German TerraSAR-X and the Canadian RADARSAT-2, both equipped with phased array antennas and multiple receiver channels, synthetic aperture radar, ground moving target indication (SAR-GMTI) data are now routinely being acquired from space. Defence R&D Canada has been conducting SAR-GMTI trials to assess the performance and limitations of the RADARSAT-2 GMTI system. Several SAR-GMTI modes developed for RADARSAT-2 are described and preliminary test results of these modes are presented. Detailed equations of motion of a moving target for multiaperture spaceborne SAR geometry are derived and a moving target parameter estimation algorithm developed for RADARSAT-2 (called the Fractrum Estimator) is presented. Limitations of the simple dual-aperture SAR-GMTI mode are analysed as a function of the signal-to-noise ratio and target speed. Recently acquired RADARSAT-2 GMTI data are used to demonstrate the capability of different system modes and to validate the signal model and the algorithm.
1. Introduction
1.1. Motivation
Due to the significant clutter Doppler spread that is imparted by a fast-moving space-based radar (SBR) platform (typically over 7 km/s) and the large footprints (of the order of kilometers) that result from space observation of the earth, detection of airborne and ground vehicles is a difficult problem. Strong mainbeam clutter can impede even the detection of large targets unless it is suppressed, in which case the detection of small targets might still be hindered by possible sidelobe clutter. Therefore,efficient ground moving target indication (GMTI) and target parameter estimation can be achieved only after sufficient suppression of interfering clutter, particularly for space-based SARs with typically small exoclutter regions (clutter-free Doppler bands in the spectral domain). In its simplest form, this is accomplished using two radar receiver channels, such as the dual-receive antenna mode of RADARSAT-2 (R2) Moving Object Detection EXperiment (MODEX).In this mode of operation, the full antenna is split into two subapertures with two parallel receivers to create two independent phase centers. It is known, however, that two degrees of freedom are suboptimum for simultaneous suppression of the clutter and estimation of targets' properties, such as velocity and position [1]. Parameter estimation is often compromised and limited by clutter contamination of the target signal [2]. This deficiency has led to exploration of means of increasing the spatial diversity for RADARSAT-2. One such method is the so-called "sub-aperture switching" or "toggling" to create virtual channels [3], a technique originally proposed by Ender [4]. From January to May 2008, the RADARSAT-2 satellite underwent a set of on-orbit commissioning tests, which included the MODEX mode set. Three variants of the originally proposed virtual multichannel concepts [5] (collectively called MODEX-2) have been successfully evaluated using the RADARSAT-2 satellite, in addition to the standard dual-channel mode (referred to as MODEX-1), and impressive MODEX data sets, to be presented in this paper, have been collected.
This paper first describes the MODEX modes that have been investigated to date in Section 2 with preliminary test results also presented. In Section 3, a set of equations of motion of a ground moving target is derived for a multichannel spaceborne SAR. These equations of motion are shown to be applicable to both airborne and spaceborne stripmap imaging geometries. Assuming that the SAR platform state vectors (position, velocity and acceleration) will be available, these equations serve as a physical basis for the development of a parameter estimation algorithm, called the Fractrum Estimator, in Section 4. The effects of clutter contamination are analysed in Section 5 explaining why MODEX-1 is suboptimum. Fractrum Estimator is then applied to recently acquired RADARSAT-2 MODEX-1 and MODEX-2 data and the results are presented in Section 6, followed by concluding remarks in Section 7.
1.2. Background Work
The history of synthetic aperture radar dates back to 1951 when Carl Wiley of Goodyear postulated the Doppler beam-sharpening concept [6], but unclassified SAR papers only appeared in the literature a decade later [7]. The effects of moving targets in a SAR image were first discussed and published by Raney [8] in 1971, twenty years after the conception of SAR. Before the launches of German TerraSAR-X [9], Canadian RADARSAT-2 [10], and Italian COSMO-SkyMed [11] in 2007-2008, spaceborne SARs were only single-aperture systems. Such systems have a very limited GMTI capability due to dominant radar clutter, which prevents slowly moving targets from being detected. The three SAR satellites mentioned above are the first (in the unclassified world) to be equipped with a phased array, programmable antenna, and two physical receiver channels, permitting multiple independent phase centers (or virtual channels) to be synthesized. Although first advertised in [11] as GMTI capable SAR satellites with a few proposed modifications, COSMO Sky-Med have yet to produce their first GMTI results. TerraSAR-X and RADARSAT-2, on the other hand, have collected numerous GMTI data and the results have been published in several papers, for example, [12–19].
There are two major approaches to detection of ground moving targets with a multichannel SAR: Space-Time Adaptive Processing (STAP) and Along-Track Interferometry (ATI). A comparison of the two techniques has recently been presented in [20] and an excellent review of these two methods and others is given in [21]. The ATI is a nonadaptive method, which requires proper channel coregistration and balancing for it to work. Many research groups have developed detection algorithms based on these two approaches. The groups adopting mainly the ATI methodology include, for example, [22–25] and those following the STAP stream are, for example, [26–28]. In the following, SAR-GMTI processing algorithms developed by the German Aerospace Center (DLR) and the Institute for High Frequency Physics and Radar Techniques (FGAN-FHR) are discussed in more details, as they have adopted two very different approaches and assumptions for the detection and estimation of ground moving targets.
The DLR researchers have adopted very similar techniques as our group, namely using the ATI and/or the Displaced Phase Center Antenna (DPCA) in combination with a Matched Filter Bank (MFB) [29] for the detection and estimation of ground movers [24]. The fundamental difference between their approach and ours is the DLR's assumption that vehicles travel on roads of a known road network, which provide a priori information that can be effectively exploited [9]. Although not valid in military scenarios, the assumption is definitely legitimate for civilian applications such as traffic monitoring (except for marine or dense urban traffic). With this a priori knowledge, detections from an ATI (across-track) detector and an MFB (along-track or Doppler rate) detector can be weighted accordingly depending on the road orientation [24]. Also, the target range (across-track) speed can be accurately estimated from the azimuth displacement from the road based on the ATI phase of the target. In addition, the along-track speed can be derived from the range speed using the road orientation as a priori knowledge. Interestingly, once the along-track speed is known the acceleration of the target (if any) can also be inferred based on the estimated Doppler rate (from the MFB) that best focuses or maximizes the target energy. The Fractrum Estimator described in this paper is an alternate way of accomplishing what an MFB does, namely, estimating the true target Doppler (FM) rate by maximizing the target energy.
The FGAN-FHR has adopted primarily the STAP approach to SAR-GMTI for their airborne PAMIR system. A post-Doppler STAP clutter cancellation scheme was implemented, which permits the asymptotic decoupling of the different Doppler frequency contributions given that the time base is sufficiently long for the case of a SAR acquisition [20, 26]. A two-stage detection scheme was applied: the predetection and the postdetection. Since the PAMIR is a multifunction, multifrequency X-band (i.e., five sub-bands) radar, the predetection is performed on each sub-band as part of an elaborate CFAR detector [30, 31]. The target radial speed is estimated from the analysis of the Doppler frequency of the received pulses induced by both the target motion and the known platform velocity. The target localization is accomplished via the estimation of the target azimuth direction in the antenna coordinate system using the maximum-likelihood method [31]. For the existing spaceborne SAR-GMTI systems like TerraSAR-X and RADARSAST-2, equipped with only two physical receiver channels, a similar approach is not very effective, unless a sub-aperture switching (or toggling) scheme is used in order to generate multiple virtual channels. The performance of Direction-Of-Arrival (DOA) approach using such a sub-aperture antenna switching was presented in [32, 33]. We note that similar limitations exist for the ATI method for radial speed estimation and for the DOA-based estimator of the radial speed described in [13] as the Azimuth Displacement Indicator (ADI).
With a sub-aperture switching or toggling scheme (as presented in the next section for RADARSAT-2), however, there is always a trade-off between more phase centers and a reduced SNR (Signal-to-Noise Ratio) as several transmitter and/or receiver elements are turned off during the switching process. In the case of RADARSAT-2, a duty cycle (or maximum transmit power) constraint forces the pulse length to be reduced by half (from 0.42 to 0.21  s) when a switching mode is employed. This would further reduce the achievable SNR. However, a performance improvement to target parameter estimation using the sub-aperture switching methodology has been established theoretically in [32, 33] and will be here demonstrated using recently acquired RADARSAT-2 MODEX data in Section 6.
s) when a switching mode is employed. This would further reduce the achievable SNR. However, a performance improvement to target parameter estimation using the sub-aperture switching methodology has been established theoretically in [32, 33] and will be here demonstrated using recently acquired RADARSAT-2 MODEX data in Section 6.
2. RADARSAT-2 MODEX Modes
The 512 transmit-receive modules (TRMs) in the RADARSAT-2 two-dimensional active phased array are organized as 16 columns, as depicted by little rectangles in Figure 1, with 32 TRMs per column. All TRMs have independent control of transmitter phase and receiver phase and amplitude for both vertical and horizontal polarizations [34]. The phase and amplitude controls in the elevation dimension allow for the formation and steering of all beams. Transmitter phase control in the azimuth dimension allows the formation of the wider beams required for the Ultrafine resolution mode. This is accomplished by the deliberate defocussing of the beam [35].
RADARSAT-2 MODEX modes: (a) standard two-channel receive mode, (b) three-channel half-aperture toggle-transmit mode, (c) four-channel 3/4-aperture toggle-transmit mode, and (d) four-channel quarter-aperture toggle-receive mode. Shaded rectangles constitute active antenna panels with different shades representing different channels; down/up arrows represent transmitter/receiver physical center positions, respectively; black down-pointing triangles denote two-way effective phase centers.
The proposed virtual channel modes take advantage of the flexible programming capabilities of the RADARSAT-2 antenna to generate two, three, or four phase centers, as illustrated in Figure 1, using a sub-aperture switching (or toggling) technique originally proposed by Ender [4]. The spatial diversity of the standard dual-receive mode, Figure 1(a), can be increased by either transmitter toggling between pulses, Figures 1(b) and 1(c), or smart receiver excitation schemes, Figure 1(d). These are only a few methods for achieving multichannel capability and are by no means exhaustive. Due to transmitter/receiver toggling between pulses, the pulse repetition frequency (PRF) per virtual channel is effectively cut by one half. This may lead to clutter band aliasing (non-Nyquist sampling), which may be partially compensated for by doubling the original PRF.
The half-aperture, toggled-transmit (toggled-Tx) approach (between fore and aft subapertures), shown in Figure 1(b), has the advantage of maintaining the same phase-center distance (or the along-track baseline) as the standard dual-channel case (Figure 1(a)), which is nominally 3.75 m for RADARSAT-2, and is capable of generating three independent phase centers, shown as down-pointing triangles. The down/up arrows denote the transmitter/receiver physical phase center positions, respectively. However, the two-way beamwidth is significantly increased compared to the standard dual-channel case due to the half-aperture transmit. This could lead to clutter band aliasing (as confirmed by recently acquired MODEX data) even at RADARSAT-2's maximum PRF of 3800 Hz (or 1900 Hz per virtual channel). Also, the half-aperture transmit leads to a decrease in the transmit power and may severely limit the attainable SNR. The proposed solution to mitigate this shortcoming is to increase the transmitter aperture size from half to three-quarter aperture, as depicted in Figure 1(c). This sub-aperture switching configuration generates four independent phase centers (or virtual channels) as represented by down-pointing triangles at four different positions along the antenna.
The last approach is the toggled-receive (toggled-Rx) or sub-aperture switching mode where pulses are transmitted with the full aperture and returns are received using two alternating quarter subapertures as shown in Figure 1(d). Both (c) and (d) modes generate four independent phase centers and produce an effective phase-center distance that is one-half that of the standard dual-receive case. The (d) configuration has a slightly narrower two-way azimuth beam pattern than that of the (c) case.
The actual antenna patterns of the first three MODEX modes of Figure 1 have been estimated from recently acquired RADARSAT-2 MODEX data and are shown in Figure 2. The corresponding correlation plots between coregistered channels are also shown. The antenna patterns for the standard dual-receive mode (Figure 2(a)) and the  -aperture toggled-Tx mode (Figure 2(e)) show that the clutter bands are adequately sampled using a PRF of 1900 Hz (per channel). The
-aperture toggled-Tx mode (Figure 2(e)) show that the clutter bands are adequately sampled using a PRF of 1900 Hz (per channel). The  -aperture toggled-Tx mode, on the other hand, shows a 3 dB beamwidth of about 1800 Hz, which is just below the maximum sampling frequency of 1900 Hz (per channel). Often, the maximum PRF is not achievable due to the duty cycle limitation of RADARSAT-2. More realistic maximum PRF values often fall in the range of 3600–3700 Hz (or 1800–1850 Hz per channel). Therefore, clutter ambiguities can become quite severe for the
-aperture toggled-Tx mode, on the other hand, shows a 3 dB beamwidth of about 1800 Hz, which is just below the maximum sampling frequency of 1900 Hz (per channel). Often, the maximum PRF is not achievable due to the duty cycle limitation of RADARSAT-2. More realistic maximum PRF values often fall in the range of 3600–3700 Hz (or 1800–1850 Hz per channel). Therefore, clutter ambiguities can become quite severe for the  -aperture toggled-Tx mode. It is important to note that ambiguities must be avoided or minimized, because they cause decorrelation between coregistered channels due to interpolation errors [36, 37] as seen in Figure 2(d) and often generate false moving targets as a result of the erroneous phase imparted on the ambiguous clutter. These interpolation errors are illustrated in Figure 3. To coregister channels, the spatially displaced channel signals are time-shifted, via interpolation, to align them in space. This time shift is accomplished by applying a phase ramp on the signals in the frequency domain as illustrated by a solid peach line in the figure. As the ambiguities fold back into the Doppler band, the phase ramp is incorrectly applied and imparts a positive or negative constant phase error (or bias) on these ambiguous clutter signals, depending on the sign of their original frequencies. Therefore, ambiguous clutter shows up as false moving targets in an interferometric SAR image. The constant phase errors imparted on the ambiguities can be derived from the Fourier transformation pair:
-aperture toggled-Tx mode. It is important to note that ambiguities must be avoided or minimized, because they cause decorrelation between coregistered channels due to interpolation errors [36, 37] as seen in Figure 2(d) and often generate false moving targets as a result of the erroneous phase imparted on the ambiguous clutter. These interpolation errors are illustrated in Figure 3. To coregister channels, the spatially displaced channel signals are time-shifted, via interpolation, to align them in space. This time shift is accomplished by applying a phase ramp on the signals in the frequency domain as illustrated by a solid peach line in the figure. As the ambiguities fold back into the Doppler band, the phase ramp is incorrectly applied and imparts a positive or negative constant phase error (or bias) on these ambiguous clutter signals, depending on the sign of their original frequencies. Therefore, ambiguous clutter shows up as false moving targets in an interferometric SAR image. The constant phase errors imparted on the ambiguities can be derived from the Fourier transformation pair:  , where
, where  is the slope of the phase ramp applied to signal
is the slope of the phase ramp applied to signal  in the frequency domain to effect the desired time shift
in the frequency domain to effect the desired time shift  on
on  in the time domain. Therefore, the constant phase error can be shown to be
in the time domain. Therefore, the constant phase error can be shown to be

where  corresponds to
corresponds to  sign in the original frequency of ambiguous signals, assuming a positive ramp slope, and
sign in the original frequency of ambiguous signals, assuming a positive ramp slope, and  and
and  are the pulse repetition frequency (PRF) and pulse repetition interval (PRI), respectively. Signs are reversed in case of a negative ramp. Moreover, one observes from (1) that the interpolation does not lead to channel decorrelation if the PRF is chosen to be
are the pulse repetition frequency (PRF) and pulse repetition interval (PRI), respectively. Signs are reversed in case of a negative ramp. Moreover, one observes from (1) that the interpolation does not lead to channel decorrelation if the PRF is chosen to be  , such that the so-called Displaced Phase Center Antenna (DPCA) condition is met. Under this condition, there is no sub-sample interpolation (only integer sample shifting) and the phase errors imparted on the ambiguities are exactly multiples of
, such that the so-called Displaced Phase Center Antenna (DPCA) condition is met. Under this condition, there is no sub-sample interpolation (only integer sample shifting) and the phase errors imparted on the ambiguities are exactly multiples of  , which have no effect on the signal (including both main and side beams). The channel-to-channel decorrelation can also be caused by beam pointing errors, as the beam footprints for different channels do not coincide perfectly, generating slightly different clutter Doppler centroid for each channel. This effect is clearly seen in Figure 2(c), where the Doppler centroids of different channels differ by up to a few hundreds of Hertz. The decorrelation caused by the beam pointing errors is most noticeable for the toggled modes, as seen in Figure 2(d), where a drop in the correlation is observed for the interpulse channels. Fortunately, the beam pointing errors can be easily compensated for by applying a corrective phase ramp across the elements of a phased array, as was done for the last case shown in Figure 2(e), where the errors are reduced down to less than a few tens of Hertz. With this corrective measure, there is now virtually no drop in the correlation between the interpulse channels and all the channels have now correlations over 0.96, as shown in Figure 2(f).
, which have no effect on the signal (including both main and side beams). The channel-to-channel decorrelation can also be caused by beam pointing errors, as the beam footprints for different channels do not coincide perfectly, generating slightly different clutter Doppler centroid for each channel. This effect is clearly seen in Figure 2(c), where the Doppler centroids of different channels differ by up to a few hundreds of Hertz. The decorrelation caused by the beam pointing errors is most noticeable for the toggled modes, as seen in Figure 2(d), where a drop in the correlation is observed for the interpulse channels. Fortunately, the beam pointing errors can be easily compensated for by applying a corrective phase ramp across the elements of a phased array, as was done for the last case shown in Figure 2(e), where the errors are reduced down to less than a few tens of Hertz. With this corrective measure, there is now virtually no drop in the correlation between the interpulse channels and all the channels have now correlations over 0.96, as shown in Figure 2(f).
3. Equations of Motion of a Moving Target
High resolution Synthetic Aperture Radar (SAR) processing requires that a highly accurate imaging geometry model be first established. For SAR Ground Moving Target Indication (SAR-GMTI), the underlying assumption that the radar scene is stationary must be extended to include nonstationary scenes or moving targets. This can be quite easily accomplished for the case of an airborne platform [38], which is assumed to be moving along a straight line and transmitting uniformly spaced pulses. This assumption requires good platform motion compensation and good control of the PRF as a function of ground speed. The same cannot be said about a spaceborne platform, where the earth's gravitational force plays a key role in defining the platform trajectory and the velocity of the radar antenna footprint as it sweeps along the surface of the earth. The modeling of a moving target for a single channel spaceborne SAR geometry has already been accomplished to a high degree of accuracy by Eldhuset [39] and Curlander and McDonough [40]. However, the extension of the model to include a SAR system that is equipped with multiple apertures is evidently absent in the open literature, partly because there were no existing spaceborne SAR systems in the unclassified world equipped with such a capability up until the recent launches of COSMO-SkyMed [11], TerraSAR-X [41] and RADARSAT-2 [13] in 2007. In the following, equations of motion of a ground moving target for a multichannel spaceborne SAR are derived. The full derivation is presented here for the first time, although this model has been used in our previous work.
Several assumptions are used to simplify the model. The SAR pointing angles, measured from a reference pointing direction, are assumed to be small. The along-track speed of the target is assumed to be much smaller than the SAR platform speed, which is warranted in the case of spaceborne SAR and typical ground vehicles. It is also assumed that the rate of change is very slow for certain orbital parameters, such as the linear speed, which is true for nearly circular orbits. For the sake of generality, these assumptions are not incorporated in the statement of the problem. They are introduced, where appropriate, only to simplify the final formulae. For a different SAR system, they may be reviewed or removed at the expense of model complexity.
The relative position vector of a moving target with respect to an imaging SAR satellite, in the earth centered earth fixed (ECEF) system, can be written as

where indices "t" and "s" denote "target" and "satellite," respectively. A bold letter indicates a vector and the corresponding regular italic font (of the same symbol) represents the magnitude of the vector, and a bold upper case letter represents a matrix. In the ECEF frame, the earth motion is absorbed into the relative satellite motion.
The Doppler centroid and Doppler rate are proportional to  and
and  , respectively, where the dot and double-dot notations indicate first and second derivatives with respect to time. A common approach to the derivation of
, respectively, where the dot and double-dot notations indicate first and second derivatives with respect to time. A common approach to the derivation of  and
and  is to start from the identity [40]
is to start from the identity [40]

and to differentiate it with respect to time, where superscript  denotes the vector (or matrix) transpose.
denotes the vector (or matrix) transpose.
Differentiating both sides of (3) with respect to time, we get


Equation (4b) can be rewritten as


where  is the velocity vector of the moving target,
is the velocity vector of the moving target,  is the velocity vector of the satellite, and
is the velocity vector of the satellite, and

are the projections of the target and satellite velocity vectors, respectively, onto the line of sight (LOS) or the radial direction. Also, the radial speed of a stationary target as "seen" by the radar due to the platform motion is equal to  . Therefore, the Doppler shift at the beam center induced by the motion of the platform (or the stationary clutter Doppler centroid) is given by
. Therefore, the Doppler shift at the beam center induced by the motion of the platform (or the stationary clutter Doppler centroid) is given by

and the Doppler shift due to the target's radial speed is

Therefore, the total Doppler shift is given by

Again, differentiating both sides of (4a) with respect to time yields


Using the following definitions

Equation (10b) can be rewritten as

Therefore,

where


 is the so-called "effective velocity" often used in the spaceborne SAR processing to model the range equation and
is the so-called "effective velocity" often used in the spaceborne SAR processing to model the range equation and  is the projection of the target velocity onto the direction of platform velocity
is the projection of the target velocity onto the direction of platform velocity  (also called the along-track direction) and needs not to be parallel to the ground track.
(also called the along-track direction) and needs not to be parallel to the ground track.
The instantaneous slant range equation (or history)  is the key to high precision SAR processing. Accurate estimation of the effective velocity
is the key to high precision SAR processing. Accurate estimation of the effective velocity  allows complicated mathematical manipulations involving a satellite/earth geometry model to be avoided and a simple hyperbolic approximation to be adopted in most high precision SAR processing algorithms [42]. The hyperbolic model can be further simplified and approximated using a second-order Taylor series expansion or a parabolic model without significantly incurring further loss of accuracy for typical RADARSAT-2 dwell times and resolutions. However, this may not be true in general.
allows complicated mathematical manipulations involving a satellite/earth geometry model to be avoided and a simple hyperbolic approximation to be adopted in most high precision SAR processing algorithms [42]. The hyperbolic model can be further simplified and approximated using a second-order Taylor series expansion or a parabolic model without significantly incurring further loss of accuracy for typical RADARSAT-2 dwell times and resolutions. However, this may not be true in general.
If  and
and  in (5a) and (13) are evaluated at some arbitrary time
in (5a) and (13) are evaluated at some arbitrary time  , then the range equation can be approximated by the Taylor series expansion:
, then the range equation can be approximated by the Taylor series expansion:

where




 and
and  are considered negligible with respect to
are considered negligible with respect to  and, therefore, are dropped in (16d). If
and, therefore, are dropped in (16d). If  is chosen to be the broadside time
is chosen to be the broadside time  , then
, then  by definition and the radial direction (subscripted by "
by definition and the radial direction (subscripted by " ") becomes exactly perpendicular to the flight direction or the along-track direction (subscripted by "
") becomes exactly perpendicular to the flight direction or the along-track direction (subscripted by " "). Under this condition, (16b) and (16d) become
"). Under this condition, (16b) and (16d) become


where  and
and  are now the target's down-range (or across-track) velocity and acceleration components, respectively, and
are now the target's down-range (or across-track) velocity and acceleration components, respectively, and  is the broadside range of the moving target. In the vicinity of
is the broadside range of the moving target. In the vicinity of  , therefore, the Taylor series expansion reads
, therefore, the Taylor series expansion reads

The use of a parabolic model is convenient in the derivation of range equations for multichannel SAR systems. In the following, the range equation for the second aperture of a two-channel SAR is derived.
3.1. Local Frame of Reference
In order to continue with our derivations, we first define a local flight (LF) frame of reference for the radar as shown in Figure 4, where  is defined as the unit vector pointing down from the radar's center of gravity to the center of the earth. To define the second axis, we cross (vector) multiply
is defined as the unit vector pointing down from the radar's center of gravity to the center of the earth. To define the second axis, we cross (vector) multiply  with the radar's velocity vector
with the radar's velocity vector  to form the right pointing unit vector
to form the right pointing unit vector  :
:

Then the third unit vector, which completes the local reference frame, is given by

We should point out that  is not necessarily in the exact same direction as
is not necessarily in the exact same direction as  , as illustrated in Figure 4.
, as illustrated in Figure 4.
3.2. Transformation Matrix
We now derive the transformation matrix from the LF reference frame to the ECEF reference frame. To begin, we express the unit vector  in the ECEF frame:
in the ECEF frame:

Then  becomes
becomes

where

 is obviously the horizontal velocity component of the radar and can be easily shown to be
is obviously the horizontal velocity component of the radar and can be easily shown to be

where  is the vertical velocity component of the radar platform and is given by
is the vertical velocity component of the radar platform and is given by

We are now ready to express the forward unit vector  in the ECEF frame as
in the ECEF frame as

Finally, the transformation matrix from the LF reference frame to the ECEF frame [43] is simply


3.3. Antenna Look Vector
Let the ideal look direction of the antenna in the LF frame, with an off-nadir angle  pointing at a zero Doppler point on the surface of the earth, be
pointing at a zero Doppler point on the surface of the earth, be

Then the actual antenna look vector (or pointing vector) in the local reference frame of the radar is given by


where  is the yaw-pitch rotation matrix, and
is the yaw-pitch rotation matrix, and  and
and  are the yaw and pitch angles about the axes
are the yaw and pitch angles about the axes  and
and  , respectively. We are assuming that
, respectively. We are assuming that  and
and  correspond to a LOS within the beam, but not necessarily at its center. For RADARSAT-2,
correspond to a LOS within the beam, but not necessarily at its center. For RADARSAT-2,  and
and  are typically small (
are typically small ( 1) in the ECEF frame due to the mechanical zero-Doppler beam steering. The rotation matrix
1) in the ECEF frame due to the mechanical zero-Doppler beam steering. The rotation matrix  can, therefore, be shown to be
can, therefore, be shown to be


where

The term,  , is considered negligible [43] and is set to zero in (29b) and (30b). In the ECEF frame, the antenna look vector
, is considered negligible [43] and is set to zero in (29b) and (30b). In the ECEF frame, the antenna look vector  is then given by
is then given by

Note that the look vector  is not necessarily in the direction of the beam center, rather it points to the direction of the target of interest within the beam footprint.
is not necessarily in the direction of the beam center, rather it points to the direction of the target of interest within the beam footprint.
3.4. Displacement Vector
Let  denote the vector pointing from the effective phase center of the aft sub-aperture to the effective phase center of the fore sub-aperture in the LF frame, then
denote the vector pointing from the effective phase center of the aft sub-aperture to the effective phase center of the fore sub-aperture in the LF frame, then  can be expressed as
can be expressed as

where

and  and
and  are the pitch and yaw angles (or the orientation) of the antenna, representing the attitude of the spacecraft in the LF frame of reference. In the ECEF frame,
are the pitch and yaw angles (or the orientation) of the antenna, representing the attitude of the spacecraft in the LF frame of reference. In the ECEF frame,  becomes
becomes

3.5. Range Equations for Multiple Phase Centers
A two-aperture SAR-GMTI system is again assumed in the following derivations with the understanding that the derived equations can be generalized to a multiaperture system. Let  and
and  denote the position vectors of the antenna's two effective (or two-way) phase centers in the ECEF frame, respectively. The aft antenna phase center
denote the position vectors of the antenna's two effective (or two-way) phase centers in the ECEF frame, respectively. The aft antenna phase center  is then displaced from the fore antenna phase center
is then displaced from the fore antenna phase center  by
by  . For the case of RADARSAT-2, the displacement vector
. For the case of RADARSAT-2, the displacement vector  is closely aligned with the radar's velocity vector
is closely aligned with the radar's velocity vector  . Perfect alignment would be optimal because it would allow the aft phase center to pass through the same ECEF position as the fore phase center with a time delay of
. Perfect alignment would be optimal because it would allow the aft phase center to pass through the same ECEF position as the fore phase center with a time delay of  , where
, where  is the distance between the two effective phase centers. This perfect alignment would also mean that the whole antenna is ideally steered, generating a zero Doppler centroid in the clutter Doppler spectrum. In the presence of a nonzero Doppler centroid, there exists a nonzero across-track component of
is the distance between the two effective phase centers. This perfect alignment would also mean that the whole antenna is ideally steered, generating a zero Doppler centroid in the clutter Doppler spectrum. In the presence of a nonzero Doppler centroid, there exists a nonzero across-track component of  , which translates into a small across-track baseline. In the case of a real spaceborne SAR-GMTI system, such as the RADARSAT-2 MODEX, this small cross-track component is always present and, therefore, must be compensated for or taken into account in the system modeling [19].
, which translates into a small across-track baseline. In the case of a real spaceborne SAR-GMTI system, such as the RADARSAT-2 MODEX, this small cross-track component is always present and, therefore, must be compensated for or taken into account in the system modeling [19].
The slant-range vector  from the aft antenna phase center to the target can, therefore, be expressed as
from the aft antenna phase center to the target can, therefore, be expressed as


where  and
and  . Then the projections of these slant-range vectors,
. Then the projections of these slant-range vectors,  and
and  , along the look vector
, along the look vector  direction are given by
direction are given by




From (29b) and (33), (37d) becomes



where

 and
and  are now measured in the slant-range plane. As the antenna footprint sweeps across the target, the pitch angle
are now measured in the slant-range plane. As the antenna footprint sweeps across the target, the pitch angle  hardly changes (i.e., remains virtually constant) such that
hardly changes (i.e., remains virtually constant) such that  , resulting in
, resulting in  . In the case of RADARSAT-2,
. In the case of RADARSAT-2,  and
and  are usually small but nonzero such that the beam center is not located exactly at the zero-Doppler point on the surface of the earth (in the ECEF frame). This residual beam squint
are usually small but nonzero such that the beam center is not located exactly at the zero-Doppler point on the surface of the earth (in the ECEF frame). This residual beam squint  generates a small constant along-track interferometric phase, which is usually removed by the digital-balance processing of the signal channels and can, therefore, be ignored. For the sake of completeness, however, we shall keep the term in (38c). Then, the zeroth-order coefficient of the Taylor expansion of
generates a small constant along-track interferometric phase, which is usually removed by the digital-balance processing of the signal channels and can, therefore, be ignored. For the sake of completeness, however, we shall keep the term in (38c). Then, the zeroth-order coefficient of the Taylor expansion of  evaluated at arbitrary time
evaluated at arbitrary time  can be expressed as
can be expressed as

Next, we derive the first-order coefficient of the Taylor series expansion of  . From (36b), we obtain
. From (36b), we obtain






where it can be shown that  , and the
, and the  term can be neglected.
term can be neglected.
First, we derive the second term in (41f):

where we have assumed that the spacecraft attitude is not changing in the LF frame such that time derivatives of  and
and  (or
(or  ) are equal to zero in the imaging time interval. We also assume, for simplicity, that
) are equal to zero in the imaging time interval. We also assume, for simplicity, that  and
and  are small (normally true for RADARSAT-2). Therefore, (42) becomes
are small (normally true for RADARSAT-2). Therefore, (42) becomes

Here, we need to find the first time derivative of  (i.e.,
(i.e.,  ), which can be shown to be
), which can be shown to be

where terms of the type  ,
,  , and
, and  cancel out in the second column of (44) and are, therefore, dropped. We can further simplify (44) by noting that
cancel out in the second column of (44) and are, therefore, dropped. We can further simplify (44) by noting that  ,
,  , and
, and  :
:

Therefore, (43) becomes



The last term in (46b) is ignored since the look vector  is virtually perpendicular to
is virtually perpendicular to  .
.
We now derive the last term of (41f). From (27b) and (35),


where  , and they are neglected in (47b). Also by noting that
, and they are neglected in (47b). Also by noting that

where  is virtually perpendicular to
is virtually perpendicular to  for ground moving targets, we can rewrite (47b) as
for ground moving targets, we can rewrite (47b) as


Finally, (49b) can be further simplified by noting that  and
and  , yielding
, yielding

Putting everything together, (41f) becomes



where we make use of  (14a) and
(14a) and  . The latter is the velocity of the beam footprint that moves along the surface of the earth and the approximation is mainly due to the fact that the satellite orbit is only approximately circular. Therefore, the first-order coefficient of the Taylor expansion of
. The latter is the velocity of the beam footprint that moves along the surface of the earth and the approximation is mainly due to the fact that the satellite orbit is only approximately circular. Therefore, the first-order coefficient of the Taylor expansion of  evaluated at time
evaluated at time  can be written as
can be written as

Similarly, we derive the second-order coefficient of the Taylor series expansion of  by taking the time derivative of (51c), which simply yields
by taking the time derivative of (51c), which simply yields  . Therefore, the Taylor expansion of
. Therefore, the Taylor expansion of  (up to the second order) evaluated at arbitrary time
(up to the second order) evaluated at arbitrary time  can be written as
can be written as

We are now ready to generalize the moving target range equation (53) for a multichannel SAR system (i.e., with multiple phase centers)

where  ,
,  ;
;  ,
,  , and
, and  are defined for time
are defined for time  ;
;  (for equidistant phase center 1, 2, 3, etc.);
(for equidistant phase center 1, 2, 3, etc.);  depends on
depends on  and
and  in a predictable way;
in a predictable way;  ,
,  , and
, and  vary slowly with time and, therefore, may be evaluated anywhere in the neighborhood of
vary slowly with time and, therefore, may be evaluated anywhere in the neighborhood of  .
.
If we choose  to be the broadside time
to be the broadside time  , then
, then  and
and  become zero, resulting in
become zero, resulting in

where subscript "b" denotes the broadside time. In order to generate an interferogram or a SAR-DPCA image, one normally performs coregistration of channels with respect to channel 1 ( ). Therefore, the range history (55) of a coregistered channel
). Therefore, the range history (55) of a coregistered channel  becomes
becomes

where terms containing  or
or  have been neglected in the equation.
have been neglected in the equation.
When examining a target track acquired by a real-world SAR, one observes that it has breaks and missing portions [38], during which times the target fades out and appears invisible to the radar. As a result, the effective center of the track may not always correspond to the boresight (or the beam-center) time of the target. If the actual measured target track (or range history) is centered at  for
for  , where
, where  and
and  are the time offsets due to the beam squint and the target track not being effectively centered at the beam boresight, respectively, then the coregistered signals for channels 1 and
are the time offsets due to the beam squint and the target track not being effectively centered at the beam boresight, respectively, then the coregistered signals for channels 1 and  can be written, respectively, as
can be written, respectively, as


where  ,
,  (
( ) is the length of the signal, and, for simplicity,
) is the length of the signal, and, for simplicity,  is the idealized two-way antenna pattern.
is the idealized two-way antenna pattern.
The accuracy of the equations of motion derived above is validated and demonstrated in Section 6 by applying the parameter estimation algorithm, described in Section 4, to the recently acquired RADARSAT-2 MODEX data.
4. Parameter Estimation Algorithm
We describe here a target parameter estimation algorithm based on the fractional Fourier transform (FrFT) [44] and along-track interferometry (ATI) [45], also called the Fractrum Estimator, for the RADARSAT-2 imaging geometry. Equations that relate various target parameters are derived.
The FrFT, with fractional frequency variable  and rotational angle
and rotational angle  , of a signal
, of a signal  is defined as [44]
is defined as [44]

where, for  being not equal to zero or a multiple of
being not equal to zero or a multiple of  , the kernel
, the kernel  is given by
is given by

The FrFT with parameter  can be considered as a generalization of the conventional Fourier transform (FT). Thus, the FrFT for
can be considered as a generalization of the conventional Fourier transform (FT). Thus, the FrFT for  and
and  reduces to the conventional and inverse FT, respectively.
reduces to the conventional and inverse FT, respectively.
The FrFT is first applied to each detected target to focus its signals (received at different channels or subapertures) in the fractional Fourier domain. The best focus is achieved by searching for a fractional parameter  that maximizes the DPCA output of the target. Combining (18) and (57a) into (58) and integrating to maximize the target signal in the fractional Fourier domain yield
that maximizes the DPCA output of the target. Combining (18) and (57a) into (58) and integrating to maximize the target signal in the fractional Fourier domain yield




where one gathers the terms for  ,
,  , and
, and  , respectively, to yield
, respectively, to yield



where  is the wavenumber,
is the wavenumber,  is the number of processed pulses, and time scaling
is the number of processed pulses, and time scaling  has been applied. The scaling is necessary when passing from physical quantities to the normalized unitless variables used in the digital implementation of the FrFT.
has been applied. The scaling is necessary when passing from physical quantities to the normalized unitless variables used in the digital implementation of the FrFT.
The target signal amplitude is maximized in the fractional Fourier domain if  in (64c) is set equal to zero, which yields a "sinc" function in (63) and the optimum fractional angle
in (64c) is set equal to zero, which yields a "sinc" function in (63) and the optimum fractional angle  :
:

Similarly, the optimum fractional Fourier transform of the signal received at channel  can be shown to be
can be shown to be

where


Therefore, the phase of the interferogram ( ) evaluated at the optimum fractional Fourier angle
) evaluated at the optimum fractional Fourier angle  yields
yields



Equation (68c) seems to indicate that  is sensitive to both the across-track (or slant-range) speed
is sensitive to both the across-track (or slant-range) speed  and the along-track speed
and the along-track speed  . This is due to RADARSAT-2's antenna squint, which introduces the along-track velocity dependence of
. This is due to RADARSAT-2's antenna squint, which introduces the along-track velocity dependence of  in the direction of radar-to-target line of sight. The result differs from that of the nonsquint case, which depends only on the target's across-track velocity component [38]. However, from (17b) the second term inside the square bracket of (68c) is shown to be
in the direction of radar-to-target line of sight. The result differs from that of the nonsquint case, which depends only on the target's across-track velocity component [38]. However, from (17b) the second term inside the square bracket of (68c) is shown to be

which is negligible compared to the first term in (68c) for typical RADARSAT-2 imaging geometries and common ground vehicles. This important result, which differs from that of an airborne case [38], essentially decouples the parameter estimation equations, even for large  values. Therefore, the formula for estimating the target range speed
values. Therefore, the formula for estimating the target range speed  simplifies to
simplifies to

where  in (68c) can be estimated from the phase of the clutter interferogram (for any two coregistered channels) and is removed during the channel-balance processing and, therefore, dropped in (70).
in (68c) can be estimated from the phase of the clutter interferogram (for any two coregistered channels) and is removed during the channel-balance processing and, therefore, dropped in (70).
The positions of a moving target in the fractional Fourier axis for channels 1 and  can be derived by setting
can be derived by setting  (64b) and
(64b) and  (67b), respectively. That is, evaluating at the maxima of the "sinc" functions in (63) and (66) yields
(67b), respectively. That is, evaluating at the maxima of the "sinc" functions in (63) and (66) yields


The third and fourth terms in (71b) can be ignored compared to the first two terms, and  is smaller than the spatial resolution of "sinc" functions, implying spatial overlap on the fractional Fourier axis or
is smaller than the spatial resolution of "sinc" functions, implying spatial overlap on the fractional Fourier axis or  . Therefore, the target broadside azimuth position
. Therefore, the target broadside azimuth position  (=
(= ) can be obtained directly from (71a) by solving for
) can be obtained directly from (71a) by solving for  :
:

where  is the measured target position on the unitless fractional Fourier axis and
is the measured target position on the unitless fractional Fourier axis and  is obtained from the estimated
is obtained from the estimated  that best focuses the target energy in the fractional Fourier domain using (65):
that best focuses the target energy in the fractional Fourier domain using (65):

Finally, the target along-track speed is estimated from (17b):

where a nonaccelerating target is assumed (i.e.,  ). If the target is accelerating with a constant
). If the target is accelerating with a constant  , then one must use other information to decouple
, then one must use other information to decouple  and
and  contained in
contained in  . This case, however, will not be considered in this paper.
. This case, however, will not be considered in this paper.
In summary, the equations used for estimating  ,
,  , and
, and  are
are

where

 satellite effective speed, calculated from satellite state vectors,
satellite effective speed, calculated from satellite state vectors,  satellite velocity in ECEF frame,
satellite velocity in ECEF frame,  distance from radar to detected target when it is at radar broadside,
distance from radar to detected target when it is at radar broadside,  interferometric phase of coregistered channels (1 and
interferometric phase of coregistered channels (1 and  ) focused via FrFT,
) focused via FrFT,  channel number,
channel number,  wavenumber,
wavenumber,  distance between two effective phase centers,
distance between two effective phase centers,  position of focused target on fractional Fourier axis,
position of focused target on fractional Fourier axis,  azimuth sampling or pulse repetition frequency,
azimuth sampling or pulse repetition frequency,  target signal length or the number of azimuth pulses,
target signal length or the number of azimuth pulses,  fractional angle or parameter used to best focus the target,
fractional angle or parameter used to best focus the target,  target's estimated azimuth speed,
target's estimated azimuth speed,  target's estimated slant-range speed, and
target's estimated slant-range speed, and  target's estimated broadside time.
target's estimated broadside time.
The FrFT-ATI parameter estimation algorithm (or the Fractrum Estimator) can be summarized as consisting of the following nine steps
-
(1)
after detection, extract moving target signals from range-compressed, azimuth-uncompressed raw data for channels 1 and
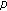 ;
; -
(2)
apply DPCA processing on the signals;
-
(3)
find fractional parameter
 that best focuses the DPCA image of the moving target;
that best focuses the DPCA image of the moving target; -
(4)
measure target position
 on the fractional Fourier axis;
on the fractional Fourier axis; -
(5)
using the optimum
 value, calculate
value, calculate 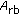 ;
; -
(6)
form an interferogram from the FrFT focused signals of the two coregistered channels;
-
(7)
measure the interferometric phase
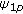 ;
; -
(8)
solve (75) for
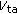 ,
, 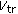 , and
, and  using
using  ,
, 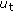 ,
, 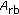 , and
, and 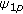 ;
; -
(9)
then
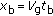 , where
, where  is the target's broadside azimuth position.
is the target's broadside azimuth position.
5. Interferometric Phase Properties in the Presence of Clutter
As one of the key steps in the described Fractrum Algorithm, the extraction of the interferometric phase  has a strong impact on the estimation accuracy of target's range speed and broadside time. In a dual-aperture configuration, in particular,
has a strong impact on the estimation accuracy of target's range speed and broadside time. In a dual-aperture configuration, in particular,  is inevitably affected by clutter. At positions
is inevitably affected by clutter. At positions  in the fractional Fourier domain, the focused moving target signature is superimposed on the signature of a stationary background target acquired at a different time, namely,
in the fractional Fourier domain, the focused moving target signature is superimposed on the signature of a stationary background target acquired at a different time, namely,  later than the moving target. Since the returns of the two targets partially overlap in the time domain, the
later than the moving target. Since the returns of the two targets partially overlap in the time domain, the  samples processed by the FrFT include, at least partially, the interfering stationary clutter. The interferogram is formed between the resulting superimposed samples in the two coregistered channels that can be modelled as
samples processed by the FrFT include, at least partially, the interfering stationary clutter. The interferogram is formed between the resulting superimposed samples in the two coregistered channels that can be modelled as

where  and
and  are the complex samples from the same location in the two channels,
are the complex samples from the same location in the two channels,  and
and  are the sample amplitudes,
are the sample amplitudes,  and
and  are the corresponding phases,
are the corresponding phases,  and
and  represent the amplitudes of the clutter and target component, respectively,
represent the amplitudes of the clutter and target component, respectively,  is the phase of the clutter sample,
is the phase of the clutter sample,  is the common-mode phase of the target sample,
is the common-mode phase of the target sample,  is the channel-to-channel phase difference of the target sample, which is proportional to the target radial speed
is the channel-to-channel phase difference of the target sample, which is proportional to the target radial speed  , and
, and  and
and  represent two statistically independent noise processes. In this section, we will discuss some properties of the resulting interferometric phase.
represent two statistically independent noise processes. In this section, we will discuss some properties of the resulting interferometric phase.
Ignoring the system noise,  and
and  , and focusing on the clutter-dominated case, the interferogram can be represented as
, and focusing on the clutter-dominated case, the interferogram can be represented as

where " " denotes complex conjugate, and the interferometric phase is
" denotes complex conjugate, and the interferometric phase is

In this model, both the target and the clutter portion are assumed to be fully coherent because temporal decorrelation is negligible for short ATI baselines and the cross-track baseline has been compensated.
Since  is used as an estimate of
is used as an estimate of  , the first property that is examined is the bias.
, the first property that is examined is the bias.
In (78),  is the relative phase of the background clutter at the apparent position of the target. It is reasonable to assume that the probability density function (pdf) of the relative clutter phase,
is the relative phase of the background clutter at the apparent position of the target. It is reasonable to assume that the probability density function (pdf) of the relative clutter phase,  , is uniform and independent of the clutter amplitude pdf,
, is uniform and independent of the clutter amplitude pdf,  , which may be unknown. It can now be shown that the conditional expectation
, which may be unknown. It can now be shown that the conditional expectation

where  .
.
It is sufficient to consider only positive radial speeds, that is,  . Similar argumentation applies to the case of negative radial speeds. To prove (80), components of
. Similar argumentation applies to the case of negative radial speeds. To prove (80), components of  and
and  are shown as phasors in the complex plane in Figure 5.
are shown as phasors in the complex plane in Figure 5.
The case of  is obvious from Figure 5(a), which shows a simplified phasor diagram of
is obvious from Figure 5(a), which shows a simplified phasor diagram of  in the absence of noise, with
in the absence of noise, with  chosen without loss of generality. Under the assumption of uniform
chosen without loss of generality. Under the assumption of uniform  , clutter phase
, clutter phase  (shown by a solid red line) is equally probable as
(shown by a solid red line) is equally probable as  (indicated by a dotted black line). It is easy to show that these two equally probable clutter realizations cause opposite offsets,
(indicated by a dotted black line). It is easy to show that these two equally probable clutter realizations cause opposite offsets,  , of
, of  about
about  (represented by a solid and a dotted line). Clutter also induces an offset in
(represented by a solid and a dotted line). Clutter also induces an offset in  relative to
relative to  . Similarly, this offset has a zero average because clutter phase
. Similarly, this offset has a zero average because clutter phase  and
and  have equal probability. In the case shown in Figure 5(a),
have equal probability. In the case shown in Figure 5(a),  for all
for all  , that is,
, that is,  is unambiguous and its mean is equal to the sum of the means of
is unambiguous and its mean is equal to the sum of the means of  and
and  , which is
, which is  .
.
The case of  can be represented by a phasor of
can be represented by a phasor of  assuming, without loss of generality, that
assuming, without loss of generality, that  , while
, while  is uniformly distributed. As shown in Figure 5(b), now the mover causes
is uniformly distributed. As shown in Figure 5(b), now the mover causes  (and, similarly,
(and, similarly,  ) to have an offset,
) to have an offset,  , from 0, where
, from 0, where  for all
for all  . Considering that
. Considering that  and
and  are equally probable, as are
are equally probable, as are  and
and  , and applying the same reasoning as above, both
, and applying the same reasoning as above, both  and
and  are found to have a zero mean and so does
are found to have a zero mean and so does  .
.
The special case  is interesting. It can be shown that for this case
is interesting. It can be shown that for this case

which produces a zero phase on the average.
Unlike all of the above cases, if  , neither clutter nor the mover is prevalent. There are some values of
, neither clutter nor the mover is prevalent. There are some values of  for which
for which  , thus mapping
, thus mapping  to a negative value when
to a negative value when  . In this case, the conditional expectation of the ATI phase depends on the resolution of the
. In this case, the conditional expectation of the ATI phase depends on the resolution of the  ambiguity in the implemented ATI algorithm and in (78). The equality
ambiguity in the implemented ATI algorithm and in (78). The equality  is valid only if the ATI phase is not restricted to the
is valid only if the ATI phase is not restricted to the  interval and if a suitable ambiguity resolution is applied (e.g., using a priori information or Doppler offsets).
interval and if a suitable ambiguity resolution is applied (e.g., using a priori information or Doppler offsets).
Averaging (80) over  , one finds the expectation of
, one finds the expectation of 


where 
 depends on the ambiguity resolution policy and is bound on both sides by the probability
depends on the ambiguity resolution policy and is bound on both sides by the probability  that
that  lies below a certain value. This result is obtained without presuming any particular pdf for
lies below a certain value. This result is obtained without presuming any particular pdf for  . As expected,
. As expected,  is a biased estimate of
is a biased estimate of  . According to (82b), bias
. According to (82b), bias  is proportional to
is proportional to  , that is, to the probability that
, that is, to the probability that  exceeds a certain threshold. Thus, bias is more pronounced for long-tailed
exceeds a certain threshold. Thus, bias is more pronounced for long-tailed  . Bias is also proportional to
. Bias is also proportional to  ; it is larger for faster moving targets, assuming invariant clutter pdf and signal-to-clutter ratio. The assumption of invariant signal to clutter ratio is true if
; it is larger for faster moving targets, assuming invariant clutter pdf and signal-to-clutter ratio. The assumption of invariant signal to clutter ratio is true if  samples extracted for FrFT processing include the interfering clutter echoes completely. However, as the temporal overlap between the interfering clutter and the moving target decreases in the time domain with increasing
samples extracted for FrFT processing include the interfering clutter echoes completely. However, as the temporal overlap between the interfering clutter and the moving target decreases in the time domain with increasing  of the target, there is, in principle, a possibility to cut out a portion of the interfering clutter returns, thus improving the signal to clutter ratio. This option is of limited benefit in practice (as a consequence of a typically narrow exoclutter zone and the initial uncertainty about the actual target's broadside time
of the target, there is, in principle, a possibility to cut out a portion of the interfering clutter returns, thus improving the signal to clutter ratio. This option is of limited benefit in practice (as a consequence of a typically narrow exoclutter zone and the initial uncertainty about the actual target's broadside time  ).
).
The next property that will be examined is the interval  , where
, where  is the maximum and
is the maximum and  is the minimum interferometric phases attainable for a given ratio
is the minimum interferometric phases attainable for a given ratio  , a given
, a given  , and a variable relative phase
, and a variable relative phase  . Using geometry, it can be readily seen that
. Using geometry, it can be readily seen that  is reached for
is reached for  , while
, while  is reached for
is reached for  . We will consider only the case of
. We will consider only the case of  , illustrated in Figure 6. Other cases can be analysed easily, but they are of little practical interest. From Figure 6, we note that
, illustrated in Figure 6. Other cases can be analysed easily, but they are of little practical interest. From Figure 6, we note that

By applying the well-known formula  , it is easy to show that
, it is easy to show that

which is a monotonically increasing function of both  and
and  (on the interval of unambiguous interferometric phases). Therefore, under equal signal-to-noise conditions, we can expect a larger interval of variation of the interferometric phase
(on the interval of unambiguous interferometric phases). Therefore, under equal signal-to-noise conditions, we can expect a larger interval of variation of the interferometric phase  around the ideal value
around the ideal value  for faster targets than for slower targets. From (84), it is also clear that suppression of the interfering clutter plays an important role, especially when dealing with faster targets.
for faster targets than for slower targets. From (84), it is also clear that suppression of the interfering clutter plays an important role, especially when dealing with faster targets.
The analysis also implies that this dependence on  may be mitigated or minimized by canceling the clutter prior to forming the interferogram
may be mitigated or minimized by canceling the clutter prior to forming the interferogram  , using the sub-aperture toggling (or switching) techniques as described in Section 2. An excellent theoretical review of various receiver and transmitter switching strategies is provided in [33]. If clutter is successfully suppressed, the interferometric system becomes noise limited in terms of ATI phase variance.
, using the sub-aperture toggling (or switching) techniques as described in Section 2. An excellent theoretical review of various receiver and transmitter switching strategies is provided in [33]. If clutter is successfully suppressed, the interferometric system becomes noise limited in terms of ATI phase variance.
6. MODEX Results
First, we carry out simulations of a deterministic target moving in Gaussian clutter for various SCR (Signal-to-Clutter Ratio) scenarios. The standard dual-receive mode (or MODEX-1) of Figure 1(a) is simulated and the target's range speed statistics are computed from (70). Figure 7 plots the results, which indicate that the range speed estimate improves with increasing SCR, as expected. The results also show that the standard deviation ( ) of the estimate of the range speed, indicated by the length of the error bars, increases with increasing target range speed
) of the estimate of the range speed, indicated by the length of the error bars, increases with increasing target range speed  . This effect was clearly observed from recently collected RADARSAT-2 data (in the MODEX-1 configuration) of the Trenton (Ontario) area. Two trains (moving in opposite direction and at different speeds) and many targets on the MacDonald Cartier Freeway are detected in the scene as shown in Figure 8, where green markers represent the receding targets and red markers are the approaching ones. The movers are detected using the Histogram Along-Track Interferometry (HATI) Detector [25] and their position and velocity vectors are estimated using the Fractrum Estimator, as described in Section 4. The estimated range speeds with the corresponding standard deviations for trains 1 and 2 are
. This effect was clearly observed from recently collected RADARSAT-2 data (in the MODEX-1 configuration) of the Trenton (Ontario) area. Two trains (moving in opposite direction and at different speeds) and many targets on the MacDonald Cartier Freeway are detected in the scene as shown in Figure 8, where green markers represent the receding targets and red markers are the approaching ones. The movers are detected using the Histogram Along-Track Interferometry (HATI) Detector [25] and their position and velocity vectors are estimated using the Fractrum Estimator, as described in Section 4. The estimated range speeds with the corresponding standard deviations for trains 1 and 2 are  m/s and
m/s and  m/s, respectively. These estimates are consistent with the true range speeds of the two trains (
m/s, respectively. These estimates are consistent with the true range speeds of the two trains ( 3.08 and 12.20 m/s for trains 1 and 2, resp.), which can be accurately inferred from the positions of the railway tracks in the SAR image. It is noted that the standard deviation of the estimated range speed of the fast train is about three times larger than that of the slow train. This effect is somewhat counter intuitive, since the ease of target detection usually improves with increasing
3.08 and 12.20 m/s for trains 1 and 2, resp.), which can be accurately inferred from the positions of the railway tracks in the SAR image. It is noted that the standard deviation of the estimated range speed of the fast train is about three times larger than that of the slow train. This effect is somewhat counter intuitive, since the ease of target detection usually improves with increasing  . However, this phenomenon can be understood by the simple phasor analysis presented in the previous section. It is also in agreement with the theoretical bounds derived in [33], keeping in mind the actual conditions and physical limitations of our data sets (such as typically moderate vehicle speeds, relatively tight PRF sampling).
. However, this phenomenon can be understood by the simple phasor analysis presented in the previous section. It is also in agreement with the theoretical bounds derived in [33], keeping in mind the actual conditions and physical limitations of our data sets (such as typically moderate vehicle speeds, relatively tight PRF sampling).
We show in Figure 9 the results of a MODEX experiment in the Ottawa (Ontario) area, where azimuth-shifted moving targets are detected using the HATI detector. The MODEX-2 mode used in this experiment is a 3/4-aperture toggled-Tx configuration as depicted in Figure 1(c), where pulses are transmitted alternately with the first and the last three quarters of the aperture and the echoes are received simultaneously with two half subapertures. The effective distance (or baseline) between the four phase centers is 1.875 m. Figure 9(a) shows the estimation results of azimuth positioning of the detected targets with clutter cancellation prior to forming the interferogram. All channels are spatially coregistered with respect to channel 1 prior to DPCA and ATI operations. The clutter suppression is first accomplished via the DPCA subtraction of channel 1 with channel 3 ( ) and of channel 2 with channel 4 (
) and of channel 2 with channel 4 ( ). The resulting interferogram becomes
). The resulting interferogram becomes  , where subscript "t" signifies target without clutter.
, where subscript "t" signifies target without clutter.
The estimation performance of the MODEX-2 mode (Figure 9(b)) is perceptibly better than that without the clutter cancellation (Figure 9(a)), where only two channels are used to form the interferogram and the estimated target azimuth positions exhibit a noticeably larger standard deviation than that of Figure 9(b). The effectiveness of clutter cancellation may be further appreciated when one examines the interferograms of a detected target (target ID: T1093) in the scene for cases with (Figure 10(b)) and without (Figure 10(a)) the DPCA clutter cancellation prior to forming the interferogram. The interferogram with clutter cancellation shows a well defined (localized) phase, whereas the interferogram without the prior clutter cancellation displays a phase spread and a small bias. As the target must move on a road, its true azimuth position (thus, its true interferometric phase and range speed) can be inferred from Hwy 417, which is the main road going through the scene center in Figure 9. The inferred true range speed of the target is, therefore, 17.84 m/s and its true interferometric phase is  for the 1.875 m baseline or
for the 1.875 m baseline or  for the 3.75 m baseline. The MODEX-2 estimation of the target's range speed is
for the 3.75 m baseline. The MODEX-2 estimation of the target's range speed is  m/s compared to
m/s compared to  m/s for the two-channel case (without the clutter cancellation). The target's estimated azimuth position (in pulse number) is
m/s for the two-channel case (without the clutter cancellation). The target's estimated azimuth position (in pulse number) is  for the MODEX-2 mode and
for the MODEX-2 mode and  for the two-channel case, and the inferred true azimuth position is 1852. The conversion factor from pulse number to azimuth distance is 3.5346 [m/pulse], which translates to standard deviations of the estimated azimuth positions of 7 m and 233 m for the MODEX-2 mode and for the two-channel case, respectively.
for the two-channel case, and the inferred true azimuth position is 1852. The conversion factor from pulse number to azimuth distance is 3.5346 [m/pulse], which translates to standard deviations of the estimated azimuth positions of 7 m and 233 m for the MODEX-2 mode and for the two-channel case, respectively.
Comparison of (a) the clutter-contaminated interferogram (from channels 1 and 3) and (b) the clutter-canceled interferogram for a detected target ("T1093") from Figure 9. The baseline between channels 1 and 3 is 3.75 m, twice that of the MODEX-2 mode; therefore, the phase of (a) is roughly twice that of (b).
For the along-track speed estimation, the two trains detected in the Trenton area (Figure 8) have the along-track speed estimates of  m/s and
m/s and  m/s for train 1 and train 2, respectively. Based on the geometry of the railway track with respect to the radar, the inferred true range speeds of
m/s for train 1 and train 2, respectively. Based on the geometry of the railway track with respect to the radar, the inferred true range speeds of  3.08 m/s and 12.20 m/s would translate to along-track speeds of
3.08 m/s and 12.20 m/s would translate to along-track speeds of  1.09 m/s and 9.15 m/s, respectively, which are consistent with our estimated values. Also, we have observed significantly greater spreads (
1.09 m/s and 9.15 m/s, respectively, which are consistent with our estimated values. Also, we have observed significantly greater spreads ( ) in
) in  measurements than in
measurements than in  estimates. Typically,
estimates. Typically,  is two to seven times larger than
is two to seven times larger than  , depending on the range speed of the target. This is expected since the along-track speed is estimated from the slope of the target Doppler history or the Doppler rate, which is directly proportional to
, depending on the range speed of the target. This is expected since the along-track speed is estimated from the slope of the target Doppler history or the Doppler rate, which is directly proportional to  , and
, and  is in turn dominated by the large satellite effective velocity
is in turn dominated by the large satellite effective velocity  . Therefore, the target Doppler rate is expected to be not very sensitive to
. Therefore, the target Doppler rate is expected to be not very sensitive to  . It is further noted that while the variance of the estimated range speed is a function of both the range speed and the SCR, the variance of the estimated along-track speed does not appear to be sensitive to the target range speed.
. It is further noted that while the variance of the estimated range speed is a function of both the range speed and the SCR, the variance of the estimated along-track speed does not appear to be sensitive to the target range speed.
7. Conclusions
This paper first describes the various MODEX modes that were evaluated to date and shows that very high channel correlations ( 0.96) can be achieved by compensating for subbeam pointing errors and by operating the radar at near the DPCA condition. A set of equations of motion that accurately describes a ground moving target in spaceborne multichannel SAR imaging geometry is derived in the ECEF frame of reference using linearization for small angles as a function of the receive phase center. Using these equations of motion, a moving target parameter estimation algorithms is developed. A simple phasor analysis is used to describe the target-clutter interaction. The accuracy of the equations of motion, the effectiveness of the parameter estimation algorithm and the benefits of the advanced antenna configurations have been tested and demonstrated using recently acquired RADARSAT-2 MODEX data.
0.96) can be achieved by compensating for subbeam pointing errors and by operating the radar at near the DPCA condition. A set of equations of motion that accurately describes a ground moving target in spaceborne multichannel SAR imaging geometry is derived in the ECEF frame of reference using linearization for small angles as a function of the receive phase center. Using these equations of motion, a moving target parameter estimation algorithms is developed. A simple phasor analysis is used to describe the target-clutter interaction. The accuracy of the equations of motion, the effectiveness of the parameter estimation algorithm and the benefits of the advanced antenna configurations have been tested and demonstrated using recently acquired RADARSAT-2 MODEX data.
References
Stockburger EF, Held DN: Interferometric moving ground target imaging. Proceedings of the IEEE International Radar Conference, May 1995, Alexandria, Va, USA 438-443.
Chiu S, Gierull CH, Durak A: Clutter effects on ground moving targets' interferometric phase. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS '05), July 2005 4: 2928-2931.
Ender JHG, Cerutti-Maori D, Bürger W: Radar antenna architectures and sampling strategies for space based moving target recognition. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '05), July 2005 4: 2921-2924.
Ender JHG: Detectability of slowly moving targets using a multi channel SAR with an along track antenna array. Proceedings of the SEE/IEE Conference (SAR '93), 1993
Chiu S: Performance analysis of RADARSAT-2 multi-channel MODEX modes. Proceedings of the 4th European Radar Conference (EuRAD '07), October 2007, Munich, Germany 170-173.
Gart JH: Electronics and aerospace industry in cold war arizona,1945–1968: Motorola, Hughes Aircraft, Ph.D. thesis. Arizona State University, Tempe, Ariz, USA; 2006.
Cutrona LJ, Vivian WE, Leith EN, Hall GO: A high resolution radar combat-surveillance system. IRE Transactions on Military Electronics 1961, 6: 119-133.
Raney RK: Synthetic aperture imaging radar and moving targets. IEEE Transactions on Aerospace and Electronic Systems 1971, 7(3):499-505.
Meyer F, Hinz S, Laika A, Weihing D, Bamler R: Performance analysis of the TerraSAR-X traffic monitoring concept. Journal of Photogrammetry and Remote Sensing 2006, 61(3-4):225-242. 10.1016/j.isprsjprs.2006.08.002
Dragošević MV, Vachon PW: Estimation of ship radial speed by adaptive processing of RADARSAT-1 fine mode data. IEEE Geoscience and Remote Sensing Letters 2008, 5(4):678-682.
Lombardo P: A multichannel spaceborne radar for the COSMO-Skymed satellite constellation. Proceedings of the IEEE Aerospace Conference Proceedings, March 2004, Big Sky, Mont, USA 1: 111-119.
Chiu S, Livingstone C, Sikaneta I, Gierull C, Beaulne P: RADARSAT-2 moving object detection experiment (MODEX). Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '08), July 2008, Boston, Mass, USA 1(1):I13-I16.
Dragošević MV, Chiu S: Space-based motion estimators—evaluation with the first RADARSAT-2 MODEX data. IEEE Geoscience and Remote Sensing Letters 2009, 6(3):438-442.
Chiu S, Dragošević MV: Velocity estimation with RADARSAT-2 moving object detection experiment mode. Proceedings of the International Conference on Space Technology (ICST '09), August 2009, Thessaloniki, Greece
Chiu S, Beaulne P, Livingstone C, Sikaneta I: Spaceborne SAR-MTI experiments with Canadian RADARSAT-2. Proceedings of the International Radar Symposium (IRS '09), 2009, Hamburg, Germany
Weihing D, Suchandt S, Hinz S, Runge H, Bamler R: Traffic parameter estimation using TerraSAR-X data. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2008, 37: 153-156.
Palubinskas G, Runge H: Change detection for traffic monitoring in TerraSAR-X imagery. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '08), July 2008 1(1):I169-I172.
Hinz S, Weihing D, Suchandt S, Bamler R: Detection and velocity estimation of moving vehicles in high-resolution spaceborne synthetic aperture radar data. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPR '08), June 2008 1-8.
Dragosevic MV, Livingstone C: Demonstration of RADARSAT-2 moving object detection experiment (MODEX) capabilities for maritime surveillance. International Radar Symposium (IRS '09), September 2009, Hamburg, Germany
Cristallini D, Colone F, Pastina D, Lombardo P: STAP versus ATI for detection of moving target with along-track velocity in M-SAR images. Proceedings of the International Radar Symposium (IRS '09), 2009, Hamburg, Germany
Farina A: STAP for SAR. In Military Application of Space-Time Adaptive Processing, RTO SET Lecture Series. NATO Research and Technology Organization; 2003.
Budillon A, Pascazio V, Schirinzi G: Multichannel along-track interferometric SAR systems: moving tagets detection and velocity estimation. International Journal of Navigation and Observation 2008, 2008:-16.
Chen CW: Performance assessment of along-track interferometry for detecting ground moving targets. Proceedings of the IEEE National Radar Conference, April 2004, Philadelphia, Pa, USA 99-104.
Hinz S, Meyer F, Eineder M, Bamler R: Traffic monitoring with spaceborne SAR—theory, simulations, and experiments. Computer Vision and Image Understanding 2007, 106(2-3):231-244. 10.1016/j.cviu.2006.09.008
Chiu S: A constant false alarm rate (CFAR) detector for RADARSAT-2 along-track interferometry. Canadian Journal of Remote Sensing 2005, 31(1):73-84. 10.5589/m04-057
Ender JHG: Space-time processing for multichannel synthetic aperture radar. Electronics & Communication Engineering Journal 1999, 11(1):29-38. 10.1049/ecej:19990106
Farina A, Lombardo P: Space-time techniques for SAR—part I. In Applications of Space-Time Adaptive Processing. Edited by: Klemm R. IEE Publisher, London, UK; 2004:73-120.
Wei J, Yuan Y, Sun J, Liu S, Mao S: A new multi-channel SAR-GMTI algorithm based on frequency STAP and FrFT. The 2nd International Conference on Space Information Technology, November 2007, Wuhan, China, Proceedings of SPIE 6795:
Gierull CH, Sikaneta I: Ground moving target parameter estimation for two-channel SAR. Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR '04), May 2004, Ulm, Germany 799-802.
Cerutti-Maori D, Bürger W, Ender JHG: Experimental results of ground moving target detection achieved with the multi-channel SAR/MTI system PAMIR. Journal of the European Microwave Association 2006, 2: 122-127.
Cerutti-Maori D, Klare J, Brenner AR, Ender JHG: Wide-area traffic monitoring with the SAR/GMTI system PAMIR. IEEE Transactions on Geoscience and Remote Sensing 2008, 46(10):3019-3030.
Ender JHG, Gierull CH, Cerutti-Maori D: Spaced-based moving target positioning using radar with a switched aperture antenna. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '07), July 2007, Barcelona, Spain 101-106.
Ender JHG, Gierull CH, Cerutti-Maori D: Improved space-based moving target indication via alternate transmission and receiver switching. IEEE Transactions on Geoscience and Remote Sensing 2008, 46(12):3960-3974.
Uher J, Grenier C, Lefebvre G: RADARSAT-2 SAR antenna. Canadian Journal of Remote Sensing 2004, 30(3):287-294. 10.5589/m04-009
Fox PA, Luscombe AP, Thompson AA: RADARSAT-2 SAR modes development and utilization. Canadian Journal of Remote Sensing 2004, 30(3):258-264. 10.5589/m04-014
Cerutti-Maori D, Sikaneta IC: System-dependent decorrelation sources in multi-channel SAR-GMTI and their impact on DPCA. Proceedings of the International Radar Conference, October 2009, Bordeaux, France
Bamler R, Hanssen R: Decorellation induced by interpolation errors in InSAR processing. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS '97), August 1997, Singapore 4: 1710-1712.
Chiu S: Application of fractional Fourier transform to moving target indication via along-track interferometry. EURASIP Journal on Applied Signal Processing 2005, 2005(20):3293-3303. 10.1155/ASP.2005.3293
Eldhuset K: A new fourth-order processing algorithm for spaceborne SAR. IEEE Transactions on Aerospace and Electronic Systems 1998, 34(3):824-835. 10.1109/7.705890
Curlander JC, McDonough RN: Synthetic Aperture Radar. John Wiley & Sons, New York, NY, USA; 1991.
Meyer F, Hinz S: The feasibility of traffic monitoring with TerraSAR-X—analyses and consequences. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '04), September 2004 2: 1502-1505.
Cumming IG, Wong FH: Digital Processing of Synthetic Aperture Radar Data. Artech House, Boston, Mass, USA; 2005.
Dragošević MV, Plache B: Doppler tracker for a spaceborne ScanSAR system. IEEE Transactions on Aerospace and Electronic Systems 2000, 36(3, part 1):907-924. 10.1109/7.869510
Almeida LB: The fractional Fourier transform and time-frequency representations. IEEE Transactions on Signal Processing 1994, 42(11):3084-3091. 10.1109/78.330368
Livingstone CE, Sikaneta I, Gierull CH, et al.: An airborne synthetic aperture radar (SAR) experiment to support RADARSAT-2 ground moving target indication (GMTI). Canadian Journal of Remote Sensing 2002, 28(6):794-813. 10.5589/m02-074
Acknowledgments
The authors are grateful to the RADARSAT-2 GMTI team for their support in the experiments. Special thanks go to Dr. Ishuwa Sikaneta who provided us with MATLAB routines to generate antenna patterns and channel correlation plots. They also would like to thank their visiting scientists Dr. Delphine Cerutti-Maori of German FGAN-FHR, who performed theoretical analyses on the MODEX system and led the entire benchmark experimental campaign and Mr. Thomas Jensen of German MOD for supporting all our MODEX trials.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chiu, S., Dragošević, M.V. Moving Target Indication via RADARSAT-2 Multichannel Synthetic Aperture Radar Processing. EURASIP J. Adv. Signal Process. 2010, 740130 (2009). https://doi.org/10.1155/2010/740130
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/740130




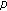 ;
; that best focuses the DPCA image of the moving target;
that best focuses the DPCA image of the moving target; on the fractional Fourier axis;
on the fractional Fourier axis; value, calculate
value, calculate 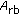 ;
;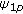 ;
;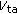 ,
, 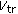 , and
, and  using
using  ,
, 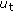 ,
, 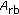 , and
, and 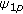 ;
;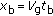 , where
, where  is the target's broadside azimuth position.
is the target's broadside azimuth position.
 . Solid lines correspond to one given
. Solid lines correspond to one given  value, while dotted lines represent the case of an alternative, equally probable,
value, while dotted lines represent the case of an alternative, equally probable, 


 , the maximum phase
, the maximum phase  (solid lines), and the minimum phase
(solid lines), and the minimum phase  (dotted lines) for given S and C.
(dotted lines) for given S and C.
 m/s.
m/s.

 estimation, with (b) and Without (a) clutter cancellation before forming the interferogram.
estimation, with (b) and Without (a) clutter cancellation before forming the interferogram.
