- Research Article
- Open access
- Published:
Pilot-Based Synchronization and Equalization in Filter Bank Multicarrier Communications
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 741429 (2010)
Abstract
This paper presents a detailed analysis of synchronization methods based on scattered pilots for filter bank based multicarrier (FBMC) communications, taking into account the interplay of the synchronization, channel estimation, and equalization methods. We show that by applying pilots designed specifically for filter banks, the carrier frequency offset (CFO), fractional time delay (FTD), and channel response can be accurately estimated. Further, a novel joint FTD and channel estimation scheme, based on iterative interference cancelation, permits extending the FTD estimation range well beyond the limit imposed by the pilot separation. The channel parameter estimation and compensation are successfully performed totally in the frequency domain, in a subchannel-wise fashion, which is appealing in spectrally agile and cognitive radio scenarios. The performance evaluation is done in a hypothetical WiMAX scenario in which an FBMC system would substitute OFDM maintaining as much physical layer compatibility as possible.
1. Introduction
Research on increasing data transmission rates and the development of applications exploiting these improved rates, or requiring even more bandwidth, have been fueling each other for decades already, and it seems that this trend will continue. The challenge is therefore to boost high data rates in wireless communications.
Multicarrier (MC) techniques have proven to be a means to adequately overcome many challenges of wide bandwidth transmission while providing also high spectral efficiency. Using MC communications, a frequency selective channel can be divided into several parallel subchannels with flat or mildly selective fading, facilitating channel estimation and equalization (the terms "subchannel", "subband" and "subcarrier" are used interchangeably throughout the whole text, referring to the frequency subband centered at the subcarrier frequency). Timing synchronization is also easier and limited narrowband interference can be easily mitigated. In fact, the division of the whole bandwidth into many subchannels provides scalability and flexibility when configuring the communication link [1].
The flagship of MC techniques is orthogonal frequency division multiplexing (OFDM) with cyclic prefix (CP) [1]. A correctly chosen CP elegantly turns severely frequency selective channels into flat fading ones at subcarrier level, enabling very simple subcarrier-wise equalization (one complex coefficient per subcarrier). OFDM has become the MC technique of choice in a number of communication systems, including emerging cellular standards such as WiMAX [2] (based on the IEEE 802.16e [3] standard) and E-UTRA LTE (Evolved UMTS Terrestrial Radio Access Long Term Evolution) [4]. These two exploit the flexibility of OFDM to also provide multiple access in time and frequency through orthogonal frequency division multiple access (OFDMA).
Filter bank based multicarrier (FBMC) modulation can be considered an evolved OFDM due to the advantages it presents and also because it can easily be implemented building on the core blocks of OFDM, that is, the IFFT/FFT pair [5]. The filter banks (FBs) display the following two highly desirable properties. Firstly, their subchannels can be optimally designed in the frequency domain to have desired spectral containment [6]. Secondly, FBMC systems do not make use of the CP, which is pure redundancy, enabling a more efficient use of channel resources. Basically, the subchannel filters are designed with the Nyquist pulse shaping principle, which means that the consecutive symbol waveforms are overlapping in time. Compared to OFDM, where the adjacent subbands are only attenuated 13 dB, the excellent spectral containment allowed by the FBs is crucial for avoiding distortion from asynchronous signals in adjacent bands. Further savings in spectral resources appear at the edges of the transmission band, where ideally only one subchannel can be used as guard band to the next transmission band. An OFDM system with slowly decaying sidelobes would need more subbands or very sharp additional filtering to provide similar attenuation outside the transmission band. In the context of cognitive radio [7, 8], where a secondary user scans the spectrum assigned to primary users for a transmission opportunity (spectral sensing), the high spectral definition of FBMC is especially valuable. The performance of Haykin's method of choice for radio scene analysis, the multitaper method [9], can be well approximated using FBs with greatly reduced complexity [10].
In order to synchronize and equalize the channel, there are methods to perform timing, frequency offset and channel estimation. In the MC context, timing estimation involves locating the start of a transmission burst, finding the first multicarrier symbol, and estimating the fractional time delay (FTD), which is a fraction of the multicarrier symbol period. Since OFDM is the most widespread MC technique, many methods for synchronization and channel estimation can be found for it. They are based on scattered pilots and training sequences [11, 12], on exploiting the redundancy of the CP [13] or even blind methods that do not make use of overheads in the signal [12].
Due to the different nature of the FB waveforms, some of the OFDM methods can be applied to FBMC and others, such as the CP-based ones, cannot. Although there exist preamble based [14], training sequence based [15] and blind [16] approaches, we focus our interest here towards scattered-pilot-based approaches. However, when using efficient filter bank implementations, as for example the FBMC/OQAM (offset quadrature amplitude modulation) [5], the application of scattered pilots is not as straightforward as in OFDM due to the complementary interference that a low-rate symbol suffers from adjacent symbols in time and frequency. This has motivated different proposals for generating pilots [17, 18] compatible with the filter bank class of interest. In this paper, we build our synchronization and channel estimation subsystem based on pilots and auxiliary pilots [19] similarly to [18] because of good estimation performance.
Here it is interesting to mention that the authors of [20] also present an approach to perform full synchronization in both FBMC/OQAM and OFDM/QAM systems based on scattered pilots. However, in that publication the time domain properties of the regularly scattered pilots are exploited and synchronization takes place in the time domain instead of subcarrier-wise, as is our goal in this paper. Both approaches complement each other and could be used together, for example, for performing coarse acquisition and fine tuning or to improve their respective performances.
In order to obtain results of practical relevance, we develop a testbed system that aims to maintain a certain resemblance and even compatibility up to a degree with the WiMAX profile. Also the channel model and distortion parameters are chosen to be typical of WiMAX communications. We use rather basic synchronization parameter estimation, and compensation methods, many of which are known from the literature in the OFDM context, and adapt them to the FBMC/OQAM system model. Our focus is on understanding the interplay of different synchronization and channel equalization functions. We also explore the possibilities to enhance the overall performance by iterating the estimation and compensation tasks. It is important to underline, that all the necessary synchronization, channel estimation and equalization operations take place after the analysis bank at the receiver, at the low sampling rate. This makes it possible to utilize the filter bank itself for efficient implementation of the needed frequency channelization selectivity for all signal processing functions. Further, the channelization can be done in a dynamically adjustable manner, efficiently suppressing immediately adjacent and even (narrow) in-band interference components.
The paper is structured as follows: first, we review the concept of efficient filter bank based multicarrier communications. In Section 2, we describe how to implement the filter banks and perform efficient subchannel-wise equalization. In Section 3, we first discuss the synchronization requirements in spectrally agile radios. Then we present the method for obtaining pilots for FBMC/OQAM and study the effect of the channel distortions on these pilots. In the end of this section, we present solutions for correcting the distortions, including a novel, iterative interference canceling, joint FTD, and channel estimating algorithm. In Section 4, we introduce the design of the WiMAX-like simulation testbed based on FBMC. Section 5 presents the estimation and correction performance of the studied methods. Finally, Section 6 draws the conclusions from this research.
2. FBMC and Efficient Subchannel-Wise Equalization
2.1. Filter Bank Based Multicarrier Communications
Exponentially modulated filter banks (EMFB) [21], modified DFT (MDFT) filter banks [22], and OFDM with offset QAM (OFDM/OQAM or FBMC/OQAM) [5], among others, are complex filter bank structures that can produce complex I/Q baseband signals for transmission, making them suitable for FBMC systems in spectrally efficient radio communications. In FBMC communications, the filter banks are used in the transmultiplexer (TMUX) configuration [23], with the synthesis filter bank (SFB) in the transmitter and the analysis filter bank (AFB) in the receiver. Figure 1 shows the filter banks in this configuration as fundamental part of a complete FBMC/OQAM transmission/reception system. This FB technique builds on uniform modulated filter banks [23], in which a prototype filter  of length
of length  is shifted in frequency to generate subbands which cover the whole system bandwidth. The output of such a synthesis filter bank can be expressed by
is shifted in frequency to generate subbands which cover the whole system bandwidth. The output of such a synthesis filter bank can be expressed by

where

 is the sample index at the output of the SFB (at high rate),
is the sample index at the output of the SFB (at high rate),  is the number of subchannels in the filter bank, and
is the number of subchannels in the filter bank, and  are the real-valued data symbols in subchannel
are the real-valued data symbols in subchannel  , transmitted at a rate
, transmitted at a rate  . The signaling interval is defined as
. The signaling interval is defined as  , where
, where  is the subcarrier spacing. The pair of symbols
is the subcarrier spacing. The pair of symbols  and
and  can be interpreted as carrying the in-phase and quadrature information of a complex-valued symbol transmitted at rate
can be interpreted as carrying the in-phase and quadrature information of a complex-valued symbol transmitted at rate  . Therefore, the filter bank presented in Figure 1 is critically sampled. The "
. Therefore, the filter bank presented in Figure 1 is critically sampled. The " "-blocks indicate the conversion into real-valued data from the real and imaginary parts of the complex-valued input symbols
"-blocks indicate the conversion into real-valued data from the real and imaginary parts of the complex-valued input symbols  and can be considered as introducing upsampling by 2. "
and can be considered as introducing upsampling by 2. " " carries out the inverse operation after the AFB in the receiver, effectively downsampling the signal by 2. In FBMC/OQAM,
" carries out the inverse operation after the AFB in the receiver, effectively downsampling the signal by 2. In FBMC/OQAM,  belongs to a QAM alphabet and the real and imaginary parts are interleaved with a relative time offset of
belongs to a QAM alphabet and the real and imaginary parts are interleaved with a relative time offset of  (hence offset QAM) and
(hence offset QAM) and  performs the following mapping:
performs the following mapping:


Note that the signs of the sequences in (2)–(4) could be chosen arbitrarily, but the pattern of real and imaginary symbols after multiplication by  has to follow the above definitions to maintain orthogonality [5].
has to follow the above definitions to maintain orthogonality [5].
This type of filter bank pairs can be efficiently implemented using FFT and IFFT of size  aided by polyphase filtering structures. The different parts of the polyphase SFB structure of Figure 1(a) can be better identified by noting that
aided by polyphase filtering structures. The different parts of the polyphase SFB structure of Figure 1(a) can be better identified by noting that  and rewriting (1) as
and rewriting (1) as

where

Here, the factor  centers the low-rate output signal of each subchannel
centers the low-rate output signal of each subchannel  of the analysis filter bank around DC.
of the analysis filter bank around DC.
The synthesis and analysis banks in Figure 1, between the OQAM modulation and the subchannel processing parts, respectively, can also be understood from the classical FB presentation: each subchannel  with its own up/downsampling and subchannel filters. The synthesis/analysis subchannel filters are, respectively, obtained from the prototype filter
with its own up/downsampling and subchannel filters. The synthesis/analysis subchannel filters are, respectively, obtained from the prototype filter  as
as

where  and
and  indicates complex conjugation.
indicates complex conjugation.
Further, the length  of the prototype filter
of the prototype filter  depends on the size of the filter bank and the integer overlapping factor
depends on the size of the filter bank and the integer overlapping factor  as
as  , where the factor
, where the factor  indicates the number of FBMC/OQAM symbol waveforms that overlap in time. In [24], other lengths of the prototype filter, close to
indicates the number of FBMC/OQAM symbol waveforms that overlap in time. In [24], other lengths of the prototype filter, close to  , are explored. High values for
, are explored. High values for  allow more freedom in designing the prototype filter, for example to achieve very high stopband attenuation. On the other hand, it increases the time required for processing each symbol. The prototype filter
allow more freedom in designing the prototype filter, for example to achieve very high stopband attenuation. On the other hand, it increases the time required for processing each symbol. The prototype filter  can be designed in such a way that the filter bank pair yields perfect reconstruction (PR) of the transmitted data in case of an ideal channel, that is, the received data sequence
can be designed in such a way that the filter bank pair yields perfect reconstruction (PR) of the transmitted data in case of an ideal channel, that is, the received data sequence  equals the transmitted data
equals the transmitted data  (except for the FB processing delay), if there is no additional processing involved. Methods to design PR prototype filters can be found in [25]. However, in practical communication systems, the channel will always introduce some distortion to the signal. Therefore, the design constraints can be somewhat relaxed and the prototype can be optimized to achieve nearly PR (NPR). The trade-off, when comparing with PR designs, is that for prototype filters of the same length, NPR designs can achieve higher stopband attenuations, or with fixed stopband attenuations, the NPR prototype filter can be shorter. This happens at the cost of allowing some marginal intersymbol (ISI) and intercarrier (ICI) interference from the filter bank, well under the noise level of the communication channel.
(except for the FB processing delay), if there is no additional processing involved. Methods to design PR prototype filters can be found in [25]. However, in practical communication systems, the channel will always introduce some distortion to the signal. Therefore, the design constraints can be somewhat relaxed and the prototype can be optimized to achieve nearly PR (NPR). The trade-off, when comparing with PR designs, is that for prototype filters of the same length, NPR designs can achieve higher stopband attenuations, or with fixed stopband attenuations, the NPR prototype filter can be shorter. This happens at the cost of allowing some marginal intersymbol (ISI) and intercarrier (ICI) interference from the filter bank, well under the noise level of the communication channel.
The NPR prototype can be designed using, among others, window-based techniques [26] or the frequency sampling approach [27, 28]. In the studies described here, the prototype is obtained using the latter method, in which the filter impulse response is obtained by the inverse Fourier transform of the desired frequency response at certain frequency locations. The design of such an NPR prototype filter under different optimization criteria has been addressed in [24].
2.2. Subchannel-Wise Equalization in FBMC
In OFDM, as long as the channel delay spread and the possible synchronization errors remain within the cyclic prefix time, equalization can simply be done with a complex coefficient multiplication at subcarrier level. This approach is also applicable to FBMC, if the ratio of channel delay spread in samples and number of subchannels is sufficiently low, since the frequency variation within a subchannel is then small enough that it can be considered flat fading. But as this is not the general case, more effective channel equalization methods have been developed for FBMC. The single complex coefficient is usually considered when the FB waveforms are well localized in time and frequency domains to limit the effect on consecutive symbols and neighboring subchannels [5, 29, 30]. Longer finite impulse response (FIR) filters as subcarrier equalizers with cross-connections between the adjacent subchannels to cancel the ICI are studied in [31, 32]. To avoid the cross-connections between subchannels, an oversampled receiver filter bank structure with per-subcarrier FIR equalizers can restore the orthogonality of the subcarrier waveforms. This approach is followed in [33–37] and more recently with MMSE equalizers explicitly for FBMC/OQAM in [38].
The authors of this paper have worked on a low-complexity, subcarrier-wise FBMC equalizer using oversampled subcarrier signals [39, 40]. The equalizers were considered earlier for the exponential modulation type of filter banks, which are basically a generalization of the sine and cosine modulated filter banks to complex-valued signals. Nevertheless, these equalizers can readily be applied to FBMC/OQAM receivers by noting that now the filter bank is even stacked, as compared to the odd stacking of the EMFB-based system. We base the equalization in the current study on this approach because it yields good equalization performance with practical channels and subcarrier spacings of up to 100 kHz, which is more than enough for the WiMAX-like system under consideration.
The working principle is based on frequency sampling: assuming a roll-off factor of the prototype filter  or smaller, each subchannel overlaps only with the immediately neighboring subchannels. At the oversampled part of the receiver bank, before taking the real part of the subcarrier signals, the equalizer can perform equalization at a number of frequency points according to its complexity. For example, if the equalizer is a 3-tap complex FIR filter, 3 frequency points within the subchannel can be completely equalized, according to the zero-forcing (ZF) or the mean squared error (MSE) criterion. With the filter bank structure in Figure 1, all the subchannels alias to frequencies centered around DC, and a straightforward choice is to equalize at DC and at
or smaller, each subchannel overlaps only with the immediately neighboring subchannels. At the oversampled part of the receiver bank, before taking the real part of the subcarrier signals, the equalizer can perform equalization at a number of frequency points according to its complexity. For example, if the equalizer is a 3-tap complex FIR filter, 3 frequency points within the subchannel can be completely equalized, according to the zero-forcing (ZF) or the mean squared error (MSE) criterion. With the filter bank structure in Figure 1, all the subchannels alias to frequencies centered around DC, and a straightforward choice is to equalize at DC and at  , that is, the center of the subchannel and the passband edge frequencies, respectively. Also other frequencies can be used, as well as longer filters, but the described solution is the computationally least demanding.
, that is, the center of the subchannel and the passband edge frequencies, respectively. Also other frequencies can be used, as well as longer filters, but the described solution is the computationally least demanding.
In the 3-tap complex FIR equalizer of subchannel  at time
at time  with (noncausal) transfer function
with (noncausal) transfer function

the filter coefficients  , with
, with  can be tuned in a way that the filter achieves at the mentioned frequency points the following target values:
can be tuned in a way that the filter achieves at the mentioned frequency points the following target values:

Here,  , where
, where  corresponds to the lower subband edge,
corresponds to the lower subband edge,  to the subband center, and
to the subband center, and  to the upper subband edge frequency.
to the upper subband edge frequency.  is the channel frequency response in subchannel
is the channel frequency response in subchannel  and time
and time  at frequency position given by
at frequency position given by  , and
, and  and
and  are scaling factors. If the equalizer applies the ZF criterion,
are scaling factors. If the equalizer applies the ZF criterion,  and
and  . In the MSE case,
. In the MSE case,  is the noise-to-signal power ratio and the choice of
is the noise-to-signal power ratio and the choice of

removes the bias of the MSE solution.
Taking into account these assumptions, the equalizer coefficients can readily be derived from the target values in (9) above as [39]

Furthermore, it is worth mentioning here that this equalizer can perform also limited FTD and CFO correction in addition to channel equalization, as will be discussed in the next section.
3. Pilot-Based Synchronization in FBMC
3.1. Synchronization in Spectrally Agile Radios
Traditional wireless communication systems are characterized by dedicated frequency bands and well-defined frequency channels. After analog and digital receiver front-ends, the signal contains only the transmissions allocated to that channel, which have well-controlled dynamics under the radio resource management functionalities of the wireless network.
The scarcity of frequency spectrum which can be used in wireless communications is a significant factor that has given raise to the concepts of flexible dynamic spectrum use and cognitive radio. In this context, the used frequency band is not anymore dedicated to a specific service and specific waveforms. The band cannot be expected anymore to be free of other waveforms, the utilized frequency spectrum may be noncontiguous, and the dynamics of signal power levels are not well-controlled anymore. This calls for efficient means to dynamically separate the used portions of the frequency spectrum from other portions that are considered interference. Filter banks are ideal for this purpose. It should be noted that in OFDM, the plain FFT processing does not provide effective filtering to signal elements that are not synchronized to the CP structure, and the frequency channelization selectivity has to be implemented in the analog and digital front-end.
As for the synchronization functionalities in case of spectrally agile radios, it is clear that synchronization parameter estimation cannot be implemented in time domain before major part of the selectivity is implemented and strong interferers are suppressed. As the filter bank itself can be used effectively for implementing the selectivity, the feasibility of time domain synchronization becomes questionable. Therefore, in the context of cognitive radio, there is a strong motivation to develop synchronization methods which are operating in frequency domain, utilizing the subchannel signals only. However, for compensation of coarse synchronization errors, time domain methods are still favorable. In the following discussion, it is assumed that coarse timing and frequency offsets have been compensated in time domain. The required accuracy of coarse CFO and FTD estimates is an outcome of this study.
The primary use of these methods is for channel tracking. In normal tracking mode, with continuous flow of data packets, only small CFO and FTD values are expected, and it is enough to use only the estimation algorithms in conjunction with basic time domain compensation methods and some filtering to reduce the random variations of block-wise estimates. However, in advanced packet-based radio interfaces, there can be long gaps in the packet flow, especially when the terminal is in idle mode. This may result in significant drift of the CFO and FTD values, and it is advantageous to be able to compensate significant synchronization errors right away for the first received data packet.
For initial synchronization, the developed scheme could be a part of a search procedure, where different coarse CFO and FTD values are tested until synchronization can be established.
3.2. Signal Models
In order to perform channel equalization and synchronization with the presented equalizer, it has to be fed with channel estimates that provide information about the channel state and the possible synchronization errors. In this paper, we study only the effect of a linear multipath channel with additive white Gaussian noise (AWGN), fractional time delay, and carrier frequency offset. In this scenario, the baseband signal model at the receiver input can be expressed as

where  represents the convolution operation,
represents the convolution operation,  is the continuous time version of (1) (or (5)),
is the continuous time version of (1) (or (5)),  is the time-varying transmission channel, and
is the time-varying transmission channel, and  is the Dirac delta. Moreover,
is the Dirac delta. Moreover,  is the fractional time delay as a fraction of the signalling interval
is the fractional time delay as a fraction of the signalling interval  ,
,  is the CFO as a fraction of the subcarrier spacing
is the CFO as a fraction of the subcarrier spacing  , and
, and  is complex valued AWGN. At the receiver,
is complex valued AWGN. At the receiver,  is sampled at
is sampled at  into
into  and then passes the analysis bank. Before the subchannel processing stage (estimation and synchronization/equalization in our case), the
and then passes the analysis bank. Before the subchannel processing stage (estimation and synchronization/equalization in our case), the  th subchannel sequence
th subchannel sequence  can be expressed as
can be expressed as

where

Above,  is the subchannel-dependent 2-dimensional impulse response, including the channel effects, from subchannel
is the subchannel-dependent 2-dimensional impulse response, including the channel effects, from subchannel  to subchannel
to subchannel  , and (see Figure 1)
, and (see Figure 1)

The discrete-time time varying channel is  , the delay
, the delay  is assumed in this paper to be an integer number of samples, for simplicity, and
is assumed in this paper to be an integer number of samples, for simplicity, and  M/2 represents the downsampling by
M/2 represents the downsampling by  of the preceding expression. The sampled and filtered noise is
of the preceding expression. The sampled and filtered noise is  .
.
In an FB system with a sufficiently frequency selective prototype filter and roll-off  , only adjacent subchannels overlap and have an effect on subchannel
, only adjacent subchannels overlap and have an effect on subchannel  of interest. This implies that the sum in (13), which is basically a 2-dimensional convolution, can be limited to run from
of interest. This implies that the sum in (13), which is basically a 2-dimensional convolution, can be limited to run from  to
to  :
:

This also assumes a reasonably small frequency offset  , in which case the overlaps with subchannels
, in which case the overlaps with subchannels  remain limited.
remain limited.
3.3. Pilots for FBMC
In a multicarrier system with sufficient number of subcarriers, it is just intuitive to obtain information about a doubly selective (in frequency and time) transmission channel by sampling it in frequency and time directions at certain intervals. The samples are obtained by known data symbols (pilots) that are transmitted at given time and frequency locations and from which the channel information at these locations is recovered. This information is extended to cover the whole signal domain by interpolating between the pilots. In OFDM the application and exploitation of the pilots is straightforward: the channel state in subchannel  at time instant
at time instant  is just the received symbol divided by the transmitted symbol (this implies ignoring the additive noise). In efficient modulated filter banks it is not that simple, as a closer look into (14) reveals. Indeed, if we first remove all the channel effects in that equation, that is,
is just the received symbol divided by the transmitted symbol (this implies ignoring the additive noise). In efficient modulated filter banks it is not that simple, as a closer look into (14) reveals. Indeed, if we first remove all the channel effects in that equation, that is,  ,
,  , and
, and  ,
,  becomes the time- and frequency invariant 2-dimensional impulse response of the TMUX, relating
becomes the time- and frequency invariant 2-dimensional impulse response of the TMUX, relating  with
with  (or equivalently
(or equivalently  with the received
with the received  th subchannel signal before the operation of taking its real part,
th subchannel signal before the operation of taking its real part,  ). In this case, (16) can be expressed as
). In this case, (16) can be expressed as

Equivalently, we can write


The elements  and
and  within the parentheses of (19) are obtained by, respectively, taking the real and imaginary part of the summation term in (18). They can be considered interference on the desired symbol
within the parentheses of (19) are obtained by, respectively, taking the real and imaginary part of the summation term in (18). They can be considered interference on the desired symbol  . Now, even in a PR TMUX, in which the real-valued term
. Now, even in a PR TMUX, in which the real-valued term  , the imaginary-valued interference
, the imaginary-valued interference  does not add up to 0. The orthogonality is only obtained after taking the real part, that is, this interference summation has only imaginary values [5]. In an NPR design,
does not add up to 0. The orthogonality is only obtained after taking the real part, that is, this interference summation has only imaginary values [5]. In an NPR design,  is a small real-valued contribution, generally well below the level of
is a small real-valued contribution, generally well below the level of  , and will be ignored from now on. Another property of the imaginary-valued interference
, and will be ignored from now on. Another property of the imaginary-valued interference  is that it is time-varying, since it depends on the data in the adjacent channels and on the symbols preceding and following
is that it is time-varying, since it depends on the data in the adjacent channels and on the symbols preceding and following  .
.
For simplicity of notation, we define the noncausal TMUX response at subchannel  and instant
and instant  as
as  . It is assumed that it is normalized at
. It is assumed that it is normalized at  and
and  as
as  . Table 1 presents the interference weights that multiply neighboring symbols in the case of an NPR prototype designed with the frequency sampling method in [28] and with an overlapping factor
. Table 1 presents the interference weights that multiply neighboring symbols in the case of an NPR prototype designed with the frequency sampling method in [28] and with an overlapping factor  . Thus, we obtain at the location
. Thus, we obtain at the location  of interest
of interest

where the imaginary interference is

with

and  is the set of subcarrier and time indices that are considered to contribute to the interference on the symbol at
is the set of subcarrier and time indices that are considered to contribute to the interference on the symbol at  . Without channel distortions,
. Without channel distortions,  and
and  are related as
are related as  .
.
Table 1 shows that the interference from subchannels not adjacent to the subchannel of interest have negligible effect and that in time direction the interference goes  symbols from the symbol of interest in both directions. With this design, the residual distortion on the real part is less than
symbols from the symbol of interest in both directions. With this design, the residual distortion on the real part is less than  65 dB compared to the actual data.
65 dB compared to the actual data.
It is clear that a pilot located at subcarrier  and time
and time  cannot be immediately recovered even if the channel at that subcarrier is a simple complex coefficient
cannot be immediately recovered even if the channel at that subcarrier is a simple complex coefficient  (flat fading), because the pilot information and the complex-valued, time-varying, and data-dependent interference will be mixed by the channel. In the following paragraphs we describe the method we use to handle the described complex-valued interference in order to make pilot-based channel sampling feasible and briefly point out several alternative approaches. The interested reader is referred to the cited references for detailed description of the methods. We first consider a channel with neither FTD nor CFO.
(flat fading), because the pilot information and the complex-valued, time-varying, and data-dependent interference will be mixed by the channel. In the following paragraphs we describe the method we use to handle the described complex-valued interference in order to make pilot-based channel sampling feasible and briefly point out several alternative approaches. The interested reader is referred to the cited references for detailed description of the methods. We first consider a channel with neither FTD nor CFO.
3.3.1. Auxiliary Pilots
This approach is based on an elegant idea presented in [18] utilizing an auxiliary pilot located at  adjacently to the pilot
adjacently to the pilot  and which cancels the interference
and which cancels the interference  of (21). The advantage of eliminating the interference is that the pilots can be used at the receiver in a similar fashion as OFDM pilots are used; the estimate of the channel at the pilot location is
of (21). The advantage of eliminating the interference is that the pilots can be used at the receiver in a similar fashion as OFDM pilots are used; the estimate of the channel at the pilot location is

assuming that the channel is constant over the whole subchannel bandwidth. The auxiliary pilot is indeed one element of the sum (21) and has to be calculated on-line with data transmission every time a pilot is inserted since the interference terms vary with the data. In [18], the auxiliary pilot is chosen to cancel the interference from the 8 surrounding symbols. This is a good approximation in well time-frequency localized prototype filters, such as the ones based on the isotropic orthogonal transform algorithm (IOTA) function [29]. Here we chose to include more terms in the calculation of the interference because also symbols located further away can add significant interference. The auxiliary pilot that cancels the imaginary interference can be calculated as

In typical filter bank designs it is wise to locate the auxiliary pilot immediately preceding or following the pilot, that is,  or
or  . This way, the absolute value of the denominator
. This way, the absolute value of the denominator  is maximized (see Table 1) and the magnitude of the auxiliary pilot is minimized on the average, wasting less transmission energy on the pilot/auxiliary pilot pair and preventing possible strong effects on the peak-to-average-power ratio (PAPR) due to excessively strong auxiliary pilots. As an example, with the prototype filter presented above, it is sensible to use the shaded area of Table 1 for the computation of the interference and the auxiliary pilot. This leaves the residual imaginary interference below
is maximized (see Table 1) and the magnitude of the auxiliary pilot is minimized on the average, wasting less transmission energy on the pilot/auxiliary pilot pair and preventing possible strong effects on the peak-to-average-power ratio (PAPR) due to excessively strong auxiliary pilots. As an example, with the prototype filter presented above, it is sensible to use the shaded area of Table 1 for the computation of the interference and the auxiliary pilot. This leaves the residual imaginary interference below  dB level with respect to the data. Further, if the auxiliary pilot is chosen to precede or succeed the pilot, then the auxiliary pilot power is on the average 3.3 dB stronger than the data surrounding the pilot/auxiliary pilot pair. Note that the use of two real-valued symbols as pilots does not mean a penalty in overhead with respect to OFDM, since there the pilot is complex-valued.
dB level with respect to the data. Further, if the auxiliary pilot is chosen to precede or succeed the pilot, then the auxiliary pilot power is on the average 3.3 dB stronger than the data surrounding the pilot/auxiliary pilot pair. Note that the use of two real-valued symbols as pilots does not mean a penalty in overhead with respect to OFDM, since there the pilot is complex-valued.
3.3.2. Alternative Pilot Techniques for Channel Estimation
The pair of real pilots (POP) [17] method also uses two consecutive OQAM subsymbols to send known pilots, in the simplest case, similar pilots. Ignoring the noise and assuming that the channel remains unchanged during both subsymbols, an equation system yields the equalizer coefficient (the same for both pilots) that restores the pilots to their original phase. Its inverse is the estimate for the channel at the positions of the POP. This method places the computational complexity on the receiver part and has the advantage that it is independent from the prototype filter design, since the interference term is not used explicitly in the equations. However, if the noise is not negligible, it will be enhanced in a random fashion, depending on the data surrounding the pilots, which makes the performance unpredictable and generally worse.
The authors of [17] present also the interference approximation method (IAM). The philosophy here is that most of the symbols surrounding the pilot in time and frequency are fixed and known at the receiver. In this case, the interference  can be approximatively calculated with (21), which leads to the estimate
can be approximatively calculated with (21), which leads to the estimate  . The more symbols in the shaded area of Table 1 are fixed, the better is the approximation of
. The more symbols in the shaded area of Table 1 are fixed, the better is the approximation of  . Unfortunately, this approach leads to an unacceptable overhead if a good approximation of the interference, necessary for accurate channel estimates, is desired. Therefore, it is practical only in situations in which pilots are packed closely together, for example, in preambles, where the fixed symbols can be simultaneously utilized by nearby located pilots.
. Unfortunately, this approach leads to an unacceptable overhead if a good approximation of the interference, necessary for accurate channel estimates, is desired. Therefore, it is practical only in situations in which pilots are packed closely together, for example, in preambles, where the fixed symbols can be simultaneously utilized by nearby located pilots.
More sophisticated methods for scattered-pilot-based channel estimation in FBMC/OQAM are presented in [41]. By means of an orthonormal transformation of the data around the pilot, the imaginary-valued term can be nulled while avoiding the need of an auxiliary pilot with increased power. Nevertheless, it is still necessary to fix one of the surrounding symbols, which cannot be used for data transmission. Another approach in [41, 42] consists of iteratively approximating  at the receiver with help of the demodulated data. At first, it is considered that
at the receiver with help of the demodulated data. At first, it is considered that  , and the channel is estimated based on this assumption. The equalization and detection then yield estimates of the data surrounding the pilot, which, in turn, permit calculating a better estimate of
, and the channel is estimated based on this assumption. The equalization and detection then yield estimates of the data surrounding the pilot, which, in turn, permit calculating a better estimate of  . This technique converges in 3-4 iterations.
. This technique converges in 3-4 iterations.
The methods presented above provide a way of sampling the time-varying frequency response of the transmission channel. The estimates required at the remaining subchannels and time-instants can be obtained by interpolating between the estimates obtained at the pilot locations. Note that for the 3-tap subcarrier equalizer presented in Section 2.2, the interpolation has to return estimates not only at the center frequencies of the subcarriers, but also at the subband edges in the middle of those frequencies. Studying how improved interpolation techniques [12] affect the FBMC channel estimation performance is an interesting research subject but goes beyond the scope of this paper.
3.4. Timing Estimation and Correction
Assuming that the coarse location of a transmission frame is obtained by other means, the effect of not synchronizing exactly with the MC symbols, hence introducing a fractional time delay, can be understood with help of (14). In the frequency domain we can write

which shows that FTD introduces a phase term that linearly varies with the frequency. This frequency-dependent phase term destroys the orthogonality of the subchannels and causes the appearance of ICI.
For estimation purposes, let us first assume that there is neither channel distortion nor CFO present. In this case, (16) can be approximated as

where the term  at
at  and
and  , respectively, causes the interference
, respectively, causes the interference  not to be purely imaginary anymore (after compensation of the common phase rotation
not to be purely imaginary anymore (after compensation of the common phase rotation  and multiplication by
and multiplication by  ), hence causing ICI. However, from (26) it seems straightforward to estimate the FTD from a transmitted pilot at
), hence causing ICI. However, from (26) it seems straightforward to estimate the FTD from a transmitted pilot at  , allowing for some uncertainty caused by the ICI. In practice, the estimate is obtained from the phase difference between two pilots separated by
, allowing for some uncertainty caused by the ICI. In practice, the estimate is obtained from the phase difference between two pilots separated by  subcarriers, since the signal can have a constant random phase rotation that is eliminated when calculating the phase difference. Thus,
subcarriers, since the signal can have a constant random phase rotation that is eliminated when calculating the phase difference. Thus,

where  is the phase of
is the phase of  and
and  comes from the
comes from the  that relate
that relate  and
and  . This result limits the carrier separation for the pilots, if unambiguous phase differences are to be calculated. The phase difference remains below
. This result limits the carrier separation for the pilots, if unambiguous phase differences are to be calculated. The phase difference remains below  if
if  . For example, if pilot subcarriers are separated by
. For example, if pilot subcarriers are separated by  , only a delay of
, only a delay of  samples (
samples ( rounds to the closest smaller integer) can be estimated without phase ambiguity.
rounds to the closest smaller integer) can be estimated without phase ambiguity.
The estimate can be improved by averaging techniques such as least squares linear curve fitting over all pilot pairs that are sufficiently closely placed within a frame. In case of CFO, consecutive symbols within a subcarrier are rotated with respect to each other, as will soon be discussed, forcing the averaging to be independently done over the subchannels for every MC symbol time. The CFO additionally increases the additive distortion. Finally, in presence of the transmission channel, the (flat-fading) channel coefficient within the subchannel of interest also multiplies the transmitted signal, introducing additional rotation. Since in general this rotation is different at different subcarriers, it would be expected that this method cannot be used anymore with practical transmission channels. Nevertheless, if the effect of the FTD on the phase is predominant, the phase difference introduced by the channel coefficients will add up as noise at the end. Consequently, we can consider  , where
, where  is an additive phase term, which depends on how much the channel is correlated in frequency direction at the pilot distance. Again, averaging over a sufficient number of pilots reduces the harmful effect of this additional phase term. In general, the FTD estimation can be seen as a problem of phase slope estimation over the active subcarriers.
is an additive phase term, which depends on how much the channel is correlated in frequency direction at the pilot distance. Again, averaging over a sufficient number of pilots reduces the harmful effect of this additional phase term. In general, the FTD estimation can be seen as a problem of phase slope estimation over the active subcarriers.
To compensate for the FTD, an equalizer can be designed to reverse the effect of the frequency-varying phase. The 3-tap complex FIR equalizer presented in Section 2.2 is well suited for performing this task simply by including the FTD effect on the phase of the channel estimates at the subband edges. When computing these estimates for all subcarriers and time instants, the correct interpolation of the channel from the estimates at the pilots is not a trivial problem in the case of FTD due to the modulo  phase ambiguity. For example, if amplitude and phase are interpolated separately, in order to include the FTD estimation for compensating the phase,
phase ambiguity. For example, if amplitude and phase are interpolated separately, in order to include the FTD estimation for compensating the phase,  hops can result in a very unsmooth 2-D channel interpolation. In our studies using very basic linear interpolation we obtained the smoothest results by first eliminating the phase slope from the center frequencies of the pilots. Then, 2-D complex interpolation to obtain the channel estimates for the data symbols both at the center and edge frequencies is performed, and finally the phase slope is restored to the whole estimation matrix for final calculation of the equalizer coefficients.
hops can result in a very unsmooth 2-D channel interpolation. In our studies using very basic linear interpolation we obtained the smoothest results by first eliminating the phase slope from the center frequencies of the pilots. Then, 2-D complex interpolation to obtain the channel estimates for the data symbols both at the center and edge frequencies is performed, and finally the phase slope is restored to the whole estimation matrix for final calculation of the equalizer coefficients.
3.5. Joint FTD and Channel Estimation Based on Iterative Interference Cancelation
The analysis above shows a clear interplay between the quality of the estimates and the presence of FTD and CFO. Therefore, it is desirable to apply the information of the estimated synchronization parameters to the estimated pilots in order to improve the quality of all the pilot-based estimates. One way to achieve this is by jointly estimating the subcarrier-wise channel coefficients and the phase slope. Here, we present a new approach that utilizes the FTD-induced linear phase slope within each pilot subcarrier. We assume a simplified signal model, where the amplitude response is assumed to be constant within each subchannel and the phase is assumed to be a linear function of frequency. This is motivated by the observation that, in many cases, a 1-tap equalizer is able to equalize the channel quite well in the absence of timing offsets. The joint channel-FTD estimation includes two parts: estimation of the complex channel coefficient for each pilot, and estimation of the phase slope jointly for all pilots participating in the estimation window  .
.
Simplifying the notation for the 1-tap equalizer coefficient at  in (11) as
in (11) as  , the FTD-compensating target response of the 3-tap subcarrier equalizer presented in Section 2.2 can be written as
, the FTD-compensating target response of the 3-tap subcarrier equalizer presented in Section 2.2 can be written as

where the equalizer phase difference correction between the subchannel center frequency and the edge is

The subcarrier equalizer in the frequency sampling design can now be written as

resulting in the following signal model for the subcarrier equalizer output:

If small  is assumed we can approximate (31) as
is assumed we can approximate (31) as

This can be rewritten as

where we define

Using the auxiliary pilot scheme, for the pilot symbols the ideal output is  (the subindices
(the subindices  are ignored here for readability). Now, the channel equalization problem can be formulated as
are ignored here for readability). Now, the channel equalization problem can be formulated as

where  is the set of subcarrier symbols used in the joint estimation. The idea is to adjust
is the set of subcarrier symbols used in the joint estimation. The idea is to adjust  and
and  in such a way that the difference between the equalizer output and the known pilot
in such a way that the difference between the equalizer output and the known pilot  is minimized in the least-squares sense. This is a nonlinear optimization problem, which can be solved for example by iterating the following two steps.
is minimized in the least-squares sense. This is a nonlinear optimization problem, which can be solved for example by iterating the following two steps.
-
(1)
Assuming that the phase slope is known from the previous iteration (0 in the beginning),
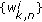 are solved from pilots
are solved from pilots  . Note that here
. Note that here  is the iteration index.
is the iteration index. -
(2)
Assuming that
 are known, the observation is a linear function of
are known, the observation is a linear function of  and the optimum
and the optimum  can easily be calculated with the derivative of the expression in brackets in (35) with respect to
can easily be calculated with the derivative of the expression in brackets in (35) with respect to 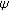 and setting the result to 0, yielding
and setting the result to 0, yielding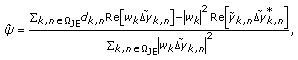 (36)
(36)which, from (29), yields
 . Note that
. Note that  is here the average of
is here the average of 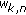 within subchannel
within subchannel  . This process converges typically in 5–10 iterations, depending on the FTD and
. This process converges typically in 5–10 iterations, depending on the FTD and 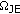 . Moreover, the estimates
. Moreover, the estimates  are quite accurate even for higher values of
are quite accurate even for higher values of 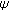 , as will be seen in Section 5.
, as will be seen in Section 5.
Since this method relies on iteratively canceling the ICI, it will hereafter be referred to as iterative interference cancelation (IIC) approach.
3.6. CFO Estimation and Correction
The effect of carrier frequency offset can be analyzed with help of (12), (14), and (25). We observe that before the AFB, the complex exponential that represents the frequency shift induces a linearly time-varying phase rotation of  on consecutive high-rate samples. Recall that
on consecutive high-rate samples. Recall that  is the normalized CFO with respect to the subcarrier separation
is the normalized CFO with respect to the subcarrier separation  . After the receiver bank and downsampling by
. After the receiver bank and downsampling by  , the phase rotation between two consecutive symbols at rate
, the phase rotation between two consecutive symbols at rate  is
is  radians. This leads to ISI from symbols in the same subchannel and ICI from symbols in neighboring subchannels at earlier and later time-instants (the neighboring symbols located at the same timing instant have the same phase rotation as the symbol under study, so they do not contribute to ICI, if only CFO is present). The linearly time-varying phase rotation is the property exploited in the forthcoming pilot-based CFO estimation and permits also to implement the basic compensation scheme.
radians. This leads to ISI from symbols in the same subchannel and ICI from symbols in neighboring subchannels at earlier and later time-instants (the neighboring symbols located at the same timing instant have the same phase rotation as the symbol under study, so they do not contribute to ICI, if only CFO is present). The linearly time-varying phase rotation is the property exploited in the forthcoming pilot-based CFO estimation and permits also to implement the basic compensation scheme.
A further effect of the CFO that can be deduced from (25) is that the subchannel filter at the AFB is not frequency-aligned with the corresponding subchannel filter at the SFB. This distorts the effective impulse response of the synthesis-analysis cascade by a factor

where  is the normalized angular frequency at subchannel sample rate and
is the normalized angular frequency at subchannel sample rate and  is the prototype filter frequency response in the filter bank design. In filter banks with linear-phase channel filters in the analysis (and synthesis) filter banks and in the zero-phase subchannel processing model, only the magnitude of the distorting frequency response is significant. The described distortion on the frequency response for the prototype filter introduced above is shown in Figure 2 for some selected CFO values.
is the prototype filter frequency response in the filter bank design. In filter banks with linear-phase channel filters in the analysis (and synthesis) filter banks and in the zero-phase subchannel processing model, only the magnitude of the distorting frequency response is significant. The described distortion on the frequency response for the prototype filter introduced above is shown in Figure 2 for some selected CFO values.
Finally, there are some effects like aliasing effects close to the subband edges and the appearance of distortion from the subchannel located 2 subcarrier spacings away.
3.6.1. CFO Estimation
Based on the CFO effects described above, pilot-based frequency offset estimation is straightforward. If a pilot at  is followed by another one
is followed by another one  samples later at
samples later at  , the phase rotation between them will cover
, the phase rotation between them will cover  radians. This yields an estimate
radians. This yields an estimate

where  comes from the
comes from the  that relate
that relate  and
and  .
.
The performance of the estimation can be improved by averaging over many pilots to reduce the effect of the distortion. For example, if pilots are all separated by the same number of samples, the following expression [43] can be used for estimating the CFO, while simultaneously weighting the subcarrier pilots according to their powers:

This way, stronger subcarriers are favored over weaker ones. Again the subindices  indicating pilot locations are not included in the equation for readability. Here,
indicating pilot locations are not included in the equation for readability. Here,  is the set of pilot locations used for CFO estimation. Note that the same problem of phase-ambiguity appears as in FTD estimation when
is the set of pilot locations used for CFO estimation. Note that the same problem of phase-ambiguity appears as in FTD estimation when  .
.
3.6.2. CFO Compensation
If the CFO is moderate, for example, in CFO tracking scenarios, or the subchannel signal modulation is robust, then the offset compensation can be performed subchannel-wise, as sketched in Figure 3(a) with the multiplication by the complex exponential sequence that undoes the frequency shift:  . The performance of this CFO correction on a WiMAX-like FBMC system is presented in [19], although there no other synchronization tasks are considered. The frequency shifting correction will obviously not recover the information leaked to the neighboring channel nor get rid of the distortion coming from 2 subchannels away, since the frequency shift is circular when performed at subchannel level. Further, the amplitude distortion due to the subchannel filter misalignments, depicted in Figure 2, is also ignored when shifting the signal back to its original location subchannel-wise.
. The performance of this CFO correction on a WiMAX-like FBMC system is presented in [19], although there no other synchronization tasks are considered. The frequency shifting correction will obviously not recover the information leaked to the neighboring channel nor get rid of the distortion coming from 2 subchannels away, since the frequency shift is circular when performed at subchannel level. Further, the amplitude distortion due to the subchannel filter misalignments, depicted in Figure 2, is also ignored when shifting the signal back to its original location subchannel-wise.
It is possible, however, to compensate for this amplitude distortion in a simple way with the help of the 3-tap equalizer presented above. Similarly as with the phase slope in the presence of FTD, the low complexity equalizer can approximatively correct the amplitude distortion given by (37). This is achieved by setting the desired target responses to

for  .
.
Figure 3 presents the subchannel model with the effect of the first two mentioned distortion types, which are predominating. It includes also the basic subchannel-wise CFO correction that undoes the CFO phase rotation according to the estimated frequency shift  . In the equivalent model (b), the effect of inaccurate CFO estimation is represented by the residual frequency modulation
. In the equivalent model (b), the effect of inaccurate CFO estimation is represented by the residual frequency modulation  .
.
When the frequency shift is too large, the degradation of the signal advocates for time domain solutions for correcting and possibly also for estimating the CFO. The compensation performance degrades faster than the estimation performance: At sufficiently high CFO, the subcarrier-wise compensation cannot recover enough of the signal of interest that has leaked to the neighboring subchannel and eliminate the interference. This logically affects higher order modulations most. However, since several pilots are used for CFO estimation, it is possible that the CFO estimate is still acceptable at the given CFO level. In this case, CFO estimation may still be done at subcarrier level, but compensation has to take place before the analysis filter bank.
It is also worth underlining that when multipath channel, FTD and CFO concur in a communication link, the low-complexity subband equalizer can compensate for the three distortions at the desired frequency locations by combining (multiplying) the target frequency responses needed for correcting each of the estimated distortions.
3.7. Synchronization Scheme with Iteration
In order to estimate and compensate the effect of CFO and FTD and the interplay between these effects shown in (14) and (25) we propose a receiver to jointly estimate and correct the channel impairments subchannel-wise. First, the pilots are recovered from the received signal and from them, the CFO is estimated and the frequency shift is reverted. Then, the synchronization block estimates the FTD and uses the obtained information when interpolating the channel between the pilots. Finally, at the equalization stage, the channel estimates at the equalization frequency points are weighted by the frequency-dependent amplitude distortion caused by the CFO (Figure 2) and the 3-tap equalizer then equalizes the signal. It is also possible to iterate this loop, since the 3-tap equalizer is able to remove a lot of distortion from the pilots, allowing for better estimates after the iteration.
4. FBMC for WiMAX
Next we describe the parameters and adjustments required for an FBMC communication system that aims to maintain a certain degree of compatibility with WiMAX specifications. We have aimed to design a system taking as much parameters from the mobile WiMAX specifications [2] and the underlying 802.16e standard [3] as possible. For our setup, we have selected the time division duplexing (TDD) specification for the 10 MHz bandwidth at sampling rate  MHz. With a transform size
MHz. With a transform size  , the subcarrier spacing is
, the subcarrier spacing is  kHz. The frame duration of 5 ms allows for transmission of 47 OFDMA symbols with the cyclic prefixes permitted in the specifications. If the whole frame was to be used for a downlink (DL) transmission, FBMC could fit 53 FBMC symbols in the same time because of the absence of the CP. In a more realistic scenario including the uplink (UL) subframe, one or two FBMC symbols would have to be sacrificed for guard times between the forward and reverse links. WiMAX provides for different data configuration modes. Here, we observe two of the possible configurations: the downlink partial usage of subcarriers (DL-PUSC) and the adaptive modulation and coding (AMC23). PUSC and AMC23 use 840 and 864 active consecutive subcarriers, respectively, and have a null subcarrier at the center of the transmission band. Compared to AMC23 in OFDMA without additional filtering, if an attenuation of 40 dB outside the 10 MHz transmission band is desired, the FBMC design with the prototype filter presented above could transmit on around 50 additional subcarriers thanks to its good spectral containment. The configurations also define the size of the transmission slots and how the pilots are located within the frame. Figure 4 shows these pilot configurations for the mentioned cases. Here, each OFDMA symbol corresponds to two consecutive subcarrier samples in the FBMC model.
kHz. The frame duration of 5 ms allows for transmission of 47 OFDMA symbols with the cyclic prefixes permitted in the specifications. If the whole frame was to be used for a downlink (DL) transmission, FBMC could fit 53 FBMC symbols in the same time because of the absence of the CP. In a more realistic scenario including the uplink (UL) subframe, one or two FBMC symbols would have to be sacrificed for guard times between the forward and reverse links. WiMAX provides for different data configuration modes. Here, we observe two of the possible configurations: the downlink partial usage of subcarriers (DL-PUSC) and the adaptive modulation and coding (AMC23). PUSC and AMC23 use 840 and 864 active consecutive subcarriers, respectively, and have a null subcarrier at the center of the transmission band. Compared to AMC23 in OFDMA without additional filtering, if an attenuation of 40 dB outside the 10 MHz transmission band is desired, the FBMC design with the prototype filter presented above could transmit on around 50 additional subcarriers thanks to its good spectral containment. The configurations also define the size of the transmission slots and how the pilots are located within the frame. Figure 4 shows these pilot configurations for the mentioned cases. Here, each OFDMA symbol corresponds to two consecutive subcarrier samples in the FBMC model.
The auxiliary pilot scheme introduced in Section 3.3.1 can directly be applied to the AMC23 pilot configuration. However, if the auxiliary pilot is to be placed in the advantageous position preceding or succeeding the actual pilot, the proximity of the pilots in DL-PUSC poses a computational problem. As shown in Figure 5, directly allocating the pilot and auxiliary pilot fixes a previous auxiliary pilot inside the range used for calculating the complex interference needed for obtaining the auxiliary pilot of interest. If the contribution of this previous auxiliary pilot is not to be ignored, the calculation requires optimization of the auxiliary pilots over the whole burst duration, taking into account their interdependencies (basically, the first auxiliary pilot would need to be calculated, then the next one and so on successively). It is more practical to be able to calculate the interference-nulling auxiliary pilots only from the surrounding data. This can be achieved by switching the positions of the pilot/auxiliary pilot pair every other pilot. The lower part of Figure 5 shows this convenient allocation, where the interference window extends only over data and a known pilot.
5. Simulation Setup and Results
We have tested the filter bank based multicarrier system with WiMAX-like parameters and using the synchronization and channel equalization methods that have been described above. The prototype filter is the NPR optimized design with  described in Section 3.3. The FBMC signal is sent through a quasistatic channel, if not indicated otherwise, modeled according to the International Telecommunication Union ITU-R Vehicular-A Channel guidelines [44]. This means, that for the duration of a transmission burst, the channel remains constant in time unless a certain mobility is indicated. In this case, the fading varies with time according to the mobile velocity. For each simulation, 3000 independent burst transmissions with independent channel realizations are performed. The estimation of the synchronization parameters and the channel state relies on scattered pilots obtained with the auxiliary pilot technique. The combined pilot/auxiliary pilot symbol is boosted on average by 4.5 dB with respect to the data. The overall channel response is obtained from the scattered channel estimates by triangulation-based linear interpolation between the pilots. It is important to note that all the processing is done subcarrier-wise, after the AFB.
described in Section 3.3. The FBMC signal is sent through a quasistatic channel, if not indicated otherwise, modeled according to the International Telecommunication Union ITU-R Vehicular-A Channel guidelines [44]. This means, that for the duration of a transmission burst, the channel remains constant in time unless a certain mobility is indicated. In this case, the fading varies with time according to the mobile velocity. For each simulation, 3000 independent burst transmissions with independent channel realizations are performed. The estimation of the synchronization parameters and the channel state relies on scattered pilots obtained with the auxiliary pilot technique. The combined pilot/auxiliary pilot symbol is boosted on average by 4.5 dB with respect to the data. The overall channel response is obtained from the scattered channel estimates by triangulation-based linear interpolation between the pilots. It is important to note that all the processing is done subcarrier-wise, after the AFB.
Extensive results presented in [45] justify favoring the 3-tap equalizer over the single tap solution. With perfect synchronization in the Veh-A channel model, the differences are hardly visible, but in channel models with longer delay spreads and especially when correcting synchronization errors, the performance advantage of the 3-tap equalizer is overwhelming. With respect to the OFDM-based WiMAX, Figure 6 shows the BER performance in the synchronized case of FBMC and OFDM in a system with around 1000 subcarriers that transmit during a whole frame of 5 ms. The OFDM pilots are boosted by 4.5 dB with respect to the data, that is, by the same boost applied to the FBMC pilot/auxiliary pilot pair. The obtained BER curves are quite similar. The better performance of FBMC with perfect knowledge of the channel (PCI) is due to the power that goes into the OFDM CP of length  of the OFDM symbol [2]. This advantage is almost completely used up when channel estimation takes place because in OFDM all the pilot power is used but in FBMC part of it is dedicated to the auxiliary pilot, which does not contribute to the actual estimation.
of the OFDM symbol [2]. This advantage is almost completely used up when channel estimation takes place because in OFDM all the pilot power is used but in FBMC part of it is dedicated to the auxiliary pilot, which does not contribute to the actual estimation.
In an actual communication system there are synchronization mismatches, and a receiver has to be able to cope with the joint effect of CFO and FTD. The approach detailed above in Section 4, including the iteration of the synchronization/equalization stage, is applied. In our simulations we have concluded that the described synchronization and equalization chain plus one iteration delivers nearly all the improvement, since the differences in offset estimates with additional iterations are marginal.
The first results in Figure 7 show the BER-performance of the mentioned system with 64-QAM at  dB in a quasistatic Vehicular-A channel. All the subcarriers are used, and the pilots are in the DL-PUSC configuration, simulating a downlink scenario. The transmitted burst consists of 4 FBMC symbols. Until otherwise mentioned, the FTD is calculated through averaging the phase differences between pilots. Figure 7(a) presents the BER results with changing CFO for two fixed FTD values, while Figure 7(b) presents the BER as a function of the FTD for two fixed CFO values. These figures show a clear improvement in performance with respect to CFO due to the CFO amplitude compensation. Further, the iteration of the synchronization and equalization stages also improves the BER, especially with respect to
dB in a quasistatic Vehicular-A channel. All the subcarriers are used, and the pilots are in the DL-PUSC configuration, simulating a downlink scenario. The transmitted burst consists of 4 FBMC symbols. Until otherwise mentioned, the FTD is calculated through averaging the phase differences between pilots. Figure 7(a) presents the BER results with changing CFO for two fixed FTD values, while Figure 7(b) presents the BER as a function of the FTD for two fixed CFO values. These figures show a clear improvement in performance with respect to CFO due to the CFO amplitude compensation. Further, the iteration of the synchronization and equalization stages also improves the BER, especially with respect to  . Because improvements in 4-QAM are not that visible (since the modulation is very robust by itself), these results are not shown here. Nevertheless, a slight improvement can still be achieved.
. Because improvements in 4-QAM are not that visible (since the modulation is very robust by itself), these results are not shown here. Nevertheless, a slight improvement can still be achieved.
Next, a situation similar to an uplink is tested. The pilots are now placed according to the AMC23 configuration, as in Figure 4(b), and the user sends its data in AMC23 slots, each slot consisting of 18 consecutive subcarriers and 3 MC symbols. Within each slot there are 6 pilot/auxiliary pilot pairs, as can be seen from the figure. We have studied two sizes for the transmitted bursts:  and
and  slots, where the first number indicates the number of slots in frequency direction and the second number in time direction. The smaller burst includes 48 pilot/auxiliary pilot pairs, the larger one has 768. We assume that other users are separated by the required guard band and that they do not produce multiuser interference.
slots, where the first number indicates the number of slots in frequency direction and the second number in time direction. The smaller burst includes 48 pilot/auxiliary pilot pairs, the larger one has 768. We assume that other users are separated by the required guard band and that they do not produce multiuser interference.
Figures 8 and 9 present the BER performances for 64-QAM and 4-QAM, respectively. The degradation that occurs when using a smaller burst size can be observed. This is due to the lower number of pilots available to perform synchronization and estimation. We further see that the range in which the synchronization is successful is much smaller than in the downlink case, but this is mainly due to the larger pilot separation. The effect of this is that the phase ambiguity when estimating FTD or CFO appears for  between 0.05 to 0.1
between 0.05 to 0.1 and
and  between 0.15 to 0.2
between 0.15 to 0.2 (at around
(at around  , because only every 6th symbol is a pilot in time direction). Figure 9 also compares the BER performance of an OFDM-based WiMAX system using the same synchronization and estimation methods as its FBMC counterpart. It occupies
, because only every 6th symbol is a pilot in time direction). Figure 9 also compares the BER performance of an OFDM-based WiMAX system using the same synchronization and estimation methods as its FBMC counterpart. It occupies  AMC23 slots and the BER results are similar to the FBMC case. The main difference is that in the CFO axis the performance degradation commences earlier. Due to the CP extension of the OFDM symbols, effectively slightly "separating" the pilots in time, the phase ambiguity appears approximately when
AMC23 slots and the BER results are similar to the FBMC case. The main difference is that in the CFO axis the performance degradation commences earlier. Due to the CP extension of the OFDM symbols, effectively slightly "separating" the pilots in time, the phase ambiguity appears approximately when  . Further, Figure 10 shows the effects on the FBMC system of user mobility and low SNR on the smaller burst with robust subchannel modulation. The performance is barely affected at this speed and only when the CFO approaches the nonambiguity limit the difference becomes visible. On the other hand, the stronger noise is evidently worsening the BER, but still allowing for a certain synchronization range. The following simulation results prove this by taking a closer look at the estimation performance of the synchronization parameters.
. Further, Figure 10 shows the effects on the FBMC system of user mobility and low SNR on the smaller burst with robust subchannel modulation. The performance is barely affected at this speed and only when the CFO approaches the nonambiguity limit the difference becomes visible. On the other hand, the stronger noise is evidently worsening the BER, but still allowing for a certain synchronization range. The following simulation results prove this by taking a closer look at the estimation performance of the synchronization parameters.
The CFO estimator performance is evaluated with help of the root mean square (RMS) error with respect to the actual CFO. The RMS error of the previously presented simulation scenarios is shown for a fixed  in Figure 11(a). The CFO estimation performance proves to be quite independent from the actual FTD, having only a minor degradation with increasing
in Figure 11(a). The CFO estimation performance proves to be quite independent from the actual FTD, having only a minor degradation with increasing  , as the interested reader can verify in [45]. In the low SNR scenario, even with the small burst and with FTD present, the estimate for the frequency offset is acceptable if the CFO stays below 7% of the subcarrier spacing. Also the user with vehicular mobility can be synchronized well by the base station. The other considered cases have a low variation of the performance with increasing CFO, until the ambiguity limit is reached. Although not presented here, the RMS CFO error of
, as the interested reader can verify in [45]. In the low SNR scenario, even with the small burst and with FTD present, the estimate for the frequency offset is acceptable if the CFO stays below 7% of the subcarrier spacing. Also the user with vehicular mobility can be synchronized well by the base station. The other considered cases have a low variation of the performance with increasing CFO, until the ambiguity limit is reached. Although not presented here, the RMS CFO error of  increases slightly if the synchronization procedure is iterated. Nevertheless, the estimates are still good enough for accurate synchronization within the WiMAX requirements for maximum CFO offset, specifically,
increases slightly if the synchronization procedure is iterated. Nevertheless, the estimates are still good enough for accurate synchronization within the WiMAX requirements for maximum CFO offset, specifically,  2% of the subcarrier spacing [3].
2% of the subcarrier spacing [3].
Similar results, now for the FTD RMS estimation error at the fixed CFO  , are summarized in Figure 11(b). Here the estimation error with iteration of the synchronization part is almost overlaying with the presented results. Also the case with the AMC23 mobile at 60 km/h has been omitted for readability, since the estimation RMS error is similar to the other AMC23 results. As in the CFO case, also here the FTD error is very much independent of the CFO (see again [45]) and is almost constant within the nonambiguous estimation range, between 5 and 10 high rate samples. This error floor for the different scenarios is caused by the inherent delay the channel introduces due to the delay spread distribution. Its effect is a mild slope in the phase with respect to the subcarrier index, even in the absence of proper FTD. This mild slope is also detected by the estimation methods as part of the FTD, inducing the error floor when comparing it to the actual FTD.
, are summarized in Figure 11(b). Here the estimation error with iteration of the synchronization part is almost overlaying with the presented results. Also the case with the AMC23 mobile at 60 km/h has been omitted for readability, since the estimation RMS error is similar to the other AMC23 results. As in the CFO case, also here the FTD error is very much independent of the CFO (see again [45]) and is almost constant within the nonambiguous estimation range, between 5 and 10 high rate samples. This error floor for the different scenarios is caused by the inherent delay the channel introduces due to the delay spread distribution. Its effect is a mild slope in the phase with respect to the subcarrier index, even in the absence of proper FTD. This mild slope is also detected by the estimation methods as part of the FTD, inducing the error floor when comparing it to the actual FTD.
Figures 11(a) and 11(b) include the RMS estimation error performance of the OFDM-based system. It can be seen that due to the higher available power boost for the OFDM pilots, the CFO estimates are better than in the FBMC system in the nonambiguous region. The FTD estimation error almost matches the error in the FBMC system because the mild slope of the inherent channel delay mentioned in the previous paragraph is detected here, too. The better CFO estimation performance does not translate into a better BER performance, as can be verified above in Figure 9.
The FTD estimation range can be extended further than the limit imposed by the frequency separation of the pilots by applying the interference minimization approach described in Section 3.5, yielding (36). The BER performance of the IIC technique for the AMC23 transmission configuration is shown in Figure 12, where the novel method is iterated 10 times. Figure 13 presents the corresponding RMS FTD estimation error. The extension into longer delay operating ranges is evident, and the BER performance for this  achieves the same level as the conventional technique when the larger bursts are compared. However, when a mobile user transmits using small bursts, and consequently few pilots, the BER and estimation performances of the IIC approach suffer greatly. If the interference cancelation method does not perform well enough in estimating the FTD because it has not enough pilots, it can, nevertheless, be applied for a coarse estimation within a wide FTD range to pin the delay to a value from where the conventional FTD estimation can take over the task.
achieves the same level as the conventional technique when the larger bursts are compared. However, when a mobile user transmits using small bursts, and consequently few pilots, the BER and estimation performances of the IIC approach suffer greatly. If the interference cancelation method does not perform well enough in estimating the FTD because it has not enough pilots, it can, nevertheless, be applied for a coarse estimation within a wide FTD range to pin the delay to a value from where the conventional FTD estimation can take over the task.
Figure 14 presents the performance of the IIC method for AMC23 transmission of  slots under different channel conditions. We see that this method is more sensitive to the mobility conditions than the conventional FTD and channel estimation method (see Figure 10). The BER performance with low SNR is also worse in this small burst case. If only 5 iterations in the IIC are performed, then the BER worsens for longer fractional time delays. Although not presented here, 5 iterations suffice if the larger burst of
slots under different channel conditions. We see that this method is more sensitive to the mobility conditions than the conventional FTD and channel estimation method (see Figure 10). The BER performance with low SNR is also worse in this small burst case. If only 5 iterations in the IIC are performed, then the BER worsens for longer fractional time delays. Although not presented here, 5 iterations suffice if the larger burst of  slots is sent, since the performance is practically the same as with 10 iterations.
slots is sent, since the performance is practically the same as with 10 iterations.
BER performance versus CFO and FTD of the IIC joint FTD and channel estimation method in different channel scenarios. 4-QAM transmission of 4 × 2 AMC23 slots in Vehicular-A channel at  dB and
dB and  dB and at different velocities. 5 and 10 iterations in the IIC technique. No additional synchronization iteration.
dB and at different velocities. 5 and 10 iterations in the IIC technique. No additional synchronization iteration.
6. Conclusions
In this contribution we proposed an integrated synchronization subsystem for filter bank based multicarrier communications. If the dimensioning of the filter bank leads to approximately flat fading subchannels, scattered pilots can be used to perform the synchronization and channel estimation tasks. Spectrally efficient filter banks with efficient implementations, such as the FBMC/OQAM transmultiplexer, can provide well-contained communication channels with high isolation to adjacent, nonsynchronous signals. However, the orthogonality conditions between subchannels for this kind of systems require special solutions in pilot design. The auxiliary pilot approach permits creating pilots that can take advantage of the basic synchronization procedures for OFDM to estimate the fractional time delay, carrier offsets, and communication channel. More important, it enables the design of FBMC-specific synchronization and channel estimation methods taking into account the interplay of the different stages involved in estimating and compensating for the distortions experienced by the signal. The utilized low-complexity subchannel-wise equalizer for filter banks can use these estimates for equalizing the channel and also to correct distortions caused by incorrect timing or frequency tuning in an efficient way. We have also presented a novel iterative interference cancelation (IIC) approach that estimates the fractional time delay and can return channel estimates by iterating an optimization routine specific to the low-complexity equalizer.
The mentioned synchronization apparatus was put to test in a 10 MHz WiMAX-like communications scenario, where the discussed tools succeed in estimating and compensating the channel distortions. Special emphasis is put on maintaining as many compatible physical layer elements with WiMAX as possible. As a matter of fact, the FBMC system can be updated to send over more subchannels and more MC symbols within the given time frame and system bandwidth, compared to the OFDM-based WiMAX, while achieving similar BER performance. For example, if a whole frame is used for downlink transmission and a 40 dB attenuation is assumed at the transmission band limits, the additional MC symbols and subcarriers in the FBMC-based system permit transmitting 16% more QAM symbols.
Clever reuse of the subchannel equalizer leads to improved BER performance, compared to basic techniques, especially for higher order modulations, for example, 64-QAM. In this case, performance degradation with significant synchronization offsets is due to insufficient compensation by the synchronization subsystem, whereas with more robust modulations, such as 4-QAM, the bottleneck is in the estimation performance, that is, the performance after compensation is satisfactory as long as estimation is acceptable, which mainly depends on the pilot distribution. In this sense, the introduced joint FTD and channel estimation approach can outperform the conventional method under favorable channel conditions (good SNR and low mobility) allowing acceptable reception under severe FTD. In adverse conditions, it provides sufficiently good estimates for a wide range of FTD, making it suitable for coarse estimation and synchronization of robust data signals.
This can also be exploited when multiple-input multiple-output (MIMO) techniques are used to improve the throughput. The pilots of one transmit antenna have to coincide with "silence" on the other antennas to enable MIMO channel estimation similar as in the single stream case. If the pilot (including the "silent pilots") overhead is to remain the same, as for example in the optional 2 antenna WiMAX AMC transmission [3], the density of active pilots that can be used for actual estimation of the MIMO channel diminishes. In this scenario of greater separation of active pilots, the new FTD estimation with its wider estimation range can prove itself very practical.
Some of the simulation results of Section 5 were obtained for small- and medium-sized transmission bursts. Since the FTD and CFO values are relatively slowly changing in most wireless communication scenarios, it is always possible to refine the estimates by filtering them over multiple transmission bursts to reduce the random variations of block-wise estimates.
An attractive aspect of the presented method is that it operates completely in the frequency domain, after the analysis filter bank. This is especially useful in cognitive radio scenarios, in which high spectral containment and resolution permit secondary users to exploit appearing and vanishing spectral time-frequency holes in the communications of the primary system. Processing after the AFB means that the signal has been well delimited in frequency domain.
In an uplink multiuser scenario, a base station using the presented synchronization, estimation, and equalization methods for FBMC can independently synchronize different users in different bands transmitting in an unsynchronized way, that is, with different FTDs, as long as they are separated by a guard band of at least one subchannel. The bands assigned to each user are processed subcarrier-wise and independently. It is not necessary for the users to transmit synchronously because the guard subchannel assures that the signals remain orthogonal to each other, independently of their relative timings.
A possible direction of future work is to examine the behavior of smaller filter banks in the same bandwidth, with higher subcarrier spacings. This situation poses challenges to the estimation part, since the use of scattered pilots is not that well justified when the subchannel channel is not flat fading anymore.
All in all, we conclude that FBMC can perform sufficiently well to offer an alternative to OFDM as modulation and multiple access technique, offering several advantages especially as a cognitive radio physical layer.
References
van Nee R, Prasad R: OFDM for Wireless Multimedia Communications. Artech House, Boston, Mass, USA; 2000.
WiMAX Forum : Mobile system profile. Release 1.0 Approved Specification, Revision 1.5.0, November 2007
IEEE standard for local and metropolitan area networks. Part 16: air interface for fixed and mobile broadband wireless access systems. Amendment 2: physical and medium access control layers for combined fixed and mobile operation in licensed bands and corrigendum 1 IEEE Std 802.16e-2005 and IEEE Std 802.16-2004/Cor 1-2005 (Amendment and Corrigendum to IEEE Std 802.16-2004), pp. 1–822, 2006
TSG-RAN 3GPP TS 36.211 : Physical channels and modulation. Release 8, February 2009
Siohan P, Siclet C, Lacaille N: Analysis and design of OFDM/OQAM systems based on filterbank theory. IEEE Transactions on Signal Processing 2002, 50(5):1170-1183. 10.1109/78.995073
Malvar HS: Signal Processing with Lapped Transforms. Artech House, Boston, Mass, USA; 1992.
Mitola J III, Maguire GQ Jr.: Cognitive radio: making software radios more personal. IEEE Personal Communications 1999, 6(4):13-18. 10.1109/98.788210
Haykin S: Cognitive radio: brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications 2005, 23(2):201-220.
Thomson D: Spectrum estimation and harmonic analysis. Proceedings of the IEEE 1982, 70(9):1055-1096.
Farhang-Boroujeny B, Kempter R: Multicarrier communication techniques for spectrum sensing and communication in cognitive radios. IEEE Communications Magazine 2008, 46(4):80-85.
Manton JH: Optimal training sequences and pilot tones for OFDM systems. IEEE Communications Letters 2001, 5(4):151-153. 10.1109/4234.917097
Pun M, Morelli M, Jay Kuo C: Multi-Carrier Techniques for Broadband Wireless Communications. A Signal Processing Perspective. Imperial College Press, London, UK; 2007.
van de Beek J-J, Sandell M, Börjesson PO: ML estimation of time and frequency offset in OFDM systems. IEEE Transactions on Signal Processing 1997, 45(7):1800-1805. 10.1109/78.599949
Fusco T, Petrella A, Tanda M: Data-aided symbol timing and CFO synchronization for filter bank multicarrier systems. IEEE Transactions on Wireless Communications 2009, 8(5):2705-2715.
Hidalgo Stitz T, Ihalainen T, Renfors M: Practical issues in frequency domain synchronization for filter bank based multicarrier transmission. Proceedings of the 3rd International Symposium on Communications, Control, and Signal Processing (ISCCSP '08), March 2008, St. Julians, Malta 411-416.
Bölcskei H: Blind estimation of symbol timing and carrier frequency offset in wireless OFDM systems. IEEE Transactions on Communications 2001, 49(6):988-999. 10.1109/26.930629
Lélé C, Javaudin J-P, Legouable R, Skrzypczak A, Siohan P: Channel estimation methods for preamble-based OFDM/OQAM modulations. Proceedings of the European Wireless Conference, April 2007, Paris, France
Javaudin J-P, Lacroix D, Rouxel A: Pilot-aided channel estimation for OFDM/OQAM. Proceedings of the 57th IEEE Semiannual Vehicular Technology Conference (VTC '03), April 2003 3: 1581-1585.
Hidalgo Stitz T, Viholainen A, Ihalainen T, Renfors M: CFO estimation and correction in a WiMAX-like FBMC system. Proceedings of IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '09), June 2009, Perugia, Italy 633-637.
Jahan B, Lanoiselée M, Degoulet G, Rabineau R: Full synchronization method for OFDM/OQAM and OFDM/QAM modulations. Proceedings of IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA), June 2008, Perugia, Italy 344-348.
Alhava J, Renfors M: Exponentially-modulated filter bank-based transmultiplexer. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS), May 2003, Bangkok, Thailand 4: 233-236.
Mirabbasi S, Martin K: Overlapped complex-modulated transmultiplexer filters with simplified design and superior stopbands. IEEE Transactions on Circuits and Systems II 2003, 50(8):456-469. 10.1109/TCSII.2003.813592
Vaidyanathan PP: Multirate Systems and Filter Banks. Prentice-Hall, Englewood Cliffs, NJ, USA; 1993.
Viholainen A, Ihalainen T, Hidalgo Stitz T, Renfors M, Bellanger M: Prototype filter design for filter bank based multicarrier transmission. Proceedings of European Signal Processing Conference (EUSIPCO), August 2009, Glasgow, Scotland
Bregović R: Optimal design of perfect-reconstruction and nearly perfect-reconstruction multirate filter banks, Ph.D. dissertation. Tampere University of Technology, TUT Publications 428, Tampere, Finland; 2003.
Martín-Martín P, Bregović R, Martín-Marcos A, Cruz-Roldán F, Saramäki T: A generalized window approach for designing transmultiplexers. IEEE Transactions on Circuits and Systems I 2008, 55(9):2696-2706.
Martin KW: Small side-lobe filter design for multitone data-communication applications. IEEE Transactions on Circuits and Systems II 1998, 45(8):1155-1161. 10.1109/82.718830
Bellanger MG: Specification and design of a prototype filter for filter bank based multicarrier transmission. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '01), May 2001 4: 2417-2420.
Le Floch B, Alard M, Berrou C: Coded orthogonal frequency division multiplex. Proceedings of the IEEE 1995, 83(6):829-996.
Vahlin A, Holte N: Optimal finite duration pulses for OFDM. IEEE Transactions on Communications 1996, 44(1):10-14. 10.1109/26.476088
Sandberg SD, Tzannes MA: Overlapped discrete multitone modulation for high speed copper wire communications. IEEE Journal on Selected Areas in Communications 1995, 13(9):1571-1585. 10.1109/49.475531
Vandendorpe L, Cuvelier L, Deryck F, Louveaux J, Van de Wiel O: Fractionally spaced linear and decision-feedback detectors for transmultiplexers. IEEE Transactions on Signal Processing 1998, 46(4):996-1011. 10.1109/78.668552
Hirosaki B: An analysis of automatic equalizers for orthogonally multiplexed QAM systems. IEEE Transactions on Communications Systems 1980, 28(1):73-83. 10.1109/TCOM.1980.1094576
Wiegand T, Fliege NJ: Equalizers for transmultiplexers in orthogonal multiple carrier data transmission. Proceedings of European Signal Processing Conference (EUSIPCO), September 1996, Trieste, Italy 2: 1211-1214.
Nedic S: An unified approach to equalization and echo cancellation in OQAM-based multi-carrier data transmission. Proceedings of the IEEE Global Telecommunications Conference, November 1997, Phoenix, Ariz, USA 3: 1519-1523.
van Acker K, Leus G, Moonen M, van de Wiel O, Pollet T: Per tone equalization for DMT-based systems. IEEE Transactions on Communications 2001, 49(1):109-119. 10.1109/26.898255
Wyglinski AM, Kabal P, Labeau F: Adaptive filterbank multicarrier wireless systems for indoor environments. Proceddings of IEEE Vehicular Technology Conference, September 2002, Vancouver, Canada 336-340.
Waldhauser DS, Baltar LG, Nossek JA: MMSE subcarrier equalization for filter bank based multicarrier systems. Proceedings of IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '08), July 2008 525-529.
Ihalainen T, Hidalgo Stitz T, Rinne M, Renfors M: Channel equalization in filter bank based multicarrier modulation for wireless communications. EURASIP Journal on Advances in Signal Processing 2007, 2007:-18.
Renfors M, Ihalainen T, Hidalgo Stitz T: Channel equalization. Patent EP1 716 681, November 2008
Lélé C: OFDM/OQAM modulation: channel estimation methods, and applications to multicarrier CDMA and multi-antenna transmission, Ph.D. dissertation. Conservatoire National des Arts et Métiers; November 2008.
Lélé C, Legouable R, Siohan P: Iterative scattered pilot channel estimation in OFDM/OQAM. Proceedings of IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '09), June 2009 176-180.
Kay S: Fast and accurate single frequency estimator. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(12):1987-1990. 10.1109/29.45547
ITU-R : Guidelines for evaluation of radio transmission technologies for IMT-2000. Recommendation M.1225, 1997
INFSO-ICT-211887 Project PHYDYAS : Deliverable 2.2: synchronization and initialization with single antenna. Blind techniques. January 2009, http://www.ict-phydyas.org/userfiles/file/Phydyas-D2-2.pdf
Acknowledgments
This research was supported in part by the European Commission under Project PHYDYAS (FP7-ICT-2007-1-211887). The authors would like to acknowledge the valuable contributions of their colleagues in the PHYDYAS project. They also wish to thank the reviewers and the editor for their comments that helped to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Stitz, T., Ihalainen, T., Viholainen, A. et al. Pilot-Based Synchronization and Equalization in Filter Bank Multicarrier Communications. EURASIP J. Adv. Signal Process. 2010, 741429 (2010). https://doi.org/10.1155/2010/741429
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/741429

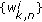 are solved from pilots
are solved from pilots  . Note that here
. Note that here  is the iteration index.
is the iteration index. are known, the observation is a linear function of
are known, the observation is a linear function of  and the optimum
and the optimum  can easily be calculated with the derivative of the expression in brackets in (35) with respect to
can easily be calculated with the derivative of the expression in brackets in (35) with respect to 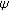 and setting the result to 0, yielding
and setting the result to 0, yielding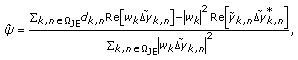
 . Note that
. Note that  is here the average of
is here the average of  within subchannel
within subchannel  . This process converges typically in 5–10 iterations, depending on the FTD and
. This process converges typically in 5–10 iterations, depending on the FTD and  . Moreover, the estimates
. Moreover, the estimates  are quite accurate even for higher values of
are quite accurate even for higher values of  , as will be seen in Section 5.
, as will be seen in Section 5.




 . 64-QAM transmission with perfect channel information (PCI) and pilot-based estimation in a quasistatic channel.
. 64-QAM transmission with perfect channel information (PCI) and pilot-based estimation in a quasistatic channel.
 dB, 64-QAM modulation. BER versus CFO with fixed FTD
dB, 64-QAM modulation. BER versus CFO with fixed FTD  and
and  BER versus FTD with fixed CFO
BER versus FTD with fixed CFO  and
and 

 dB using 64-QAM. Different synchronization options.
dB using 64-QAM. Different synchronization options.
 dB using 4-QAM. OFDM- and FBMC-based WiMAX. FBMC Synchronization performed with CFO amplitude compensation in the 3-tap equalizer and one synchronization iteration.
dB using 4-QAM. OFDM- and FBMC-based WiMAX. FBMC Synchronization performed with CFO amplitude compensation in the 3-tap equalizer and one synchronization iteration.
 and
and dB using 4-QAM. Static user and user with 60 km/h mobility. Synchronization with CFO amplitude distortion correction and one iteration.
dB using 4-QAM. Static user and user with 60 km/h mobility. Synchronization with CFO amplitude distortion correction and one iteration.
 values are referred to 4-QAM modulation.RMS CFO error versus CFO at fixed FTD
values are referred to 4-QAM modulation.RMS CFO error versus CFO at fixed FTD  RMS FTD error versus FTD at fixed CFO
RMS FTD error versus FTD at fixed CFO 

 dB. Static user. No additional synchronization iteration.
dB. Static user. No additional synchronization iteration.
 dB. Static user. No additional synchronization iteration.
dB. Static user. No additional synchronization iteration.