- Research Article
- Open access
- Published:
Application of Linear Prediction Technique to Passive Synthetic Aperture Processing
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 751069 (2010)
Abstract
A method for the synthesis of an aperture with improved angular resolution and array gain is described. The proposed method explores the merit of linear prediction technique to improve the performance of conventional ETAM (extended towed array measurements) method. Previous efforts to improve the ETAM method generally focused on how to get more accurate estimation of overlap correlator, with an aim to reduce bearing estimation variance. In this paper, however, we discuss how to further improve the angular resolution when the effective synthetic aperture is rather limited. We resort to linear prediction technique to further extend the synthetic aperture obtained by ETAM, which produces a much longer virtual aperture. Results from simulations and lake experiment showed that the proposed LP-ETAM method achieved better angular resolution than ETAM.
1. Introduction
Line arrays are widely used in underwater acoustics to measure the spatial field of propagating acoustic waves. When employing conventional beamforming techniques, the angular resolution and the signal gain are proportional to the ratio of aperture length to signal wavelength. High bearing resolution becomes more important and more difficult to achieve as the frequency regime is made lower in order to increase the detection range. Because increased low-frequency bearing resolution means longer hydrophone arrays, it is not practical to increase the physical length of line arrays in order to match the coherence length of signals. An alternative approach in this case is to employ coherent synthesis of subapertures, namely, synthetic aperture technique.
Application of synthetic aperture technique to passive sonar has received a sustained interest for more than twenty years. This technique exploits the array motion and the temporal coherence of narrow band received signals to build a large synthetic array, resulting in an improvement in beamforming performance compared with that of the short physical array.
As it is widely known, there are four typical methods for passive synthetic array, namely, the method introduced by Yen and Carey [1], Extended towed-array measurements (ETAM) [2], Maximum Likelihood method (ML) [3], and FFT Synthetic Aperture processing method (FFTSA) [4]. The method introduced by Yen and Carey is a processing technique in the beam domain which provides coherent processing of subapertures by proper selection of a phase term based on knowledge or the use of a velocity filter concept for the source-receiver relative speed. In the ETAM algorithm, developed by Stergiopoulos and Sullivan, the successive subaperture signals are coherently synthesized in the aperture domain into an extended aperture size by using a phase correction factor, which is derived by cross-correlating overlapping space samples of the acoustic signal received at successive moments by the moving array. The ML method requires the acquisition of very long hydrophone time series over an interval which is required by the moving towed array to travel a distance equivalent to the desired length of the synthetic aperture. It performs a two-dimensional search in equivalent phase and frequency domains to yield the best estimates of the unknown parameters. FFTSA method is like the method introduced by Yen and Carey, but it does not need the velocity information. It performs coherent processing of subaperture signals at successive time intervals in the beam domain via FFT transformations. Theoretical studies and sea experiments showed that ETAM method yielded the best performance among them [5, 6].
So far, there have emerged many improved versions of ETAM method, most of which endeavor to improve the bearing estimation precision by working on the overlap correlator [7, 8]. But in this paper, we try to improve the angular resolution of ETAM method. As well known, in real sea environment, the effective synthetic aperture is limited by the coherence length of underwater signals. In some adverse sea environments [9], the effective synthetic aperture size is only 1.5 times of the physical array. Thus, how to further improve the bearing resolution within the effective synthetic aperture is a meaningful problem.
Linear prediction (LP) is a technique widely used in the data processing field. It predicts the time series in the future or in the past according to obtained time series. In recent years linear prediction technique has found extensive applications in the fields of voice identification, image processing, and signal frequency estimation [10–12]. This paper incorporates spatial linear prediction technique into the ETAM method to propose a new hybrid technique called LP-ETAM method for the bearing estimation of multiple coherent underwater targets. The proposed method employs spatial linear prediction technique to do extrapolation on the synthetic aperture obtained by ETAM to further enlarge the aperture size, which is the main reason leading to superior bearing resolution to ETAM method. Results from simulations and applications of the ETAM and LP-ETAM method on real data with pure tone CW signals showed that the proposed LP-ETAM method achieved better angular resolution than ETAM method.
2. Review of Conventional ETAM Method
In this section we describe the conventional ETAM method for underwater towed arrays.
Consider an  -element uniform line array moving at constant speed in the direction of
-element uniform line array moving at constant speed in the direction of  -axis. There exists a signal with a frequency of
-axis. There exists a signal with a frequency of  and with an azimuth of
and with an azimuth of  (relative to the array normal) in the farfield. Suppose that the signal is sampled at an interval of
(relative to the array normal) in the farfield. Suppose that the signal is sampled at an interval of  we denote
we denote  =
=  =
=  Then the output of the
Then the output of the  th array sensor at time
th array sensor at time  is
is

where 
 is signal amplitude and
is signal amplitude and  is sound velocity.
is sound velocity.
The  in (1) includes Doppler shift caused by the relative movement between the array and the signal. It is generally expressed as
in (1) includes Doppler shift caused by the relative movement between the array and the signal. It is generally expressed as

Substitute (2) into (1) and omit the high-order terms  we have
we have

Then the output of the  th array element at time
th array element at time  is
is

Select  and
and  so that
so that  where
where  represents the number of sensor positions that has moved during time
represents the number of sensor positions that has moved during time  Thus (4) can be rewritten as
Thus (4) can be rewritten as

From (3) it is easy to know that the output of the  th array element at time
th array element at time  is
is

For two consecutive sets of measurements,  and
and  represent the outputs of array elements which have the same position in space but differ by time
represent the outputs of array elements which have the same position in space but differ by time 
Comparing (5) and (6), we know the only difference between them is the term  if their noise terms are omitted
if their noise terms are omitted

In view of the systematic and random effects due to physical processes, we introduce a phase  thus (7) is modified as
thus (7) is modified as

Here we denote  as the phase correction factor. In order to compute the least-square estimate of
as the phase correction factor. In order to compute the least-square estimate of  first we compute
first we compute

where the superscript  denotes complex conjugate,
denotes complex conjugate,  is the number of overlapped sensors between two consecutive sets of measurements. So a least-square estimate of the phase correction factor is given by
is the number of overlapped sensors between two consecutive sets of measurements. So a least-square estimate of the phase correction factor is given by

So at time  the output of the (
the output of the ( )th sensor (a virtual extended sensor)
)th sensor (a virtual extended sensor)  is equal to the product of
is equal to the product of  and
and  , namely,
, namely,

In other words, the number of array sensors is increased from  to
to  through one measurement. Repeat the same process, after
through one measurement. Repeat the same process, after  measurements the total number of the synthetic array sensors is
measurements the total number of the synthetic array sensors is 
3. Basic Concepts for Linear Prediction Technique
Linear prediction (LP) is a technique widely used in the data processing field. It predicts the time series in the future or in the past according to obtained time series, which are called forward prediction and backward prediction, respectively. Assuming that the signal output  is the linear combination of
is the linear combination of  samples before time
samples before time  and the coefficients maintain the same value from one sample to the next, this is called forward prediction. Next, we outline the process of the linear prediction technique by taking forward prediction as an example.
and the coefficients maintain the same value from one sample to the next, this is called forward prediction. Next, we outline the process of the linear prediction technique by taking forward prediction as an example.
Assuming that  is a random series then the
is a random series then the  -order forward prediction
-order forward prediction  of
of  is defined as
is defined as

where  is called linear prediction coefficient, when
is called linear prediction coefficient, when  satisfies Yule-Walker equation as follows
satisfies Yule-Walker equation as follows

The averaged squared value  of linear prediction error
of linear prediction error  reaches its minimum where
reaches its minimum where

Obviously, the calculation of the prediction coefficients  for the
for the  th order filter is of paramount importance. The classical method to calculate prediction coefficient
th order filter is of paramount importance. The classical method to calculate prediction coefficient  is to solve (13) directly. In practice, since
is to solve (13) directly. In practice, since  is usually unknown, (14) is estimated by obtained sample series
is usually unknown, (14) is estimated by obtained sample series 
4. LP-ETAM Method
According to linear prediction theory, the delayed sample points in the time domain correspond to the array sensors in the spatial domain. For the  -sensor uniform line array, the
-sensor uniform line array, the  -order forward prediction filter in the spatial domain uses the data of the first
-order forward prediction filter in the spatial domain uses the data of the first  sensors to estimate the data of the
sensors to estimate the data of the  th sensor, while the
th sensor, while the  -order backward prediction filter in the spatial domain uses the data of the last
-order backward prediction filter in the spatial domain uses the data of the last  sensors to estimate the data of the sensor before them.
sensors to estimate the data of the sensor before them.
Assume the data vector for the  snapshots of the
snapshots of the  th sensor as
th sensor as  then the
then the  -order forward prediction filter is
-order forward prediction filter is

The equation (15) can be written in short as

From (16) we can get the vector for the forward prediction coefficients

In the same way,  -order backward prediction filter is
-order backward prediction filter is

The equation (18) can be written in short as

Then the vector for the backward prediction coefficients is

After we get the prediction coefficients, we can use them to extrapolate the array sensors. The array is extended as a sensor at one time. The forward prediction coefficients are used to extend the array forwardly. The backward prediction coefficients are used to extend the array backwardly.
The formula for forward prediction is

where  is the forward prediction coefficient appearing in (15).
is the forward prediction coefficient appearing in (15).
Similarly, the formula for backward prediction is

where  is the backward prediction coefficient appearing in (18).
is the backward prediction coefficient appearing in (18).
Figure 1 illustrates the forward prediction process described by (21). In our proposed LP-ETAM method, abovementioned linear prediction technique is applied to the synthetic array obtained by ETAM method to further enlarge the aperture size, which results in improved performance over ETAM method.
Now we summarize the steps of the proposed LP-ETAM method in the following.
-
(1)
To extend the
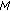 -sensor physical array to
-sensor physical array to 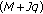 -sensor synthetic array by conventional ETAM method.
-sensor synthetic array by conventional ETAM method. -
(2)
To determine the prediction filter order
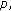 calculate the forward and backward prediction coefficients according to (17) and (20).
calculate the forward and backward prediction coefficients according to (17) and (20). -
(3)
To extend the
 -sensor synthetic array to
-sensor synthetic array to 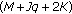 -sensor virtual array by forward and backward prediction filter. In this process,
-sensor virtual array by forward and backward prediction filter. In this process,  sensors are extrapolated to the left and right of the synthetic array, respectively.
sensors are extrapolated to the left and right of the synthetic array, respectively. -
(4)
To get the bearing estimation of targets by applying conventional beamforming technique to the virtual array obtained in step 3. Notice that the dimension of the steering vector is
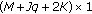 .
.
Figure 2 gives the array aperture extension process in the proposed LP-ETAM method.
5. Performance Analysis
5.1. Angular Resolution
The performance of the LP-ETAM method has been tested with synthetic data; the relevant results are presented in this section. The far-field acoustic pressure measurements of a towed array have been simulated according to (1). In the numerical experiment, an 8-hydrophone towed array is considered with 1 m spacing moving with 5-knot speed. The received signal is assumed to be a narrow-band CW at 330 Hz. The  at the hydrophone is
at the hydrophone is 
 . In our simulations, the performance of the LP-ETAM method is compared with conventional beamforming method (CBF) and ETAM method. The integration time used to synthesize the aperture is 24
. In our simulations, the performance of the LP-ETAM method is compared with conventional beamforming method (CBF) and ETAM method. The integration time used to synthesize the aperture is 24  , and the 8-hydrophone towed array is extended to a 64-hydrophone synthetic aperture by ETAM and a 192-hydrophone virtual aperture by LP-ETAM. The values of other parameters are
, and the 8-hydrophone towed array is extended to a 64-hydrophone synthetic aperture by ETAM and a 192-hydrophone virtual aperture by LP-ETAM. The values of other parameters are  ,
,  and
and 
Figure 3 shows the directivity power patterns of the beamformer output for the three different methods when there is a single source with bearings at  . It is obvious that the mainlobe of LP-ETAM is much narrower than that of ETAM and CBF, indicating that LP-ETAM has the best angular resolution ability.
. It is obvious that the mainlobe of LP-ETAM is much narrower than that of ETAM and CBF, indicating that LP-ETAM has the best angular resolution ability.
Figure 4 shows the directivity power patterns of the beamformer output for the three different methods when there are two widely spaced sources with bearings at  and
and  We notice that CBF cannot resolve the two sources but both LP-ETAM and ETAM can resolve them. Though both LP-ETAM and ETAM can resolve the two sources, the detection threshold for LP-ETAM is much lower than that of ETAM. This is easily deduced from the fact that the valley between the two source directions for LP-ETAM is deeper than the valley between the two source directions for ETAM.
We notice that CBF cannot resolve the two sources but both LP-ETAM and ETAM can resolve them. Though both LP-ETAM and ETAM can resolve the two sources, the detection threshold for LP-ETAM is much lower than that of ETAM. This is easily deduced from the fact that the valley between the two source directions for LP-ETAM is deeper than the valley between the two source directions for ETAM.
Figure 5 shows similarly the directivity power patterns when there are two closely spaced sources with bearings at  and
and  We notice that both CBF and ETAM cannot resolve the two sources while LP-ETAM can resolve them, which means that LP-ETAM is superior to the other methods in angular resolution.
We notice that both CBF and ETAM cannot resolve the two sources while LP-ETAM can resolve them, which means that LP-ETAM is superior to the other methods in angular resolution.
Figure 6 compares the probability of resolution for ETAM and LP-ETAM according to various  . Two sources with azimuths
. Two sources with azimuths  and
and  are considered successfully "resolved" if both
are considered successfully "resolved" if both  and
and  are less than
are less than  , where
, where  is the estimate of
is the estimate of  and
and  is the estimate of
is the estimate of  . If two sources are successfully resolved
. If two sources are successfully resolved  times in
times in  independent trials, the probability of resolution is
independent trials, the probability of resolution is  . In this simulation two sources are assumed to be located at
. In this simulation two sources are assumed to be located at  and
and  and 100 independent trials are performed. We can see that the proposed LP-ETAM method has better resolution at low
and 100 independent trials are performed. We can see that the proposed LP-ETAM method has better resolution at low  compared with ETAM method.
compared with ETAM method.
Figure 7 shows the root mean squared errors (RMSE) of ETAM and LP-ETAM according to various  . The simulation conditions are the same as those used for Figure 6. It can be seen that the proposed LP-ETAM method does not produce better RMSE result. It is easy to understand since the proposed method is based on ETAM that the linear prediction technique helps extend the aperture but contributes little to reduce the bearing estimation variance.
. The simulation conditions are the same as those used for Figure 6. It can be seen that the proposed LP-ETAM method does not produce better RMSE result. It is easy to understand since the proposed method is based on ETAM that the linear prediction technique helps extend the aperture but contributes little to reduce the bearing estimation variance.
5.2. Array Gain
In order to discuss array gain, we first define cross-correlation coefficients between different hydrophones. For a frequency band  with central frequency
with central frequency  the normalized cross-correlation coefficient between the
the normalized cross-correlation coefficient between the  th and
th and  th hydrophones is defined as [9]
th hydrophones is defined as [9]

where 
 are the frequency bins in the band
are the frequency bins in the band  with central frequency
with central frequency 
The performance of a line array to an acoustic signal embodied in a noise field is characterized by the "array gain" parameter. When the noise field is white and isotropic, array gain is expressed as

where  is the number of hydrophones in the physical array or extended array.
is the number of hydrophones in the physical array or extended array.
Figure 8 presents the normalized cross-correlation coefficients  (
( ) for the ETAM results of Figure 5 for the 100 Hz band in the frequency range 280–380 Hz with central frequency 330 Hz, which is the frequency of the two CW sources. The value of each coefficient is expressed as a circle in figure. The results in Figure 8 provide a quantitative estimate of the effectiveness of the extended aperture. Since the magnitude values of the coefficients are close to unity, it is apparent that the 64-hydrophone extended aperture is equivalent to a fully populated physical array.
) for the ETAM results of Figure 5 for the 100 Hz band in the frequency range 280–380 Hz with central frequency 330 Hz, which is the frequency of the two CW sources. The value of each coefficient is expressed as a circle in figure. The results in Figure 8 provide a quantitative estimate of the effectiveness of the extended aperture. Since the magnitude values of the coefficients are close to unity, it is apparent that the 64-hydrophone extended aperture is equivalent to a fully populated physical array.
Figure 9 presents the normalized cross-correlation coefficients  (
( ,
,  ) for the LP-ETAM results of Figure 5. We can see that the values are still close to unity even if the array aperture has been further extended, indicating the degree of coherence of the phase information related to the bearings of the sources across the extended apertures
) for the LP-ETAM results of Figure 5. We can see that the values are still close to unity even if the array aperture has been further extended, indicating the degree of coherence of the phase information related to the bearings of the sources across the extended apertures
The next step is to calculate the array gain for the physical and the synthetic apertures by using (24) and the values of the coefficients  shown in Figures 8 and 9. The expected array gain estimates for an 8-hydrophone, a 64-hydrophone, and a 192-hydrophone physical arrays are 9 dB, 18 dB, and 22.8 dB, respectively. The experimental array gain estimates for the 8-hydrophone physical array, the 64-hydrophone and the 192-hydrophone extended aperture are 6.9 dB, 15.8 dB, and 20.6 dB, respectively.
shown in Figures 8 and 9. The expected array gain estimates for an 8-hydrophone, a 64-hydrophone, and a 192-hydrophone physical arrays are 9 dB, 18 dB, and 22.8 dB, respectively. The experimental array gain estimates for the 8-hydrophone physical array, the 64-hydrophone and the 192-hydrophone extended aperture are 6.9 dB, 15.8 dB, and 20.6 dB, respectively.
6. Lake Experiments
The lake experiment was designed to evaluate the angular resolution provided by the LP-ETAM method and the ETAM method in comparison with that provided by the physical array.
The measurement procedure in this experiment included one tow ship and two stationary projectors. The tow ship was used to tow a receiving array along a straight line course at 5 knots with 8 hydrophones spaced at 1 m and at 20 m depth. The experiments were carried out in a lake in south China. The water depth was 40 m. The data acquisition and control system included amplification of the hydrophone signals, bandpass filtering, digitization, and continuous recording on a high performance digital recorder for offline processing of the time series. Two projectors transmitting CW signals at 650 Hz were placed 400 meters apart, and they were moored at 20 m depth approximately 10 km from the towed array.
Results from the application of the LP-ETAM on the 8-hydrophone towed array for a 24-second observation period are shown in Figure 10. Hamming shading is adopted in each method prior to beamforming. The bearing estimates from the LP-ETAM method, shown by the dotted line in Figure 10, indicate the presence of the two expected sources while CBF and ETAM fail. This demonstrates the effectiveness of the proposed LP-ETAM method to provide improved angular resolution with respect to that provided by CBF and ETAM.
7. Conclusion
This paper focuses on the development of a new passive synthetic aperture technique that explores the merits of both linear prediction technique and ETAM method. The proposed LP-ETAM method employs spatial linear prediction technique to do extrapolation on the synthetic aperture obtained by ETAM to further enlarge the aperture size, which leads to superior angular resolution to conventional ETAM method. Simulation analysis shows that the proposed LP-ETAM method yields narrower beams and higher array gain than ETAM method. Results from application of ETAM method and the proposed LP-ETAM method on real data with very stable CW signals have shown that the angular resolution provided by LP-ETAM resolves two closely spaced sources that are unresolvable by the ETAM method.
References
Yen N-C, Carey W: Application of synthetic-aperture processing to towed-array data. Journal of the Acoustical Society of America 1989, 86(2):754-765. 10.1121/1.398758
Stergiopoulos S: Extended towed array processing by an overlap correlator. Journal of the Acoustical Society of America 1989, 86(1):158-171. 10.1121/1.398335
Nuttall AH: The maximum likelihood estimator for acoustic synthetic aperture processing. IEEE Journal of Oceanic Engineering 1992, 17(1):26-29. 10.1109/48.126951
Stergiopoulos S, Urban H: A new passive synthetic aperture technique for towed arrays. IEEE Journal of Oceanic Engineering 1992, 17(1):16-25. 10.1109/48.126950
Edelson GS, Tufts DW: On the ability to estimate narrow-band signal parameters using towed arrays. IEEE Journal of Oceanic Engineering 1992, 17(1):48-61. 10.1109/48.126954
Rajagopal R, Rao PR: Performance comparison of PASA beamforming algorithms. Proceedings of the International Symposium on Signal Processing and Its Applications (ISSPA '96), August 1996, Gold Coast, Australia 2: 825-828.
Rajagopal R, Rao PR: Modified extended towed array method (METAM) for passive synthetic aperture beamforming. Proceedings of the International Symposium on Signal Processing and Its Applications (ISSPA '96), August 1996, Gold Coast, Australia 2: 772-775.
Kim S, Youn DH, Lee C: Temporal domain processing for a synthetic aperture array. IEEE Journal of Oceanic Engineering 2002, 27(2):322-327. 10.1109/JOE.2002.1002487
Stergiopoulos S, Urban H: An experimental study in forming a long synthetic aperture at sea. IEEE Journal of Oceanic Engineering 1992, 17(1):62-72. 10.1109/48.126955
Zhang ZG, Chan SC, Tsui KM: A recursive frequency estimator using linear prediction and a Kalman-filter-based iterative algorithm. IEEE Transactions on Circuits and Systems II 2008, 55(6):576-580.
Ekman LA, Kleijn WB, Murthi MN: Regularized linear prediction of speech. IEEE Transactions on Audio, Speech and Language Processing 2008, 16(1):65-73.
Andriani S, Calvagno G: Lossless compression of color sequences using optimal linear prediction theory. IEEE Transactions on Image Processing 2008, 17(11):2102-2111.
Acknowledgment
This work was supported by the National Natural Science Foundation of China (60972152), Aeronautical Science Foundation of China (2009ZC53031), and the Basic Research Foundation of Northwestern Polytechnical University (NPU-FFR-W018102).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hou, Y., Huang, J., Jiang, M. et al. Application of Linear Prediction Technique to Passive Synthetic Aperture Processing. EURASIP J. Adv. Signal Process. 2010, 751069 (2010). https://doi.org/10.1155/2010/751069
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/751069

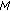 -sensor physical array to
-sensor physical array to 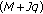 -sensor synthetic array by conventional ETAM method.
-sensor synthetic array by conventional ETAM method.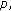 calculate the forward and backward prediction coefficients according to (17) and (20).
calculate the forward and backward prediction coefficients according to (17) and (20). -sensor synthetic array to
-sensor synthetic array to 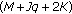 -sensor virtual array by forward and backward prediction filter. In this process,
-sensor virtual array by forward and backward prediction filter. In this process,  sensors are extrapolated to the left and right of the synthetic array, respectively.
sensors are extrapolated to the left and right of the synthetic array, respectively.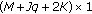 .
.







