- Research Article
- Open access
- Published:
Hidden Markov Model with Duration Side Information for Novel HMMD Derivation, with Application to Eukaryotic Gene Finding
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 761360 (2010)
Abstract
We describe a new method to introduce duration into an HMM using side information that can be put in the form of a martingale series. Our method makes use of ratios of duration cumulant probabilities in a manner that meshes with the column-level dynamic programming construction. Other information that could be incorporated, via ratios of sequence matches, includes an EST and homology information. A familiar occurrence of a martingale in HMM-based efforts is the sequence-likelihood ratio classification. Our method suggests a general procedure for piggybacking other side information as ratios of side information probabilities, in association (e.g., one-to-one) with the duration-probability ratios. Using our method, the HMM can be fully informed by the side information available during its dynamic table optimization—in Viterbi path calculations in particular.
1. Introduction
Hidden Markov models have been extensively used in speech recognition since the 1970s and in bioinformatics since the 1990s. In automated gene finding, there are two types of approaches based on data intrinsic to the genome under study or extrinsic to the genome (e.g., homology and EST data). Since around 2000, the best gene finders have been based on combined intrinsic/extrinsic statistical modeling [1]. The most common intrinsic statistical model is an HMM, so the question naturally arises—how to incorporate side information into an HMM? We resolve that question in this paper by treating duration distribution information itself as side information and demonstrate a process for incorporating that side information into an HMM. We thereby bootstrap from an HMM formalism to a HMM-with-duration (more generally, a hidden semi-Markov model or HSMM). Our method for incorporating side information incorporates duration information precisely as needed to yield an HMMD. In what follows, we apply this capability to actual gene finding, where model sophistication in the choice of emission variables is used to obtain a highly accurate ab initio gene finder.
The original description of an explicit HMMD required computation of order  [2], where
[2], where  is the period of observations,
is the period of observations,  is the number of states, and
is the number of states, and  is the maximum duration of state transitions to self allowed in the model (where
is the maximum duration of state transitions to self allowed in the model (where  is typically >500 in gene-structure identification and channel-current analysis [3]). This is generally too prohibitive (computationally expensive) in practical operations and introduces a severe maximum-interval constraint on the self-transition distribution model. Improvements via hidden semi-Markov models to computations of order
is typically >500 in gene-structure identification and channel-current analysis [3]). This is generally too prohibitive (computationally expensive) in practical operations and introduces a severe maximum-interval constraint on the self-transition distribution model. Improvements via hidden semi-Markov models to computations of order  were described in [4, 5], where the Viterbi and Baum-Welch algorithms were implemented, the latter improvement only obtained as of 2003. In these derivations, however, the maximum-interval constraint is still present (comparisons of these methods were subsequently detailed in [6]). Other HMM generalizations include factorial HMMs [7] and hierarchical HMMs [8]. For the latter, inference computations scaled as
were described in [4, 5], where the Viterbi and Baum-Welch algorithms were implemented, the latter improvement only obtained as of 2003. In these derivations, however, the maximum-interval constraint is still present (comparisons of these methods were subsequently detailed in [6]). Other HMM generalizations include factorial HMMs [7] and hierarchical HMMs [8]. For the latter, inference computations scaled as  in the original description and have since been improved to
in the original description and have since been improved to  by [9]. The above HMMD variants all have a computational inefficiency problem which limits their applications in real-world settings. In [10], a hidden Markov model with binned duration (HMMBD) is shown to be possible with computation complexity of
by [9]. The above HMMD variants all have a computational inefficiency problem which limits their applications in real-world settings. In [10], a hidden Markov model with binned duration (HMMBD) is shown to be possible with computation complexity of  , where
, where  is typically <50 (and can often be as small as 4 or 5, as in the application that follows). These bins are generated by analyzing the state-duration distribution and grouping together neighboring durations if their differences are below some cutoff. In this way, we now have an efficient HMM with duration model that can be applied in many areas that were originally thought impractical. Furthermore, the binning allows us to have a "tail bin" and thereby eliminate the maximum duration restriction.
is typically <50 (and can often be as small as 4 or 5, as in the application that follows). These bins are generated by analyzing the state-duration distribution and grouping together neighboring durations if their differences are below some cutoff. In this way, we now have an efficient HMM with duration model that can be applied in many areas that were originally thought impractical. Furthermore, the binning allows us to have a "tail bin" and thereby eliminate the maximum duration restriction.
In DNA sequence analysis, the observation sequences consist of the nucleotide bases: adenine, thymine, cytosine, and guanine  , and the hidden states are labels associated with regions of exon, intron, and junk
, and the hidden states are labels associated with regions of exon, intron, and junk  . In gene finding, the hidden Markov models usually have to be expanded to include additional requirements, such as the codon frame information, site-specific statistics, and state-duration probability information, and must also follow some exception rules. For example, the start of an initial exon typically begins with "ATG", final exons end with a stop codon
. In gene finding, the hidden Markov models usually have to be expanded to include additional requirements, such as the codon frame information, site-specific statistics, and state-duration probability information, and must also follow some exception rules. For example, the start of an initial exon typically begins with "ATG", final exons end with a stop codon  , and the introns generally follow the GT-AG rule. There are many popular gene finder application programs: AUGUSTUS, Gene Mark, GeneScan, Genie, and so forth [11]. The statistical models employed by Gene Mark and AUGUSTUS involve implementations or approximations of an HMM with duration (HMMD), where state durations are not restricted to be geometric, as in the standard HMM modeling (further details are given in the background section to follow). For the Gene Mark HMMD, the state-duration distributions are an estimation of the length distributions from the training set of sequences, and are characterized by the minimum and maximum duration length allowed. For example, the minimum and maximum durations of introns and intergenic sequences are set to 20 and 10,000 nts. For the AUGUSTUS HMMD, an intron submodel is introduced on durations [12], providing an approximate HMMD modeling on the introns (but not exons, etc.). The improvement to HMMD modeling on the introns is critical to an HMM-based gene finder that can be used in "general use" situations, such as applications to raw genomic sequence (not preprocessed situations, such as one coding sequence in a selected genomic subsequence, as discussed in [13]). The hidden Markov model with binned duration (HMMBD) algorithm, presented in [10], offers a significant reduction in computational time for all HMMD-based methods, to approximately the computational time of the HMM-process alone, while not imposing a maximum duration cutoff, and is used in the implementations and tuning described here. In adopting any model with "more parameters", such as an HMMD over an HMM, there is potentially a problem with having sufficient data to support the additional modeling. This is generally not a problem in any HMM model that requires thousands of samples of nonself transitions for sensor modeling, however, since knowing the boundary positions allows the regions of self-transitions (the durations) to be extracted with similar high sample number as well, for effective modeling of the duration distributions in the HMMD (as will be the case in the genomics analysis to follow).
, and the introns generally follow the GT-AG rule. There are many popular gene finder application programs: AUGUSTUS, Gene Mark, GeneScan, Genie, and so forth [11]. The statistical models employed by Gene Mark and AUGUSTUS involve implementations or approximations of an HMM with duration (HMMD), where state durations are not restricted to be geometric, as in the standard HMM modeling (further details are given in the background section to follow). For the Gene Mark HMMD, the state-duration distributions are an estimation of the length distributions from the training set of sequences, and are characterized by the minimum and maximum duration length allowed. For example, the minimum and maximum durations of introns and intergenic sequences are set to 20 and 10,000 nts. For the AUGUSTUS HMMD, an intron submodel is introduced on durations [12], providing an approximate HMMD modeling on the introns (but not exons, etc.). The improvement to HMMD modeling on the introns is critical to an HMM-based gene finder that can be used in "general use" situations, such as applications to raw genomic sequence (not preprocessed situations, such as one coding sequence in a selected genomic subsequence, as discussed in [13]). The hidden Markov model with binned duration (HMMBD) algorithm, presented in [10], offers a significant reduction in computational time for all HMMD-based methods, to approximately the computational time of the HMM-process alone, while not imposing a maximum duration cutoff, and is used in the implementations and tuning described here. In adopting any model with "more parameters", such as an HMMD over an HMM, there is potentially a problem with having sufficient data to support the additional modeling. This is generally not a problem in any HMM model that requires thousands of samples of nonself transitions for sensor modeling, however, since knowing the boundary positions allows the regions of self-transitions (the durations) to be extracted with similar high sample number as well, for effective modeling of the duration distributions in the HMMD (as will be the case in the genomics analysis to follow).
The breadth of applications for HMMs goes beyond the aforementioned to include gesture recognition [14, 15], handwriting and text recognition [16–19], image processing [20, 21], computer vision [22], communication [23], climatology [24], and acoustics [25, 26] to list a few. HMMs are a central method in all of these approaches not because they are the simplest, most efficient, modeling approach that is obtained when one combines a Bayesian statistical foundation for stochastic sequential analysis with the efficient dynamic programming table constructions possible on a computer. As mentioned above, in many applications, the ability to incorporate the state duration into the HMM is very important because the standard, HMM-based, the Viterbi, and Baum-Welch algorithms are otherwise critically constrained in their modeling ability to distributions on state intervals that are geometric. This can lead to a significant decoding failure in noisy environments when the state-interval distributions are not geometric (or approximately geometric). The starkest contrast occurs for multimodal distributions and heavy-tailed distributions. Critical improvement to overall HMM application rests not only with generalization to HMMD, however, but also to a generalized, fully interpolated, clique HMM, the "meta-HMM" described in [27], and also with the ability to incorporate external information, "side-information", into the HMM, as described in this paper.
2. Background
2.1. Markov Chains and Standard Hidden Markov Models
A Markov chain is a sequence of random variables  ;
;  ;
;  ; … with the Markov property of limited memory, where a first-order Markov assumption on the probability for observing a sequence "
; … with the Markov property of limited memory, where a first-order Markov assumption on the probability for observing a sequence " " is
" is

In the Markov chain model, the states are also the observables. For a hidden Markov model (HMM), we generalize to where the states are no longer directly observable (but still 1st-order Markov), and for each state, say  , we have a statistical linkage to a random variable,
, we have a statistical linkage to a random variable,  , that has an observable base emission, with the standard (0th-order) Markov assumption on prior emissions (see [27] for clique-HMM generalizations). The probability for observing base sequence "
, that has an observable base emission, with the standard (0th-order) Markov assumption on prior emissions (see [27] for clique-HMM generalizations). The probability for observing base sequence " " with state sequence taken to be "
" with state sequence taken to be " " is then
" is then

A hidden Markov model is a "doubly embedded stochastic process with an underlying stochastic process that is not observable, but can only be observed through another set of stochastic process that produce the sequence of observations" [25].
2.2. HMM with Duration Modeling
In the standard HMM, when a state  is entered, that state is occupied for a period of time, via self-transitions, until transiting to another state
is entered, that state is occupied for a period of time, via self-transitions, until transiting to another state  . If the state interval is given as
. If the state interval is given as  , the standard HMM description of the probability distribution on state intervals is implicitly given by
, the standard HMM description of the probability distribution on state intervals is implicitly given by

where  is self-transition probability of state
is self-transition probability of state  . This geometric distribution is inappropriate in many cases. The standard HMMD replaces (3) with a
. This geometric distribution is inappropriate in many cases. The standard HMMD replaces (3) with a  that models the real duration distribution of state
that models the real duration distribution of state  . In this way, explicit knowledge about the duration of states is incorporated into the HMM. A general HMMD can be illustrated as
. In this way, explicit knowledge about the duration of states is incorporated into the HMM. A general HMMD can be illustrated as

When entered, state  will have a duration of
will have a duration of  according to its duration density
according to its duration density  , and it then transits to another state
, and it then transits to another state  according to the state transition probability
according to the state transition probability  (self-transitions,
(self-transitions,  , are not permitted in this formalism). It is easy to see that the HMMD will turn into an HMM if
, are not permitted in this formalism). It is easy to see that the HMMD will turn into an HMM if  is set to the geometric distribution shown in (3). The first HMMD formulation was studied by Ferguson [2]. A detailed HMMD description was later given by [28] (we follow much of the [28] notation in what follows). There have been many efforts to improve the computational efficiency of the HMMD formulation given its fundamental utility in many endeavors in science and engineering. Notable amongst these are the variable transition HMM methods for implementing the Viterbi algorithm introduced in [4] and the hidden semi-Markov model implementations of the forward-backward algorithm [5].
is set to the geometric distribution shown in (3). The first HMMD formulation was studied by Ferguson [2]. A detailed HMMD description was later given by [28] (we follow much of the [28] notation in what follows). There have been many efforts to improve the computational efficiency of the HMMD formulation given its fundamental utility in many endeavors in science and engineering. Notable amongst these are the variable transition HMM methods for implementing the Viterbi algorithm introduced in [4] and the hidden semi-Markov model implementations of the forward-backward algorithm [5].
2.3. Significant Distributions That Are Not Geometric
Nongeometric duration distributions occur in many familiar areas, such as the length of spoken words in phone conversation, as well as other areas in voice recognition. The Gaussian distribution occurs in many scientific fields, and there are huge number of other (skewed) types of distributions, such as heavy-tailed (or long-tailed) distributions and multimodal distributions.
Heavy-tailed distributions are widespread in describing phenomena across the sciences [29]. The log-normal and Pareto distributions are heavy-tailed distributions that are almost as common as the normal and geometric distributions in descriptions of physical phenomena or man-made phenomena and many other phenomena. Pareto distribution was originally used to describe the allocation of wealth of the society, known as the famous 80–20 rule; namely, about 80% of the wealth was owned by a small amount of people, while "the tail", the large part of people only have the rest 20% wealth [30]. Pareto distribution has been extended to many other areas. For example, internet file-size traffic is a long-tailed distribution; that is, there are a few large-sized files and many small-sized files to be transferred. This distribution assumption is an important factor that must be considered to design a robust and reliable network and Pareto distribution could be a suitable choice to model such traffic. (Internet applications have found more and more heavy-tailed distribution phenomena.) Pareto distribution's can also be found in a lot of other fields, such as economics.
Log-normal distributions are used in geology and mining, medicine, environment, atmospheric science, and so on, where skewed distribution occurrences are very common [29]. In Geology, the concentration of elements and their radioactivity in the Earth's crust are often shown to be log-normaly distributed. The infection latent period, the time from being infected to disease symptoms occurs, is often modeled as a log-normal distribution. In the environment, the distribution of particles, chemicals, and organisms is often log-normal distributed. Many atmospheric physical and chemical properties obey the log-normal distribution. The density of bacteria population often follows the log-normaly distribution law. In linguistics, the number of letters per words and the number of words per sentence fit the log-normal distribution. The length distribution for introns, in particular, has very strong support in an extended heavy-tail region, likewise for the length distribution on exons or open reading frames (ORFs) in genomic DNA [31, 32]. The anomalously long-tailed aspect of the ORF-length distribution is the key distinguishing feature of this distribution and has been the key attribute used by biologists using ORF finders to identify likely protein-coding regions in genomic DNA since the early days of (manual) gene structure identification.
2.4. Significant Series That Are Martingale
A discrete-time martingale is a stochastic process where a sequence of random variables  has conditional expected value of the next observation equal to the last observation
has conditional expected value of the next observation equal to the last observation  , where
, where  . Similarly, one sequence, say
. Similarly, one sequence, say  , is said to be martingale with respect to another, say
, is said to be martingale with respect to another, say  , if for all
, if for all  , where
, where  . Examples of martingales are rife in gambling. For our purposes, the most critical example is the likelihood-ratio testing in statistics, with test statistic, the "likelihood ratio", given as
. Examples of martingales are rife in gambling. For our purposes, the most critical example is the likelihood-ratio testing in statistics, with test statistic, the "likelihood ratio", given as  , where the population densities considered for the data are
, where the population densities considered for the data are  and
and  . If the better (actual) distribution is
. If the better (actual) distribution is  , then
, then  is martingale with respect to
is martingale with respect to  . This scenario arises throughout the HMM Viterbi derivation if local "sensors" are used, such as with profile HMMs or position-dependent Markov models in the vicinity of transition between states. This scenario also arises in the HMM Viterbi recognition of regions (versus transition out of those regions), where length-martingale side information will be explicitly shown in what follows, providing a pathway for incorporation of any martingale-series side information (this fits naturally with the clique-HMM generalizations described in [27] as well). Given that the core ratio of cumulant probabilities that is employed is itself a martingale, this then provides a means for incorporation of side information in general.
. This scenario arises throughout the HMM Viterbi derivation if local "sensors" are used, such as with profile HMMs or position-dependent Markov models in the vicinity of transition between states. This scenario also arises in the HMM Viterbi recognition of regions (versus transition out of those regions), where length-martingale side information will be explicitly shown in what follows, providing a pathway for incorporation of any martingale-series side information (this fits naturally with the clique-HMM generalizations described in [27] as well). Given that the core ratio of cumulant probabilities that is employed is itself a martingale, this then provides a means for incorporation of side information in general.
3. Methods
3.1. The Hidden Semi-Markov Model Via Length Side Information
In this section, we present a means to lift side information that is associated with a region, or transition between regions, by "piggybacking" that side information along with the duration side information. We use the example of such a process for HMM incorporation of duration itself as the guide. In doing so, we arrive at a hidden semi-Markov model (HSMM) formalism. (Throughout the derivation to follow, we try to stay consistent with the notation introduced by [28].) An equivalent formulation of the HSMM was introduced in [4] for the Viterbi algorithm and in [5] for Baum-Welch. The formalism introduced here, however, is directly amenable to incorporation of side information and to adaptive speedup (as described in [10]).
For the state duration density  ,
,  , we have
, we have

where  is abbreviated as
is abbreviated as  if no ambiguity. Define "self-transition" variable
if no ambiguity. Define "self-transition" variable  = probability that next state is still
= probability that next state is still  , given that
, given that  has consecutively occurred
has consecutively occurred  times up to now
times up to now

We see with comparison of (5) and (3) that we now have similar form; there are " " factors of "
" factors of " " instead of "
" instead of " ", with a "cap term" "(
", with a "cap term" "( )" instead of "(
)" instead of "( )", where the "
)", where the " " terms are not constant, but only depend on the state's duration probability distribution. In this way, "
" terms are not constant, but only depend on the state's duration probability distribution. In this way, " " can mesh with the HMM's dynamic programming table construction for the Viterbi algorithm at the column level in the same manner that "
" can mesh with the HMM's dynamic programming table construction for the Viterbi algorithm at the column level in the same manner that " " does. Side information about the local strength of EST matches or homology matches, and so forth, that can be put in similar form can now be "lifted" into the HMM model on a proper, locally optimized Viterbi-path sense (see Appendices A and B for details). The length probability in the above form, with the cumulant-probability ratio terms, is a form of martingale series (more restrictive than that seen in likelihood ratio martingales).
" does. Side information about the local strength of EST matches or homology matches, and so forth, that can be put in similar form can now be "lifted" into the HMM model on a proper, locally optimized Viterbi-path sense (see Appendices A and B for details). The length probability in the above form, with the cumulant-probability ratio terms, is a form of martingale series (more restrictive than that seen in likelihood ratio martingales).
The derivation of the Baum-Welch and Viterbi HSMM algorithm, given (5), is outlined in Appendices A and B (where (A.1)–(B.8) are located). A summary of the Baum-Welch training algorithm is as follows:
-
(1)
initialize elements (
 ) of HMMD,
) of HMMD, -
(2)
calculate
 using (A.6) and (A.7) (save the two tables:
using (A.6) and (A.7) (save the two tables: 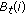 and
and  ),
), -
(3)
calculate
 using (A.4) and (A.5),
using (A.4) and (A.5), -
(4)
re-estimate elements (
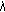 ) of HMMD using (A.9)–(A.10),
) of HMMD using (A.9)–(A.10), -
(5)
terminate if stop condition is satisfied, else go to step (2).
The memory complexity of this method is  . As shown above, the algorithm first does backward computing (step (2)) and saves two tables: one is
. As shown above, the algorithm first does backward computing (step (2)) and saves two tables: one is  , the other is
, the other is  . Then, at very time index
. Then, at very time index  , the algorithm can group the computation of steps (3) and (4) together. So, no forward table needs to be saved. We can do a rough estimation of HMMD's computation cost by counting multiplications inside the loops of ΣT ΣN (which corresponds to the standard HMM computational cost) and ΣT ΣD (the additional computational cost incurred by the HMMD). The computation complexity is
, the algorithm can group the computation of steps (3) and (4) together. So, no forward table needs to be saved. We can do a rough estimation of HMMD's computation cost by counting multiplications inside the loops of ΣT ΣN (which corresponds to the standard HMM computational cost) and ΣT ΣD (the additional computational cost incurred by the HMMD). The computation complexity is  . In an actual implementation, a scaling procedure may be needed to keep the forward-backward variables within a manageable numerical interval. One common method is to rescale the forward-backward variables at every time index
. In an actual implementation, a scaling procedure may be needed to keep the forward-backward variables within a manageable numerical interval. One common method is to rescale the forward-backward variables at every time index  using the scaling factor
using the scaling factor  . Here we use a dynamic scaling approach. For this, we need two versions of
. Here we use a dynamic scaling approach. For this, we need two versions of  . Then, at every time index, we test if the numerical values is too small if so, we use the scaled version to push the numerical values up; if not, we keep using the unscaled version. In this way, no additional computation complexity is introduced by scaling.
. Then, at every time index, we test if the numerical values is too small if so, we use the scaled version to push the numerical values up; if not, we keep using the unscaled version. In this way, no additional computation complexity is introduced by scaling.
As with Baum-Welch, the Viterbi algorithm for the HMMD is  . Because logarithm scaling can be performed for Viterbi in advance; however, the Viterbi procedure consists only of additions to yield a very fast computation. For both the Baum-Welch and Viterbi algorithms, use of the HMMBD algorithm [10] can be employed (as in this work) to further reduce computational time complexity to
. Because logarithm scaling can be performed for Viterbi in advance; however, the Viterbi procedure consists only of additions to yield a very fast computation. For both the Baum-Welch and Viterbi algorithms, use of the HMMBD algorithm [10] can be employed (as in this work) to further reduce computational time complexity to  , thus obtaining the speed benefits of a simple HMM, with the improved modeling capabilities of the HMMD.
, thus obtaining the speed benefits of a simple HMM, with the improved modeling capabilities of the HMMD.
3.2. Method for Modeling Gene-Finder State Structure [27]
3.2.1. The Exon Frame States and Other HMM States
Exons have a 3-base encoding as directly revealed in a mutual information analysis of gapped base statistical linkages in prokaryotic DNA, as shown in [3]. The 3-base encoding elements are called codons, and the partitioning of the exons into 3-base subsequences is known as the codon framing. A gene's coding length must be a multiple of 3 bases. The term frame position is used to denote one of the 3 possible positions—0, 1, or 2 by our convention—relative to the first base of a codon. Introns may interrupt genes after any frame position. In other words, introns can split the codon framing either at a codon boundary or one of the internal codon positions.
Although there is no need for framing among introns, for convenience, we associate a fixed frame label with the intron as a tracking device in order to ensure that the frame of the following exon transition is constrained appropriately. The primitive states of the individual bases occurring in exons, introns, and junk are denoted by

The vicinity around the transitions between exon, intron and junk usually contains rich information for gene identification. The junk to exon transition usually starts with an ATG, the exon to junk transition, ends with one of the stop codons  . Nearly all eukaryotic introns start with GT and end with with AG (the AG-GT rule). To capture the information at these transition areas, we build a position-dependent emission (pde) table for base positions around each type of transition point. It is called "position-dependent" since we make estimation of occurrence of the bases (emission probabilities) in this area according to their relative distances to the nearest nonself state transition. For example, the start codon "ATG" is the first three bases at the junk-exon transition. The size of the pde region is determined by a window-size parameter centered at the transition point (thus, only even numbered window sizes are plotted in the Results). We use four transition states to collect such position-dependent emission probabilities
. Nearly all eukaryotic introns start with GT and end with with AG (the AG-GT rule). To capture the information at these transition areas, we build a position-dependent emission (pde) table for base positions around each type of transition point. It is called "position-dependent" since we make estimation of occurrence of the bases (emission probabilities) in this area according to their relative distances to the nearest nonself state transition. For example, the start codon "ATG" is the first three bases at the junk-exon transition. The size of the pde region is determined by a window-size parameter centered at the transition point (thus, only even numbered window sizes are plotted in the Results). We use four transition states to collect such position-dependent emission probabilities  ;
;  ;
;  ;
;  . Considering the framing information, we can expand the above four transition into eight transitions
. Considering the framing information, we can expand the above four transition into eight transitions  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  . We make
. We make  ;
;  ;
;  share the same
share the same  emission table and
emission table and  ;
;  ;
;  share the same
share the same  emission tables. Since we process both the forward-strand and reverse-strand gene identifications simultaneously in one pass, there is another set of eight state transitions for the reverse strand. Forward states and their reverse state counterparts also share the same emission table (i.e., their instance counts and associated statistics are merged). Based on the training sequences' properties and the size of the training data set, we adjust the window size and use different Markov emission orders to calculate the estimated occurrence probabilities for different bases inside the window (e.g., interpolated Markov models are used [3]).
emission tables. Since we process both the forward-strand and reverse-strand gene identifications simultaneously in one pass, there is another set of eight state transitions for the reverse strand. Forward states and their reverse state counterparts also share the same emission table (i.e., their instance counts and associated statistics are merged). Based on the training sequences' properties and the size of the training data set, we adjust the window size and use different Markov emission orders to calculate the estimated occurrence probabilities for different bases inside the window (e.g., interpolated Markov models are used [3]).
The regions on either side of a pde window often include transcription factor binding sites such as the promoter for the  window. Statistics from these regions provide additional information needed to identify start of gene coding and alternative splicing. The statistical properties in these regions are described according to zone-dependent emission (zde) statistics. The signals in these areas can be very diverse, and their exact relative positions are typically not fixed positionally. We apply a 5th-order Markov model on instances in the zones indicated (further refinements with hash-interpolated Markov models [3] have also met with success but are not discussed further here). The size of the "zone" region extends from the end of the position-dependent emission table's coverage to a distance specified by a parameter. For the dataruns shown in the Results, this parameter was set to 50.
window. Statistics from these regions provide additional information needed to identify start of gene coding and alternative splicing. The statistical properties in these regions are described according to zone-dependent emission (zde) statistics. The signals in these areas can be very diverse, and their exact relative positions are typically not fixed positionally. We apply a 5th-order Markov model on instances in the zones indicated (further refinements with hash-interpolated Markov models [3] have also met with success but are not discussed further here). The size of the "zone" region extends from the end of the position-dependent emission table's coverage to a distance specified by a parameter. For the dataruns shown in the Results, this parameter was set to 50.
There are eight zde tables:  , where ieeeee corresponds to the exon emission table for the downstream side of an
, where ieeeee corresponds to the exon emission table for the downstream side of an  transition, with zde region 50 bases wide, for example, the zone on the downstream side of a non-self transition with positions in the domain (window, window + 50]. We build another set of eight hash tables for states on the reverse strand. We see 2% performance improvement when the zde regions are separated from the bulk-dependent emissions (bde), the standard HMM emission for the regions. When outside the pde and zde regions, thus in a bde region, there are three emission tables for both the forward and reverse strands exon, intron, and junk states, corresponding to the normal exon emission table, the normal intron emission table and the normal junk emission table. The three kinds of emission processing are shown in Figure 1.
transition, with zde region 50 bases wide, for example, the zone on the downstream side of a non-self transition with positions in the domain (window, window + 50]. We build another set of eight hash tables for states on the reverse strand. We see 2% performance improvement when the zde regions are separated from the bulk-dependent emissions (bde), the standard HMM emission for the regions. When outside the pde and zde regions, thus in a bde region, there are three emission tables for both the forward and reverse strands exon, intron, and junk states, corresponding to the normal exon emission table, the normal intron emission table and the normal junk emission table. The three kinds of emission processing are shown in Figure 1.
Three kinds of emission mechanisms: (1) position-dependent emission, (2) hash-interpolated emission, and (3) normal emission. Based on the relative distance from the state transition point, we first encounter the position-dependent emissions (denoted as (1)), then we use the zone-dependent emissions (2), and finally, we encounter the normal state emissions (denoted as (3)).
The model contains the following 27 states in total for each strand, three each of  , corresponding to the different reading frames, and one each of
, corresponding to the different reading frames, and one each of  . As before, there is another set of corresponding reverse-strand states, with junk as the shared state. When a state transition happens, junk to exon for example, the positional-dependent emissions inside the window
. As before, there is another set of corresponding reverse-strand states, with junk as the shared state. When a state transition happens, junk to exon for example, the positional-dependent emissions inside the window  will be referenced first, then the state travels to the zone-dependant emission zone
will be referenced first, then the state travels to the zone-dependant emission zone  , then travels to the state of the normal emission region
, then travels to the state of the normal emission region  , then travels to another state of zone-dependent emissions
, then travels to another state of zone-dependent emissions  or
or  , then to a bulk region of self-transitions
, then to a bulk region of self-transitions  , and so forth, The duration information of each state is represented by the corresponding bin assigned by the algorithm, according to [10]. For convenience in calculating emissions in the Viterbi decoding, we precompute the cumulant emission tables for each of 54 substates (states of the forward and reverse strand), then as the state transitions, its emission contributions can be determined by the differences between two references to the precomputed cumulant array data.
, and so forth, The duration information of each state is represented by the corresponding bin assigned by the algorithm, according to [10]. For convenience in calculating emissions in the Viterbi decoding, we precompute the cumulant emission tables for each of 54 substates (states of the forward and reverse strand), then as the state transitions, its emission contributions can be determined by the differences between two references to the precomputed cumulant array data.
The occurrence of a stop codon (TAA, TAG, or TGA) that is in reading frame 0 and located inside an exon, or across two exons because of the intron interruption, is called as an "in-frame stop". In general, the occurrences of in-frame stops are considered very rare. We designed our in-frame stop filter to penalize such Viterbi paths. A DNA sequence has six reading frames (read in six ways based on frames), three for the forward strand and three for the reverse strand. When precomputing the emission tables in the above for the sub-states, for those sub-states related to exons we consider the occurrences of in-frame stop codons in the six reading frames. For each reading frame, we scan the DNA sequence from left to the right, and whenever a stop codon is encountered in-frame, we add to the emission probability for that position a user defined stop penalty factor. In this way, the in-frame stop filter procedure is incorporated into the emission table building process and does not bring the additional computational complexity to the program. The algorithmic complexity of the whole program is  where
where  sub-states and
sub-states and  is the number of bins for each sub-state, and the memory complexity is
is the number of bins for each sub-state, and the memory complexity is  , via the HMMBD method described in [10].
, via the HMMBD method described in [10].
3.3. Hardware Implementation
The whole program for this application is written in the C programming language. The GNU Compiler Collection (GCC) is used to compile the codes. The Operating system used is Ubuntu/Linux, running on a server with 8 GB RAM. In general, the measure of prediction performance is taken at both individual nucleotide level and the full exon level, according to the specification in [33], where we calculate sensitivity (SN), specificity (SP), and take their average as our final accuracy rate (AC).
3.4. Prediction Accuracy Measures
The sensitivity (SN), specificity (SP), and accuracy (AC) are defined at the base or nucleotide level, or complete exon match level

where TP: true positive count; FN: false negative count; and FP: false positive count.
3.5. Data Preparation
The data we use in the experiment are Chromosomes I–V of C. elegans that were obtained from release WS200 of Wormbase [34]. The data preparation is described in [27] and is done exactly the same in order to perform a precise comparison with the meta-HMM method. The reduced data set, without the coding regions that have (known) alternative splicing, or any kind of multiple encoding, is summarized in Tables 1 and 2.
4. Results
We take advantage of the parallel presentation in [27] to start the tuning with a parameter set that is already nearly optimized (i.e., the Markov emissions, window size, and other genome-dependent tuning parameters is already close to optimal). For verification purposes, we first do training and testing using the same folds, the results for each of the five folds indicated above are very good, a 99%-100% accuracy rate (not shown). We then do a "proper" single train/test fold from the fivefold cross-validation set (i.e., folds 1–4 to train, and the 5th fold as test), and explore the tuning on Markov model and window size as shown in Figures 2–5. We then perform a complete fivefold cross-validation with the five folds for the model identified as best (i.e., train on four folds, test on one, permute over the five holdout test possibilities and take their average accuracies of the different train/tests as the overall accuracy).
In Figures 2 and 3, we show the results of the experiments where we tune the Markov order and window size parameters to try to reach a local maximum in the predication performance for both the full exon level and the individual nucleotide level. We compare the results of three kinds of different configurations. In the first configuration, shown in Figures 2 and 3, we have the HMM with binned duration (HMMBD) with position-dependent emissions (pde's) and zone-dependent emissions (i.e., HMMBD + pde + zde).
In the second configuration, we turn off the zone-dependent emissions (so, HMMBD + pde), the resulting accuracy suffers a 1.5%–2.0% drop as shown in Figures 4 and 5. In the third setting, we use the same setting as the first setting except that we now use the geometric distribution that is implicitly incorporated by HMM as the duration distribution input to the HMMBD (HMMBD + pde + zde + Geometric). The purpose is have an approximation of the performance of the standard HMM with pde and zde contributions. As show in Figures 4 and 5, the performance of the result has about 3% to 4% drop (conversely, the performance improvement with HMMD modeling, with the duration modeling on the introns in particular, is improved 3%-4% in this case, with a notable robustness at handling multiple genes in a sequence—as seen in the intron submodel that includes duration information in [12]). When the window size becomes 0, that is, when we turn off the setting of position-dependent emissions, the performances of the results drop sharply as shown in Figures 4 and 5. This is because the strong information at the transitions, such as the start codon with ATG or stop codons with TAA, TAG, or TGA, and so forth, are now "buried" in the bulk statistics of the exon, intron, or junk regions.
A full fivefold cross validation is performed for the HMMBD + pde + zde case, as shown in Figures 6 and 7. The fifth- and second-order Markov models work best, with the fifth order Markov model having a notably smaller spread in values consistent with [27] and validating the rapid tuning performed in Figures 2–5 (that proceeded with analysis using only one fold). The best case performance was 86% accuracy at the nucleotide level and 70% accuracy at the base level (compared with 90% on nucleotides and 74% on exons on the exact same datasets in the meta-HMM described in [27]).
5. Discussion and Conclusions
The gap and hash interpolating Markov models (gIMM and hIMM) [3] will eventually be incorporated into the model, since they are already known to extract additional information that may prove useful, particularly in the zde regions where promoters and other gapped motifs might exist. This is because promoters and transcription factor-binding sites often have lengthy overall gapped motif structure, and with the hash-interpolated Markov models, it is possible to capture the conserved higher order sequence information in the zde sample space. The hIMM and gIMM methods will not only strengthen the gene structure recognition, but also the gene-finding accuracy, and they can also provide the initial indications of anomalous motif structure in the regions identified by the gene finder (in a postgenomic phase of the analysis) [3].
In this paper we present a novel formulation for inclusion of side information, beginning with treating the state duration as side information and thereby bootstrapping from an HMM to a HMMD modeling capability. We then apply the method, using binned duration for speedup, HMMBD [10], to eukaryotic gene-finding analysis and compare to the meta-HMM [27]. In further work, we plan to merged the methods to obtain a meta-HMMBD + zde that is projected to have at least a 3% improvement over the meta-HMM at comparable time complexity.
Appendices
A. Baum-Welch Algorithm in HMMD Side-Information Formalism
The Baum-Welch algorithm in the length-martingale side-information HMMD formalism.
We define the following three variables to simplify what follows:


Define 

Define

where

Define

where

Now,  ,
,  ,
,  and
and  can be expressed as
can be expressed as

Now, define

Using the above equations

B. Viterbi Algorithm in HMMD Side-Information Formalism
The Viterbi algorithm in the length-martingale side-information HMMD formalism.
Define  the most probable path that consecutively occurred
the most probable path that consecutively occurred  times at state
times at state  at time
at time 

where

The goal is to find

Define

where

The goal is now

If we do a logarithm scaling on  ,
,  and
and  in advance, the final Viterbi path can be calculated by:
in advance, the final Viterbi path can be calculated by:


where the argmax goal above stays the same.
In Appendix A that follows, we present a description of the Baum-Welch algorithm in the hidden semi-Markov model (HSMM) formalism. In Appendix B, we present a description of the Viterbi algorithm in the HSMM formalism.
References
Mathé C, Sagot M-F, Schiex T, Rouzé P: Current methods of gene prediction, their strengths and weaknesses. Nucleic Acids Research 2002, 30(19):4103-4117. 10.1093/nar/gkf543
Ferguson JD: Variable duration models for speech. Proceedings of the Symposium on the Application of Hidden Markov models to Text and Speech, 1980 143-179.
Winters-Hilt S: Hidden Markov model variants and their application. BMC Bioinformatics 2006., 7(2, article no. S14):
Ramesh P, Wilpon JG: Modeling state durations in hidden markov models for automatic speech recognition. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, 1992 1: 381-384.
Yu S-Z, Kobayashi H: An efficient forward-backward algorithm for an explicit-duration hidden Markov model. IEEE Signal Processing Letters 2003, 10(1):11-14. 10.1109/LSP.2002.806705
Johnson MT: Capacity and complexity of HMM duration modeling techniques. IEEE Signal Processing Letters 2005, 12(5):407-410.
Ghahramani Z, Jordan MI: Factorial hidden Markov models. Machine Learning 1997, 29(2-3):245-273.
Fine S, Singer Y, Tishby N: The hierarchical hidden Markov model: analysis and applications. Machine Learning 1998, 32(1):41-62. 10.1023/A:1007469218079
Murphy K, Paskin M: Linear time inference in hierarchical hmms. Proceedings of Neural Information Processing Systems (NIPS '01), December 2001 833-840.
Winters-Hilt S, Jiang Z: A hidden markov model with binned duration algorithm. IEEE Transactions on Signal Processing 2010, 58(2):948-952.
Stanke M, Steinkamp R, Waack S, Morgenstern B: AUGUSTUS: a web server for gene finding in eukaryotes. Nucleic Acids Research 2004, 32: W309-W312. 10.1093/nar/gkh379
Stanke M, Waack S: Gene prediction with a hidden Markov model and a new intron submodel. Bioinformatics 2003, 19(2):215-225.
Guigó R, Agarwal P, Abril JF, Burset M, Fickett JW: An assessment of gene prediction accuracy in large DNA sequences. Genome Research 2000, 10(10):1631-1642. 10.1101/gr.122800
Stoll PA, Ohya J: Applications of HMM modeling to recognizing human gestures in image sequences for a man-machine interface. Proceedings of the 4th IEEE International Workshop on Robot and Human Communication (RO-MAN '95), July 1995 129-134.
Elmezain M, Al-Hamadi A, Appenrodt J, Michaelis B: A hidden markov model-based continuous gesture recognition system for hand motion trajectory. Proceedings of the 19th International Conference on Pattern Recognition (ICPR '08), December 2008
Appenrodt J, Elmezain M, Al-Hamadi A, Michaelis B: A hidden markov model-based isolated and meaningful hand gesture recognition. International Journal of Electrical, Computer, and Systems Engineering 2009, 3: 156-163.
Knerr S, Augustin E, Baret O, Price D: Hidden Markov model based word recognition and its application to legal amount reading on french checks. Computer Vision and Image Understanding 1998, 70(3):404-419. 10.1006/cviu.1998.0685
Schenkel M, Jabri M: Low resolution, degraded document recognition using neural networks and hidden markov models. Pattern Recognition Letters 1998, 19(3-4):365-371. 10.1016/S0167-8655(97)00176-1
Vlontzos J, Kung S: Hidden markov models for character recognition. IEEE Transactions on Image Processing 1992, 1(4):539-543. 10.1109/83.199925
Li J, Najmi A, Gray RM: Image classification by a two-dimensional hidden Markov model. IEEE Transactions on Signal Processing 2000, 48(2):517-533. 10.1109/78.823977
Li J, Gray RM, Olshen RA: Multiresolution image classification by hierarchical modeling with two-dimensional hidden Markov models. IEEE Transactions on Information Theory 2000, 46(5):1826-1841. 10.1109/18.857794
Huang C-L, Wu M-S, Jeng S-H: Gesture recognition using the multi-PDM method and hidden Markov model. Image and Vision Computing 2000, 18(11):865-879. 10.1016/S0262-8856(99)00042-6
Garcia-Frias J: Hidden markov models for burst error characterization in indoor radio channels. IEEE Transactions on Vehicular Technology 1997, 46(4):1006-1020. 10.1109/25.653074
Bellone E, Hughes JP, Guttorp P: A hidden Markov model for downscalling synoptic atmospheric patterns to precipitation amounts. Climate Research 2000, 15(1):1-12.
Raphael C: Automatic segmentation of acoustic musical signals using hidden Markov models. IEEE Transactions on Pattern Analysis and Machine Intelligence 1999, 21(4):360-370. 10.1109/34.761266
Kogan JA, Margoliash D: Automated recognition of bird song elements from continuous recordings using dynamic time warping and hidden Markov models: a comparative study. Journal of the Acoustical Society of America 1998, 103(4):2185-2196. 10.1121/1.421364
Winters-Hilt S, Baribault C: A meta-state hmm with application to gene-structure identification in eukaryotes. submitted to EURASIP Genomic Signal Processing
Rabiner LR: Tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE 1989, 77(2):257-286. 10.1109/5.18626
Limpert E, Stahel WA, Abbt M: Log-normal distributions across the sciences: keys and clues. BioScience 2001, 51(5):341-352. 10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2
Lorenz MO: Methods of measuring the concentration of wealth. Publications of the American Statistical Association 1905, 9(70):209-219. 10.2307/2276207
Krogh A, Mian IS, Haussler D: A hidden Markov model that finds genes in E. coli DNA. Nucleic Acids Research 1994, 22(22):4768-4778. 10.1093/nar/22.22.4768
Hong X, Scofield DG, Lynch M: Intron size, abundance, and distribution within untranslated regions of genes. Molecular Biology and Evolution 2006, 23(12):2392-2404. 10.1093/molbev/msl111
Burset M, Guigó R: Evaluation of gene structure prediction programs. Genomics 1996, 34(3):353-367. 10.1006/geno.1996.0298
wormbase 2009, http://www.wormbase.org/
Acknowledgment
Funding for this research was provided by an NIH K-22 Grant (5K22LM008794, SWH PI).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Winters-Hilt, S., Jiang, Z. & Baribault, C. Hidden Markov Model with Duration Side Information for Novel HMMD Derivation, with Application to Eukaryotic Gene Finding. EURASIP J. Adv. Signal Process. 2010, 761360 (2010). https://doi.org/10.1155/2010/761360
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/761360
 ) of HMMD,
) of HMMD, using (A.6) and (A.7) (save the two tables:
using (A.6) and (A.7) (save the two tables: 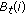 and
and  ),
), using (A.4) and (A.5),
using (A.4) and (A.5),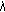 ) of HMMD using (A.9)–(A.10),
) of HMMD using (A.9)–(A.10),





