- Research Article
- Open access
- Published:
Distributed Encoding Algorithm for Source Localization in Sensor Networks
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 781720 (2010)
Abstract
We consider sensor-based distributed source localization applications, where sensors transmit quantized data to a fusion node, which then produces an estimate of the source location. For this application, the goal is to minimize the amount of information that the sensor nodes have to exchange in order to attain a certain source localization accuracy. We propose a distributed encoding algorithm that is applied after quantization and achieves significant rate savings by merging quantization bins. The bin-merging technique exploits the fact that certain combinations of quantization bins at each node cannot occur because the corresponding spatial regions have an empty intersection. We apply the algorithm to a system where an acoustic amplitude sensor model is employed at each node for source localization. Our experiments demonstrate significant rate savings (e.g., over 30%, 5 nodes, and 4 bits per node) when our novel bin-merging algorithms are used.
1. Introduction
In sensor networks, multiple correlated sensor readings are available from many sensors that can sense, compute and communicate. Often these sensors are battery-powered and operate under strict limitations on wireless communication bandwidth. This motivates the use of data compression in the context of various tasks such as detection, classification, localization, and tracking, which require data exchange between sensors. The basic strategy for reducing the overall energy usage in the sensor network would then be to decrease the communication cost at the expense of additional computation in the sensors [1].
One important sensor collaboration task with broad applications is source localization. The goal is to estimate the location of a source within a sensor field, where a set of distributed sensors measures acoustic or seismic signals emitted by a source and manipulates the measurements to produce meaningful information such as signal energy, direction-of-arrival (DOA), and time difference-of-arrival (TDOA) [2, 3].
Localization based on acoustic signal energy measured at individual acoustic amplitude sensors is proposed in [4], where each sensor transmits unquantized acoustic energy readings to a fusion node, which then computes an estimate of the location of the source of these acoustic signals. Localization can be also performed using DOA sensors (sensor arrays) [5]. The sensor arrays generally provide better localization accuracy, especially in far field, as compared to amplitude sensors, while they are computationally more expensive. TDOA can be estimated by using various correlation operations and a least squares (LS) formulation can be used to estimate source location [6]. Good localization accuracy for the TDOA method can be accomplished if there is accurate synchronization among sensors, which will tend to require a high cost in wireless sensor networks [3].
None of these approaches take explicitly into account the effect of sensor reading quantization. Since practical systems will require quantization of sensor readings before transmission, estimation algorithms will be run on quantized sensor readings. Thus, it would be desirable to minimize the information in terms of rate before being transmitted to a fusion node. It is noted that there exists some degree of redundancy between the quantized sensor readings since each sensor collects information (e.g., signal energy or direction) regarding a source location. Clearly, this redundancy can be reduced by adopting distributed quantizers designed to maximize the localization accuracy by exploiting the correlation between the sensor readings (see [7, 8]).
In this paper, we observe that the redundancy can be also reduced by encoding the quantized sensor readings for a situation, where a set of nodes (Each node may employ one sensor or an array of sensors, depending on the applications) and a fusion node wish to cooperate to estimate a source location (see Figure 1). We assume that each node can estimate noise-corrupted source characteristics (zi in Figure 1), such as signal energy or DOA, using actual measurements (e.g., time-series measurements or spatial measurements). We also assume that there is only one way communication from nodes to the fusion node; that is, there is no feedback channel, the nodes do not communicate with each other (no relay between nodes), and these various communication links are reliable.
In our problem, a source signal is measured and quantized by a series of distributed nodes. Clearly, in order to make localization possible, each possible location of the source produces a different vector of sensor readings at the nodes. Thus, the vector of the readings  should uniquely define the localization. Quantization of the readings at each node reduces the accuracy of the localization. Each quantized value (e.g.,
should uniquely define the localization. Quantization of the readings at each node reduces the accuracy of the localization. Each quantized value (e.g.,  at node
at node  ) of a sensor reading can then be linked to a region in space, where the source can be found. For example, if distance information is provided by sensor readings, the regions corresponding to sensor readings will be circles centered on the nodes and thus quantized values of those readings will then be mapped to "rings" centered on the nodes. Figure 2 illustrates the case, where 3 nodes equipped with acoustic amplitude sensors measure the distance information for source localization. Denote
) of a sensor reading can then be linked to a region in space, where the source can be found. For example, if distance information is provided by sensor readings, the regions corresponding to sensor readings will be circles centered on the nodes and thus quantized values of those readings will then be mapped to "rings" centered on the nodes. Figure 2 illustrates the case, where 3 nodes equipped with acoustic amplitude sensors measure the distance information for source localization. Denote  the
the  th quantization bin at node
th quantization bin at node  ; that is, whenever sensor reading
; that is, whenever sensor reading  at node
at node  belongs to
belongs to  th bin, the node will transmit
th bin, the node will transmit  to the fusion node. From the discussion, it should be clear that since each quantized sensor reading
to the fusion node. From the discussion, it should be clear that since each quantized sensor reading  can be associated with the corresponding ring, the fusion node can locate the source by computing the intersection of those 3 rings from the combination (
can be associated with the corresponding ring, the fusion node can locate the source by computing the intersection of those 3 rings from the combination ( ) received from the 3 nodes. (In a noiseless case, there always exists a nonempty intersection corresponding to each received combination, where a source is located. However, empty intersections may be constructed in a noisy case. In Figure 2, suppose that node
) received from the 3 nodes. (In a noiseless case, there always exists a nonempty intersection corresponding to each received combination, where a source is located. However, empty intersections may be constructed in a noisy case. In Figure 2, suppose that node  transmits
transmits  instead of
instead of  due to measurement noise. Then, the fusion node will receive
due to measurement noise. Then, the fusion node will receive  which leads to an empty intersection. Probabilistic localization methods should be employed to handle empty intersections. For further details, see [9].) Therefore, the combinations such as
which leads to an empty intersection. Probabilistic localization methods should be employed to handle empty intersections. For further details, see [9].) Therefore, the combinations such as  or
or  transmitted from the nodes will tend to produce nonempty intersections (the shaded regions in Figure 2, resp.) while numerous other combinations randomly collected may lead to empty intersections, implying that such combinations are very unlikely to be transmitted from the nodes (e.g.,
transmitted from the nodes will tend to produce nonempty intersections (the shaded regions in Figure 2, resp.) while numerous other combinations randomly collected may lead to empty intersections, implying that such combinations are very unlikely to be transmitted from the nodes (e.g.,  and many others). In this work, we focus on developing tools that allow us to exploit this observation in order to eliminate the redundancy. More specifically, we consider a novel way of reducing the effective number of quantization bins consumed by all the nodes involved while preserving localization performance. Suppose that one of the nodes reduces the number of bins that are being used. This will cause a corresponding increase of uncertainty. However, the fusion node that receives a combination of the bins from all the nodes should be able to compensate for the increase by using the data from the other nodes as side information.
and many others). In this work, we focus on developing tools that allow us to exploit this observation in order to eliminate the redundancy. More specifically, we consider a novel way of reducing the effective number of quantization bins consumed by all the nodes involved while preserving localization performance. Suppose that one of the nodes reduces the number of bins that are being used. This will cause a corresponding increase of uncertainty. However, the fusion node that receives a combination of the bins from all the nodes should be able to compensate for the increase by using the data from the other nodes as side information.
We propose a novel distributed encoding algorithm that allows us to achieve significant rate savings [8, 10]. With our method, we merge (non-adjacent) quantization bins in a given node whenever we determine that the ambiguity created by this merging can be resolved at the fusion node once information from other nodes is taken into account. In [11], the authors focused on encoding the correlated measurements by merging the adjacent quantization bins at each node so as to achieve rate savings at the expense of distortion. Notice that they search the quantization bins to be merged that show redundancy in encoding perspective while we find the bins for merging that produce redundancy in localization perspective. In addition, while in their approach each computation of distortion for pairs of bins will be required to find the bins for merging, we develop simple techniques that choose the bins to be merged in a systematic way.
It is noted that our algorithm is an example of binning as can be found in Slepian-Wolf and Wyner-Ziv techniques [11, 12]. In our approach, however, we achieve rate savings purely through binning and provide several methods to select candidate bins for merging. We apply our distributed encoding algorithm to a system, where an acoustic amplitude sensor model proposed in [4] is considered. Our experiments show rate savings (e.g., over  5 nodes, and
5 nodes, and  bits per node) when our novel bin-merging algorithms are used.
bits per node) when our novel bin-merging algorithms are used.
This paper is organized as follows. The terminologies and definitions are given in Section 2, and the motivation is explained in Section 3. In Section 4, we consider quantization schemes that can be used with the encoding at each node. An iterative encoding algorithm is proposed in Section 5. For a noisy situation, we consider the modified encoding algorithm in Section 6 and describe the decoding process and how to handle decoding errors in Section 7. In Section 8, we apply our encoding algorithm to the source localization system, where an acoustic amplitude sensor model is employed. Simulation results are given in Section 9, and the conclusions are found in Section 10.
2. Terminologies and Definitions
Within the sensor field  of interest, assume that there are
of interest, assume that there are  nodes located at known spatial locations, denoted
nodes located at known spatial locations, denoted  where
where  The nodes measure signals generated by a source located at an unknown location
The nodes measure signals generated by a source located at an unknown location  Denote by
Denote by  the measurement (equivalently, sensor reading) at the
the measurement (equivalently, sensor reading) at the  th node over a time interval
th node over a time interval 

where  denotes the sensor model employed at node
denotes the sensor model employed at node  and the measurement noise
and the measurement noise  can be approximated using a normal distribution,
can be approximated using a normal distribution,  (The sensor models for acoustic amplitude sensors and DOA sensors can be expressed in this form [4, 13].)
(The sensor models for acoustic amplitude sensors and DOA sensors can be expressed in this form [4, 13].)  is the parameter vector for the sensor model (an example of
is the parameter vector for the sensor model (an example of  for an acoustic amplitude sensor case is given in Section 8). It is assumed that each node measures its sensor reading
for an acoustic amplitude sensor case is given in Section 8). It is assumed that each node measures its sensor reading  at time interval
at time interval  quantizes it and sends it to a fusion node, where all sensor readings are used to obtain an estimate
quantizes it and sends it to a fusion node, where all sensor readings are used to obtain an estimate  of the source location.
of the source location.
At node  we use a
we use a  -bit quantizer with a dynamic range
-bit quantizer with a dynamic range  We assume that the quantization range can be selected for each node based on desirable properties of their respective sensing ranges [14]. Denote by
We assume that the quantization range can be selected for each node based on desirable properties of their respective sensing ranges [14]. Denote by  the quantizer with quantization level
the quantizer with quantization level  at node
at node  which generates a quantization index
which generates a quantization index  In what follows,
In what follows,  will be also used to denote the quantization bin to which measurement
will be also used to denote the quantization bin to which measurement  belongs.
belongs.
This formulation is general and captures many scenarios of practical interest. For example,  could be the energy captured by an acoustic amplitude sensor (this will be the case study presented in Section 8), but it could also be a DOA measurement. (In the DOA case, each measurement at a given node location will be provided by an array of collocated sensors.) Each scenario will obviously lead to a different sensor model
could be the energy captured by an acoustic amplitude sensor (this will be the case study presented in Section 8), but it could also be a DOA measurement. (In the DOA case, each measurement at a given node location will be provided by an array of collocated sensors.) Each scenario will obviously lead to a different sensor model  We assume that the fusion node needs measurements,
We assume that the fusion node needs measurements,  fromall nodes in order to estimate the source location.
fromall nodes in order to estimate the source location.
Let  be the cartesian product of the sets of quantization indices.
be the cartesian product of the sets of quantization indices.  contains
contains  -tuples representing all possible combinations of quantization indices
-tuples representing all possible combinations of quantization indices

We denote  the subset of
the subset of  that contains all the quantization index combinations that can occur in a real system, that is, all those generated as a source moves around the sensor field and produces readings at each node
that contains all the quantization index combinations that can occur in a real system, that is, all those generated as a source moves around the sensor field and produces readings at each node

For example, assuming that each node measures noiseless sensor readings (i.e.,  ), we can construct the set
), we can construct the set  by collecting only the combinations that lead to nonempty intersections. (The combinations
by collecting only the combinations that lead to nonempty intersections. (The combinations  corresponding to the shaded regions in Figure 2 will belong to
corresponding to the shaded regions in Figure 2 will belong to  ) In a noisy situation, how to construct
) In a noisy situation, how to construct  will be further explained in Section 6.
will be further explained in Section 6.
We denote  the subset of
the subset of  that contains all
that contains all  -tuples in which the
-tuples in which the  th node is assigned the
th node is assigned the  th quantization bin
th quantization bin

This set will provide all possible combinations of ( ) tuples that can be transmitted from other nodes when the
) tuples that can be transmitted from other nodes when the  th bin at node
th bin at node  was actually transmitted. In other words, the fusion node will be able to identify which bin actually occurred at node
was actually transmitted. In other words, the fusion node will be able to identify which bin actually occurred at node  by exploiting the set as side information, when there is uncertainty induced by merging bins at node
by exploiting the set as side information, when there is uncertainty induced by merging bins at node 
Since ( ) quantized measurements out of each
) quantized measurements out of each  -tuple in
-tuple in  are used in actual process of encoding, it would be useful to construct the set of (
are used in actual process of encoding, it would be useful to construct the set of ( ) tuples generated from
) tuples generated from  We denote by
We denote by  the set of
the set of  -tuples obtained from
-tuples obtained from  -tuples in
-tuples in  where only the quantization bins at positions other than position
where only the quantization bins at positions other than position  are stored. That is, if
are stored. That is, if  then we always have
then we always have  Clearly, there is one to one correspondence between the elements in
Clearly, there is one to one correspondence between the elements in  and
and  so that
so that 
3. Motivation: Identifiability
In this section, we assume that  that is, only combinations of quantization indices belonging to
that is, only combinations of quantization indices belonging to  can occur and those combinations belonging to
can occur and those combinations belonging to  never occur. These sets can be easily obtained when there is no measurement noise (i.e.,
never occur. These sets can be easily obtained when there is no measurement noise (i.e.,  ) and no parameter mismatches. As discussed in the introduction, there will be numerous elements in
) and no parameter mismatches. As discussed in the introduction, there will be numerous elements in  that are not in
that are not in  Therefore, simple scalar quantization at each node would be inefficient because a standard scalar quantizer would allow us to represent any of the
Therefore, simple scalar quantization at each node would be inefficient because a standard scalar quantizer would allow us to represent any of the  -tuples in
-tuples in  What we would like to determine now is a method such that independent quantization can still be performed at each node, while at the same time, we reduce the redundancy inherent in allowing all the combinations in
What we would like to determine now is a method such that independent quantization can still be performed at each node, while at the same time, we reduce the redundancy inherent in allowing all the combinations in  to be chosen. Note that, in general, determining that a specific quantizer assignment in
to be chosen. Note that, in general, determining that a specific quantizer assignment in  does not belong to
does not belong to  requires having access to the whole vector, which obviously is not possible if quantization has to be performed independently at each node.
requires having access to the whole vector, which obviously is not possible if quantization has to be performed independently at each node.
In our design, we will look for quantization bins in a given node that can be merged without affecting localization. As will be discussed next, this is because the ambiguity created by the merger can be resolved once information obtained from the other nodes is taken into account. Note that this is the basic principle behind distributed source coding techniques: binning at the encoder, which can be disambiguated once side information is made available at the decoder [11, 12, 15] (in this case, quantized values from other nodes).
Merging of bins results in bit rate savings because fewer quantization indices have to be transmitted. To quantify the bit rate savings, we need to take into consideration that quantization indices will be entropy coded (in this paper, Huffman coding is used). Thus, when evaluating the possible merger of two bins, we will compute the probability of the merged bin as the sum of the probabilities of the bins merged. Suppose that  and
and  are merged into
are merged into  Then, we can construct the set
Then, we can construct the set  and compute the probability for the merged bin as follows:
and compute the probability for the merged bin as follows:

where  is the pdf of the source position and
is the pdf of the source position and  is given by
is given by

Since the encoder at node  merges
merges  and
and  into
into  with
with  , it sends the corresponding index,
, it sends the corresponding index,  to the fusion node whenever the sensor reading belongs to
to the fusion node whenever the sensor reading belongs to  or
or  The decoder will try to determine which of the two merged bins (
The decoder will try to determine which of the two merged bins ( or
or  in this case) actually occurred at node
in this case) actually occurred at node  To do so, the decoder will use the information provided by the other nodes, that is, the quantization indices
To do so, the decoder will use the information provided by the other nodes, that is, the quantization indices  Consider one particular source position
Consider one particular source position  for which node
for which node  produces
produces  and the remaining nodes produce a combination of
and the remaining nodes produce a combination of  quantization indices
quantization indices  (To avoid confusion, we denote
(To avoid confusion, we denote  a vector of
a vector of  quantization indices and
quantization indices and  a vector of
a vector of  -1 quantization indices, resp.) Then, for this
-1 quantization indices, resp.) Then, for this  there would be no ambiguity at the decoder, even if bins
there would be no ambiguity at the decoder, even if bins  and
and  were to be merged, as long as
were to be merged, as long as  This follows because if
This follows because if  the decoder would be able to determine that only
the decoder would be able to determine that only  is consistent with receiving
is consistent with receiving  With the notation adopted earlier this leads to the following definition:
With the notation adopted earlier this leads to the following definition:
Definition 1.
 and
and  are identifiable, and therefore can be merged, if and only if
are identifiable, and therefore can be merged, if and only if 
Figure 3 illustrates how to merge quantization bins for a simple case, where there are 3 nodes deployed in a sensor field. It is noted that the first bin  (equivalently,
(equivalently,  and the fourth bin
and the fourth bin  at node
at node  can be merged since the sets
can be merged since the sets  and
and  have no elements in common. This merging process will be repeated in the other nodes until there are no quantization bins that can be merged.
have no elements in common. This merging process will be repeated in the other nodes until there are no quantization bins that can be merged.
4. Quantization Schemes
As mentioned in the previous section, there will be redundancy in  -tuples after quantization which can be eliminated by our merging technique. However, we can also attempt to reduce the redundancy during quantizer design before the encoding of the bins is performed. Thus, it would be worth considering the effect of selection of a given quantization scheme on system performance when the merging technique is employed. In this section, we consider three schemes as follows.
-tuples after quantization which can be eliminated by our merging technique. However, we can also attempt to reduce the redundancy during quantizer design before the encoding of the bins is performed. Thus, it would be worth considering the effect of selection of a given quantization scheme on system performance when the merging technique is employed. In this section, we consider three schemes as follows.
(i) Uniform quantizers
Since they do not utilize any statistics about the sensor readings for quantizer design, there will be no reduction in redundancy by the quantization scheme. Thus only the merging technique plays a role in improving the system performance.
(ii) L1oyd quantizers
Using the statistics about the sensor reading  available at node
available at node  the
the  th quantizer
th quantizer  is designed using the generalized L1oyd algorithm [16] with the cost function
is designed using the generalized L1oyd algorithm [16] with the cost function  which is minimized in an iterative fashion. Since each node consider only the information available to it during quantizer design, there will still exist much redundancy after quantization which the merging technique can attempt to reduce.
which is minimized in an iterative fashion. Since each node consider only the information available to it during quantizer design, there will still exist much redundancy after quantization which the merging technique can attempt to reduce.
(iii) Localization specific quantizers (LSQs) proposed in [7]
While designing a quantizer at node  we can take into account the effect of quantized sensor readings at other nodes on the quantizer design by introducing the localization error in a new cost function, which will be minimized in an iterative manner. (The new cost function to be minimized is expressed as the Lagrangian functional
we can take into account the effect of quantized sensor readings at other nodes on the quantizer design by introducing the localization error in a new cost function, which will be minimized in an iterative manner. (The new cost function to be minimized is expressed as the Lagrangian functional  The topic of quantizer design in distributed setting goes beyond the scope of this work. See [7, 8] for detailed information.) Since the correlation between sensor readings is exploited during quantizer design, LSQ along with our merging technique will show the best performance of all.
The topic of quantizer design in distributed setting goes beyond the scope of this work. See [7, 8] for detailed information.) Since the correlation between sensor readings is exploited during quantizer design, LSQ along with our merging technique will show the best performance of all.
We will discuss the effect of quantization and encoding on the system performance based on experiments for an acoustic amplitude sensor system in Section 9.1.
5. Proposed Encoding Algorithm
In general, there will be multiple pairs of identifiable quantization bins that can be merged. Often, all candidate identifiable pairs cannot be merged simultaneously; that is, after a pair has been merged, other candidate pairs may become nonidentifiable. In what follows, we propose algorithms to determine in a sequential manner which pairs should be merged.
In order to minimize the total rate consumed by  nodes, an optimal merging technique should attempt to reduce the overall entropy as much as possible, which can be achieved by
nodes, an optimal merging technique should attempt to reduce the overall entropy as much as possible, which can be achieved by  merging high probability bins together and
merging high probability bins together and  merging as many bins as possible. It should be observed that these two strategies cannot be pursued simultaneously. This is because high probability bins (under our assumption of uniform distribution of the source position) are large and thus merging large bins tends to result in fewer remaining merging choices (i.e., a larger number of identifiable bin pairs may become nonidentifiable after two large identifiable bins have been merged). Conversely, a strategy that tries to maximize the number of merged bins will tend to merge many small bins, leading to less significant reductions in overall entropy. In order to strike a balance between these two strategies, we define a metric,
merging as many bins as possible. It should be observed that these two strategies cannot be pursued simultaneously. This is because high probability bins (under our assumption of uniform distribution of the source position) are large and thus merging large bins tends to result in fewer remaining merging choices (i.e., a larger number of identifiable bin pairs may become nonidentifiable after two large identifiable bins have been merged). Conversely, a strategy that tries to maximize the number of merged bins will tend to merge many small bins, leading to less significant reductions in overall entropy. In order to strike a balance between these two strategies, we define a metric,  attached to each quantization bin
attached to each quantization bin

where  This is a weighted sum of the bin probability and the number of the combinations of
This is a weighted sum of the bin probability and the number of the combinations of  -tuples that include
-tuples that include  If
If  is large the corresponding bin would be a good candidate for merging under criterion (1) whereas a small value of
is large the corresponding bin would be a good candidate for merging under criterion (1) whereas a small value of  will indicate a good choice under criterion (2). In our proposed procedure, for a suitable value of
will indicate a good choice under criterion (2). In our proposed procedure, for a suitable value of  we will seek to prioritize the merging of those identifiable bins having the largest total weighted metric. This will be repeated iteratively until there are no identifiable bins left. The selection of
we will seek to prioritize the merging of those identifiable bins having the largest total weighted metric. This will be repeated iteratively until there are no identifiable bins left. The selection of  can be heuristically made so as to minimize the total rate. For example, several different
can be heuristically made so as to minimize the total rate. For example, several different  could be evaluated in (7) to first determine its applicable range which will be then searched to find a proper value of
could be evaluated in (7) to first determine its applicable range which will be then searched to find a proper value of  Clearly,
Clearly,  depends on the application.
depends on the application.
The proposed global merging algorithm is summarized as follows.
Step 1.
Set  where
where  indicating that none of the bins,
indicating that none of the bins,  have been merged yet.
have been merged yet.
Step 2.
Find  that is, we search over all the nonmerged bins for the one with the largest metric
that is, we search over all the nonmerged bins for the one with the largest metric 
Step 3.
Find  such that
such that  where the search for the maximum is done only over the bins identifiable with
where the search for the maximum is done only over the bins identifiable with  at node
at node  and go to Step 4. If there are no bins identifiable with
and go to Step 4. If there are no bins identifiable with  set
set  indicating the bin
indicating the bin  is no longer involved in the merging process. If
is no longer involved in the merging process. If  stop; otherwise, go to Step 2.
stop; otherwise, go to Step 2.
Step 4.
Merge  and
and  to
to  with
with  Set
Set  Go to Step 2.
Go to Step 2.
In the proposed algorithm, the search for the maximum of the metric is done for the bins of all nodes involved. However, different approaches can be considered for the search. These are explained as follows.
Method 1 (Complete sequential merging).
In this method, we process one node at a time in a specified order. For each node, we merge the maximum number of bins possible before proceeding to the next node. Merging decisions are not modified once made. Since we exhaust all possible mergers in each node, after scanning all the nodes no more additional mergers are possible.
Method 2 : (Partial sequential merging).
In this method, we again process one node at a time in a specified order. For each node, among all possible bin mergers, the best one according to a criterion is chosen (the criterion could be entropy based and e.g., (7) is used in this paper) and after the chosen bin is merged we proceed to the next node. This process is continued until no additional mergers are possible in any node. This may require multiple passes through the set of nodes.
These two methods can be easily implemented with minor modifications to our proposed algorithm. Notice that the final result of the encoding algorithm will be  merging tables, each of which has the information about which bins can be merged at each node in real operation. That is, each node will merge the quantization bins using the merging table stored at the node and will send the merged bin to the fusion node which then tries to determine which bin actually occurred via the decoding process using
merging tables, each of which has the information about which bins can be merged at each node in real operation. That is, each node will merge the quantization bins using the merging table stored at the node and will send the merged bin to the fusion node which then tries to determine which bin actually occurred via the decoding process using  merging tables and
merging tables and 
5.1. Incremental Merging
The complexity of the above procedures is a function of the total number of quantization bins, and thus of the number of the nodes involved. These approaches could potentially be complex for large sensor fields. We now show that incremental merging is possible; that is, we can start by performing the merging based on a subset consisting of  sensor nodes,
sensor nodes,  and it can be guaranteed that the merging decisions that were valid when
and it can be guaranteed that the merging decisions that were valid when  nodes were considered will remain valid even when all
nodes were considered will remain valid even when all  nodes are taken into account. To see this, suppose that
nodes are taken into account. To see this, suppose that  and
and  are identifiable when only
are identifiable when only  nodes are considered. From Definition 1,
nodes are considered. From Definition 1,  where
where  indicates the number of nodes involved in the merging process. Note that since every element
indicates the number of nodes involved in the merging process. Note that since every element  (In this section, we denote by
(In this section, we denote by  an element
an element  Later, it will be also used to denote an
Later, it will be also used to denote an  th element in
th element in  in Section 8 without confusion) is constructed by concatenating
in Section 8 without confusion) is constructed by concatenating  indices
indices  with the corresponding element,
with the corresponding element,  we have that
we have that  if
if  By the property of the intersection operator
By the property of the intersection operator  we can claim that
we can claim that  implying that
implying that  and
and  are still identifiable even when we consider
are still identifiable even when we consider  nodes. Thus, we can start the merging process with just two nodes and continue to do further merging by adding one node (or a few) at a time without change in previously merged bins. When many nodes are involved, this would lead to significant savings in computational complexity. In addition, if some of the nodes are located far away from the nodes being added (i.e., the dynamic ranges of their quantizers do not overlap with those of the nodes being added), they can be skipped for further merging without loss of merging performance.
nodes. Thus, we can start the merging process with just two nodes and continue to do further merging by adding one node (or a few) at a time without change in previously merged bins. When many nodes are involved, this would lead to significant savings in computational complexity. In addition, if some of the nodes are located far away from the nodes being added (i.e., the dynamic ranges of their quantizers do not overlap with those of the nodes being added), they can be skipped for further merging without loss of merging performance.
6. Extension of Identifiability: 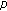 -Identifiability
-Identifiability
Since for real operating conditions, there exist measurement noise ( and/or parameter mismatches, it is computationally impractical to construct the set
and/or parameter mismatches, it is computationally impractical to construct the set  satisfying the assumption of
satisfying the assumption of  under which the merging algorithm was derived in Section 3. Instead, we construct
under which the merging algorithm was derived in Section 3. Instead, we construct  such that
such that  and propose an extended version of identifiability that allows us to still apply the merging technique under noisy situations. With this consideration, Definition 1 can be extended as follows.
and propose an extended version of identifiability that allows us to still apply the merging technique under noisy situations. With this consideration, Definition 1 can be extended as follows.
Definition 2.
 and
and  are
are  -identifiable, and therefore can be merged, if and only if
-identifiable, and therefore can be merged, if and only if  where
where  and
and  are constructed from
are constructed from  as
as  from
from  in Section 2. Obviously, to maximize the rate gain achievable by the merging technique, we need to construct
in Section 2. Obviously, to maximize the rate gain achievable by the merging technique, we need to construct  as small as possible given
as small as possible given  Ideally, we can build the set
Ideally, we can build the set  by collecting the
by collecting the  -tuples with high probability although it would require huge computational complexity especially when many nodes are involved at high rates. In this work, we suggest following the procedure stated below for construction of
-tuples with high probability although it would require huge computational complexity especially when many nodes are involved at high rates. In this work, we suggest following the procedure stated below for construction of  with reduced complexity.
with reduced complexity.
Step 1.
Compute the interval  such that
such that  Since
Since  where
where  in (1), we can construct the interval that is symmetric with respect to
in (1), we can construct the interval that is symmetric with respect to  that is,
that is,  so that
so that  Notice that
Notice that  is determined by
is determined by  and
and  (not a function of
(not a function of  ). For example, if
). For example, if  is given by
is given by  and
and  with
with 
Step 2.
From  intervals
intervals  we generate possible
we generate possible  -tuples
-tuples  satisfying that
satisfying that  Denote by
Denote by  a set containing such
a set containing such  tuples. It is noted that the process of generating
tuples. It is noted that the process of generating  -tuples from
-tuples from  intervals is deterministic, given
intervals is deterministic, given  quantizers. (Simple programming allows us to generate
quantizers. (Simple programming allows us to generate  -tuples from
-tuples from  intervals. For example, suppose that
intervals. For example, suppose that  and
and  and
and  are computed given
are computed given  in Step 1. Pick an
in Step 1. Pick an  -tuple
-tuple  with
with  and
and  Then, we determine whether or not
Then, we determine whether or not  by checking
by checking  In this example, we have
In this example, we have  )
)
Step 3.
Construct  We have
We have 
As  approaches
approaches  will be asymptotically reduced to
will be asymptotically reduced to  the set constructed in a noiseless case. It should be mentioned that this procedure provides a tool that enables us to change the size of
the set constructed in a noiseless case. It should be mentioned that this procedure provides a tool that enables us to change the size of  by simply adjusting
by simply adjusting  Obviously, computation of
Obviously, computation of  is unnecessary.
is unnecessary.
Notice that all the merged bins are  -identifiable (or identifiable) at the fusion node as long as the
-identifiable (or identifiable) at the fusion node as long as the  -tuple to be encoded belongs to
-tuple to be encoded belongs to  (or
(or  ). In other words, decoding errors will be generated when elements in
). In other words, decoding errors will be generated when elements in  occur and there will be tradeoff between rate savings and decoding errors. If we choose
occur and there will be tradeoff between rate savings and decoding errors. If we choose  to be as small as possible, yielding a small set
to be as small as possible, yielding a small set  , we can achieve good rate savings at the expense of large decoding error (equivalently,
, we can achieve good rate savings at the expense of large decoding error (equivalently,  large), which could lead to degradation of localization performance. Handling of decoding errors will be discussed in Section 7.
large), which could lead to degradation of localization performance. Handling of decoding errors will be discussed in Section 7.
7. Decoding of Merged Bins and Handling Decoding Errors
In the decoding process, the fusion node will first decompose the received  -tuple
-tuple  into the possible
into the possible  -tuples,
-tuples,  by using the
by using the  merging tables (see Figure 4). Note that the merging process is done offline in a centralized manner. In real operation, each node stores its merging table which is constructed from the proposed merging algorithm and used to perform the encoding and the fusion node uses
merging tables (see Figure 4). Note that the merging process is done offline in a centralized manner. In real operation, each node stores its merging table which is constructed from the proposed merging algorithm and used to perform the encoding and the fusion node uses  and
and  merging tables to do the decoding. Revisit the simple case in Figure 3. According to node
merging tables to do the decoding. Revisit the simple case in Figure 3. According to node  merging table,
merging table,  and
and  can be merged into
can be merged into  implying that node
implying that node  will transmit
will transmit  to the fusion node whenever
to the fusion node whenever  belongs to
belongs to  or
or  Suppose that the fusion node receives
Suppose that the fusion node receives  Then, it decomposes
Then, it decomposes  into
into  and
and  by using node
by using node  merging table. This decomposition will be performed for the other
merging table. This decomposition will be performed for the other  merging tables. Note that
merging tables. Note that  is discarded since it does not belong to
is discarded since it does not belong to  implying that
implying that  actually occurred at node
actually occurred at node 
Suppose that we have a set of K  -tuples,
-tuples,  decomposed from
decomposed from  via
via  merging tables. Then, clearly,
merging tables. Then, clearly,  and
and  where
where  is the true
is the true  -tuple before encoding (see Figure 4). Notice that if
-tuple before encoding (see Figure 4). Notice that if  then all merged bins would be identifiable at the fusion node; that is, after decomposition, there is only one decomposed
then all merged bins would be identifiable at the fusion node; that is, after decomposition, there is only one decomposed  -tuple,
-tuple,  belonging to
belonging to  , (As the decomposition is processed, all the decomposed
, (As the decomposition is processed, all the decomposed  -tuples except
-tuples except  will be discarded since they do not belong to
will be discarded since they do not belong to  .) and we declare decoding successful. Otherwise, we declare decoding errors and apply the decoding rules which will be explained in the following subsections, to handle those errors. Since the decoding error occurs only when
.) and we declare decoding successful. Otherwise, we declare decoding errors and apply the decoding rules which will be explained in the following subsections, to handle those errors. Since the decoding error occurs only when  the decoding error probability will be less than
the decoding error probability will be less than 
It is observed that since the decomposed  -tuples are produced via the
-tuples are produced via the  merging tables from
merging tables from  it is very likely that
it is very likely that  where
where  In other words, since the encoding process merges the quantization bins whenever any
In other words, since the encoding process merges the quantization bins whenever any  -tuples that contain either of them are very unlikely to happen at the same time, the
-tuples that contain either of them are very unlikely to happen at the same time, the  -tuples
-tuples  tend to take very low probability.
tend to take very low probability.
7.1. Decoding Rule 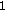 : Simple Maximum Rule
: Simple Maximum Rule
Since the received  -tuple
-tuple  has ambiguity produced by encoders at each node, the decoder at fusion node should be able to find the true
has ambiguity produced by encoders at each node, the decoder at fusion node should be able to find the true  -tuple by using appropriate decoding rules. As a simple rule, we can take the
-tuple by using appropriate decoding rules. As a simple rule, we can take the  -tuple (out of
-tuple (out of  ) that is most likely to happen. Formally,
) that is most likely to happen. Formally,

where  is the decoded
is the decoded  -tuple which will be forwarded to the localization routine.
-tuple which will be forwarded to the localization routine.
7.2. Decoding Rule 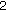 : Weighted Decoding Rule
: Weighted Decoding Rule
Instead of choosing only one decoded  -tuple, we can treat each decomposed
-tuple, we can treat each decomposed  -tuple as a candidate for the decoded
-tuple as a candidate for the decoded  -tuple,
-tuple,  with its corresponding weight obtained from the likelihood. That is, we can view
with its corresponding weight obtained from the likelihood. That is, we can view  as one decoded
as one decoded  -tuple with weight
-tuple with weight  It should be noted that the weighted decoding rule should be used along with the localization routine as follows:
It should be noted that the weighted decoding rule should be used along with the localization routine as follows:

where  is the estimated source location assuming
is the estimated source location assuming  For simplicity, we can take a few dominant
For simplicity, we can take a few dominant  -tuples for the weighted decoding and localization
-tuples for the weighted decoding and localization

where  is the weight of
is the weight of  and
and  if
if  Typically,
Typically,  is chosen as a small number (e.g.,
is chosen as a small number (e.g.,  in our experiments). Note that the weighted decoding rule with
in our experiments). Note that the weighted decoding rule with  is equivalent to the simple maximum rule in (8).
is equivalent to the simple maximum rule in (8).
8. Application to Acoustic Amplitude Sensor Case
As an example of the application, we consider the acoustic amplitude sensor system, where an energy decay model of sensor signal readings proposed in [4] is used for localization. The energy decay model was verified by the field experiment in [4] and was also used in [9, 13, 17].) This model is based on the fact that the acoustic energy emitted omnidirectionally from a sound source will attenuate at a rate that is inversely proportional to the square of the distance in free space [18]. When an acoustic sensor is employed at each node, the signal energy measured at node  over a given time interval
over a given time interval  and denoted by
and denoted by  can be expressed as follows:
can be expressed as follows:

where the parameter vector  in (1) consists of the gain factor of the
in (1) consists of the gain factor of the  th node
th node  an energy decay factor
an energy decay factor  which is approximately equal to
which is approximately equal to  in free space, and the source signal energy
in free space, and the source signal energy  The measurement noise term
The measurement noise term  can be approximated using a normal distribution,
can be approximated using a normal distribution,  In (11), it is assumed that the signal energy,
In (11), it is assumed that the signal energy,  is uniformly distributed over the range
is uniformly distributed over the range  .
.
In order to perform distributed encoding at each node, we first need to obtain the set  which can be constructed from (3) as follows:
which can be constructed from (3) as follows:

where the  th sensor reading
th sensor reading  is expressed by the sensor model
is expressed by the sensor model  and the measurement noise,
and the measurement noise, 
When the signal energy  is known, and there is no measurement noise (
is known, and there is no measurement noise ( ), it would be straightforward to construct the set
), it would be straightforward to construct the set  That is, each element in
That is, each element in  corresponds to one region in sensor field which is obtained by computing the intersection of
corresponds to one region in sensor field which is obtained by computing the intersection of  ring-shaped areas (see Figure 2). For example, using an j th element
ring-shaped areas (see Figure 2). For example, using an j th element  in
in  we can compute the corresponding intersection
we can compute the corresponding intersection  as follows:
as follows:

Since the nodes involved in localization of any given source generate the same  -tuple, the set
-tuple, the set  will be computed deterministically and we have
will be computed deterministically and we have  Thus, using
Thus, using  we can apply our merging technique to this case and achieve significant rate savings without any degradation of localization accuracy (no decoding error).
we can apply our merging technique to this case and achieve significant rate savings without any degradation of localization accuracy (no decoding error).
However, measurement noise and/or unknown signal energy will make this problem complicated by allowing random realizations of  -tuples generated by
-tuples generated by  nodes for any given source location. For this case, we construct
nodes for any given source location. For this case, we construct  by following the procedure in Section 6 and apply our decoding rules explained in Section 7 to handle decoding errors.
by following the procedure in Section 6 and apply our decoding rules explained in Section 7 to handle decoding errors.
9. Experimental Results
The distributed encoding algorithm described in Section 5 is applied to the system, where each node employs an acoustic amplitude sensor model given by (11) for source localization. The experimental results are provided in terms of average localization error. (Clearly, the localization error would be affected by the estimators employed at the fusion node. The estimation algorithms go beyond the scope of this work. For detailed information, see [9].)  and rate savings (%) computed by
and rate savings (%) computed by  where
where  is the rate consumed by
is the rate consumed by  nodes when only the independent entropy coding (Huffman coding) is used after quantization and
nodes when only the independent entropy coding (Huffman coding) is used after quantization and  is the rate by
is the rate by  nodes when the merging technique is applied to quantized data before the entropy coding. We assume that each node uses LSQ described in Section 4 (for further details, refer to [7]) except for the experiments where otherwise stated.
nodes when the merging technique is applied to quantized data before the entropy coding. We assume that each node uses LSQ described in Section 4 (for further details, refer to [7]) except for the experiments where otherwise stated.
9.1. Distributed Encoding Algorithm: Noiseless Case
It is assumed that each node can measure the known signal energy without measurement noise. Figure 5 shows the overall performance of the system for each quantization scheme. In this experiment, 100 different 5-node configurations were generated in a sensor field  For each configuration, a test set of 2000 random source locations was used to obtain sensor readings, which are then quantized by three different quantizers, namely, uniform quantizers, L1oyd quantizers, and LSQs. The average localization error and total rate
For each configuration, a test set of 2000 random source locations was used to obtain sensor readings, which are then quantized by three different quantizers, namely, uniform quantizers, L1oyd quantizers, and LSQs. The average localization error and total rate  are averaged over 100 node configurations. As expected, the overall performance for LSQ is the best of all since the total reduction in redundancy can be maximized when the application-specific quantization such as LSQ and the distributed encoding are used together.
are averaged over 100 node configurations. As expected, the overall performance for LSQ is the best of all since the total reduction in redundancy can be maximized when the application-specific quantization such as LSQ and the distributed encoding are used together.
Our encoding algorithm with the different merging techniques outlined in Section 5 is applied for comparison, and the results are provided in Table 1. Methods 1 and 2 are as described in Section 5, and Method 3 is the global merging algorithm discussed in that section. We can observe that even with relative low rates (4 bits per node) and a small number of nodes (only 5) significant rate gains (over 30%) can be achieved with our merging technique.
 in bits (rate savings) achieved by various merging techniques.
in bits (rate savings) achieved by various merging techniques.The encoding algorithm was also applied to many different node configurations to characterize the performance. In this experiment, 500 different node configurations were generated for each  in a sensor field
in a sensor field  The global merging technique has been applied to obtain the rate savings. In computing the metric in (7), the source distribution is assumed to be uniform. The average rate savings is plotted by varying
The global merging technique has been applied to obtain the rate savings. In computing the metric in (7), the source distribution is assumed to be uniform. The average rate savings is plotted by varying  and
and  in Figure 6. Clearly, the better rate savings is achieved with larger
in Figure 6. Clearly, the better rate savings is achieved with larger  and/or at higher rate since there exists more redundancy expressed as
and/or at higher rate since there exists more redundancy expressed as  as more nodes become involved at higher rate.
as more nodes become involved at higher rate.
Since there are a large number of nodes in typical sensor networks, our distributed algorithms have been applied to the system in a larger sensor field  In this experiment, 20 different node configurations are generated for each
In this experiment, 20 different node configurations are generated for each  Note that the node density for
Note that the node density for  in
in  is equal to
is equal to  which is also the node density for the case of
which is also the node density for the case of  in
in  In Table 2, it is worth noting that the system with a larger number of nodes outperforms the system with a smaller number of nodes
In Table 2, it is worth noting that the system with a larger number of nodes outperforms the system with a smaller number of nodes  although the node density is kept the same. This is because the incremental property of the merging technique allows us to find more identifiable bins at each node.
although the node density is kept the same. This is because the incremental property of the merging technique allows us to find more identifiable bins at each node.
 in bits (rate savings) achieved by distributed encoding algorithm (global merging technique). The rate savings is averaged over 20 different node configurations, where each node uses LSQ with
in bits (rate savings) achieved by distributed encoding algorithm (global merging technique). The rate savings is averaged over 20 different node configurations, where each node uses LSQ with 
9.2. Encoding with 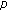 -Identifiability and Decoding Rules: Noisy Case
-Identifiability and Decoding Rules: Noisy Case
The distributed encoding algorithm with  -identifiability described in Section 6 was applied to the case, where each node collects noise-corrupted measurements of unknown source signal energy. First, assuming known signal energy, we checked the effect of measurement noise on the rate savings, and thus the decoding error by varying the size of
-identifiability described in Section 6 was applied to the case, where each node collects noise-corrupted measurements of unknown source signal energy. First, assuming known signal energy, we checked the effect of measurement noise on the rate savings, and thus the decoding error by varying the size of  Note that as
Note that as  becomes increased, the total rate
becomes increased, the total rate  tends to be increased since small rate gain is achieved with
tends to be increased since small rate gain is achieved with  large. In this experiment, the variance of measurement noise,
large. In this experiment, the variance of measurement noise,  varies from
varies from  to
to  and for each
and for each  a test set of 2000 source locations was generated with
a test set of 2000 source locations was generated with  Figure 7 illustrates that good rate savings can be still achieved in a noisy situation by allowing small decoding errors. It can be noted that better rate savings can be achieved at higher SNR (Note that for practical vehicle target, the SNR is often much higher than 40 dB and a typical value of the variance of measurement noise
Figure 7 illustrates that good rate savings can be still achieved in a noisy situation by allowing small decoding errors. It can be noted that better rate savings can be achieved at higher SNR (Note that for practical vehicle target, the SNR is often much higher than 40 dB and a typical value of the variance of measurement noise  is
is  [4, 13].) and/or with larger decoding errors allowed (Pr [decoding error]
[4, 13].) and/or with larger decoding errors allowed (Pr [decoding error] in this experiments).
in this experiments).
For the case of unknown signal energy, where we assume that  we constructed
we constructed  with
with  by varying
by varying  where
where  is constructed when
is constructed when  using the procedure in Section 6. Using
using the procedure in Section 6. Using  we applied the merging technique with
we applied the merging technique with  -identifiability to evaluate the performance (rate savings versus localization error). In the experiment, a test set of 2000 samples is generated from uniform priors for
-identifiability to evaluate the performance (rate savings versus localization error). In the experiment, a test set of 2000 samples is generated from uniform priors for  and
and  with each noise variance (
with each noise variance ( and
and  ). In order to deal with decoding errors, two decoding rules in Section 7 were applied. In Figure 8, the performance curves for two decoding rules were plotted for comparison. As can be seen, the weighted decoding rule performs better than the simple maximum rule since the former takes into account the effect of the other decomposed
). In order to deal with decoding errors, two decoding rules in Section 7 were applied. In Figure 8, the performance curves for two decoding rules were plotted for comparison. As can be seen, the weighted decoding rule performs better than the simple maximum rule since the former takes into account the effect of the other decomposed  -tuples on localization accuracy by adjusting their weights. It is also noted that when decoding error is very low (equivalently,
-tuples on localization accuracy by adjusting their weights. It is also noted that when decoding error is very low (equivalently,  ), both of them show almost the same performance.
), both of them show almost the same performance.
Average localization error versus total rate  achieved by the distributed encoding algorithm (global merging algorithm) with simple maximum decoding and weighted decoding, respectively. Total rate increases by changing
achieved by the distributed encoding algorithm (global merging algorithm) with simple maximum decoding and weighted decoding, respectively. Total rate increases by changing  from
from  to
to  and weighted decoding is conducted with
and weighted decoding is conducted with  Solid line
Solid line  weighted decoding. Solid line +
weighted decoding. Solid line +  simple maximum decoding.
simple maximum decoding.
To see how much gain we can obtain from the encoding under noisy situations, we compared this to the system which uses only the entropy coding without applying the merging technique. In Figure 9, the performance curves (R-D curves) are plotted with  and
and  for
for  and
and  It should be noted that we can determine the size of
It should be noted that we can determine the size of  (equivalently,
(equivalently,  ) that provides the best performance from this experiment.
) that provides the best performance from this experiment.
9.3. Performance Comparison
For the purpose of evaluation, it would be meaningful to compare our encoding technique with LSQ algorithm since both of them are optimized for source localization and can be viewed as DSC (distributed source coding) techniques which are developed as a tool to reduce the rate required to transmit data from all nodes to the sink. In Figure 10, the R-D curve for LSQ only (without our encoding technique) is plotted for comparison. It should be observed that at high rate, the encoding technique will outperform LSQ since the better rate savings will be achieved as the total rate increases.
We address the question of how our technique compares with the best achievable performance for this source localization scenario. As a bound on achievable performance we consider a system where (i) each node quantizes its measurement independently and (ii) the quantization indices generated by all nodes for a given source location are jointly coded (in our case, we use the joint entropy of the vector of measurements as the rate estimate).
Note that this is not a realistic bound because joint coding cannot be achieved unless the nodes are able to communicate before encoding. In order to approximate the behavior of the joint entropy coder via DSC techniques one would have to transmit multiple sensor readings of the source energy from each node, as the source is moving around the sensor field. Some of the nodes could send measurements that are directly encoded, while others could transmit a syndrome produced by an error correcting code based on the quantized measurements. Then, as the fusion node receives all the information from the various nodes it would be able to exploit the correlation from the measurements and approximate the joint entropy. This method would not be desirable, however, because the information in each node depends on the location of the source and thus to obtain a reliable estimate of the measurement at all nodes one would have to have measurements at a sufficient number of positions of the source. Thus, instantaneous localization of the source would not be possible. The key point here, then, is that the randomness between measurements across nodes is based on the localization of the source, which is precisely what we wish to observe.
For a 5-node configuration, the average rate per node was plotted with respect to the localization error in Figure 11, with assumption of no measurement noise ( ) and known signal energy. For this particular configuration we can observe a gap of less than
) and known signal energy. For this particular configuration we can observe a gap of less than  at high rates, between the performance achieved by the distributed encoding and that achievable by the joint entropy coding when the same quantizers (LSQ) are employed. In summary, our merging technique provides substantial gain which comes close to the optimal achievable performance.
at high rates, between the performance achieved by the distributed encoding and that achievable by the joint entropy coding when the same quantizers (LSQ) are employed. In summary, our merging technique provides substantial gain which comes close to the optimal achievable performance.
10. Conclusion and Future Works
Using the distributed property of the quantized sensor readings, we proposed a novel encoding algorithm to achieve significant rate savings by merging quantization bins. We also developed decoding rules to deal with the decoding errors which can be caused by measurement noise and/or parameter mismatches. In the experiment, we showed that the system equipped with the distributed encoders achieved significant data compression as compared with standard systems.
So far, we have considered encoding algorithms by fixing quantizers. However, since there exists dependency between quantization and encoding of quantized data which can be exploited to obtain better performance gain, it would be worth considering a joint design of quantizers and encoders.
References
Zhao F, Shin J, Reich J: Information-driven dynamic sensor collaboration. IEEE Signal Processing Magazine 2002, 19(2):61-72. 10.1109/79.985685
Chen JC, Yao K, Hudson RE: Source localization and beamforming. IEEE Signal Processing Magazine 2002, 19(2):30-39. 10.1109/79.985676
Li D, Wong KD, Hu YH, Sayeed AM: Detection, classification, and tracking of targets. IEEE Signal Processing Magazine 2002, 19(2):17-29. 10.1109/79.985674
Li D, Hu YH: Energy-based collaborative source localization using acoustic microsensor array. EURASIP Journal on Applied Signal Processing 2003, 2003(4):321-337. 10.1155/S1110865703212075
Chen JC, Yao K, Hudson RE: Acoustic source localization and beamforming: theory and practice. EURASIP Journal on Applied Signal Processing 2003, 2003(4):359-370. 10.1155/S1110865703212038
Chen JC, Yip L, Elson J, Wang H, Maniezzo D, Hudson RE, Yao K, Estrin D: Coherent acoustic array processing and localization on wireless sensor networks. Proceedings of the IEEE 2003, 91(8):1154-1161. 10.1109/JPROC.2003.814924
Kim YH, Ortega A: Quantizer design for source localization in sensor networks. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '05), March 2005 857-860.
Kim YH: Distrbuted algorithms for source localization using quantized sensor readings, Ph.D. dissertation. USC; December 2007.
Kim YH, Ortega A: Maximum a posteriori (MAP)-based algorithm for distributed source localization using quantized acoustic sensor readings. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006 1053-1056.
Kim YH, Ortega A: Quantizer design and distributed encoding algorithm for source localization in sensor networks. Proceedings of the 4th International Symposium on Information Processing in Sensor Networks (IPSN '05), April 2005 231-238.
Flynn TJ, Gray RM: Encoding of correlated observations. IEEE Transactions on Information Theory 1988, 33(6):773-787.
Ishwar P, Puri R, Ramchandran K, Pradhan SS: On rate-constrained distributed estimation in unreliable sensor networks. IEEE Journal on Selected Areas in Communications 2005, 23(4):765-774.
Liu J, Reich J, Zhao F: Collaborative in-network processing for target tracking. EURASIP Journal on Applied Signal Processing 2003, 2003(4):378-391. 10.1155/S111086570321204X
Yang H, Sikdar B: A protocol for tracking mobile targets using sensor networks. Proceedings of IEEE Workshop on Sensor Network Protocols and Applications (SNPA '03), May 2003, Anchorage, Alaska, USA 71-81.
Cover TM, Thomas JA: Elements of Information Theory. Wiley-Interscience, New York, NY, USA; 1991.
Sayood K: Introduction to Data Compression. 2nd edition. Morgan Kaufmann Publishers, San Fransisco, Calif, USA; 2000.
Hero AO III, Blatt D: Sensor network source localization via projection onto convex sets (POCS). Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '05), March 2005 689-692.
Rappaport TS: Wireless Communications:Principles and Practice. Prentice-Hall, Upper Saddle River, NJ, USA; 1996.
Acknowledgments
The authors would like to thank the anonymous reviewers for their careful reading of the paper and useful suggestions which led to significant improvements in the paper. This research has been funded in part by the Pratt & Whitney Institute for Collaborative Engineering (PWICE) at USC, and in part by NASA under the Advanced Information Systems Technology (AIST) program. The work was presented in part in IEEE International Symposium on Information Processing in Sensor Networks (IPSN), April 2005.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, Y., Ortega, A. Distributed Encoding Algorithm for Source Localization in Sensor Networks. EURASIP J. Adv. Signal Process. 2010, 781720 (2010). https://doi.org/10.1155/2010/781720
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/781720

 ) and encoded (ENC block) measurement to the fusion node, where decoding and localization are conducted in a distributed manner.
) and encoded (ENC block) measurement to the fusion node, where decoding and localization are conducted in a distributed manner.

 ). In this case, it is assumed that
). In this case, it is assumed that 
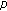 -Identifiability
-Identifiability
 : Simple Maximum Rule
: Simple Maximum Rule : Weighted Decoding Rule
: Weighted Decoding Rule
 for three different quantization schemes with distributed encoding algorithm. Average rate savings is achieved by the distributed encoding algorithm (global merging algorithm).
for three different quantization schemes with distributed encoding algorithm. Average rate savings is achieved by the distributed encoding algorithm (global merging algorithm).
 with
with
 (left) and number of nodes with
(left) and number of nodes with
 (right).
(right).
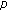 -Identifiability and Decoding Rules: Noisy Case
-Identifiability and Decoding Rules: Noisy Case
 and
and



 achieved by the distributed encoding algorithm (global merging algorithm) with
achieved by the distributed encoding algorithm (global merging algorithm) with
 and
and
 is varied from
is varied from
 Weighted decoding with
Weighted decoding with
 is applied in this experiment.
is applied in this experiment.

 are averaged for 100 different 5-node configurations.
are averaged for 100 different 5-node configurations.