- Research Article
- Open access
- Published:
Spectral Correlation of Multicarrier Modulated Signals and Its Application for Signal Detection
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 794246 (2009)
Abstract
Spectral correlation theory for cyclostationary time-series signals has been studied for decades. Explicit formulas of spectral correlation function for various types of analog-modulated and digital-modulated signals are already derived. In this paper, we investigate and exploit the cyclostationarity characteristics for two kinds of multicarrier modulated (MCM) signals: conventional OFDM and filter bank based multicarrier (FBMC) signals. The spectral correlation characterization of MCM signal can be described by a special linear periodic time-variant (LPTV) system. Using this LPTV description, we have derived the explicit theoretical formulas of nonconjugate and conjugate cyclic autocorrelation function (CAF) and spectral correlation function (SCF) for OFDM and FBMC signals. According to theoretical spectral analysis, Cyclostationary Signatures (CS) are artificially embedded into MCM signal and a low-complexity signature detector is, therefore, presented for detecting MCM signal. Theoretical analysis and simulation results demonstrate the efficiency and robustness of this CS detector compared to traditionary energy detector.
1. Introduction
A cyclostationary process is an appropriate probabilistic model for the signals that undergo periodic transformation, such as sampling, modulating, multiplexing, and coding operations, provided that the signal is appropriately modeled as a stationary process before undergoing the periodic transformation [1]. Increasing demands on communication system performance indicate the importance of recognizing the cyclostationary character of communicated signals. The growing role of the cyclostationarity is illustrated by abundant works in the detection area and other signal processing areas. Spectral correlation is an important characteristic property of wide sense cyclostationarity, and a spectral correlation function is a generalization of the power spectral density (PSD) function. Recently, the spectral correlation function has been largely exploited for signal detection, estimation, extraction and classification mainly because different types of modulated signals have highly distinct spectral correlation functions and the fact stationary noise and interference exhibit no spectral correlation property. Furthermore, the spectral correlation function contains phase and frequency information related to timing parameters in modulated signals.
In [1, 2], explicit formulas of the CAF and SCF for various types of single carrier modulated signals are derived. The cyclostationary properties of OFDM have been analyzed in [3, 4], and the formulas of CAF and SCF of OFDM signal are derived by a mathematic deduce process in [3], whereas the authors in [4] provide a straightforward derivation of CAF and SCF for OFDM signal by a matrix-based stochastic method without involving complicated theory. For FBMC signals, the second-order syclostationarity properties of FBMC signal are exploited in [5, 6] for blind joint carrier-frequency offset (CFO) and symbol timing estimation.
The main objective of this article is to obtain the general formulas for calculating the CAF and SCF of MCM signals using a common derivation model. A particularly convenient method for calculating the CAF and SCF for many types of modulated signals is to model the signal as a purely stationary waveform transformed by a Linear Periodically Time-Variant (LPTV) transformation [7, 8]. Multicarrier modulated signal can be regarded as a special model with the multi-input transformed by LPTV transformation and one scalar output. By modeling MCM signal into a LPTV system it is convenient to analyze MCM signal using the known LPTV theory. With the help of the mature LPTV theory, herein we derive the explicit formulas for nonconjugate and conjugate cyclic autocorrelation function and spectral correlation function of OFDM and FBMC signals, which are very useful for blind MCM signals detection and classification.
Cognitive Radio (CR) has recently been proposed as a possible solution to improve spectrum utilization via dynamic spectrum access, and spectrum sensing has also been identified as a key enabling functionality to ensure that cognitive radios would not interference with primary users. We are interested in various efficient (low Signal-to-Noise Ratio, (SNR), detection requirement of licensed signal) and low-complex methods for the detection of free bands at the worst situation that we know only few information about the received signal. Cyclostationary based detector is efficient and more robust than energy detector [9], which is highly susceptible to noise uncertainty. In most of practical situations, it is not very likely that the cognitive radio has access to the nature of licensed signal, hence rendering noise estimation impossible. The worse thing is that energy detector cannot differentiate between modulated signals, noise and interference. Feature detector such as cyclostationarity is, therefore, proposed for signal detection in CR context. An inherent cyclostationary detection method, by detecting the presence of nonconjugate cyclostationarity in some non-zero cyclic frequency, is proposed in [3]. Although this detector exhibits good detection performance, it cannot achieve the low SNR requirement of CR system specified by FCC. In addition, the computation of the proposed cyclostationarity detection algorithm is complex.
Therefore, in order to alleviate the computation complexity and achieve better detection performance for low SNR level, we apply a conjugate cyclostationarity detector by inserting Cyclostationary Signature [10] (CS), which is realized by redundantly transmitting message symbols at some predetermined cyclic frequency based on the theoretical spectral analysis and the fact that most of the MCM signals and noise do not exhibit conjugate cyclostationarity. Previous works introducing artificially cyclostationarity for OFDM signal at the transmitter can be found in [10–12]. In this paper, the signal detection between FBMC signal and noise is investigated. We implement the spectral detection of FBMC signal embedded by CS using a low-complexity conjugate cyclostationarity detector considering both AWGN and Rayleigh fading environments in the CR domain. Experimental results are provided to show the efficiency and the robustness compared to the traditionary energy detector.
The remainder of this paper is organized as follows: Section 2 presents the basic definition of spectral correlation. The fundamental concepts of LPTV system are mentioned in Section 3. Through the aforementioned theoretical knowledge, Section 4 analyzes and derives the theoretical formulas of nonconjugate and conjugate cyclic autocorrelation and spectral correlation functions of OFDM and FBMC signals. In Section 5, corresponding spectral analysis for FBMC signals with CS is investigated. A low-complexity CS detector is presented in Section 6. Simulation results are given in Section 7. Finally, conclusions are drawn in Section 8.
2. Definition of Cyclic Spectral Correlation
A complete understanding of the concept of spectral correlation is given in the tutorial paper [8]. This section is a very brief review of the fundamental definitions for spectral correlation.
The probabilistic nonconjugate autocorrelation of a stochastic process  is
is

where the superscript asterisk denotes complex conjugation.  is defined to be second-order cyclostationary (in the wide sense) if
is defined to be second-order cyclostationary (in the wide sense) if  is the periodic function about
is the periodic function about  with period
with period  and can be represented as a Fourier series:
and can be represented as a Fourier series:

which is called periodic autocorrelation function, where the sum is taken over integer multiples of the fundamental frequency " ". The Fourier coefficients can be calculated as
". The Fourier coefficients can be calculated as

where  , and
, and  is called the cyclic autocorrelation function. The idealized cyclic spectrum function can be characterized as the Fourier transform
is called the cyclic autocorrelation function. The idealized cyclic spectrum function can be characterized as the Fourier transform

In the nonprobabilistic approach, for a time-series  that contains second-order periodicity, synchronized averaging applied to the lag product time-series "
that contains second-order periodicity, synchronized averaging applied to the lag product time-series " " yields
" yields

which is referred to as the limit periodic autocorrelation function. The nonprobabilistic counterpart of (3) is given by

which is recognized as the limit cyclic autocorrelation function. The limit cyclic spectrum function can be characterized as the Fourier transform like (4):

The limit cyclic spectrum function is also called spectral correlation function. Fourier transform relation in (7) is called the cyclic Wiener relation.
In summary, the limit cyclic autocorrelation can be interpreted as a Fourier coefficient in the Fourier series expansion of the limit periodic autocorrelation like (2). If  for all
for all  and
and  , then
, then  is purely stationary. If
is purely stationary. If  only for
only for  for some period
for some period  , then
, then  is purely cyclostationary with period
is purely cyclostationary with period  . If
. If  for values of
for values of  that are not all integer multiples of some fundamental frequency
that are not all integer multiples of some fundamental frequency  , then
, then  is said to exhibit cyclostationary [1]. For modulated signals, the periods of cyclostationarity correspond to carrier frequencies, pulse rates, spreading code repetition rates, time-division multiplexing rates, and so on.
is said to exhibit cyclostationary [1]. For modulated signals, the periods of cyclostationarity correspond to carrier frequencies, pulse rates, spreading code repetition rates, time-division multiplexing rates, and so on.
In paper [8], an useful modification of the CAF called conjugate cyclic autocorrelation function is given as

with  , and the corresponding SCF called conjugate spectral correlation function is
, and the corresponding SCF called conjugate spectral correlation function is

For a noncyclostationary signal,  for all
for all  , and for a cyclostationary signal, any nonzero value of the frequency parameter
, and for a cyclostationary signal, any nonzero value of the frequency parameter  , for which the nonconjugate and conjugate CAFs and SCFs differ from zero is called a cycle frequency. Both nonconjugate and conjugate CAFs and SCFs are discrete functions of the cycle frequency
, for which the nonconjugate and conjugate CAFs and SCFs differ from zero is called a cycle frequency. Both nonconjugate and conjugate CAFs and SCFs are discrete functions of the cycle frequency  and are continuous in the lag parameter
and are continuous in the lag parameter  and frequency parameter
and frequency parameter  , respectively.
, respectively.
3. LPTV System
LPTV is a special case of linear almost-periodically time-variant (LAPTV), which is introduced in [7]. A linear time-variant system with input  , output
, output  , impulse response function
, impulse response function  , and input-output relation
, and input-output relation

is said to be LAPTV if the impulse response function admits the Fourier series expansion:

where  is a countable set.
is a countable set.
By substituting (11) into (10) the output  can be expressed in the two equivalent forms
can be expressed in the two equivalent forms


where " " denotes convolution operation, and
" denotes convolution operation, and

From (12) it follows that a LAPTV system performs a linear time-invariant filtering of frequency-shifted version of the input signal. For this reason LAPTV is also referred to as frequency-shift filtering. Equivalently, form (13) it follows that a LAPTV system performs a frequency shift of linear time-invariant filtered versions of the input.
In the special case for which  for some period
for some period  , the system becomes the linear periodically time-variant (LPTV).
, the system becomes the linear periodically time-variant (LPTV).
LPTV transformation is defined as follows [8]:

where  is a
is a  -element column vector input (
-element column vector input ( is any non-zero positive integer) and
is any non-zero positive integer) and  is a scalar response.
is a scalar response.  is the periodically time-variant (
is the periodically time-variant ( -element row vector) of impulse response functions that specify the transformation. The function
-element row vector) of impulse response functions that specify the transformation. The function  is periodic in
is periodic in  with a period
with a period  for each
for each  represented by the Fourier series
represented by the Fourier series

where

The Fourier transform of function  is defined as a system function:
is defined as a system function:

which can be also represented by a Fourier series:

where

By substitution of (15) and (16) into the definition of (3) and (4), it can be shown that the nonconjugate cyclic autocorrelation and cyclic spectrum of the input  and output
and output  of the LPTV system are related by the formulas
of the LPTV system are related by the formulas


where " " denotes convolution operation, the superscript symbol "
" denotes convolution operation, the superscript symbol " " denotes matrix transposition, and "
" denotes matrix transposition, and " " denotes conjugation.
" denotes conjugation.  is the matrix of cyclic cross-correlation of the elements of the vector
is the matrix of cyclic cross-correlation of the elements of the vector 

and  is the matrix of finite cyclic cross correlation
is the matrix of finite cyclic cross correlation

Formulas (21) and (22) reveal that the cyclic autocorrelation and spectra of a modulated signal are each self-determinant characteristics under an LPTV transformation.
The conjugate cyclic autocorrelation and cyclic spectrum of the input  and output
and output  of the LPTV system are obtained similarly:
of the LPTV system are obtained similarly:




4. Spectral Correlation of MCM Signals
Generally, the carrier modulated passband MCM signal  can be expressed as
can be expressed as

where  denotes the real part of
denotes the real part of  ,
,  is the baseband envelope of the actual transmitted MCM signal, and
is the baseband envelope of the actual transmitted MCM signal, and  is the carrier frequency.
is the carrier frequency.
If the baseband envelope signal  is cyclostationary, the spectral correlation function of its corresponding carrier modulated signal
is cyclostationary, the spectral correlation function of its corresponding carrier modulated signal  can be expressed as [13]
can be expressed as [13]

where  and
and  are the nonconjugate and conjugate spectral correlation function of the complex envelope
are the nonconjugate and conjugate spectral correlation function of the complex envelope  , respectively. We can observe that the spectral correlation of the carrier modulated signal
, respectively. We can observe that the spectral correlation of the carrier modulated signal  is determined by the nonconjugate and conjugate spectral correlation of the complex envelope signal
is determined by the nonconjugate and conjugate spectral correlation of the complex envelope signal  and is related to the double carrier frequency, so the problem of spectral analysis correlation analysis of passband carrier modulated signal can be reduced to the spectral correlation analysis of the complex baseband signal.
and is related to the double carrier frequency, so the problem of spectral analysis correlation analysis of passband carrier modulated signal can be reduced to the spectral correlation analysis of the complex baseband signal.
The spectral correlation analysis of MCM signals is the theoretical basis for further signal processing. In this section, we investigate two typical MCM signals: OFDM and FBMC signals. Other MCM signals share similar spectral correlation properties with these two signals.
4.1. Spectral Correlation of OFDM Signal Using LPTV
Figure 1 shows a filter bank based schematic baseband equivalent of transmultiplexer system, based on the LPTV theory  parallel complex data streams are passed to
parallel complex data streams are passed to  subcarrier transmission filters. OFDM system is special filter bank based multicarrier system with the rectangular pulse filters. The baseband OFDM signal can be expressed as a sum of
subcarrier transmission filters. OFDM system is special filter bank based multicarrier system with the rectangular pulse filters. The baseband OFDM signal can be expressed as a sum of  single carrier signals like (15)
single carrier signals like (15)

where  is the element of the input vector of LPTV system and
is the element of the input vector of LPTV system and  is the element of impulse response of LPTV:
is the element of impulse response of LPTV:

for which  is the purely stationary data,
is the purely stationary data,  is one OFDM symbol duration, where
is one OFDM symbol duration, where  is the useful symbol duration and
is the useful symbol duration and  is the length of the guard interval where the OFDM signal is extended cyclically.
is the length of the guard interval where the OFDM signal is extended cyclically.  is the rectangular pulse function, and
is the rectangular pulse function, and  can be regarded as the periodic function in
can be regarded as the periodic function in  with the period
with the period  for
for  .
.
Element of input vector  can also be regarded as an inherent LPTV transformation of data
can also be regarded as an inherent LPTV transformation of data  with the time-invariant filters
with the time-invariant filters  :
:

where

Assuming  , each entity of matrix
, each entity of matrix  and
and  in (21) and (22) reduce to
in (21) and (22) reduce to

where  is the Fourier transform of
is the Fourier transform of  and
and

Other terms corresponding to the LPTV system can be similarly calculated:

Substituting (31) (37) into (21) and (22), the nonconjugate cyclic autocorrelated and cyclic spectra of OFDM signal are transformed into
(37) into (21) and (22), the nonconjugate cyclic autocorrelated and cyclic spectra of OFDM signal are transformed into


where  is the time length of one OFDM symbol,
is the time length of one OFDM symbol,  is the Fourier transform of
is the Fourier transform of  . The magnitudes of nonconjugate CAF and SCF of OFDM signal are drawn in graphical terms as the heights of surfaces above a bifrequency plane in Figures 2 and 3.
. The magnitudes of nonconjugate CAF and SCF of OFDM signal are drawn in graphical terms as the heights of surfaces above a bifrequency plane in Figures 2 and 3.
For the conjugate case, according to (25) and (26), the conjugate cyclic autocorrelation and cyclic spectra of OFDM signal are transformed into


Consequently, the explicit spectral correlation function of the carrier modulated OFDM signal can be derived by substituting (39) and (41) into (30):

where  . Since
. Since  for MPSK
for MPSK or QAM modulation types, given that
or QAM modulation types, given that  is centered and i.i.d.. According to (41), it can be seen that the OFDM signal does not exhibit conjugate cyclostationarity, that is
is centered and i.i.d.. According to (41), it can be seen that the OFDM signal does not exhibit conjugate cyclostationarity, that is  . The spectral correlation function of the carrier-modulated signal for MPSK
. The spectral correlation function of the carrier-modulated signal for MPSK or QAM modulation can be simplified as
or QAM modulation can be simplified as

4.2. Spectral Correlation of FBMC Signal Using LPTV
An efficient FBMC scheme based on offset quadrature amplitude modulation (OQAM) system has been developed [14–19]. OQAM in [15] can achieve smaller intersymbol interference (ISI) and interchannel interference (ICI) without using the cyclic prefix by utilizing well designed pulse shapes. Saltzberg in [16] showed that by designing a transmit pulse-shape in a multichannel QAM system, and by introducing a half symbol space delay between the in-phase and quadrature components of QAM symbols, it is possible to achieve a baud-rate spacing between adjacent subcarrier channels and still recover the information symbol free of ISI and ICI. Further development was made by Hirosaki [17], who showed that the transmitter and receiver part of this modulation method could be implemented efficiently in a polyphase Discrete Fourier Transform (DFT) structure. Some new progress about OQAM system can be found in [18, 19].
The principle of OQAM multicarrier modulation system is to divide the transmission into  independent transmissions using
independent transmissions using  subcarriers. Instead of a Fast Fourier Transform (rectangular shape filters), a more normal filter bank
subcarriers. Instead of a Fast Fourier Transform (rectangular shape filters), a more normal filter bank  is used. Subcarrier bands are spaced by the symbol rate
is used. Subcarrier bands are spaced by the symbol rate  (
( is one OQAM symbol period). An introduced orthogonality condition between subcarriers guarantees that the transmitted symbols arrive at the receiver free of ISI and ICI, which is achieved through time staggering the in-phase and quadrature components of the subcarrier symbols by half a symbol period
is one OQAM symbol period). An introduced orthogonality condition between subcarriers guarantees that the transmitted symbols arrive at the receiver free of ISI and ICI, which is achieved through time staggering the in-phase and quadrature components of the subcarrier symbols by half a symbol period  . The typical baseband OQAM transmitter system is shown in Figure 4.
. The typical baseband OQAM transmitter system is shown in Figure 4.
Supposing the complex input symbols of OQAM system are

where  and
and  are, respectively, the real and imaginary parts of the kth subcarrier of the lth symbol. The complex-values baseband OQAM signal is defined as
are, respectively, the real and imaginary parts of the kth subcarrier of the lth symbol. The complex-values baseband OQAM signal is defined as

From (45) and Figure 4 we can see that OQAM signal is a special model with  -input
-input  transformed by LPTV transformation
transformed by LPTV transformation  and one scalar output
and one scalar output  . The baseband OQAM signal (45) can also be expressed as a sum of
. The baseband OQAM signal (45) can also be expressed as a sum of  single carrier signals like (15)
single carrier signals like (15)

where  is the element of the input vector of LPTV system and
is the element of the input vector of LPTV system and  is the element of impulse response of LPTV
is the element of impulse response of LPTV

for which  and
and  are the purely stationary data,
are the purely stationary data,  is one OQAM symbol duration,
is one OQAM symbol duration,  is the prototype filter bank pulse function, and
is the prototype filter bank pulse function, and  can be regarded as the periodic function in
can be regarded as the periodic function in  with the period
with the period  for
for  .
.
 also can be regarded as a two-element vector LPTV transformation of input data
also can be regarded as a two-element vector LPTV transformation of input data  and
and  with the time-invariant filters
with the time-invariant filters  and
and  :
:

where

Assuming  , each entity of matrices
, each entity of matrices  and
and  in (21) and (22) reduces to
in (21) and (22) reduces to

where  is the Fourier Transform of
is the Fourier Transform of  and
and

Other terms corresponding to the LPTV system can be similarly calculated:

By the substitution of (46) (52) into (21) and (22), the nonconjugate cyclic autocorrelation and cyclic spectra of OQAM signal are transformed into
(52) into (21) and (22), the nonconjugate cyclic autocorrelation and cyclic spectra of OQAM signal are transformed into


where  is the time length of the prototype filter bank,
is the time length of the prototype filter bank,  is the Fourier transform of
is the Fourier transform of  and
and  is described as (51). The magnitudes of nonconjugate CAF and SCF of OQAM signal are shown in Figures 5 and 6. We unfortunately found that OQAM signal has very poor inherent cyclostationary property when the cyclic frequency is not equal to zero, which can be interpreted by (54), where the value of cross product "
is described as (51). The magnitudes of nonconjugate CAF and SCF of OQAM signal are shown in Figures 5 and 6. We unfortunately found that OQAM signal has very poor inherent cyclostationary property when the cyclic frequency is not equal to zero, which can be interpreted by (54), where the value of cross product " " tends to zero when "
" tends to zero when " " due to the low sidelobes property of OQAM prototype function.
" due to the low sidelobes property of OQAM prototype function.
For the conjugate situation, assuming  , in the same way we can get each entity of matrices
, in the same way we can get each entity of matrices  and
and  in (25) and (26):
in (25) and (26):


Substitution of (52), (55), and (56) into (25) and (26), the conjugate cyclic autocorrelation and cyclic spectra of OQAM signal is transformed into


As same as OFDM signal (except BPSK), OQAM signal does not exhibit conjugate cyclostationarity, either. This property can be exactly interpreted by (58), where the value of cross product " " equals to zero due to neighbored offset effect. The explicit spectral correlation function of the carrier modulated FBMC signal can be obtained by substituting (54) into (30):
" equals to zero due to neighbored offset effect. The explicit spectral correlation function of the carrier modulated FBMC signal can be obtained by substituting (54) into (30):

5. Cyclostationary Signature for MCM Signal
The poor inherent cyclostationarity is unsuitable for practically applications in the context of cognitive radio. Even for OFDM signals which contain inherent cyclostationary features due to the underlying periodicities properties (Figure 3), as the power of inherent OFDM features are relative low to the power of signal, reliable detection of these features requires complex architecture and long observation time.
In this paper we study the detection problem of MCM signals considering the AWGN and Rayleigh fading environment by using an induced cyclostationary scheme [20], which is realized by intentionally embedding some cyclostationary signatures. Cyclostationarity-inducing method enables the recognition among primary system and secondary system or among multiple secondary systems competing for the same space spectrum, which is important as it may facilitate the setting of advanced spectrum policy such as multilevel priority or advanced access control [12]. Cyclostationary signature has been shown to be a powerful tool in overcoming the challenge of the distributed coordination of operating frequencies and bandwidths between co-existing systems [10]. A cyclostationary signature is a feature, intentionally embedded in the physical properties of a digital communication signal. CSs are effectively applied to overcome the limitations associated with the use of inherent cyclostationary features for signal detection and analysis with minimal additional complexity for existing transmitter architectures. Detection and analysis of CS may be also achieved using low-complexity receiver architectures and short observation durations. CS provides a robust mechanism for signal detection, network identification and signal frequency acquisition.
As illustrated in Figure 7, CSs are easily created by mapping a set of subcarriers onto a second set as

where  is the
is the  independent and identically distributed message at
independent and identically distributed message at  subcarrier frequency,
subcarrier frequency,  is the set of subcarrier values to be mapped and
is the set of subcarrier values to be mapped and  is the number of subcarriers between mapped subcarriers. So a correlation pattern is created and a cyclostationary feature is embedded in the signal by redundantly transmitting message symbols.
is the number of subcarriers between mapped subcarriers. So a correlation pattern is created and a cyclostationary feature is embedded in the signal by redundantly transmitting message symbols.
In order to avoid redundant theoretical analysis, herein we just discuss the cyclostationary signature for FBMC signal. According to (21), (22), (53), (54), and (60), we can rewrite the nonconjugate cyclic autocorrelation and spectral correlation formulas of FBMC signal with cyclostationary signatures:


where  is the set of subcarriers to be mapped and
is the set of subcarriers to be mapped and  .
.
The magnitudes of nonconjugate CAF and SCF of FBMC signal with CS are drawn in Figures 8 and 9, where four cyclostationary signatures are embedded corresponding to two different values of  (choosing
(choosing  and
and  ), and a reference filter bank is designed using the method given in [21]. We can see that for the FBMC signal with CS the strong cyclostationary features appear at the cyclic frequency "
), and a reference filter bank is designed using the method given in [21]. We can see that for the FBMC signal with CS the strong cyclostationary features appear at the cyclic frequency " " and "
" and " ".
".
OFDM and FBMC signals detection utilizing CSs by nonconjugate operation are already investigated in [10, 14], respectively. They both exhibit good performances, but the experiments using CSs by conjugate operation are still an open topic. In the following, we will insert the CSs by conjugate operation aiming at generating cyclostationary features on some predefined cyclic frequency, which is feasible based on the fact that most of MCM signals and noise don't display cyclostationarity under the conjugate operation for all the cyclic frequencies. (Herein the noise is assumed to be circularly symmetric.) Therefore, a simple cyclostationarity detector for the presence of conjugate cyclostationarity over the predefined cyclic frequency can be given to detect MCM signal and noise or detect two different MCM signals. (Recognition is feasible between the MCM signal embedded by CS and the other MCM signal without CS at a predetermined cyclic frequency.)
Contrary to the nonconjugate operation, a CS is created by mapping the conjugate formation of a set of subcarriers onto a second set as

by which a correlation pattern is created and a cyclostationary feature is embedded in the signal.
According to (25), (26), (57), (58), and (63), we can rewrite the conjugate cyclic autocorrelation and spectral correlation formulas of FBMC signal with cyclostationary signatures


where  is the set of subcarriers to be mapped and
is the set of subcarriers to be mapped and  . From (65) we can embed the CSs at zero cyclic frequency by setting a group of mapping subcarriers according to (63) under the condition "
. From (65) we can embed the CSs at zero cyclic frequency by setting a group of mapping subcarriers according to (63) under the condition " ". The magnitudes of conjugate CAF and SCF of FBMC signal with CS are drawn in Figures 10 and 11, where two subcarriers are repeated transmitted at the value of
". The magnitudes of conjugate CAF and SCF of FBMC signal with CS are drawn in Figures 10 and 11, where two subcarriers are repeated transmitted at the value of  . We can see that the strong cyclostationary features appear at the cyclic frequency "
. We can see that the strong cyclostationary features appear at the cyclic frequency " ".
".
6. Signature Detector
Since complex noise does not exhibit nonconjugate (conjugate) cyclostationarity, the presence of the MCM signal under noise and interference is equivalent to the detection of the presence of nonconjugate (conjugate) cyclostationarity in the received composite signal  on the predetermined cyclic frequency, where
on the predetermined cyclic frequency, where  is the contribution from noise.
is the contribution from noise.
The signature detector in [10] can be used for efficient FBMC signal detection. Cyclostationary features generated by subcarriers set mapping can be successfully detected using spectral resolution (subcarrier spacing  ). So the low-complexity signature detector can be designed by sliding a window
). So the low-complexity signature detector can be designed by sliding a window  with the width
with the width  (
( is the number of subcarriers in the mapped set) around estimated nonconjugate (conjugate) SCF at the cyclic frequency
is the number of subcarriers in the mapped set) around estimated nonconjugate (conjugate) SCF at the cyclic frequency  :
:

where  is estimated using a time-smoothed cyclic cross periodogram [8].
is estimated using a time-smoothed cyclic cross periodogram [8].
7. Simulations
Instead of discussing the detection applications of various MCM signals, in this section only the performance of the conjugate cyclostationarity detector between FBMC signal inserted by CS and noise signal is investigated. A 512-subcarrier FBMC signal is chosen and the following assumptions are made.
-
(1)
Cognitive radio system with a bandwidth of 5?MHz, and assuming signals are transmitted at carrier frequency
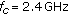 .
. -
(2)
The Additive White Gaussian Noise (AWGN) and Rayleigh fading channel are considered, respectively. A typical urban channel [22] is used with a maximum spread delay
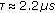 and a Doppler frequencies
and a Doppler frequencies  , which corresponds to a moving speed 30?m/s.
, which corresponds to a moving speed 30?m/s. -
(3)
Subcarriers are modulated using OQAM.
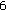 ,
, 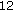 ,
, 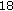 and
and 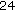 subcarriers are respectively used as the mapping subcarrier sets at zero cyclic frequency.
subcarriers are respectively used as the mapping subcarrier sets at zero cyclic frequency. -
(4)
Using the detector (66), the entry
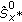 is estimated using time-smoothed cyclic periodogram, where a Hamming window is used. For simplicity, a rectangular sliding window
is estimated using time-smoothed cyclic periodogram, where a Hamming window is used. For simplicity, a rectangular sliding window 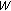 is chosen.
is chosen. -
(5)
For comparison, the traditional energy detector proposed by Urkowitz [9] is applied under the assumption of noise uncertainty indicated by
 , which is defined in [23].
, which is defined in [23].
Receiver operating characteristic (ROC) curves are drawn in Figures 12–15 by averaging 500 Monte Carlo simulations for AWGN channel and Rayleigh fading channel, respectively. Figure 12 gives the experimental results for an AWGN channel at different SNR levels (0 dB,  dB,
dB,  dB,
dB,  dB, and
dB, and  dB) with
dB) with  subcarriers mapping set and an observation time
subcarriers mapping set and an observation time  (10 FBMC symbols). As a comparison, the energy detector proposed in [9] with a noise uncertainty
(10 FBMC symbols). As a comparison, the energy detector proposed in [9] with a noise uncertainty  is used. It can be seen that desired detection performance can be achieved for CS detector at the low SNR level, and almost
is used. It can be seen that desired detection performance can be achieved for CS detector at the low SNR level, and almost  detection rate can be achieved when the SNR level is more than 0 dB. We can also observe that the energy detector significantly outperforms the CS detector when the noise power is well estimated. Effects of observation time and mapping set are shown in Figure 13 at a fixed SNR
detection rate can be achieved when the SNR level is more than 0 dB. We can also observe that the energy detector significantly outperforms the CS detector when the noise power is well estimated. Effects of observation time and mapping set are shown in Figure 13 at a fixed SNR , where the ROC curves show that the performance of the CS detector improves when longer observation time and larger mapping set are applied. In addition, energy detector performance for different noise uncertainty values is depicted in Figure 13, which verifies that energy detector is very susceptible to noise uncertainty at low SNR level. Due to the noise uncertainty, the performance of energy detector does not improve even if the observation time increases. This behavior is predicted by the so called "SNR wall" in [24]. Namely, the energy detector can't distinguish the weak received signal form slightly higher noise power below some SNR level.
, where the ROC curves show that the performance of the CS detector improves when longer observation time and larger mapping set are applied. In addition, energy detector performance for different noise uncertainty values is depicted in Figure 13, which verifies that energy detector is very susceptible to noise uncertainty at low SNR level. Due to the noise uncertainty, the performance of energy detector does not improve even if the observation time increases. This behavior is predicted by the so called "SNR wall" in [24]. Namely, the energy detector can't distinguish the weak received signal form slightly higher noise power below some SNR level.
The results deteriorate when more realistic time variant Rayleigh fading channels are considered. As shown in Figure 14, effects of SNR are illustrated at different SNR levels (3 dB, 0 dB,  dB,
dB,  dB, and
dB, and  dB) with
dB) with  subcarriers mapping set and an observation time
subcarriers mapping set and an observation time  (30 FBMC symbols). Compared with Figure 12, it can be seen that Rayleigh fading channel affects detection performance significantly. The energy detector with noise uncertainty
(30 FBMC symbols). Compared with Figure 12, it can be seen that Rayleigh fading channel affects detection performance significantly. The energy detector with noise uncertainty  is compared with CS detector in Figure 14, which once again shows the advantage of energy detector when the SNR level is below the SNR wall. In order to achieve higher detection reliability for CS detector, longer observation time or more mapping subcarriers are needed as shown in Figure 15. It can be noted that from Figures 13 and 15 at a low SNR level (
is compared with CS detector in Figure 14, which once again shows the advantage of energy detector when the SNR level is below the SNR wall. In order to achieve higher detection reliability for CS detector, longer observation time or more mapping subcarriers are needed as shown in Figure 15. It can be noted that from Figures 13 and 15 at a low SNR level ( ) energy detector is not robust under the condition of a noise uncertainty
) energy detector is not robust under the condition of a noise uncertainty  .
.
Simulations show that the energy detector is very susceptible to noise uncertainties and its performance is dictated by the accuracy of the noise power estimate. Moreover, energy detector can't differentiate different modulated signals, noise and interference. Conversely, good performance can be achieved for CS detector with a short observation time. Detection reliability can be seriously impacted by time-variant Rayleigh fading channel, which can be overcome through the use of longer observation time and more mapping subcarriers. Besides, CS detector is not susceptible to noise uncertainty and can distinguish different modulated signals by inserting CSs at different frequency positions.
8. Conclusion
This paper firstly analyzes the cyclic spectral correlation of both OFDM and FBMC signals. By utilizing an LPTV model, we have derived the explicit formulas of nonconjugate and conjugate cyclic autocorrelation and spectral correlation functions for OFDM and FBMC signals, which provide the theoretical basis for further signal detection.
Secondly, a strategy for the detection of MCM signals by embedding cyclostationary signature at the predefined cyclic frequency is investigated. Because of the LPTV structure of the FBMC signal, the explicit formulas of nonconjugate and conjugate CAF and SCF with CS for FBMC signal are derived and CS can be accordingly easily inserted into the FBMC signal at some predetermined frequency position. During the simulation, a low-complexity conjugate detector is applied for detecting FBMC signal by embedding the CS at zero cyclic frequency in the AWGN and Rayleigh fading situations, respectively. All the cyclic operations at zero cyclic frequency are actually the conventional correlation and power spectral operations, which in some way reduce the computation complexity. Experimental results show that CS is an effective and robust tool for signal detection in cognitive radio network. We can improve the performance with increased subcarriers mapping size, but this causes a reduction in overall date rate because of the increased overhead. Via flexible CS position design for different MCM signals (different CR networks), identification among different modulated signals can be implemented in the same way.
Future work will be undertaken to examine the uses of pilots for generating cyclostationary signatures. In addition, further applications of CSs will be carried out in a practical cognitive radio platform.
References
Gardner WA: Spectral correlation of modulated signal—part I: analog modulation. IEEE Transactions on Communications 1987, 35(6):584-594. 10.1109/TCOM.1987.1096820
Gardner WA, Brown WA, Chen C-K: Spectral correlation of modulated signals—part II: digital modulation. IEEE Transactions on Communications 1987, 35(6):595-601. 10.1109/TCOM.1987.1096816
Öner M, Jondral F: On the extraction of the channel allocation information in spectrum pooling systems. IEEE Journal on Selected Areas in Communications 2007, 25(3):558-565.
Vučić D, Obradović M, Obradović D: Spectral correlation of OFDM signals related to their PLC applications. Proceedings of the 6th International Symposium on Power-Line Communications and Its Applications (ISMPLC '02), 2002
Bölcskei H: Blind estimation of symbol timing and carrier frequency offset in wireless OFDM systems. IEEE Transactions on Communications June 2001, 49(6):988-999. 10.1109/26.930629
Ciblat P, Serpedin E: A fine blind frequency offset estimator for OFDM/OQAM systems. IEEE Transactions on Signal Processing 2004, 52(1):291-296. 10.1109/TSP.2003.820062
Gardner WA, Napolitano A, Paura L: Cyclostationarity: half a century of research. Signal Processing 2006, 86(4):639-697. 10.1016/j.sigpro.2005.06.016
Gardner WA: The spectral correlation theory of cyclostationary time-series. Signal Processing 1986, 11(1):13-36. 10.1016/0165-1684(86)90092-7
Urkowitz H: Energy detection of unknown deterministic signals. Proceeding of the IEEE 1967, 55(4):523-531.
Sutton PD, Nolan KE, Doyle LE: Cyclostationary signatures in practical cognitive radio applications. IEEE Journal on Selected Areas in Communications 2008, 26(1):13-24.
Chevreuil A, Serpedin E, Loubaton P, Giannakis G: Blind channel identification and equalization using non-redundant periodic modulation precoders: performance analysis. IEEE Transactions on Signal Processing 2000, 48(6):1570-1586. 10.1109/78.845916
Maeda K, Benjebbour A, Asai T, Furuno T, Ohya T: Cyclostationarity-inducing transmission methods for recognition among OFDM-Based systems. EURASIP Journal on Wireless Communications and Networking 2008, 2008:-14.
Vučić D, Obradović M: Matrix-based stochastic method for the spectral correlation characterization of digital modulation. Facta Universitatis, Series: Electronics and Energetics 1998, 11(3):271-284.
Zhang H, Le Ruyet D, Terre M: Signal detection for OFDM/OQAM system using cyclostationary signatures. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), September 2008 1-5.
Chang RW: Synthesis of band-limited orthogonal signals for multicarrier data transmission. Bell System Technical Journal 1966, 45: 1775-1796.
Saltzberg BR: Performance of an efficient parallel data transmission system. IEEE Transactions on Communication Technology 1967, 15(6):805-811.
Hirosaki B: An orthogonally multiplexed QAM system using the discrete Fourier transform. IEEE transactions on communications systems 1981, 29(7):982-989. 10.1109/TCOM.1981.1095093
Bolcskei H, Duhamel P, Hleiss R: Orthogonalization of OFDM/OQAM pulse shaping filters using the discrete Zak transform. Signal Processing 2003, 83(7):1379-1391. 10.1016/S0165-1684(03)00087-2
Siohan P, Siclet C, Lacaille N: Analysis and design of OFDM/OQAM systems based on filterbank theory. IEEE Transactions on Signal Processing 2002, 50(5):1170-1183. 10.1109/78.995073
Tsatsanis MK, Giannakis GB: Transmitter induced cyclostationarity for blind channel equalization. IEEE Transactions on Signal Processing 1997, 45(7):1785-1794. 10.1109/78.599947
Bellanger MG: Specification and design of a prototype filter for filter bank based multicarrier transmission. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01), 2001 4: 2417-2420.
3GPP : ARIB TR-T12-25.943 V4.2.0 Deployment aspects (Release 4). 3GPP, June 2002
Sonnenschein A, Fishman PM: Radiometric detection of spread-spectrum signals in noise of uncertain power. IEEE Transactions on Aerospace and Electronic Systems 1992, 28(3):654-660. 10.1109/7.256287
Tandra R, Sahai A: SNR walls for signal detection. IEEE Journal on Selected Topics in Signal Processing 2008, 2(1):4-17.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, H., Le Ruyet (EURASIPMember), D. & Terré, M. Spectral Correlation of Multicarrier Modulated Signals and Its Application for Signal Detection. EURASIP J. Adv. Signal Process. 2010, 794246 (2009). https://doi.org/10.1155/2010/794246
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/794246








 and
and
 .
.

 and
and
 .
.

 .
.
 .
.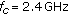 .
.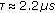 and a Doppler frequencies
and a Doppler frequencies  , which corresponds to a moving speed 30?m/s.
, which corresponds to a moving speed 30?m/s.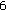 ,
, 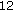 ,
, 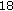 and
and 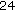 subcarriers are respectively used as the mapping subcarrier sets at zero cyclic frequency.
subcarriers are respectively used as the mapping subcarrier sets at zero cyclic frequency.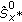 is estimated using time-smoothed cyclic periodogram, where a Hamming window is used. For simplicity, a rectangular sliding window
is estimated using time-smoothed cyclic periodogram, where a Hamming window is used. For simplicity, a rectangular sliding window 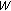 is chosen.
is chosen. , which is defined in [
, which is defined in [
 subcarriers mapping set and an observation time
subcarriers mapping set and an observation time
 .
.

 .
.
 subcarriers mapping set and an observation time
subcarriers mapping set and an observation time
 .
.

 .
.