- Research Article
- Open access
- Published:
Enhanced JPEG2000 Quality Scalability through Block-Wise Layer Truncation
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 803542 (2010)
Abstract
Quality scalability is an important feature of image and video coding systems. In JPEG2000, quality scalability is achieved through the use of quality layers that are formed in the encoder through rate-distortion optimization techniques. Quality layers provide optimal rate-distortion representations of the image when the codestream is transmitted and/or decoded at layer boundaries. Nonetheless, applications such as interactive image transmission, video streaming, or transcoding demand layer fragmentation. The common approach to truncate layers is to keep the initial prefix of the to-be-truncated layer, which may greatly penalize the quality of decoded images, especially when the layer allocation is inadequate. So far, only one method has been proposed in the literature providing enhanced quality scalability for compressed JPEG2000 imagery. However, that method provides quality scalability at the expense of high computational costs, which prevents its application to the aforementioned applications. This paper introduces a Block-Wise Layer Truncation (BWLT) that, requiring negligible computational costs, enhances the quality scalability of compressed JPEG2000 images. The main insight behind BWLT is to dismantle and reassemble the to-be-fragmented layer by selecting the most relevant codestream segments of codeblocks within that layer. The selection process is conceived from a rate-distortion model that finely estimates rate-distortion contributions of codeblocks. Experimental results suggest that BWLT achieves near-optimal performance even when the codestream contains a single quality layer.
1. Introduction
Quality scalability is an important feature provided by modern image and video coding systems to allow the transmission and/or decoding of compressed codestreams at several bitrates without sacrificing coding performance. Quality scalability is key in applications like interactive image transmission, video streaming, or transcoding, among others. Commonly, it is achieved by means of the formation of successive layers of quality that, progressively decoded, provide optimal rate-distortion representations of the image.
JPEG2000 [1] is a prominent image coding standard that provides advanced features such as lossy and lossy-to-lossless compression, random codestream access, and five different progression orders: scalability by quality, by spatial location, by resolution, and by component. To suit quality scalability requirements of applications, JPEG2000 permits the user to specify the layer allocation of the codestream. The density and bitrate distribution of layers are selected at encoding time, determining the rate-distortion optimality of the codestream [2]. It is important to construct codestreams containing a layer allocation that works well for most applications. Nonetheless, the practical use of quality layers must consider that, once the codestream is constructed, the layer allocation cannot be modified without the full reencoding of the image, or the use of computationally intensive techniques like for example [3] or [4]. If the codestream had an inadequate layer allocation, the quality of decoded images could be penalized by more than 10 dB, especially when insufficient quality layers are available (see Section 4).
The high degree of flexibility provided by JPEG2000 is adjusted through several coding parameters that are all set at encoding time. For simplicity, applications and libraries commonly use the default parameters of the underlying JPEG2000 implementation. The layer allocation of most implementations, including Kakadu, JJ2000, Jasper, OpenJPEG, ECW, and LeadTools, constructs by default codestreams containing a single quality layer. Though single quality layer codestreams may be adequate for the basic requirements of applications, this default layer allocation may become inadequate when extended functionalities are required. Such a case is found, for example, in the medical environment. Before the advent of interactive image transmission, the main concern of medical institutions was to compress images losslessly, thus imagery compressed using single quality layer codestreams were sufficient. If these images need to be interactively transmitted in, for instance, current telemedicine environments, the lack of quality scalability becomes an unacceptable shortcoming. Another example is the compression and distribution of digital cinema, in which frames of a movie are compressed using single quality layer codestreams [5]. This restrains the real-time rendering, or the video streaming, of such movies in personal computers, or over the Internet, due to the lack of quality scalability. Functional changes in such environments may trigger important problems for the adequate manipulation of already compressed images. Reencoding is not a viable solution because of the large amount of data or, in some cases, due to limited computational resources. Hence, enhanced quality scalability for already compressed images is a need of pressing importance in environments that deal with JPEG2000 imagery.
The purpose of this paper is to introduce a simple yet efficient strategy of quality layer truncation for JPEG2000 that, requiring negligible computational cost, can be employed in most applications to enhance the quality scalability of already compressed codestreams constructed through an inadequate layer allocation. A preliminary version of this work was presented at the Workshop on Scalable Coded Media Beyond Compression [6]. This paper extends that prior work with a better description, justification, and comparison between the proposed layer truncation and state-of-the-art methods. In addition, the research has been extended implementing the proposed strategy of layer truncation into interactive image and video transmission scenarios, which are niche applications of our method. This paper also contributes extensive experimental results considering computational costs, visual performance, and several configurations of quality layers allocation.
The paper is structured as follows. Section 2 overviews the JPEG2000 core coding system and reviews the state-of-the-art of layer formation and rate-distortion optimization. Section 3 introduces the proposed strategy of layer truncation, and Section 4 evaluates its performance in three applications that require enhanced quality scalability. The last section provides concluding remarks.
2. JPEG2000 Overview
2.1. JPEG2000 Core Coding System
The JPEG2000 core coding system (ISO/IEC 15444-1) is constituted by four main stages (see Figure 1): sample data transformations, sample data coding, rate-distortion optimization, and codestream reorganization. The first sample data transformations stage compacts the energy of the image through the Discrete Wavelet Transform (DWT), and sets the range of image samples. Then, the image is logically partitioned into codeblocks that are independently coded by the sample data coding stage, also called Tier-1.
Tier-1 successively refines the coefficients' distortion by means of a fractional bitplane coder that encodes all coefficients of codeblock  from the highest bitplane
from the highest bitplane  to the lowest bitplane
to the lowest bitplane  ,
,  denoting the number of minimum magnitude bitplanes needed to represent all coefficients of
denoting the number of minimum magnitude bitplanes needed to represent all coefficients of  . In each bitplane, Tier-1 carries out three subbitplane coding passes that are called Significance Propagation Pass (SPP), Magnitude Refinement Pass (MRP), and Cleanup Pass (CP). Each bit produced by the bitplane coder is encoded by the binary arithmetic coder MQ, which employs contextual information to adaptively encode input data. This encoding process produces a quality embedded bitstream for each codeblock that contains first the coding passes with the greatest distortion reductions, and that contains a large collection of potential truncation points (one at the end of each coding pass).
. In each bitplane, Tier-1 carries out three subbitplane coding passes that are called Significance Propagation Pass (SPP), Magnitude Refinement Pass (MRP), and Cleanup Pass (CP). Each bit produced by the bitplane coder is encoded by the binary arithmetic coder MQ, which employs contextual information to adaptively encode input data. This encoding process produces a quality embedded bitstream for each codeblock that contains first the coding passes with the greatest distortion reductions, and that contains a large collection of potential truncation points (one at the end of each coding pass).
The main purpose of the rate-distortion optimization stage is to optimally truncate and select those bitstream segments included in each layer while attaining target bitrates determined by the encoder. The first method to approach this problem in the context of JPEG2000 was the postcompression rate-distortion optimization (PCRD) introduced in [7], which employs Lagrange optimization. Let  denote the target bitrate for one layer, or for the final codestream, and let
denote the target bitrate for one layer, or for the final codestream, and let  denote the potential truncation points of the bitstream produced for codeblock
denote the potential truncation points of the bitstream produced for codeblock  , with
, with  ,
,  denoting the number of coding passes of
denoting the number of coding passes of  . For each codeblock, PCRD first identifies those truncation points lying on the convex hull, that is, those truncation points with strictly decreasing distortion-rate slope. If
. For each codeblock, PCRD first identifies those truncation points lying on the convex hull, that is, those truncation points with strictly decreasing distortion-rate slope. If  and
and  denote, respectively, the bitrate and distortion of
denote, respectively, the bitrate and distortion of  's truncation points, with
's truncation points, with  , the operational points on the convex hull are determined as those ones fulfilling
, the operational points on the convex hull are determined as those ones fulfilling  , with
, with

Computing the total distortion of the image and the total bitrate of the final codestream as  and
and  respectively, and considering only the truncation points lying on the convex hull, the set of truncation points that minimizes the overall image distortion can be determined through the Lagrange multiplier
respectively, and considering only the truncation points lying on the convex hull, the set of truncation points that minimizes the overall image distortion can be determined through the Lagrange multiplier  that minimizes the following expression yielding
that minimizes the following expression yielding 

Though  may not perfectly attain
may not perfectly attain  , close approximations are enough to achieve near optimal performance.
, close approximations are enough to achieve near optimal performance.
Once bitstream segments included in each quality layer are selected, the codestream reorganization stage encodes auxiliary data needed to properly identify the content of quality layers through Tier-2 coding. The final codestream is organized in several containers that encapsulate and sort the bitstream segments of codeblocks. As Figure 3 depicts, containers within the codestream are closely related with the partitioning system defined by JPEG2000. First, the dyadic decomposition carried out by the wavelet transform produces a multiresolution representation of the image. Second, each resolution level is composed of three subbands, denoted as HL, LH, and HH, that contain low and high frequencies in the horizontal and vertical direction, respectively. The lowest resolution level (also referred to as LL subband) is the only resolution level that contains only one subband with low frequencies. As depicted in Figure 3, the third image partition are precincts, which are defined as the same spatial region of all subbands within one resolution level. Finally, each precinct is subdivided in codeblocks. Data belonging to codeblocks within one precinct are coded in the smallest accessible container of the codestream, the packet. This sophisticated partitioning system is aimed to the rapid editing and management of the image in the compressed domain.
The progression order defines how packets are sorted in the final codestream. JPEG2000 defines 5 progression orders denoted as LRCP, RLCP, RPCL, PCRL, and CPRL. Characters L, R, C, and P stand for quality Layer, Resolution, Component, and spatial Position, respectively. The most common progression order is LRCP, in which the primary sorting directive is by quality. This means that all packets belonging to the first quality layer are situated at the very beginning of the codestream. After them, packets belonging to the second quality layer are included, and so on. Within each quality layer, packets are sorted by resolution level (second sorting directive), that is, first all packets belonging to precincts of the lowest resolution level are included, then those ones belonging to the second resolution level, and so on. Within each resolution level, packets are sorted by component (third sorting directive), and the last sorting directive is by position, which sorts packets depending on the spatial location. An illustrative example of the LRCP progression is depicted in Figure 3. The remaining progression orders employ same principles as LRCP but directives are in different order.
2.2. Review of Layer Formation and Rate-Distortion Optimization
Even though PCRD achieves optimal results in terms of rate-distortion performance, in some scenarios it cannot be applied as it was originally formulated due to restrictions inherent in applications, such as limited computational resources, and scan-based acquisition. Several alternatives to PCRD have been proposed in the literature, most of them focused on the reduction of the Tier-1's computational load that can be achieved when only those coding passes included in the final codestream are encoded. These methods might be roughly classified in four classes as characterized in [8]: ( ) the sample data coding and rate-distortion optimization is carried out simultaneously [9–11]; (
) the sample data coding and rate-distortion optimization is carried out simultaneously [9–11]; ( ) statistics from the already encoded codeblocks are collected to decide which coding passes need to be encoded in the remaining codeblocks [12, 13]; (
) statistics from the already encoded codeblocks are collected to decide which coding passes need to be encoded in the remaining codeblocks [12, 13]; ( ) rate-distortion contributions of codeblocks are estimated before the encoding process [14]; and (
) rate-distortion contributions of codeblocks are estimated before the encoding process [14]; and ( ) suitable step sizes for the wavelet subbands are determined before encoding [15, 16]. The complementary problem of the optimization of the bitrate for a target quality is addressed in [17, 18], reducing the computational load of Tier-1 too. Specific techniques of rate-distortion optimization are also developed in scenarios such as scan-based applications [19], the coding of hyperspectral data [20], implementations of motion JPEG2000 [21], and for images containing tiles [22].
) suitable step sizes for the wavelet subbands are determined before encoding [15, 16]. The complementary problem of the optimization of the bitrate for a target quality is addressed in [17, 18], reducing the computational load of Tier-1 too. Specific techniques of rate-distortion optimization are also developed in scenarios such as scan-based applications [19], the coding of hyperspectral data [20], implementations of motion JPEG2000 [21], and for images containing tiles [22].
Most of the proposed methods of rate-distortion optimization can be employed to allocate successive layers of quality at increasing bitrates. The most common strategy for the layer allocation is to distribute layers in terms of bitrate through a uniform or a logarithmic function [1, Chapter 8.4.1], employing PCRD or derived approaches afterward. Another approach is to let the bitplane coder self-determine the layer allocation [23], or to optimally allocate layers considering the expected multirate-distortion measure introduced in [2].
Despite the use of different techniques to tackle the optimization problem, none of the aforementioned approaches can be directly applied to avoid loss when decoding, transmitting, or transcoding codestreams containing an inadequate layer allocation. The main difficulty to apply rate-distortion optimization once the codestream is constructed is that rate-distortion statistics collected during the encoding process are no longer available. More precisely, neither distortion-rate slopes nor truncation points of codeblocks are maintained in the final codestream because they are not needed for the decoding process. Thus, this information is disregarded to minimize the size of the codestream. Only some coders, like for example Kakadu, may record distortion-rate slope thresholds achieved at each quality layer in a COM marker of the codestream. Even so, when the layer is truncated, only the distortion-rate slope threshold for that layer is available, which reveals nothing with regard to individual distortion-rate slopes of coding passes and truncation points. The lack of rate-distortion statistics once the image is compressed prevents the use of classic rate-distortion optimization techniques. Though techniques to estimate distortion [24, 25] may aid transcoding procedures, their practical use require partial decoding of the codestream. To the best of our knowledge, only our previous work [4, 26, 27] addresses the lack of quality scalability of codestreams containing an inadequate layer allocation through models that characterize the rate-distortion contributions of codeblocks. The main idea behind that approach is to estimate distortion-rate slopes of coding passes without using distortion measures based on the original image, or related with the encoding process. Again, applicability of such approach is limited since lengths of individual coding passes are required, hence its use may compel partial decoding of the codestream. We recall that coding passes lengths are not commonly maintained in the codestream. They are only available when the restart coding variation [1, Chapter 12.4] is active. The restart coding variation is devised to allow intracodeblock parallelization for the bitplane coding, and for error resilience, hence its use may compel partial decoding of the codestream. Our objective is to truncate quality layers in the compressed domain, without needing to decode any part of the codestream.
3. Block-Wise Truncation of Quality Layers
Let a codestream primarily progressive by quality contain  quality layers allocated at bit-rates
quality layers allocated at bit-rates  , with
, with  . When the codestream is truncated at quality layer boundaries
. When the codestream is truncated at quality layer boundaries  , the decoded image is optimal in the rate-distortion sense. However, when the codestream needs to be truncated at bitrate
, the decoded image is optimal in the rate-distortion sense. However, when the codestream needs to be truncated at bitrate  , with
, with  , the common approach of simply truncating layer
, the common approach of simply truncating layer  by keeping the first
by keeping the first  portion does not guarantee optimal decoding. None of the rate-distortion optimization methods and techniques employed during encoding time can be used once the codestream is already constructed, since neither the rate-distortion statistics collected during the encoding process, nor the lengths of individual coding passes are available.
portion does not guarantee optimal decoding. None of the rate-distortion optimization methods and techniques employed during encoding time can be used once the codestream is already constructed, since neither the rate-distortion statistics collected during the encoding process, nor the lengths of individual coding passes are available.
The strategy of layer truncation introduced in this work only uses the auxiliary information included in packet headers. Packet headers, which are generated during Tier-2 coding, contain information regarding codeblocks. They include:
-
(1)
whether or not the codeblock contributes to the quality layer,
-
(2)
number of included coding passes,
-
(3)
length of encoded data, and
-
(4)
number of the magnitude bit-planes
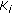 of the codeblock.
of the codeblock.
Instead of truncating a quality layer by keeping its initial prefix, we propose a Block-Wise Layer Truncation (BWLT) that modifies the number of bytes included for each codeblock within the truncated layer. The key point of this method is to determine an adequate number of bytes to keep for each codeblock. The main insight to do so is to use the rate-distortion model deployed by the Coding Passes Interleaving (CPI) method [8, 26], jointly with an estimation of the lengths of individual coding passes.
The main assumption behind CPI is that coding passes belonging to the highest bitplanes have greater rate-distortion contributions than coding passes belonging to the lowest bitplanes. More precisely, let us define a coding level  as the coding pass of all codeblocks of the image at the same level, defined as
as the coding pass of all codeblocks of the image at the same level, defined as  , with
, with  standing for the bitplane, and
standing for the bitplane, and  standing for the coding pass type with
standing for the coding pass type with  . Through this rate-distortion model, coding passes are included from the highest coding level to the lowest one until the target bitrate is achieved.
. Through this rate-distortion model, coding passes are included from the highest coding level to the lowest one until the target bitrate is achieved.
CPI was originally conceived to aid transcoding or decoding procedures, assuming that coding passes lengths are available. In the current framework, coding passes lengths are not available, so the efficiency achieved by the rate-distortion model relies, completely, on a precise estimation of the bitstream lengths generated for each coding pass. We have evaluated the relation between the coding pass order and the bitstream length for the images of the ISO 12640-1 corpus. To ease the visual interpretation, Figure 2(a) depicts the average bitstream lengths of codeblocks with the same number of coding passes for the "Portrait" image, that is, codeblocks with the same number of coding passes are grouped in one plot. Both the coding pass length and coding pass order are normalized to the nominal range. Results suggest that all codeblocks have a similar relation between the coding pass order and the bitstream length, generating the shortest bitstreams for the first coding passes of the codeblock. Same results hold for all images of the corpus.
(a) Experimental results depicting coding passes lengths (normalized to the nominal range) generated for codeblocks of the "Portrait" image (8-bit gray-scale, size 2048  2560), grouping those codeblocks with the same number of coding passes. Coding parameters are: JPEG2000 lossy mode, 5 DWT levels, codeblock size 64
2560), grouping those codeblocks with the same number of coding passes. Coding parameters are: JPEG2000 lossy mode, 5 DWT levels, codeblock size 64  64. (b) Models to estimate coding passes lengths of codeblocks. Experimental resultsModels
64. (b) Models to estimate coding passes lengths of codeblocks. Experimental resultsModels
We model the relation between the coding pass order and the bitstream length according to the exponential function

which is defined in the range  , and fulfills
, and fulfills  ,
,  . As Figure 2(b) depicts, the base
. As Figure 2(b) depicts, the base  (with
(with  ) of the exponential function determines its convexity, and it is set to
) of the exponential function determines its convexity, and it is set to  in our experiments. Through this function, the determination of the bitstream lengths corresponding to coding passes is rather simple. Let
in our experiments. Through this function, the determination of the bitstream lengths corresponding to coding passes is rather simple. Let  and
and  respectively denote the highest and the lowest coding level corresponding to coding passes of codeblock
respectively denote the highest and the lowest coding level corresponding to coding passes of codeblock  included in the to-be-truncated layer
included in the to-be-truncated layer  . The BWLT strategy determines the bitrate
. The BWLT strategy determines the bitrate  of the bitstream corresponding to coding pass
of the bitstream corresponding to coding pass  , with
, with  , as
, as

where  stands for the length of
stands for the length of  's bitstream segment included in layer
's bitstream segment included in layer  , and
, and  stands for the number of coding passes of the codeblock. Note that
stands for the number of coding passes of the codeblock. Note that  , and
, and  can be extracted from packet headers of layers
can be extracted from packet headers of layers  ,
,  .
.
When the codestream has to be truncated to bitrate  , with
, with  , BWLT selects segments of bitstreams included in the to-be-truncated layer
, BWLT selects segments of bitstreams included in the to-be-truncated layer  using the following procedure.
using the following procedure.
Algorithm 1 includes first the full content of layers  ,
,  in the final codestream. For the layer
in the final codestream. For the layer  , BWLT selects coding passes from the highest coding level to the lowest coding level within
, BWLT selects coding passes from the highest coding level to the lowest coding level within (line 3). In each coding level, coding passes are selected from the lowest resolution level (i.e., subband LL), to the highest resolution level. If codeblock
(line 3). In each coding level, coding passes are selected from the lowest resolution level (i.e., subband LL), to the highest resolution level. If codeblock  has a coding pass corresponding to the currently included coding level (line 7), the increment on the
has a coding pass corresponding to the currently included coding level (line 7), the increment on the  's bitstream length for that coding pass is estimated according to expression (4) (line 8). If the bitrate of the final codestream
's bitstream length for that coding pass is estimated according to expression (4) (line 8). If the bitrate of the final codestream  does not exceed the target bitrate
does not exceed the target bitrate  , that coding pass is included in the final codestream. The algorithm finishes execution when the bitrate for the final codestream is attained and, then, packet headers of the truncated layer
, that coding pass is included in the final codestream. The algorithm finishes execution when the bitrate for the final codestream is attained and, then, packet headers of the truncated layer  are regenerated to adjust bitstream lengths of codeblocks.
are regenerated to adjust bitstream lengths of codeblocks.
Algorithm 1: Procedure carried out by the Block-Wise Layer Truncation strategy.
( ) Include full content of layers
) Include full content of layers  ,
,  in the final codestream
in the final codestream
( )
) 
( ) for
) for  to
to  do
do
( ) for
) for  lowest resolution level to highest resolution level do
lowest resolution level to highest resolution level do
( ) for each subband
) for each subband  resolution level
resolution level  do
do
( ) for each codeblock
) for each codeblock  subband
subband  do
do
( ) if
) if  then
then
( )
)  (where
(where  are computed according to expression (4))
are computed according to expression (4))
( ) if
) if  then
then
( ) Include coding pass
) Include coding pass  of codeblock
of codeblock  to the final codestream
to the final codestream
( )
) 
( ) else
) else
( ) STOP truncation
) STOP truncation
( ) end if
) end if
( ) end if
) end if
( ) end for
) end for
( ) end for
) end for
( ) end for
) end for
( ) end for
) end for
( ) Re-generate packet headers of layer
) Re-generate packet headers of layer 
Algorithm 1 uses a fixed scanning order to select codestream segments of codeblocks (loops of lines 3, 4, and 5). Our experience suggests that to modify this scanning order does not change results significantly since, in practice, the truncated layer  includes segments of most codeblocks. This is caused due to the outer loop in line 3 that selects coding passes from the highest to the lowest coding level within
includes segments of most codeblocks. This is caused due to the outer loop in line 3 that selects coding passes from the highest to the lowest coding level within  , so small increments for all codeblocks are added progressively until the target bitrate is achieved. Figure 3 depicts an illustrative example of the layer truncation carried out by BWLT compared to the common approach of truncation by keeping the initial prefix.
, so small increments for all codeblocks are added progressively until the target bitrate is achieved. Figure 3 depicts an illustrative example of the layer truncation carried out by BWLT compared to the common approach of truncation by keeping the initial prefix.
For the sake of simplicity, throughout this section we have assumed that the base quantization step sizes, corresponding to bitplane  , are chosen accordingly to the
, are chosen accordingly to the  -norm of the DWT synthesis basis vectors of the subband. This orthonormalizes wavelet coefficients, which is a common practice in JPEG2000, hence coding levels are weighted according to the coding gain of the wavelet subband. When nonorthonormal filter-banks are employed, the number of coding passes of codeblocks must be multiplied by the energy gain factor of the subband to which they belong. This can be employed to weight coloured-transformed components, or for the JPEG2000 lossless mode.
-norm of the DWT synthesis basis vectors of the subband. This orthonormalizes wavelet coefficients, which is a common practice in JPEG2000, hence coding levels are weighted according to the coding gain of the wavelet subband. When nonorthonormal filter-banks are employed, the number of coding passes of codeblocks must be multiplied by the energy gain factor of the subband to which they belong. This can be employed to weight coloured-transformed components, or for the JPEG2000 lossless mode.
The application of the BWLT strategy raises the issue of how the decoder deals with bitstreams truncated at any point rather than at the end of coding passes. The simplest and most effective strategy is to stop the decoding of the bitstream when the MQ decoder starts synthesizing FF's, which occurs when the bitstream terminates. Although this may cause the loss of the last coded coefficients, whether the bitstream is correctly truncated or not, experimental evidence suggests that these losses are in practice negligible.
4. Experimental Results
4.1. Transcoding and Decoding
The BWLT strategy is implemented in Kakadu (see http://www.kakadusoftware.com/), and evaluated in three different applications. The first application uses BWLT as a transcoder to generate, from an already compressed image, new codestreams with different sizes. All images of the ISO 12640-1 corpus are compressed to codestreams containing 1, 4, and 8 quality layers, distributing layers logarithmically spaced in terms of bitrate. Images are 8-bit gray-scale, size  . Coding parameters are: JPEG2000 lossy mode, 5 levels of DWT, codeblock size
. Coding parameters are: JPEG2000 lossy mode, 5 levels of DWT, codeblock size  . Then, BWLT is employed to generate—from the already compressed images—100 codestreams with target bitrates uniformly distributed between 0.01 to 4 bps. The BWLT strategy achieves same coding performance regardless of the progression order of the codestream. When layers are truncated through the common approach, the LRCP progression order is used to minimize the impact on coding performance. Figure 4(a) depicts results obtained for the "Portrait" and "Cafeteria" images when BWLT is applied (dashed plot), and when the original codestreams are truncated by keeping the initial prefix (solid plot), which is the common approach. Results of Figure 4(a) suggest that the BWLT strategy significantly enhances the coding performance of codestreams containing few quality layers, especially at low bitrates. Same results hold for the other images of the corpus.
. Then, BWLT is employed to generate—from the already compressed images—100 codestreams with target bitrates uniformly distributed between 0.01 to 4 bps. The BWLT strategy achieves same coding performance regardless of the progression order of the codestream. When layers are truncated through the common approach, the LRCP progression order is used to minimize the impact on coding performance. Figure 4(a) depicts results obtained for the "Portrait" and "Cafeteria" images when BWLT is applied (dashed plot), and when the original codestreams are truncated by keeping the initial prefix (solid plot), which is the common approach. Results of Figure 4(a) suggest that the BWLT strategy significantly enhances the coding performance of codestreams containing few quality layers, especially at low bitrates. Same results hold for the other images of the corpus.
It is worth noting that the selected layer allocation is the most adequate one in this context to benefit the performance of the common truncation. Other layer allocations, such as uniformly distributed layers in terms of bitrate, penalize more the coding performance of truncated codestreams. The common approach of layer truncation, for instance, requires 12 uniformly distributed quality layers or more to reach the performance that is achieved by BWLT when truncating codestreams containing a single quality layer. In general, the more inadequate the layer distribution, the more layers the common truncation requires to achieve competitive performance. BWLT achieves virtually the same performance regardless of the number of quality layers.
To assess the performance of BWLT when nonorthonormal filter-banks are employed, Figure 4(b) depicts results obtained when transcoding the "Portrait" and "Cafeteria" images encoded using the JPEG2000 lossless mode. The JPEG2000 lossless mode employs the 5/3 Integer Wavelet Transform (IWT), and no quantization is performed on wavelet data, therefore, the coding pass order used by BWLT is multiplied by the energy gain factor of the subband. Results are similar to the ones achieved with the JPEG2000 lossy mode, suggesting that BWLT can be employed with nonorthonormal transforms.
Results of Figures 4(a) and 4(b) also hold when BWLT is employed to decode a portion of a codestream, rather than generating a new one. This may be useful, for example, in real-time video rendering applications with limited computational resources, in which the full decoding of the codestream might force subsampling.
4.2. Interactive Image Transmission
The second application in which BWLT is applied is interactive transmission of JPEG2000 imagery. In this case, BWLT is implemented in the Kakadu server and client. The implementation of BWLT maintains compliance with the JPIP protocol (ISO/IEC 15444-9), which is supported in Kakadu. JPIP specifies a rich syntax to interchange JPEG2000 imagery over the network, and it is employed in several environments like remote sensing or telemedicine. In the server, the implemented BWLT strategy aids the procedure that extracts the window-of-interest (WOI) requested by the client from the codestream. The WOI is delivered progressively so that it can be rendered at increasing quality at the client side.
The test used to evaluate the performance of BWLT employs an aerial image provided by the Cartographic Institute of Catalonia (8-bit gray-scale, size 7168  4096) that is encoded to codestreams containing 1, 4, 8, and 16 quality layers logarithmically spaced in terms of bitrate. The client requests a WOI of size 830
4096) that is encoded to codestreams containing 1, 4, 8, and 16 quality layers logarithmically spaced in terms of bitrate. The client requests a WOI of size 830  660, which is delivered in portions of 8 KB. Figure 5 depicts the quality of the decoded WOI when BWLT is applied, and when codestreams are truncated using the common approach. Results indicate that the BWLT strategy can improve the quality of the delivered WOI in more than 10 dB when few quality layers are available.
660, which is delivered in portions of 8 KB. Figure 5 depicts the quality of the decoded WOI when BWLT is applied, and when codestreams are truncated using the common approach. Results indicate that the BWLT strategy can improve the quality of the delivered WOI in more than 10 dB when few quality layers are available.
To better appraise the enhancement of BWLT over the common approach, Figure 6 depicts the WOIs decoded by BWLT and by the common truncation when 105 KB of data are transmitted from a codestream containing a single quality layer. BWLT significantly enhances the quality of the interactive transmission, enabling the transmission of codestreams that contain few quality layers.
4.3. Video Streaming
The third application that may require enhanced quality scalability is video streaming. In the same framework of interactive transmission, BWLT is used to optimally truncate and transmit the codestreams belonging to the frames of a motion JPEG2000 sequence. A sub-sequence of the "Standard Evaluation Material" (StEM) video, provided by the Digital Cinema Initiatives Consortium, is selected and codestreams containing 4 and 12 quality layers logarithmically spaced in terms of bitrate are constructed. Frames #2700 through #2999 are selected. The frame size is  , 8-bit gray-scale versions are used. The performance of the BWLT strategy does not depend on the policy of video transmission, therefore, a constant bitrate policy is employed for simplicity. This policy delivers the same amount of bytes for all frames. The capacity of the channel is chosen as 440,000 bytes per second, and video is rendered at 10 frames per second. Figure 7 depicts the results obtained by BWLT and by the common approach. Note that BWLT is able to achieve similar performance for all codestreams, regardless of their layer density. Contrarily, the common approach significantly penalizes performance when few layers are available. Furthermore, in these experiments the common layer truncation leads to a flickering problem due to irregularities in quality of the transmitted frames. See in Figure 8 the decoded images of two consecutive frames of this sequence when codestreams containing 4 quality layers are used. The common layer truncation produces disturbing visual differences between the quality of consecutive frames, whereas BWLT achieves a more regular performance.
, 8-bit gray-scale versions are used. The performance of the BWLT strategy does not depend on the policy of video transmission, therefore, a constant bitrate policy is employed for simplicity. This policy delivers the same amount of bytes for all frames. The capacity of the channel is chosen as 440,000 bytes per second, and video is rendered at 10 frames per second. Figure 7 depicts the results obtained by BWLT and by the common approach. Note that BWLT is able to achieve similar performance for all codestreams, regardless of their layer density. Contrarily, the common approach significantly penalizes performance when few layers are available. Furthermore, in these experiments the common layer truncation leads to a flickering problem due to irregularities in quality of the transmitted frames. See in Figure 8 the decoded images of two consecutive frames of this sequence when codestreams containing 4 quality layers are used. The common layer truncation produces disturbing visual differences between the quality of consecutive frames, whereas BWLT achieves a more regular performance.
Visual comparison between BWLT (c), (d) and the common layer truncation (a), (b) for two frames of the "StEM" sequence. The common truncation produces irregular quality, which leads to flickering.Common approach, frame #259: 30.34 dBCommon approach, frame #260: 25.75 dBBWLT, frame #259: 33.13 dBBWLT, frame #260: 32.86 dB
4.4. Comparison with State-of-the-Art Methods
To compare the BWLT's performance to a state-of-the-art method, Figure 9 depicts the results when the "Portrait" and "Cafeteria" images are transcoded to codestreams with different sizes using the CoRD method introduced in [4]. CoRD proved to achieve near-optimal performance at the expense of requiring coding passes lengths, so that partial decoding of the codestream may be necessary. It is worth noting that the performance achieved by CoRD marks the maximum coding performance that can be achieved in the framework of JPEG2000 [4]. Results in Figure 9 shows that BWLT is able to achieve performance similar to that of CoRD—even when the codestream contains a single quality layer—requiring only decoding of packet headers. When the codestreams contains 4 quality layers or more, the performance achieved by BWLT is virtually the same as that of CoRD. Figure 9 also reports the performance achieved when a codestream containing an adequate layer allocation, namely, 32 quality layers logarithmically distributed in terms of bitrate, is truncated using the common approach. Results suggest that BWLT achieves performance similar to the one achieved with a codestream containing an adequate layer allocation, regardless of the layer allocation of the codestream. Same results hold for other images.
4.5. Computational Cost
To implement BWLT in niche applications such as interactive image and video transmission, or codestream transcoding, BWLT is required to spend few computational resources. This section evaluates computational time of four methods of layer truncation. All codestreams employed in the previous experiments—that include several codestreams with different layer configurations per image—are used in this test. Results are reported as the CPU time needed to truncate the codestreams (as truncated in Section 4.1), on average for all codestreams constructed for each image. Experiments are carried out on an Intel Core 2 CPU at 2 GHz. Table 1 reports achieved results. The strategy labeled "full reencoding" decodes the full image and encodes it at the desired target bitrate. The strategy labeled "CoRD" employs the CoRD method, which requires partial decoding of the codestream. The strategy labeled "BWLT" reports results for the truncation strategy proposed in this paper. The strategy labeled "common" uses the common approach of layer truncation, which keeps the initial prefix of the layer. The operations required by BWLT are the decoding of packet headers, and the regeneration of packet headers for the truncated layer. Both operations have low computational cost. Results suggest that, commonly, the time spent by BWLT is around 5% of the time spent to re-encode the full codestream. Compared to CoRD, BWLT is more than 10 times faster. Compared to the common approach, BWLT is 2 to 3 times slower. Scenarios in which high resolution images are used, such as in remote sensing or telemedicine, the improvement of BWLT may save significant computational time. When BWLT is applied in interactive image transmission, computational time is negligible since most JPIP servers decompress packet headers to obtain the codestream's characteristics.
5. Conclusions
Quality scalability is achieved in JPEG2000 through the use of quality layers. Even though the definition of quality layers is a sound mechanism of JPEG2000, their practical use must take into account that codestreams containing an inadequate layer allocation may greatly penalize the coding performance.
This paper introduces a Block-Wise Layer Truncation (BWLT) strategy based on a well-known rate-distortion model and on an accurate estimation of the bitstream lengths generated for coding passes. The proposed BWLT strategy only uses the auxiliary information included in packet headers, without requiring decoding of the image. Experimental results suggest that BWLT may significantly improve the quality of decoded images, especially when few quality layers are available. To the best of our knowledge, the proposed BWLT is the only strategy of layer truncation that, with negligible computation cost, provides enhanced quality scalability to JPEG2000 codestreams achieving near-optimal performance. Applications that can benefit from the proposed strategy are interactive image and video transmission, video streaming, transcoding of codestreams, and real-time video rendering.
References
Taubman DS, Marcellin MW: JPEG2000 Image Compression Fundamentals, Standards and Practice. Kluwer Academic Publishers, Norwell, Mass, USA; 2002.
Wu X, Dumitrescu S, Zhang N: On multirate optimality of JPEG2000 code stream. IEEE Transactions on Image Processing 2005, 14(12):2012-2023.
Apostolopoulos JG: Secure media streaming & secure adaptation for non-scalable video. Proceedings of the IEEE International Conference on Image Processing (ICIP '04), October 2004 3: 1763-1766.
Auli-Llinas F, Serra-Sagrista J: JPEG2000 quality scalability without quality layers. IEEE Transactions on Circuits and Systems for Video Technology 2008, 18(7):923-936.
Digital cinema system specification, version 1.2 2008.http://www.dcimovies.com
Auli-Llinas F, Taubman D: JPEG2000 block-wise truncation of quality layers. Proceedings of the IEEE/IET International Conference on Visual Information Engineering, August 2008 711-716.
Taubman D: High performance scalable image compression with EBCOT. IEEE Transactions on Image Processing 2000, 9(7):1158-1170. 10.1109/83.847830
Auli-Llinas F: Model-based JPEG2000 rate control methods, Ph.D. dissertation. Universitat Autònoma de Barcelona, Barcelona, Spain; December 2006.
Kim T, Kim HM, Tsai P-S, Acharya T: Memory efficient progressive rate-distortion algorithm for JPEG 2000. IEEE Transactions on Circuits and Systems for Video Technology 2005, 15(1):181-187.
Yeung YM, Au OC: Efficient rate control for JPEG2000 image coding. IEEE Transactions on Circuits and Systems for Video Technology 2005, 15(3):335-344.
Yu W, Sun F, Fritts JE: Efficient rate control for JPEG-2000. IEEE Transactions on Circuits and Systems for Video Technology 2006, 16(5):577-589.
Taubman D: Software architectures for JPEG2000. Proceedings of the IEEE International Conference on Digital Signal Processing, July 2002 1: 197-200.
Du W, Sun J, Ni Q: Fast and efficient rate control approach for JPEG2000. IEEE Transactions on Consumer Electronics 2004, 50(4):1218-1221. 10.1109/TCE.2004.1362522
Vikram KN, Vasudevan V, Srinivasan S: Rate-distortion estimation for fast JPEG2000 compression at low bit-rates. Electronics Letters 2005, 41(1):16-18. 10.1049/el:20057147
Parisot C, Antonini M, Barlaud M: High performance coding using a model-based bit allocation with EBCOT. Proceedings of the EURASIP European Signal Processing Conference, September 2002 2: 510-513.
Gaubatz MD, Hemami SS: Robust rate-control for wavelet-based image coding via conditional probability models. IEEE Transactions on Image Processing 2007, 16(3):649-663.
Liu Z, Karam LJ, Watson AB: JPEG2000 encoding with perceptual distortion control. IEEE Transactions on Image Processing 2006, 15(7):1763-1778.
Chang Y-W, Fang H-C, Cheng C-C, Chen C-C, Chen L-G: Precompression quality-control algorithm for JPEG 2000. IEEE Transactions on Image Processing 2006, 15(11):3279-3293.
Kulkarni P, Bilgin A, Marcellin MW, et al.: Compression of earth science data with JPEG2000. In Hyperspectral Data Compression. Springer, New York, NY, USA; 2006:347-378.
Kosheleva OM, Usevitch BE, Cabrera SD, Vidal E Jr.: Rate distortion optimal bit allocation methods for volumetric data using JPEG 2000. IEEE Transactions on Image Processing 2006, 15(8):2106-2112.
Dagher JC, Bilgin AH, Marcellin MW: Resource-constrained rate control for motion JPEG2000. IEEE Transactions on Image Processing 2003, 12(12):1522-1529. 10.1109/TIP.2003.819228
Wu Z, Zheng N: Efficient rate-control system with three stages for JPEG2000 image coding. IEEE Transactions on Circuits and Systems for Video Technology 2006, 16(9):1063-1073.
Auli-Llinas F, Bartrina-Rapesta J, Serra-Sagrista J: Self-conducted allocation strategy of quality layers for JPEG2000. EURASIP Journal on Advances in Signal Processing 2008, 2008:-7.
Taubman DS: Localized distortion estimation from already compressed JPEG2000 images. Proceedings of the IEEE International Conference on Image Processing, October 2006 3089-3092.
Auli-Llinas F, Marcellin MW: Distortion estimators for bitplane image coding. IEEE Transactions on Image Processing 2009, 18(8):1772-1781.
Auli-Llinas F, Serra-Sagrista J, Monteagudo-Pereira JL, Bartrina-Rapesta J: Efficient rate control for JPEG2000 coder and decoder. Proceedings of the IEEE Data Compression Conference, March 2006 282-291.
Auli-Llinas F, Serra-Sagrista J: Low complexity JPEG2000 rate control through reverse subband scanning order and coding passes concatenation. IEEE Signal Processing Letters 2007, 14(4):251-254.
Acknowledgments
The authors thank the associate editor supervising the review process of this paper, and the anonymous referees for their remarks. The authors thank D. Taubman for his help with Kakadu, and for hosting the first author during his stay in Australia. This paper has been partially supported by the Spanish Government (MICINN), by FEDER, and by the Catalan Government, under Grants 2008-BPB-0010, TIN2009-14426-C02-01, TIN2009-05737-E/TIN, and 2009-SGR-1224.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Auli-Llinas, F., Serra-Sagristà, J. & Bartrina-Rapesta, J. Enhanced JPEG2000 Quality Scalability through Block-Wise Layer Truncation. EURASIP J. Adv. Signal Process. 2010, 803542 (2010). https://doi.org/10.1155/2010/803542
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/803542

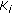 of the codeblock.
of the codeblock.




 660, and belongs to an aerial image compressed to a single quality layer codestream (transmitted 105 KB).Common approach: 17.65 dBBWLT: 26.05 dB
660, and belongs to an aerial image compressed to a single quality layer codestream (transmitted 105 KB).Common approach: 17.65 dBBWLT: 26.05 dB

