- Research Article
- Open access
- Published:
A Ramp Cosine Cepstrum Model for the Parameter Estimation of Autoregressive Systems at Low SNR
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 808312 (2010)
Abstract
A new cosine cepstrum model-based scheme is presented for the parameter estimation of a minimum-phase autoregressive (AR) system under low levels of signal-to-noise ratio (SNR). A ramp cosine cepstrum (RCC) model for the one-sided autocorrelation function (OSACF) of an AR signal is first proposed by considering both white noise and periodic impulse-train excitations. Using the RCC model, a residue-based least-squares optimization technique that guarantees the stability of the system is then presented in order to estimate the AR parameters from noisy output observations. For the purpose of implementation, the discrete cosine transform, which can efficiently handle the phase unwrapping problem and offer computational advantages as compared to the discrete Fourier transform, is employed. From extensive experimentations on AR systems of different orders, it is shown that the proposed method is capable of estimating parameters accurately and consistently in comparison to some of the existing methods for the SNR levels as low as −5 dB. As a practical application of the proposed technique, simulation results are also provided for the identification of a human vocal tract system using noise-corrupted natural speech signals demonstrating a superior estimation performance in terms of the power spectral density of the synthesized speech signals.
1. Introduction
The parameter estimation of autoregressive (AR) systems under noisy conditions has been extensively studied in areas of signal processing, communication, and control. For example, estimating the AR or linear predictive coding (LPC) parameters of a vocal tract (VT) system from an observed noisy speech plays an important role in speech coding, synthesis, and recognition [1]. Numerous system identification methods have been developed for both noise-free and noisy AR systems. The maximum likelihood (ML) methods are asymptotically consistent but their convergence performance relies heavily on the initialization process of the methods [2, 3]. In [3], Xie and Leung have proposed a genetic algorithm to be employed to solve the ML estimation problem at a low SNR, where they consider an AR system driven by chaos. The Yule-Walker (YW) methods have been widely employed to identify the AR systems [2]. The estimation performance of noise compensation-based identification schemes, such as the low-order Yule-Walker (LOYW) method, depend heavily on the accuracy of a priori knowledge of the noise corrupting the signal [2]. Although the high-order Yule-Walker (HOYW) method does not require a priori estimate of the noise variance, it suffers from a singularity problem and has a large estimation variance [4]. To reduce the estimation variance, a least-squares HOYW (LSYW) method can be used [2]. However, in the presence of a reasonable level of noise, the estimation variance of the LSYW method is still large. In order to overcome this problem, in [5], Davila has proposed a signal/noise subspace YW (SSYW) method by introducing a noise compensation in the LOYW method. In [6], by deriving a method of removing the noise-induced bias from the standard least-squares (LS) estimator, Zheng has proposed a method known as the improved least-squares fast-converging (ILSF) algorithm. Both the SSYW and ILSF methods are computationally fast and provide estimation results that are quite satisfactory for low levels of signal-to-noise ratio (SNR).
Identifying AR systems from cepstral coefficients has been attempted only by a few researchers [7, 8]. In [7], a homomorphic LPC (HLPC) method has been proposed for both the white noise and periodic impulse-train excitations in a noise-free environment. The HLPC method cannot guarantee the stability of the estimated AR model. The ramp-cepstrum method proposed in [8] overcomes this problem even in a noisy environment. The method employs conventional cepstrum of a correlation function to formulate a ramp-cepstrum for the estimation of the AR parameters. Since conventional cepstrum is based on Fourier analysis, even for applications dealing with real data it involves complex computation and phase unwrapping operation during its implementation via the discrete Fourier transform (DFT) and inverse DFT (IDFT). In comparison to the DFT, the discrete cosine transform (DCT) is much better in many applications dealing with real signals, for example speech enhancement and speech recognition [1, 9], since it avoids complex computations. Also DCT requires relatively less number of coefficients to represent the signal/image data as compared to DFT. Moreover, it uses a very simple algorithm for phase unwrapping. Nevertheless, the DCT has rarely been employed for system identification problems [10]. In [10], the real spectrum computed by the DCT is employed to obtain an AR model describing the squared Hilbert temporal envelope of a sequence. In this paper, motivated by the advantageous features of DCT, we develop an AR system identification technique in the cepstral domain where DCT rather than DFT is employed. To this end, unlike the conventional cepstrum determined via Fourier and inverse Fourier transforms, a cosine cepstrum is first formally defined through cosine and inverse cosine transforms, and then utilized to develop a theory for the AR parameter estimation.
The objective of this paper is to develop an effective cosine-cepstrum-based methodology for the identification of AR systems from very heavily noise-corrupted samples of the output observations. The main idea of the proposed methodology is to achieve the above stated goal by having a transformed version of the corrupted signal for model-fitting so that the process of transformation itself is noise-robust, and by developing a corresponding target model for the purpose of fitting. In the proposed technique, the noise-robust approach of obtaining the transformed signal is to use the ramp cosine cepstrum (RCC) of one-sided autocorrelation function (OSACF) of an AR signal for both white noise and periodic impulse-train excitations. With this transformation for the signal, we are able to develop the corresponding target model, referred to as the RCC model, for the estimation of the system parameters. The motivation behind using the OSACF for the cosine cepstrum computation is to reduce the effect of the noise. Unlike conventional methods, we deal with both white noise and periodic impulse-train excitations. By employing the RCC model, a residue-based least-squares (RBLS) optimization scheme is presented for the estimation of the AR parameters. For the purpose of implementation, the DCT, which is capable of handling the phase unwrapping problem and offers computational advantages over the DFT, is employed in the proposed method. The proposed method is tested for the estimation of the AR parameters of different synthetic AR systems and also for the identification of a human vocal tract system using natural speech signals.
The paper is organized as follows. In Section 2, the problem of AR system identification in the presence of noise is formulated in the cepstral domain. In Section 3, first, a ramp cosine cepstrum model based on a one-sided ACF of an AR signal for the two types of input excitations is derived and then the DCT is employed for the realization of the derived model. Section 4 presents a residue-based least-squares optimization scheme for the AR parameter estimation using the proposed ramp cosine cepstrum model under noisy conditions. The performance of the proposed method is demonstrated in Section 5 through extensive computer simulations for both synthetic and natural speech signals. Finally, in Section 6, salient features of the proposed algorithm are summarized with some concluding remarks.
2. Problem Statement
The input-output relationship of a real causal stable linear time-invariant autoregressive (AR) system can be described as

where  and
and  are, respectively, the excitation and the response of the AR system,
are, respectively, the excitation and the response of the AR system,  the AR parameters to be estimated, and
the AR parameters to be estimated, and  the system order assumed to be known in this paper. Note that when the system order is unknown, different standard techniques, available in the literature [2], can be employed to estimate the order. The system output in (1) can be considered as a convolution of the input
the system order assumed to be known in this paper. Note that when the system order is unknown, different standard techniques, available in the literature [2], can be employed to estimate the order. The system output in (1) can be considered as a convolution of the input  and the impulse-response
and the impulse-response  of the system, represented as
of the system, represented as

The transfer function of the AR system described by (1) can be written as
system described by (1) can be written as

where  is the AR polynomial and
is the AR polynomial and  represents the
represents the  th pole with a magnitude
th pole with a magnitude  and angle
and angle  . In most of the system identification problems,
. In most of the system identification problems,  is modeled to be a stationary zero-mean white Gaussian noise with an unknown variance
is modeled to be a stationary zero-mean white Gaussian noise with an unknown variance  . For some practical applications, such as speech signal processing, seismology, and communication, however, the excitation may have other forms [1, 11–13]. For example, in speech signal processing, a periodic impulse-train is often used as an excitation of the vocal tract system [1, 11, 13]. As such, in this paper, both the white Gaussian noise and the periodic impulse-train excitations are considered as input to the AR system.
. For some practical applications, such as speech signal processing, seismology, and communication, however, the excitation may have other forms [1, 11–13]. For example, in speech signal processing, a periodic impulse-train is often used as an excitation of the vocal tract system [1, 11, 13]. As such, in this paper, both the white Gaussian noise and the periodic impulse-train excitations are considered as input to the AR system.
Cepstrum analysis has become a very important tool in signal processing, especially in different speech processing applications. It has been proposed as a method for separating signals that have been combined through convolution [1, 11]. For an  -point real sequence
-point real sequence  , in general, the cepstrum of
, in general, the cepstrum of  can be defined as [9]
can be defined as [9]

where  and
and  , respectively, represent a transform and its inverse operator. When
, respectively, represent a transform and its inverse operator. When  is a z-transform, for example,
is a z-transform, for example,  , and the natural logarithm yields
, and the natural logarithm yields

Definition in (4) is valid provided  is deterministic. Since a numerical computation of (5) provides only the principal or wrapped phase, a phase unwrapping algorithm is necessary to restore the phase continuity [11, 14].
is deterministic. Since a numerical computation of (5) provides only the principal or wrapped phase, a phase unwrapping algorithm is necessary to restore the phase continuity [11, 14].
In the current system identification problem, the system response  , as described in (2), is a convolution of the input and the impulse-response of the system. In such a situation, (2) can be expressed in the cepstral domain by applying (4), where
, as described in (2), is a convolution of the input and the impulse-response of the system. In such a situation, (2) can be expressed in the cepstral domain by applying (4), where  is either
is either  -transform or Fourier transform, as
-transform or Fourier transform, as

where  is the cepstrum of the impulse response and
is the cepstrum of the impulse response and  represents the cepstrum of one realization of the input signal. Utilizing such an advantage of homomorphic deconvolution, cepstrum domain methods have been proposed for system identification in [7, 15, 16]. For example, in [7], in order to estimate the AR parameters, a mean-squared error minimization involving (6) is used by employing the Cholesky decomposition. However, as mentioned in [7], the problem of this method is that the stability of the estimated AR model is not guaranteed. It is to be noted that all the cepstral domain methods mentioned above deal only with the noise-free environment.
represents the cepstrum of one realization of the input signal. Utilizing such an advantage of homomorphic deconvolution, cepstrum domain methods have been proposed for system identification in [7, 15, 16]. For example, in [7], in order to estimate the AR parameters, a mean-squared error minimization involving (6) is used by employing the Cholesky decomposition. However, as mentioned in [7], the problem of this method is that the stability of the estimated AR model is not guaranteed. It is to be noted that all the cepstral domain methods mentioned above deal only with the noise-free environment.
In the presence of additive noise  , the observed signal
, the observed signal  is given by
is given by

where  is assumed to be a zero mean stationary process and is independent of
is assumed to be a zero mean stationary process and is independent of  . In [17], the behavior of the cepstral coefficients in the presence of additive noise has been investigated for the purpose of speech recognition by assuming that the noise spectrum can be obtained during the experiment, and it has been shown that the cepstral vector of noisy data can be expressed as the sum of the cepstral vector of its clean version and a scaled deviation vector. In our identification problem, however, we handle a more common and critical situation where only noisy observations are available. Given one realization of input excitation and the observation noise, using the definition in (4), the complex cepstrum of
. In [17], the behavior of the cepstral coefficients in the presence of additive noise has been investigated for the purpose of speech recognition by assuming that the noise spectrum can be obtained during the experiment, and it has been shown that the cepstral vector of noisy data can be expressed as the sum of the cepstral vector of its clean version and a scaled deviation vector. In our identification problem, however, we handle a more common and critical situation where only noisy observations are available. Given one realization of input excitation and the observation noise, using the definition in (4), the complex cepstrum of  can be expressed as
can be expressed as

where  arises because of the noise. The term
arises because of the noise. The term  determines as to how the noise affects
determines as to how the noise affects  and it vanishes altogether in the absence of noise. In order to estimate the AR system parameters from
and it vanishes altogether in the absence of noise. In order to estimate the AR system parameters from  , the effect of
, the effect of  has to be reduced. It is difficult to obtain an accurate estimate of
has to be reduced. It is difficult to obtain an accurate estimate of  from
from  , since the cepstrum decomposition techniques are very sensitive to the noise level [17, 18]. In this paper, in order to reduce the effect of noise in extracting the AR parameters, first, we avoid computing cepstrum directly from the noise-corrupted observations by using a one-sided ACF, and then develop a ramp cosine cepstrum (RCC) model for a model-fitting based least-squares optimization in the cepstral domain. Moreover, in the proposed method, the DCT, instead of the conventional DFT, is employed for computing the cepstrum so as to overcome the problem of phase unwrapping and to achieve computational savings in dealing with real signals.
, since the cepstrum decomposition techniques are very sensitive to the noise level [17, 18]. In this paper, in order to reduce the effect of noise in extracting the AR parameters, first, we avoid computing cepstrum directly from the noise-corrupted observations by using a one-sided ACF, and then develop a ramp cosine cepstrum (RCC) model for a model-fitting based least-squares optimization in the cepstral domain. Moreover, in the proposed method, the DCT, instead of the conventional DFT, is employed for computing the cepstrum so as to overcome the problem of phase unwrapping and to achieve computational savings in dealing with real signals.
3. Proposed Ramp Cosine Cepstrum (RCC) Model Based on One-Sided ACF
In the cepstral analysis, cepstral coefficients are, generally, computed from an observed signal or from an estimate of its nonparametric power spectral density (PSD) [2, 19]. In this section we propose to develop a ramp cosine cepstrum model utilizing a one-sided ACF (OSACF) of  , which can be defined as
, which can be defined as

where  is the conventional two-sided ACF of
is the conventional two-sided ACF of  which, in general, is estimated as [2, 13]
which, in general, is estimated as [2, 13]

where  is the data length. This equation provides an accurate estimate of
is the data length. This equation provides an accurate estimate of  when
when  is sufficiently large. Some important properties of the OSACF of
is sufficiently large. Some important properties of the OSACF of  relevant to the development of the proposed model can be summarized as follows.
relevant to the development of the proposed model can be summarized as follows.
-
(1)
As
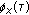 is a symmetric two-sided sequence, the corresponding OSACF
is a symmetric two-sided sequence, the corresponding OSACF 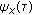 is related to
is related to 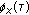 by
by (11)
(11) -
(2)
For a real signal
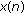 , its OSACF
, its OSACF  is also real.
is also real. -
(3)
The function
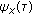 retains the pole-preserving property of
retains the pole-preserving property of 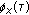 .
. -
(4)
The OSACF exhibits a higher noise immunity than the conventional ACF does [20]. Since the spectral envelope of the OSACF of noisy observations, in comparison to the conventional two-sided conventional ACF, strongly enhances the highest power frequency bands corresponding to the spectral peaks, a large attenuation of the noise components lying outside the enhanced frequency bands would occur.
Taking the  -transform of both sides of (11) results in
-transform of both sides of (11) results in

The Fourier domain representation of (11) is given by

where  represents the Fourier transform and the operator
represents the Fourier transform and the operator  gives the real part of a complex number. As we are interested to perform cepstrum domain computation with
gives the real part of a complex number. As we are interested to perform cepstrum domain computation with  , the relation in (13) favors the use of the cosine transform, which is the real part of the Fourier transform. The cosine transform, denoted as
, the relation in (13) favors the use of the cosine transform, which is the real part of the Fourier transform. The cosine transform, denoted as  , of a real signal
, of a real signal  can be written as
can be written as

From (4) and (14), one can define the cosine cepstrum of a real signal  as
as

where  denotes the inverse operator for the cosine transform, that is, for a given frequency domain spectrum
denotes the inverse operator for the cosine transform, that is, for a given frequency domain spectrum  , the inverse cosine transform can be defined as
, the inverse cosine transform can be defined as

In the following, we will develop a ramp cosine cepstrum model for the estimation of the AR parameters under the white Gaussian noise and periodic impulse-train excitations. To this end, we first show that the cosine cepstrum  can be expressed in terms of the system poles. Using (13) and (14),
can be expressed in terms of the system poles. Using (13) and (14),  in (15) can be expressed as
in (15) can be expressed as

Here,  is by definition the PSD of the real signal
is by definition the PSD of the real signal  , and it can be shown that
, and it can be shown that  is real, even, and nonnegative. From (2), the PSD of the output
is real, even, and nonnegative. From (2), the PSD of the output  for the linear time-invariant system with the transfer function
for the linear time-invariant system with the transfer function  given by (3) can be expressed as
given by (3) can be expressed as

where  is the PSD of the input signal. Using (18),
is the PSD of the input signal. Using (18),  in (17) can be written as
in (17) can be written as

It is observed from (19) that the effect of input excitation  has been made additive by using the homomorphic deconvolution. Now, we consider each of the four terms in (19) individually. From (3),
has been made additive by using the homomorphic deconvolution. Now, we consider each of the four terms in (19) individually. From (3),  can be expanded as
can be expanded as

where  . Using (16), the inverse cosine transform of
. Using (16), the inverse cosine transform of  , with
, with  being real and minimum phase, can be calculated by
being real and minimum phase, can be calculated by

Noting that

we have

Similarly, the inverse cosine transform of  can be obtained as
can be obtained as

It is observed from (16) that for a constant value of  for all
for all  . Thus for
. Thus for  , the last term on the right side of (19) vanishes. Let us now consider the remaining third term of (19) that depends on the characteristics of the input excitation
, the last term on the right side of (19) vanishes. Let us now consider the remaining third term of (19) that depends on the characteristics of the input excitation  . In the following section we consider separately the white Gaussian noise and a periodic impulse-train as an input excitation.
. In the following section we consider separately the white Gaussian noise and a periodic impulse-train as an input excitation.
3.1. White Noise Excitation
For a zero mean white Gaussian noise with a variance  . Thus, the third term on the right side of (19) reduces to
. Thus, the third term on the right side of (19) reduces to

Hence, for the white noise excitation, the cosine cepstrum  in (19) can finally be expressed as
in (19) can finally be expressed as

It can be observed from this equation that  decays rapidly with increasing
decays rapidly with increasing  , thus making it difficult to use
, thus making it difficult to use  for the estimation of the system poles. In order to overcome this problem, we propose an easy-to-handle ramp cosine cepstrum (RCC) for the OSACF of
for the estimation of the system poles. In order to overcome this problem, we propose an easy-to-handle ramp cosine cepstrum (RCC) for the OSACF of  , defined as
, defined as

Since the poles in a system could appear as real or as complex conjugate pair, (27) can be rewritten as

where  is the number of real poles plus the number of complex conjugate pole pairs,
is the number of real poles plus the number of complex conjugate pole pairs,  and
and  are, respectively, the magnitude and the argument of
are, respectively, the magnitude and the argument of  . In (28),
. In (28),  is introduced to distinguish real and complex poles and is given by
is introduced to distinguish real and complex poles and is given by

The model given by (28) is termed as the AR ramp cosine cepstrum (RCC) model for the OSACF of  . This model will be used in the next section to formulate an objective function for the least-squares fitting problem in a noisy environment.
. This model will be used in the next section to formulate an objective function for the least-squares fitting problem in a noisy environment.
3.2. Periodic Impulse-Train Excitation
In the derivation of the RCC model with the white noise excitation, it was observed that the term containing the effect of white noise excitation becomes zero for  , since the PSD of the input
, since the PSD of the input  is a constant. However, the situation is more complicated in the case of a periodic impulse-train excitation
is a constant. However, the situation is more complicated in the case of a periodic impulse-train excitation  where the corresponding PSD is no longer a constant. Next, we analyze the effect of the third term
where the corresponding PSD is no longer a constant. Next, we analyze the effect of the third term  of (19), which is now denoted as
of (19), which is now denoted as  , on
, on  .
.
A periodic impulse-train excitation  with a given period
with a given period  can be expressed as [13]
can be expressed as [13]

where  denoting the ceiling operator, is the total number of impulses within the finite duration of excitation. Using (10), an estimate of the ACF of
denoting the ceiling operator, is the total number of impulses within the finite duration of excitation. Using (10), an estimate of the ACF of  is obtained as
is obtained as

It is observed from (31) that  decays with increasing values of
decays with increasing values of  and has nonzero values at
and has nonzero values at  and at integer multiples of
and at integer multiples of  for the case of finite data operation with
for the case of finite data operation with  . Thus,
. Thus,  can be expressed alternately as
can be expressed alternately as

where

Note that  is an even symmetric triangular sequence and from (32) and (33), it is evident that
is an even symmetric triangular sequence and from (32) and (33), it is evident that  can be obtained by down-sampling
can be obtained by down-sampling  with a factor
with a factor  . Thus the
. Thus the  transform of
transform of  can be expressed as
can be expressed as

where  is the
is the  transform of
transform of  and the sequence
and the sequence  can be generated through a convolution between a rectangular pulse train of width
can be generated through a convolution between a rectangular pulse train of width  and its time reversal sequence. An expression for
and its time reversal sequence. An expression for  can be obtained as
can be obtained as

Based on the relation between  and
and  , as described in (32), (33), and (34), it can be shown that
, as described in (32), (33), and (34), it can be shown that

where

It is evident from (36) that  assumes nonzero values at
assumes nonzero values at  and at integral multiples of
and at integral multiples of  for
for  . Thus, the third term on the right side of (19) reduces to
. Thus, the third term on the right side of (19) reduces to

Note that the RCC given by (27) for the white noise excitation can be modified for the impulse-train excitation as

From (27) and (39), it is observed that the RCC model derived for the white noise excitation is also valid for the case of periodic impulse-train excitation when  .
.
3.3. Computation of RCC Model via DCT/IDCT
The RCC model derived in the previous subsections is obtained from the cosine cepstrum of the OSACF of  , where the logarithm operation is performed on the cosine transform of
, where the logarithm operation is performed on the cosine transform of  . As explained earlier, the difficulty in the complex cepstral analysis is the necessity to unwrap the phase to make it a continuous function of
. As explained earlier, the difficulty in the complex cepstral analysis is the necessity to unwrap the phase to make it a continuous function of  . A major advantage of using cosine transform lies in its binary phase information, i.e.,
. A major advantage of using cosine transform lies in its binary phase information, i.e.,  or
or  which, as shown later, can significantly simplify the phase unwrapping process. From the implementation point of view, different types of discrete cosine-transforms (DCTs) can be employed. It is known that the DCT is far superior to the DFT for the transformation of real signals. For a real signal, DFT gives complex spectrum and leaves nearly one-half of data unused. In contrast, the DCT generates real spectrum of real signals and thereby makes the computation of redundant data unnecessary. Being a real function, the DCT offers an added advantage that it requires only a simple phase unwrapping algorithm. Also, as the DCT is derived from the DFT, all the desirable properties of DFT are preserved, and fast algorithms for its computation exist. As a result, using a DCT and inverse DCT (IDCT) pair, a complex-cepstrum corresponding to (15) can be implemented as follows
which, as shown later, can significantly simplify the phase unwrapping process. From the implementation point of view, different types of discrete cosine-transforms (DCTs) can be employed. It is known that the DCT is far superior to the DFT for the transformation of real signals. For a real signal, DFT gives complex spectrum and leaves nearly one-half of data unused. In contrast, the DCT generates real spectrum of real signals and thereby makes the computation of redundant data unnecessary. Being a real function, the DCT offers an added advantage that it requires only a simple phase unwrapping algorithm. Also, as the DCT is derived from the DFT, all the desirable properties of DFT are preserved, and fast algorithms for its computation exist. As a result, using a DCT and inverse DCT (IDCT) pair, a complex-cepstrum corresponding to (15) can be implemented as follows

For a real sequence  with
with  , the most commonly used DCT-IDCT pair is defined as
, the most commonly used DCT-IDCT pair is defined as


where  is a normalization coefficient defined as
is a normalization coefficient defined as

Since the bases of the cosine transform are real functions, the principal phases of DCT coefficients can only be  or
or  . Accordingly, we can represent the phase as
. Accordingly, we can represent the phase as  when the cosine transform is negative sign and as
when the cosine transform is negative sign and as  when it is positive. With this representation, the logarithm operation in (40) can be easily carried out and (40) can be expressed as
when it is positive. With this representation, the logarithm operation in (40) can be easily carried out and (40) can be expressed as

where

Thus, this representation clearly supports a simple phase unwrapping. On the other hand, in the case of using DFT for the computation of cepstrum, complicated phase unwrapping algorithms as proposed in literature [11, 14] need to be used, since the phase in this case has no longer binary values.
4. The RCC Model-Based Parameter Estimation
4.1. Effect of Additive Noise
In the presence of noise, the observed signal gets heavily corrupted especially when the signal-to-noise ratio (SNR) is very low. In this paper, a more general noisy environment is considered where it is assumed that the noise variance is unknown and noise-only data is not available. In Section 2, the effect of noise on cepstral coefficients has been described for the case when cepstrum is computed in the signal domain. It is well-known that the autocorrelation of a noisy signal offers more noise-robustness in comparison to the noisy signal itself [20]. Thus, the RCC model that we have developed based on the OSACF  of noise-free signal can be used as a target function even when RCC is computed based on the OSACF of the noisy observation of the signal. In what follows, our objective is to investigate the effect of the noise on the RCC computed from noisy observations. In the presence of an additive noise
of noise-free signal can be used as a target function even when RCC is computed based on the OSACF of the noisy observation of the signal. In what follows, our objective is to investigate the effect of the noise on the RCC computed from noisy observations. In the presence of an additive noise  , the ACF of the noisy observation
, the ACF of the noisy observation  can be expressed as
can be expressed as

where

Here,  is the ACF of noise
is the ACF of noise  , and
, and  and
and  are crosscorrelation terms. Equation (46) is valid for both the estimated and the theoretical ACFs. It can be observed that
are crosscorrelation terms. Equation (46) is valid for both the estimated and the theoretical ACFs. It can be observed that  corrupts
corrupts  in an additive fashion like the signal. The effect of
in an additive fashion like the signal. The effect of  cannot be neglected, especially when the SNR is very low. Note that the effect of crosscorrelation terms on
cannot be neglected, especially when the SNR is very low. Note that the effect of crosscorrelation terms on  is negligible when
is negligible when  and
and  are assumed to be uncorrelated. However, at a very low SNR, this is not so when the length of the observed data is finite. Even for an uncorrelated additive white Gaussian noise, all the lags of the noisy ACF are corrupted at a very low SNR. Under such a noisy condition, the conventional correlation based methods employing directly
are assumed to be uncorrelated. However, at a very low SNR, this is not so when the length of the observed data is finite. Even for an uncorrelated additive white Gaussian noise, all the lags of the noisy ACF are corrupted at a very low SNR. Under such a noisy condition, the conventional correlation based methods employing directly  cannot provide a good estimation performance. This motivates us to switch to the cepstral domain where the logarithmic smoothing would help in preserving the RCC model under heavy noisy conditions. The OSACF
cannot provide a good estimation performance. This motivates us to switch to the cepstral domain where the logarithmic smoothing would help in preserving the RCC model under heavy noisy conditions. The OSACF  of noisy observations
of noisy observations  can be obtained as
can be obtained as

From (46) and (48), the OSACF of  can be written as
can be written as

where  indicates the effect of noise on
indicates the effect of noise on  and it can be expressed in a form similar to that of
and it can be expressed in a form similar to that of  given by (9). Thus, in the presence of noise, the cosine cepstrum of
given by (9). Thus, in the presence of noise, the cosine cepstrum of  can be expressed as
can be expressed as

where

Therefore, the ramp cosine cepstrum of  can be expressed as
can be expressed as

Here, the term  arises because of the noise. Like
arises because of the noise. Like  in (8),
in (8),  would vanish in the absence of noise. Now, the RCC model derived in Section 3 can be used in (52) for a ramp cosine cepstral model fitting to minimize the error between
would vanish in the absence of noise. Now, the RCC model derived in Section 3 can be used in (52) for a ramp cosine cepstral model fitting to minimize the error between  and
and  . By this approach the RCC model parameters, and thus the AR parameters are estimated.
. By this approach the RCC model parameters, and thus the AR parameters are estimated.
Since, in the presence of additive white Gaussian noise, the zero lag of the noisy ACF  is most severely corrupted in comparison to other lags, if the zero lag is kept as it is during the computation of the RCC of the OSACF, it may result in a more erroneous value of RCC. On the other hand, excluding the zero lag, although it may reduce the effect of noise, would remove the average power of the observed data
is most severely corrupted in comparison to other lags, if the zero lag is kept as it is during the computation of the RCC of the OSACF, it may result in a more erroneous value of RCC. On the other hand, excluding the zero lag, although it may reduce the effect of noise, would remove the average power of the observed data  . Since
. Since  for
for  , we replace
, we replace  by
by  with
with  in order to reduce the effect of noise. This is suitable especially for a difficult situation where noise variance and/or noise-only data are not available. The process can efficiently suppress the level of
in order to reduce the effect of noise. This is suitable especially for a difficult situation where noise variance and/or noise-only data are not available. The process can efficiently suppress the level of  while leaving the shape of
while leaving the shape of  similar to that of
similar to that of  .
.
4.2. Ramp Cosine Cepstral Fitting: Residue-Based Least-Squares Optimization
As discussed in the previous sub-section following (52) that a ramp cosine cepstral fitting approach can be developed to determine the RCC model parameters from the RCC of the OSACF of noisy observations. We now propose a residue-based least-squares (RBLS) fitting scheme to estimate the model parameters in (28) and (39). Then, the AR parameters can be obtained from the RCC model parameters  and
and  . Each of the
. Each of the  component terms in (28) contains a pair
component terms in (28) contains a pair  . In order to estimate each of the
. In order to estimate each of the  such pairs,
such pairs,  values of
values of  are used, where
are used, where  for the periodic impulse-train excitation. The objective function to determine the values of one pair
for the periodic impulse-train excitation. The objective function to determine the values of one pair  is defined as the total squared error between the
is defined as the total squared error between the  th residual function
th residual function  and the
and the  th component of the RCC model, that is
th component of the RCC model, that is

where the residual function is updated as follows

Note that  and
and  are independent variables and
are independent variables and  depends on
depends on  as seen from (29). We would like to find the optimal solution for
as seen from (29). We would like to find the optimal solution for  and
and  by a search algorithm based on the computation of (53) and (54). In order to reduce the computational burden, a two-step search algorithm is adopted. In the first step, a coarse-search based on the DCT spectrum of the OSACF of the observed data is employed to find out the initial estimate of
by a search algorithm based on the computation of (53) and (54). In order to reduce the computational burden, a two-step search algorithm is adopted. In the first step, a coarse-search based on the DCT spectrum of the OSACF of the observed data is employed to find out the initial estimate of  and
and  . In the second step, a fine-search is carried out around each initially estimated pair of
. In the second step, a fine-search is carried out around each initially estimated pair of  and
and  to obtain a more accurate estimate. In the fine-search, a neighborhood centered at each initial estimate of
to obtain a more accurate estimate. In the fine-search, a neighborhood centered at each initial estimate of  and
and  is searched with a prescribed search resolution in a bounded region. A pair of
is searched with a prescribed search resolution in a bounded region. A pair of  and
and  that globally minimizes
that globally minimizes  is selected as the estimate of a desired pole. It can be observed from (54) that, in order to determine the
is selected as the estimate of a desired pole. It can be observed from (54) that, in order to determine the  th residual function
th residual function  , the computed values of
, the computed values of  and
and  are utilized. Proceeding in this manner, the AR parameters can be determined using (3) once all the
are utilized. Proceeding in this manner, the AR parameters can be determined using (3) once all the  poles have been estimated. In the proposed search scheme, restricting the search range of
poles have been estimated. In the proposed search scheme, restricting the search range of  within the stable region inherently guarantees the stability of the estimated AR system. Another advantage of the RBLS scheme is that in each fine-search, instead of the entire RCC model with all
within the stable region inherently guarantees the stability of the estimated AR system. Another advantage of the RBLS scheme is that in each fine-search, instead of the entire RCC model with all  constituent terms, only one such term is estimated in (53), and in this fashion each term of the RCC model is sequentially obtained. This is done with a view to convert a multivariable optimization problem into a set of two-variable optimization scheme which makes the problem much simpler.
constituent terms, only one such term is estimated in (53), and in this fashion each term of the RCC model is sequentially obtained. This is done with a view to convert a multivariable optimization problem into a set of two-variable optimization scheme which makes the problem much simpler.
5. Simulation Results
In this section, extensive simulations are carried out in order to demonstrate the effectiveness of the proposed technique in identifying the AR systems in the presence of noise. We investigate the identification performance for synthetic AR signals as well as natural speech signals corrupted by additive noise. The estimation performance of the proposed method in terms of the accuracy and consistency of the estimated parameters is obtained and compared with that of the existing methods including the improved least-squares fast-converging (ILSF) method [6], the signal/noise subspace Yule-Walker (SSYW) method [5], and the modified least-squares Yule-Walker (MLSYW) method [2].
5.1. Results on Synthetic AR Systems
5.1.1. White Noise Excitation
A noisy signal is generated according to (1) and (7) with  and
and  , where the variance of the white Gaussian noise
, where the variance of the white Gaussian noise  is appropriately set based on a specified level of SNR defined as
is appropriately set based on a specified level of SNR defined as

From the noisy observations, first, the OSACF  is computed using (48) and (10). Note that for the purpose of implementing the cosine cepstrum, generally the continuous frequency
is computed using (48) and (10). Note that for the purpose of implementing the cosine cepstrum, generally the continuous frequency  is sampled as
is sampled as  for
for  resulting in a
resulting in a  -point Discrete Cosine Transform (DCT). According to the description provided in Section 3.3 for the noise-free observations, DCT-IDCT-based ramp-cosine cepstrum (RCC) is computed using
-point Discrete Cosine Transform (DCT). According to the description provided in Section 3.3 for the noise-free observations, DCT-IDCT-based ramp-cosine cepstrum (RCC) is computed using  . The RCC model parameters are then determined using the residue-based least-squares optimization technique introduced in Section 4.2. In the proposed optimization scheme, the search range for
. The RCC model parameters are then determined using the residue-based least-squares optimization technique introduced in Section 4.2. In the proposed optimization scheme, the search range for  is chosen in the range
is chosen in the range  , that allows the identification of systems even with a very fast decaying autocorrelations. The initial estimates of
, that allows the identification of systems even with a very fast decaying autocorrelations. The initial estimates of  are obtained from the location of the peaks of the smoothed DCT of the OSACF of
are obtained from the location of the peaks of the smoothed DCT of the OSACF of  . The search range for
. The search range for  is in a range of
is in a range of  chosen symmetrically around the neighborhood of the initial estimates. Search resolutions of
chosen symmetrically around the neighborhood of the initial estimates. Search resolutions of  and
and  are used for
are used for  and
and  , respectively. It has been experimentally found that, in order to obtain a better estimate of the
, respectively. It has been experimentally found that, in order to obtain a better estimate of the  unknown AR coefficients, the number of RCC samples to be considered in the model-fitting operation should be higher than
unknown AR coefficients, the number of RCC samples to be considered in the model-fitting operation should be higher than  . In our experiment, the number of RCC samples is taken as
. In our experiment, the number of RCC samples is taken as  .
.
As discussed in Section 4.1, in order to reduce the effect of the most corrupted zero lag on the OSACF of the noisy observations, the value of  is chosen as
is chosen as  . Several experiments, each consisting of
. Several experiments, each consisting of  independent trials, are conducted to find the means and variances of the estimated AR parameters under noisy observations in which the SNR varies from
independent trials, are conducted to find the means and variances of the estimated AR parameters under noisy observations in which the SNR varies from  dB to
dB to  dB at steps of
dB at steps of  dB. The performance measurement criteria considered in our simulation study are
dB. The performance measurement criteria considered in our simulation study are  the mean of estimated parameters,
the mean of estimated parameters,  the standard deviation from the mean (SDM),
the standard deviation from the mean (SDM),  the standard deviation from the given value, that is, the true value (SDT), and
the standard deviation from the given value, that is, the true value (SDT), and  the average sum-squared error (ASSE) given by
the average sum-squared error (ASSE) given by

where  represents the estimated parameter at the
represents the estimated parameter at the  th trial and
th trial and  the corresponding true value of the parameter.
the corresponding true value of the parameter.
Different AR systems are investigated in order to cover a wide range of possible locations of poles, their numbers and types (i.e., real or complex conjugate). Tables 1 and 2 show the estimation results for the AR and AR
and AR systems at an SNR level of
systems at an SNR level of  dB, respectively. The AR
dB, respectively. The AR system with
system with  contains a real pole and a pair of complex conjugate pole, and the AR
contains a real pole and a pair of complex conjugate pole, and the AR system with
system with  contains two real poles and a pair of complex conjugate poles. As the real and complex types of poles exhibit quite different behaviors, in our experiments various combinations of real and complex poles are considered to show the capability of the proposed algorithm in dealing with real life situations. In each table, the second column lists the true values of the AR parameters and the remaining four columns list the estimated values of corresponding parameters obtained from the proposed and the three other methods. The values for the SDM and SDT corresponding to estimated AR coefficients are also given below the estimated parameter value. The last row of each table provides the ASSE measure in dB. Table 1 shows that at
contains two real poles and a pair of complex conjugate poles. As the real and complex types of poles exhibit quite different behaviors, in our experiments various combinations of real and complex poles are considered to show the capability of the proposed algorithm in dealing with real life situations. In each table, the second column lists the true values of the AR parameters and the remaining four columns list the estimated values of corresponding parameters obtained from the proposed and the three other methods. The values for the SDM and SDT corresponding to estimated AR coefficients are also given below the estimated parameter value. The last row of each table provides the ASSE measure in dB. Table 1 shows that at  dB, when the other methods fail to identify the system, the proposed method successfully estimates the parameters quite accurately. It is seen from Table 2, although some of the other methods provide an acceptable performance, the estimation accuracy achieved by the proposed method is much higher. It is seen from these tables that the proposed method exhibits a superior estimation performance with respect to all the four performance indices at such a low level of SNR. Very small values of SDM and SDT obtained from the proposed technique indicate a high degree of estimation consistency and accuracy.
dB, when the other methods fail to identify the system, the proposed method successfully estimates the parameters quite accurately. It is seen from Table 2, although some of the other methods provide an acceptable performance, the estimation accuracy achieved by the proposed method is much higher. It is seen from these tables that the proposed method exhibits a superior estimation performance with respect to all the four performance indices at such a low level of SNR. Very small values of SDM and SDT obtained from the proposed technique indicate a high degree of estimation consistency and accuracy.
 dB for AR
dB for AR system with white noise excitation.
system with white noise excitation. dB for AR
dB for AR system with white noise excitation.
system with white noise excitation.Figure 1 shows the ASSE values as a function of SNR levels for the AR system obtained by each of the four methods with the true parameters as specified in Table 1. It is observed from Figure 1 that the ILSF and the SSYW methods give estimation accuracy comparable to that provided by the proposed method for SNR levels above
system obtained by each of the four methods with the true parameters as specified in Table 1. It is observed from Figure 1 that the ILSF and the SSYW methods give estimation accuracy comparable to that provided by the proposed method for SNR levels above  dB. However, the proposed method performs significantly better for levels of SNR as low as
dB. However, the proposed method performs significantly better for levels of SNR as low as  dB.
dB.
Figure 2 depicts the superimposed plots of the estimated poles from  independent realizations obtained by the four methods at
independent realizations obtained by the four methods at  dB along with their true locations for an AR
dB along with their true locations for an AR system with parameters
system with parameters  1, −3.2229, 5.2862, −5.0095, 2.7875, −0.7362
1, −3.2229, 5.2862, −5.0095, 2.7875, −0.7362 . Clearly, the estimated values obtained using the proposed method in comparison to that achieved by the other methods are much less scattered around the true values indicating a very high estimation accuracy. Similar to AR
. Clearly, the estimated values obtained using the proposed method in comparison to that achieved by the other methods are much less scattered around the true values indicating a very high estimation accuracy. Similar to AR , AR
, AR , and AR
, and AR systems described above, the performance of the proposed method has been investigated for a number of other AR systems with different orders. As an illustration of the effectiveness of the proposed RCC method with larger model orders, an AR
systems described above, the performance of the proposed method has been investigated for a number of other AR systems with different orders. As an illustration of the effectiveness of the proposed RCC method with larger model orders, an AR system is considered with parameters
system is considered with parameters  1, −2.1953, 3.7702, −5.7045, 7.9177, −9.0049, 9.2872, −8.8448, 7.5863, −5.3168, 3.4542, −1.9537, 0.8162
1, −2.1953, 3.7702, −5.7045, 7.9177, −9.0049, 9.2872, −8.8448, 7.5863, −5.3168, 3.4542, −1.9537, 0.8162 . In Figure 3, the superimposed plots of the estimated poles of the AR
. In Figure 3, the superimposed plots of the estimated poles of the AR system obtained by the four methods at
system obtained by the four methods at  dB along with their true locations are shown. Similar to Figure 2 that portrays the estimation accuracy of the proposed method for the case of AR
dB along with their true locations are shown. Similar to Figure 2 that portrays the estimation accuracy of the proposed method for the case of AR system, Figure 3 clearly exhibits the effectiveness of the proposed method in estimating poles of the high-order AR system. As expected, the estimation accuracy of this large order AR system is somewhat reduced, but the performance of the proposed RCC method still remains considerably superior to that provided by the other techniques.
system, Figure 3 clearly exhibits the effectiveness of the proposed method in estimating poles of the high-order AR system. As expected, the estimation accuracy of this large order AR system is somewhat reduced, but the performance of the proposed RCC method still remains considerably superior to that provided by the other techniques.
5.1.2. Impulse-Train Excitation
We now consider the problem of AR system identification with periodic impulse-train excitations of different periods for various levels of noise. An impulse-train is generated using (30) with a known value of  . We choose the number of RCC samples less than
. We choose the number of RCC samples less than  ; thus,
; thus,  . A noisy AR signal is generated according to (1) and (7) with
. A noisy AR signal is generated according to (1) and (7) with  . The simulations are carried out for
. The simulations are carried out for  independent trials and the results averaged.
independent trials and the results averaged.
Tables 3 and 4 provide the estimation results for the impulse-train excited AR and AR
and AR systems with
systems with  at
at  dB, respectively. It is seen from these tables that the proposed method provides quite accurate estimation of the AR parameters with very small values of SDM and SDT, whereas the other methods are unable to identify the systems at
dB, respectively. It is seen from these tables that the proposed method provides quite accurate estimation of the AR parameters with very small values of SDM and SDT, whereas the other methods are unable to identify the systems at  dB. Similar result is observed for the AR
dB. Similar result is observed for the AR system that was considered for the white noise excitation.
system that was considered for the white noise excitation.
 dB for AR
dB for AR system with impulse train excitation.
system with impulse train excitation. dB for AR
dB for AR system with impulse train excitation.
system with impulse train excitation.The ASSE resulting from using the various methods under the impulse-train excitation for the estimation of the same AR system as the one considered for the white noise excitation is shown in Figure 4. It is seen from the figure that, the proposed RCC method provides a significantly better performance even at a very low SNR, whereas the performance of other methods deteriorates at low levels of SNR.
system as the one considered for the white noise excitation is shown in Figure 4. It is seen from the figure that, the proposed RCC method provides a significantly better performance even at a very low SNR, whereas the performance of other methods deteriorates at low levels of SNR.
It is to be mentioned that, we have also compared the proposed ramp cosine cepstrum (RCC) method with our ramp cepstrum (RC) method previously developed in [8] which employs conventional cepstrum of a correlation function via DFT and IDFT. It has been observed that the estimation performance of the RCC method is slightly better than our previous RC method at a very low SNR of around −5 dB, and remains comparable for other levels of SNR. Although the two methods exhibit quite a similar estimation performance, yet the RCC method based on the DCT-IDCT implementation offers significant computational advantages as opposed to the RC approach.
5.2. An Application for Vocal Tract System Identification
As a practical application of the proposed method, the identification of a vocal tract system is performed from natural speech signals. Since, in this case, the true system parameters are not known, for the purpose of evaluating the estimation accuracy, nonparametric PSD is used. In addition, an estimate of the poles under a noise-free condition is also obtained by using some commonly used technique for the LPC analysis, such as the MLSYW method. The corresponding wide-band spectrogram of the noise-free speech gives information on possible pole locations. In order to estimate the vocal tract system parameters, some English natural voiced phonemes from the TIMIT and the North Texas standard databases [21, 22] with a sampling frequency of  KHz are used as the noise-free output observations. Instances of the phonemes for the TIMIT database are extracted from the database according to the given transcriptions, and the North Texas is a database containing natural vowels. Low-pass filtering up to a certain high-frequency range, such as
KHz are used as the noise-free output observations. Instances of the phonemes for the TIMIT database are extracted from the database according to the given transcriptions, and the North Texas is a database containing natural vowels. Low-pass filtering up to a certain high-frequency range, such as  KHz, is not performed in order to observe the accuracy of the pole estimation over the entire range of frequency. With the estimated parameters of the vocal tract considered as an AR system and the pitch-period (or the excitation signal), a speech phoneme can be synthesized using an appropriate value of the vocal tract filter gain, which is determined based on the RMS power level and the peak PSD of the natural speech frames [1]. For computing synthesized speech signals by different methods, the same excitation signal is used for a particular phoneme. In order to verify the estimation accuracy, first, the PSD of the synthesized speech is compared with that of the noise-free natural speech, and then the estimated poles at a noisy condition are compared with that obtained in a noise-free condition by using the MLSYW method. Figure 5(a) shows a comparison of the PSDs of the vocal tract system obtained from the different methods considered in noisy environments with respect to noise-free PSD. Considering the fact that the choice of the order of the vocal tract filter depends on the spectral characteristics of the specific phoneme, an AR
KHz, is not performed in order to observe the accuracy of the pole estimation over the entire range of frequency. With the estimated parameters of the vocal tract considered as an AR system and the pitch-period (or the excitation signal), a speech phoneme can be synthesized using an appropriate value of the vocal tract filter gain, which is determined based on the RMS power level and the peak PSD of the natural speech frames [1]. For computing synthesized speech signals by different methods, the same excitation signal is used for a particular phoneme. In order to verify the estimation accuracy, first, the PSD of the synthesized speech is compared with that of the noise-free natural speech, and then the estimated poles at a noisy condition are compared with that obtained in a noise-free condition by using the MLSYW method. Figure 5(a) shows a comparison of the PSDs of the vocal tract system obtained from the different methods considered in noisy environments with respect to noise-free PSD. Considering the fact that the choice of the order of the vocal tract filter depends on the spectral characteristics of the specific phoneme, an AR model is used for a naturally spoken sound
model is used for a naturally spoken sound  of the word "head" uttered by a female speaker. In this case, the vowel duration is
of the word "head" uttered by a female speaker. In this case, the vowel duration is  ms with
ms with  samples. In order to test the performance of the methods in estimating the AR parameters of a vocal tract system, twenty independent experiments were performed by adding to the same original speech
samples. In order to test the performance of the methods in estimating the AR parameters of a vocal tract system, twenty independent experiments were performed by adding to the same original speech  different realizations of white Gaussian noise, thus obtaining
different realizations of white Gaussian noise, thus obtaining  realizations of noisy observations each with a SNR value of
realizations of noisy observations each with a SNR value of  dB. These
dB. These  realizations of the noisy observations are then used one by one in twenty independent experiments. In each experiment, one set of AR parameters is obtained by employing a given method of parameter estimation. The AR parameter values of the vocal tract are averaged over
realizations of the noisy observations are then used one by one in twenty independent experiments. In each experiment, one set of AR parameters is obtained by employing a given method of parameter estimation. The AR parameter values of the vocal tract are averaged over  sets and then used to obtain the synthesized speech corresponding to the given method of parameter estimation. We choose the number of RCC samples
sets and then used to obtain the synthesized speech corresponding to the given method of parameter estimation. We choose the number of RCC samples  less than the pitch period
less than the pitch period  ; thus,
; thus,  . According to the general behavior of the vocal tract parameter,
. According to the general behavior of the vocal tract parameter,  is searched in the range
is searched in the range  [23]. The search range for
[23]. The search range for  can be narrowed down based on the knowledge of the pole locations of a particular phoneme [1, 23]. In order to have a better understanding of the level of noise, the PSD of one of the
can be narrowed down based on the knowledge of the pole locations of a particular phoneme [1, 23]. In order to have a better understanding of the level of noise, the PSD of one of the  noisy signals is also included in obtaining the results of Figure 5(a). It is seen from this figure that the PSD of the synthesized signal obtained by using the estimated vocal tact system parameters resulting from the proposed scheme is quite accurate relative to that obtained by the other methods. The estimated average poles are also shown in Figure 5(b) along with the noise-free estimates obtained by the MLSYW method. In Figure 5(b), the noise-free wide-band spectrogram and the noise-free nonparametric PSD are included in order to clearly visualize the pole locations and strength in the natural phoneme. The pole-plot clearly shows a high estimation accuracy of the proposed method even at a low level of SNR.
noisy signals is also included in obtaining the results of Figure 5(a). It is seen from this figure that the PSD of the synthesized signal obtained by using the estimated vocal tact system parameters resulting from the proposed scheme is quite accurate relative to that obtained by the other methods. The estimated average poles are also shown in Figure 5(b) along with the noise-free estimates obtained by the MLSYW method. In Figure 5(b), the noise-free wide-band spectrogram and the noise-free nonparametric PSD are included in order to clearly visualize the pole locations and strength in the natural phoneme. The pole-plot clearly shows a high estimation accuracy of the proposed method even at a low level of SNR.
Estimation results for a natural speech phoneme  in the presence of white noise at
in the presence of white noise at  dB. (a) PSD obtained by using different methods, (b) Average estimated poles (
dB. (a) PSD obtained by using different methods, (b) Average estimated poles ( ) obtained from noise-corrupted speech by using the proposed method along with the noise-free estimates (
) obtained from noise-corrupted speech by using the proposed method along with the noise-free estimates ( ) obtained by the MLSYW method, spectrogram of the noise-free speech, and noise-free PSD.
) obtained by the MLSYW method, spectrogram of the noise-free speech, and noise-free PSD.
In a similar fashion, using an AR model, PSD results are obtained by employing different schemes under a real noisy environment of a multitalker babble noise (multiple background competing speakers) taken from the Noisex92 database [24]. In Figure 6(a), the results obtained at an SNR of
model, PSD results are obtained by employing different schemes under a real noisy environment of a multitalker babble noise (multiple background competing speakers) taken from the Noisex92 database [24]. In Figure 6(a), the results obtained at an SNR of  dB for a naturally spoken sound
dB for a naturally spoken sound  of the word "Rob" uttered by a male speaker are presented. In this case, the vowel duration is
of the word "Rob" uttered by a male speaker are presented. In this case, the vowel duration is  ms with
ms with  samples. The multiplicity of speakers produces a flatter short-term spectrum which has greater spectral and temporal modulation than a white Gaussian noise. It is observed from Figure 6(a) that the PSD obtained using the proposed method closely matches the noise-free PSD, and all pole locations are accurately estimated. The pole estimation accuracy of the proposed method is better revealed in Figure 6(b). In this figure, the estimated average poles along with the noise-free pole estimates, the wide-band spectrogram, and the nonparametric PSD are shown. Figure 6 clearly shows that the proposed method is capable of providing a satisfactory estimation performance also in the presence of babble noise at a very low level of SNR.
samples. The multiplicity of speakers produces a flatter short-term spectrum which has greater spectral and temporal modulation than a white Gaussian noise. It is observed from Figure 6(a) that the PSD obtained using the proposed method closely matches the noise-free PSD, and all pole locations are accurately estimated. The pole estimation accuracy of the proposed method is better revealed in Figure 6(b). In this figure, the estimated average poles along with the noise-free pole estimates, the wide-band spectrogram, and the nonparametric PSD are shown. Figure 6 clearly shows that the proposed method is capable of providing a satisfactory estimation performance also in the presence of babble noise at a very low level of SNR.
Estimation results for a natural speech phoneme /a/ in the presence of a multitalker babble noise at  dB. (a) PSD obtained by using different methods, (b) Average estimated poles (
dB. (a) PSD obtained by using different methods, (b) Average estimated poles ( ) obtained from noise-corrupted speech by using the proposed method along with the noise-free estimates (
) obtained from noise-corrupted speech by using the proposed method along with the noise-free estimates ( ) obtained by the MLSYW method, wide-band spectrogram of the noise-free speech, and noise-free PSD.
) obtained by the MLSYW method, wide-band spectrogram of the noise-free speech, and noise-free PSD.
6. Conclusion
In this paper, a new technique for the parameter estimation of an AR system, given its noise-corrupted output observations, has been proposed. A comprehensive and accurate ramp cosine cepstrum (RCC) model of the one-sided ACF of an AR signal, valid for both white noise and periodic impulse-train excitations, has been developed in a unified fashion in order to identify the AR systems. A residue-based least-squares ramp cosine cepstral fitting scheme employing the RCC model has been presented. It has been shown that the proposed method is able to provide a more accurate estimate of the AR parameters. It combines the attractive features of the correlation- and cepstral-domain system identifications, and has the advantage of providing the flexibility in incorporating some a priori knowledge of the parameters, if available, to facilitate the process of parameter estimation. Extensive experimentation performed on different AR systems has demonstrated that the proposed method is sufficiently accurate and consistent in estimating the parameters of the AR signals at very low levels of SNR. The method has also been applied to noise-corrupted natural speech signals for the estimation of human vocal tract system parameters, the accuracy of which is demonstrated in terms of the PSD of the resulting synthesized speech. The simulation results have revealed that the proposed method is superior to some of the existing methods in handling the parameter estimation problem of natural speech signals under white or real-life babble noise degradation.
References
O'Shaughnessy D: Speech Communications Human and Machine. 2nd edition. IEEE Press, New York, NY, USA; 2000.
Kay SM: Modern Spectral Estimation, Theory and Application. Prentice-Hall, Englewood Cliffs, NJ, USA; 1988.
Xie N, Leung H: Blind identification of autoregressive system using chaos. IEEE Transactions on Circuits and Systems I 2005, 52(9):1953-1964.
Vergara-Dominguez L: New insights into the high-order Yule-Walker equations. IEEE Transactions on Acoustics, Speech, and Signal Processing 1990, 38(9):1649-1651. 10.1109/29.60088
Davila CE: A subspace approach to estimation of autoregressive parameters from noisy measurements. IEEE Transactions on Signal Processing 1998, 46(2):531-534. 10.1109/78.655442
Zheng WX: Fast identification of autoregressive signals from noisy observations. IEEE Transactions on Circuits and Systems II 2005, 52(1):43-48.
Huang Z, Yang X, Zhu X, Kuh A: Homomorphic linear predictive coding. A new estimation algorithm for all-pole speech modelling. IEE Proceedings, Part I: Communications, Speech and Vision 1990, 137(2):103-108. 10.1049/ip-i-2.1990.0014
Fattah SA, Zhu W-P, Ahmad MO: Identification of autoregressive systems in noise based on a ramp-cepstrum model. IEEE Transactions on Circuits and Systems II 2008, 55(10):1051-1055.
Wang F, Yip P: Cepstrum analysis using discrete trigonometric transforms. IEEE Transactions on Signal Processing 1991, 39(2):538-541. 10.1109/78.80852
Athineos M, Ellis DPW: Autoregressive modeling of temporal envelopes. IEEE Transactions on Signal Processing 2007, 55(11):5237-5245.
Oppenheim AV, Schafer RW: Discrete-Time Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 1989.
de Almeida SJM, Bermudez JCM, Bershad NJ, Costa MH: A statistical analysis of the affine projection algorithm for unity step size and autoregressive inputs. IEEE Transactions on Circuits and Systems I 2005, 52(7):1394-1405.
Fattah SA, Zhu W-P, Ahmad MO: A novel technique for the identification of ARMA systems under very low levels of SNR. IEEE Transactions on Circuits and Systems I 2008, 55(7):1988-2001.
Long DG: Exact computation of the unwrapped phase of a finite-length time series. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988, 36(11):1787-1790. 10.1109/29.9019
Verhelst W, Steenhaut O: A new model for the short-time complex cepstrum of voiced speech. IEEE Transactions on Acoustics, Speech, and Signal Processing 1986, 34(1):43-51. 10.1109/TASSP.1986.1164787
Kobayashi T, Imai S: Spectrum analysis using generalized cepstrum. IEEE Transactions on Acoustics, Speech, and Signal Processing 1984, 32(5):1087-1089. 10.1109/TASSP.1984.1164416
Hwang T-H, Lee L-M, Wang H-C: Cepstral behaviour due to additive noise and a compensation scheme for noisy speech recognition. IEE Proceedings Vision, Image and Signal Processing 1998, 145(5):316-321. 10.1049/ip-vis:19982319
Kim HK, Rose RC: Cepstrum-domain acoustic feature compensation based on decomposition of speech and noise for ASR in noisy environments. IEEE Transactions on Speech and Audio Processing 2003, 11(5):435-446. 10.1109/TSA.2003.815515
Byrnes CI, Enqvist P, Lindquist A: Cepstral coefficients, covariance lags, and pole-zero models for finite data strings. IEEE Transactions on Signal Processing 2001, 49(4):677-693. 10.1109/78.912912
Hernando J, Nadeu C: Linear prediction of the one-sided autocorrelation sequence for noisy speech recognition. IEEE Transactions on Speech and Audio Processing 1997, 5(1):80-84. 10.1109/89.554273
Garofolo JS, Lamel LF, Fisher WM, et al.: Timit acoustic-phonetic continuous speech corpus. Proceedings of Linguistic Data Consortium, 1993, Philadelphia, PA, USA
Hillenbrand JM, Getty LA, Clark MJ, Wheeler K: Acoustic characteristics of American English vowels. Journal of the Acoustical Society of America 1995, 97(5 I):3099-3111.
Yegnanarayana B, Veldhuis RNJ: Extraction of vocal-tract system characteristics from speech signals. IEEE Transactions on Speech and Audio Processing 1998, 6(4):313-327. 10.1109/89.701359
Varga A, Steeneken HJM: Assessment for automatic speech recognition: II. NOISEX-92: A database and an experiment to study the effect of additive noise on speech recognition systems. Speech Communication 1993, 12(3):247-251. 10.1016/0167-6393(93)90095-3
Acknowledgments
This work was supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada and the Regroupement Stratégique en Microsystèmes du Québec (ReSMiQ).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fattah, S., Zhu, WP. & Ahmad, M. A Ramp Cosine Cepstrum Model for the Parameter Estimation of Autoregressive Systems at Low SNR. EURASIP J. Adv. Signal Process. 2010, 808312 (2010). https://doi.org/10.1155/2010/808312
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/808312
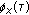 is a symmetric two-sided sequence, the corresponding OSACF
is a symmetric two-sided sequence, the corresponding OSACF 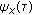 is related to
is related to 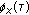 by
by
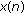 , its OSACF
, its OSACF  is also real.
is also real.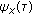 retains the pole-preserving property of
retains the pole-preserving property of 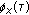 .
.

 system at
system at  dB.
dB. : true poles and
: true poles and  : estimated poles. (a) Proposed, (b) ILSF, (c) SSYW, and (d) MLSYW method.
: estimated poles. (a) Proposed, (b) ILSF, (c) SSYW, and (d) MLSYW method.
 system at
system at  dB.
dB. : true poles and
: true poles and  : estimated poles. (a) Proposed, (b) ILSF, (c) SSYW, and (d) MLSYW method.
: estimated poles. (a) Proposed, (b) ILSF, (c) SSYW, and (d) MLSYW method.

