- Research Article
- Open access
- Published:
On Optimizing H. 264/AVC Rate Control by Improving R-D Model and Incorporating HVS Characteristics
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 830605 (2010)
Abstract
The state-of-the-art JVT-G012 rate control algorithm of H.264 is improved from two aspects. First, the quadratic rate-distortion (R-D) model is modified based on both empirical observations and theoretical analysis. Second, based on the existing physiological and psychological research findings of human vision, the rate control algorithm is optimized by incorporating the main characteristics of the human visual system (HVS) such as contrast sensitivity, multichannel theory, and masking effect. Experiments are conducted, and experimental results show that the improved algorithm can simultaneously enhance the overall subjective visual quality and improve the rate control precision effectively.
1. Introduction
Rate control plays an important role in the field of video coding and transmission, which has been extensively studied in the literature. Strictly speaking, rate control technology is not a normative part of video coding standards. However, due to its importance for video coding and transmission, rate control has been widely studied, and several rate control algorithms have been proposed for inclusion in the reference software implementations of the existing video coding standards such as the TM5 for MPEG-2, the TMN8 for H.263, the VM8 for MPEG-4, and the F086 and G012 for H.264 [1–4]. Of all those algorithms the JVT-G012 has attracted great attention over the last few years and is being widely used.
R-D models describe the relationships between the bitrates and the distortions in the reconstructed video, which can enable an encoder to determine the required bit rate to achieve a target quality. For a rate control algorithm, the R-D model is a key part, and its accuracy greatly affects the rate control performance. Hence, how to improve the prediction accuracy of R-D model is the key to enhance the performance of rate control algorithm. Quite a few R-D models have been proposed such as the logarithm model, exponential model, and quadratic model [5]. Of all these models the quadratic model is adopted by JVT-G012 which is derived based on the assumption that video source follows Gaussian distribution. However, as analyzed in Section 2, it is not accurate enough in practical applications. There also exist several works where the quadratic models have been improved [6, 7]. However, almost all of them have just emphasized on how to improve the accuracy of frame complexity prediction, and their R-D models' structure is very similar to that of the original quadratic model. At the same time, studies on visual physiology and visual psychology indicate that observers usually have different sensitivities and interests to different video contents in video sequence, and the contents with more attention-attraction and higher visual sensitivity will be more sensitive to coding error. Hence, during video coding process, the regions with high sensitivities can be allocated more bits to acquire a higher overall subjective quality. Many scholars have been working on HVS-based video coding technologies, and many achievements have been made. For example, a novel subjective criteria for video quality evaluation based on the foveal characteristics has been developed in [8]. Nguyen and Hwang have presented a rate control approach for low bit-rate streaming video by incorporating the HVS characteristic of smooth pursuit eye movement, which can improve the quality of moving scenes in a video sequence [9]. Tang et al. have also proposed a novel rate control algorithm by considering the motion and texture structures of video contents [10]. However, since HVS is extremely complex, it is very difficult to obtain perfect perceptually consistent result during rate control and video coding. Thus, this topic should be further studied [11–13].
Based on above observations, the G012 algorithm is optimized from two aspects in this paper. First, the traditional quadratic R-D model is improved based on both empirical observations and theoretical analysis. Second, based on current physiological and psychological research findings of HVS, the main HVS characteristics such as contrast sensitivity, multichannel theory, and masking effect are analyzed, and then the G012 algorithm is optimized by incorporating these characteristics.
This paper is organized as follows. In Section 2, the quadratic model is analyzed and improved. In Section 3, some main HVS characteristics and the HVS-based rate control optimization are introduced. Experiments are conducted in Section 4, and Section 5 concludes the paper.
2. Improved R-D Model
The classical quadratic model is derived based on the assumption that video source follows Gaussian distribution [14]. Its R-D function can be formulated as follows:

After expanded with Taylor series, the above formula can be expressed as

Let , then the quadratic R-Q model can be acquired
, then the quadratic R-Q model can be acquired

where are model parameters,
are model parameters,  denotes quantization step, and
denotes quantization step, and  is the residual.
is the residual.
The above derivation is not very precise for the following several reasons. Firstly, the assumption that the DCT coefficients follow Gaussian distribution is not always true in practical applications. Secondly, only the first and the second items in expanded Taylor series are retained in (2). The constant and high-order items are totally discarded, which will introduce errors. In addition, it is not accurate to just let .
.
To further investigate the accuracy of the quadratic model, experiments have been performed. The actual relationship between the bitrates and the quantization steps has been analyzed. Nearly twenty video sequences have been tested, including Alex, Claire, Train, Discus, Mom, Grandmom, Mom_daughter, Trevor, Tennis, Foreman, Sergio, Susan, Miss, Sflowg, Janine, Pascal, and Herve sequences. For each sequence, more than 50 frames are tested. Our experiments are performed on our improved JM 10.2 platform, and the IBBP structure is used, where I denotes "Intracoded frame,"  denotes "Predicted frame," and
denotes "Predicted frame," and  denotes "Bipredictive frame." For H.264/AVC, quantization parameter's range is within
denotes "Bipredictive frame." For H.264/AVC, quantization parameter's range is within  . The corresponding quantization step's range is within [0.625, 224]. In our experiments, 30 quantization parameters from 1 to 30 are used. Each sequence is firstly encoded with different quantization steps. Then the acquired R-Q data are fitted by the quadratic R-Q model, and the fit errors are analyzed. From experimental results of nearly one thousand frames, we have found that, as shown in Figure 1, the actual bit-rate does not always decrease obviously with the increment of
. The corresponding quantization step's range is within [0.625, 224]. In our experiments, 30 quantization parameters from 1 to 30 are used. Each sequence is firstly encoded with different quantization steps. Then the acquired R-Q data are fitted by the quadratic R-Q model, and the fit errors are analyzed. From experimental results of nearly one thousand frames, we have found that, as shown in Figure 1, the actual bit-rate does not always decrease obviously with the increment of  , while the fitted curve of the quadratic R-Q model almost decreases obviously with the increment of
, while the fitted curve of the quadratic R-Q model almost decreases obviously with the increment of  . Hence, there exists considerable gap between the actual R-Q curve and the fitted curve of the quadratic R-Q model. As a result, the quadratic model is not accurate enough in practical rate control applications.
. Hence, there exists considerable gap between the actual R-Q curve and the fitted curve of the quadratic R-Q model. As a result, the quadratic model is not accurate enough in practical rate control applications.
Some experimental results on R-Q models. Results of four frames of Train sequence (the top-left is an I-frame; others are P-frames) Results of four frames of Discus sequence (the top-left is an I-frame; others are P-frames)Results of four frames of Trevor sequence (the top-left is an I-frame; others are P-frames)
Based on above observations, the quadratic model is adapted to be

where  ,
,  , and
, and  are model parameters and they can be computed based on linear regression method, which is briefly introduced as follows.
are model parameters and they can be computed based on linear regression method, which is briefly introduced as follows.
-
(1)
Firstly, let
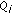 denote the quantization step of the i th frame, and define
denote the quantization step of the i th frame, and define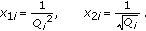 (5)
(5)Suppose that
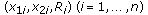 are existing samples from previously coded frames, where
are existing samples from previously coded frames, where  is the number of the previously coded frames and
is the number of the previously coded frames and 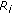 is the corresponding bit rate of the i th frame.
is the corresponding bit rate of the i th frame. -
(2)
Secondly, define
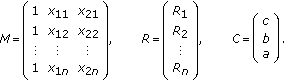 (6)
(6)Then (4) can be rewritten in matrix form as
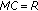 using (6).
using (6). -
(3)
Finally, based on linear regression method, the parameters in
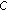 can be estimated by
can be estimated by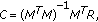 (7)
(7)where
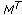 is the transpose of
is the transpose of 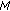 and
and 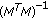 is the inverse matrix of
is the inverse matrix of 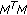 .
.
In order to evaluate the performance of the new proposed R-D model, the actual R-Q data are also fitted by the proposed R-D model, and the fitted result is compared with that of the quadratic model. Some simulation results are shown in Figure 1, where the actual R-Q curve and the fitted R-Q curve of each frame with two models are drawn on the same figure. From the simulation results, it can be found that, compared with the old model, the new one can more accurately approach the actual R-Q relation.
3. HVS-Based Rate Control
G012 can be viewed as performing rate control at three different layers: GOP layer, frame layer, and basic unit (BU) layer. Within a BU, all the macroblocks (MB) are encoded with the same quantization parameter, which does not consider the visual sensitivity difference between MBs. Thus, it is hard to obtain perceptually consistent results in practical applications.
HVS is so complex that it is impossible to incorporate the whole HVS characteristics during rate control and video coding. This paper only discusses several important HVS characteristics including the contrast sensitivity, multichannel theory, and masking effect [15–17]. HVS-related research findings contend that there exists a threshold contrast for an observer to detect the change in intensity. The inverse of the contrast threshold is usually defined as contrast sensitivity, which is a function of spatial frequency with a bandpass nature [18]. The multichannel theory of human vision states that different stimuli are processed in different channels in the human visual system. Both physiological and psychophysical experiments carried out on perception have given the evidence of the bandpass nature of the cortical cells' response in the spectral domain, and the human brain seems therefore to possess a collection of separate mechanisms, each being more sensitive to a portion of the frequency domain. Masking effect can be explained as the interaction among stimuli. The detection threshold of a stimulus may vary due to the existence of another. This kind of variation can be either positive or negative. Due to masking effect, similar artifacts may be disturbing in certain regions of an image while they are hardly noticeable elsewhere. Hence, during rate control the masking effect can be used to deal with different scenarios with different tips to acquire perceptually consistent result [19].
In the proposed algorithm, the quantization step for each MB will be adjusted by its visual sensitivity. MBs with high visual sensitivity will be encoded with small quantization parameters, and MBs with low visual sensitivities are encoded with large quantization parameters so that better subjective visual quality could be obtained under the same given bit rate constraint. In order to incorporate HVS characteristics, three new modules are added to the original G012 framework, which are preprocessing module, visual sensitivity calculation module, and quantization step modification module. The three new added modules are briefly introduced as follows.
3.1. Preprocessing
In this module, the background intensity and the average spatial frequency of each image are calculated. For an image, its background intensity,  , is calculated by averaging the values of all pixels
, is calculated by averaging the values of all pixels

where  is the value of thei th pixel,
is the value of thei th pixel,  denotes the image width, and
denotes the image width, and  denotes the image height.
denotes the image height.
The average spatial frequency,  , is defined as the average spatial frequency of all the MBs, that is,
, is defined as the average spatial frequency of all the MBs, that is,

where

where NUM denotes the number of MBs in the image,  denotes the spatial frequency of thei th MB,
denotes the spatial frequency of thei th MB,  and
and  denote the horizontal and vertical frequencies, respectively, and
denote the horizontal and vertical frequencies, respectively, and  denotes the
denotes the  th pixel' value.
th pixel' value.
3.2. Calculation of Visual Sensitivity
In the proposed algorithm, the quantization step for an MB will be adjusted according to its visual sensitivity. For each MB, we consider its visual sensitivity from four aspects: motion sensitivity, brightness sensitivity, contrast sensitivity, and position sensitivity.
(1) Motion Sensitivity
Studies on human perception indicate that motion has a strong influence on visual attention, and people often pay more attention to fast moving objects than to low or still background regions [20, 21]. Hence, compared with still background regions, the moving regions are considered to have high visual sensitivities. In the proposed algorithm, each frame is divided into moving regions and background regions, and different sensitivities are defined for each region

where  denotes the motion sensitivity,
denotes the motion sensitivity,  and
and  denote the sensitivities of background region and moving object, respectively. In this paper,
denote the sensitivities of background region and moving object, respectively. In this paper,  is set to 0.5, and
is set to 0.5, and  is set to 1.5. For moving objects detection, our earlier proposed object extraction and tracking algorithm based on spatio-temporal information is employed [22].
is set to 1.5. For moving objects detection, our earlier proposed object extraction and tracking algorithm based on spatio-temporal information is employed [22].
(2) Brightness Sensitivity
For a digital image, its pixels' values are represented by a finite number of intensity levels. For example, a gray image with 8 bits per pixel is represented by 256 intensity levels, where 0 usually corresponds to the darkest level and 255 corresponds to the brightest level. According to the Weber's law, the perceived brightness of HVS is a nonlinear function of intensity, which can be modeled by nonlinear monotonically increasing functions. Various models have been proposed such as the logarithmic model, and cube root model. In this paper, the following nonlinear model is used:

where I denotes image intensity, B denotes the corresponding perceived brightness,  is the threshold for intensity,
is the threshold for intensity,  is the maximum value of intensity, and
is the maximum value of intensity, and  is the maximum value of perceived brightness [23]. Suppose that
is the maximum value of perceived brightness [23]. Suppose that  is the perceived global brightness of an image and
is the perceived global brightness of an image and  is the perceived brightness of the current MB, then the brightness sensitivity of the MB,
is the perceived brightness of the current MB, then the brightness sensitivity of the MB,  is defined by
is defined by

(3) Contrast Sensitivity
HVS-related researches have shown that HVS is not equally sensitive to all spatial frequencies and CSFs are defined to describe the frequency response of HVS. Various CSFs have been proposed, and most of them are bandpass in nature, but maximum at different frequencies. In practical applications, due to the difference of video content, the peak frequencies are also various for different video sequences. Hence, the following improved CSF function is used in this paper:

where  denotes the peak frequency,
denotes the peak frequency,  denotes the contrast sensitivity, and f denotes the spatial frequency in cycles per degree.
denotes the contrast sensitivity, and f denotes the spatial frequency in cycles per degree.
(4) Position Sensitivity
Many HVS-related research experiments have indicated that people usually pay more attention to the central region than to the side regions, and the visual sensitivity decreases progressively from central region to side regions. Based on this observation, we define a new sensitivity, position sensitivity termed  , to model this effect
, to model this effect

where denotes the center of the current MB,
denotes the center of the current MB,  denotes the center of the image, and max represents the maximum distance from the side to the center of the image.
denotes the center of the image, and max represents the maximum distance from the side to the center of the image.
3.3. Quantization Parameter Modification Based on Visual Sensitivity
In our proposed algorithm, the quantization step for each MB will be adjusted by its visual sensitivity. For each MB, we compute a quantization adjustment according to each kind of sensitivity. The finally overall adjustment for each MB is the sum of them. The quantification adjustment induced by each kind of sensitivity is calculated as follows.
-
(1)
The motion sensitivity-induced quantization adjustment,
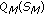 , is defined by
, is defined by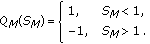 (16)
(16) -
(2)
The brightness sensitivity-induced quantization adjustment,
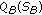 , is defined by
, is defined by (17)
(17)where
 is a weighting factor of background intensity,
is a weighting factor of background intensity, 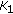 and
and 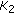 are thresholds for intensity.
are thresholds for intensity. -
(3)
The contrast sensitivity-induced quantization adjustment,
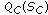 , is defined by
, is defined by (18)
(18) -
(4)
The position sensitivity-induced quantization adjustment,
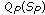 , is defined by
, is defined by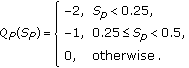 (19)
(19)
Finally, the overall quantization adjustment for each MB  is given by
is given by

And during rate control and video coding, the finally used quantization step, , is determined by
, is determined by

where  is the quantization step for the whole BU acquired during BU layer rate control. For practical rate control, MB-based quantization adjustment may lead to visual discomfort such as artifact. Hence, in our actual implementations, the quantization adjustment
is the quantization step for the whole BU acquired during BU layer rate control. For practical rate control, MB-based quantization adjustment may lead to visual discomfort such as artifact. Hence, in our actual implementations, the quantization adjustment  for each MB is confined to
for each MB is confined to  .
.
4. Experimental Results
In order to evaluate the performance of the improved rate-control algorithm, experiments are performed based on our improved JM 10.2 platform. Some test parameters are given in Table 1. Several test sequences are used including the Alex, Claire, and Train sequences. For each sequence, over 100 frames are encoded. We mainly investigate the rate-control precision and the image quality of decoded videos. Therefore, two metrics are defined for algorithm evaluation, rate-control deviation  and average peak signal-to-noise ratio (PSNR)
and average peak signal-to-noise ratio (PSNR) is defined to reflect the rate-control precision. The smaller the
is defined to reflect the rate-control precision. The smaller the  is, the better the rate-control precision will be. The two metrics are defined as
is, the better the rate-control precision will be. The two metrics are defined as

where  and
and  are the target and actual bitrates, respectively,
are the target and actual bitrates, respectively,  is the number of frames encoded, and
is the number of frames encoded, and  denotes the PSNR of the i th frame.
denotes the PSNR of the i th frame.
To evaluate the proposed algorithm objectively, subjective tests are also performed. To implement subjective evaluation, our test procedure is set up similar to the double stimulus impairment scale (DSIS) method formalized in ITU-R Recommendation BT.500-10 [24]. In our experiments, for every test sequence, both the decoded versions with the original and the proposed algorithms are presented to the observers under the same lighting and viewing conditions. Fifteen observers participated in the test, and they are asked to rate the perceptual quality of the decoded versions and make a mean opinion score (MOS) between 0 and 10 for each version. The mean opinion scores are made according to the principle given in Table 2.
Partial experimental results are shown in Figures 2, 3, 4, 5, 6, and 7 and Tables 3, 4, 5, 6, and 7. Table 3 shows the average intensities and the average spatial frequencies of the test sequences. Figure 2 gives the moving segmentation results. Tables 4, 5, 6, and 7 show partial comparison results of the two algorithms with respect to rate control precision, average PSNR, while Figures 3–6 show partial results with respect to subjective quality of the decoded image sequences. Figure 7 shows some frame by frame results in terms of PSNR of Train sequence at some bitrates. From Tables 4–7, it can be observed that, compared with the original algorithm, the rate control precision of the proposed algorithm is improved obviously at most bit-rates, which is mainly attributed to the improved R-Q model. From Figures 3–7, it can be seen that, though the average PSNR of reconstructed video of the proposed algorithm decreases slightly, the overall subjective visual quality is enhanced due to the incorporation of main HVS characteristics. From the results in Figure 7, one can also tell that, compared with the original one, the image quality of the successive frames changes more smoothly in the proposed algorithm.
However, rate control is a comprehensive technology whose performance is affected by many factors in practical applications. There also exist some limitations for our algorithm. For example, we also used the same temporal Mean Absolute Difference (MAD) prediction method as JVT-G012, which has the following drawbacks: (a) inaccurate MAD prediction for sudden changes; (b) inaccurate bit allocation since the header bits of the current basic unit are predicted from previous encoded basic units. Another limitation is the algorithm complexity. Compared with the original one, the proposed algorithm has higher computational load. Our future work will be on how to handle these limitations.
5. Conclusion
Rate control plays an important role in the field of video coding and transmission, and its performance is of great importance to the video coding effectiveness. In this paper, by adapting quadratic R-D model and incorporating the main HVS characteristics, the classic JVT-G012 rate control algorithm has been improved, which can both improve the rate control precision and enhance the overall subjective quality of the reconstructed video images. However, rate control is a comprehensive technology whose performance is affected by many factors in practical applications, and there still exist some limitations for the proposed algorithm. Hence, it should be further optimized if only better performance is expected.
References
Merritt L, Vanam R: Improved rate control and motion estimation for H.264 encoder. Proceedings of the 14th IEEE International Conference on Image Processing (ICIP '07), September 2007 V309-V312.
Kamaci N, Altunbasak Y, Mersereau RM: Frame bit allocation for the H.264/AVC video coder via cauchy-density-based rate and distortion models. IEEE Transactions on Circuits and Systems for Video Technology 2005, 15(8):994-1006.
Chen Z, Ngan KN: Recent advances in rate control for video coding. Signal Processing: Image Communication 2007, 22(1):19-38. 10.1016/j.image.2006.11.002
Li ZG, Pan F, Lin KP, Feng G, Lin X, Rahardja S: Adaptive basic unit layer rate control for JVT. Proceedings of the 7th JVT Meeting, 2003, Pattaya II, Thailand
Yuan W: Research for the rate control algorithm in H.264, M.S. thesis. Hefei University of Technology, China; 2006.
Yi X, Ling N: Improved H.264 rate control by enhanced MAD-based frame complexity prediction. Journal of Visual Communication and Image Representation 2006, 17(2):407-424. 10.1016/j.jvcir.2005.04.005
Kim J-Y, Kim S-H, Ho Y-S: A frame-layer rate control algorithm for H.264 using rate-dependent mode selection. Proceedings of the 6th Pacific Rim Conference on Multimedia (PCM '05), 2005, Lecture Notes in Computer Science 3768: 477-488.
Lee S, Pattichis MS, Bovik AC: Foveated video compression with optimal rate control. IEEE Transactions on Image Processing 2001, 10(7):977-992. 10.1109/83.931092
Nguyen AG, Hwang J-N: A novel hybrid HVPC/mathematical model rate control for low bit-rate streaming video. Signal Processing: Image Communication 2002, 17(5):423-440. 10.1016/S0923-5965(02)00011-5
Tang C-W, Chen C-H, Yu Y-H, Tsai C-J: Visual sensitivity guided bit allocation for video coding. IEEE Transactions on Multimedia 2006, 8(1):11-18.
Chen ZZ, Ngan KN: A unified framework of unsupervised subjective optimized bit allocation for video coding using visual attention model. Multimedia Systems and Applications VIII, 2005, Boston, Mass, USA, Proceedings of SPIE
Liu Z, Karam LJ, Watson AB: JPEG2000 encoding with perceptual distortion control. IEEE Transactions on Image Processing 2006, 15(7):1763-1778.
Jiang M, Ling N: On lagrange multiplier and quantizer adjustment for H.264 frame-layer video rate control. IEEE Transactions on Circuits and Systems for Video Technology 2006, 16(5):663-669.
Chiang T, Zhang Y-Q: A new rate control scheme using quadratic rate distortion model. IEEE Transactions on Circuits and Systems for Video Technology 1997, 7(1):246-250. 10.1109/76.554439
Wang Z, Sheikh RH, Bovik CA: Objective video quality assessment. In The Handbook of Video Databases: Design and Applications. Edited by: Furht B, Marqure O. CRC Press, Boca Raton, Fla, USA; 2003:1041-1078.
Simoncelli EP, Olshausen BA: Natural image statistics and neural representation. Annual Review of Neuroscience 2001, 24: 1193-1216. 10.1146/annurev.neuro.24.1.1193
Sheikh HR, Bovik AC: Image information and visual quality. IEEE Transactions on Image Processing 2006, 15(2):430-444.
Wei CK: Image quality assessment model via HVS, M.S. thesis. National University of Defense Technology, China; 2003.
Mannos JL, Sakrison DJ: The effects of a visual fidelity criterion on the encoding of images. IEEE Transactions on Information Theory 1974, 20(4):525-536. 10.1109/TIT.1974.1055250
Cheng W-H, Chu W-T, Kuo J-H, Wu J-L: Automatic video region-of-interest determination based on user attention model. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '05), May 2005 3219-3222.
Osberger W, Maeder A, Bergmann N: A technique for image quality assessment based on a human visual system model. Proceedings of the European Signal Processing Conference, 1998 1049-1052.
Zhu ZJ, Jiang GY, Yu M, Wu XW: New algorithm for extracting moving object based on spatio-temporal information. Chinese Journal of Image and Graphics 2003, 8(4):422-425.
Ivkovic G, Sankar R: An algorithm for image quality assessment. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '04), May 2004 713-716.
ITU-R : Methodology for the subjective assessment of the quality of television pictures. ITU-R Recommendation BT.500-10, Geneva, Switzerland; 2000.
Acknowledgments
This paper was supported in part by the National Natural Science Foundation of China (no. 60902066, 60872094, 60832003), the Zhejiang Provincial Natural Science Foundation (no. Y107740), the Projects of Chinese Ministry of Education (no. 200816460003), the Open Project Foundation of Ningbo Key Laboratory of DSP (no. 2007A22002), and the Scientific Research Fund of Zhejiang Provincial Education Department (Grant no. Z200909361).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhu, Z., Wang, Y., Bai, Y. et al. On Optimizing H. 264/AVC Rate Control by Improving R-D Model and Incorporating HVS Characteristics. EURASIP J. Adv. Signal Process. 2010, 830605 (2010). https://doi.org/10.1155/2010/830605
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/830605

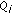 denote the quantization step of the i th frame, and define
denote the quantization step of the i th frame, and define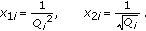
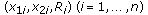 are existing samples from previously coded frames, where
are existing samples from previously coded frames, where  is the number of the previously coded frames and
is the number of the previously coded frames and 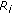 is the corresponding bit rate of the i th frame.
is the corresponding bit rate of the i th frame.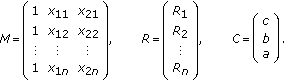
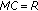 using (6).
using (6).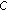 can be estimated by
can be estimated by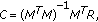
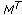 is the transpose of
is the transpose of 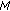 and
and 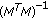 is the inverse matrix of
is the inverse matrix of 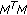 .
.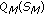 , is defined by
, is defined by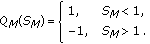
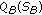 , is defined by
, is defined by
 is a weighting factor of background intensity,
is a weighting factor of background intensity, 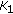 and
and 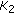 are thresholds for intensity.
are thresholds for intensity.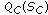 , is defined by
, is defined by
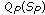 , is defined by
, is defined by