- Research Article
- Open access
- Published:
Decentralized Detection in Censoring Sensor Networks under Correlated Observations
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 838921 (2010)
Abstract
The majority of optimal rules derived for different decentralized detection application scenarios are based on an assumption that the sensors' observations are statistically independent. Deriving the optimal decision rule in the canonical decentralized setting with correlated observations was shown to be complicated even for the simple case of two sensors. We introduce an alternative suboptimal rule to deal with correlated observations in decentralized detection with censoring sensors using a modified generalized likelihood ratio test (mGLRT). In the censoring scheme, sensors either send or do not send their complete observations to the fusion center. Using ML estimation to estimate the censored values, the decentralized problem is converted to a centralized problem. Our simulation results indicate that, when sensor observations are correlated, the mGLRT gives considerably better performance in terms of probability of detection than does the optimal decision rule derived for uncorrelated observations.
1. Introduction
The theory of signal detection and estimation is used in a wide variety of target-detection applications. Different formulations for the target detection problem have been suggested depending on the cost of communication. The classical detection theory considered the canonical detection problem in which a decision is made based on observations present in one central location, that is, centralized detection. The classical detection theory suits applications in which the complete observations are available at one location for decision making, for example, detection of the presence of a target using a radar.
Decentralized detection addresses the issue of detection in sensor networks. A typical decentralized detection system with fusion is shown in Figure 1, in which a fusion-center produces an estimate of the state of nature based on the data sent by geographically dispersed sensor nodes. Some preliminary processing of data is carried out at each sensor node. For example, in the canonical decentralized detection problem, each sensor node quantizes the likelihood ratio of its observation before sending it [1]. The performance of decentralized detection systems is suboptimal compared to the centralized systems because the decision maker (fusion-center) does not receive a sufficient statistic. Nonetheless, factors such as communication bandwidth and limited energy motivate the use of decentralized detection systems. Moreover, in systems with a large number of sensor nodes, uncompressed information could overwhelm the fusion-center.
In battery-powered sensor networks, the most valuable resource is the limited energy available to each sensor. In a scenario where the absence of the target (null hypothesis) is much more likely than its presence (target hypothesis), an alternative formulation of the decentralized detection problem would allow the sensors to not communicate all the time to the fusion center, and thereby conserve energy. In such a case, the sensors are said to censor their observations by not sending observations that fall within a certain criterion. Rago et al. [2] considered a censoring scheme in which sensors either send or do not send some real-valued function of their observation to a fusion center based on a communication-rate constraint. The work in [2] shows that in the censoring scenario with independent sensors' observations, it is optimal (in both the Bayesian and the Neyman-Pearson (NP) sense) for the sensors to not send their likelihood ratios if they fall in a particular interval and that the optimal censoring region is a single interval of the likelihood ratio.
In the canonical decentralized detection problem introduced in [1], an optimal decision rule should come up with the optimal quantizer at each sensor and the optimal decision rule at the fusion center. To obtain the censoring thresholds and the optimum decision rule in the censoring formulation, joint optimization is required across the sensors and the fusion center. Appadwedula et al. [3, 4] provided a useful simplification of the censoring interval  . It was proven in [3, 4] that setting the lower threshold of the censoring interval to 0 for any false-alarm constraints less than or equal to
. It was proven in [3, 4] that setting the lower threshold of the censoring interval to 0 for any false-alarm constraints less than or equal to  is optimal in the NP sense, where
is optimal in the NP sense, where  is the communication rate constraint for sensor
is the communication rate constraint for sensor  . This reduces the complexity of finding the censoring region to dealing with one threshold per sensor instead of two thresholds per sensor.
. This reduces the complexity of finding the censoring region to dealing with one threshold per sensor instead of two thresholds per sensor.
Most of the work done in the area of deriving optimal rules was based on an assumption that the observations at each sensor node are conditionally independent. Although such an assumption reduces the complexity of analysis noticeably, many wireless sensor network applications experience correlated observations, for example, in target-detection problems in which the sensors are close to each other and are prone to the same noise sources.
The effect of correlation on the performance of a decentralized detection system has been explored in the literature. Some of this work was done in [5–9]. The results obtained are often not easy to implement because the observation space cannot be divided into two contiguous portions. Willett et al. [8], for example, derive the optimal sensor rule for a two-sensor system with correlated noise. Their findings show that as the correlation between the sensors' observations increases, the optimal detection scheme cannot use single-interval decision regions at both sensors. In fact, the optimal scheme, if present, would be that either one sensor uses a single-interval decision region and the other sensor's observation is ignored, or both sensors use non-single-interval decision regions and neither sensor is ignored. Furthermore, it was shown in [9] that finding the optimal decision rule at the fusion center requires complete knowledge of the observation statistics.
In Section 2, we introduce the problem of detection under correlated observations. We propose a modified generalized likelihood ratio test (mGLRT) as a test implemented at a fusion-center receiving correlated observations. We then show how the mGLRT could be applied in censoring sensor networks. In Section 3, we evaluate the performance of the mGLRT through simulations. We consider two examples, a two-sensor network, and an eight-sensor network. We then find when the mGLRT has a performance similar to that of the optimal centralized test. In Section 4 we consider an example with real data.
2. Correlated Observations and the mGLRT
In wireless sensor networks used for detection applications, sensors communicate to detect a certain phenomenon. As mentioned earlier, the sensor observations are sent to a fusion center for decision making. The observations received at the fusion center may have a certain degree of correlation depending on the nature of the communication links between the sensors and the fusion center and the sources of signal and noise. Correlated noise is encountered in different communication scenarios such as wireless communication in fading channels. In the following discussion, we consider the problem of detection using censoring sensors under correlated noise. We introduce the problem by considering a simple sensor network consisting of two sensors communicating to a fusion center.
Consider a decentralized detection system consisting of two sensors sending their censored observations to a fusion center in which the final decision is made. The optimal fusion rule in the NP sense would be one that solves the following optimization problem:

where  is the probability of detection,
is the probability of detection,  is the probability of false alarm,
is the probability of false alarm,  is the conditional probability under
is the conditional probability under  ,
,  ,
,  is
is  (first sensor censors, second sensor sends),
(first sensor censors, second sensor sends),  is
is  (first sensor sends, second sensor censors),
(first sensor sends, second sensor censors),  is
is  (first sensor sends, second sensor sends), and
(first sensor sends, second sensor sends), and  is the fusion center's decision-rule threshold.
is the fusion center's decision-rule threshold.
Finding the optimal solution requires joint optimization for the censoring and the fusion center decision thresholds even with the assumption of independence across sensor observations. With the independence assumption removed, finding the optimal decision rule becomes intractable for the original decentralized detection problem [1, 6–8]. For a two-sensor system, censoring converts the simple binary hypothesis problem to a composite hypothesis problem in which we get four different sensor-output combinations under each hypothesis. These combinations are

where 
 (
( ,
, ) is the received data at the fusion center from sensor 1 and sensor 2, respectively. When the sensor censors its observation, the received data at the fusion-center will be zero.
) is the received data at the fusion center from sensor 1 and sensor 2, respectively. When the sensor censors its observation, the received data at the fusion-center will be zero.  and
and  are the target absent and the target present hypotheses, respectively.
are the target absent and the target present hypotheses, respectively.
The optimal NP test in such a case is a uniformly most powerful (UMP) test. However, the UMP test does not exist in this case because the likelihood ratio between the pair of observations depends on which one of the four different sensor-output combinations was received at the fusion center.
When the UMP test fails, a common practice in solving composite hypothesis problems is to apply a generalized likelihood ratio test (GLRT) which is known to give a performance close to the optimal rule in a wide range of detection problems when the optimal rule is hard to find [10]. The GLRT uses the following likelihood ratio test (LRT) for the case of two sensors:

where  ,
,  , is the set of all possible parameters (
, is the set of all possible parameters ( ) under hyposthesis
) under hyposthesis  . The GLRT uses the probability distribution that corresponds to the parameter (
. The GLRT uses the probability distribution that corresponds to the parameter ( ) with the highest posterior probability based on the observations in the LRT. A modified generalized likelihood ratio test (mGLRT) proposed here uses the following likelihood ratio for decision:
) with the highest posterior probability based on the observations in the LRT. A modified generalized likelihood ratio test (mGLRT) proposed here uses the following likelihood ratio for decision:

If none of the sensors' observations are censored, then the optimal NP test in the centralized case is applied. However, if observations get censored, then the ML estimate of each censored observation under both hypotheses is used in the LRT.
For a composite hypothesis-testing problem, the generalized likelihood ratio test uses the probability density function (pdf) of the state of nature with the highest posterior probability based on the observations under the two hypotheses in the final likelihood ratio. We use the mGLRT to estimate the values of the censored observations under both hypotheses. The use of mGLRT in the censoring sensors scenario will be illustrated for a two-sensor network. The generalization to an N-sensor network will then be considered. The following assumptions are made throughout the discussion.
-
(i)
The sensors censor their observations; that is, they either send their complete observations to a fusion center or send nothing.
-
(ii)
The sensors communicate with the fusion center through an ideal noise-free channel.
-
(iii)
The noise accompanied with the sensors' observations is Gaussian. Therefore, the notions of statistical correlation and dependence will be used interchangeably [11].
-
(iv)
The fusion center knows the statistics of the sensors' observations.
-
(v)
The covariance matrix of the sensors' observations is positive definite.
-
(vi)
If all sensors' observations are censored, then decide
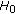 .
.
2.1. A Two-Sensor Network
To demonstrate how the mGLRT can be applied to a censoring sensor network, we begin with a simple two-sensor network. Consider the problem of detecting a mean-shift in Gaussian noise using a censoring two-sensor network. In detection-theory terminology, the problem can be expressed as  versus
versus  where the covariance matrix
where the covariance matrix

is assumed to be positive definite and  . The joint probability density function of the sensor observations is
. The joint probability density function of the sensor observations is

where  ,
,  , and
, and  are sensor observations.
are sensor observations.
To limit our attention to finding the fusion-center decision rule, the communication-rate constraints are assumed to be identical across the sensors, and so  for each sensor. We found experimentally that assigning an equal communication-rate constraint among the sensors performs best. This agrees with the finding in [12] for the statistically independent observations case. When one of the sensors sends its observation to the fusion center and the other does not, the censored observation could be estimated based on the correlation information. For example, if sensor 1 censors while sensor 2 sends, the fusion center could estimate the value of
for each sensor. We found experimentally that assigning an equal communication-rate constraint among the sensors performs best. This agrees with the finding in [12] for the statistically independent observations case. When one of the sensors sends its observation to the fusion center and the other does not, the censored observation could be estimated based on the correlation information. For example, if sensor 1 censors while sensor 2 sends, the fusion center could estimate the value of  using maximum likelihood (ML) estimation based on
using maximum likelihood (ML) estimation based on  under each hypothesis:
under each hypothesis:

where  is the joint pdf of the observations under
is the joint pdf of the observations under  .
.
Let

with  . Applying (7) results in
. Applying (7) results in

The likelihood ratio of the censored and uncensored observations at the fusion center is

which can be expressed as a function of  alone
alone

which can easily be simplified to

So, by calculating the inverse of the covariance matrix and estimating the mean of the observations,  can be estimated based on the observation
can be estimated based on the observation  .
.
2.2. Applying mGLRT to an N-Sensor System
In the previous discussion, we considered applying the mGLRT to a system consisting of two sensors communicating with a fusion center. The mGLRT can be easily generalized to N sensors using the same mathematical formulation. Consider a system with N sensors that detect the presence of a target under correlated Gaussian noise. Let
-
(i)
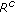 be the set of indices of the sensors that censored their observations,
be the set of indices of the sensors that censored their observations, -
(ii)
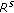 be the set of indices of the sensors that sent their complete observations to the fusion center,
be the set of indices of the sensors that sent their complete observations to the fusion center, -
(iii)
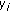 be the observation of the
be the observation of the  th sensor,
th sensor, -
(iv)
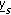 be the vector containing the uncensored observations.
be the vector containing the uncensored observations.
The fusion center will have  observations and
observations and  . Using ML estimation, the fusion center can estimate the censored observations based on the received observations and the knowledge of the sensors' observation statistics (covariance matrix,
. Using ML estimation, the fusion center can estimate the censored observations based on the received observations and the knowledge of the sensors' observation statistics (covariance matrix,  , and mean of the observations,
, and mean of the observations,  ). Since the observations are assumed to be Gaussian, we need to estimate the censored observations such that they minimize the exponent, or equivalently maximize the negative of the exponent, of the joint probability density of the sensors' observations under each hypothesis. This is done by solving the following two optimization problems.
). Since the observations are assumed to be Gaussian, we need to estimate the censored observations such that they minimize the exponent, or equivalently maximize the negative of the exponent, of the joint probability density of the sensors' observations under each hypothesis. This is done by solving the following two optimization problems.
Problem 1 (under  ).
).
We have

such that  .
.
Problem 2 (under  ).
).
We have

such that  ,
,  , where
, where  is the censoring threshold for the
is the censoring threshold for the  th sensor.
th sensor.
The censoring interval of the  th sensor is assumed to be
th sensor is assumed to be  . Again, the communication-rate constraints are chosen to be identical across all sensors. The results in [2] state that choosing the censoring interval to be a single interval does not reduce the probability of detection. The choice of
. Again, the communication-rate constraints are chosen to be identical across all sensors. The results in [2] state that choosing the censoring interval to be a single interval does not reduce the probability of detection. The choice of  and
and  depends on the nature of correlation between the observations. For observations with positive correlations and a positive mean, the negative observations are considered uninformative, and therefore
depends on the nature of correlation between the observations. For observations with positive correlations and a positive mean, the negative observations are considered uninformative, and therefore  is chosen to be
is chosen to be  .
.  is then found based on the communication rate constraint imposed on each sensor. When the observations are negatively correlated, the negative observations may be informative; therefore, the censoring intervals should be chosen differently [13].
is then found based on the communication rate constraint imposed on each sensor. When the observations are negatively correlated, the negative observations may be informative; therefore, the censoring intervals should be chosen differently [13].
The optimization problems under consideration are convex because the equations to be maximized are quadratic. Also, the set over which the optimization is carried out is convex because the censoring intervals are continuous in  . The solution of those problems gives us an estimate of the censored observations. The objective function of Problem 1 can be rewritten as
. The solution of those problems gives us an estimate of the censored observations. The objective function of Problem 1 can be rewritten as

where  , and for Problem 2
, and for Problem 2

The solution to Problem 1 is

and to Problem 2 is

where
-
(i)
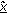 ,
,  are vectors with elements
are vectors with elements (19)
(19)and
 is the element in the
is the element in the  th row and
th row and 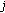 th column of
th column of 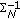 (inverse of the covariance matrix).
(inverse of the covariance matrix). -
(ii)
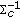 is an
is an 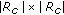 matrix obtained by eliminating the elements in
matrix obtained by eliminating the elements in 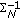 that are related to the uncensored observations.
that are related to the uncensored observations.
After estimating the censored observations under the two hypotheses, the values of the received observations  and the estimated observations under both hypotheses
and the estimated observations under both hypotheses  are plugged into a regular LRT at the fusion center, so
are plugged into a regular LRT at the fusion center, so

3. Performance Evaluation of the mGLRT through Simulations
Analytically comparing mGLRT to the optimal independent test is difficult. Therefore, in this section, we compare the proposed mGLRT to the optimal independent test through simulations. Two sensor-network scenarios will be considered, a two-sensor network and a network consisting of eight sensors. The results are obtained using Monte Carlo (MC) simulations. Table 1 shows the required number of trials for each figure. The second column shows the number of points per MC trial. At each point, a value is obtained on the graph.
Decentralized detection has a suboptimal performance when compared to centralized detection, because in centralized detection all the data are available at one location for decision making; therefore, the performance of the centralized detector is an upper bound on the decentralized detection performance. Consequently, when evaluating a decentralized detection scheme, our comparison criteria will be based on the difference between the centralized detection performance and the performance of the scheme under consideration. We assume the following about the fusion center in the centralized detection:
-
(i)
complete observations are available at the fusion center with no censoring or quantization.
-
(ii)
the fusion center has complete knowledge of the correlation structure between the observations.
3.1. Two-Sensor Network
In the following simulations, the performance of the mGLRT is compared to the optimal independent test for a two-sensor network that communicates to a fusion center. The sensors receive Gaussian observations that have a certain correlation structure.
As discussed earlier, the mGLRT test exploits the correlation information with a slight increase in computations compared to the optimal independent test derived in [3, 4]. Therefore, we expect the mGLRT to have a better performance compared to the optimal independent test when the observations are significantly correlated. The results of our simulations match the expectation. Figure 2 shows the performance of the mGLRT compared to the optimal independent test in the case of correlated observations for different values of signal amplitudes. The figure shows that there is a slight degradation in performance when using the mGLRT in a censoring environment compared to our performance benchmark. This degradation in performance is sacrificed to save energy in the sensors via censoring. It is worth noting that for low probabilities of false alarm, there is essentially no loss in performance due to using censoring with the mGLRT.
The performance of the mGLRT compared to the optimal independent test should vary depending on the degree of correlation between the sensor observations. The reason is that the fusion center using the mGLRT uses the correlation information and thus gets better performance, unlike the optimal independent test which assumes that the sensor observations are independent. To examine the effect of correlation, we define a correlation index  that captures the degree of correlation:
that captures the degree of correlation:

Figure 3 shows that as the sensor observations become more correlated with unequal variance (i.e., the diagonal elements in the covariance matrix are not equal), the mGLRT performs considerably better than the optimal independent test and does not differ much from the ideal centralized detector. The optimal independent test has a better performance than the mGLRT when  is in the vicinity of 0 (i.e., closer to the independent case), since it is optimal. Also, in the case of equal variance, the performance of the optimal independent test is close to that of the ideal centralized detector.
is in the vicinity of 0 (i.e., closer to the independent case), since it is optimal. Also, in the case of equal variance, the performance of the optimal independent test is close to that of the ideal centralized detector.
As seen in Figure 3, the structure of the correlation matrix plays a role in the performance of the mGLRT compared to the optimal independent test. Figure 4 shows that as the diagonal elements of the correlation matrix (variance of each sensor's observation) get close to each other, the performance of the mGLRT degrades until it matches the optimal independent test when the variance of the sensor observations is equal. However, as the diagonal elements of the covariance matrix stray from each other, the mGLRT performs better.
Based on the observations from Figures 3 and 4, we conclude that when the sensor observations are highly correlated with unequal variances the mGLRT performs much better than the optimal independent test. When the variances are equal and the sensor observations are highly correlated, either both sensors get the same reading, which is equivalent to a one-sensor observation, or both sensors do not get any. Therefore, the performance of the mGLRT degrades since the fusion-center receives less information. Also, the optimal independent test appears to be optimal for correlated observations when the correlation matrix is symmetric. Since the optimal independent rule partitions the observation space into two continuous parts via the censoring threshold, the result obtained here agrees with Corollary 1 in [14] which states that for a two-sensor system with  ,
,  , and nonnegative correlation, an optimal solution exists in which both quantizers use the same contiguous partition of the observation space.
, and nonnegative correlation, an optimal solution exists in which both quantizers use the same contiguous partition of the observation space.
The performance loss due to using the optimal independent test is higher compared to the mGLRT as the correlation increases. However, when the sensors' observations are of equal variance and all observations are highly correlated, the performance of the optimal independent test matches that of the mGLRT. The reader is referred to [13] for a more thorough comparison between the mGLRT and the optimal independent test.
3.2. Eight-Sensor Network
In the following simulations, the performance of the mGLRT is compared to the optimal independent test for an eight-sensor network that communicates to a fusion center with the following assumptions.
-
(i)
The sensors are placed as shown in Figure 5.
-
(ii)
The amplitude of the signal emitted by the source to be detected decreases as
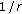 , where
, where  is the distance from the source to the sensor.
is the distance from the source to the sensor. -
(iii)
The observations of the sensors contained in the circle and the square are highly correlated among their peers in the same group; whereas the sensors in the circle are weakly correlated with the sensors in the square.
Figure 6 shows the performance of the mGLRT compared to the optimal independent test and our performance benchmark for the system described above. The figure shows that the mGLRT performs better even when the sensors' observations are of equal variance. Moreover, the ideal centralized detection performs slightly better than the mGLRT at low false-alarm probabilities. Because of censoring, the mGLRT and the optimal independent test could not get to the point where  . This agrees with the results in [3].
. This agrees with the results in [3].
The performance of the mGLRT compared to the optimal independent and centralized tests depends on the communication-rate constraint. As the communication-rate constraint increases, the mGLRT should get closer in performance to the centralized test because they both have similar structure. Figure 7 shows a comparison between the mGLRT and the optimal independent test as the communication-rate constraint changes. The optimal independent test does not take advantage from increasing the communication rate constraint beyond  .
.
4. A Real-Life Application
The performance analysis carried out for the detection tests so far was based on pure simulations. We will now consider a real-world detection problem from the work in [15], where the presence of a frog is to be detected using sound signals collected from an array of microphones placed as shown in Figure 8. For our censoring setup, the sensors (microphone and a transmitter) are assumed to have a communication-rate constraint of 0.33; that is, the sensors will communicate at most one-third of the time when the frog is not active. The signals collected from the microphones are shown in Figure 9. The spikes represent the call of a frog.
To apply the mGLRT, we assume that the noise is Gaussian,  , where
, where  is known and obtained by calculating the correlation between the different microphone signals during an interval when the frog is not calling. For the signals shown in Figure 9,
is known and obtained by calculating the correlation between the different microphone signals during an interval when the frog is not calling. For the signals shown in Figure 9,  has both negative and positive entries. Figure 10 shows the performance of the mGLRT compared to the optimal centralized test. The performance of the mGLRT is almost similar to that of the optimal centralized test while saving energy through censoring. On the other hand, using the optimal independent test results in a degradation in performance especially for low false alarm probabilities.
has both negative and positive entries. Figure 10 shows the performance of the mGLRT compared to the optimal centralized test. The performance of the mGLRT is almost similar to that of the optimal centralized test while saving energy through censoring. On the other hand, using the optimal independent test results in a degradation in performance especially for low false alarm probabilities.
5. Conclusion
A modified GLRT provides a simple and well-performing method for decentralized detection with censoring sensors in correlated noise. Our proposed mGLRT generally performs better than the optimal independent test when the sensor observations are significantly correlated. In our analysis, we showed where the mGLRT could be used while preserving performance and saving energy.
The mGLRT uses the knowledge of correlation between sensor observations to estimate the censored values at the fusion center. Depending on the degree of correlation between the sensors' observations and the variance of the noise affecting the sensors, the performance of the mGLRT varies when compared to the optimal independent test. The mGLRT out-performs the optimal independent test the most when the sensors' observations are highly correlated and the variances of the sensors' observations are not equal. Interestingly, when the sensors' observations are of equal variance and all observations are highly correlated, the performance of the optimal independent test matches that of the mGLRT.
Allowing sensors to censor in the case when the null hypothesis is more likely to occur prolongs the lifetime of battery-powered sensors by saving energy while sacrificing some of the system's performance. Our simulations showed that for a wide range of values for the correlation indices and variance ratios, the degradation in performance when using the mGLRT with censoring is very low. Moreover, as the variance of the observations increases, the mGLRT gets closer in performance to the optimal centralized test.
In a scenario where the fusion center could estimate the covariance matrix of the sensors' observations, the fusion center could choose between either using the optimal independent test or resorting to the mGLRT. If the observations are statistically independent, the fusion center could save on computations by using the optimal independent test. However, if the mGLRT is used all the time, a slight degradation in performance will be experienced in the following two cases.
-
(i)
The sensors' observations are independent.
-
(ii)
The sensors' observations have equal variance and the correlation among them is equal.
References
Tenney RR, Sandell NR Jr.: Detection with distributed sensors. IEEE Transactions on Aerospace and Electronic Systems 1981, 17(4):501-510.
Rago C, Willett P, Bar-Shalom Y: Censoring sensors: a low-communication-rate scheme for distributed detection. IEEE Transactions on Aerospace and Electronic Systems 1996, 32(2):554-568.
Appadwedula S, Veeravalli V, Jones D: Robust and locally-optimum decentralized detection with censoring sensors. Proceedings of the 5th International Conference on Information Fusion, 2002 1: 56-63.
Appadwedula S, Veeravalli VV, Jones DL: Decentralized detection with censoring sensors. IEEE Transactions on Signal Processing 2008, 56(4):1362-1373.
Aalo V, Viswanathou R: On distributed detection with correlated sensors: two examples. IEEE Transactions on Aerospace and Electronic Systems 1989, 25(3):414-421. 10.1109/7.30797
Blum RS, Kassam SA: Optimum distributed detection of weak signals in dependent sensors. IEEE Transactions on Information Theory 1992, 38(3):1066-1079. 10.1109/18.135646
Drakopoulos E, Lee C-C: Optimum multisensor fusion of correlated local decisions. IEEE Transactions on Aerospace and Electronic Systems 1991, 27(4):593-606. 10.1109/7.85032
Willett P, Swaszek PF, Blum RS: The good, bad, and ugly: distributed detection of a known signal in dependent Gaussian noise. IEEE Transactions on Signal Processing 2000, 48(12):3266-3279. 10.1109/78.886990
Unnikrishnan J, Veeravalli V: Decentralized detection with correlated observations. Proceedings of the 41st Asilomar Conference on Signals, Systems and Computers, November 2007 381-385.
Van Trees HL: Detection, Estimation, and Modulation Theory. 1st edition. Wiley-Interscience, New York, NY, USA; 2001.
Hajek B: An exploration of random processes for engineers. January 2009.http://www.ifp.illinois.edu/~hajek/Papers/randomprocJan09.pdf
Appadwedula S: Energy-efficient sensor networks for detection applications, Ph.D. dissertation. University of Illinois, Urbana, Ill, USA; 2003.
Abu-Romeh A: Decentralized detection with censoring sensors and correlated observations using a modified generalized likelihood ratio test, M.S. thesis. University of Illinois, Urbana, Ill, USA; 2009.
Chen P-N, Papamarcou : Likelihood ratio partitions for distributed signal detection in correlated Gaussian noise. Proceedings of the IEEE International Symposium on Information Theory, 1995 118.
Jones DL, Ratnam R: Dynamical interactions in a green treefrog chorus. Journal of the Acoustical Society of America 2009, 126(4):2270.
Acknowledgments
This work was partially supported by the Gigascale Systems Research Center and the Multiscale Systems Center, funded under the Focus Center Research Program (FCRP), a Semiconductor Research Corporation program.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abu-Romeh, A.S., Jones, D.L. Decentralized Detection in Censoring Sensor Networks under Correlated Observations. EURASIP J. Adv. Signal Process. 2010, 838921 (2010). https://doi.org/10.1155/2010/838921
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/838921

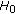 .
.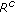 be the set of indices of the sensors that censored their observations,
be the set of indices of the sensors that censored their observations,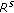 be the set of indices of the sensors that sent their complete observations to the fusion center,
be the set of indices of the sensors that sent their complete observations to the fusion center,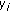 be the observation of the
be the observation of the  th sensor,
th sensor,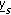 be the vector containing the uncensored observations.
be the vector containing the uncensored observations.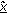 ,
,  are vectors with elements
are vectors with elements
 is the element in the
is the element in the  th row and
th row and 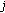 th column of
th column of 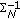 (inverse of the covariance matrix).
(inverse of the covariance matrix).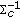 is an
is an 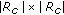 matrix obtained by eliminating the elements in
matrix obtained by eliminating the elements in 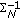 that are related to the uncensored observations.
that are related to the uncensored observations.
 ,
,  = 0. 75, and different signal amplitudes (
= 0. 75, and different signal amplitudes ( ).
).
 with:
with:  (unequal variance),
(unequal variance),  (equal variance).
(equal variance).
 as the variances of the sensors become closer to each other for
as the variances of the sensors become closer to each other for  .
.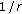 , where
, where  is the distance from the source to the sensor.
is the distance from the source to the sensor.

 for sensors in the same set,
for sensors in the same set,  for sensors in different sets. The communication rate constraint for each sensor is
for sensors in different sets. The communication rate constraint for each sensor is  = 0.375.
= 0.375.
 for the eight-sensor example with
for the eight-sensor example with
 for sensors in the same set,
for sensors in the same set,
 for sensors in different sets.
for sensors in different sets.


