- Research Article
- Open access
- Published:
Vector-Sensor Array Processing for Polarization Parameters and DOA Estimation
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 850265 (2010)
Abstract
This paper presents a method allowing a complete characterization of wave signals received on a vector-sensor array. The proposed technique is based on wavefields separation processing and on estimation of fundamental waves attributes as the state of polarization state and the direction of arrival. Estimation of these attributes is an important step in data processing for a wide range of applications where vector sensor antennas technology is involved such as seismic processing, electromagnetic fields studies, and telecommunications. Compared to the classic techniques, the proposed method is based on computation of multicomponent wideband spectral matrices which enable to take into account all information given by the vector sensor array structures and thus provide a complete characterization of a larger number of sources.
1. Introduction
Over the past decade, the use of vector-sensor array (VSA) technology for source localization has significantly increased allowing a better characterization of the recorded phenomena in a wide range of applications (e.g., acoustics, electromagnetism, radar, sonar, geophysics, etc.) [1–5]. For instance in seismic acquisition case, vector sensors are nowadays widely used, allowing a better characterization of the layers thanks to the state of polarization dimension added to detection process. With a vector sensor, we can have access to the particle-displacement vector that describes the particle motion in 3D at a given point in space. As the state of polarization is wavefield dependent, it can be used as an essential attribute to separate waves in addition to their different DOAs. To resume, multicomponent acquisitions provide more detailed information on the recorded wavefield and VSA-recorded signals allow the estimation of the directions of arrival (DOA) and the polarizations of multiple waves (or sources) impinging the array. In the case of elastic and acoustic seismic surveys, the VSA-recorded signals are a mixture of various wave types (body waves, surface waves, converted waves, multiples, noise, etc.). Combined multicomponent acquisition and multicomponent processing and analysis provide better wave characterizations and enhance the imaging resolution of geological features. In order to perform the characterization of each wave, separation of interfering wavefields is a crucial step. In the case of multicomponent sensor arrays, methods of filtering, of source localization, and of polarization estimation have already been developed for acoustics and electromagnetic sources. In the last decade, many array processing techniques for source localization and polarization estimation using vector sensors have been developed, mainly in electromagnetics. Nehorai and Paldi [1] proposed the Cramer-Rao bound and the vector cross-product DOA. Li and Compton Jr [3] developed the ESPRIT algorithm for a vector-sensor array. MUSIC-based algorithms were also proposed by Wong and Zoltowski [6–8], who also developed vector-sensors versions of ESPRIT [9–13]. These approaches represent a highly popular subspace-based parameter estimation method and use matrix techniques directly derived from scalar-sensor array processing. Such a method is based on the long-vector approach, consisting in the concatenation of all components of the vector-sensor array in a long vector [9].
The originality of our method consists in keeping multidimensional structures of data organization for processing. These structures are more adapted to the nature of seismic polarized signals, allowing data organization closer to its multimodal intrinsic structure. This paper presents a novel subspace separation method performing wavefields separation. This method issued from the Multicomponent Wideband Spectral Matrix Filtering (MWSMF) technique [14, 15] is a subspace separation algorithm derived from the classic spectral matrix filtering presented in [16, 17]. After a separation step where each wavefield has been isolated, we propose polarization and DOA estimations for each separated wavefield that takes all frequencies and all components into account. The algorithm treats the various components as a whole rather than individually. In Section 2, we summarize the noise filtering and wavefields separation principles. In Sections 3 and 4, we present the technique using the estimated multicomponent wideband spectral matrices of sources leading to the estimations of the polarization and of the DOA parameters for each wavefield. Finally in Section 5, we present the performances of the algorithm on several simulated 2C-datasets.
2. Noise Filtering and Wavefield Separation
In this section, the proposed subspace separation technique based on Multicomponent Wideband Spectral Matrix Filtering (MWSMF) is briefly explained (for more details, the reader might refer to [14, 15]).
2.1. Model Formulation and Hypothesis
Let us consider an uniform linear array composed of  omnidirectional sensors uniformly spaced by distance
omnidirectional sensors uniformly spaced by distance  and receiving
and receiving  waves with
waves with  . A convolutive model of seismic signal was first suggested by Robinson [18] and, using the superposition principle, the signal
. A convolutive model of seismic signal was first suggested by Robinson [18] and, using the superposition principle, the signal  recorded on sensor
recorded on sensor  is a linear combination of the
is a linear combination of the  waves received on the array added with noise
waves received on the array added with noise  . Waves have been propagated through a medium and could have been attenuated, time delayed, or phase shifted. The signal
. Waves have been propagated through a medium and could have been attenuated, time delayed, or phase shifted. The signal  recording all wavefieds can be expressed as
recording all wavefieds can be expressed as

with
-
(i)
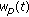 , the waveform signal emitted by a source
, the waveform signal emitted by a source 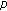 (or a wavefied
(or a wavefied 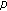 ),
), -
(ii)
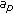 , a random amplitude of the source
, a random amplitude of the source  ,
, -
(iii)
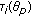 , a time propagation between source
, a time propagation between source 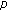 and sensor depending of
and sensor depending of  (the direction-of-arrival (DOA) of source
(the direction-of-arrival (DOA) of source 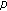 ),
), -
(iv)
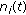 , a random noise supposed to be additive, temporally and spatially white, uncorrelated with the sources, nonpolarized and with a power spectral density given by
, a random noise supposed to be additive, temporally and spatially white, uncorrelated with the sources, nonpolarized and with a power spectral density given by 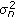 .
.
In frequential domain, the problem can be divided into a set of instantaneous mixtures of signals as

with 
 and
and  , respectively, the Fourier transform of
, respectively, the Fourier transform of  ,
,  and
and  . The time delay
. The time delay  can be expressed as summation of two terms
can be expressed as summation of two terms

with  the time of propagation between the source and a referenced sensor (classically, the first sensor is used as reference) also called offset.
the time of propagation between the source and a referenced sensor (classically, the first sensor is used as reference) also called offset.  is the time of propagation between the reference and sensor
is the time of propagation between the reference and sensor  depending of the DOA (
depending of the DOA ( ) of source
) of source  as
as

where  characterizes the apparent wave velocity and
characterizes the apparent wave velocity and  the distance between two adjacent sensors.
the distance between two adjacent sensors.
In matrix formulation, (2) can be written as

with
-
(i)
 , a vector of size
, a vector of size 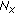 describing signals recorded on array at frequency bin
describing signals recorded on array at frequency bin 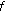
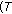 stands transposition operator),
stands transposition operator), -
(ii)
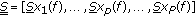 , a matrix of size
, a matrix of size 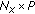 whose columns are steering vectors describing the propagation of each wave with
whose columns are steering vectors describing the propagation of each wave with 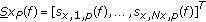 and
and 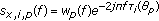 ,
, -
(iii)
 , a vector of size
, a vector of size 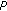 which contains the random amplitudes of the waves,
which contains the random amplitudes of the waves, -
(iv)
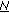 is a vector of size
is a vector of size 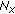 which corresponds to the additive noise.
which corresponds to the additive noise.
In case of multicomponent acquisition with vector sensor array, seismic data depend on three parameters: time ( samples), distance (
samples), distance ( sensors), and number of components (
sensors), and number of components ( components). These components, recording signals in three directions as
components). These components, recording signals in three directions as  (for in-line axis),
(for in-line axis),  (for cross-line axis), and
(for cross-line axis), and  for vertical axis, allow to express the state of polarization of the different wavefields.
for vertical axis, allow to express the state of polarization of the different wavefields.
On component  we can write the recorded signal as
we can write the recorded signal as

where  and
and  are, respectively, the amplitude ratio and the phase-shift between components
are, respectively, the amplitude ratio and the phase-shift between components  and
and  characterizing polarization parameters for a source
characterizing polarization parameters for a source  .
.
In time domain, dataset recorded on a vector array of  sensors (during
sensors (during  samples) can be expressed as
samples) can be expressed as

In the frequency domain, this dataset is

with  the number of frequency bins. To simplify notations, we will consider the case of 2-component sensors (
the number of frequency bins. To simplify notations, we will consider the case of 2-component sensors ( and
and  so
so  ). Nevertheless, proposed method can be used for higher number of components (3, 4, 6,
). Nevertheless, proposed method can be used for higher number of components (3, 4, 6, ). Dataset
). Dataset  is concatenated into a long-vector noted
is concatenated into a long-vector noted  of size
of size  which contains all frequencies of all sensors and all components:
which contains all frequencies of all sensors and all components:

where  and
and  are vectors of size
are vectors of size  which corresponds to the
which corresponds to the  th frequency bin received on the
th frequency bin received on the  sensors, respectively, on components
sensors, respectively, on components  and
and  So the mixture model is rewritten as
So the mixture model is rewritten as

where
-
(i)
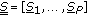 , a matrix of size
, a matrix of size 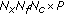 whose columns are steering vectors describing the propagation of the
whose columns are steering vectors describing the propagation of the 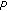 waves along the antenna for all frequencies and all components,
waves along the antenna for all frequencies and all components, -
(ii)
 , a vector of size
, a vector of size 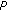 which contains the random amplitudes of the waves,
which contains the random amplitudes of the waves, -
(iii)
 , a vector of size
, a vector of size 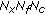 which corresponds to the additive noises supposed to be additive, temporally and spatially white, uncorrelated with sources, nonpolarized and with identical power spectral density
which corresponds to the additive noises supposed to be additive, temporally and spatially white, uncorrelated with sources, nonpolarized and with identical power spectral density  .
.
2.2. Estimation of the Multicomponent Wideband Spectral Matrix
Relations between components and sensors are expressed in the calculation of the Multicomponent Wideband Spectral Matrix (MWSM)  of
of  as
as

with  the expectation operator and
the expectation operator and  the transpose conjugate operation.
the transpose conjugate operation.
To avoid the fact that  is noninvertible (not full rank) and to decorrelate sources from noise and from themselves, we perform smoothing operators to estimate the matrix
is noninvertible (not full rank) and to decorrelate sources from noise and from themselves, we perform smoothing operators to estimate the matrix  . This step is crucial since the effectiveness of filtering depends on this estimation. In practice, mathematical expectation operator
. This step is crucial since the effectiveness of filtering depends on this estimation. In practice, mathematical expectation operator  is an averaging operation, like spatial or frequential smoothing or both of them [19–22]. Objective of these averaging operations is to reduce the influence of terms corresponding to the interactions between different sources in order to uncorrelate them, and to uncorrelate sources and noise, making the inversion of the spectral matrix possible. The spatial smoothing could be done by averaging spatial sub-bands. The uniform linear array with
is an averaging operation, like spatial or frequential smoothing or both of them [19–22]. Objective of these averaging operations is to reduce the influence of terms corresponding to the interactions between different sources in order to uncorrelate them, and to uncorrelate sources and noise, making the inversion of the spectral matrix possible. The spatial smoothing could be done by averaging spatial sub-bands. The uniform linear array with  sensors is subdivided into overlapping subarrays in order to have several identical arrays, which will be used to estimate spectral matrices in order to build a smoothed matrix. Shan et al. [21] have proven that if the number of subarrays is greater than or equal to the number of sources Nw, then the spectral matrix of the sources is nonsingular. However, one assumption is that the wave does not vary rapidly over the number of sensors used in the average, in particular, amplitude fluctuations must be smoothed out. To introduce frequency smoothing, two ways can be performed: either by weighting the autocorrelation and cross-correlation functions (in the time domain) or by averaging frequential sub-bands (in the frequential domain). For a better estimation of the multicomponent wideband spectral matrix, it is suitable to realize jointly spatial and frequential smoothing. For more details on averaging operators, we suggest to read [14].
sensors is subdivided into overlapping subarrays in order to have several identical arrays, which will be used to estimate spectral matrices in order to build a smoothed matrix. Shan et al. [21] have proven that if the number of subarrays is greater than or equal to the number of sources Nw, then the spectral matrix of the sources is nonsingular. However, one assumption is that the wave does not vary rapidly over the number of sensors used in the average, in particular, amplitude fluctuations must be smoothed out. To introduce frequency smoothing, two ways can be performed: either by weighting the autocorrelation and cross-correlation functions (in the time domain) or by averaging frequential sub-bands (in the frequential domain). For a better estimation of the multicomponent wideband spectral matrix, it is suitable to realize jointly spatial and frequential smoothing. For more details on averaging operators, we suggest to read [14].
The multicomponent wideband spectral matrix  is a matrix of dimension
is a matrix of dimension  . The structure of
. The structure of  is presented diagrammatically on Figure 1.
is presented diagrammatically on Figure 1.  and
and  correspond to the single-component wideband spectral matrix for
correspond to the single-component wideband spectral matrix for  and
and  components, respectively. These terms are located on the main diagonal of
components, respectively. These terms are located on the main diagonal of  . The other blocks correspond to the cross-component spectral matrices which contain information relating to the interaction between the components and especially information on polarization. The results obtained by multicomponent wideband matrix filtering are better than the ones obtained applying classical filtering methods on each components for the reason that the former contains more information on the signal especially on polarization Since the multicomponent wideband matrix filtering provides more information on the signal and especially on polarization, better filtering results are obtained rather than results based on classical filtering methods used independently on each component.
. The other blocks correspond to the cross-component spectral matrices which contain information relating to the interaction between the components and especially information on polarization. The results obtained by multicomponent wideband matrix filtering are better than the ones obtained applying classical filtering methods on each components for the reason that the former contains more information on the signal especially on polarization Since the multicomponent wideband matrix filtering provides more information on the signal and especially on polarization, better filtering results are obtained rather than results based on classical filtering methods used independently on each component.
2.3. Estimation of Signal Subspace
Following the assumptions made in Section 2.1,  can be written as
can be written as

After smoothing (averaging) operators step,  is nonsingular (with full rank equals to
is nonsingular (with full rank equals to  in case of free noise dataset or equals to
in case of free noise dataset or equals to  in case of noisy dataset). As columns of
in case of noisy dataset). As columns of  are linearly independent, then the rank of the signal part
are linearly independent, then the rank of the signal part  is
is  So the estimated spectral matrix can be decomposed uniquely using an eigenvalue decomposition as
So the estimated spectral matrix can be decomposed uniquely using an eigenvalue decomposition as

where  and
and  are, respectively, the real eigenvalues, the orthonormal eigenvectors of
are, respectively, the real eigenvalues, the orthonormal eigenvectors of  . Eigenvalues can be arranged in decreasing order (
. Eigenvalues can be arranged in decreasing order ( ). Each eigenvalue
). Each eigenvalue  corresponds to the energy of the data associated with their respective eigenvector
corresponds to the energy of the data associated with their respective eigenvector  . The space generated by the smallest eigenvectors associated to the smallest eigenvalues is referred to as the noise subspace
. The space generated by the smallest eigenvectors associated to the smallest eigenvalues is referred to as the noise subspace  , and its orthogonal complement as the signal subspace
, and its orthogonal complement as the signal subspace  , spanned by the steering vectors of the signal [23]. Estimated Multicomponent Wideband Spectral Matrix can be written as
, spanned by the steering vectors of the signal [23]. Estimated Multicomponent Wideband Spectral Matrix can be written as

After performing efficient average, a decorrelation of waves from themselves and waves from noise is obtained and the spectral matrix is well estimated. Under these conditions, Thirion et al. in [24–26] have shown that the steering vectors are identifiable to the eigenvectors. In fact steering vectors that account several frequencies (wideband context) can easily show to be asymptotically orthogonal. In that case, the spectral matrix corresponding to the  th source (wave) is noted
th source (wave) is noted  and is equal to
and is equal to

2.4. Filtering by Projection onto the Signal Subspace
The filtering step corresponds to an orthogonal projection of the initial data  onto the first
onto the first  eigenvectors corresponding to the signal subspace:
eigenvectors corresponding to the signal subspace:

The projection onto the noise subspace ( ) is obtained by subtraction of
) is obtained by subtraction of  from the initial data
from the initial data

The final steps consist of rearranging the long-vectors  and
and  in its initial form and computing an inverse Fourier transform in order to come back to the time-distance-component domain.
in its initial form and computing an inverse Fourier transform in order to come back to the time-distance-component domain.
3. Polarization Estimation
3.1. Introduction
After presenting the separation processing part, we propose to find polarization parameters on each separated wavefield. State of polarization analysis is based on the computation of parameters describing the particle movement associated with wave propagation. That movement of the ground induced useful parameters which were first identified by Jolly in 1956 [27], whereas the first attempt to measure this movement was done by Shimshoni and Smith in 1964 [28]. They introduced a successful method of polarization analysis for earthquake data. Many other algorithms were developed subsequently for seismic exploration applications [29–31]. One of the most effective and stable approaches in this regards is the algorithm developed by Flinn [32, 33] using the covariance matrix of the data. In the following part, we compare our proposed method (based on MWSM) with Flinn's algorithm.
3.2. Proposed Method
We propose to use the spectral matrices of rank one (linked to each  th source) obtained from the decomposition of the multicomponent wideband spectral matrix (see (15)). Thus, once a wavefield has been separated from other waves and from noise, we show that its polarization parameters can be characterized from the matrix elements of wavefield,
th source) obtained from the decomposition of the multicomponent wideband spectral matrix (see (15)). Thus, once a wavefield has been separated from other waves and from noise, we show that its polarization parameters can be characterized from the matrix elements of wavefield,  . After separation processing, the signal, noted
. After separation processing, the signal, noted  , corresponding to the
, corresponding to the  th source received on component
th source received on component  at frequency
at frequency  and on sensor
and on sensor  can be expressed as
can be expressed as

where  is the time of propagation between the source and the sensor
is the time of propagation between the source and the sensor  (for wave
(for wave  ). For the second component
). For the second component  we obtain
we obtain

The diagonal element of  at the frequency
at the frequency  on the
on the  th sensor which corresponds to the interaction of the
th sensor which corresponds to the interaction of the  component with itself could be expressed by
component with itself could be expressed by

Likewise, the term corresponding to the interaction of Z component with itself is

and finally, the cross-term corresponding to the interaction between component  and
and  could be written as
could be written as

All these terms are located either on the principal diagonal or on the secondary diagonals of the matrix  (see Figure 2). Based on these structures, we deduce estimators for polarization parameters of the
(see Figure 2). Based on these structures, we deduce estimators for polarization parameters of the  th wave on each sensor
th wave on each sensor  at frequency
at frequency  . In fact, polarization parameters
. In fact, polarization parameters  expressed as amplitude ratio between components
expressed as amplitude ratio between components  and
and  and phase shift for wave
and phase shift for wave  can be expressed, respectively, by
can be expressed, respectively, by

Classically, the propagation medium is regarded as isotropic (nondispersive for frequency) so that the polarization parameters are independent of frequency and sensor. But in more realistic context where some dispersion appears, a better estimate of the polarization parameters can thus be obtained by averaging them over a range of frequencies and sensors. However, in order to have a correct estimate, the averaging must be done only on the frequencies belonging to the signal bandwidth ( ). The estimators thus obtained are
). The estimators thus obtained are


with  being the cardinal of
being the cardinal of  .
.
3.3. Comparison between Flinn's Method and Proposed Method Based on MWSM
MWSM's and Flinn's methods are two different approaches for polarization analysis. Flinn's method uses a covariance matrix and proposes a temporal approach on a single trace whereas our proposed method is a frequential approach which can either be on a single trace or on the whole array. In the case studied here, the waves' state of polarization can be considered as constant over distance. Consequently, for a given wave, we can estimate the amplitude ratio and phase shift between the components by carrying out an averaging of the parameters found on each sensor.
To compare Flinn's and our method and to illustrate polarization estimation, we consider the trivial case of a single wave with infinite velocity, received on a 2C-sensors array, whose phase shift  (= 0.4 rad) and amplitude ratio
(= 0.4 rad) and amplitude ratio  (= 0.8) are constant over the array.
(= 0.8) are constant over the array.
Figures 3 and 4 correspond respectively to the Mean Absolute Error (MAE) between the theoretical and the estimated values of phase shift and amplitude ratio for various signal-to-noise ratio (SNR) from  10 dB to 15 dB. The average is done for 500 noisy realizations.
10 dB to 15 dB. The average is done for 500 noisy realizations.
These figures show that for both methods, polarization analysis is very sensitive to noise and thus the estimates are better when SNR increases. We can notice that our MWSM-based method always gives better estimation than the Flinn's method for small SNR.
4. Direction-of-Arrival Estimation
4.1. Proposed Method
Just as we did for polarization state estimation, we propose a DOA estimation method based on the structure of Multicomponent Wideband Spectral Matrix. We call it MW-MUSIC for Multicomponent Wideband-MUSIC as it is an extension of the MUSIC (MUltiple SIgnal Classification) algorithm [34–37]. This method is an extension of the MUSIC algorithm for vector-sensor arrays called LV-MUSIC for Long-Vector MUSIC [1]. The first extensions of MUSIC algorithm to polarized sources were made by Schmidt [34], Ferrara and Parks [38], Wong and Zoltowski [6, 8], and Wong et al. [13]. Algorithms to estimate DOAs of polarized sources in electromagnetism were also proposed in [1, 39, 40]. Our proposed method has the advantage of being able to compute both DOA and offset.
We define two matrices  (
( size) and
size) and  (
( size), containing the eigenvectors corresponding to signal subspace and noise subspace, respectively,
size), containing the eigenvectors corresponding to signal subspace and noise subspace, respectively,

These complex matrices enable us to write MWSM as

with  being a diagonal matrix containing the
being a diagonal matrix containing the  highest eigenvalues. If we multiply (12) on the right by
highest eigenvalues. If we multiply (12) on the right by  , we obtain
, we obtain

By combining (27) and (28) and by using the orthogonality property of the matrices  and
and  , we obtain
, we obtain

which implies:

We can rewrite it as

with  , being the propagation vector corresponding to the wave
, being the propagation vector corresponding to the wave  . Thereafter, we note
. Thereafter, we note  , the matrix corresponding to the projection on noise subspace.
, the matrix corresponding to the projection on noise subspace.
According to relation (31), propagation vectors are orthogonal to noise subspace. Consequently, their projection on  is zero. MW-MUSIC algorithm exploits this idea by carrying out the projection of directional vector
is zero. MW-MUSIC algorithm exploits this idea by carrying out the projection of directional vector  on the estimated noise subspace. This vector models the arrival of a polarized wave of direction
on the estimated noise subspace. This vector models the arrival of a polarized wave of direction  on multicomponent sensors' antenna and is expressed as
on multicomponent sensors' antenna and is expressed as

with

The extended MUSIC functional, calculated by projection of  on the noise subspace is given by
on the noise subspace is given by

The functional allows local maxima for a set of values  and
and  . We use the fact that two parameters
. We use the fact that two parameters  have been already found by the method proposed on Section 3. After this stage, the functional only depends on two parameters,
have been already found by the method proposed on Section 3. After this stage, the functional only depends on two parameters,  the direction of arrival and
the direction of arrival and  the offset, and it will give maximum for values of
the offset, and it will give maximum for values of  corresponding to the sources present in the signal. It is clear that processing will work with lot of efficiency in case of far field sources (waves can be considered as locally plane).
corresponding to the sources present in the signal. It is clear that processing will work with lot of efficiency in case of far field sources (waves can be considered as locally plane).
4.2. Study of Estimator Variance
In this part, we compare variances of various estimators: MUSIC, LV-MUSIC and MW-MUSIC. Mean Square Error (MSE) for DOA estimation is presented for various SNRs (Figure 5). Each point corresponds to an average over 200 realizations. In this case under study, a polarized source is received on an array of 30 2C-sensors. The DOA of the source, expressed in terms of samples of delay between two sensors, is 1 sample. A white Gaussian noise is added to the signal with a SNR from  18 dB to 0 dB. For classical MUSIC algorithm which operates only on one component, we carry out an average of the results obtained from the two components. Figure 5 shows clearly that when we take into account the polarization information and frequential coherency given by the MWSM's structure, statistical performances of the estimator are improved. This induces that MW-MUSIC gives better results rather than Classical-MUSIC algorithm.
18 dB to 0 dB. For classical MUSIC algorithm which operates only on one component, we carry out an average of the results obtained from the two components. Figure 5 shows clearly that when we take into account the polarization information and frequential coherency given by the MWSM's structure, statistical performances of the estimator are improved. This induces that MW-MUSIC gives better results rather than Classical-MUSIC algorithm.
5. Synthetic Examples
Proposed method consisting of wavefield separation followed by polarization and DOA estimation steps is applied on a 2-Components synthetic seismic profile to validate the efficiency of the method. Figure 6 plots two waves received on an array of 24 2C-sensors superimposed by a white gaussian noise (SNR = 4 dB). The fastest wave, (called wave 1) has a linear polarization parameter (
dB). The fastest wave, (called wave 1) has a linear polarization parameter ( and
and  ) and the slowest wave (called wave 2) is characterized by an elliptic polarization (
) and the slowest wave (called wave 2) is characterized by an elliptic polarization ( and
and  ).
).
5.1. Wavefield Separation
The first step of proposed method consists of separating the two waves and the noise using the multicomponent wideband spectral matrix filtering technique (see Section 2). Estimation of the Multicomponent Wideband Spectral Matrix (MWSM) is done using both spatial and frequential smoothing. Its modulus of this matrix is presented in Figure 7. We observe the same structure as in Figure 1 where the large energetic pattern is associated to wave 1 (low frequency content), and smaller energetic pattern to wave 2 (high frequency content). The MWS Matrix is then decomposed using eigenvalue decomposition. Observing the decrease of eigenvalues, we decide to keep the two first eigen sections, corresponding to modeled waves:

Modulus of the Multicomponent Wideband Spectral Matrix of the initial dataset (of size 3072 × 3072 with 3072 = 24 × 64 × 2). Compared with Figure 1, block 1 is  , block 4 is
, block 4 is  and blocks 2 and 3 are
and blocks 2 and 3 are  ,
,  respectively.
respectively.
Figures 8 and 9 show the modulus of  (wave 1) and
(wave 1) and  (wave 2). We can observe from these figures that separation of waves is efficient since patterns are well separated and no energetic interferences appear. Thus, by projecting the initial data on the first eigenvector
(wave 2). We can observe from these figures that separation of waves is efficient since patterns are well separated and no energetic interferences appear. Thus, by projecting the initial data on the first eigenvector  , we obtain the first extracted wavefield (wave 1) (Figure 10) and on the second eigenvector
, we obtain the first extracted wavefield (wave 1) (Figure 10) and on the second eigenvector  , the second extracted wavefield (wave 2) (Figure 11). These two figures clearly show that the noise has been removed and the waves have been well separated.
, the second extracted wavefield (wave 2) (Figure 11). These two figures clearly show that the noise has been removed and the waves have been well separated.
5.2. Polarization Estimation
After separation of waves, the second step consists of making the polarization analysis of the two waves using the matrix elements of  and
and  (see Section 3). As previously presented, in Figure 8 (resp., Figure 9), blocks
(see Section 3). As previously presented, in Figure 8 (resp., Figure 9), blocks  and
and  correspond to wideband spectral matrices of wave 1 (resp., wave 2) on components
correspond to wideband spectral matrices of wave 1 (resp., wave 2) on components  and
and  respectively. We denote them by
respectively. We denote them by  and
and  (resp.,
(resp.,  and
and  ). Blocks
). Blocks  and
and  correspond to the cross-spectral matrices of wave 1 (resp., wave 2) containing the interactions between components
correspond to the cross-spectral matrices of wave 1 (resp., wave 2) containing the interactions between components  and
and  We denote them by
We denote them by  and
and  (resp.,
(resp.,  and
and  ).
).
Figure 12 shows two graphs. The upper plot corresponds to the modulus of diagonals of blocks  and
and  of
of  . It enables to determine the frequency band
. It enables to determine the frequency band  used to estimate the polarization parameters as well as to carry out the estimation of the amplitude ratio
used to estimate the polarization parameters as well as to carry out the estimation of the amplitude ratio  between components
between components  and
and  (see (25)). The bottom graph of Figure 12 shows the phase of blocks
(see (25)). The bottom graph of Figure 12 shows the phase of blocks  and
and  diagonals. It allows to obtain phase shift
diagonals. It allows to obtain phase shift  between components
between components  and
and  (see (25)). In a similar way, it is possible to estimate the polarization parameters of wave 2 by using the principal and secondary diagonals of the spectral matrix
(see (25)). In a similar way, it is possible to estimate the polarization parameters of wave 2 by using the principal and secondary diagonals of the spectral matrix  .
.
The values obtained for the polarization parameters of each wave are summarized in Table 1. The phase shift  estimation results are really satisfactory as we find less than
estimation results are really satisfactory as we find less than  error. The amplitude ratio
error. The amplitude ratio  is also well estimated with a bigger error (
is also well estimated with a bigger error ( ). This can be attributed to the spectral matrix estimation step. Infact, the spatial smoothing used to estimate MWSM might affect the wave amplitudes since smoothing is equivalent to an averaging in distance over a small number of sensors.
). This can be attributed to the spectral matrix estimation step. Infact, the spatial smoothing used to estimate MWSM might affect the wave amplitudes since smoothing is equivalent to an averaging in distance over a small number of sensors.
5.3. DOA Estimation
The last step is the estimation of DOA and offset of each wave (see Section 4). We compute the MW-MUSIC functional for values of the DOA,  , between
, between  with a step of 0.01 and for the offset
with a step of 0.01 and for the offset  , between
, between  with a step of 1. The results obtained are shown in Figure 13. The two main lobes are found at the original values of offsets and DOAs of the two waves samples. Figure 14 corresponds to the cross-sections of the 3D-function (Figure 13) for fixed offsets. The vertical lines show the theoretical values of the DOAs. The estimated values for the DOAs and the offsets are recapitulated in Table 2. One can note that the estimated values are very close to the true values (percentages of error between
with a step of 1. The results obtained are shown in Figure 13. The two main lobes are found at the original values of offsets and DOAs of the two waves samples. Figure 14 corresponds to the cross-sections of the 3D-function (Figure 13) for fixed offsets. The vertical lines show the theoretical values of the DOAs. The estimated values for the DOAs and the offsets are recapitulated in Table 2. One can note that the estimated values are very close to the true values (percentages of error between  and
and  ).
).
5.4. A More Realistic Example
Now, we consider a 2-Component acquisition simulation recording two waves (15). These two waves called  and
and  have shown same spectrum, same offset, same polarisation parameters, and two very close DOAs
have shown same spectrum, same offset, same polarisation parameters, and two very close DOAs  ;
;  . The Signal-to-Noise ratio is estimated at 0 dB (Figure 16).
. The Signal-to-Noise ratio is estimated at 0 dB (Figure 16).
We propose to compare Long Vector-MUSIC and Multi-component Wideband-MUSIC algorithms. We show on Figure 17, that resolution given by MW-MUSIC is better than LV-MUSIC. A full separation, polarisation and DOA's estimation have been also realized on a real seismic example [41].
6. Conclusion
A novel method providing wavefields separation along with an estimation of both the polarization parameters and the directions of arrival was presented. Taking into account the polarization and the widebandness of the signal leads to a better characterization of a greater number of waves ( ) as opposed to the monocomponent array case (
) as opposed to the monocomponent array case ( ). The performance and efficiency of the method was proven using several simulations. Comparison of the wideband matrix filtering method with those of the classic filtering technique has already been done [15] and gave encouraging result for wideband case. We also obtained promising results for DAO estimation using the proposed method which can be attributed to the fact that our method takes into account the entire frequency information and is therefore insensitive to frequency band selection.
). The performance and efficiency of the method was proven using several simulations. Comparison of the wideband matrix filtering method with those of the classic filtering technique has already been done [15] and gave encouraging result for wideband case. We also obtained promising results for DAO estimation using the proposed method which can be attributed to the fact that our method takes into account the entire frequency information and is therefore insensitive to frequency band selection.
References
Nehorai A, Paldi E: Vector-sensor array processing for electromagnetic source localization. IEEE Transactions on Signal Processing 1994, 42(2):376-398. 10.1109/78.275610
Nehorai A, Paldi E: Acoustic vector-sensor array processing. IEEE Transactions on Signal Processing 1994, 42(9):2487-2491.
Li J, Compton RT Jr.: Angle and polarization estimation using ESPRIT with a polarization sensitive array. IEEE Transactions on Antennas and Propagation 1991, 39(9):1376-1383. 10.1109/8.99047
Rahamim D, Tabrikian J, Shavit R: Source localization using vector sensor array in a multipath environment. IEEE Transactions on Signal Processing 2004, 52(11):3096-3103. 10.1109/TSP.2004.836456
Chen H-W, Zhao J-W: Wideband MVDR beamforming for acoustic vector sensor linear array. IEE Proceedings: Radar, Sonar and Navigation 2004, 151(3):158-162. 10.1049/ip-rsn:20040651
Wong KT, Zoltowski MD: Self-initiating MUSIC-based direction finding and polarization estimation in spatio-polarizational beamspace. IEEE Transactions on Antennas and Propagation 2000, 48(8):1235-1245. 10.1109/8.884492
Wong KT, Zoltowski MD: Diversely polarized root-MUSIC for azimuth-elevation angle-of-arrival estimation. Proceedings of the AP-S International Symposium & URSI Radio Science Meeting, July 1996 1352-1355.
Wong KT, Zoltowski MD: Root-MUSIC-based azimuth-elevation angle-of-arrival estimation with uniformly spaced but arbitrarily oriented velocity hydrophones. IEEE Transactions on Signal Processing 1999, 47(12):3250-3260. 10.1109/78.806070
Wong KT, Zoltowski MD: Uni-vector-sensor ESPRIT for multisource azimuth, elevation, and polarization estimation. IEEE Transactions on Antennas and Propagation 1997, 45(10):1467-1474. 10.1109/8.633852
Zoltowski MD, Wong KT: Closed-form eigenstructure-based direction finding using arbitrary but identical subarrays on a sparse uniform Cartesian array grid. IEEE Transactions on Signal Processing 2000, 48(8):2205-2210. 10.1109/78.852001
Zoltowski MD, Wong KT: ESPRIT-based 2-D direction finding with a sparse uniform array of electromagnetic vector sensors. IEEE Transactions on Signal Processing 2000, 48(8):2195-2204. 10.1109/78.852000
Wong KT, Zoltowski MD: Closed-form direction finding and polarization estimation with arbitrarily spaced electromagnetic vector-sensors at unknown locations. IEEE Transactions on Antennas and Propagation 2000, 48(5):671-681. 10.1109/8.855485
Wong KT, Li L, Zoltowski MD: Root-MUSIC-based direction-finding and polarization estimation using diversely polarized possibly collocated antennas. IEEE Antennas and Wireless Propagation Letters 2004, 3(1):129-132.
Paulus C, Mars J, Gounon P: Wideband spectral matrix filtering for multicomponent sensors array. Signal Processing 2005, 85(9):1723-1743. 10.1016/j.sigpro.2005.03.018
Paulus C, Mars JI: New multicomponent filters for geophysical data processing. IEEE Transactions on Geoscience and Remote Sensing 2006, 44(8):2260-2270.
Mermoz H: Imagerie, corrélation et modèles. Annales des Telecommunications 1976, 31(1-2):17-36.
Samson JC: The spectral matrix, eigenvalues, and principal components in the analysis of multichannel geophysical data. Annales Geophysicae 1983, 1(2):115-119.
Robinson EA: Predictive decomposition of time series with application to seismic exploration. Geophysics 1967, 32: 418-484. 10.1190/1.1439873
Rao BD, Hari KVS: Weighted subspace methods and spatial smoothing. Analysis and comparison. IEEE Transactions on Signal Processing 1993, 41(2):788-803. 10.1109/78.193218
Reddi SS: On a spatial smoothing technique for multiple source location. IEEE Transactions on Acoustics, Speech, and Signal Processing 1987, 35(5):709. 10.1109/TASSP.1987.1165190
Shan T, Wax M, Kailath T: On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Transactions on Acoustics, Speech, and Signal Processing 1985, 33(4):806-811. 10.1109/TASSP.1985.1164649
Pillai SU, Kwon BH: Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(1):8-15. 10.1109/29.17496
Wang H, Kaveh M: Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Transactions on Acoustics, Speech, and Signal Processing 1985, 33(4):823-831. 10.1109/TASSP.1985.1164667
Thirion N, Mars JI, Lacoume J-L: Analytical links between steering vectors and eigenvectors. Proceedings of the European Signal Processing Conference (EUSIPCO '96), 1996, Trieste, Italy 81-84.
Thirion N, Lacoume J, Mars J: Resolving power of spectral matrix filtering: a discussion on the links steering vectors /eigenvectors. Proceedings of the 8th IEEE Signal Processing Workshop on Statistical Signal and Array Processing (SSAP '96), June 1996 340-343.
Thirion N, Mars JI, Boelle J-L: Separation of seismic signals: a new concept based on blind algorithm. Proceedings of the European Signal Processing Conference (EUSIPCO '96), 1996, Trieste, Italy 85-88.
Jolly RN: Investigation of shear waves. Geophysics 1956, 21(4):905-938. 10.1190/1.1438310
Shimshoni M, Smith SW:Linear end parabolic
 -p revisited. Geophysics 1964, 29(5):664-671. 10.1190/1.1439402
-p revisited. Geophysics 1964, 29(5):664-671. 10.1190/1.1439402Greenhalgh SA, Mason IM, Mosher CC, Lucas E: Seismic wavefield separation by multicomponent tau-p polarisation filtering. Tectonophysics 1990, 173(1-4):53-61. 10.1016/0040-1951(90)90203-K
Shieh C-S, Herrmann RB: Ground roll: rejection using polarization filters. Geophysics 1990, 55(9):1216-1222. 10.1190/1.1442937
Jackson GM, Mason IM, Greenhalgh SA: Principal component transforms of triaxial recordings by singular value decomposition. Geophysics 1991, 56(4):528-533. 10.1190/1.1443068
Flinn EA: Signal analysis using rectilinearity and direction of particule motion. Proceedings of the IEEE 1965, 56: 1874-1876.
Archambeau CB, Flinn EA: Automated analysis of seismic radiation for source characteristics. Proceedings of the IEEE 1965, 53: 1876-1884.
Schmidt RO: A signal subspace approach to multiple emitter location and spectral estimation, Ph.D. dissertation. Stanford University, Stanford, Calif, USA; 1981.
Schmidt RO: Multiple emitter location and signal parameter estimation. IEEE Transactions on Antennas and Propagation 1986, 34(3):276-280. 10.1109/TAP.1986.1143830
Kaveh M, Barabell AJ: The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise. IEEE Transactions on Acoustics, Speech, and Signal Processing 1986, 34(2):331-341. 10.1109/TASSP.1986.1164815
Stoica P, Nehorai A: MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(5):720-741. 10.1109/29.17564
Ferrara ER Jr., Parks TM: Direction finding with an array of antennas having diverse polarizations. IEEE Transactions on Antennas and Propagation 1983, 31(2):231-236. 10.1109/TAP.1983.1143038
Hua Y: Pencil-MUSIC algorithm for finding two-dimensional angles and polarizations using crossed dipoles. IEEE Transactions on Antennas and Propagation 1993, 41(3):370-376. 10.1109/8.233122
Swindlehurst A, Viberg M: Subspace fitting with diversely polarized antenna arrays. IEEE Transactions on Antennas and Propagation 1993, 41(12):1687-1694. 10.1109/8.273313
Paulus C, Mars JI: Polarization analysis on seismic data after multicomponent wavefield filtering. Proceedings of EAGE/SEG Research Workshop, Multicomponent Seismic—Past, Present and Future, September 2005, Pau, France
Acknowledgments
The authors would like to thank reviewers for interesting remarks and A. A. Khan for improving the language.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Paulus, C., Mars, J.I. Vector-Sensor Array Processing for Polarization Parameters and DOA Estimation. EURASIP J. Adv. Signal Process. 2010, 850265 (2010). https://doi.org/10.1155/2010/850265
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/850265
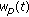 , the waveform signal emitted by a source
, the waveform signal emitted by a source 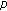 (or a wavefied
(or a wavefied 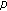 ),
),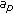 , a random amplitude of the source
, a random amplitude of the source  ,
,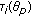 , a time propagation between source
, a time propagation between source 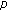 and sensor depending of
and sensor depending of  (the direction-of-arrival (DOA) of source
(the direction-of-arrival (DOA) of source 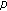 ),
),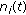 , a random noise supposed to be additive, temporally and spatially white, uncorrelated with the sources, nonpolarized and with a power spectral density given by
, a random noise supposed to be additive, temporally and spatially white, uncorrelated with the sources, nonpolarized and with a power spectral density given by 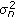 .
. , a vector of size
, a vector of size 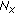 describing signals recorded on array at frequency bin
describing signals recorded on array at frequency bin 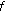
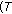 stands transposition operator),
stands transposition operator),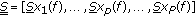 , a matrix of size
, a matrix of size 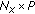 whose columns are steering vectors describing the propagation of each wave with
whose columns are steering vectors describing the propagation of each wave with 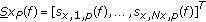 and
and 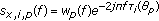 ,
, , a vector of size
, a vector of size 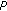 which contains the random amplitudes of the waves,
which contains the random amplitudes of the waves,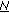 is a vector of size
is a vector of size 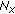 which corresponds to the additive noise.
which corresponds to the additive noise.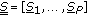 , a matrix of size
, a matrix of size 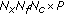 whose columns are steering vectors describing the propagation of the
whose columns are steering vectors describing the propagation of the 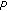 waves along the antenna for all frequencies and all components,
waves along the antenna for all frequencies and all components, , a vector of size
, a vector of size 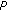 which contains the random amplitudes of the waves,
which contains the random amplitudes of the waves, , a vector of size
, a vector of size 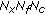 which corresponds to the additive noises supposed to be additive, temporally and spatially white, uncorrelated with sources, nonpolarized and with identical power spectral density
which corresponds to the additive noises supposed to be additive, temporally and spatially white, uncorrelated with sources, nonpolarized and with identical power spectral density  .
.

 , the 2-Component wideband spectral matrix of the wave
, the 2-Component wideband spectral matrix of the wave







 .
.

 .
.








 -p revisited. Geophysics 1964, 29(5):664-671. 10.1190/1.1439402
-p revisited. Geophysics 1964, 29(5):664-671. 10.1190/1.1439402