- Research Article
- Open access
- Published:
Low Complexity MLSE Equalization in Highly Dispersive Rayleigh Fading Channels
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 874874 (2010)
Abstract
A soft output low complexity maximum likelihood sequence estimation (MLSE) equalizer is proposed to equalize M-QAM signals in systems with extremely long memory. The computational complexity of the proposed equalizer is quadratic in the data block length and approximately independent of the channel memory length, due to high parallelism of its underlying Hopfield neural network structure. The superior complexity of the proposed equalizer allows it to equalize signals with hundreds of memory elements at a fraction of the computational cost of conventional optimal equalizer, which has complexity linear in the data block length but exponential in die channel memory length. The proposed equalizer is evaluated in extremely long sparse and dense Rayleigh fading channels for uncoded BPSK and 16-QAM-modulated systems and remarkable performance gains are achieved.
1. Introduction
Multipath propagation in wireless communication systems is a challenge that has enjoyed much attention over the last few decades. This phenomenon, caused by the arrival of multiple delayed copies of the transmitted signal at the receiver, results in intersymbol interference (ISI), severely distorting the transmitted signal at the receiver.
Channel equalization is necessary in the receiver to mitigate the effect of ISI, in order to produce reliable estimates of the transmitted information. In the early 1970s, Forney proposed an optimal equalizer [1] based on the Viterbi algorithm (VA) [2], able to optimally estimate the most likely sequence of transmitted symbols. The VA was proposed a few years before for the optimal decoding of convolutional error-correction codes. Shortly afterward, the BCJR algorithm [3], also known as the maximum a posterior probability (MAP) algorithm, was proposed, able to produce optimal estimates of the transmitted symbols.
The development of an optimal MLSE equalizer was an extraordinary achievement, as it enabled wireless communication system designers to design receivers that can optimally detect a sequence of transmitted symbols, corrupted by ISI, for the first time. Although the Viterbi MLSE algorithm and the MAP algorithm estimate the transmitted information with maximum confidence, their computational complexities are prohibitive, increasing exponentially with an increase in channel memory [4]. Their complexity is  , where
, where  is the data block length,
is the data block length,  is the channel impulse response (CIR) length and
is the channel impulse response (CIR) length and  is the modulation alphabet size. Due to the complexity of optimal equalizer, they are rendered infeasible in communication systems with moderate to large bandwidth. For this reason, communication system designers are forced to use suboptimal equalization algorithms to alleviate the computational strain of optimal equalization algorithms, sacrificing system performance.
is the modulation alphabet size. Due to the complexity of optimal equalizer, they are rendered infeasible in communication systems with moderate to large bandwidth. For this reason, communication system designers are forced to use suboptimal equalization algorithms to alleviate the computational strain of optimal equalization algorithms, sacrificing system performance.
A number of suboptimal equalization algorithms have been considered where optimal equalizers cannot be used due to constrains on the processing power. Although these equalizers allow for decreased computational complexity, their performance is not comparable to that of optimal equalizers. The minimum mean squared error (MMSE) equalizer and the decision feedback equalizer (DFE) [5–7], and variants thereof, are often used in systems where the channel memory is too long for optimal equalizers to be applied [4, 8]. Orthogonal frequency division multiplexing (OFDM) modulation can be used to completely eliminate the effect of multipath on the system performance by exploiting the orthogonality properties of the Fourier matrix and through the use of a cyclic prefix, while maintaining trivial per symbol complexity. OFDM, however, is very susceptible to Doppler shift, suffers from a large peak-to-average power ratio (PAPR), and requires large overhead when the channel delay spread is very long compared to the symbol period [4, 9].
There are a number of communication channels that have extremely long memory. Among these are underwater channels (UAC), magnetic recording channels (MRC), power line channels (PLC), and microwave channels (MWC) [10–13]. In these channels, there may be hundreds of multipath components, leading to severe ISI. Due to the large amount of interfering symbols in these channels, the use of conventional optimal equalization algorithms are infeasible.
In this paper, a low complexity MLSE equalizer, first presented by the authors in [14], (in this paper, the M-QAM HNN MLSE equalizer in [14] is presented in much greater detail. Here, a complete complexity analysis, as well as the performance of the proposed equalizer in sparse channels, are presented) is developed for equalization in M-QAM-modulated systems with extremely long memory. Using the Hopfield neural network (HNN) [15] as foundation, this equalizer has complexity quadratic in the data block length and approximately independent of the channel memory length for practical systems. (In practical systems, the data block length is larger that the channel memory length.) Its complexity is roughly  , where
, where  is the number of iterations performed during equalization and
is the number of iterations performed during equalization and  and
and  are the data block length and CIR length as before. (A complete computational complexity analysis is presented in Section 5) Its superior computational complexity, compared to that of the Viterbi MLSE and MAP algorithms, is due to the high parallelism and high level of interconnection between the neurons of its underlying HNN structure.
are the data block length and CIR length as before. (A complete computational complexity analysis is presented in Section 5) Its superior computational complexity, compared to that of the Viterbi MLSE and MAP algorithms, is due to the high parallelism and high level of interconnection between the neurons of its underlying HNN structure.
This equalizer, henceforth referred to as the HNN MLSE equalizer, iteratively mitigates the effect of ISI, producing near-optimal estimates of the transmitted symbols. The proposed equalizer is evaluated for uncoded BPSK and 16-QAM modulated single-carrier mobile systems with extremely long memory—for (CIRs) of multiple hundreds—where its performance is compared to that of an MMSE equalizer for BPSK modulation. Although there currently exist various variants of the MMSE equalizer in the literature [16–21]—some less computationally complex and others more efficient in terms of performance—the conventional MMSE is nevertheless used in this paper as a benchmark since it is well-known and well-studied. It is shown that the performance of the HNN MLSE equalizer approaches unfaded, zero ISI, matched filter performance as the effective time-diversity due to multipath increases. The performance of the proposed equalizer is also evaluated for sparse channels and it is shown that its performance in sparse channels is superior to its performance in equivalent dense, or nonsparse, channels, (equivalent dense channels will be explained in Section 7) with a negligible computational complexity increase.
It was shown by various authors [22–25] that the problem of MLSE can be solved using the HNN. However, none of the authors applied the equalizer model to systems with extremely long memory in mobile fading channels. Also, none of the authors attempted to develop an HNN-based equalizer for higher order signal constellations. (Only BPSK and QPSK modulation were addressed using short length static channels whereas the proposed equalizer is able to equalize M-QAM signals.) The HNN-based MLSE equalizer was neither evaluated for sparse channels in previous work.
This paper is organized as follows. Section 2 discussed the HNN model, followed by a discussion on the basic principles of MLSE equalization in Section 3. In Section 4, the derivation of the proposed M-QAM HNN MLSE equalizer is discussed, followed by a complete computational complexity analysis of the proposed equalizer in Section 5. Simulation results are presented in Section 6, and conclusions are drawn in Section 7.
2. The Hopfield Neural Network
The HNN is a recurrent neural network and can be applied to combinatorial optimization and pattern recognition problems, of which the former of interest in this paper. In 1985, Hopfield and Tank showed how neurobiological computations can be modeled with the use of an electronic circuit [15]. This circuit is shown in Figure 1.
By using basic electronic components, they constructed a recurrent neural network and derived the characteristic equations for the network. The set of equations that describe the dynamics of the system is given by [26]

with  , the dots, describing the interconnections between the amplifiers,
, the dots, describing the interconnections between the amplifiers,  the input voltages of the amplifiers,
the input voltages of the amplifiers,  the output voltages of the amplifiers,
the output voltages of the amplifiers,  the capacitor values,
the capacitor values,  the resistivity values, and
the resistivity values, and  the bias voltages of each amplifier. Each amplifier represents a neuron. The transfer function of the positive outputs of the amplifiers represents the positive part of the activation function
the bias voltages of each amplifier. Each amplifier represents a neuron. The transfer function of the positive outputs of the amplifiers represents the positive part of the activation function  and the transfer function of the negative outputs represents the negative part of the activation function
and the transfer function of the negative outputs represents the negative part of the activation function  (negative outputs are not shown here).
(negative outputs are not shown here).
It was shown in [15] that the stable state of this circuit network can be found by minimizing the function

provided that  and
and  , implying that
, implying that  is symmetric around the diagonal and its diagonal is zero [15]. There are therefore no self-connections. This function is called the energy function or the Lyapunov function which, by definition, is a monotonically decreasing function, ensuring that the system will converge to a stable state [15]. When minimized, the network converges to a local minimum in the solution space to yield a "good" solution. The solution is not guaranteed to be optimal, but by using optimization techniques, the quality of the solution can be improved. To minimize (2) the system equations in (1) are solved iteratively until the outputs
is symmetric around the diagonal and its diagonal is zero [15]. There are therefore no self-connections. This function is called the energy function or the Lyapunov function which, by definition, is a monotonically decreasing function, ensuring that the system will converge to a stable state [15]. When minimized, the network converges to a local minimum in the solution space to yield a "good" solution. The solution is not guaranteed to be optimal, but by using optimization techniques, the quality of the solution can be improved. To minimize (2) the system equations in (1) are solved iteratively until the outputs  settle.
settle.
Hopfield also showed that this kind of network can be used to solve the travelling salesman problem (TSP). This problem is of a class called NP-complete, the class of nondeterministic polynomial problems. Problems that fall in this class, can be solved optimally if each possible solution is enumerated [27]. However, complete enumeration is a time-consuming exercise, especially as the solution space grows. Complete enumeration is often not a feasible solution for real-time problems, of which MLSE equalization is considered in this paper.
3. MLSE Equalization
In a single-carrier frequency-selective Rayleigh fading environment, assuming a time-invariant channel impulse response (CIR), the received symbols are described by [1, 4]

where  denotes the
denotes the  th complex symbol in the transmitted sequence of
th complex symbol in the transmitted sequence of  symbols chosen from an alphabet
symbols chosen from an alphabet  containing
containing  complex symbols,
complex symbols,  is the
is the  th received symbol,
th received symbol,  is the
is the  th Gaussian noise sample
th Gaussian noise sample  , and
, and  is the
is the  th coefficient of the estimated CIR [7]. The equalizer is responsible for reversing the effect of the channel on the transmitted symbols in order to produce the sequence of transmitted symbols with maximum confidence. To optimally estimate the transmitted sequence of length
th coefficient of the estimated CIR [7]. The equalizer is responsible for reversing the effect of the channel on the transmitted symbols in order to produce the sequence of transmitted symbols with maximum confidence. To optimally estimate the transmitted sequence of length  in a wireless communication system, the cost function [1]
in a wireless communication system, the cost function [1]

must be minimized. Here,  is the most likely transmitted sequence that will maximize
is the most likely transmitted sequence that will maximize  . The Viterbi MLSE equalizer is able to solve this problem exactly, with computational complexity linear in
. The Viterbi MLSE equalizer is able to solve this problem exactly, with computational complexity linear in  and exponential in
and exponential in  [1]. The HNN MLSE equalizer is also able to minimizes the cost function in (4), with computational complexity quadratic in
[1]. The HNN MLSE equalizer is also able to minimizes the cost function in (4), with computational complexity quadratic in  but approximately independent of
but approximately independent of  , thus enabling it to perform near-optimal sequence estimation in systems with extremely long CIR lengths at very low computational cost.
, thus enabling it to perform near-optimal sequence estimation in systems with extremely long CIR lengths at very low computational cost.
4. The HNN MLSE Equalizer
It was observed [22–25] that (4) can be written as

where  is a column vector with
is a column vector with  elements,
elements,  is an
is an  matrix, and
matrix, and  implies the Hermitian transpose, where (5) corresponds to the HNN energy function in (2). In order to use the HNN to perform MLSE equalization, the cost function (4) that is minimized by the Viterbi MLSE equalizer must be mapped to the energy function (5) of the HNN. This mapping is performed by expanding (4) for a given block length
implies the Hermitian transpose, where (5) corresponds to the HNN energy function in (2). In order to use the HNN to perform MLSE equalization, the cost function (4) that is minimized by the Viterbi MLSE equalizer must be mapped to the energy function (5) of the HNN. This mapping is performed by expanding (4) for a given block length  and a number of CIR lengths
and a number of CIR lengths  , starting from
, starting from  and increasing
and increasing  until a definite pattern emerges in
until a definite pattern emerges in  and
and  in (5). The emergence of a pattern in
in (5). The emergence of a pattern in  and
and  enables the realization of an MLSE equalizer for the general case, that is, for systems with any
enables the realization of an MLSE equalizer for the general case, that is, for systems with any  and
and  , yielding a generalized HNN MLSE equalizer that can be used in a single-carrier communication system.
, yielding a generalized HNN MLSE equalizer that can be used in a single-carrier communication system.
Assuming that  ,
,  , and
, and  contain complex values these variables can be written as [22–25]
contain complex values these variables can be written as [22–25]

where  and
and  are column vectors of length
are column vectors of length  , and
, and  is an
is an  matrix, where subscripts
matrix, where subscripts  and
and  are used to denote the respective in-phase and quadrature components.
are used to denote the respective in-phase and quadrature components.  is the cross-correlation matrix of the complex received symbols such that
is the cross-correlation matrix of the complex received symbols such that

implying that it is Hermitian. Therefore,  is symmetric and
is symmetric and  is skew symmetric [22, 23]. By using the symmetric properties of
is skew symmetric [22, 23]. By using the symmetric properties of  , (5) can be expanded and rewritten as
, (5) can be expanded and rewritten as

which in turn can be rewritten as [22–25]

It is clear that (9) is in the form of (5), where the variables in (5) are substituted as follows:

Equation (9) will be used to derive a general model for M-QAM equalization.
4.1. Systematic Derivation
The transmitted and received data block structures are shown in Figure 2, where it is assumed that  known tail symbols are appended and prepended to the block of payload symbols. (The transmitted tails are
known tail symbols are appended and prepended to the block of payload symbols. (The transmitted tails are  to
to  and
and  to
to  and are equal to
and are equal to  )
)
The expressions for the unknowns in (9) are found by expanding (4), for a fixed data block length  and increasing CIR length
and increasing CIR length  and mapping it to (9). Therefore, for a single-carrier system with a data block of length
and mapping it to (9). Therefore, for a single-carrier system with a data block of length  and CIR of length
and CIR of length  , with the data block initiated and terminated by
, with the data block initiated and terminated by  known tail symbols,
known tail symbols,  and
and  are given by
are given by


where  and
and  are respectively determined by
are respectively determined by


where  and
and  and
and  denote the real and complex components of the CIR coefficients. Also,
denote the real and complex components of the CIR coefficients. Also,


where  and
and  is determined by
is determined by

and  is determined by
is determined by

where  with
with  and
and  again denoting the real and complex components of the respective vectors.
again denoting the real and complex components of the respective vectors.
4.2. Training
Since the proposed equalizer is based on a neural network, it has to be trained. The HNN MLSE equalizer does not have to be trained by providing a set of training examples as in the case of conventional supervised neural networks [28]. Rather, the HNN MLSE equalizer is trained anew in an unsupervized fashion for each received data block by using the coefficients of the estimated CIR to determine  in (13) and
in (13) and  in (14), for
in (14), for  , which serve as the connection weights between the neurons.
, which serve as the connection weights between the neurons.  ,
,  ,
,  , and
, and  fully describes the structure of the equalizer for each received data block, which are determined according to (11), (12), (15) and (16), using the estimated CIR and the received symbol sequence.
fully describes the structure of the equalizer for each received data block, which are determined according to (11), (12), (15) and (16), using the estimated CIR and the received symbol sequence.  and
and  therefore describe the connection weights between the neurons, and
therefore describe the connection weights between the neurons, and  and
and  represent the input of the neural network.
represent the input of the neural network.
4.3. The Iterative System
In order for the HNN to minimize the energy function (5), the following dynamic system is used

where  is an arbitrary constant and
is an arbitrary constant and  is the internal state of the network. An iterative solution for (19) is given by
is the internal state of the network. An iterative solution for (19) is given by

where again  is the internal state of the network,
is the internal state of the network,  is the vector of estimated symbols,
is the vector of estimated symbols,  is the decision function associated with each neuron and
is the decision function associated with each neuron and  indicates the iteration number.
indicates the iteration number.  is a function used for optimization.
is a function used for optimization.
To determine the MLSE estimate for a data block of length  with
with  CIR coefficients for a M-QAM system, the following steps are executed:
CIR coefficients for a M-QAM system, the following steps are executed:
-
(1)
Use the received symbols
 and the estimated CIR
and the estimated CIR 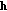 to calculate
to calculate 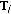 ,
, 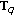 ,
, 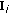 and
and 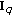 according to (11), (12), (15) and (16).
according to (11), (12), (15) and (16). -
(2)
Initialize all elements in [
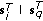 ] to
] to  .
. -
(3)
Calculate
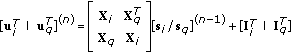 .
. -
(4)
Calculate [
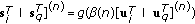 .
. -
(5)
Go to step
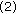 and repeat until
and repeat until 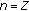 , where
, where 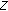 is the predetermined number of iterations. (
is the predetermined number of iterations. ( iterations are used for the proposed equalizer.)
iterations are used for the proposed equalizer.)
As is clear from the algorithm, the estimated symbol vector  is updated with each iteration.
is updated with each iteration.  contains the best linear estimate for
contains the best linear estimate for  (it can be shown that
(it can be shown that  contains the output of a RAKE reciever used in DSSS systems) and is therefore used as input to the network, while
contains the output of a RAKE reciever used in DSSS systems) and is therefore used as input to the network, while  contains the cross-correlation information of the received symbols. The system solves (4) by iteratively mitigating the effect of ISI and produces the MLSE estimates in
contains the cross-correlation information of the received symbols. The system solves (4) by iteratively mitigating the effect of ISI and produces the MLSE estimates in  after
after  iterations.
iterations.
4.4. The Decision Function
4.4.1. Bipolar Decision Function
When BPSK modulation is used, only two signal levels are required to transmit information. Therefore, since only two signal levels are used, a bipolar decision function is used in the HNN BPSK MLSE equalizer. This function, also called a bipolar sigmoid function, is expressed as

and is shown in Figure 3. It must also be noted that the bipolar decision can also be used in the M-QAM model for equalization in 4-QAM systems. This is an exception, since, although 4-QAM modulation uses four signal levels, there are only two signal levels per dimension. By using the model derived for M-QAM modulation, 4-QAM equalization can be performed by using the bipolar decision function in (21), with the output scaled by 'n factor  .
.
4.4.2. Multilevel Decision Function
Apart from 4-QAM modulation, all other M-QAM modulation schemes use multiple amplitude levels to transmit information as the "AM" in the acronym M-QAM implies. A bipolar decision function will therefore not be sufficient; a multilevel decision function with  distinct signal levels must be used, where
distinct signal levels must be used, where  is the modulation alphabet size.
is the modulation alphabet size.
A multilevel decision function can be realized by adding several bipolar decision functions and shifting each by a predetermined value, and scaling the result accordingly [29, 30]. To realize a  -level decision function for use in an M-QAM HNN MLSE equalizer, the following function can be used:
-level decision function for use in an M-QAM HNN MLSE equalizer, the following function can be used:

where  is the modulation alphabet size and
is the modulation alphabet size and  is the value by which the respective bipolar decision functions are shifted. Figure 4 shows the four-level decision function used for the 16-QAM HNN MLSE equalizer, for
is the value by which the respective bipolar decision functions are shifted. Figure 4 shows the four-level decision function used for the 16-QAM HNN MLSE equalizer, for  ,
,  and
and  .
.
Due to the time-varying nature of a mobile wireless communication channel and energy losses caused by absorption and scattering, the total power in the received signal is also time-variant. This complicates equalization when using the M-QAM HNN MLSE equalizer, since the value by which the respective bipolar decision functions are shifted,  , is dependent on the power in the channel and will therefore have a different value for every new data block arriving at the receiver. For this reason the
, is dependent on the power in the channel and will therefore have a different value for every new data block arriving at the receiver. For this reason the  -level decision function in (22) will change slightly for every data block.
-level decision function in (22) will change slightly for every data block.  is determined by the Euclidean norm of the estimated CIR and is given by
is determined by the Euclidean norm of the estimated CIR and is given by

where  and
and  are the
are the  th respective in-phase and quadrature components of the estimated CIR of length
th respective in-phase and quadrature components of the estimated CIR of length  as before.
as before.
Figure 4 shows the four-level decision function for different values of  to demonstrate the effect of varying power levels in the channel. Higher power in
to demonstrate the effect of varying power levels in the channel. Higher power in  will cause the outer neurons to move away from the origin whereas lower power will cause the outer neurons to move towards the origin. Therefore, upon reception of a complete data block,
will cause the outer neurons to move away from the origin whereas lower power will cause the outer neurons to move towards the origin. Therefore, upon reception of a complete data block,  is determined according to the power of the CIR, after which equalization commences.
is determined according to the power of the CIR, after which equalization commences.
4.5. Optimization
Because MLSE is an NP-complete problem, there are a number of possible "good" solutions in the multidimensional solution space. By enumerating every possible solution, it will be possible to find the best solution, that is, the sequence of symbols that minimizes (4) and (5), but it is not computationally feasible for systems with large  and
and  . The HNN is used to minimize (5) to find a near-optimal solution at very low computational cost. Because the HNN usually gets stuck in suboptimal local minima, it is necessary to employ optimization techniques as suggested [31]. To aid the HNN in escaping less optimal basins of attraction simulated annealing and asynchronous neuron updates are often used.
. The HNN is used to minimize (5) to find a near-optimal solution at very low computational cost. Because the HNN usually gets stuck in suboptimal local minima, it is necessary to employ optimization techniques as suggested [31]. To aid the HNN in escaping less optimal basins of attraction simulated annealing and asynchronous neuron updates are often used.
Markov Chain Monte Carlo (MCMC) algorithms are used together with Gibbs sampling in [32] to aid optimization in the solution space. According to [32], however, the complexity of the MCMC algorithms may become prohibitive due to the so called stalling problem, which result from low probability transitions in the Gibbs sampler. To remedy this problem an optimization variable referred to as the "temperature" can be adjusted in order to avoid these small transition probabilities. This idea is similar to simulated annealing, where the temperature is adjusted to control the rate of convergence of the algorithm as well as the quality of the solution it produces.
4.5.1. Simulated Annealing
Simulated annealing has its origin in metallurgy. In metallurgy annealing is the process used to temper steel and glass by heating them to a high temperature and then gradually cooling them, thus allowing the material to coalesce into a low-energy crystalline state [28]. In neural networks, this process is imitated to ensure that the neural network escapes less optimal local minima to converge to a near-optimal solution in the solution space. As the neural network starts to iterate, there are many candidate solutions in the solution space, but because the neural network starts to iterate at a high temperature, it is able to escape the less optimal local minima in the solutions space. As the temperature decreases, the network can still escape less optimal local minima, but it will start to gradually converge to the global minimum in the solution space to minimize the energy. This state of minimum energy corresponds to the optimal solution.
The output of the function  in (20) is used for simulated annealing. As the system iterates,
in (20) is used for simulated annealing. As the system iterates,  is incremented with each iteration, and
is incremented with each iteration, and  produces a value according to an exponential function to ensure that the system converges to a near-optimal local minimum in the solution space. This function is give by
produces a value according to an exponential function to ensure that the system converges to a near-optimal local minimum in the solution space. This function is give by

and shown in Figure 5. This causes the output of  to start at a near-zero value and to exponentially converge to 1 with each iteration.
to start at a near-zero value and to exponentially converge to 1 with each iteration.
The effect of annealing on the bipolar and four-level decision function during the iteration cycle is shown in Figures 6 and 7, respectively, with the slope of the decision function increasing as  is updated with each iteration. Simulated annealing ensures near-optimal sequence estimation by allowing the system to escape less optimal local minima in the solution space, leading to better system performance.
is updated with each iteration. Simulated annealing ensures near-optimal sequence estimation by allowing the system to escape less optimal local minima in the solution space, leading to better system performance.
Figures 8 and 9 show the neuron outputs, for the real and complex symbol components, of the 16-QAM HNN MLSE equalizer for each iteration of the system with and without annealing. It is clear that annealing allows the outputs of the neurons to gradually evolve in order to converge to near-optimal values in the  -dimensional solution space, not produce reliable transmitted symbol estimates.
-dimensional solution space, not produce reliable transmitted symbol estimates.
4.5.2. Asynchronous Updates
In artificial neural networks, the neurons in the network can either be updated using parallel or asynchronous updates. Consider the iterative solution of the HNN in (20). Assume that  ,
,  and
and  each contain
each contain  elements and that
elements and that  is an
is an  matrix with
matrix with  iterations as before.
iterations as before.
When parallel neuron updates are used,  elements in
elements in  are calculated before
are calculated before  elements in
elements in  are determined, for each iteration. This implies that the output of the neurons will only be a function of the neuron outputs from the previous iteration. On the other hand, when using asynchronous neuron updates, one element in
are determined, for each iteration. This implies that the output of the neurons will only be a function of the neuron outputs from the previous iteration. On the other hand, when using asynchronous neuron updates, one element in  is determined for every corresponding element in
is determined for every corresponding element in  . This is performed
. This is performed  times per iteration—once for each neuron. Asynchronous updates allow the changes of the neuron outputs to propagate to the other neurons immediately [31], while the output of all of the
times per iteration—once for each neuron. Asynchronous updates allow the changes of the neuron outputs to propagate to the other neurons immediately [31], while the output of all of the  neurons will only be propagated to the other neurons after all of them have been updated when parallel updates are used.
neurons will only be propagated to the other neurons after all of them have been updated when parallel updates are used.
With parallel updates the effect of the updates propagates through the network only after one complete iteration cycle. This implies that the energy of the network might change drastically, because all of the neurons are updated together. This will cause the state of the neural network to "jump" around on the solution space, due to the abrupt changes in the internal state of the network. This will lead to degraded performance, since the network is not allowed to gradually evolve towards an optimal, or at least a near-optimal, basin of attraction.
With asynchronous updates the state of the network changes after each element in  is determined. This means that the state of the network undergoes
is determined. This means that the state of the network undergoes  gradual changes during each iteration. This ensures that the network traverses the solution space using small steps while searching for the global minimum. The computational complexity is identical for both parallel and asynchronous updates [31]. Asynchronous updates are therefore used for the HNN MLSE equalizer. The neurons are updated in a sequential order:
gradual changes during each iteration. This ensures that the network traverses the solution space using small steps while searching for the global minimum. The computational complexity is identical for both parallel and asynchronous updates [31]. Asynchronous updates are therefore used for the HNN MLSE equalizer. The neurons are updated in a sequential order:  .
.
4.6. Convergence and Performance
The rate of convergence and the performance of the HNN MLSE equalizer are dependent on the number of CIR coefficients  as well as the number of iterations
as well as the number of iterations  . Firstly, the number of CIR coefficients determines the level of interconnection between the neurons in the network. A long CIR will lead to dense population of the connection matrix in
. Firstly, the number of CIR coefficients determines the level of interconnection between the neurons in the network. A long CIR will lead to dense population of the connection matrix in  (10), consisting of
(10), consisting of  in (11) and
in (11) and  (12), which translates to a high level of interconnection between the neurons in the network. This will enable the HNN MLSE equalizer to converge faster while producing better maximum likelihood sequence estimates, which is ultimately the result of a high level of diversity provided by a highly dispersive channel. Similarly, a short CIR will result in a sparse connection matrix
(12), which translates to a high level of interconnection between the neurons in the network. This will enable the HNN MLSE equalizer to converge faster while producing better maximum likelihood sequence estimates, which is ultimately the result of a high level of diversity provided by a highly dispersive channel. Similarly, a short CIR will result in a sparse connection matrix  , where the HNN MLSE equalizer will converge slower while yielding less optimal maximum likelihood sequence estimates.
, where the HNN MLSE equalizer will converge slower while yielding less optimal maximum likelihood sequence estimates.
Second, simulated annealing, which allows the neuron outputs to be forced to discrete decision levels when the iteration number reaches the end of the iteration cycle (when  ), ensures that the HNN MLSE equalizer will have converged by the last iteration (as dictated by
), ensures that the HNN MLSE equalizer will have converged by the last iteration (as dictated by  ). This is clear from Figure 9. For small
). This is clear from Figure 9. For small  , the output of the HNN MLSE equalizer will be less optimal than for large
, the output of the HNN MLSE equalizer will be less optimal than for large  . It was found that the HNN MLSE equalizer produces acceptable performance without excessive computational complexity for
. It was found that the HNN MLSE equalizer produces acceptable performance without excessive computational complexity for  .
.
4.7. Soft Outputs
To enable the HNN MLSE equalizer to produce soft outputs,  in (24) is scaled by a factor
in (24) is scaled by a factor  . This allows the outputs of the equalizer to settle between the discrete decision levels instead of being forced to settle on the decision levels.
. This allows the outputs of the equalizer to settle between the discrete decision levels instead of being forced to settle on the decision levels.
5. Computational Complexity Analysis
The computational complexity of the HNN MLSE equalizer is quadratic in the data block length  and approximately independent of the CIR length
and approximately independent of the CIR length  for practical systems where the data block length is larger than channel memory length. This is due to the high parallelism of its underlying neural network structure an high level of interconnection between the neurons. The approximate independence of the complexity from the channel memory is significant, as the CIR length is the dominant term in the complexity of all optimal equalizers, where the complexity is
for practical systems where the data block length is larger than channel memory length. This is due to the high parallelism of its underlying neural network structure an high level of interconnection between the neurons. The approximate independence of the complexity from the channel memory is significant, as the CIR length is the dominant term in the complexity of all optimal equalizers, where the complexity is  .
.
In this section, the computational complexity of the HNN MLSE equalizer is analyzed, where it is compared to that of the Viterbi MLSE equalizer. The computational complexities of these algorithms are analyzed by assuming that an addition as well as a multiplication are performed using one machine instruction. It is also assumed that variable initialization does not add to the cost.
5.1. HNN MLSE Equalizer
The M-QAM HNN MLSE equalizer performs the following steps. (The computational complexity of the BPSK HNN MLSE equalizer is easily derived from that of the M-QAM HNN MLSE equalizer.)
(1) Determine and
and values using the estimated CIR: There are
values using the estimated CIR: There are  distinct
distinct  values and
values and  distinct
distinct  values.
values.  and
and  both contain
both contain  terms, each consisting of a multiplication between two values. Also,
terms, each consisting of a multiplication between two values. Also,  and
and  both contain one term. Therefore the number of computations to determine all
both contain one term. Therefore the number of computations to determine all  - and
- and  values can be written as
values can be written as

(2) Populate matrices and
and (of size
(of size ) and vectors
) and vectors and
and (of size
(of size ). Under the assumption that variable initialization does not add to the total cost, the population of
). Under the assumption that variable initialization does not add to the total cost, the population of  and
and  does not add to the cost. However,
does not add to the cost. However,  and
and  are not only populated, but some calculations are performed before population. All elements in
are not only populated, but some calculations are performed before population. All elements in  and
and  need
need  additions of two multiplicative terms. Also, the first and the last
additions of two multiplicative terms. Also, the first and the last  elements in
elements in  and
and  together contain
together contain 
 and
and  addition and/or subtraction terms. Therefore, the cost of populating
addition and/or subtraction terms. Therefore, the cost of populating  and
and  is given by
is given by

(3) Initialize and
and , both of length
, both of length . Under the assumption that variable initialization does not add to the total cost, initialization of these variables does not add to the cost.
. Under the assumption that variable initialization does not add to the total cost, initialization of these variables does not add to the cost.
(4) Iterate the system times:
times:
-
(i)
Determine the state vector
 . The cost of multiplying a matrix of size
. The cost of multiplying a matrix of size 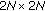 with a vector of size
with a vector of size 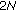 and adding another vector of length
and adding another vector of length 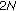 to the result,
to the result, 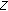 times, is given by
times, is given by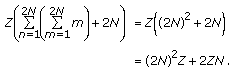 (27)
(27) -
(ii)
Calculate

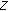 times. The cost of calculating the estimation vector
times. The cost of calculating the estimation vector  of length
of length 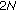 by using every value in state vector
by using every value in state vector  , also of length
, also of length  , assuming that the sigmoid function uses three instructions to execute,
, assuming that the sigmoid function uses three instructions to execute,  times, is given by (it is assumed that the values of
times, is given by (it is assumed that the values of 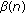 is stored in a lookup table, where
is stored in a lookup table, where 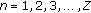 , to trivialize the computational complexity of simulated annealing)
, to trivialize the computational complexity of simulated annealing) (28)
(28)
Thus, by adding all of the computations above, the total computational complexity for the M-QAM HNN MLSE equalizer is

The structure of the M-QAM HNN MLSE equalizer is identical to that of the BPSK HNN MLSE equalizer. The only difference is that, for the BPSK HNN MLSE equalizer, all matrices and vectors are of dimension  and instead of
and instead of  , as only the in-phase component of the estimated symbol vector is considered. Therefore, it follows that the computational complexity of the BPSK HNN MLSE equalizer will be
, as only the in-phase component of the estimated symbol vector is considered. Therefore, it follows that the computational complexity of the BPSK HNN MLSE equalizer will be

5.2. Viterbi MLSE Equalizer
The Viterbi equalizer performs the following steps:
-
(1)
Setup trellis of length
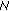 , where each stage contains
, where each stage contains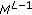 states, where
states, where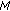 is the constellation size: It is assumed that this does not add to the complexity. It must however be noted that the dimensions of the trellis is
is the constellation size: It is assumed that this does not add to the complexity. It must however be noted that the dimensions of the trellis is 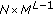 .
. -
(2)
Determine two Euclidean distances for each node. The Euclidean distance is determined by subtracting
 addition terms, each containing one multiplication, from the received symbol at instant
addition terms, each containing one multiplication, from the received symbol at instant  . The cost for determining one Euclidean distance is therefore given by
. The cost for determining one Euclidean distance is therefore given by (31)
(31) -
(3)
Eliminate contending paths at each node. Two path costs are compared using an if-statement, assumed to count one instruction. The cost is therefore
 (32)
(32) -
(4)
Backtrack the trellis to determine the MLSE solution. Backtracking accross the trellis, where each time instant
 requires an if-statement. The cost is therefore
requires an if-statement. The cost is therefore (33)
(33)Adding all costs to give the total cost results in
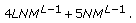 (34)
(34)
5.3. HNN MLSE Equalizer and Viterbi MLSE Equalizer Comparison
Figure 10 shows the computational complexities of the HNN MLSE equalizer and the Viterbi MLSE equalizer as a function of the CIR length  , for
, for  to
to  , where the number of iterations is
, where the number of iterations is  . For the HNN MLSE equalizer, it is shown for BPSK and M-QAM modulation, since the computational complexities of all M-QAM HNN MLSE equalizers are equal. Also, for the Viterbi MLSE equalizer, it is shown for BPSK and 4-QAM modulation. It is clear that the computational complexity of the HNN MLSE equalizer is superior to that of the Viterbi MLSE equalizer for system with larger memory. For BPSK, the break-even mark between the HNN MLSE equalizer and the Viterbi MLSE equalizer is at
. For the HNN MLSE equalizer, it is shown for BPSK and M-QAM modulation, since the computational complexities of all M-QAM HNN MLSE equalizers are equal. Also, for the Viterbi MLSE equalizer, it is shown for BPSK and 4-QAM modulation. It is clear that the computational complexity of the HNN MLSE equalizer is superior to that of the Viterbi MLSE equalizer for system with larger memory. For BPSK, the break-even mark between the HNN MLSE equalizer and the Viterbi MLSE equalizer is at  , and for 4-QAM it is at
, and for 4-QAM it is at  .
.
The complexity of the HNN MLSE equalizer for both BPSK and M-QAM seems constant whereas that of the Viterbi MLSE equalizer increases exponentially as the CIR length increases. Also, note the difference in complexity between the BPSK HNN MLSE equalizer and the M-QAM HNN MLSE equalizer. This is due to the quadratic relationship between the complexity and the data block length, which dictates the size of the vectors and matrices in the HNN MLSE equalizer. The HNN MLSE equalizer is however not well-suited for systems with short CIRs, as the complexity of the Viterbi MLSE equalizer is less than that of the HNN MLSE equalizer for short CIRs. This is however not a concern, since the aim of the proposed equalizer is on equalization of signals in systems with extremely long memory.
Figure 11 shows the computational complexity of the HNN MLSE equalizer for BPSK and M-QAM modulation for block lengths of  and
and  respectively, indicating the quadratic relationship between the computational complexity and the data block length, also requiring larger vectors and matrices in the HNN MLSE equalizer. It is clear that, as the data block length increases, the data block length
respectively, indicating the quadratic relationship between the computational complexity and the data block length, also requiring larger vectors and matrices in the HNN MLSE equalizer. It is clear that, as the data block length increases, the data block length  , rather than the CIR length
, rather than the CIR length  , is the dominant factor contributing to the computational complexity. However, due to the approximate independence of the complexity on the CIR length, the HNN MLSE equalizer is able to equalize signals in systems with hundreds of CIR elements for large data block lengths. This should be clear from Figures 10 and 11.
, is the dominant factor contributing to the computational complexity. However, due to the approximate independence of the complexity on the CIR length, the HNN MLSE equalizer is able to equalize signals in systems with hundreds of CIR elements for large data block lengths. This should be clear from Figures 10 and 11.
The scenario in Figure 11 is somewhat unrealistic, since the data block length must at least be as long as the CIR length. However, Figure 12 serves to show the effect of the data block length and the CIR length on the computational complexity of the HNN MLSE equalizer. Figure 12 shows the computational complexity for a more realistic scenario. Here the complexity of the BPSK HNN MLSE and the M-QAM HNN MLSE equalizer is shown for  ,
,  and
and  , for
, for  to
to  .
.
From Figure 12 it is clear that the computational complexity increases quadratically as the data block length linearly increases. It is quite significant that the complexity is nearly independent of the CIR length when the data block length is equal to or great then the CIR length, which is the case in practical communication systems. It should now be clear why the HNN MLSE equalizer is able to equalize signals in systems, employing BPSK or M-QAM modulation, with hundreds and possibly thousands of resolvable multipath elements.
The superior computational complexity of the HNN MLSE equalizer is obvious. Its low complexity makes it suitable for equalization of signals with CIR lengths that are beyond the capabilities of optimal equalizers like the Viterbi MLSE equalizer and the MAP equalizer, for which the computational complexity increases exponentially with an increase in the channel memory (note that the computational complexity graphs of the Viterbi MLSE equalizer cannot be presented on the same scale as that of the HNN MLSE equalizer, as shown in Figure 10 through Figure 12), and it is also exponentially related to the number of symbols in the modulation alphabet. On the other hand, the computational complexity of the HNN MLSE equalizer is quadratically related to the data block length and almost independent of the CIR length for realistic scenarios. Also, the complexity of the HNN MLSE equalizer is independent of the modulation alphabet size for M-QAM systems, making it suitable for equalization in higher order M-QAM system with even moderate channel memory, where optimal equalizer cannot be applied.
6. Simulation Results
In this section, the HNN MLSE equalizer is evaluated. The low computational complexity of the HNN MLSE equalizer allows it to equalize signals in systems with extremely long memory, well beyond the capabilities of conventional optimal equalizers like the Viterbi MLSE and the MAP equalizers. The HNN MLSE equalizer is evaluated for long sparse and dense Rayleigh fading channels. It will be established that the HNN MLSE equalizer outperforms the MMSE equalizer in long fading channels and it will be shown that the performance of the HNN MLSE equalizer in sparse channels is better than its performance in equivalent dense channels, that is, longer channels with the same amount of nonzero CIR taps.
The communication system is simulated for a GSM mobile fading environment, where the carrier frequency is  MHz, the symbol period is
MHz, the symbol period is 
 s and the relative speed between the transmitter and receiver is
s and the relative speed between the transmitter and receiver is  km/h. To simulate the fading effect on each tap, the Rayleigh fading simulator proposed in [33] is used to generate uncorrelated fading vectors. Least Squares (LS) channel estimation is used to determine an estimate for the CIR, in order to include the effect of imperfect channel state information (CSI) in the simulation results. Where perfect CSI is assumed, however, the statistical average of each fading vector is used to construct the CIR vector for each received data block. In all simulations, the nominal CIR weights are chosen as
km/h. To simulate the fading effect on each tap, the Rayleigh fading simulator proposed in [33] is used to generate uncorrelated fading vectors. Least Squares (LS) channel estimation is used to determine an estimate for the CIR, in order to include the effect of imperfect channel state information (CSI) in the simulation results. Where perfect CSI is assumed, however, the statistical average of each fading vector is used to construct the CIR vector for each received data block. In all simulations, the nominal CIR weights are chosen as  such that
such that  , where
, where  is the CIR length, and
is the CIR length, and  is a column vector of length
is a column vector of length  , in order to normalize the energy in the channel. The normalized nominal taps are used to scale the uncorrelated fading vectors produced by the Rayleigh fading simulator. To simulated dense channels, all the nominal tap weights are chosen as 1, after which the taps are normalized as explained. To simulated sparse channels,
, in order to normalize the energy in the channel. The normalized nominal taps are used to scale the uncorrelated fading vectors produced by the Rayleigh fading simulator. To simulated dense channels, all the nominal tap weights are chosen as 1, after which the taps are normalized as explained. To simulated sparse channels,  % of the nominal taps weights are chosen as 1 (for sparse channels the nonzero taps are evenly spaced), while the rest are set to zero. Again the taps are normalized, but now only
% of the nominal taps weights are chosen as 1 (for sparse channels the nonzero taps are evenly spaced), while the rest are set to zero. Again the taps are normalized, but now only  % of
% of  taps are nonzero.
taps are nonzero.
In order to compare the performance of the HNN MLSE equalizer in dense channels to its performance in sparse channels, an equivalent dense channel is used. An equivalent dense channel is a dense channel with an equal amount of nonzero taps as that of a sparse channel of any length. A sparse channel of length  , where only
, where only  % of the taps are nonzero, is compared to a dense channel of length
% of the taps are nonzero, is compared to a dense channel of length  , so that the number of nonzero taps in the sparse channel is equal to that in the equivalent dense channel. Figure 13 shows the evenly spaced normalized nominal CIR taps of sparse channels of length
, so that the number of nonzero taps in the sparse channel is equal to that in the equivalent dense channel. Figure 13 shows the evenly spaced normalized nominal CIR taps of sparse channels of length  , where
, where  % (a),
% (a),  % (b),
% (b),  % (c) and
% (c) and  % (d), reducing the number of nonzero CIR taps to
% (d), reducing the number of nonzero CIR taps to  % of the CIR length.
% of the CIR length.
6.1. Performance in Dense Channels
The performance of the BPSK HNN MLSE equalizer and 16-QAM HNN MLSE equalizers is evaluated for long dense channels, for perfect CSI, with channel delays from 
 s to
s to  ms (
ms ( to
to  ). The performance of the BPSK HNN MLSE equalizer is also compared to that of an MMSE equalizer for imperfect CSI.
). The performance of the BPSK HNN MLSE equalizer is also compared to that of an MMSE equalizer for imperfect CSI.
Figure 14 shows the performance of the BPSK HNN MLSE equalizer for perfect CSI, where the uncoded data block length is  and the CIR lengths range from
and the CIR lengths range from  to
to  , corresponding to channel delay spreads of
, corresponding to channel delay spreads of  s to
s to  ms. As the channel memory increases, the performance increases correspondingly, approaching unfaded matched filter performance as a result of the effective time diversity provided by the multipath channels. It is clear the BSPK HNN MLSE equalizer performs near-optimal, if not optimal, equalization. Note that for
ms. As the channel memory increases, the performance increases correspondingly, approaching unfaded matched filter performance as a result of the effective time diversity provided by the multipath channels. It is clear the BSPK HNN MLSE equalizer performs near-optimal, if not optimal, equalization. Note that for  , a Viterbi MLSE equalizer would require
, a Viterbi MLSE equalizer would require  states in its trellis per transmitted symbol.
states in its trellis per transmitted symbol.
Figure 15 shows the performance of the 16-QAM HNN MLSE equalizer, where again perfect CSI and an uncoded data block length of  are assumed. Here, the CIR length ranges from
are assumed. Here, the CIR length ranges from  to
to  which corresponds to channel delay spreads of
which corresponds to channel delay spreads of 
 s to
s to  ms. Here, it is also clear that the performance approaches unfaded matched filter performance as the channel memory increases. Note that a Viterbi MLSE equalizer would require
ms. Here, it is also clear that the performance approaches unfaded matched filter performance as the channel memory increases. Note that a Viterbi MLSE equalizer would require  states in its trellis per transmitted symbol for
states in its trellis per transmitted symbol for  .
.
Figure 16 shows the performance of the BPSK HNN MLSE equalizer compared to that of an MMSE equalizer, for moderate to long channels, using channel estimation. It is assumed that  training symbols are available for channel estimation per data block of length
training symbols are available for channel estimation per data block of length  . For the HNN MLSE equalizer the LS channel estimator is used to estimate the CIR using
. For the HNN MLSE equalizer the LS channel estimator is used to estimate the CIR using  training symbols, and for the MMSE equalizer the channel is estimated as part of the filter coefficient optimization—an integral part of MMSE equalization—where the filter smoothing length is
training symbols, and for the MMSE equalizer the channel is estimated as part of the filter coefficient optimization—an integral part of MMSE equalization—where the filter smoothing length is  . From Figure 16 it is clear that the HNN MLSE equalizer outperforms the MMSE equalizer for high
. From Figure 16 it is clear that the HNN MLSE equalizer outperforms the MMSE equalizer for high  -levels and when the channel memory is large.
-levels and when the channel memory is large.
From these results it is clear that the HNN MLSE equalizer effectively equalizes the received signal and performs near-optimally when the channel memory is large, if perfect CSI is assumed.
6.2. Performance in Sparse Channels
The performance of the BSPK HNN MLSE equalizer, and 16-QAM HNN MLSE equalizers is evaluated for sparse channels, where their performance is compared to equivalent dense channels. The equalizer is simulated for various levels op sparsity, where  indicates the percentage of nonzero CIR taps. The performance of the HNN MLSE equalizers in these sparse channels is compared to their performance in equivalent dense channels of length
indicates the percentage of nonzero CIR taps. The performance of the HNN MLSE equalizers in these sparse channels is compared to their performance in equivalent dense channels of length  to
to  . Perfect CSI is assumed.
. Perfect CSI is assumed.
For the BPSK HNN MLSE equalizer an uncoded data block length of  is used where the channel delay of the sparse channel is
is used where the channel delay of the sparse channel is  ms, corresponding to a CIR length of
ms, corresponding to a CIR length of  . To simulate the BPSK equalizer
. To simulate the BPSK equalizer  is chosen as
is chosen as  %,
%,  %,
%,  %,
%,  %, and
%, and  %, such that the number of nonzero taps in the CIR is 10, 20, 40, 60, and 80, respectively. Figure 17 shows the performance of the BPSK HNN MLSE equalizer in a sparse channel of length
%, such that the number of nonzero taps in the CIR is 10, 20, 40, 60, and 80, respectively. Figure 17 shows the performance of the BPSK HNN MLSE equalizer in a sparse channel of length  , compared to its performance in dense channels of length
, compared to its performance in dense channels of length  to
to  . It is clear from Figure 17 that the performance of the BPSK HNN MLSE equalizer in sparse is better compared to the corresponding equivalent dense channels. Because of the approximate independence of the computational complexity on the CIR length, the increase in complexity due to larger
. It is clear from Figure 17 that the performance of the BPSK HNN MLSE equalizer in sparse is better compared to the corresponding equivalent dense channels. Because of the approximate independence of the computational complexity on the CIR length, the increase in complexity due to larger  is negligible.
is negligible.
The 16-QAM HNN MLSE equalizer is also simulated for sparse channels, where the uncoded block length is  and the channel delay spread is
and the channel delay spread is  which corresponds to
which corresponds to  ms. Here,
ms. Here,  is chosen as
is chosen as  % and
% and  % such that the number of nonzero taps in the CIR is 25 and 40, respectively. Figure 18 shows the performance of the 16-QAM HNN MLSE equalizer in a sparse channel of length
% such that the number of nonzero taps in the CIR is 25 and 40, respectively. Figure 18 shows the performance of the 16-QAM HNN MLSE equalizer in a sparse channel of length  , compared to its performance in dense channels of length
, compared to its performance in dense channels of length  to
to  . Here, again it is clear that the performance of the equalizer in sparse channels is better than its performance in the corresponding equivalent dense channels. Again, the complexity increase for equalization in sparse channels is negligible.
. Here, again it is clear that the performance of the equalizer in sparse channels is better than its performance in the corresponding equivalent dense channels. Again, the complexity increase for equalization in sparse channels is negligible.
From the simulation results in Figures 17 and 18 it is clear that the HNN MLSE equalizer performs well in sparse channels compared to its performance in equivalent dense channels. Having an equal amount of nonzero nominal CIR taps, the performance increase in the sparse channels is not attributed to more diversity due to extra multipath, but rather to the higher level of interconnection between the neurons in the HNN. (Longer estimated CIRs will allow the connection matrix of the HNN to be more densely populated, increasing the level of interconnection between the neurons.) This allows the HNN MLSE equalizer to mitigate the effect of multipath more effectively to produce better performance in sparse channels than in their corresponding equivalent dense channels.
Figure 19 shows the performance of the BPSK HNN MLSE equalizer for various sparse channels, all with a fixed amount of nonzero nominal CIR taps such that the level of diversity due to multipath remains constant. Using an uncoded data block length of  and with
and with  such that
such that  for
for  %,
%,  %,
%,  % and
% and  % (corresponding to
% (corresponding to  ,
,  ,
,  and
and  ), it is clear that the performance increases as the CIR length
), it is clear that the performance increases as the CIR length  increases, although the number of multipath channels remains unchanged for all cases. Also, Figure 20 shows the performance of the 16-QAM HNN MLSE equalizer. Using an uncoded data block length of
increases, although the number of multipath channels remains unchanged for all cases. Also, Figure 20 shows the performance of the 16-QAM HNN MLSE equalizer. Using an uncoded data block length of  and with
and with  such that
such that  for
for  %,
%,  %,
%,  % and
% and  % (corresponding to
% (corresponding to  ,
,  ,
,  and
and  ), the performance increases with an increase in
), the performance increases with an increase in  .
.
From these results in is clear that the BER performance increases with an increase in  . The HNN MLSE equalizer thus exploits sparsity in communication channels by reducing the BER as the level of sparsity increases, given that the nonzero CIR taps remains constant.
. The HNN MLSE equalizer thus exploits sparsity in communication channels by reducing the BER as the level of sparsity increases, given that the nonzero CIR taps remains constant.
7. Conclusion
In this paper, a low complexity MLSE equalizer was proposed for use in single-carrier M-QAM modulated systems with extremely long memory. The equalizer has computational complexity quadratic in the data block length and approximately independent of the channel memory length. An extensive computational complexity analysis was performed, and the superior computational complexity of the proposed equalizer was graphically presented. The HNN was used as the basis of this equalizer due to its low complexity optimization ability. It was also highlighted that the complexity of the equalizer for any single carrier M-QAM system is independent of the number of symbols in the modulation alphabet, allowing for equalization in 256-QAM systems with equal computational cost as for 4-QAM systems, which is not possible with conventional optimal equalizers like the VA and MAP.
When the equalizer was evaluated for extremely long channels for perfect CSI its performance matched unfaded AWGN performance, providing enough evidence to assume that the equalizer performs optimally for extremely long channels. It is therefore assumed that the performance of the equalizer approaches optimality as the connection matrix of the HNN is populated. It was also shown that the HNN MLSE equalizer outperforms an MMSE equalizer at high  values.
values.
The HNN MLSE equalizer was evaluated for sparse channels and it was shown that its performance was better compared to its performance in equivalent dense channels, with a negligible increase in computational complexity. It was also shown how the equalizer exploits channel sparsity. The HNN MLSE equalizer is therefore very attractive for equalization in sparse channels, due to its low complexity and good performance.
With its low complexity equalization ability, the HNN MLSE equalizer can find application in systems with extremely long memory lengths, where conventional optimal equalizers cannot be applied.
References
Forney GD Jr.: Maximum likelihood sequence estimation of digital sequences in the presence of intersymbol interference. IEEE Transactions on Information Theory 1972, 18(3):363-378. 10.1109/TIT.1972.1054829
Viterbi AD: Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory 1967, 13(1):260-269.
Bahl LR, Cocke J, Jelinek F, Raviv J: Optimal decoding of linear codes for minimizing symbol error rate. IEEE Transactions on Information Theory 1974, 20(2):284-287.
Proakis JG: Digital Communications. 4th edition. McGraw-Hill, New York, NY, USA; 2001.
Duel-Hallen A, Heegard C: Delayed decision-feedback sequence estimation. IEEE Transactions on Communications 1989, 37(5):428-436. 10.1109/26.24594
Lee WU, Hill FS Jr.: A maximum likelihood sequence estimator with decision feedback equalizer. IEEE Transactions on Communications 1977, 25(9):971-979. 10.1109/TCOM.1977.1093930
Gerstacker WH, Schober R: Equalization concepts for EDGE. IEEE Transactions on Wireless Communications 2002, 1(1):190-199. 10.1109/7693.975457
Goldsmith A: Wireless Communications. Cambridge University Press, Cambridge, UK; 2005.
Terry J, Heiskala J: OFDM Wireless LANs: A Theoretical and Practical Guide. Sams, Indianapolis, Ind, USA; 2001.
Lopes RR, Barry JR: The soft-feedback equalizer for turbo equalization of highly dispersive channels. IEEE Transactions on Communications 2006, 54(5):783-788.
Stojanovic M, Freitag L, Johnson M: Channel-estimation-based adaptive equalization of underwater acoustic signals. Oceans 1999, 2: 985-990.
Zimmermann M, Dostert K: A multipath model for the powerline channel. IEEE Transactions on Communications 2002, 50(4):553-559. 10.1109/26.996069
Bergmans JWM: Digital Baseband Transmission and Recording. Springer, New York, NY, USA; 1996.
Myburgh HC, Olivier JC: Low complexity iterative MLSE equalization of M-QAM signals in extremely long rayliegh fading channels. Proceedings of the European International Science Fiction Convention (EUROCON '09), 2009 1632-1637.
Hopfield JJ, Tank DW: Neural computation of decisions in optimization problems. Biological Cybernetics 1985, 52(3):141-152.
Zeng HH, Ye L, Winters JH: Improved spatial-temporal equalization for EDGE: a fast selective-direction MMSE timing recovery algorithm and two-stage soft-output equalizer. IEEE Transactions on Communications 2001, 49(12):2124-2134. 10.1109/26.974259
Dayong X, Yang X, Haifeng D: An improved algorithm of MMSE multiuser detection for CDMA systems. Proceedings of the International Symposium on Communications and Information Technologies (ISCIT '05), 2005 1: 552-555.
Zhou H, Zhou S: Improved adaptive MMSE detector for downlink multi-cell MIMO signals. Proceedings of the 60th IEEE Vehicular Technology Conference (VTC '04), September 2004 3733-3737.
Czink N, Matz G, Seethaler D, Hlawatsch F: Improved MMSE estimation of correlated MIMO channels using a structured correlation estimator. Proceedings of the IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '05), 2005 595-599.
Park J-H, Whang Y, Kim KS: Low complexity MMSE-SIC equalizer employing time-domain recursion for OFDM systems. IEEE Signal Processing Letters 2008, 15: 633-636.
Rong Z, Guangqiu L: Low complexity code multiplexed pilot aided adaptive MMSE equalizerfor CDMA systems. Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, 2008 1-4.
Bang SH, Sheu BJ, Chang RC-H: Maximum likelihood sequence estimation of communication signals by a Hopfield neural network. Proceedings of the IEEE International Conference on Neural Networks, July 1994 5: 3369-3374.
Bang SH, Sheu BJ: A neural network for detection of signals in communication. IEEE Transactions on Circuits and Systems I 1996, 43(8):644-655. 10.1109/81.526680
Provence JD: Neural network implementation for an adaptive maximum-likelihood receiver. Proceedings of the IEEE International Symposium on Circuits and Systems, June 1988 3: 2381-2385.
Chen DC, Sheu BJ, Chou EY: A neural network communication equalizer with optimized solution capability. Proceedings of the IEEE International Conference on Neural Networks, June 1996 4: 1957-1962.
Hopfield JJ: Artificial neural networks. IEEE Circuits and Devices Magazine 1988, 4(5):3-10. 10.1109/101.8118
Olivier JC: Essential Digital Communication Theory. ESF320 Lecture notes, 2007
Russell S, Norvig P: Artificial Intelligence: AModern Approach. 2nd edition. Prentice-Hall, Upper Saddle River, NJ, USA; 2003.
Bang SH, Chen OT-C, Chang JC-F, Sheu BJ: Paralleled hardware annealing in multilevel Hopfield neural networks for optimal solutions. IEEE Transactions on Circuits and Systems II 1995, 42(1):46-49. 10.1109/82.363542
Bang SH, Sheu BJ, Chang JC-F: Search of optimal solutions in multi-level neural networks. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '94), June 1994 6: 423-426.
Halici U: Artificial Neural Networks. EE 543 Lecture notes, 2004
Farhang-Boroujeny B, Zhu H, Shi Z: Markov chain Monte Carlo algorithms for CDMA and MIMO communication systems. IEEE Transactions on Signal Processing 2006, 54(5):1896-1909.
Zheng YR, Xiao C: Improved models for the generation of multiple uncorrelated Rayleigh fading waveforms. IEEE Communications Letters 2002, 6(6):256-258. 10.1109/LCOMM.2002.1010873
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Myburgh, H.C., Olivier, J.C. Low Complexity MLSE Equalization in Highly Dispersive Rayleigh Fading Channels. EURASIP J. Adv. Signal Process. 2010, 874874 (2010). https://doi.org/10.1155/2010/874874
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/874874


 and the estimated CIR
and the estimated CIR 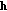 to calculate
to calculate 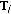 ,
, 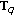 ,
, 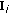 and
and 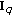 according to (11), (12), (15) and (16).
according to (11), (12), (15) and (16).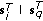 ] to
] to  .
.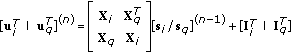 .
.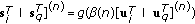 .
. and repeat until
and repeat until  , where
, where  is the predetermined number of iterations. (
is the predetermined number of iterations. ( iterations are used for the proposed equalizer.)
iterations are used for the proposed equalizer.)






 . The cost of multiplying a matrix of size
. The cost of multiplying a matrix of size 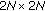 with a vector of size
with a vector of size 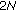 and adding another vector of length
and adding another vector of length 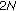 to the result,
to the result, 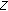 times, is given by
times, is given by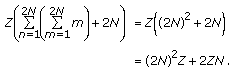

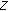 times. The cost of calculating the estimation vector
times. The cost of calculating the estimation vector  of length
of length 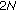 by using every value in state vector
by using every value in state vector  , also of length
, also of length  , assuming that the sigmoid function uses three instructions to execute,
, assuming that the sigmoid function uses three instructions to execute,  times, is given by (it is assumed that the values of
times, is given by (it is assumed that the values of 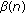 is stored in a lookup table, where
is stored in a lookup table, where 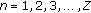 , to trivialize the computational complexity of simulated annealing)
, to trivialize the computational complexity of simulated annealing)
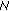 , where each stage contains
, where each stage contains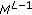 states, where
states, where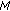 is the constellation size: It is assumed that this does not add to the complexity. It must however be noted that the dimensions of the trellis is
is the constellation size: It is assumed that this does not add to the complexity. It must however be noted that the dimensions of the trellis is 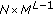 .
. addition terms, each containing one multiplication, from the received symbol at instant
addition terms, each containing one multiplication, from the received symbol at instant  . The cost for determining one Euclidean distance is therefore given by
. The cost for determining one Euclidean distance is therefore given by

 requires an if-statement. The cost is therefore
requires an if-statement. The cost is therefore




 (b)
(b)  (c)
(c)  (d)
(d)  .
.





