- Research Article
- Open access
- Published:
Improved Adaptive LSB Steganography Based on Chaos and Genetic Algorithm
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 876946 (2010)
Abstract
We propose a novel steganographic method in JPEG images with high performance. Firstly, we propose improved adaptive LSB steganography, which can achieve high capacity while preserving the first-order statistics. Secondly, in order to minimize visual degradation of the stego image, we shuffle bits-order of the message based on chaos whose parameters are selected by the genetic algorithm. Shuffling message's bits-order provides us with a new way to improve the performance of steganography. Experimental results show that our method outperforms classical steganographic methods in image quality, while preserving characteristics of histogram and providing high capacity.
1. Introduction
Steganography is the science of hiding messages in a medium called carrier or cover object in such a way that existence of the message is concealed. The cover object could be a digital still image, an audio file, or a video file. The hidden message called payload could be a plain text, an audio file, a video file, or an image [1, 2].
Steganographic methods can be classified into spatial domain embedding and frequency domain embedding. Least Significant Bit (LSB) replacing is the most widely used steganographic method in spatial domain, which replaces the cover image's LSBs with message bits directly. Although it has several disadvantages such as vulnerable to attacks, LSB steganography is a popular method because of its low computational complexity and high embedding capacity. In frequency domain, popular steganographic methods mostly base on Discrete Cosine Transformation (DCT). After performing DCT on each  block and quantizing the DCT coefficients, message bits are embedded into the quantized DCT (qDCT) coefficients. Recently, many steganographic schemes using LSB and its improved versions on qDCT have been invented, which offer reasonably high embedding capacity while attempting to preserve the marginal statistics of the cover image, such as J-Steg [3], F5 [4], and OutGuess [5]. It is well known that J-Steg is detectable using the
block and quantizing the DCT coefficients, message bits are embedded into the quantized DCT (qDCT) coefficients. Recently, many steganographic schemes using LSB and its improved versions on qDCT have been invented, which offer reasonably high embedding capacity while attempting to preserve the marginal statistics of the cover image, such as J-Steg [3], F5 [4], and OutGuess [5]. It is well known that J-Steg is detectable using the  attack [6, 7] since it is based on simply flipping LSBs. F5 employs matrix encoding to decrease the change for one payload, but its shrinkage at 0s makes it detectable. OutGuess embeds message bits into a part of coefficients and uses the other part to compensate artifacts on the histogram, so it preserves characteristics of histogram. But its embedding efficiency and capacity are low because of compensation.
attack [6, 7] since it is based on simply flipping LSBs. F5 employs matrix encoding to decrease the change for one payload, but its shrinkage at 0s makes it detectable. OutGuess embeds message bits into a part of coefficients and uses the other part to compensate artifacts on the histogram, so it preserves characteristics of histogram. But its embedding efficiency and capacity are low because of compensation.
Our contributions are in two folds. First, we present improved adaptive LSB steganography that can embed messages adaptively and thus can satisfy various requirements (high capacity, high security, high image quality, etc.). Second, our method minimizes degradation of the stego image through finding the best mapping between the secret message and the cover image based on chaos and the genetic algorithm (GA).
The rest of the paper is organized as follows. Section 2 introduces general principles of chaos and GA. Section 3 illustrates our proposed method in detail, which includes the improved adaptive LSB steganography, a method to shuffle message bits based on the logistic map and GA, the embedding procedure and the extraction procedure. Experimental results are shown in Section 4, where we demonstrate that our method has good stego image quality, high security-preserving characteristics of histogram, and high capacity. Finally, conclusions are addressed in Section 5.
2. Preliminary
2.1. Chaos and Its Application in Information Hiding
The chaos phenomenon is a deterministic and analogously stochastic process appearing in a nonlinear dynamical system [8, 9]. Because of its extreme sensitivity to initial conditions and the outspreading of orbits over the entire space, it has been used in information hiding to increase security [10, 11].
Logistic map is one of the simplest chaotic maps, described by

where  ,
,  .
.
Researches on chaotic dynamical systems show that the logistic map stands in chaotic state when  . That is, the sequence
. That is, the sequence  generated by the logistic map is nonperiodic and nonconvergent. All the sequences generated by the logistic map are very sensitive to initial conditions, in the sense that two logistic sequences generated from different initial conditions are uncorrelated statistically. The logistic map was used to generate a sequence as the watermark [11] or to encrypt the embedded position [10, 11] in former works. In our algorithm to be described below, we use the logistic map to shuffle bits-order of the message.
generated by the logistic map is nonperiodic and nonconvergent. All the sequences generated by the logistic map are very sensitive to initial conditions, in the sense that two logistic sequences generated from different initial conditions are uncorrelated statistically. The logistic map was used to generate a sequence as the watermark [11] or to encrypt the embedded position [10, 11] in former works. In our algorithm to be described below, we use the logistic map to shuffle bits-order of the message.
2.2. Genetic Algorithm
The genetic algorithm (GA), introduced by Holland [12] in his seminal work, is commonly used as an adaptive approach that provides a randomized, parallel, and global search. It bases on the mechanics of natural selection and genetics to find the exact or approximate solution for a given optimization problem.
GA is implemented as a computer simulation in which a population of abstract representations of candidate solutions to an optimization problem evolves toward better solutions. The evolution usually starts with some randomly selected genes as the first generation. All genes in a generation form a population. Each individual in the population is called chromosome, which corresponds to a solution in the optimization problem domain. An objective, called fitness function, is used to evaluate the quality of each chromosome. A new generation is recombined to find the best solution by using three operators: selection, crossover, and mutation [13]. The process is repeated until a predefined condition is satisfied.
Once we have the genetic representation and the fitness function defined, pseudocode algorithm of GA is illustrated as follows.
-
(1)
Generate initial population.
-
(2)
Evaluate the fitness of each individual in the population.
-
(3)
Select best-ranking individuals to reproduce.
-
(4)
Breed a new generation through crossover and mutation (genetic operations) and give birth to offspring.
-
(5)
Evaluate the individual fitness of the offspring.
-
(6)
Replace the worst ranked part of population with offspring.
-
(7)
Repeat
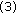 to (6) until termination condition is satisfied.
to (6) until termination condition is satisfied.
3. Our Proposed Method
3.1. Improved Adaptive LSB (IA-LSB) Steganography
The classical LSB steganography replaces cover images' LSBs with messages' bits directly. This embedding strategy leads to dissymmetry. When the LSB of a coefficient in the cover image equals to its corresponding message bit, no change is made. Otherwise, this coefficient is changed from  to
to  or from
or from  to
to  —changes from
—changes from  to
to  or from
or from  to
to  never happen. This dissymmetry is utilized by steganalysis, known as
never happen. This dissymmetry is utilized by steganalysis, known as  attack [6, 7].
attack [6, 7].
In order to avoid dissymmetry, improved adaptive LSB (IA-LSB) steganography is proposed. First, the number of bits to be embedded in a certain coefficient is adaptive. With proper parameters, we can get high capacity while preserving high security. Second, less modification rule (LMR) is used to minimize modification.
3.1.1. Adaptively Decide Bits to be Embedded in Each Coefficient
Let  denote the sequence of quantized DCT coefficients in a certain
denote the sequence of quantized DCT coefficients in a certain  JPEG block of the cover image. loc divides 64 coefficients into two parts. In the first part,
JPEG block of the cover image. loc divides 64 coefficients into two parts. In the first part,  bits are embedded into each valid coefficient, and in the second part,
bits are embedded into each valid coefficient, and in the second part,  bits are embedded (shown in Figure 1). We can adjust
bits are embedded (shown in Figure 1). We can adjust  ,
,  , and loc to get high performance according to the content of the cover image.
, and loc to get high performance according to the content of the cover image.
3.1.2. Less Modification Rule (LMR)
Suppose  is assigned to hold
is assigned to hold  bits. Denote
bits. Denote  's corresponding
's corresponding  message bits as
message bits as  decimally, and denote its corresponding coefficient in the stego image as
decimally, and denote its corresponding coefficient in the stego image as  . Let
. Let  be the decimal expression of the least significant
be the decimal expression of the least significant  bits of
bits of  . That is,
. That is,  .
.
Let  ,
,  be two candidates for
be two candidates for  . Because
. Because  ,
,  and
and  hold the same message bits. In classical LSB steganography,
hold the same message bits. In classical LSB steganography,  . In our method,
. In our method,  or
or  is chosen according to less modification rule formulated as follows:
is chosen according to less modification rule formulated as follows:

In this rule, we always choose the change that introduces less modification. For example, if  ,
,  , and
, and  , then
, then  ,
,  ,
,  .
.  , but the absolute value of change from
, but the absolute value of change from  to
to  is 3 while to
is 3 while to  is 1, so choose
is 1, so choose  as
as  . Take another example,
. Take another example,  ,
,  and
and  , then
, then  ,
,  ,
,  . In this case, choose
. In this case, choose  , which is closer to
, which is closer to  , as
, as  .
.
3.2. Shuffle Message Bits Based on Chaos and Genetic Algorithm
Shuffling message bits changes the way of modifying the cover image during embedding thus influences image quality and security of the stego image. By finding a proper way to shuffle, we can improve the image quality or security or both. In this paper, we use the logistic map for shuffling and use GA to find proper parameters for the logistic map.
Denote the message with length  as
as  . The process of using the logistic map to shuffle is stated as follows.
. The process of using the logistic map to shuffle is stated as follows.
-
(1)
Given a pair of input
 , the logistic map will generate a sequence
, the logistic map will generate a sequence 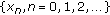 . Wipe off the first
. Wipe off the first 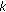 (e.g. 1000) elements of the sequence, and use the consecutive
(e.g. 1000) elements of the sequence, and use the consecutive 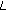 different elements to form a vector
different elements to form a vector 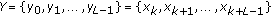 .
. -
(2)
Sort the elements of
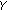 in descending order. The suffixes of the sorted elements form a sequence
in descending order. The suffixes of the sorted elements form a sequence  .
. -
(3)
Shuffle message bits according to
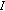 . That is, the message bit with suffix
. That is, the message bit with suffix  in
in 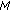 is put to position
is put to position  .
.
Here comes an example of using the logistic map to shuffle message bits. Let  ,
,  , then
, then  , and shuffled message sequence is
, and shuffled message sequence is  .
.
From the shuffling process mentioned above, we can see that the pair of parameters  decides the order of shuffled message bits. In order to improve the performance of the shuffling method, GA is used to select a proper pair of
decides the order of shuffled message bits. In order to improve the performance of the shuffling method, GA is used to select a proper pair of  . In our scheme, we choose to improve quality of the stego image in the sense of PSNR and select PSNR as GA's fitness function:
. In our scheme, we choose to improve quality of the stego image in the sense of PSNR and select PSNR as GA's fitness function:

where  and
and  are number of rows and columns of the cover image, respectively;
are number of rows and columns of the cover image, respectively;  is the difference between coefficients in spatial domain at position
is the difference between coefficients in spatial domain at position  in the cover image and in the stego image. The process of using GA to maximize PSNR is shown in Figure 2 and stated as follows.
in the cover image and in the stego image. The process of using GA to maximize PSNR is shown in Figure 2 and stated as follows.
-
(1)
Initialize population. Randomly generate
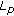 pairs of
pairs of 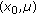 ,
, 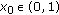 ,
, 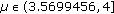 .
.  is the size of population and each
is the size of population and each  is an individual.
is an individual. -
(2)
For each
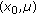 , shuffle message bits and embed the reordered message bits into the cover image using IA-LSB steganography, then compute PSNR between the cover image and the stego image, which is the fitness function of GA. In the following operations, the individual with larger fitness function will be considered better.
, shuffle message bits and embed the reordered message bits into the cover image using IA-LSB steganography, then compute PSNR between the cover image and the stego image, which is the fitness function of GA. In the following operations, the individual with larger fitness function will be considered better. -
(3)
GA operators—selection, crossover, and mutation—are operated to generate the next generation.
-
(4)
Repeat
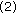 and
and 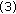 till the number of generations equals maximum generation
till the number of generations equals maximum generation 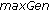 (e.g., 100).
(e.g., 100). -
(5)
Put out the best pair of
 selected by GA.
selected by GA.
3.3. Embedding Procedure
A coefficient  is valid, if
is valid, if  and it is not a DC coefficient. The whole embedding procedure is depicted in Figure 3. Firstly, the message bits are shuffled by the logistic map whose input pair
and it is not a DC coefficient. The whole embedding procedure is depicted in Figure 3. Firstly, the message bits are shuffled by the logistic map whose input pair  is selected by GA. Secondly, the cover JPEG file is decoded, obtaining quantized DCT coefficients. Thirdly, the shuffled message bits are embedded into the valid quantized DCT coefficients using IA-LSB steganography. Finally, stego quantized DCT coefficients are encoded to the stego JPEG file.
is selected by GA. Secondly, the cover JPEG file is decoded, obtaining quantized DCT coefficients. Thirdly, the shuffled message bits are embedded into the valid quantized DCT coefficients using IA-LSB steganography. Finally, stego quantized DCT coefficients are encoded to the stego JPEG file.
It needs to be taken into consideration that valid coefficients after embedding should still be valid, that is, valid coefficients should not be changed to 0. On one hand, characteristics of histogram can be preserved; on the other hand, message bits can be extracted correctly and simply. If  ,
,  . To add or subtract
. To add or subtract  is determined randomly.
is determined randomly.
3.4. Extracting Procedure
After receiving the stego JPEG file and  , we can extract the message bits as showed in Figure 4. First, the stego JPEG file is entropy decoded to obtain stego quantized DCT coefficients. Second, the shuffled message bits are extracted from LSBs of valid coefficients. Thirdly, the shuffled message bits are reordered to there natural order using logistic map with
, we can extract the message bits as showed in Figure 4. First, the stego JPEG file is entropy decoded to obtain stego quantized DCT coefficients. Second, the shuffled message bits are extracted from LSBs of valid coefficients. Thirdly, the shuffled message bits are reordered to there natural order using logistic map with  as input. Message bits are obtained.
as input. Message bits are obtained.
4. Experiments
In this section, we demonstrate the performance of our proposed method and compare it with that of F5 [14], MB1 [15], and Outguess [16]. The image quality of each steganography method is expressed objectively in PSNR. Standard  gray-level and true color images with sizes of
gray-level and true color images with sizes of  are used as covers, such as Lena, Baboon, and Couple. The JPEG quality factor is set to
are used as covers, such as Lena, Baboon, and Couple. The JPEG quality factor is set to  during compression in each method.
during compression in each method.
4.1. Image Quality
In order to demonstrate validity of shuffling message bits, we compare the PSNR of images embedded by IA-LSB steganography with and without shuffling message bits. The results of gray images are shown in Table 1. Shuffling message bits does improve the PSNR of the stego image. It can also be applied to other steganographic algorithms and provides us with a new way to improve performance of steganography. Moreover, Table 2 shows that this scheme of shuffling is not only applicable to gray images but also color images.
Figure 5 shows the PSNR of our method, F5, and MB1. The results are averaged on 50 gray-level images. We can see that the PSNR of our proposed method is higher than that of F5 and MB1. For the capacity of Outguess is around 0.3 bpc, it is not shown in the figure. The PSNR of Outguess is not higher than 32.86 db at 0.3 bpc (bit per nonzero AC coefficient) but of our method is higher than 37 db even at 0.72 bpc. We can conclude that our method outperforms F5, MB1, and Outguess in image quality.
4.2. Preserving Characteristics of Histogram
As a representative example, Figure 6 plots distribution of the (2,1)th quantized AC components for cover image "Lena" and its corresponding stego image with an embedding rate of 0.46 bpc. The red line illustrates the coefficients distribution of a stego image with our proposed method, and green bars illustrate that of the cover image. Figure 6 shows that our method preserves the characteristics of histogram. This is also true for the other components (e.g., (1,2)th, (2,2)th AC components) and the other testing images.
5. Conclusion
A steganographic method uses IA-LSB based on chaos and genetic algorithm is proposed. After finding the best parameters for the logistic map using GA, rearrange the secret message and embed it into the cover image using IA-LSB. Experimental results demonstrate that our algorithm achieves high embedding capacity while preserving good image quality and high security.
The important and distinctive features in the proposed method are to minimize the degradation of stego image by shuffling the secret message based on the logistic map and GA. To find better mapping between the secret message and the cover image so as to improve the steganographic performance is our future work.
References
Silman J: Steganography and steganalysis: an overview. SANS Institute; 2001.
Jamil T: Steganography: the art of hiding information in plain sight. IEEE Potentials 1999, 18(1):10-12. 10.1109/45.747237
Upham D1997, http://zooid.org/~paul/crypto/jsteg/
Westfeld A: F5-a steganographic algorithm. Proceedings of the 4th International Workshop on Information Hiding, 2001, Pittsburgh, Pa, USA 289-302.
Provos N: Defending against statistical steganalysis. Proceedings of the 10th USENIX Security Symposium, 2001, Washington, DC, USA 323-335.
Westfeld A, Pfitzmann A: Attacks on steganographic systems. Proceedings of the 3rd International Workshop on Information Hiding, 2000
Provos N, Honeyman P: Detecting steganographic content on the internet. Center for Information Technology Integration, University of Michigan; 2001.
Liu Z, Xi L: Image information hiding encryption using chaotic sequence. Proceedings of the 11th International Conference on Knowledge-Based Intelligent Information and Engineering Systems and the XVII Italian Workshop on Neural Networks, 2007 202-208.
Zhang Y, Zuo F, Zhai Z, Xiaobin C: A new image encryption algorithm based on multiple chaos system. Proceedings of the International Symposium on Electronic Commerce and Security (ISECS '08), August 2008 347-350.
Munir R, Riyanto B, Sutikno S, Agung WP: Secure spread spectrum watermarking algorithm based on chaotic map for still images. Proceedings of the International Conference on Electrical Engineering and Informatics, 2007
Dawei Z, Guanrong C, Wenbo L: A chaos-based robust wavelet-domain watermarking algorithm. Chaos, Solitons and Fractals 2004, 22(1):47-54. 10.1016/j.chaos.2003.12.104
Holland JH: Adaptation in Natural and Artificial Systems. MIT Press, Cambridge, Mass, USA; 1992.
Wu Y-T, Shih FY: Genetic algorithm based methodology for breaking the steganalytic systems. IEEE Transactions on Systems, Man, and Cybernetics B 2006, 36(1):24-31.
http://os.inf.tu-dresden.de/~westfeld/publikationen/f5r11.zip
Acknowledgments
This work was supported in part by National Natural Science Foundation of China (no. 60776794, no. 90604032, and no. 60702013), 973 program (no. 2006CB303104), 863 program (no. 2007AA01Z175), Beijing NSF (no. 4073038), and Specialized Research Foundation of BJTU (no. 2006XM008 and no. 2005SZ005).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yu, L., Zhao, Y., Ni, R. et al. Improved Adaptive LSB Steganography Based on Chaos and Genetic Algorithm. EURASIP J. Adv. Signal Process. 2010, 876946 (2010). https://doi.org/10.1155/2010/876946
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/876946
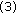 to (6) until termination condition is satisfied.
to (6) until termination condition is satisfied.
 , the logistic map will generate a sequence
, the logistic map will generate a sequence 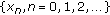 . Wipe off the first
. Wipe off the first 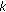 (e.g. 1000) elements of the sequence, and use the consecutive
(e.g. 1000) elements of the sequence, and use the consecutive 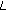 different elements to form a vector
different elements to form a vector 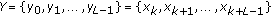 .
.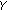 in descending order. The suffixes of the sorted elements form a sequence
in descending order. The suffixes of the sorted elements form a sequence  .
.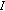 . That is, the message bit with suffix
. That is, the message bit with suffix  in
in 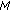 is put to position
is put to position  .
.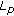 pairs of
pairs of 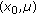 ,
, 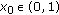 ,
, 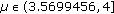 .
.  is the size of population and each
is the size of population and each  is an individual.
is an individual.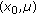 , shuffle message bits and embed the reordered message bits into the cover image using IA-LSB steganography, then compute PSNR between the cover image and the stego image, which is the fitness function of GA. In the following operations, the individual with larger fitness function will be considered better.
, shuffle message bits and embed the reordered message bits into the cover image using IA-LSB steganography, then compute PSNR between the cover image and the stego image, which is the fitness function of GA. In the following operations, the individual with larger fitness function will be considered better.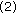 and
and 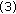 till the number of generations equals maximum generation
till the number of generations equals maximum generation 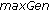 (e.g., 100).
(e.g., 100). selected by GA.
selected by GA.



