- Research Article
- Open access
- Published:
Adaptive Wavelet Transform Method to Identify Cracks in Gears
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 879875 (2010)
Abstract
Many damages and faults can cause problems in gear unit operation. A crack in the tooth root is probably the least desirable among them. It often leads to failure of gear unit operation. By monitoring vibrations, it is possible to determine the presence of a crack. Signals are, however, very noisy. This makes it difficult to define properties of individual components. Wavelet analysis is an effective tool for analysing signals and for defining properties. In this paper, a denoising method based on wavelet analysis, which takes prior information about impulse probability density into consideration, is used to identify transient information from vibration signals of a gear unit with a fatigue crack in the tooth root.
1. Introduction
The aim of maintenance is to keep a technical system (gear unit) in the most suitable working condition, and its purpose is to discover, to diagnose, to foresee, to prevent and to eliminate damages. The purpose of modern maintenance, however, is not only to eliminate failures but also to define the stage of a potential danger of a sudden failure of system operation. The aim of diagnostics is to define the current condition of the system and the location, shape, and reason of damage formation. The following diagnostic values are used to define incorrect operation, the possibility and location of damages, and the possibility of elimination of these damages: different signals, condition parameters, and other indirect signs. Identification of the form of damage is based on deviations from the values typical of a faultless gear system.
Gear units are often used in various industrial applications. Consequently, it is of utmost significance to identify fault symptoms of a gear unit at an early stage. It is vibration signals that are primarily used to identify faults but they are always complex and it is difficult to identify faults in gear units on the basis of vibration signals. Acquired vibration signals often contain a lot of noise. With too much noise, the useful information is corrupted to such an extent that it is impossible to establish the condition or that a wrong conclusion is made.
A gear unit consists of elements enabling the transmission of rotating movement. Although a gear unit is a complex dynamic model, its movement is usually periodical; faults and damages represent a disturbing quantity or impulse. Local and time changes in vibration signals indicate the disturbance [1, 2] and it is possible to expect time-frequency changes [3]. This idea is based on kinematics and operating characteristics [4, 5].
It is of key importance to apply effective methods for the identification (extraction) of properties from noisy signals. Wavelet analysis is one such effective tool. It is especially suitable when it comes to processing nonstationary signals. Local energy distributions in time domain and frequency domain are typical of transient property components of vibration signals, which resemble a wavelet function. It is possible to use wavelet functions to detect transient property components due to similar structures.
It is possible to apply wavelets to extract features and purge noise. Matching pursuits by Mallat [6] and soft-threshold denoising by Donoho and Johnstone [7, 8] are among such procedures. Threshold in the wavelet domain is used for threshold denoising. It is possible to present that this is asymptotically almost optimal for many signals, which have been corrupted by additive white Gaussian noise. However, feature components of many mechanical dynamic signals consist of impulse components. This method, however, has not been proved effective for impulse component extraction. Smoothness of the signal that will be isolated is assumed by all previously mentioned methods, based on orthogonal wavelet transforms. The transient components, which are treated as noise, vary quickly. Some of these methods result in an even greater smoothness than in case of the original signal. Consequently, existing denoising methods are not suitable for vibration analysis of signals produced by gears as impulses that need to be isolated are not smooth. For threshold denoising, Morlet wavelet is used, and similarity between the Morlet wavelet and impulse is applied. If nonorthogonal wavelet transform is used, this does not ensure that, after the transform, independent and identically distributed noise retains this characteristic on each scale. After nonorthogonal wavelet transforms, statistical noise attributes become different as rules that apply for thresholding when orthogonal wavelet transforms are used are not suitable for thresholding when nonorthogonal wavelet transforms are involved.
The technique with high-order statistics was sometimes more successful. The shape of the amplitude distribution of vibration data is described on the basis of statistical moments. However, oversensitivity to vibration and noise is characteristic of higher moments whereas lower moments are less sensitive to early-stage fault. As a result, in relation to statistical moments used in practice, only the fourth normalized moment (kurtosis) and third normalized moment are useful. If a defect must be identified at a very early stage, kurtosis is preferred over the third moment as this implies higher sensitivity to impulse signals [9]. Thus, the third and fourth moments have some disadvantages, and to eliminate these disadvantages, a class of new diagnostic gear failure indexes have been derived, based on Renyi entropy, to describe vibration signature and to optimise the parameter of the wavelets. They present, so to speak, a generalization of traditional statistical moments. Nannone and Morabito [10] used wavelet entropy to extract features from complex signals in medicine, and Tao et al. [11] and Qiu et al. [12] used in mechanical systems.
In order to make denoising more effective, a new denoising method based on Morlet wavelet with adjustment of the shape of the wavelet filter based on the Renyi entropy and maximum likelihood estimation denoising method for non-Gaussian data is proposed in this paper; this method is particularly useful to extract impulse components. With the new specific threshold rule, based on the maximum likelihood estimation, the information regarding the probability density function of the impulse is taken into consideration.
2. Wavelet Analysis
The continuous wavelet transform of function  at the time and scale is expressed as follows [6]:
at the time and scale is expressed as follows [6]:



where the transform is presented as the product of convolution; (2) presents the expression of an average wavelet function and the corresponding Fourier integral transform, (3).
At the continuous wavelet transform, the observed function  is multiplied by a group of shifted and scaled wavelet functions. A simultaneous change in time and frequency dissemination of the continuous wavelet transform can be observed. Wavelets, as locally limited functions, are used to analyse the observed function
is multiplied by a group of shifted and scaled wavelet functions. A simultaneous change in time and frequency dissemination of the continuous wavelet transform can be observed. Wavelets, as locally limited functions, are used to analyse the observed function  . The continuous wavelet transform is very sensitive to local nonstationarities.
. The continuous wavelet transform is very sensitive to local nonstationarities.
Morlet wavelet function, which is a representative of a nonorthogonal wavelet function:

Equation (5) yields a family of wavelet functions or a shifted  and scaled
and scaled  Morlet wavelet function is
Morlet wavelet function is

Various wavelet basis functions were selected in wavelet applications. Theoretically speaking, any function that is finite in time and frequency can be used for the basis function. Several types of functions can be used as a wavelet basis; the selection depends on the application-related requirements [13, 14].
The Morlet wavelet was used as the basis function due to the similarity of formulation with Gabor transform function that was researched in our laboratory. The Gabor transform has some properties in Fourier transforms. The only difference between the Morlet wavelet and Gabor transform is in the exponent term, which helps determine the shape of the wavelet.
Using the expression in (5), the time function can be further transformed to the frequency domain as shown below:

The Morlet wavelet is a complex wavelet and it can be decomposed into two parts—one of them for the real part and the other one for the imaginary part:

where  is the shape parameter, balancing time resolution and frequency resolution of the Morlet wavelet.
is the shape parameter, balancing time resolution and frequency resolution of the Morlet wavelet.
It is evident from (6) that the shape of the basic wavelet is controlled by parameter  . With the reduction of
. With the reduction of  , the frequency resolution will increase whereas time resolution will decrease. When
, the frequency resolution will increase whereas time resolution will decrease. When  tends to be infinite, the Morlet wavelet becomes a Dirac function with the finest time resolution. With
tends to be infinite, the Morlet wavelet becomes a Dirac function with the finest time resolution. With  tending to be 0, the Morlet wavelet becomes a cosine function with the finest frequency resolution. Therefore, there is always an optimal
tending to be 0, the Morlet wavelet becomes a cosine function with the finest frequency resolution. Therefore, there is always an optimal  with the best time-frequency resolution for a certain signal localized in the time-frequency plane.
with the best time-frequency resolution for a certain signal localized in the time-frequency plane.
Only the real part is usually used. The real part of the Morlet wavelet is a cosine signal decaying exponentially on the left and right side, and its function shape is similar to an impulse. Because of this similarity the Morlet wavelet is widely used in mechanical fault diagnostic applications.
By time translation and scale dilation, a daughter Morlet wavelet is acquired from the mother wavelet:

where  is the scale parameter for dilation and
is the scale parameter for dilation and  for time translation. It is possible to construct, by selecting parameters
for time translation. It is possible to construct, by selecting parameters  and
and  , a daughter Morlet wavelet closely matching the shape of a mechanical impulse.
, a daughter Morlet wavelet closely matching the shape of a mechanical impulse.
It is required to first define the location and shape of the frequency band corresponding to the impulses in order to define the impulses by means of filtering. Location and shape of the daughter Morlet wavelet are controlled by scale  and parameter
and parameter  . Due to this, it is possible to, by optimising the two parameters for a daughter wavelet, build an adaptive wavelet filter. The selection of the mother wavelet that adapts best to the signal to be isolated was dealt with by several researchers [15–17]. It is not required to carry out optimal wavelet reconstruction but to find the best daughter wavelet. Differences between single- and double-sided Morlet wavelets were dealt with by Wang [18]. Their frequency spectra are quite different. A real impulse is usually nonsymmetric, and, consequently, the right-hand side of Morlet wavelet was selected to be used as the basis. Such wavelets should be most appropriate to match the behaviour of hidden impulses.
. Due to this, it is possible to, by optimising the two parameters for a daughter wavelet, build an adaptive wavelet filter. The selection of the mother wavelet that adapts best to the signal to be isolated was dealt with by several researchers [15–17]. It is not required to carry out optimal wavelet reconstruction but to find the best daughter wavelet. Differences between single- and double-sided Morlet wavelets were dealt with by Wang [18]. Their frequency spectra are quite different. A real impulse is usually nonsymmetric, and, consequently, the right-hand side of Morlet wavelet was selected to be used as the basis. Such wavelets should be most appropriate to match the behaviour of hidden impulses.
It is required to determine the location and shape of the frequency band corresponding to the impulses in order to identify the immersed impulses by means of filtering. As a result, it is possible to form an adaptive wavelet filter by optimising the parameter  for a daughter wavelet. Here it is presented how to find the best wavelet filter (the daughter wavelet of a Morlet wavelet) instead of optimal wavelet reconstruction.
for a daughter wavelet. Here it is presented how to find the best wavelet filter (the daughter wavelet of a Morlet wavelet) instead of optimal wavelet reconstruction.
In relation to optimising the wavelet base, sparsity is usually applied in order to evaluate the wavelet base. Since the wavelet that corresponds to the smallest number of signal wavelet transformation coefficients is the most optimal, it is possible to define the value  by establishing which wavelet coefficients are the sparsest. Renyi entropy can be applied to measure the diversity of a possibility series. It is, therefore, possible to use entropy of wavelet coefficients to measure sparsity of coefficients of these wavelets.
by establishing which wavelet coefficients are the sparsest. Renyi entropy can be applied to measure the diversity of a possibility series. It is, therefore, possible to use entropy of wavelet coefficients to measure sparsity of coefficients of these wavelets.
Renyi entropy, which is sometimes referred to as measure of uncertainty, is of a random variable and is determined on the basis of its probability distribution. It is possible to present it as a good measure of randomness and sparseness.
Entropy, as information measure of randomicity of random events, depends on event probability distribution. By analogy, considering signal amplitude distribution, entropy is sensitive also to the shape of discrete signals amplitude distribution. Small entropy values are associated with peak signals for which small numbers of large amplitude components are typical; on the other hand large entropy values are related to signals dominated by equal amplitude components. It is possible to consider wavelet transform coefficients with minimal Renyi entropy as the sparsest result. By means of this typical feature, Renyi entropy, on the basis of which a class of new diagnostic indices are derived in order to carry out condition monitoring of gear units, has introduced a generalized statistical moment concept along with its analytic expression.
Renyi entropy is sensitive to sharp variant structures in signal, for example, impulses. Consequently it is applied to detect fault symptoms [19]. The bigger the impulse in signals, the smaller the Renyi entropy value.
Renyi entropy definition is based on the theory of means [19]:

where  is a continuous and strictly monotonic function subclass of Kolmogorov-Nagumo functions. To meet the constraints of an information measure,
is a continuous and strictly monotonic function subclass of Kolmogorov-Nagumo functions. To meet the constraints of an information measure,

 is any information measure. By simplifying the above relation,
is any information measure. By simplifying the above relation,

The third order Renyi entropy  is calculated on the basis the wavelet representations:
is calculated on the basis the wavelet representations:

3. Wavelet Denoising
The aim of wavelet threshold denoising method, which was introduced by Donoho [7], is to remove independent and identically distributed Gaussian noise. A signal series  , which is acquired using a sensor, consists of impulses and noise. It is possible to express
, which is acquired using a sensor, consists of impulses and noise. It is possible to express  as follows:
as follows:

where  denotes the impulses to be determined whereas
denotes the impulses to be determined whereas  denotes the noise with mean zero and standard deviation
denotes the noise with mean zero and standard deviation  .
.
Wavelet threshold denoising method is based on the idea of the concentration of energy of the signal that needs to be identified on a few wavelet coefficients and of the spreading of noise energy throughout all wavelet coefficients. It is of importance to make signal concentrate on fewer coefficients, in relation to which similarity between basic wavelet and signal that must be identified plays an important role. The components of the impulse must be made as expressed as possible in order to improve the impulse isolation performance.
It is assumed by all traditional methods that noise properties are known, meaning that the noise is independent and identically distributed. In industrial applications, however, some data on the signal to be detected is often available but the exact behaviour of the noise is not known. The maximum likelihood estimation denoising method is suitable for non-Gaussian data.
Prior information on the impulse probability density function is taken into consideration in a specific threshold rule, based on the maximum likelihood estimation method. As to this rule, it is not necessary that the noise is independent and identically distributed Gaussian. It is, however, required to know in advance the probability density function of the impulse to be defined.
Hyvärinen introduced the so-called ''sparse code shrinkage'' method, which estimates non-Gaussian data under noisy conditions and is based on the maximum likelihood estimation principle [20].
For a very sparse probability density function, Hyvärinen [20] used the following function to represent a sparse distribution:

where  indicates the standard deviation of the impulse to be isolated whereas
indicates the standard deviation of the impulse to be isolated whereas  indicates the parameter controlling the sparseness of the probability density function.
indicates the parameter controlling the sparseness of the probability density function.
For an impulse, in relation to which the probability density function can be represented by (9), Hyvärinen used the sparse shrinkage threshold rule [20]:

where  indicates the standard deviation of the noise.
indicates the standard deviation of the noise.
The following steps are used for the denoising method based on appropriate wavelet Morlet filter.
-
(1)
The procedure of achieving the appropriate wavelet. In order to produce different daughter wavelets, modify the parameters
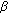 .
. -
(2)
Calculate the entropy for each daughter wavelet.
-
(3)
To identify hidden impulses, it is very appropriate to use the parameter
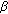 corresponding to the minimum Renyi entropy.
corresponding to the minimum Renyi entropy. -
(4)
Signal decomposition. To perform a wavelet transform for the signal, use the Morlet wavelet with appropriate parameter
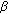 corresponding to the minimum Renyi entropy. To obtain the wavelet coefficients, use (8).
corresponding to the minimum Renyi entropy. To obtain the wavelet coefficients, use (8). -
(5)
To shrink the wavelet coefficients, use the threshold rule from (15).
-
(6)
Signal reconstruction. Perform the inverse transform of the shrunken wavelet coefficients. The result represents an approximation to the impulse to be isolated. Let
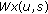 be reconstructed coefficients. Then, to purify the signal, use the following equation [6]:
be reconstructed coefficients. Then, to purify the signal, use the following equation [6]: (16)
(16)
4. Practical Example
The test used for the measurements is shown in Figure 1. It belongs to the Computer Aided Design Laboratory of the Faculty of Mechanical Engineering, University of Maribor.
A single stage gear unit EZ6.B3.132 produced by Strojna Maribor was used. A helical gear unit with straight teeth was integrated into the gear unit [9]. The pinion had 19 and the wheel 34 teeth. Each gear unit had a carburised spur gear pair (module: 4 mm). Accelometers for measuring vibrations were fixed on the housings. Tests were carried out under constant loads. The presented results refer to a nominal pinion torque of 30 Nm and a nominal pinion speed of 1200 rpm (20 Hz), which is, in industrial applications, a very typical load condition for this type of gear units.
We used a standard ground gear pair, shown in Figure 2, with teeth quality 6 but with a 4.5 mm crack in a tooth root of a pinion. Measurements were performed under the operating conditions typical of this type of a gear unit. The measurement process and analysis preparations are presented in detail in [9].
Pinion with a fatigue crack in the tooth root [ 21 ].
4.1. Comparison Analysis of Practical Signals
To carry out first comparisons, continuous wavelet transform for tested gear unit with frequency scalograms was prepared.
Morlet wavelet function represents normalised and square values of wavelet coefficients amplitudes. The representation is carried out in a time-frequency domain due to the established connection between the scale and frequency. It is much simpler to establish adequate characteristics in time-frequency domain (frequency scalogram) than in time-scale domain (scalogram). Consequently, this is very appropriate when it comes to technical diagnostics. The energy of wavelet transform equals the energy of the original signal in time domain as, on the basis of normalization, the transform matches the Parseval characteristic of energy preservation.
The continuous wavelet transform with parameters  and
and  was used. The representation of the frequency scalogram is in the form of wavelet coefficients or their square values. The analysis was based on a part of the signal only, representing one whole rotation of the gear (of a pinion with a crack), which took 50 ms.
was used. The representation of the frequency scalogram is in the form of wavelet coefficients or their square values. The analysis was based on a part of the signal only, representing one whole rotation of the gear (of a pinion with a crack), which took 50 ms.
No particularities, which would denote local changes, can be observed from the figures, in the frequency scalogram, when it comes to the faultless gear. This applies both for a normal representation (Figure 3) of wavelet coefficients and for a square representation (Figure 4) of wavelet coefficients. When it comes to normal representation of wavelet coefficients (Figure 3), the resolution is much better in the lower frequency area; the reaction of each single tooth at the frequency of 380 Hz is expressed there. A minimum local change in wavelet coefficients, at 11 ms, can be noticed in the signal caused by a gear with a crack in frequency scalograms with square representation (Figure 5). In normal representation of wavelet coefficients, it is not possible to define the changes (Figure 6). For those techniques, a reference signal was used.
To carry out next comparisons, the standard denoising method is used in concern to actual data (Figures 7 and 8) related to practical signal presented. Different thresholds are used for this method. The signal de-noised by means of Stein's Unbiased Risk Estimation (SURE), Hybrid or heuristic SURE, minimax thresholds, and universal threshold, respectively, is presented in Figures 9, 10, 11, and 12. SURE threshold is associated with a quadratic loss function. An estimate of the risk is given for a particular threshold value. Minimizing the risks yields threshold value selection. Hybrid represents a heuristic variant of the SURE threshold. A fixed threshold is applied for minimax, it gives minimax performance for mean square error. The minimax principle is applied in statistics in relation to estimators. It is possible to assimilate the de-noised signal to the estimator of the unknown regression function, therefore, the minimax estimator realizes the minimum of the maximum mean square error for the worst function in a certain set. Signal length and noise standard deviation determine universal threshold.
It is evident from denoising results, after having used four different threshold strategies, that no strategy has presented the original signal with one impulse belonging to the crack in the tooth root. Also other factors have impact upon effectiveness of denoising. These factors include wavelet decomposition level and threshold rescaling method selection.
4.2. Results Analysis Concerning Practical Signals
Morlet wavelet was used to obtain the adaptive wavelet filter. The graph of the parameter  and Renyi entropy relationship is presented in Figure 13. The entropy is very sensitive to the value
and Renyi entropy relationship is presented in Figure 13. The entropy is very sensitive to the value  . Let parameter
. Let parameter  vary from 0.1 to 5 with a step size of 0.1. The minimal value of Renyi entropy is the optimal selection of
vary from 0.1 to 5 with a step size of 0.1. The minimal value of Renyi entropy is the optimal selection of  . When
. When  , the minimum value of entropy is 5.85, as shown in Figure 13. As a denoising method, the Morlet wavelet is used. Equation (14) with
, the minimum value of entropy is 5.85, as shown in Figure 13. As a denoising method, the Morlet wavelet is used. Equation (14) with  can be used to approximate the impulse probability density function. For each scale, MAD/0.6745 is used as the noise deviation estimator. For Morlet wavelet, the same parameters are applied as described before. Measured signals of vibrations of a faultless gear and of vibrations of a gear with a crack in the tooth root are presented in Figures 7 and 8. Figure 14 shows denoising signals of a faultless gear. It can be noted that no impulses exist in the signals, whereas Figure 15 shows results of filtering with optimized wavelet filter for signals of a gear with a crack; in these signals it is possible to observe impulses at 11 ms also after the noise has been removed.
can be used to approximate the impulse probability density function. For each scale, MAD/0.6745 is used as the noise deviation estimator. For Morlet wavelet, the same parameters are applied as described before. Measured signals of vibrations of a faultless gear and of vibrations of a gear with a crack in the tooth root are presented in Figures 7 and 8. Figure 14 shows denoising signals of a faultless gear. It can be noted that no impulses exist in the signals, whereas Figure 15 shows results of filtering with optimized wavelet filter for signals of a gear with a crack; in these signals it is possible to observe impulses at 11 ms also after the noise has been removed.
The signal length is 50 ms, representing one rotation of the pinion. 19 teeth are along the circumference. The increased amplitude is located at 11 ms and belongs to the fourth tooth in the direction of rotation from the reference positional point of the gear unit.
5. Conclusion
By means of adaptive wavelet transform it is possible both to define changes and to establish the presence of a damage or fault, at the level of an individual tooth. Adaptive wavelet denoising methods are very useful to determine local changes in gears. Wavelets optimised by means of the Renyi entropy match impulses very well. Consequently, it is possible to define impulses hidden in noise signals by means of the wavelet transform. The maximum likelihood estimation threshold rule and prior information on the probability density function of the signals to be identified are used. On the basis of this method, impulses were extracted from practical engineering signals; the results of this procedure are very reliable.
When it comes to life cycle design, the actual condition of a device and of its vital component parts, which influences the operational capability significantly, can be observed. It is beyond doubt that the reliability of operation control is significantly improved with in-time detection of faults and damages. If faults are detected in a very reliable way, this leads to a better prediction of the remaining life cycle of a gear unit.
References
Adewusi SA, Al-Bedoor BO: Wavelet analysis of vibration signals of an overhang rotor with a propagating transverse crack. Journal of Sound and Vibration 2001, 246(5):777-793. 10.1006/jsvi.2000.3611
Bruce AG, Donoho DL, et al.: Smoothing and robust wavelet analysis. Proceedings of the Computational Statistics 11th Symposium, 1994, Vienna, Austria 531-547.
Taylor JI: The Vibration Analysis Handbook. Vibration Consultans; 1994.
Derrek SJ: Gear Noise and Vibration. Marcel Dekker, New York, NY, USA; 1999.
Chen VC, Ling H: Time-Frequency Transforms. Artech House Publishers, Boston, Mass, USA; 2002.
Mallat S: A Wavelet Tour of Signal Processing. Academic Press, San Diego, Calif, USA; 1999.
Donoho DL: De-noising by soft-thresholding. IEEE Transactions on Information Theory 1995, 41(3):613-627. 10.1109/18.382009
Donoho DL, Johnstone IM: Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81(3):425-455. 10.1093/biomet/81.3.425
Belsak A: Time-frequency analysis of the condition of gear units (Abstract in English), Doctoral Thesis. Faculty of Mechanical Engineering, University of Maribor, Slovenia; 2006.
Nannone M, Morabito FC: Enhanced automatic artefact detection based on independent componenet analysis and Renyi entropy. Neural Networks 2008, 21: 1029-1040. 10.1016/j.neunet.2007.09.020
Tao B, Zhu L, Ding H, Xiong Y: Rényi entropy-based generalized statistical moments for early fatigue defect detection of rolling-element bearing. Proceedings of the Institution of Mechanical Engineers 2007, 221(1):67-79.
Qiu H, Lee J, Lin J, Yu G: Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. Journal of Sound and Vibration 2006, 289(4-5):1066-1090. 10.1016/j.jsv.2005.03.007
Strang G, Nguyen T: Wavelets and Filter Banks. Wellesley-Cambridge Press, Boston, Mass, USA; 1996.
Coifman R, Beylkin G, Rokhlin V: Fast wavelet transforms and numerical algorithms. Journal of Communication on Pure and Applied Mathematics 1991, 44: 141-183. 10.1002/cpa.3160440202
Boulahbal D, Golnaraghi MF, Ismail F: Amplitude and phase wavelet maps for the detection of cracks in geared systems. Mechanical Systems and Signal Processing 1999, 13(3):423-436. 10.1006/mssp.1998.1206
Shensa MJ: The discrete wavelet transform: wedding the atrous and Mallat algorithms. IEEE Transactions on Signal Processing 1992, 40(10):2464-2482. 10.1109/78.157290
McClure MR, Carin L: Matching pursuits with a wave-based dictionary. IEEE Transactions on Signal Processing 1997, 45(12):2912-2927. 10.1109/78.650250
Wang WJ: Wavelets for detecting mechanical faults with high sensitivity. Mechanical Systems and Signal Processing 2001, 15(4):685-696. 10.1006/mssp.2000.1369
Faust O, Acharya R, Krishnan SM, Min LC: Analysis of cardiac signals using spatial filling index and time-frequency domain. BioMedical Engineering Online 2004., 3, article no. 30:
Hyvärinen A: Sparse code shrinkage: denoising of nongaussian data by maximum likelihood estimation. Neural Computation 1999, 11(7):1739-1768. 10.1162/089976699300016214
Belsak A, Flasker J: Detecting cracks in the tooth root of gears. Engineering Failure Analysis 2007, 14(8):1466-1475. 10.1016/j.engfailanal.2007.01.013
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Belsak, A., Flasker, J. Adaptive Wavelet Transform Method to Identify Cracks in Gears. EURASIP J. Adv. Signal Process. 2010, 879875 (2010). https://doi.org/10.1155/2010/879875
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/879875
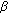 .
.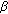 corresponding to the minimum Renyi entropy.
corresponding to the minimum Renyi entropy.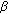 corresponding to the minimum Renyi entropy. To obtain the wavelet coefficients, use (8).
corresponding to the minimum Renyi entropy. To obtain the wavelet coefficients, use (8).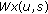 be reconstructed coefficients. Then, to purify the signal, use the following equation [
be reconstructed coefficients. Then, to purify the signal, use the following equation [














