- Research Article
- Open access
- Published:
Convergence Analysis of a Mixed Controlled 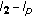 Adaptive Algorithm
Adaptive Algorithm
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 893809 (2010)
Abstract
A newly developed adaptive scheme for system identification is proposed. The proposed algorithm is a mixture of two norms, namely, the  -norm and the
-norm and the  -norm (
-norm ( ), where a controlling parameter in the range
), where a controlling parameter in the range  is used to control the mixture of the two norms. Existing algorithms based on mixed norm can be considered as a special case of the proposed algorithm. Therefore, our algorithm can be seen as a generalization to these algorithms. The derivation of the algorithm and its convexity property are reported and detailed. Also, the first moment behaviour as well as the second moment behaviour of the weights is studied. Bounds for the step size on the convergence of the proposed algorithm are derived, and the steady-state analysis is carried out. Finally, simulation results are performed and are found to corroborate with the theory developed.
is used to control the mixture of the two norms. Existing algorithms based on mixed norm can be considered as a special case of the proposed algorithm. Therefore, our algorithm can be seen as a generalization to these algorithms. The derivation of the algorithm and its convexity property are reported and detailed. Also, the first moment behaviour as well as the second moment behaviour of the weights is studied. Bounds for the step size on the convergence of the proposed algorithm are derived, and the steady-state analysis is carried out. Finally, simulation results are performed and are found to corroborate with the theory developed.
1. Introduction
The least mean square (LMS) algorithm [1] is one of the most widely used adaptive schemes. Several works have been presented using the LMS or its variants [2–14], such as signed LMS [8], the least mean fourth (LMF) algorithm and its variants [15], or the mixed LMS-LMF [16–18] all of which are intuitively motivated.
The LMS algorithm is optimum only if the noise statistics are Gaussian. However, if these statistics are different from Gaussian, other criteria, such as  -norm (
-norm ( ), perform better than the LMS algorithm. An alternative to the LMS algorithm which performs well when the noise statistics are not Gaussian is the LMF algorithm. A further improvement is possible when using a mixture of both algorithms, that is, the LMS and the LMF algorithms [16].
), perform better than the LMS algorithm. An alternative to the LMS algorithm which performs well when the noise statistics are not Gaussian is the LMF algorithm. A further improvement is possible when using a mixture of both algorithms, that is, the LMS and the LMF algorithms [16].
In this respect, existing algorithms based on mixed-norm (MN) criteria have been used in system identification behaving robustly in Gaussian and non-Gaussian environments. These algorithms are based on a fixed combination of the LMS and the LMF algorithms or a time varying combination of them. The time variation is used in adapting the mixed control parameter to compensate for nonstationarities and time-varying environments. The combination of error norms governed by a mixture parameter is introduced to yield a better performance than algorithms derived from a single error norm. Very attractive results are found through the use of mixed-norm algorithms [16–18]. These are based on the minimization of a mixed norm cost function in a controlled fashion, that is [16–18],

where the error is defined as

 is the desired value,
is the desired value,  is the filter coefficient of the adaptive filter,
is the filter coefficient of the adaptive filter,  is the input vector,
is the input vector,  is the additive noise, and
is the additive noise, and  is the mixing parameter between zero and one and set in this range to preserve the unimodal character of the cost function. It is clear from (1) that if
is the mixing parameter between zero and one and set in this range to preserve the unimodal character of the cost function. It is clear from (1) that if  the algorithm reduces to the LMS algorithm; if, however,
the algorithm reduces to the LMS algorithm; if, however,  the algorithm is the LMF. A careful choice for
the algorithm is the LMF. A careful choice for  in the interval (0,1) will enhance the performance of the algorithm. The algorithm for adjusting the tap coefficients,
in the interval (0,1) will enhance the performance of the algorithm. The algorithm for adjusting the tap coefficients,  , is given by the following recursion:
, is given by the following recursion:

Adaptive filter algorithms designed through the minimization of equation (1) have a disadvantage when the absolute value of the error is greater than one. This makes the algorithm go unstable unless either a small value of the step size or a large value of the controlling parameter is chosen such that this unwanted instability is eliminated. Unfortunately, a small value of the step size will make the algorithm converge very slowly, and a large value of the controlling parameter will make the LMS algorithm essentially dominant.
The rest of the paper is organized as follows. In Section 2, the description of the proposed algorithm is addressed, while Section 3 deals with the convergence analysis. Section 4 details the derivation of the excess mean-square-error. The simulation results are reported in Section 5, and finally Section 6 concludes the main findings of the paper and outlines possible further work.
2. Proposed Algorithm
To overcome the above-mentioned problem, a modified approach is proposed where both constraints of the step size and the control parameter are eliminated. The proposed criterion consists of the cost function (1) where the  -norm is substituted for the
-norm is substituted for the  -norm. Ultimately, this should eliminate the instability in the
-norm. Ultimately, this should eliminate the instability in the  -norm and retains the good features of (1), that is, the mixed nature of the criterion if
-norm and retains the good features of (1), that is, the mixed nature of the criterion if  . The proposed scheme is defined as,
. The proposed scheme is defined as,

If  , the cost function defined by (4) reduces to the LMS algorithm whatever the value of
, the cost function defined by (4) reduces to the LMS algorithm whatever the value of  in the range
in the range  for which the unimodality of the cost function is preserved.
for which the unimodality of the cost function is preserved.
For  , the algorithm reduces to the
, the algorithm reduces to the  -norm adaptive algorithm, and moreover if
-norm adaptive algorithm, and moreover if  results in the familiar signed LMS algorithm [14].
results in the familiar signed LMS algorithm [14].
The value range of the lower-order  is selected to be
is selected to be  because
because
-
(1)
for
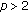 , the cost function may easily become large valued when the magnitude of the output error
, the cost function may easily become large valued when the magnitude of the output error  , leading to a potentially considerable enhancement of noise, and
, leading to a potentially considerable enhancement of noise, and -
(2)
for
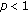 , the gradient decreases in a positive direction, resulting in an obviously undesirable attribute for being used as a cost function. Setting the value of
, the gradient decreases in a positive direction, resulting in an obviously undesirable attribute for being used as a cost function. Setting the value of 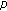 within the range
within the range 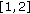 provides a situation where the gradient at
provides a situation where the gradient at  is very much lower than that for the cases with
is very much lower than that for the cases with 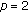 . This means that the resulting algorithm can be less sensitive to noise.
. This means that the resulting algorithm can be less sensitive to noise.
For  ,
,  gives less weight for larger error and this tends to reduce the influence of aberrant noise, while it gives relatively larger weight to smaller errors and this will improve the tracking capability of the algorithm [19].
gives less weight for larger error and this tends to reduce the influence of aberrant noise, while it gives relatively larger weight to smaller errors and this will improve the tracking capability of the algorithm [19].
2.1. Convex Property of Cost Function
The cost function  is a convex function defined on
is a convex function defined on  for
for  , where
, where  and
and  are the dimensions of
are the dimensions of  and
and  , respectively.
, respectively.
Proof.

Let  be the joint probability density function of
be the joint probability density function of  and
and  . Taking the expectation value of the above, after multiplying its both sides by
. Taking the expectation value of the above, after multiplying its both sides by  , one obtains the following:
, one obtains the following:

This shows that the cost function  is convex.
is convex.
2.2. Analysis of the Error Surface
Case 1  .
.
Let the input autocorrelation matrix be  , and the cross-correlation vector that describes the cross-correlation between the received signal (
, and the cross-correlation vector that describes the cross-correlation between the received signal ( ) and the desired data (
) and the desired data ( )
)  . The error function can be more conveniently expressed as follows:
. The error function can be more conveniently expressed as follows:

It is clear from (7) that the mean-square-error (MSE) is precisely a quadratic function of the components of the tap coefficients, and the shape associated with it is hyperparaboloid. The adaptive process continuously adjusts the tap coefficients, seeking the bottom of this hyperparaboloid.

Case 2  .
.
It can be shown as well that the error function for the feedback section will have a global minimum since the latter one is a convex function. As in the feedforward section, the adaptive process will continuously seek the bottom of the error function of the feedback section.
2.3. The Updating Scheme
The updating scheme is given by,

and sufficient condition for convergence in the mean of the proposed algorithm can be shown to be given by:

where  is the trace operation of the autocorrelation matrix
is the trace operation of the autocorrelation matrix  .
.
In general, the step size is chosen small enough to ensure convergence of the iterative procedure and produce less misadjustment error.
3. Convergence Analysis
In this section, the convergence analysis of the proposed algorithm is detailed. The following assumptions which are quite similar to what is usually assumed in literature and which can also be justified in several practical instances are used during the conver thegence analysis of the mixed controlled  algorithm. For example, these are quite similar to what is usually assumed in the literature [14, 15, 20–22], and which can also be justified in several practical instances.
algorithm. For example, these are quite similar to what is usually assumed in the literature [14, 15, 20–22], and which can also be justified in several practical instances.
-
(A1)
The input signal
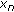 is zero mean and having variance
is zero mean and having variance 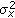 .
. -
(A2)
The noise
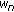 is a zero-mean independent and identically distributed process and is independent of the input signal and having zero odd moments.
is a zero-mean independent and identically distributed process and is independent of the input signal and having zero odd moments. -
(A3)
The step-size is small enough for the independence assumption [14] to be valid. As a consequence, the weight-error vector is independent of the input
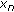 .
.
While assumptions (A1-A2) can be justified in several practical instances, assumption (A3) can only be attained asymptotically. The independence assumption [14] is very common in the literature and is justified in several practical instances [21]. The assumption of small step size is not necessarily true in practice but has been commonly used to simplify the analysis [14].
During the convergence analysis of the proposed algorithm only the case of  is considered as it is carried out for the first time. Cases for
is considered as it is carried out for the first time. Cases for  can be found, for example, in [16–18].
can be found, for example, in [16–18].
The weight error is defined to be

3.1. First Moment Behavior of the Weight Error Vector
We start by evaluating the statistical expectation of both sides of (9) which looks after subtracting  of both sides to give
of both sides to give

After substituting the error  defined by (2) in the above equation and taking the expectation of its both sides, this results in:
defined by (2) in the above equation and taking the expectation of its both sides, this results in:

Here at this point, we have to evaluate the expression  using Price's theorem [20] in the following way:
using Price's theorem [20] in the following way:

note that in the second step of this equation the error  has been substituted.
has been substituted.
Now, we are ready to evaluate expression (13), and it is given by,

It is to show that the mis-alignment vector will converge to the zero vector if the step-size,  , is given by
, is given by

A more restrictive, but sufficient and simpler, condition for convergence of (12) in the mean is

where  is the largest eigenvalue of the autocorrelation matrix
is the largest eigenvalue of the autocorrelation matrix  , since in general
, since in general  , and
, and  is the minimum MSE.
is the minimum MSE.
An inspection of (16) will immediately show that if the convergence does occur, the root mean-squared estimation error  at time
at time  is such that
is such that

where the mean-square value of the estimation error can be shown to be

(a) Discussion
It can be seen from (18) that, a sufficient condition for the algorithm to converge in the mean, the following must hold:

Consequently, when  , the convergence for the LMS algorithm is proved.
, the convergence for the LMS algorithm is proved.
3.2. Second Moment Behavior of the Weight Error Vector
From (12) we get the following expression for  :
:

Let  define the second moment of the misalignment vector therefore, the above equation becomes, after taking the expectation of both of its sides, the following:
define the second moment of the misalignment vector therefore, the above equation becomes, after taking the expectation of both of its sides, the following:

Before finalizing the above expression, let us evaluate the following quantities taking into account that they are Gaussian and zero mean [20]:



and finally,

Substituting expressions (23)–(26) in (22) results in the following:

During the derivation of the above equation, expressions  and
and  are evaluated, respectively, as follows:
are evaluated, respectively, as follows:

and

Both of these expressions are substituted in (22) to result in its simplified form (27).
Now, denote by  and
and  the limiting values of
the limiting values of  and
and  , respectively; then closed-form expressions for the limiting (steady-state) values of the second moment matrix and error power are derived next.
, respectively; then closed-form expressions for the limiting (steady-state) values of the second moment matrix and error power are derived next.
It is assumed that the autocorrelation matrix,  , is positive definite [23] with eigenvalues,
, is positive definite [23] with eigenvalues,  ; hence, it can be factorized as;
; hence, it can be factorized as;

where  is the diagonal matrix of eigenvalues
is the diagonal matrix of eigenvalues

and  is the orthonormal matrix whose
is the orthonormal matrix whose  th column is the eigenvector of
th column is the eigenvector of  associated with the
associated with the  th eigenvalue, that is,
th eigenvalue, that is,

which results in

hence (27) can be written as

We are now ready to decompose the above matrix equation into its scalar form as:

where

and  is the
is the  th scalar element of the matrix
th scalar element of the matrix  .
.
Two cases can be considered for the step size  so that the weight vector converges in the mean square sense.
so that the weight vector converges in the mean square sense.
(1) Case 
In this case, (35) consists of the off-diagonal elements of matrix  and will look like the following:
and will look like the following:

consequently, the range of the step size parameter is dictated by

As it was in the case of the mean convergence, a sufficient condition for mean square convergence is

(2) Case 
In this case, (35) consists of only the diagonal elements of matrix  and will look like the following:
and will look like the following:

correspondingly, the range of the step size parameter for convergence in the mean square sense is given by

(b) Discussion
Note that  will result in zero in the denominator of expression (41) and therefore will make
will result in zero in the denominator of expression (41) and therefore will make  take any value in the range of positive numbers, a contradiction with the ranges of values for the step sizes of LMS and LMF algorithms. Moreover, any value for
take any value in the range of positive numbers, a contradiction with the ranges of values for the step sizes of LMS and LMF algorithms. Moreover, any value for  in
in  will make of the step size
will make of the step size  set by (41) less than zero, also this condition is discarded. This concludes that it is safer to use the more realistic bounds of (39) which will guarantee stability regardless of the value of
set by (41) less than zero, also this condition is discarded. This concludes that it is safer to use the more realistic bounds of (39) which will guarantee stability regardless of the value of  , and therefore will be considered here.
, and therefore will be considered here.
Once again, it is easy to see that if the convergence in the mean-square occurs, consequently the following occurs

4. Derivation of the Excess Mean-Square-Error (EMSE)
In this section, the derivation of the EMSE will be performed for the general case of  . First, let us define the a priori estimation error
. First, let us define the a priori estimation error 

Second, the following assumption is to be used in the following ensuing analysis:
(A4)The a priori estimation error  with zero-mean is independent of
with zero-mean is independent of  .
.
The updating scheme of the proposed algorithm defined in (9) can be set up into the following recursion:

where the error function  is given by
is given by

where  .
.
In order to find the expression of the EMSE of the algorithm (defined as  ), we need to evaluate the following relation:
), we need to evaluate the following relation:

Taking the left-hand side of (46), we can write

At this point, we make use of the Taylor series expansion to expand  with respect to
with respect to  around
around  as
as

where  and
and  are, respectively, the first-order and second-order derivatives of
are, respectively, the first-order and second-order derivatives of  with respect to
with respect to  evaluated around
evaluated around  , and
, and  denotes the third, and higher-order terms of
denotes the third, and higher-order terms of  .
.
Using (45), we can write

Similarly, we can obtain

Substituting (48) in (47) we get

Using (A4) and ignoring  , we obtain
, we obtain

Using (49), we get

Using the Price's theorem to evaluate the expectation  as
as

where  . So (53) becomes
. So (53) becomes

Now taking the right-hand side of (46), we require  . So, we write
. So, we write

Therefore,

Using (A2) and (A4) and ignoring  , we write (57) as
, we write (57) as

By using (56), we can evaluate  as
as

Therefore, using (56) and (59), we can evaluate

Now letting



we can write (58) as

and subsequently (46) can be concisely expressed as

and the EMSE can be evaluated as

5. Simulation Results
In this section, the performance analysis of the proposed mixed controlled  adaptive algorithm is investigated in an unknown system identification problem for different values of
adaptive algorithm is investigated in an unknown system identification problem for different values of  and different values of the mixing parameter
and different values of the mixing parameter  . The simulations reported here are based on an FIR channel system identification defined by the following channel:
. The simulations reported here are based on an FIR channel system identification defined by the following channel:

Three different noise environments have been considered namely, Gaussian, uniform, and Laplacian. The length of the adaptive filter is the same as that of the unknown system. The learning curves are obtained by averaging 600 independent runs. Two scenarios are considered for the case of the value of  , that is,
, that is,  and
and  . The performance measure considered here is the excess mean-square-error (EMSE).
. The performance measure considered here is the excess mean-square-error (EMSE).
Figures 2, 3, and 4 depict the convergence behavior of the proposed algorithm for different values of  in a white Gaussian noise, Laplacian noise, and uniform noise, respectively, for the case of
in a white Gaussian noise, Laplacian noise, and uniform noise, respectively, for the case of  . As can be depicted from these figures the best performance is obtained when
. As can be depicted from these figures the best performance is obtained when  . More importantly, the best noise statistics for this scenario is when the noise is Laplacian distributed. An enhancement in performance is obtained, and about a 2 dB improvement is achieved for all values of
. More importantly, the best noise statistics for this scenario is when the noise is Laplacian distributed. An enhancement in performance is obtained, and about a 2 dB improvement is achieved for all values of  . Also, one can notice that the worst performance is obtained when the noise is uniformly distributed.
. Also, one can notice that the worst performance is obtained when the noise is uniformly distributed.
Figures 5, 6, 7, 8, 9 and 10 report the performance of the proposed algorithm for an SNR of 0 dB, 10 dB and 20 dB, respectively, for the case of  . Figures 5 and 6 are the result of the simulations for
. Figures 5 and 6 are the result of the simulations for  and
and  , respectively. A consistency in performance of the proposed algorithm in these scenarios for the uniform noise as far as the lowest EMSE is reached by the proposed algorithm. Similar behaviour is obtained by the proposed algorithm in Figures 7 and 8 where Figures 7 and 8 report the simulations results of the proposed algorithm for
, respectively. A consistency in performance of the proposed algorithm in these scenarios for the uniform noise as far as the lowest EMSE is reached by the proposed algorithm. Similar behaviour is obtained by the proposed algorithm in Figures 7 and 8 where Figures 7 and 8 report the simulations results of the proposed algorithm for  and
and  , respectively, for an SNR of 10 dB.
, respectively, for an SNR of 10 dB.
In the case of an SNR of 20 dB, Figures 9 and 10 depict the results. The case of  is shown in Figure 9 while that of
is shown in Figure 9 while that of  is shown in Figure 10. One can see that, even though the proposed algorithm is still performing better in the uniform noise environment, as shown in Figure 9, for
is shown in Figure 10. One can see that, even though the proposed algorithm is still performing better in the uniform noise environment, as shown in Figure 9, for  , however, identical performance is obtained by the different noise environments when
, however, identical performance is obtained by the different noise environments when  as reported in Figure 10. The theoretical findings confirm these results as will be seen later.
as reported in Figure 10. The theoretical findings confirm these results as will be seen later.
From the above results, one can conclude that when  the proposed algorithm is biased towards the LMF algorithm, in contrast to the case when
the proposed algorithm is biased towards the LMF algorithm, in contrast to the case when  , the proposed algorithm is biased towards the LMS algorithm.
, the proposed algorithm is biased towards the LMS algorithm.
Next, to assess further the performance of the proposed algorithm for the same steady-state value, two different cases for  are considered, that is,
are considered, that is,  and
and  . Figures 11 and 12 illustrate the learning behavior of the proposed algorithm for
. Figures 11 and 12 illustrate the learning behavior of the proposed algorithm for  and
and  , respectively, both are for
, respectively, both are for  . As can be seen from these figures that the best performance is obtained with uniform noise while the worst performance is obtained with Laplacian. The mixing variable
. As can be seen from these figures that the best performance is obtained with uniform noise while the worst performance is obtained with Laplacian. The mixing variable  had little effect on the speed of convergence of the proposed algorithm when the noise is uniformly and Gaussian distributed. However, as can be seen from Figure 12 in the case of Laplacian noise,
had little effect on the speed of convergence of the proposed algorithm when the noise is uniformly and Gaussian distributed. However, as can be seen from Figure 12 in the case of Laplacian noise,  has decreased the speed of convergence of the proposed algorithm from 55000 iterations (in the case of
has decreased the speed of convergence of the proposed algorithm from 55000 iterations (in the case of  ) to almost 2000 iterations. A gain of 3500 iterations in favor of the proposed algorithm when the noise is Laplacian distributed.
) to almost 2000 iterations. A gain of 3500 iterations in favor of the proposed algorithm when the noise is Laplacian distributed.
Finally, the analytical results for the steady-state EMSE derived for the proposed algorithm given in (66) are compared with the ones obtained from simulation for Gaussian, Laplacian, and uniform noise environments with an SNR of 0 dB, 10 dB, and 20 dB. This comparison is reported in Tables 1-2, and as can be seen from these tables, a close agreement exists between theory and the simulation results as mentioned earlier, for the case of  and
and  , that similar performance by the different noise environments is obtained for and SNR of 20 dB as shown in Table 2.
, that similar performance by the different noise environments is obtained for and SNR of 20 dB as shown in Table 2.
 ,
,  .
. ,
,  .
.6. Conclusion
A new adaptive scheme for system identification has been introduced, where a controlling parameter in the range  is used to control the mixture of the two norms. The derivation of the algorithm is worked out, and the convexity property is proved for this algorithm. Existing algorithms, for example [16–18] can be considered as a special case of the proposed algorithm. Also, the first moment behaviour as well as the second moment behaviour of the weights are studied. Bounds for the step size on the convergence of the proposed algorithm are derived. Finally, the steady-state analysis was carried out; simulation results performed for the purpose of validating theory are found to be in good agreement with the theory developed.
is used to control the mixture of the two norms. The derivation of the algorithm is worked out, and the convexity property is proved for this algorithm. Existing algorithms, for example [16–18] can be considered as a special case of the proposed algorithm. Also, the first moment behaviour as well as the second moment behaviour of the weights are studied. Bounds for the step size on the convergence of the proposed algorithm are derived. Finally, the steady-state analysis was carried out; simulation results performed for the purpose of validating theory are found to be in good agreement with the theory developed.
The proposed algorithm has been applied so far to a system identification scenario, for example, echo cancellation. As a future extension, recent work is going on the application of the proposed algorithm to mitigate the effects of intersymbol interference in a communication system.
References
Widrow B, Stearns SD: Adaptive Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 1985.
Sherman S: Non-mean-square error criteria. IRE Transactions on Information Theory 1958, 4(3):125-126. 10.1109/TIT.1958.1057451
Nagumo JI, Noda A: A learning method for system identification. IEEE Transactions on Automatic Control 1967, 12: 282-287.
Claasen TACM, Mecklenbraeuker WFG: Comparisons of the convergence of two algorithms for adaptive FIR digital filters. IEEE Transactions on Circuits and Systems 1981, 28(6):510-518. 10.1109/TCS.1981.1085011
Gersho A: Adaptive filtering with binary reinforcement. IEEE Transactions on Information Theory 1984, 30(2):191-199. 10.1109/TIT.1984.1056890
Feuer A, Weinstein E: Convergence analysis of LMS filters with uncorrelated data. IEEE Transactions on Acoustics, Speech, and Signal Processing 1985, 33(1):222-230. 10.1109/TASSP.1985.1164493
Bershad NJ: Behavior of the e-normalized LMS algorithm with Gaussian inputs. IEEE Transactions on Acoustics, Speech, and Signal Processing 1987, 35(5):636-644. 10.1109/TASSP.1987.1165197
Eweda E: Convergence of the sign algorithm for adaptive filtering with correlated data. IEEE Transactions on Information Theory 1991, 37(5):1450-1457. 10.1109/18.133267
Douglas SC, Meng THY: Stochastic gradient adaptation under general error criteria. IEEE Transactions on Signal Processing 1994, 42(6):1335-1351. 10.1109/78.286951
Al-Naffouri TY, Zerguine A, Bettayeb M: A unifying view of error nonlinearities in LMS adaptation. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '98), May 1998 1697-1700.
Zhang H, Peng Y:
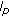 -norm based minimisation algorithm for signal parameter estimation. Electronics Letters 1999, 35(20):1704-1705. 10.1049/el:19991080
-norm based minimisation algorithm for signal parameter estimation. Electronics Letters 1999, 35(20):1704-1705. 10.1049/el:19991080Siu S, Cowan CFN: Performance analysis of the lp norm back propagation algorithm for adaptive equalisation. IEE Proceedings, Part F: Radar and Signal Processing 1993, 140(1):43-47. 10.1049/ip-f-2.1993.0006
Vargas RA, Burrus CS: The direct design of recursive or IIR digital filters. Proceedings of the 3rd International Symposium on Communications, Control, and Signal Processing (ISCCSP '08), March 2008 188-192.
Haykin S: Adaptive Filter Theory. 4th edition. Prentice-Hall, Upper-Saddle River, NJ, USA; 2002.
Walach E, Widrow B: The least mean fourth (LMF) adaptive algorithm and its family. IEEE Transactions on Information Theory 1984, 30(2):275-283. 10.1109/TIT.1984.1056886
Tanrikulu O, Chambers JA: Convergence and steady-state properties of the least-mean mixed-norm (LMMN) adaptive algorithm. IEE Proceedings Vision, Image & Signal Processing 1996, 143(3):137-142. 10.1049/ip-vis:19960449
Zerguine A, Cowan CFN, Bettayeb M: LMS-LMF adaptive scheme for echo cancellation. Electronics Letters 1996, 32(19):1776-1778. 10.1049/el:19961202
Zerguine A, Cowan CFN, Bettayeb M: Adaptive echo cancellation using least mean mixed-norm algorithm. IEEE Transactions on Signal Processing 1997, 45(5):1340-1343. 10.1109/78.575705
Siu S, Gibson GJ, Cowan CFN: Decision feedback equalisation using neural network structures and performance comparison with standard architecture. IEE Proceedings, Part I: Communications, Speech and Vision 1990, 137(4):221-225. 10.1049/ip-i-2.1990.0031
Price R: A useful theorem for non-linear devices having Gaussian inputs. IEEE Transactions on Information Theory 1958, 4: 69-72. 10.1109/TIT.1958.1057444
Mazo JE: On the independence theory of equalizer convergence. The Bell System Technical Journal 1979, 58(5):963-993.
Macchi O: Adaptive Processing: The Least Mean Squares Approach with Applications in Transmission. John Wiley & Sons, West Sussex, UK; 1995.
Sayed AH: Fundamentals of Adaptive Filtering. Wiley-Interscience, New York, NY, USA; 2003.
Acknowledgment
The author would like to acknowledge the support of King Fahd University of Petroleum and Minerals to carry out this research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zidouri, A. Convergence Analysis of a Mixed Controlled 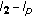 Adaptive Algorithm.
EURASIP J. Adv. Signal Process. 2010, 893809 (2010). https://doi.org/10.1155/2010/893809
Adaptive Algorithm.
EURASIP J. Adv. Signal Process. 2010, 893809 (2010). https://doi.org/10.1155/2010/893809
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/893809
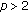 , the cost function may easily become large valued when the magnitude of the output error
, the cost function may easily become large valued when the magnitude of the output error  , leading to a potentially considerable enhancement of noise, and
, leading to a potentially considerable enhancement of noise, and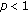 , the gradient decreases in a positive direction, resulting in an obviously undesirable attribute for being used as a cost function. Setting the value of
, the gradient decreases in a positive direction, resulting in an obviously undesirable attribute for being used as a cost function. Setting the value of 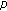 within the range
within the range 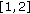 provides a situation where the gradient at
provides a situation where the gradient at  is very much lower than that for the cases with
is very much lower than that for the cases with 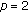 . This means that the resulting algorithm can be less sensitive to noise.
. This means that the resulting algorithm can be less sensitive to noise.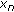 is zero mean and having variance
is zero mean and having variance 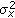 .
.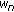 is a zero-mean independent and identically distributed process and is independent of the input signal and having zero odd moments.
is a zero-mean independent and identically distributed process and is independent of the input signal and having zero odd moments.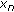 .
.











 -norm based minimisation algorithm for signal parameter estimation. Electronics Letters 1999, 35(20):1704-1705. 10.1049/el:19991080
-norm based minimisation algorithm for signal parameter estimation. Electronics Letters 1999, 35(20):1704-1705. 10.1049/el:19991080