- Research Article
- Open access
- Published:
Joint Symbol Timing and CFO Estimation for OFDM/OQAM Systems in Multipath Channels
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 897607 (2009)
Abstract
The problem of data-aided synchronization for orthogonal frequency division multiplexing (OFDM) systems based on offset quadrature amplitude modulation (OQAM) in multipath channels is considered. In particular, the joint maximum-likelihood (ML) estimator for carrier-frequency offset (CFO), amplitudes, phases, and delays, exploiting a short known preamble, is derived. The ML estimators for phases and amplitudes are in closed form. Moreover, under the assumption that the CFO is sufficiently small, a closed form approximate ML (AML) CFO estimator is obtained. By exploiting the obtained closed form solutions a cost function whose peaks provide an estimate of the delays is derived. In particular, the symbol timing (i.e., the delay of the first multipath component) is obtained by considering the smallest estimated delay. The performance of the proposed joint AML estimator is assessed via computer simulations and compared with that achieved by the joint AML estimator designed for AWGN channel and that achieved by a previously derived joint estimator for OFDM systems.
1. Introduction
In the last years, the interest for filter-bank multicarrier (FBMC) systems is increased, since they provide high spectral containment. Therefore, they have been taken into account for high-data-rate transmissions over both wired and wireless frequency-selective channels. Moreover, they have been considered for the physical layer of cognitive radio systems [1]. One of the most famous multicarrier modulation techniques is orthogonal frequency division multiplexing (OFDM), embedded in several standards such as digital audio and video broadcasting or Wi-Fi wireless LANs IEEE 802.11a/g. Other known types of FBMC systems are Filtered Multitone (FMT) systems, that have been proposed for very high-speed digital subscriber line standards [2] and are under investigation also for broadband wireless applications [3] and, moreover, OFDM based on offset QAM modulation (OQAM), considered by the 3GPP standardization forum for improved down-link UTRAN interfaces [4].
Unlike OFDM, OFDM/OQAM systems do not require the presence of a cyclic prefix (CP) in order to combat the effects of frequency selective channels. The absence of the CP implies on one hand the maximum spectral efficiency and, on the other hand, an increased computational complexity. However, since the subchannel filters are obtained by complex modulation of a single filter, efficient polyphase implementations are possible. Another fundamental difference between OFDM and OFDM/OQAM systems is the adoption in the latter case of pulse shaping filters very well localized in time and frequency [5, 6].
OFDM/OQAM systems are more sensitive to synchronization errors than single-carrier systems. In particular, carrier frequency-offset (CFO) and symbol timing (ST) estimation errors can lead to a performance degradation. For this reason, it is very important to derive efficient synchronization schemes. In the last years several studies have been focused on blind or data-aided synchronization for OFDM/OQAM systems. For example, in [7, 8] blind CFO estimators have been derived. Moreover, in [9] a blind joint CFO and ST estimator is proposed. Furthermore, in [10] a synchronization scheme for data-aided ST and CFO estimation with robust acquisition properties in dispersive channels is developed. Finally, in [11, 12] a full synchronization method utilizing frequency domain scattered pilots in the time domain is proposed. However, all cited estimators are designed for down-link communications.
In this paper we consider the problem of data-aided synchronization for OFDM/OQAM systems in multipath channels. In particular, the joint maximum-likelihood (ML) estimator for CFO, amplitudes, phases, and delays, exploiting a short known preamble, is derived. The ML estimators for phases and amplitudes are in closed form. Moreover, under the assumption that the CFO is sufficiently small, a closed form approximate ML (AML) CFO estimator is obtained. By exploiting the obtained closed form solutions a cost function whose peaks provide an estimate of the delays is derived. In particular, the ST (i.e., the delay of the first multipath component) is obtained by considering the smallest estimated delay. The proposed joint estimator is derived with reference to a down-link scenario; however, by following an approach similar to that considered in [13], it can be easily modified to be exploited for up-link communications. The performance of the proposed joint AML estimator is assessed via computer simulations and compared with that achieved by the joint AML estimator designed for AWGN channel and that achieved by a previously derived joint estimator for OFDM systems. The paper is organized as follows. In Section 2 the OFDM/OQAM system model is described. In Section 3 the proposed data-aided estimator is described. In Section 4 numerical results obtained in AWGN and multipath channel are presented and discussed. Finally, conclusions are drawn in Section 5.
Notation 1.
 , superscript
, superscript  denotes the complex conjugation,
denotes the complex conjugation,  real part,
real part,  imaginary part, and
imaginary part, and  absolute value. Moreover,
absolute value. Moreover,  denotes transpose and
denotes transpose and  the argument of a complex number in
the argument of a complex number in  . Finally, lower case boldface symbols denote column vectors.
. Finally, lower case boldface symbols denote column vectors.
2. System Model
Let us consider an OFDM/OQAM system with  subcarriers in a multipath channel. The received signal, in the presence of a CFO normalized to subcarrier spacing
subcarriers in a multipath channel. The received signal, in the presence of a CFO normalized to subcarrier spacing  , can be written as
, can be written as

where  is the information-bearing signal,
is the information-bearing signal,  is the number of multipath components, and,
is the number of multipath components, and,  ,
,  , and
, and  denote amplitude, phase, and delay, respectively, of the
denote amplitude, phase, and delay, respectively, of the  th path. Moreover, in (1)
th path. Moreover, in (1)  is a zero-mean complex-valued white Gaussian noise process with independent real and imaginary part, each with two-sided power spectral density
is a zero-mean complex-valued white Gaussian noise process with independent real and imaginary part, each with two-sided power spectral density  . The received signal
. The received signal  is filtered with an ideal lowpass filter with a bandwidth of
is filtered with an ideal lowpass filter with a bandwidth of  , where
, where  denotes the sampling period. The sampled signal
denotes the sampling period. The sampled signal  is equal to
is equal to

where  is the OFDM/OQAM symbol interval and
is the OFDM/OQAM symbol interval and  denotes the number of information-bearing symbols in the burst. Moreover, in (2)
denotes the number of information-bearing symbols in the burst. Moreover, in (2)  is the set of size
is the set of size  of used subcarriers,
of used subcarriers,  and
and  denote the real and imaginary part of the complex data symbol transmitted on the
denote the real and imaginary part of the complex data symbol transmitted on the  th subcarrier during the
th subcarrier during the  th OFDM/OQAM symbol, while the real-valued and unit-energy pulse-shaping filter
th OFDM/OQAM symbol, while the real-valued and unit-energy pulse-shaping filter  is bandlimited within
is bandlimited within  .
.
3. Joint Symbol Timing and CFO Estimator
In this section we consider the problem of data-aided synchronization for OFDM/OQAM systems in multipath channels. In particular, we derive the joint ML estimator for CFO, amplitudes, phases, and delays, exploiting a short known preamble embedded in the received burst. Specifically, the known preamble is given by

where  is the number of OFDM/OQAM symbols in the preamble,
is the number of OFDM/OQAM symbols in the preamble,  is the set of pilot subcarriers, and
is the set of pilot subcarriers, and  ,
, 
 ,
,  ,
,  , denote the known pilot symbols. Note that the duration of the preamble is
, denote the known pilot symbols. Note that the duration of the preamble is  where
where  is the overlap parameter, that is, the ratio between the length of the truncated pulse-shaping filter and the OFDM/OQAM symbol interval
is the overlap parameter, that is, the ratio between the length of the truncated pulse-shaping filter and the OFDM/OQAM symbol interval  . By considering an observations window of total length
. By considering an observations window of total length  containing the nonzero support of the received preamble, the likelihood function for the unknown parameters
containing the nonzero support of the received preamble, the likelihood function for the unknown parameters  , and,
, and,  ,
,  , and
, and  ,
,  , is given by
, is given by

where  ,
,  ,
,  ,
,

and the notation of the type  indicates trial value of
indicates trial value of  . Thus, the log-likelihood function for the parameters of interest results to be (up to irrelevant factors)
. Thus, the log-likelihood function for the parameters of interest results to be (up to irrelevant factors)

The first term in the right-hand side (RHS) of (6) for  can be approximated as
can be approximated as

Therefore, the log-likelihood function can be written as

where


with


From (8), it immediately follows that the ML estimator for phase and amplitude of the  th path is given by
th path is given by


Moreover, by replacing the estimate of the phase and the amplitude of each path in (8) we get

Therefore, the joint estimatorfor CFO and delays is given by

The derived joint ML estimator evaluates, for each trial value of each delay  ,
,  , and for each trial value of the CFO
, and for each trial value of the CFO  , the response of the filter matched to the pulse shaping filter
, the response of the filter matched to the pulse shaping filter  to the CFO compensated and downconverted signal
to the CFO compensated and downconverted signal  at the time instants
at the time instants  and
and  ,
,  . Specifically, the downconversion is performed by considering all the frequencies of the pilot subcarriers. Then, exploiting the known pilot symbols, these quantities are combined according to (11) (or (12)), (10), and (16). Note that the proposed algorithm can be exploited also in the up-link to estimate the desired parameters by considering only the subcarriers assigned to the user of interest. The joint ML estimate for delays and CFO is obtained by considering the value of
. Specifically, the downconversion is performed by considering all the frequencies of the pilot subcarriers. Then, exploiting the known pilot symbols, these quantities are combined according to (11) (or (12)), (10), and (16). Note that the proposed algorithm can be exploited also in the up-link to estimate the desired parameters by considering only the subcarriers assigned to the user of interest. The joint ML estimate for delays and CFO is obtained by considering the value of  that maximizes the statistic in (15). The
that maximizes the statistic in (15). The  -dimensional maximization required by the joint ML estimator in (16) undertakes heavy computational burden. Therefore, in the following is derived a more feasible synchronization scheme by exploiting the assumption that the CFO is sufficiently small. Specifically, taking into account that the observations window contains the nonzero support of the received preamble and that the prototype filter
-dimensional maximization required by the joint ML estimator in (16) undertakes heavy computational burden. Therefore, in the following is derived a more feasible synchronization scheme by exploiting the assumption that the CFO is sufficiently small. Specifically, taking into account that the observations window contains the nonzero support of the received preamble and that the prototype filter  is different from zero for
is different from zero for  , from (11) it follows that
, from (11) it follows that

where the integer  is the trial value of the delay
is the trial value of the delay  normalized to the sampling interval,
normalized to the sampling interval,  . Then, under the assumption that the CFO is sufficiently small within a time
. Then, under the assumption that the CFO is sufficiently small within a time  comparable with the length of the prototype filter
comparable with the length of the prototype filter  , it results that
, it results that


where

In particular, into the case of a training sequence composed of  OFDM/OQAM symbol, (10), taking into account (18)–(20), becomes
OFDM/OQAM symbol, (10), taking into account (18)–(20), becomes

with


Therefore, under the assumption  and in the case of a training sequence with
and in the case of a training sequence with  OFDM/OQAM symbol, the AML estimator for CFO, taking into account (16), is given by
OFDM/OQAM symbol, the AML estimator for CFO, taking into account (16), is given by

Moreover, from (16) and (21)–(24) it follows that

Thus, although under the assumption of small CFO values a closed form approximate estimator can be obtained, the estimation of the delays remains an  dimensional problem. To simplify the estimation of the delays the last term in the RHS of (25) can be neglected, and, then, we obtain
dimensional problem. To simplify the estimation of the delays the last term in the RHS of (25) can be neglected, and, then, we obtain

In this case, if the number of paths  is known, it immediately follows that the
is known, it immediately follows that the  -dimensional vector of delays that maximize (26) can be obtained by considering the
-dimensional vector of delays that maximize (26) can be obtained by considering the  points where the cost function
points where the cost function

presents the highest  peaks. Moreover, the lowest among the obtained delays represents an estimate of the ST. If the number of paths
peaks. Moreover, the lowest among the obtained delays represents an estimate of the ST. If the number of paths  is not known in advance, a sufficiently high number of paths should be considered to avoid to lose a strong path and, moreover, to avoid to consider very weak paths. The obtained delays can be substituted in (24) to obtain the CFO estimate, and, finally, phases and amplitudes can be obtained from (13) and (14), respectively. Note that the numerical results reported in the next section show that the considered approximation of (25) leads to a symbol timing estimator with satisfactory performance if the number of subcarriers is sufficiently large.
is not known in advance, a sufficiently high number of paths should be considered to avoid to lose a strong path and, moreover, to avoid to consider very weak paths. The obtained delays can be substituted in (24) to obtain the CFO estimate, and, finally, phases and amplitudes can be obtained from (13) and (14), respectively. Note that the numerical results reported in the next section show that the considered approximation of (25) leads to a symbol timing estimator with satisfactory performance if the number of subcarriers is sufficiently large.
In Appendix we analyzed the accuracy of the closed form AML CFO estimator (24) in the absence of noise in a single-path channel and in the case of perfect ST synchronization ( and
and  in (1)). Specifically, it is shown that in this case also if the interference from the data burst following the training symbol is neglected, the CFO estimator is expected to exhibit a performance floor. However, it is shown in the next section that this performance floor can be substantially reduced if the training symbol satisfies the condition
in (1)). Specifically, it is shown that in this case also if the interference from the data burst following the training symbol is neglected, the CFO estimator is expected to exhibit a performance floor. However, it is shown in the next section that this performance floor can be substantially reduced if the training symbol satisfies the condition

Moreover, in Appendix is derived an approximate expression for the mean square error (MSE) of the AML CFO estimator in (24) for a single-path channel and in the case of perfect ST synchronization. In particular, in Appendix it is shown that in this case the MSE can be approximated by

where  and
and  . Note that for
. Note that for  the MSE in (29) is coincident with the MSE of the CFO estimator for OFDM systems proposed by Schmidl and Cox (SC) in [14]. It is worthwhile to emphasize that the MSE in (29) has been derived by neglecting the interference at the output of each matched filter due to adjacent subcarriers. Therefore, the actual performance of the proposed AML CFO estimator presents a floor that is not predicted by (29). However, it is shown in the next section that the approximate expression in (29) can be exploited in the range of moderate
the MSE in (29) is coincident with the MSE of the CFO estimator for OFDM systems proposed by Schmidl and Cox (SC) in [14]. It is worthwhile to emphasize that the MSE in (29) has been derived by neglecting the interference at the output of each matched filter due to adjacent subcarriers. Therefore, the actual performance of the proposed AML CFO estimator presents a floor that is not predicted by (29). However, it is shown in the next section that the approximate expression in (29) can be exploited in the range of moderate  values.
values.
4. Numerical Results and Comparisons
In this section the performance of the proposed joint AML estimator is assessed via computer simulations. A number of  Monte Carlo trials has been performed under the following conditions (unless otherwise stated):
Monte Carlo trials has been performed under the following conditions (unless otherwise stated):
-
(1)
the considered OFDM/OQAM system has a bandwidth
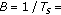 11.2 MHz;
11.2 MHz; -
(2)
the data symbols
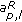 and
and 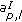 are the real and imaginary part of QPSK symbols;
are the real and imaginary part of QPSK symbols; -
(3)
the length of the considered prototype filter (designed with the frequency sampling technique [15]) is
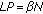 , where the overlap parameter
, where the overlap parameter 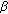 is fixed at
is fixed at  ;
; -
(4)
the considered multipath fading channel model is the ITU Vehicular A [16], which has six multipaths with differential delays 0, 0.31, 0.71, 1.09, 1.73, and 2.51 microseconds and relative powers
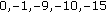 , and
, and  ;
; -
(5)
the channel is fixed in each run but it is independent from one run to another.
In the first set of simulations we have tested the sensitivity of the performance of the derived CFO estimators to the condition (28) and to the interference due to the data burst sent after the training symbol. Specifically, four operating conditions have been considered:
-
(1)
in the first case, denoted as OC1, condition (28) is satisfied and, moreover, to reduce the interference due to the data symbols, the useful data in the whole burst is delayed with respect to the preamble of the burst by one OFDM/OQAM symbol interval;
-
(2)
in the second case, denoted as OC2, condition (28) is not satisfied and the data burst is not delayed;
-
(3)
in the third case, termed OC3, condition (28) is not satisfied and the data burst is delayed;
-
(4)
in the fourth case, termed OC4, condition (28) is satisfied and the data burst is not delayed.
Figures 1 and 2 display the root mean square error (RMSE) of the considered CFO estimators as a function of  in the previously described operating conditions and in the case where the number of subcarriers is
in the previously described operating conditions and in the case where the number of subcarriers is  and the actual value of the normalized CFO is
and the actual value of the normalized CFO is  . Specifically, the AML CFO estimator for multipath channel reported in (24) is denoted as AML1 while the label AML2 indicates the AML estimator for AWGN channel, that is, that based on the choice
. Specifically, the AML CFO estimator for multipath channel reported in (24) is denoted as AML1 while the label AML2 indicates the AML estimator for AWGN channel, that is, that based on the choice  . In the case of the AML1 CFO estimator two paths have been considered to avoid to lose a strong path and, moreover, to avoid to consider very weak paths. As one would expect, the performance of both AML1 and AML2 estimators is coincident in AWGN channel (see Figure 1) while the AML1 outperforms the AML2 estimator in multipath channel (see Figure 2). Moreover, only when condition (28) is satisfied (curves labeled as OC1 and OC4), the insertion of the considered delay in the data burst can lead to a significant performance improvement both in AWGN and multipath channel. In particular, when condition (28) is satisfied and the data burst is delayed (curves labeled as OC1), a floor is observed only around
. In the case of the AML1 CFO estimator two paths have been considered to avoid to lose a strong path and, moreover, to avoid to consider very weak paths. As one would expect, the performance of both AML1 and AML2 estimators is coincident in AWGN channel (see Figure 1) while the AML1 outperforms the AML2 estimator in multipath channel (see Figure 2). Moreover, only when condition (28) is satisfied (curves labeled as OC1 and OC4), the insertion of the considered delay in the data burst can lead to a significant performance improvement both in AWGN and multipath channel. In particular, when condition (28) is satisfied and the data burst is delayed (curves labeled as OC1), a floor is observed only around  dB. In Figures 1 and 2 is also reported the theoretical RMSE (TRMSE) predicted by (29). The results show that the derived expression can be exploited in AWGN channel for
dB. In Figures 1 and 2 is also reported the theoretical RMSE (TRMSE) predicted by (29). The results show that the derived expression can be exploited in AWGN channel for  dB. As regards the performance of the AML1 and AML2 ST estimators no errors were observed in AWGN channel while in multipath channel A an RMSE (normalized to the OFDM/OQAM interval
dB. As regards the performance of the AML1 and AML2 ST estimators no errors were observed in AWGN channel while in multipath channel A an RMSE (normalized to the OFDM/OQAM interval  ) less than
) less than  was observed in all operating conditions for
was observed in all operating conditions for  dB. Taking into account the previous results in the following experiments only the operating condition OC1 is considered since it assures the best performance. In particular, in Figures 3 and 4 the normalized RMSE of the AML CFO estimators is compared with that of the SC estimator proposed in [14], both in AWGN (Figure 3) and in multipath channel A (Figure 4). Specifically, the number of subcarriers is
dB. Taking into account the previous results in the following experiments only the operating condition OC1 is considered since it assures the best performance. In particular, in Figures 3 and 4 the normalized RMSE of the AML CFO estimators is compared with that of the SC estimator proposed in [14], both in AWGN (Figure 3) and in multipath channel A (Figure 4). Specifically, the number of subcarriers is  and the actual value of the normalized CFO is
and the actual value of the normalized CFO is  . Note that the performance comparison with the SC estimator is made by exploiting the proposed algorithm in an OFDM/OQAM system and the SC algorithm in an OFDM system, and, moreover, in the case of the SC algorithm an OFDM symbol with two equal parts is exploited. The results show that in multipath channel A the performance of both estimators presents a floor, but for different reasons. In the case of the SC estimator the floor is due to the inaccuracy in the ST estimate (normalized RMSE nearly equal to
. Note that the performance comparison with the SC estimator is made by exploiting the proposed algorithm in an OFDM/OQAM system and the SC algorithm in an OFDM system, and, moreover, in the case of the SC algorithm an OFDM symbol with two equal parts is exploited. The results show that in multipath channel A the performance of both estimators presents a floor, but for different reasons. In the case of the SC estimator the floor is due to the inaccuracy in the ST estimate (normalized RMSE nearly equal to  (see Figure 5)), while in the case of the AML estimator the floor is due (as well as in the AWGN channel (see Figure 3)) to the interference from adjacent subcarriers. Moreover, in Figures 3 and 4 is reported also the Cramèr -Rao bound (CRB) on CFO estimation for OFDM/OQAM systems. The performance loss with respect to the CRB is quite contained for SNR values lower than
(see Figure 5)), while in the case of the AML estimator the floor is due (as well as in the AWGN channel (see Figure 3)) to the interference from adjacent subcarriers. Moreover, in Figures 3 and 4 is reported also the Cramèr -Rao bound (CRB) on CFO estimation for OFDM/OQAM systems. The performance loss with respect to the CRB is quite contained for SNR values lower than  dB. Specifically, as it is shown in the following the accuracy is sufficient to assure a negligible degradation with respect to the case of perfect synchronization.
dB. Specifically, as it is shown in the following the accuracy is sufficient to assure a negligible degradation with respect to the case of perfect synchronization.
To gain some insight about the acquisition range of the considered estimators in Figure 6 is reported the normalized RMSE of the AML CFO estimators as a function of the actual value of the normalized CFO  in AWGN (solid lines) and multipath channel A (dashed lines) for
in AWGN (solid lines) and multipath channel A (dashed lines) for  dB. In Figure 6 is also reported the RMSE of the SC estimator. Note that in this case a number of
dB. In Figure 6 is also reported the RMSE of the SC estimator. Note that in this case a number of  Monte Carlo trials have been performed. The results show that although the AML estimators have been derived under the assumption of small values of CFO, they assure a satisfactory performance in the range
Monte Carlo trials have been performed. The results show that although the AML estimators have been derived under the assumption of small values of CFO, they assure a satisfactory performance in the range  . Of course if the value of the normalized CFO can belong to a larger interval, an additional stage at the beginning of the preamble needs to be inserted to obtain a coarse estimate of the CFO within a sufficiently wide range.
. Of course if the value of the normalized CFO can belong to a larger interval, an additional stage at the beginning of the preamble needs to be inserted to obtain a coarse estimate of the CFO within a sufficiently wide range.
Figures 7 and 8 show the normalized RMSE of the considered CFO estimators as a function of the number of subcarriers  in AWGN (Figure 7) and in multipath channel A (Figure 8), and for two
in AWGN (Figure 7) and in multipath channel A (Figure 8), and for two  conditions. The results show that in AWGN the performance of both AML1 and AML2 estimators is coincident with that predicted by (29) for
conditions. The results show that in AWGN the performance of both AML1 and AML2 estimators is coincident with that predicted by (29) for  dB while is slightly different for
dB while is slightly different for  dB. Moreover, Figure 8 shows that in multipath channel A the AML1 CFO estimator outperforms the AML2 estimator and assures estimates whose accuracy is quite similar to that provided by the SC estimator. As regards the performance of the AML and SC ST estimators results, not reported here for the sake of brevity, have shown that the SC ST estimator assures a normalized RMSE nearly equal to
dB. Moreover, Figure 8 shows that in multipath channel A the AML1 CFO estimator outperforms the AML2 estimator and assures estimates whose accuracy is quite similar to that provided by the SC estimator. As regards the performance of the AML and SC ST estimators results, not reported here for the sake of brevity, have shown that the SC ST estimator assures a normalized RMSE nearly equal to  both in AWGN and multipath channel due to the presence of the plateau. On the other hand, as regards the AML ST estimators no errors were observed in AWGN while a normalized RMSE less than
both in AWGN and multipath channel due to the presence of the plateau. On the other hand, as regards the AML ST estimators no errors were observed in AWGN while a normalized RMSE less than  was obtained for
was obtained for  .
.
Finally, Figures 9 and 10 show, for  and
and  , the bit error rate (BER) obtained with the adoption of the AML and SC estimators followed by a one-tap equalizer with perfect knowledge of the channel and of the residual synchronization errors. The performance is compared with that of the perfectly synchronized OFDM/OQAM system (PS-OFDM/OQAM) and with that of the perfectly synchronized OFDM system (PS-OFDM) with CP
, the bit error rate (BER) obtained with the adoption of the AML and SC estimators followed by a one-tap equalizer with perfect knowledge of the channel and of the residual synchronization errors. The performance is compared with that of the perfectly synchronized OFDM/OQAM system (PS-OFDM/OQAM) and with that of the perfectly synchronized OFDM system (PS-OFDM) with CP . Note that the slight difference between the performance of the PS-OFDM/OQAM and that of the PS-OFDM is due to the fact that, to take into account the energy loss due to the CP, the amplitude of the OFDM signal has been reduced by
. Note that the slight difference between the performance of the PS-OFDM/OQAM and that of the PS-OFDM is due to the fact that, to take into account the energy loss due to the CP, the amplitude of the OFDM signal has been reduced by  where CP
where CP . The results show that both in AWGN and multipath channel A the AML estimators assure a negligible degradation with respect to the perfectly synchronized system while the adoption of the SC synchronization scheme leads to an error floor due essentially to the inaccuracy of the ST estimates.
. The results show that both in AWGN and multipath channel A the AML estimators assure a negligible degradation with respect to the perfectly synchronized system while the adoption of the SC synchronization scheme leads to an error floor due essentially to the inaccuracy of the ST estimates.
5. Conclusions
In this paper we have dealt with the problem of data-aided synchronization for OFDM/OQAM systems in multipath channels. In particular, the joint ML estimator for CFO, amplitudes, phases, and delays, exploiting a short known preamble, has been derived. Exploiting the closed form ML estimators for phases and amplitudes and the closed form AML CFO estimator for small CFO values, a cost function that can provide an estimate of the ST, has been obtained. The performance of the joint AML1 estimator for multipath channel has been assessed via computer simulations and compared with that achieved by the joint AML2 estimator designed for AWGN channel. Moreover, a comparison with the performance achieved by the SC estimator for OFDM systems has been made. The results have shown that if it satisfied a condition involving the training symbol and the data burst is delayed by one OFDM/OQAM symbol interval with respect to the training burst, the AML CFO estimators assure a performance similar to that achieved by the SC estimator in multipath channel A, while the AML ST estimators outperform the SC estimator. Moreover, an approximate expression for the MSE of the AML CFO estimators has been derived that can be exploited to predict the actual performance in the range of moderate SNR values. Finally, a comparison between the BER obtained with the adoption of the AML and SC estimators followed by a one-tap equalizer with perfect knowledge of the channel and of the residual synchronization errors has been made. The results have shown that both in AWGN and multipath channel A the AML estimators assure a negligible degradation with respect to the perfectly synchronized system while the adoption of the SC synchronization scheme leads to an error floor due essentially to the inaccuracy of the ST estimates.
References
Farhang-Boroujeny B, Kempter R: Multicarrier communication techniques for spectrum sensing and communication in cognitive radios. IEEE Communications Magazine 2008, 46(4):80-85.
Cherubini G, Eleftheriou E, Oker S, Cioffi JM: Filter bank modulation techniques for very high-speed digital subscriber lines. IEEE Communications Magazine 2000, 38(5):98-104. 10.1109/35.841832
Ihalainen T, Stitz TH, Rinne M, Renfors M: Channel equalization in filter bank based multicarrier modulation for wireless communications. EURASIP Journal on Advances in Signal Processing 2007, 2007:-18.
Lacroix D, Goudard N, Alard M: OFDM with guard interval versus OFDM/OffsetQAM for high data rate UMTS downlink transmission. Proceedings of the 54th IEEE Vehicular Technology Conference (VTC '01), October 2001, Atlantic City, NJ, USA 4: 2682-2686.
Alard CRM, Siohan P: A family of extended gaussian functions with a nearly optimal localization. Proceedings of the 1st International Workshop on Multi-Carrier Spread-Spectrum, April 1997, Oberpfaffenhofen, Germany 179-186.
Haas R, Belfiore J-C: A time-frequency well-localized pulse for multiple carrier transmission. Wireless Personal Communications 1997, 5(1):1-18. 10.1023/A:1008859809455
Ciblat P, Serpedin E: A fine blind frequency offset estimator for OFDM/OQAM systems. IEEE Transactions on Signal Processing 2004, 52(1):291-296. 10.1109/TSP.2003.820062
Fusco T, Tanda M: Blind frequency-offset estimation for OFDM/OQAM systems. IEEE Transactions on Signal Processing 2007, 55(5):1828-1838.
Bolcskei H: Blind estimation of symbol timing and carrier frequency offset in wireless OFDM systems. IEEE Transactions on Communications 2001, 49(6):988-999. 10.1109/26.930629
Fusco T, Petrella A, Tanda M: Data-aided symbol timing and cfo synchronization for filter-bank multicarrier systems. IEEE Transactions on Wireless Communications 2009, 8(5):2705-2715.
Jahan B, Lanoiselée M, Degoulet G, Rabineau R: Full synchronization method for OFDM/OQAM and OFDM/QAM modulations. Proceedings of the 10th IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA '08), August 2008 344-348.
Jahan B, Lanoiselée M, Degoulet G, Rabineau R: Frame synchronization method for OFDM/QAM and ODFM/OQAM modulations. Proceedings of the 4th IEEE International Conference on Circuits and Systems for Communications (ICCSC '08), May 2008, Shanghai, China 445-449.
Fusco T, Petrella A, Tanda M: Joint symbol timing and CFO estimation in multiuser OFDM/OQAM systems. Proceedings of the 10th IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '09), June 2009, Perugia, Italy 613-617.
Schmidl TM, Cox DC: Robust frequency and timing synchronization for OFDM. IEEE Transactions on Communications 1997, 45(12):1613-1621. 10.1109/26.650240
Bellanger MG: Specification and design of a prototype filter for filter bank based multicarrier transmission. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01), May 2001, Salt Lake, Utah, USA 4: 2417-2420.
Recommendation ITU-R M. 1225 : Guidelines for evaluation of radio transmission technologies for IMT-2000. 1997.
Acknowledgment
This work was supported in part by the European Commission under Project PHYDYAS (FP7-ICT-2007-1-211887).
Author information
Authors and Affiliations
Corresponding author
Appendices
A
In this appendix we analyze the accuracy of the AML CFO estimates in the absence of noise in a single-path channel and in the case of perfect ST synchronization ( and
and  in (1)). By considering a training symbol composed of
in (1)). By considering a training symbol composed of  OFDM/OQAM symbol, taking into account (18) and (20) it follows that
OFDM/OQAM symbol, taking into account (18) and (20) it follows that


where


Moreover, from (19) and (20) we have


where


Therefore, taking into account (18), (20), (22), and (A.1) it follows that


Moreover, from (19), (20), (23), and (A.3) we have


Note that if the training symbol satisfies the condition


it follows that




In this case, if the interference terms  and
and  in the RHS of (A.8) and (A.9), respectively, were negligible, the CFO estimate would be (see (24) for
in the RHS of (A.8) and (A.9), respectively, were negligible, the CFO estimate would be (see (24) for  )
)  . The presence of the interference terms in the RHS of (A.8) and (A.9) leads to an error floor. Moreover, if condition (A.7) is not fulfilled an error floor can be observed also when the interference terms are negligible (see (A.5) and (A.6)). However, in the section on numerical results it is shown that the error floor can be substantially reduced when condition (A.7) is satisfied.
. The presence of the interference terms in the RHS of (A.8) and (A.9) leads to an error floor. Moreover, if condition (A.7) is not fulfilled an error floor can be observed also when the interference terms are negligible (see (A.5) and (A.6)). However, in the section on numerical results it is shown that the error floor can be substantially reduced when condition (A.7) is satisfied.
B
In this appendix we derive an approximate expression for the MSE of the AML CFO estimator reported in (24) for a single-path channel and in the case of perfect ST synchronization ( and
and  in (1)). Specifically, we consider the case where the SNR is such that interference terms in (A.8) and (A.9) can be neglected with respect to the noise terms due to AWGN but it is sufficiently high that noise
in (1)). Specifically, we consider the case where the SNR is such that interference terms in (A.8) and (A.9) can be neglected with respect to the noise terms due to AWGN but it is sufficiently high that noise  noise terms can be deleted. In this case taking into account (A.1), (A.3), (A.8), and (A.9) it follows that
noise terms can be deleted. In this case taking into account (A.1), (A.3), (A.8), and (A.9) it follows that


where the last approximation has been obtained by neglecting the noise  noise term, and, moreover,
noise term, and, moreover,  and
and  represent the contribution to
represent the contribution to  and
and  (in (A.8) and (A.9), resp.) in the absence of noise and of the interference terms. The noise contributions in (B.1) are given by
(in (A.8) and (A.9), resp.) in the absence of noise and of the interference terms. The noise contributions in (B.1) are given by




where the zero-mean circular noise  has a variance
has a variance  . In this case we obtain
. In this case we obtain


where  denotes
denotes  and the last equality has been obtained by exploiting the fact that
and the last equality has been obtained by exploiting the fact that  ,
, 
 , and, moreover,
, and, moreover,


Thus, from (B.4) we obtain


Finally, under the assumption  , exploiting the condition (A.7) and the noise circularity, we have
, exploiting the condition (A.7) and the noise circularity, we have




Therefore, we can write


where  and
and  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fusco, T., Petrella, A. & Tanda, M. Joint Symbol Timing and CFO Estimation for OFDM/OQAM Systems in Multipath Channels. EURASIP J. Adv. Signal Process. 2010, 897607 (2009). https://doi.org/10.1155/2010/897607
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/897607
 11.2 MHz;
11.2 MHz;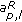 and
and 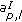 are the real and imaginary part of QPSK symbols;
are the real and imaginary part of QPSK symbols;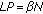 , where the overlap parameter
, where the overlap parameter 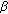 is fixed at
is fixed at  ;
;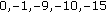 , and
, and  ;
;








