- Research Article
- Open access
- Published:
Fast Multi-Symbol Based Iterative Detectors for UWB Communications
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 903161 (2010)
Abstract
Ultra-wideband (UWB) impulse radios have shown great potential in wireless local area networks for localization, coexistence with other services, and low probability of interception and detection. However, low transmission power and high multipath effect make the detection of UWB signals challenging. Recently, multi-symbol based detection has caught attention for UWB communications because it provides good performance and does not require explicit channel estimation. Most of the existing multi-symbol based methods incur a higher computational cost than can be afforded in the envisioned UWB systems. In this paper, we propose an iterative multi-symbol based method that has low complexity and provides near optimal performance. Our method uses only one initial symbol to start and applies a decision directed approach to iteratively update a filter template and information symbols. Simulations show that our method converges in only a few iterations (less than 5), and that when the number of symbols increases, the performance of our method approaches that of the ideal Rake receiver.
1. Introduction
Ultra-wideband (UWB) impulse radio (IR) transmits ultra-short pulses at low power spectral density where the information is encoded via pulse-amplitude modulation (PAM) or via pulse-position modulation (PPM). The IR-UWB systems show some important merits including: coexistence with current narrowband signals, high multiple-access capacity and fine timing resolution [1–3]. Fine timing resolution property helps the receiver to resolve distinct dense multipath components and provides high degrees of diversity whilst the low power spectral density enables sharing of the RF spectrum with limited mutual interference.
One of the major challenges in UWB system is to deal with the dense multipath channel. Indeed, each transmitted UWB pulse arrives at the receiver as hundreds of replicas with different delays, amplitudes and phases [4–6]. To collect the available diversity, Rake receivers [7, 8] employ a large number of fingers to capture the multipath energy [9]. However, channel estimation error can degrade the Rake's performance and the accurate estimation of the gains and delays of channel paths incurs considerable computational cost [10].
As an alternative to the Rake receiver, the transmitted reference (TR) method [8, 11–14] sends a reference signal along with the data-modulated signal. The receiver can simply be an autocorrelation receiver which demodulates the data by correlating the delayed reference signal and the data-modulated signal. The advantage of the TR method compared to the Rake method is that it is easier to implement because it does not require explicit channel estimation. However, the main drawback of TR-based methods is that the noise induced in the reference signal severely degrades the error performance.
In [15], decision-directed autocorrelation (DDA) receivers are proposed to detect the current symbol by correlating the current information waveform with a waveform template generated by all previously decoded symbols. However, the DDA receivers detect the information symbols successively and the current detected symbol has no contribution to the preceding symbol detection. To relieve the noise effect of the reference signal in TR system, further enhancement techniques exploit the multi-symbol differential detection [16, 17] to jointly detect  consecutive symbols. The generalized likelihood ratio test (GLRT) approach for the multi-symbol case is derived and exhaustive search is performed on all
consecutive symbols. The generalized likelihood ratio test (GLRT) approach for the multi-symbol case is derived and exhaustive search is performed on all  symbol possibilities to find the optimal one [16]. The practical implementation of the method suffers from the exponential computational complexity in terms of block size
symbol possibilities to find the optimal one [16]. The practical implementation of the method suffers from the exponential computational complexity in terms of block size  . A reduced complexity algorithm is devised in [17] by introducing the sphere decoding algorithm (SDA). An approximate algorithm based on the Viterbi algorithm (VA) is also presented in [17]. Although SDA and VA reduce the complexity relative to exhaustive search, and are effective for small
. A reduced complexity algorithm is devised in [17] by introducing the sphere decoding algorithm (SDA). An approximate algorithm based on the Viterbi algorithm (VA) is also presented in [17]. Although SDA and VA reduce the complexity relative to exhaustive search, and are effective for small  , they require considerable computational effort when
, they require considerable computational effort when  is large.
is large.
In this paper, we propose a fast multi-symbol iterative detection method. The method harvests the benefits from the concept of the multiple symbols detection and outputs a better bit error rate (BER) performance than the single symbol TR system whilst exhibiting a low computational complexity ( , where
, where  is block size and
is block size and  is the maximum number of iterations). Following the description of general iterative method, two particular low-complexity detectors are designed and evaluated in the simulation experiments. Although the proposed method cannot guarantee to achieve the same performance as the GLRT-based detector in the general case, experimental results show that the BER performance of the method is very close to that of the GLRT when
is the maximum number of iterations). Following the description of general iterative method, two particular low-complexity detectors are designed and evaluated in the simulation experiments. Although the proposed method cannot guarantee to achieve the same performance as the GLRT-based detector in the general case, experimental results show that the BER performance of the method is very close to that of the GLRT when  (the signal-to-noise ratio (SNR) gap is less than
(the signal-to-noise ratio (SNR) gap is less than  dB). Further experiments demonstrate that a few iterations (
dB). Further experiments demonstrate that a few iterations ( iterations) are sufficient for the detectors to converge.
iterations) are sufficient for the detectors to converge.
The rest of the paper is organized as follows. Section 2 introduces the UWB signal model. Section 3 describes the multi-symbol transmitted reference system with GLRT detection. Section 4 develops two fast multi-symbol transmitted reference-based detectors. Section 5 shows the numerical results for a constant channel and random channels, respectively. Section 6 concludes the paper.
2. Signal Model
The transmitted signal in IR-UWB systems using the pulse amplitude modulation (PAM) for the  th transmitted symbol is
th transmitted symbol is

where  is a transmitted monocycle waveform with support set
is a transmitted monocycle waveform with support set  , the
, the  's are the modulated symbols, the
's are the modulated symbols, the  's are the user-specific pseudorandom time-hopping (TH) codes and
's are the user-specific pseudorandom time-hopping (TH) codes and  is its frame duration. Because the energy of one single pulse is limited in UWB communication systems, each symbol is transmitted using
is its frame duration. Because the energy of one single pulse is limited in UWB communication systems, each symbol is transmitted using  frames so that the receiver can collect enough energy to recover the signal. Thus, the symbol duration is
frames so that the receiver can collect enough energy to recover the signal. Thus, the symbol duration is  . The TH codes
. The TH codes  are integers chosen from
are integers chosen from  so that multiple users can access the channel concurrently and the transmission time of
so that multiple users can access the channel concurrently and the transmission time of  th monocycle waveform is delayed with
th monocycle waveform is delayed with  seconds. Due to the highly-frequency selective feature of UWB channel, the frame duration is chosen such that
seconds. Due to the highly-frequency selective feature of UWB channel, the frame duration is chosen such that  , where
, where  is the maximum excess delay of the channel. This condition eliminates intersymbol interference (ISI). The energy of one pulse is
is the maximum excess delay of the channel. This condition eliminates intersymbol interference (ISI). The energy of one pulse is  .
.
The channel impulse response (CIR) of the UWB system is assumed to be slow fading with multipath propagation

where  is the total number of specular propagation paths with amplitude
is the total number of specular propagation paths with amplitude  and delay
and delay  . Hence, the signal obtained from the receiver side for the
. Hence, the signal obtained from the receiver side for the  th symbol is modeled as
th symbol is modeled as

where  is the channel template,
is the channel template,  denotes the convolution operation and
denotes the convolution operation and  denotes the noise including multiple access interference (MAI) and an additive white Gaussian noise (AWGN) with zero mean and two-sided power spectral density
denotes the noise including multiple access interference (MAI) and an additive white Gaussian noise (AWGN) with zero mean and two-sided power spectral density  . The noiseless received signal energy in each frame is defined as
. The noiseless received signal energy in each frame is defined as  and is proportional to the pulse energy
and is proportional to the pulse energy  .
.
A key element to determine the receiver demodulation structure is the way to encode the information symbols  to the transmitted symbols
to the transmitted symbols  . In the following, we list three kinds of encoders:
. In the following, we list three kinds of encoders:
-
(i)
Transmitted Reference (TR) [12] with
 = 1 if
= 1 if  is even, otherwise
is even, otherwise 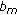 =
= 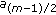 .
. -
(ii)
Multi-Symbol Differential Encoder (MSDE) [17] with
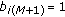 and
and 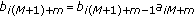 where
where  is a multi-symbol block index and
is a multi-symbol block index and 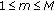 .
. -
(iii)
Multi-Symbol Transmitted Reference (MSTR) with
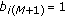 and
and 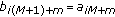 where
where  is a multi-symbol block index and
is a multi-symbol block index and  .
.
In this paper, our focus is on the MSTR encoder in this paper. All these encoders employ the first modulated symbol as the reference signal in each block and the TR scheme [12] can be viewed as a special case of MSTR scheme where  . For MSDE case, the current transmitted symbols are encoded differentially with the previous encoded symbols and the first symbol is used as an initial symbol, while in MSTR case, the current transmitted symbol is the same as the information symbol except the first one, which is used to generate the reference template.
. For MSDE case, the current transmitted symbols are encoded differentially with the previous encoded symbols and the first symbol is used as an initial symbol, while in MSTR case, the current transmitted symbol is the same as the information symbol except the first one, which is used to generate the reference template.
3. GLRT-Based Multi-Symbol Detection
In the case of multi-symbol detection, each block contains  symbols including one reference symbol and
symbols including one reference symbol and  information symbols. To simplify the equations in multi-symbol detection cases, we consider only the encoding and detecting scheme in one block of
information symbols. To simplify the equations in multi-symbol detection cases, we consider only the encoding and detecting scheme in one block of  symbols. Hence, the received signal can be rewritten as
symbols. Hence, the received signal can be rewritten as

by assuming that the channel is quasi-static over the interval  .
.
Now, our task is to determine the information symbols  without knowing the channel template
without knowing the channel template  . The relationship between information symbols
. The relationship between information symbols  and transmitted symbols
and transmitted symbols  for MSDE is
for MSDE is

and for MSTR is

Here, we resort to the generalized likelihood ratio test (GLRT) approach to detect the information symbols. The log-likelihood metric is given as

where  is the candidate waveform constructed by
is the candidate waveform constructed by 

where  is the
is the  st row of an
st row of an  matrix which comes from the encoding schemes (MSDE or MSTR) described in Section 2. All entries of
matrix which comes from the encoding schemes (MSDE or MSTR) described in Section 2. All entries of  are
are  or
or  and
and  is defined as
is defined as  . The
. The  matrices for the MSDE and MSTR are
matrices for the MSDE and MSTR are

The decision rule of GLRT algorithm is of the form

In (10), although  is unknown, it is treated as a nuisance parameter. The optimum reference template given a symbol candidate
is unknown, it is treated as a nuisance parameter. The optimum reference template given a symbol candidate  can be obtained using the variational technique (see [17])
can be obtained using the variational technique (see [17])

where  is the averaged waveform for the
is the averaged waveform for the  th received symbol signal over
th received symbol signal over  frames
frames

Incorporating the log-likelihood formula in (10) and (11), finally we have

where

where  is the integration interval of the correlator, and
is the integration interval of the correlator, and  .
.
Some remarks are now of interest.
 For the single user or multiple-orthogonal users case with
For the single user or multiple-orthogonal users case with  , (13) reduces to
, (13) reduces to

which is equivalent to averaged transmitted reference (ATR) detection for single symbol detection [12]

where  is the decision variable for ATR.
is the decision variable for ATR.
Simple mathematical manipulations yield the following expressions for the mean and variance of the decision variable  as
as


where  is the one-sided noise bandwidth of the receiver,
is the one-sided noise bandwidth of the receiver,  is the statistical expectation, and
is the statistical expectation, and  is the variance of the random variable. The BER of the detector in this case is [12]
is the variance of the random variable. The BER of the detector in this case is [12]

where  is the
is the  -function
-function 
 Unlike the ideal Rake receiver, which correlates the receive signal with noiseless template, the TR scheme uses the noisy reference signal as a template in one symbol case and the best estimated reference signal using (11) in the multi-symbol case. However, the TR system does not explicitly estimate the channel parameters and only requires the correlation coefficients
Unlike the ideal Rake receiver, which correlates the receive signal with noiseless template, the TR scheme uses the noisy reference signal as a template in one symbol case and the best estimated reference signal using (11) in the multi-symbol case. However, the TR system does not explicitly estimate the channel parameters and only requires the correlation coefficients  ,
,  ,
,  ,
,  evaluated in (14).
evaluated in (14).
 As seen in (11), the variance of the reference signal
As seen in (11), the variance of the reference signal  decays as
decays as  increases when
increases when  . In turn, the accuracy of the multi-symbol detection is improved and converges to the performance of ideal Rake receiver as
. In turn, the accuracy of the multi-symbol detection is improved and converges to the performance of ideal Rake receiver as 
 The global optimal value of
The global optimal value of  can be obtained by using exhaustive search [16] or sphere decoding [17]. However, the computational cost of the exhaustive search method grows exponentially with the number of symbols
can be obtained by using exhaustive search [16] or sphere decoding [17]. However, the computational cost of the exhaustive search method grows exponentially with the number of symbols  . Sphere decoding method searches all the lattice points inside a given radius and reduces the complexity of the exhaustive search method on average. However, the expected complexity of SDA is still exponential for fixed SNR and increases significantly when SNR is low [18].
. Sphere decoding method searches all the lattice points inside a given radius and reduces the complexity of the exhaustive search method on average. However, the expected complexity of SDA is still exponential for fixed SNR and increases significantly when SNR is low [18].
4. A Fast MSTR Detection Method
In this section, we develop an iterative MSTR detection algorithm by avoiding the high computational complexity of GLRT-based detectors (e.g., exhaustive search [16] and SDA [17]). Similar to the TR detection scheme, the proposed method first generates a reference template by using the initial symbol only, and then estimates the information symbols by correlating the reference template with the symbol waveforms. Furthermore, with the help of the information from multiple transmitted symbols, our method manages to suppress the reference template noise. However, our method also generates additional noise-cross-signal and noise-cross-noise terms which do not appear in the case of an ideal Rake receiver with perfect channel knowledge.
For the initialization, since the only known symbol is  , the best template at this stage is
, the best template at this stage is

where  can be found in (12).
can be found in (12).
The decision variables for the  information symbols are
information symbols are

The estimated information symbols in this iteration are

This means that at the first step the estimated symbols are obtained by correlating the waveform corresponding to  with the
with the  th symbol waveform. Hence, the BER performance is the same as that of the ATR in (19).
th symbol waveform. Hence, the BER performance is the same as that of the ATR in (19).
For the  th iteration, the method firstly constructs a new reference template by weighting the product of each symbol's waveform
th iteration, the method firstly constructs a new reference template by weighting the product of each symbol's waveform  and its corresponding detected symbol
and its corresponding detected symbol  obtained from the previous iteration
obtained from the previous iteration

Then, the decision variable for the  th symbol is evaluated in the same way as the one in (21)
th symbol is evaluated in the same way as the one in (21)

where  is the reference template for the
is the reference template for the  th symbol by removing the
th symbol by removing the  th waveform
th waveform  from
from 

At last, the iteration outputs the estimated symbols as

4.1. Weight Selections
A key factor that affects the method's performance and convergence is how to update the weights in each iteration. The ultimate goal of selecting the weights is to reduce BER while maintaining low computational complexity and requiring little extra knowledge (such as channel information). Here, we propose two types of rule for the choice of the weights in each iteration.
-
(i)
Hard Decision for MSTR (HD-MSTR)
The rule constructs the reference template as

which indicates that  in (23). Also note that, the template is a scaled version of the GLRT template estimate given the detected symbols
in (23). Also note that, the template is a scaled version of the GLRT template estimate given the detected symbols  as shown in (11).
as shown in (11).
An interesting observation on the reference template of HD-MSTR in (27) is that the variance of the reference template is constant given the detected symbols 

The conditional mean of the template is

where  is the number of correct symbols for the
is the number of correct symbols for the  st iteration. Hence, the mean and standard deviation ratio is
st iteration. Hence, the mean and standard deviation ratio is

where  is the standard deviation of the random variable. In general, the larger the mean-standard deviation ratio, the better the BER performance. Thus, in the case of HD-MSTR, if more correct symbols are detected for the current iteration, during the next iteration, the reference template is improved and then the method potentially results in better BER performance. The iterative procedure runs back and forth until no symbol is changed or the maximum number of iterations is reached.
is the standard deviation of the random variable. In general, the larger the mean-standard deviation ratio, the better the BER performance. Thus, in the case of HD-MSTR, if more correct symbols are detected for the current iteration, during the next iteration, the reference template is improved and then the method potentially results in better BER performance. The iterative procedure runs back and forth until no symbol is changed or the maximum number of iterations is reached.
(ii) Soft Decision for MSTR (SD-MSTR)
An intuitive idea of the SD-MSTR detector is that the decision variable  obtained in each iteration reflects the reliability of the detected symbol
obtained in each iteration reflects the reliability of the detected symbol  . The larger the value of
. The larger the value of  , the more we can trust the accuracy of the detected symbol
, the more we can trust the accuracy of the detected symbol  . Hence, the corresponding symbol deserves higher weight in the representation of the reference template for next iteration.
. Hence, the corresponding symbol deserves higher weight in the representation of the reference template for next iteration.
By facilitating the additional information from decision variables  , the SD-MSTR determines the weight values as
, the SD-MSTR determines the weight values as


where the two terms in (31) are the posterior probabilities of correct and erroneous detection of the symbol  conditioned on the decision variable
conditioned on the decision variable  . If these probabilities are the same, that means it does not matter which decision we make. This represents the most unreliable case and the weight should be set to zero. The larger the probability of correct detection, the higher weight we should put on this decision. Note that the weight
. If these probabilities are the same, that means it does not matter which decision we make. This represents the most unreliable case and the weight should be set to zero. The larger the probability of correct detection, the higher weight we should put on this decision. Note that the weight  of the known reference symbol
of the known reference symbol  is set to 1,
is set to 1,  should be
should be  and
and  ranges from
ranges from  indicating how much the averaged signal
indicating how much the averaged signal  contributes to the final template depending on accuracy of the estimated symbol
contributes to the final template depending on accuracy of the estimated symbol  .
.
By applying Bayes' rule, (31) becomes

where the probabilities rely on the distribution of  which is approximately Gaussian distributed with mean
which is approximately Gaussian distributed with mean  and variance
and variance  given
given  [13]
[13]

where  is the probability density function (pdf) of the standard normal distribution.
is the probability density function (pdf) of the standard normal distribution.
A practical issue in SD-MSTR is how to evaluate the statistics of  in each iteration since we do not have an explicit formula. An approximate solution of the problem is to utilize the known ATR statistics to evaluate the probabilities for each iteration
in each iteration since we do not have an explicit formula. An approximate solution of the problem is to utilize the known ATR statistics to evaluate the probabilities for each iteration


where  and
and  can be found in (17) and (18) which require the frame energy
can be found in (17) and (18) which require the frame energy  and the noise power
and the noise power  to evaluate
to evaluate  and
and  , but they are easy to estimate and store at the receiver side.
, but they are easy to estimate and store at the receiver side.
Now, we can summarize our method in the following steps for one block symbol detection.
Input:
Correlation matrix  defined in (14), where
defined in (14), where  ,
,  , the maximum number of iterations
, the maximum number of iterations  , channel statistics
, channel statistics  and
and  for the SD-MSTR case.
for the SD-MSTR case.
Step 1.
Initialize  ,
,  ,
,  .
.
Step 2.
 .
.
Step 3.
Obtain the decision variables by (24).
Step 4.
Obtain the detected symbols by (26).
Step 5.
Set  for the HD-MSTR case or update the weights for
for the HD-MSTR case or update the weights for  based on (31), (35), (36) in the SD-MSTR case.
based on (31), (35), (36) in the SD-MSTR case.
Step 6.
If  and
and  goto Step 2, otherwise output
goto Step 2, otherwise output  and exit.
and exit.
4.2. Convergence and Discussions
 The convergence rate also affects the practical value of the method (e.g., a system with a tight constraint on decoding delay) and the number of iterations affects the performance. These will be verified by the numerical simulation that the proposed method converges to the stable performance curve within a few iterations (usually
The convergence rate also affects the practical value of the method (e.g., a system with a tight constraint on decoding delay) and the number of iterations affects the performance. These will be verified by the numerical simulation that the proposed method converges to the stable performance curve within a few iterations (usually  iterations).
iterations).
 Comparing with MSDD, we choose MSTR as the encoding scheme which allows the algorithm to detect symbol
Comparing with MSDD, we choose MSTR as the encoding scheme which allows the algorithm to detect symbol  directly without any further processing.
directly without any further processing.
 Instead of evaluating each iteration's reference template
Instead of evaluating each iteration's reference template  explicitly, the method computes the decision variables by linear combination of the correlation coefficients
explicitly, the method computes the decision variables by linear combination of the correlation coefficients  which can be computed in the first iteration and reused later.
which can be computed in the first iteration and reused later.
 The HD-MSTR only requires the coefficients
The HD-MSTR only requires the coefficients  which is the same as the GLRT approach meanwhile the SD-MSTR requires some additional channel statistical information to update the weights for each iteration.
which is the same as the GLRT approach meanwhile the SD-MSTR requires some additional channel statistical information to update the weights for each iteration.
 For each iteration, Step 3 requires
For each iteration, Step 3 requires  multiplications and
multiplications and  additions to attain the decision variables for all
additions to attain the decision variables for all  symbols. In Step 4,
symbols. In Step 4,  sign operations are performed to obtain detected symbols. No arithmetic is required for HD-MSTR in Step 5, while the SD-MSTR performs
sign operations are performed to obtain detected symbols. No arithmetic is required for HD-MSTR in Step 5, while the SD-MSTR performs  times Gaussian pdf evaluation and needs
times Gaussian pdf evaluation and needs  additions and
additions and  divisions to normalize weights. We can treat the computational costs of sign operation and Gaussian pdf evaluation as being constant, and then the computational complexity of the both detectors for each iteration is
divisions to normalize weights. We can treat the computational costs of sign operation and Gaussian pdf evaluation as being constant, and then the computational complexity of the both detectors for each iteration is  where
where  is the block size. Note that the complexity of the proposed method is independent of the channel realizations whilst the computational complexity of SDA relies on the specific realization of channels and SNR.
is the block size. Note that the complexity of the proposed method is independent of the channel realizations whilst the computational complexity of SDA relies on the specific realization of channels and SNR.
5. Numerical Results
This section compares the BER performance of the proposed methods (HD-MSTR and SD-MSTR) and the MSTR based on exhaustive search (ES-MSTR) as benchmark. Two kinds of channel schemes are evaluated: one is a constant channel with fixed CIR parameters, and the other is a random channel based on Saleh and Valenzuela (SV) channel model.
5.1. Constant Channel
At the transmitter side, the pulse  is the second derivative of a Gaussian function with normalized unit energy and pulse width
is the second derivative of a Gaussian function with normalized unit energy and pulse width  . The number of frames per symbols is
. The number of frames per symbols is  . For the UWB channel model, we employ the resolvable multipath assumption such that
. For the UWB channel model, we employ the resolvable multipath assumption such that  as studied in [12, 13, 19] and then
as studied in [12, 13, 19] and then  in (18) can be approximated with the number of paths
in (18) can be approximated with the number of paths  . In this simulation,
. In this simulation,  is
is  and the energy of impulse channel response (CIR)
and the energy of impulse channel response (CIR)  which means
which means  in this scheme. As we have shown in Section 3, if the number of symbols in one block
in this scheme. As we have shown in Section 3, if the number of symbols in one block  is equal to
is equal to  or the maximum number of iterations
or the maximum number of iterations  is equal to
is equal to  , then the system outputs the same performance as ATR scheme in [12]. Note that there is a
, then the system outputs the same performance as ATR scheme in [12]. Note that there is a  gap between the ATR curve in the following figures and the one in [12]. This is because the definition of frame energy in [12] is twice as the one of ours. In this subsection, we only consider single user case with
gap between the ATR curve in the following figures and the one in [12]. This is because the definition of frame energy in [12] is twice as the one of ours. In this subsection, we only consider single user case with  for all
for all  . Multiuser case will be shown in next subsection.
. Multiuser case will be shown in next subsection.
5.1.1. BER with Different Block Size
Figures 1 and 2 illustrate the BER results for  for HD-MSTR and SD-MSTR, respectively. For HD-MSTR, the proposed method can obtain about
for HD-MSTR and SD-MSTR, respectively. For HD-MSTR, the proposed method can obtain about  gain relative to ATR in the case of
gain relative to ATR in the case of  and about
and about  gain if
gain if  . With the increase of the number of symbols in one block, the performance of the proposed method grows monotonically but the improvement decelerates (
. With the increase of the number of symbols in one block, the performance of the proposed method grows monotonically but the improvement decelerates ( gain for
gain for  and
and  gain for
gain for  ). In the same figure, we also depict the performance of the GLRT algorithm with exhaustive search (called ES-MSTR) as benchmarks. We also perform some simulations with very large
). In the same figure, we also depict the performance of the GLRT algorithm with exhaustive search (called ES-MSTR) as benchmarks. We also perform some simulations with very large 
 which is intractable for classical methods. The system provides similar performance to that of the ideal Rake receiver, especially in high SNR range, where the difference is less than
which is intractable for classical methods. The system provides similar performance to that of the ideal Rake receiver, especially in high SNR range, where the difference is less than  .
.
Comparing the performance of HD-MSTR and SD-MSTR detectors in Figures 1 and 2, respectively, the difference is obvious when  is small. The SD-MSTR outperforms the HD-MSTR, with about
is small. The SD-MSTR outperforms the HD-MSTR, with about  of SNR gain when
of SNR gain when  and around
and around  gain when
gain when  . The difference becomes trivial when
. The difference becomes trivial when  is
is  or larger. This indicates that the SD-MSTR method can offer additional advantages for low complexity UWB systems with small
or larger. This indicates that the SD-MSTR method can offer additional advantages for low complexity UWB systems with small  and but its advantage decreases with increasing
and but its advantage decreases with increasing  . Bearing in mind that the SD-MSTR requires some statistical channel information (
. Bearing in mind that the SD-MSTR requires some statistical channel information ( ,
,  in (17) and (18)) and the Gaussian pdf calculation of the system, it is more likely that the simpler HD-MSTR algorithm would be implemented if
in (17) and (18)) and the Gaussian pdf calculation of the system, it is more likely that the simpler HD-MSTR algorithm would be implemented if  is large.
is large.
Compared with HD-MSTR and SD-MSTR, the ES-MSTR has an advantage when  is small (if
is small (if  , about
, about  gain for HD-MSTR and
gain for HD-MSTR and  for SD-MSTR) and the performance gap becomes smaller when
for SD-MSTR) and the performance gap becomes smaller when  is larger. When
is larger. When  , the gap reduces to around
, the gap reduces to around  for HD-MSTR case and about
for HD-MSTR case and about  for the SD-MSTR case. This shows that with the increasing value of
for the SD-MSTR case. This shows that with the increasing value of  the difference between the optimal ES-MSTR method and our proposed methods decreases rapidly and that the gap can be ignored for a sufficient large
the difference between the optimal ES-MSTR method and our proposed methods decreases rapidly and that the gap can be ignored for a sufficient large  . Furthermore, the ES-MSTR incurs much higher computational cost than our MSTR method.
. Furthermore, the ES-MSTR incurs much higher computational cost than our MSTR method.
5.1.2. BER with Different Iterations
To answer the convergence question in Section 4.2, Figures 3, 4, 5, and 6 depict the BER values recorded in each iteration for  . When there is only one iteration, the system reduces to classic ATR system and the BER result overlaps with that given by (19) (see Figures 3 and 4). The BER is improved significantly in the second iteration and just after about
. When there is only one iteration, the system reduces to classic ATR system and the BER result overlaps with that given by (19) (see Figures 3 and 4). The BER is improved significantly in the second iteration and just after about  iterations, the algorithm reaches a stable BER performance curve with a small improvement in the
iterations, the algorithm reaches a stable BER performance curve with a small improvement in the  th iteration at low SNRs. These show that our methods converge fast and it is practical for UWB systems. It is also noticed that the HD-MSTR and SD-MSTR show the similar convergence rates in the figures.
th iteration at low SNRs. These show that our methods converge fast and it is practical for UWB systems. It is also noticed that the HD-MSTR and SD-MSTR show the similar convergence rates in the figures.
5.2. SV Channel Model
The more realistic UWB channel is random which significantly affects the BER performance compared with constant channels. The SV channel model which is generally statistically verified to well describe the realistic UWB channel with dense multipath is adopted in this section. The model formulates the channel impulse response (CIR) as [20]

where  models the double-sided Rayleigh distributed amplitudes with exponentially decaying profile.
models the double-sided Rayleigh distributed amplitudes with exponentially decaying profile.
In our experiments, the SV channel model parameters are:  ns,
ns,  ns,
ns,  ,
, 
 (see [20,
(see [20,  ] ). The pulse
] ). The pulse  is the monocycle which is the same as the one in Section 5.1. The energy per bit
is the monocycle which is the same as the one in Section 5.1. The energy per bit  is defined as
is defined as

where  is the average received energy per frame and the frame repetition factor is
is the average received energy per frame and the frame repetition factor is  (to compare with [17]) while the integral interval is
(to compare with [17]) while the integral interval is  ns and the frame duration is
ns and the frame duration is  ns to preclude the IFI.
ns to preclude the IFI.
5.2.1. Single User Scenario
Figures 7 and 8 plot the performance curves for both HD-MSTR and SD-MSTR in single user scenario, respectively. For random channels, SD-MSTR shows about  gain over the HD-MSTR for
gain over the HD-MSTR for  and retains the advantage even for large
and retains the advantage even for large  (
( ). For HD-MSTR case, the algorithm achieves
). For HD-MSTR case, the algorithm achieves  gain if
gain if  and about
and about  gain if
gain if  with respect to ATR. This means that with a few iterations, the algorithms efficiently exploit the multi-symbol benefits and yield a near optimal result. Furthermore, by avoiding searching the solution space which is computational complex, our iterative methods are easy to compute by adding up some correlation terms with different weights in (24).
with respect to ATR. This means that with a few iterations, the algorithms efficiently exploit the multi-symbol benefits and yield a near optimal result. Furthermore, by avoiding searching the solution space which is computational complex, our iterative methods are easy to compute by adding up some correlation terms with different weights in (24).
Furthermore, when  and BER =
and BER =  , there is about
, there is about  gap between the ideal Rake receiver and our algorithm. As we expected, the performance over random channels is worse than the one with constant channels.
gap between the ideal Rake receiver and our algorithm. As we expected, the performance over random channels is worse than the one with constant channels.
5.2.2. Multiuser Scenario
In this subsection, we consider the performance of our algorithms in the presence of multiple access interference (MAI). In the case of MAI, the chip interval is  ns and the TH codes
ns and the TH codes  are randomly generated in the range
are randomly generated in the range  where
where  . Unlike the single user scenario, we do not consider the attenuation of each individual channel and assume ideal power control among nodes such that the received energy from each interfering user is the same. Figure 9 displays the BER result in this MAI scenario. At BER
. Unlike the single user scenario, we do not consider the attenuation of each individual channel and assume ideal power control among nodes such that the received energy from each interfering user is the same. Figure 9 displays the BER result in this MAI scenario. At BER  , the HD-MSTR experiences only around
, the HD-MSTR experiences only around  performance degradation for
performance degradation for  comparing with corresponding single user scenario where
comparing with corresponding single user scenario where  is the number of users. In addition, there is less than
is the number of users. In addition, there is less than  gap between the multiple users HD-MSTR and single user ideal Rake receiver. For the SD-MSTR case, the detector outperforms the HD-MSTR detector with more than
gap between the multiple users HD-MSTR and single user ideal Rake receiver. For the SD-MSTR case, the detector outperforms the HD-MSTR detector with more than  gain in both single and multiple users scenario. In summary, our proposed detectors demonstrate significant robustness in the present of the MAI effects.
gain in both single and multiple users scenario. In summary, our proposed detectors demonstrate significant robustness in the present of the MAI effects.
6. Conclusion
In this paper, we propose fast detection methods for MSTR transmissions. The proposed MSTR detectors obtain the decision variables by summing up the correlation of different symbol waveforms, each properly weighted by the reliability of detected symbols and iteratively updating the weights and detected symbols. With different updating methods for the weights, two detectors are proposed: Hard Decision for MSTR (HD-MSTR) detector and Soft Decision for MSTR (SD-MSTR) detector, where HD-MSTR obtains the template based only on the previous detected symbols, while SD-MSTR constructs the template with additional information from the decision variables. Enhanced BER performance relative to the ATR scheme and the fast convergence property of these detectors are shown by the simulation results. Due to its simplicity, low computational complexity and near optimal performance for  , the method is promising for realistic UWB applications.
, the method is promising for realistic UWB applications.
References
Win MZ, Scholtz RA: Impulse radio: how it works. IEEE Communications Letters 1998, 2(2):36-38. 10.1109/4234.660796
Win MZ, Scholtz RA: Ultra-wide bandwidth time-hopping spread-spectrum impulse radio for wireless multiple-access communications. IEEE Transactions on Communications 2000, 48(4):679-691. 10.1109/26.843135
Yang L, Giannakis GB: Ultra-wideband communications: an idea whose time has come. IEEE Signal Processing Magazine 2004, 21(6):26-54. 10.1109/MSP.2004.1359140
Cramer RJ-M, Scholtz RA, Win MZ: Evaluation of an ultra-wide-band propagation channel. IEEE Transactions on Antennas and Propagation 2002, 50(5):561-570. 10.1109/TAP.2002.1011221
Win MZ, Scholtz RA: Characterization of ultra-wide bandwidth wireless indoor channels: a communication-theoretic view. IEEE Journal on Selected Areas in Communications 2002, 20(9):1613-1627. 10.1109/JSAC.2002.805031
Cassioli D, Win MZ, Molisch AF: The ultra-wide bandwidth indoor channel: from statistical model to simulations. IEEE Journal on Selected Areas in Communications 2002, 20(6):1247-1257. 10.1109/JSAC.2002.801228
Cassioli D, Win MZ, Vatalaro F, Molisch AF: Performance of low-complexity Rake reception in a realistic UWB channel. Proceedings of the IEEE International Conference on Communications (ICC '02), May 2002 2: 763-767.
Choi JD, Stark WE: Performance of ultra-wideband communications with suboptimal receivers in multipath channels. IEEE Journal on Selected Areas in Communications 2002, 20(9):1754-1766. 10.1109/JSAC.2002.805623
Win MZ, Scholtz RA: On the energy capture of ultrawide bandwidth signals in dense multipath environments. IEEE Communications Letters 1998, 2(9):245-247. 10.1109/4234.718491
Lottici V, D'Andrea A, Mengali U: Channel estimation for ultra-wideband communications. IEEE Journal on Selected Areas in Communications 2002, 20(9):1638-1645. 10.1109/JSAC.2002.805053
Hoctor R, Tomlinson H: Delay-hopped transmitted-reference RF communications. Proceedings of the IEEE Conference on Ultra Wideband Systems and Technologies (UWBST '02), May 2002 265-269.
Chao Y-L, Scholtz RA: Optimal and suboptimal receivers for ultra-wideband transmitted reference systems. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '03), December 2003 759-763.
Quek TQS, Win MZ: Analysis of UWB transmitted-reference communication systems in dense multipath channels. IEEE Journal on Selected Areas in Communications 2005, 23(9):1863-1874.
Yang L, Giannakis GB: Optimal pilot waveform assisted modulation for ultrawideband communications. IEEE Transactions on Wireless Communications 2004, 3(4):1236-1249. 10.1109/TWC.2004.830827
Zhao S, Liu H, Tian Z: Decision directed autocorrelation receivers for pulsed ultra-wideband systems. IEEE Transactions on Wireless Communications 2006, 5(8):2175-2184.
Guo N, Qiu RC: Improved autocorrelation demodulation receivers based on multiple-symbol detection for UWB communications. IEEE Transactions on Wireless Communications 2006, 5(8):2026-2031.
Lottici V, Tian Z: Multiple symbol differential detection for UWB communications. IEEE Transactions on Wireless Communications 2008, 7(5):1656-1666.
Jaldén J, Ottersten B: On the complexity of sphere decoding in digital communications. IEEE Transactions on Signal Processing 2005, 53(4):1474-1484.
Gezici S, Kobayashi H, Poor HV, Molisch AF: Performance evaluation of impulse radio UWB systems with pulse-based polarity randomization. IEEE Transactions on Signal Processing 2005, 53(7):2537-2549.
Saleh AAM, Valenzuela RA: A statistical model for indoor multipath propagation. IEEE Journal on Selected Areas in Communications 1987, 5(2):128-137.
Acknowledgments
Part of this work is supported by the Georgia Tech Ultrawideband Center of Excellence (http://www.uwbtech.gatech.edu/). The authors would like to thank the anonymous reviewers and the guest editor for their helpful comments which improved the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhou, Q., Ma, X. & Lottici, V. Fast Multi-Symbol Based Iterative Detectors for UWB Communications. EURASIP J. Adv. Signal Process. 2010, 903161 (2010). https://doi.org/10.1155/2010/903161
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/903161
 = 1 if
= 1 if  is even, otherwise
is even, otherwise 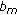 =
= 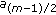 .
.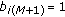 and
and 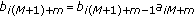 where
where  is a multi-symbol block index and
is a multi-symbol block index and 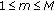 .
.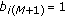 and
and 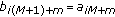 where
where  is a multi-symbol block index and
is a multi-symbol block index and  .
.







