- Research Article
- Open access
- Published:
Nyquist Filters with Alternative Balance between Time- and Frequency-Domain Parameters
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 903980 (2010)
Abstract
Designing matched pulse shaping filters with their cascade satisfying the Nyquist condition for minimum intersymbol interference constitutes an important task for almost all digital data radio transceivers processing an incoming data signal on the sample-by-sample basis. Despite their practical importance, there are only few sets of Nyquist filter definitions and design techniques to devise digital filter coefficients available for a designer. In this paper we propose a set of Nyquist filters that balance the time- and frequency-domain parameters in favor of a filter stop-band attenuation and residual intersymbol interference compared with the already existing Nyquist filter sets. Using a number of filter examples, this paper shows that the proposed Nyquist filters can be a good option for applications that need to fulfill strict limits of adjacent and alternate channel power attenuation while providing a low level of residual intersymbol interference and group delay of the digital filter.
1. Introduction
If the digital receiver processes a data signal on the sample-by-sample basis, a typical problem which arises from the strict band limitation of the signal spectrum is the phenomenon called intersymbol interference(ISI). To lower the amount of ISI to zero, the overall transmitter-channel-receiver frequency response should fulfill the first Nyquist criterion defined in the frequency domain as [1–3]

For a minimum double-sided signal bandwidth equal to the Nyquist frequency  , where
, where  is the modulation symbol period, the Nyquist condition yields a unique solution with its time representation being a sinc pulse. For the signal bandwidth exceeding the Nyquist frequency, innumerable filter characteristics should exist [1]. However, to the best of the present authors' knowledge, there are only two sets of filter frequency responses explicitly defined by their continuous piecewise function definitions [4, 5]. The first one is the well-known raised cosine (RC) filter. In spite of their practical importance there are only few design techniques that can be used to directly devise a matched combination of digital Nyquist filters. The Matlab software and its Digital Filter Design application [6] provide Nyquist filters based on a truncated version of the (square root) raised cosine filter. Such filters create a single balance between the time- and frequency-domain parameters. Additional weighting window can be used to compromise the out-of-band suppression for the excess bandwidth; however the coefficients of square root filter version cannot be explicitly calculated and for most of the windows, the minimum excess bandwidth is limited by the equivalent noise bandwidth of the window being used [7]. When the same design approach is used to calculate the coefficients of the square root RC filter directly, the residual ISI is increasing rapidly, since the design technique significantly violates the first Nyquist condition. Other techniques for designing the pulse shaping filters that have been reported are based on optimization techniques with a specific objective function such as maximizing the robustness against timing jitter [2, 3, 8–10] minimizing the duration of the impulse response [11–13] or minimizing the peak to average power ratio (PAPR) at the transmitter filter output [14]. Besides the complex way of calculating the filter coefficients, filters that are obtained by optimization techniques are usually of nonlinear phase [11, 12] or they cannot be directly partitioned into matched filter pairs [2, 3, 8–10, 15–17] having linear phase characteristic. The same holds true for the IIR Nyquist filters as discussed in [17, 18]. The most recent methods for designing Nyquist filters are based on linear programming technique [8–10, 16]. The latest and a well-written reference along this line concerning with the problem of designing matched pairs of digital Nyquist (
is the modulation symbol period, the Nyquist condition yields a unique solution with its time representation being a sinc pulse. For the signal bandwidth exceeding the Nyquist frequency, innumerable filter characteristics should exist [1]. However, to the best of the present authors' knowledge, there are only two sets of filter frequency responses explicitly defined by their continuous piecewise function definitions [4, 5]. The first one is the well-known raised cosine (RC) filter. In spite of their practical importance there are only few design techniques that can be used to directly devise a matched combination of digital Nyquist filters. The Matlab software and its Digital Filter Design application [6] provide Nyquist filters based on a truncated version of the (square root) raised cosine filter. Such filters create a single balance between the time- and frequency-domain parameters. Additional weighting window can be used to compromise the out-of-band suppression for the excess bandwidth; however the coefficients of square root filter version cannot be explicitly calculated and for most of the windows, the minimum excess bandwidth is limited by the equivalent noise bandwidth of the window being used [7]. When the same design approach is used to calculate the coefficients of the square root RC filter directly, the residual ISI is increasing rapidly, since the design technique significantly violates the first Nyquist condition. Other techniques for designing the pulse shaping filters that have been reported are based on optimization techniques with a specific objective function such as maximizing the robustness against timing jitter [2, 3, 8–10] minimizing the duration of the impulse response [11–13] or minimizing the peak to average power ratio (PAPR) at the transmitter filter output [14]. Besides the complex way of calculating the filter coefficients, filters that are obtained by optimization techniques are usually of nonlinear phase [11, 12] or they cannot be directly partitioned into matched filter pairs [2, 3, 8–10, 15–17] having linear phase characteristic. The same holds true for the IIR Nyquist filters as discussed in [17, 18]. The most recent methods for designing Nyquist filters are based on linear programming technique [8–10, 16]. The latest and a well-written reference along this line concerning with the problem of designing matched pairs of digital Nyquist ( ) filters with balanced performance and linear phase characteristic can be found in [19]. The method is based on numerical calculation and does not provide an exact definition of the filter characteristic, which complicates the design of matched filter pairs with different values of the group delay parameter and oversampling ratio. However, it offers a wide range of communication filters and will also be used for comparison in this paper.
) filters with balanced performance and linear phase characteristic can be found in [19]. The method is based on numerical calculation and does not provide an exact definition of the filter characteristic, which complicates the design of matched filter pairs with different values of the group delay parameter and oversampling ratio. However, it offers a wide range of communication filters and will also be used for comparison in this paper.
If the time- and frequency-domain parameters of the raised cosine filter are taken as a standard, the aim of this paper is to formulate an alternative Nyquist filter definition that reasonably balances the parameters in favor of filter stop-band attenuation, which is directly related to an adjacent channel power as one of the most critical parameters of the several practical applications. Giving a number of filter examples, this paper also provides a detailed comparison of the proposed filters and the existing Nyquist filter sets.
2. Nyquist Filters Design Analysis
The problem of designing a modulation filter can be seen in that the designer needs to consider carefully both representations of the signal, the time and the frequency one. Therefore, when designing modulation filters one representation has to be compromised at the expense of the other and it is a particular application that defines the final compromise. As shown in [1], the first Nyquist criterion for zero ISI level has two important implications for the modulation filter design. First, the double-sided bandwidth of the processed data signal cannot be less than  without introducing the intersymbol interference. Second, the spectrum of the signal should be symmetrical around the centre frequency, and it should also embody an odd vestigial symmetry around the frequency of
without introducing the intersymbol interference. Second, the spectrum of the signal should be symmetrical around the centre frequency, and it should also embody an odd vestigial symmetry around the frequency of  . In addition to these conditions, the overall Nyquist filter is typically split into its transmitter (TX) and receiver (RX) parts to fulfill the matched filtering condition for maximizing the signal-to-noise ratio at the decision stage [1]. The condition can be written in the frequency domain as follows:
. In addition to these conditions, the overall Nyquist filter is typically split into its transmitter (TX) and receiver (RX) parts to fulfill the matched filtering condition for maximizing the signal-to-noise ratio at the decision stage [1]. The condition can be written in the frequency domain as follows:

and in the time domain as follows:

It says that the matched filter impulse response should be the time reversed variant of the signaling pulse, where  is its time duration. Thus, to meet all these conditions the transmitter and receiver filter frequency characteristic should follow a square root version of the Nyquist filter
is its time duration. Thus, to meet all these conditions the transmitter and receiver filter frequency characteristic should follow a square root version of the Nyquist filter

Although both filters are assumed to be the same, there are different requirements placed on the design of each of them. They can be summarized into the following four conflicting requirements [19].
-
(i)
The length of the impulse response
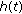 should be kept as small as possible to minimize the implementation cost and the propagation delay of the DSP part of the radio transceiver.
should be kept as small as possible to minimize the implementation cost and the propagation delay of the DSP part of the radio transceiver. -
(ii)
The Nyquist criterion should be satisfied as closely as possible to minimize intersymbol interference.
-
(iii)
At the transmitter side, the primary issue is the transmission bandwidth defined by the adjacent channel power requirements. Thus the adjacent channel and alternate channel power limits dictate the stop-band attenuation of the transmitter filter
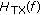 .
. -
(iv)
The lower the magnitude of the impulse response side-lobes the better is the eye opening, hence the better timing jitter immunity can be reached [3].
In several applications, there is also a demand to minimize the peak-to-average power ratio of the transmitted pulses [14, 19]. Such an optimization of the transmitter and receiver filters yields a filter pair that is no longer mutually matched and therefore it is not considered in this work.
The most widely used Nyquist filters follow the raised cosine (RC) frequency response defined by

where  is the single-sided filter bandwidth corresponding to
is the single-sided filter bandwidth corresponding to  , and
, and  is the excess bandwidth parameter usually called roll-off factor. The corresponding continuous time impulse response of the raised cosine filter can be written as
is the excess bandwidth parameter usually called roll-off factor. The corresponding continuous time impulse response of the raised cosine filter can be written as

The lower the roll-off factor, the narrower is the occupied bandwidth of the signal. However, with a low roll-off factor the original modulation (modulated) signal becomes more vulnerable to timing jitter as the eye pattern of the received signal narrows down and becomes practically almost undetectable for the roll-off factor equaling zero. The second negative effect resulting from lowering of the roll-off factor is related to the practical aspects of the digital filter design and that is the length of the filter impulse response or the decay of its tails to zero. The lower the roll-off factor, the longer the impulse response of the raised cosine filter has to be taken into account when designing a digital filter with comparable stop-band attenuation.
It is only recently that another set of modulation filters has been reported [5]. In [5], modulation filters marked as "better" than the Nyquist filter are defined in frequency domain by (7). Although, the present authors disagree with the attribute "better", because any filter fulfilling the Nyquist criterion can be regarded as a Nyquist filter, thus there cannot be a better filter in this filter family, the " " index is used for all the related characteristics of this filter in the following text
" index is used for all the related characteristics of this filter in the following text

The excess bandwidth parameter  can be used to trade off the occupied bandwidth and the time duration of the pulse. In both definitions (6) and (7) the excess bandwidth is assumed to be lower than 100%. Although there are Nyquist filters with the excess bandwidth exceeding 100% [20], they are not a primary concern of this work.
can be used to trade off the occupied bandwidth and the time duration of the pulse. In both definitions (6) and (7) the excess bandwidth is assumed to be lower than 100%. Although there are Nyquist filters with the excess bandwidth exceeding 100% [20], they are not a primary concern of this work.
From an analysis of (6) it is evident that the impulse response of the raised cosine filter differs from the minimum bandwidth Nyquist filter by the window function used to truncate the sinc pulse. The design of the digital filter thus boils down to selecting an appropriate window function [3]. The same holds true for most of the modulation filters with the zero ISI property. An example of the impulse response decomposition for the raised cosine, " " filter and weighted RC filter is shown in Figure 1.
" filter and weighted RC filter is shown in Figure 1.
In the above example, the group delay of the filters has been chosen to be six modulation symbols,  . It should be noted that this delay also determines the length of the filter impulse response
. It should be noted that this delay also determines the length of the filter impulse response  as well as the filter order
as well as the filter order  according to the following:
according to the following:

where  is the number of samples per one modulation symbol.
is the number of samples per one modulation symbol.
It can be seen from Figure 1 that both the RC and the " " filter windowing functions for the chosen parameters are in fact a cascade of the two windows, where the second window, denoted
" filter windowing functions for the chosen parameters are in fact a cascade of the two windows, where the second window, denoted  in (9), is a rectangular pulse which causes a widening of the amplitude frequency characteristic and a relatively high level and slow decay of its sidelobes
in (9), is a rectangular pulse which causes a widening of the amplitude frequency characteristic and a relatively high level and slow decay of its sidelobes

A different second window can be selected in order to improve these negative effects. In Figure 2 there is an example of the RC filter with the roll-off parameter set to 0.3 weighted by the Hann window [6, 7]. For the sake of comparison, the truncated version of the RC filter with equivalent excess bandwidth ( ) has been added to the plot.
) has been added to the plot.
It can be seen that for the same filter order ( ) the weighted version of the RC filter has a better stop-band attenuation, because its time domain characteristic (Figure 3) goes smoothly to the zero level and it is minimally influenced by the truncation operation. However, as is shown in Figure 3, there is an increase in the impulse response side lobes level. Larger tails of the impulse response typically result in a higher sensitivity to timing jitter [3]. Hence, the weighted version of the RC filter cannot be classified as a better filter; it represents an alternative balance between the studied parameters. A major obstacle of the described design method—one of the few methods available in MATLAB software [6]—is that the frequency response
) the weighted version of the RC filter has a better stop-band attenuation, because its time domain characteristic (Figure 3) goes smoothly to the zero level and it is minimally influenced by the truncation operation. However, as is shown in Figure 3, there is an increase in the impulse response side lobes level. Larger tails of the impulse response typically result in a higher sensitivity to timing jitter [3]. Hence, the weighted version of the RC filter cannot be classified as a better filter; it represents an alternative balance between the studied parameters. A major obstacle of the described design method—one of the few methods available in MATLAB software [6]—is that the frequency response  is not known and it is a problem to calculate the
is not known and it is a problem to calculate the  (4) as well as the matched filters coefficients. The numerical method based on sampling the frequency response [21] can be an option, however, such an approach yields to approximated results with a high level of residual ISI. It is therefore reasonable to start from the filter definition in the frequency domain, derive all the coefficients by calculating its inverse Fourier transform, and limit the resulting impulse response in a certain interval. In fact, the term "raised cosine filter" also originates from its definition in the frequency rather than the time domain.
(4) as well as the matched filters coefficients. The numerical method based on sampling the frequency response [21] can be an option, however, such an approach yields to approximated results with a high level of residual ISI. It is therefore reasonable to start from the filter definition in the frequency domain, derive all the coefficients by calculating its inverse Fourier transform, and limit the resulting impulse response in a certain interval. In fact, the term "raised cosine filter" also originates from its definition in the frequency rather than the time domain.
3. Nyquist  -Filter Formulation
-Filter Formulation
A closer analysis of (5) unveils the fact that the frequency response of the RC filter is a convolution of a rectangular pulse of duration  and a raised cosine window modified by the roll-off parameter.
and a raised cosine window modified by the roll-off parameter.
As shown in [7], there are other window shapes that can converge to zero more smoothly. A good alternative is a generally defined Blackmann window (10), which can be continuously changed to the Blackmann, exact-Blackmann, Blackmann-Harris, and  windows by changing the values of
windows by changing the values of  ,
,  , and
, and  in its definition
in its definition

From the comparison shown in Figure 4 it can be seen that although the general Blackmann window smoothly converges to zero level, it does so at the expense of the window width, and its shape does not satisfy the vestigial symmetry property. Nevertheless, there is still the possibility of decomposing the window into its upper and lower parts, as shown in Figure 5, and using these functions to construct a Nyquist filter by shifting them to the right by a distance marked  . Respecting the typical notation of the Nyquist RC filters, a general Nyquist
. Respecting the typical notation of the Nyquist RC filters, a general Nyquist -filter defined in the frequency domain can thus be written as follows:
-filter defined in the frequency domain can thus be written as follows:

where

For a special case, where the parameters  ,
, , and
, and  equal
equal  ,
,  , and
, and  , respectively, the equations can be effectively reduced to
, respectively, the equations can be effectively reduced to

and

The quoted values of  parameters are preferred in this paper because they represent the boundary case for which the Blackmann window approaches zero level without a discontinuity. It is important to note that the Nyquist
parameters are preferred in this paper because they represent the boundary case for which the Blackmann window approaches zero level without a discontinuity. It is important to note that the Nyquist  -filter defined by (11)–(14) differs from the RC filter also in the starting point of its stop-band region, and its first null bandwidth. Therefore, to get the filter definition directly comparable to that of the RC filter its notation is adopted where
-filter defined by (11)–(14) differs from the RC filter also in the starting point of its stop-band region, and its first null bandwidth. Therefore, to get the filter definition directly comparable to that of the RC filter its notation is adopted where

Thus, when comparing both filters (Section 5) the RC filter will have an equivalent excess bandwidth (15) adjusted by the value of the  parameter.
parameter.
The digital filter coefficients can be calculated (See the appendix) from (11) to (14) by the inverse Fourier transform of the frequency response

and equidistantly sampling the continuous impulse response (16) over the limited time interval, which is defined by the group delay parameter  as:
as:

In (17),  is the sampling period defined in relation to the modulation symbol period
is the sampling period defined in relation to the modulation symbol period  as:
as:

and  is a train of unit impulses. In order to keep the notation simple the coefficients of the Nyquist
is a train of unit impulses. In order to keep the notation simple the coefficients of the Nyquist  -filter impulse response have been denoted
-filter impulse response have been denoted  .
.
The matched filter pair (3), (4) can be calculated analogously as a square root version of the Nyquist  -filter
-filter

and its sampled version

can be used for the transmitter and receiver filter directly, since the impulse response  is symmetrical and therefore linear phase.
is symmetrical and therefore linear phase.
It is important to note that all the definitions of the Nyquist and square root Nyquist filters either in the frequency or the time domain were given in their noncausal form and thus zero phase characteristics were implicitly assumed.
4. Nyquist Filter Evaluation Criteria
Although all the studied filters calculated by their generic relations (5), (7), and (11) have a negligible level of intersymbol interference, when used as a cascade of the transmitter and receiver filters of their truncated square root versions (4), residual ISI appears and cannot be omitted. To compare this property among different filters, the relative level of residual ISI can be calculated as [19]

In addition to (21), it is also reasonable to compare the cascaded filter impulse response side lobes level according to:

The difference in stop-band attenuation between two filters can be evaluated using [7]

where the stop-band of the Nyquist and also the square root Nyquist filters is typically [4, 22] considered to start at the normalized frequency 

and to end at the normalized frequency  .
.
5. Matched Nyquist Filters Evaluation
Firstly, the proposed Nyquist  -filter has been compared with the truncated version of the RC filter. To get the numerical results presented in Table 1, the oversampling ratio of the filters has been set to 5 and the group delay parameter as well as the excess bandwidth have been varied. It can be seen that the square root Nyquist
-filter has been compared with the truncated version of the RC filter. To get the numerical results presented in Table 1, the oversampling ratio of the filters has been set to 5 and the group delay parameter as well as the excess bandwidth have been varied. It can be seen that the square root Nyquist  -filter reaches better stop-band attenuation and its cascade experiences lower residual ISI level for the same filter order, but it does so in expense of a higher impulse response side lobes level.
-filter reaches better stop-band attenuation and its cascade experiences lower residual ISI level for the same filter order, but it does so in expense of a higher impulse response side lobes level.
 [dB],
[dB],  [dB],
[dB],  [dB]. Square root RC filter versus square root Nyquist
[dB]. Square root RC filter versus square root Nyquist  -filter. The oversampling factor
-filter. The oversampling factor  is fixed and the group delay parameter
is fixed and the group delay parameter  and roll-off parameter
and roll-off parameter  of the filters vary.
of the filters vary.Secondly, the group delay parameter was set to 6 and the oversampling ratio  was changed from 4 to 6. The results shown in Table 2 express that the difference in performance of both filters is approximately the same when compared to the respective values shown in Table 1 and do not change significantly with the oversampling factor.
was changed from 4 to 6. The results shown in Table 2 express that the difference in performance of both filters is approximately the same when compared to the respective values shown in Table 1 and do not change significantly with the oversampling factor.
 [dB],
[dB],  [dB],
[dB],  [dB]. Square root RC filter versus square root Nyquist
[dB]. Square root RC filter versus square root Nyquist  -filter. The group delay parameter of the filters is fixed
-filter. The group delay parameter of the filters is fixed  and the oversampling factor
and the oversampling factor  varies.
varies.Next, there is a set of results provided in Table 3 to compare the proposed Nyquist  -filters with the digital filters designed according to (7). It is evident that the "
-filters with the digital filters designed according to (7). It is evident that the " " filters in contrast to the Nyquist
" filters in contrast to the Nyquist  -filters move a balance in favor of the time domain parameters and thus the difference in stop-band attenuation and residual ISI is even greater than in the case of the RC filter described before. Since all the values are given in their relative form, one can easily make a comparison between the RC and the "
-filters move a balance in favor of the time domain parameters and thus the difference in stop-band attenuation and residual ISI is even greater than in the case of the RC filter described before. Since all the values are given in their relative form, one can easily make a comparison between the RC and the " " filter.
" filter.
 [dB],
[dB],  [dB],
[dB],  [dB]. Square root "
[dB]. Square root " " filter versus square root Nyquist
" filter versus square root Nyquist  -filter. The oversampling factor
-filter. The oversampling factor  is fixed and the group delay parameter
is fixed and the group delay parameter  of the filters varies.
of the filters varies.The results presented express that the Nyquist  -filter represents an alternative balance between the parameters studied and can be an option in applications that require higher stop-band attenuation as well as a low level of residual intersymbol interference. It should be noted that the proposed filter set has been devised using a heuristic approach and as such cannot be considered a globally optimal solution. In fact, other filters might provide even better stop-band attenuation, but as it has been shown, at the cost of the higher residual ISI and/or worst side lobes level. Table 4 gives a comparison of the Nyquist
-filter represents an alternative balance between the parameters studied and can be an option in applications that require higher stop-band attenuation as well as a low level of residual intersymbol interference. It should be noted that the proposed filter set has been devised using a heuristic approach and as such cannot be considered a globally optimal solution. In fact, other filters might provide even better stop-band attenuation, but as it has been shown, at the cost of the higher residual ISI and/or worst side lobes level. Table 4 gives a comparison of the Nyquist  -filter with the filters devised by an iterative algorithm [19] for several choices of its design parameters. It can be seen that the stop-band attenuation of the Nyquist
-filter with the filters devised by an iterative algorithm [19] for several choices of its design parameters. It can be seen that the stop-band attenuation of the Nyquist  -filter can be just reached or can even be overcome at the additional cost of increased side lobes level or ISI.
-filter can be just reached or can even be overcome at the additional cost of increased side lobes level or ISI.
 [dB],
[dB],  [dB],
[dB],  [dB]. Square root Nyquist (
[dB]. Square root Nyquist ( ) filter versus square root Nyquist
) filter versus square root Nyquist  -filter. The
-filter. The  parameter is fixed and the group delay parameter
parameter is fixed and the group delay parameter  of the filter varies;
of the filter varies;  and
and  are the design parameters of the iteration algorithm [19].
are the design parameters of the iteration algorithm [19].To further explore the absolute levels of the parameters studied, one particular combination of filters from the studied examples has been selected and their respective characteristics have been calculated. In Figures 6, and 7 there are amplitude frequency characteristics of the square root Nyquist filter variants clearly unveiling the significant differences in stop-band attenuation. It is interesting to note also the pass band ripple (Figure 7) of the characteristics from which the " " filter is the worst due to the discontinuity already in first derivative of its frequency characteristic function (7). On the other hand, Figure 8 depicts the impulse responses of the filters, from which the increase in the side lobes level is evident. Since this is only the transmitter part of the Nyquist matched filter pair, it is reasonable to evaluate the side lobes level after the cascade of both filters as shown in Figures 10 to 12. The respective amplitude frequency characteristics of the filter cascade are shown in Figure 9. Seen in a linear scale, they should embody the vestigial symmetry to fulfill the Nyquist condition in the frequency domain (1). It can be seen from Figure 9 that this condition is not reached fully for any of the filters; however, the Nyquist
" filter is the worst due to the discontinuity already in first derivative of its frequency characteristic function (7). On the other hand, Figure 8 depicts the impulse responses of the filters, from which the increase in the side lobes level is evident. Since this is only the transmitter part of the Nyquist matched filter pair, it is reasonable to evaluate the side lobes level after the cascade of both filters as shown in Figures 10 to 12. The respective amplitude frequency characteristics of the filter cascade are shown in Figure 9. Seen in a linear scale, they should embody the vestigial symmetry to fulfill the Nyquist condition in the frequency domain (1). It can be seen from Figure 9 that this condition is not reached fully for any of the filters; however, the Nyquist  -filter is approaching the symmetrical shape very closely. From the eye diagrams shown in Figures 11 and 12 the two facts are evident that were predicted by measurement results. Firstly, the residual ISI level is the lowest for the Nyquist
-filter is approaching the symmetrical shape very closely. From the eye diagrams shown in Figures 11 and 12 the two facts are evident that were predicted by measurement results. Firstly, the residual ISI level is the lowest for the Nyquist  -filter and the highest for the "
-filter and the highest for the " " filter, the difference being 14.5 dB. And secondly, the "
" filter, the difference being 14.5 dB. And secondly, the " " filter reaches the widest eye opening and should be therefore most robust from the three studied filters as regards the timing jitter.
" filter reaches the widest eye opening and should be therefore most robust from the three studied filters as regards the timing jitter.
6. Conclusion
As has been shown in this paper, the conflicting requirements placed on the design of the digital matched Nyquist filter pair make the task complicated. From this point of view, the typical truncated raised cosine filter represents a single balance between the time- and frequency-domain parameters. The Nyquist  -filter set, which was defined throughout this paper, enlarges the family of Nyquist filters, and when compared with the truncated square root raised cosine filter cascade, it strikes the balance towards the frequency domain parameters while reaching a low level of residual intersymbol interference. It does so at the cost of a higher side lobes level of the impulse response. An exact symbolic definition of the Nyquist
-filter set, which was defined throughout this paper, enlarges the family of Nyquist filters, and when compared with the truncated square root raised cosine filter cascade, it strikes the balance towards the frequency domain parameters while reaching a low level of residual intersymbol interference. It does so at the cost of a higher side lobes level of the impulse response. An exact symbolic definition of the Nyquist  -filter in the frequency domain gives the designer scope to choose freely the arbitrary filter parameters such as equivalent excess bandwidth, group delay and oversampling parameters and derive coefficients for either the "normal" or the square root filter variants. The filters generated are of linear-phase having symmetrical impulse responses, which directly contribute to efficient hardware realization structures.
-filter in the frequency domain gives the designer scope to choose freely the arbitrary filter parameters such as equivalent excess bandwidth, group delay and oversampling parameters and derive coefficients for either the "normal" or the square root filter variants. The filters generated are of linear-phase having symmetrical impulse responses, which directly contribute to efficient hardware realization structures.
References
Burr A: Modulation and Coding for Wireless Communications. Pearson Education Ltd., Harlow, UK; 2001.
Alagha NS, Kabal P: Generalized raised-cosine filters. IEEE Transactions on Communications 1999, 47(7):989-997. 10.1109/26.774849
Farhang-Boroujeny B: Nyquist filters with robust performance against timing jitter. IEEE Transactions on Signal Processing 1998, 46(12):3427-3431. 10.1109/78.735318
Farhang-Boroujeny B: Signal Processing Techniques for Software Radios. ECE Dep. University of UTAH, Salt Lake City, Utah, USA; http://www.lulu.com
Beaulieu NC, Tan CC, Damen MO: A "better than" Nyquist pulse. IEEE Communications Letters 2001, 5(9):367-368. 10.1109/4234.951379
Mathworks Inc : Digital Filter Design DSP Blockset Description. January 2010, http://www.mathworks.com/access/helpdesk_r13/help/toolbox/dspblks/digitalfilterdesign.html
Harris FJ: On the use of windows for harmonic analysis with the discrete Fourier transform. Proceedings of the IEEE 1978, 66(1):51-83.
Boonyanant P, Tantaratana S: Design and hybrid realization of FIR Nyquist filters with quantized coefficients and low sensitivity to timing jitter. IEEE Transactions on Signal Processing 2005, 53(1):208-221.
Coleman JO: Linear programming of data communication pulses tolerant of timing jitter or multipath. Procedings of the 5th Annual Conference on Wireless Communications, July 1993, Calgary, Canada http://jocoleman.info/pubs/papers/wireless93.pdf
Muravchik CH, Guisantes JR: Optimized signaling waveforms to reduce the effects of intersymbol interference and timing jitter. IEEE Transactions on Communications 1995, 43(1):11-14. 10.1109/26.385949
Kragh F, Nga C, Hermes DJ, Robertson RC: Spectrally efficient digital modulation using new pulse shapes. In Proceedings of the Military Communications Conference (MILCOM '07), October 2007. IEEE; -5.
Hermes DJ, Kragh FE: A bandwidth efficient constant envelope modulation. Proceedings of the 40th Asilomar Conference on Signals, Systems, and Computers (ACSSC '06), November 2006 488-492.
Zhang X, Yoshikawa T: Design of FIR Nyquist filters with low group delay. IEEE Transactions on Signal Processing 1999, 47(5):1454-1458. 10.1109/78.757243
Châtelain B, Gagnon F: Peak-to-average power ratio and intersymbol interference reduction by nyquist pulse optimization. Proceedings of the IEEE 60th Vehicular Technology Conference (VTC '04), September 2004 954-958.
Tuncer TE: Optimum Nyquist filters with controlled time and frequency characteristics. Electronics Letters 2002, 38(21):1292-1293. 10.1049/el:20020880
Davidson TN: Efficient design of waveforms for robust pulse amplitude modulation. IEEE Transactions on Signal Processing 2001, 49(12):3098-3111. 10.1109/78.969517
Nakayama K, Mizukami T: A new IIR Nyquist filter with zero intersymbol interference and its frequency response approximation. IEEE transactions on circuits and systems 1982, 29(1):23-24. 10.1109/TCS.1982.1085078
Maeng SJ, Lee BGI: Design of linear-phased IIR Nyquist filters. IEEE Journal on Selected Areas in Communications 1995, 13(1):167-175. 10.1109/49.363135
Farhang-Boroujeny B: A universal square-root Nyquist (M) filter design for digital communication systems. Proceedings of the SDR Forum Technical Conference (SDR '06), November 2006, Orlando, Fla, USA http://www.sdrforum.org/pages/sdr06/sdr06_papers/2.1/2.1-3.pdf or http://www.ece.utah.edu/~farhang/Nyquist_M_r1.pdf
Benjebbour A, Asai T, Yoshino H: Nonparametric interference suppression using cyclic wiener filtering: pulse shape design and performance evaluation. EURASIP Journal on Wireless Communications and Networking 2008, 2008:-14.
Jan J: Digital Signal Filtering, Analysis and Restoration. VUTIUM BUT, Brno, Czech Republic; 2002.
Proakis J: Digital Communication. 4th edition. McGraw-Hill Higher Education, Singapore; 2000.
Acknowledgments
This work was supported by the Czech Science Foundation under project no. 102/08/0851.
Author information
Authors and Affiliations
Corresponding author
Appendix
Maple Script for Nyquist  -Filter Coefficients Calculation
-Filter Coefficients Calculation
–restart;
–S[u] := 1 − cos(Pi (B
(B (1 + alpha
(1 + alpha ) − f − delta)/(4
) − f − delta)/(4 B
B alpha
alpha ))
)) 4;
4;
–S[um] := 1 − cos(Pi (B
(B (1 + alpha
(1 + alpha ) + (f − delta))/(4
) + (f − delta))/(4 B
B alpha
alpha ))
)) 4;
4;
–S[d] := cos(Pi (B
(B (1 − alpha
(1 − alpha ) − f + delta)/(4
) − f + delta)/(4 B
B alpha
alpha ))
)) 4;
4;
–S[dm] := cos(Pi (B
(B (1 − alpha
(1 − alpha ) + (f + delta))/(4
) + (f + delta))/(4 B
B alpha
alpha ))
)) 4;
4;
–delta := 1/2 − 4 arccos((1/2)
arccos((1/2) 2
2 (3/4))
(3/4)) B
B alpha
alpha /Pi − B
/Pi − B (1 − alpha
(1 − alpha );
);
–alpha := alpha delta;
delta;
–G[d] := piecewise(abs(f) B
B (1 − alpha),1, "and" ( − B
(1 − alpha),1, "and" ( − B (1 − alpha) >f, f
(1 − alpha) >f, f B),S[um], "and" ( − B >f,f
B),S[um], "and" ( − B >f,f B
B (1+alpha)),S[dm], "and" (B
(1+alpha)),S[dm], "and" (B (1 − alpha)
(1 − alpha) f,f <B),S[u], "and" (B
f,f <B),S[u], "and" (B f,f <B
f,f <B (1 + alpha)),S[d],B
(1 + alpha)),S[d],B (1+alpha)
(1+alpha) abs(f),0);
abs(f),0);
–alpha := .25; T := 1; B := 1/(2
:= .25; T := 1; B := 1/(2 T); a
T); a := 3/8; a
:= 3/8; a := 4
:= 4 (1/8); a
(1/8); a := 1/8;
:= 1/8;
–evalf(delta);
–G[Rd]:= sqrt(G[d]);
–plot([G[d],G[Rd]],f  1 .. 1, color
1 .. 1, color [black,red]);
[black,red]);
–alpha[RC] := alpha;
–G[RC] := piecewise(abs(f) B
B (1 − alpha[RC]),1, "and" ( − B
(1 − alpha[RC]),1, "and" ( − B (1 + alpha[RC]) <f, f
(1 + alpha[RC]) <f, f B
B (1-alpha[RC])),1/2
(1-alpha[RC])),1/2 (1 + cos(Pi
(1 + cos(Pi (f + B
(f + B (1 − alpha[RC]))/(2
(1 − alpha[RC]))/(2 B
B alpha[RC]))), "and" (B
alpha[RC]))), "and" (B (1 − alpha[RC]) <f,f
(1 − alpha[RC]) <f,f B
B (1 + alpha[RC])), 1/2
(1 + alpha[RC])), 1/2 (1 + cos(Pi
(1 + cos(Pi (f − B
(f − B (1 − alpha[RC]))/(2
(1 − alpha[RC]))/(2 B
B alpha[RC]))), B
alpha[RC]))), B (1+alpha[RC])
(1+alpha[RC]) abs(f),0);
abs(f),0);
–G[RRC] := simplify(sqrt(G[RC])); plot([G[RRC],G[Rd]],f 1 .. 1,color
1 .. 1,color [black,red]);
[black,red]);
–g[Rd] := (1/2) Pi
Pi (Int(G[Rd]
(Int(G[Rd] exp((I
exp((I 2)
2) Pi
Pi f
f t), f
t), f  1.. 1));
1.. 1));
–g[delay] := 6; N := 5; step := 1/N; i := 0;
–for t from − g[delay] by step to g[delay] do t; i := i + 1; coef[i] := evalf(Re(evalf(g[Rd]))) end do; k := i;
–for i to k do print(coef[i]) end do;
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bobula, M., Prokeš, A. & Daněk, K. Nyquist Filters with Alternative Balance between Time- and Frequency-Domain Parameters. EURASIP J. Adv. Signal Process. 2010, 903980 (2010). https://doi.org/10.1155/2010/903980
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/903980
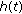 should be kept as small as possible to minimize the implementation cost and the propagation delay of the DSP part of the radio transceiver.
should be kept as small as possible to minimize the implementation cost and the propagation delay of the DSP part of the radio transceiver.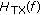 .
.


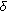 -Filter Formulation
-Filter Formulation








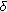 -Filter Coefficients Calculation
-Filter Coefficients Calculation