- Research Article
- Open access
- Published:
Seamless Heterogeneous 3D Tessellation via DWT Domain Smoothing and Mosaicking
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 913681 (2010)
Abstract
With todays geobrowsers, the tessellations are far from being smooth due to a variety of reasons: the principal being the light difference and resolution heterogeneity. Whilst the former has been extensively dealt with in the literature through classic mosaicking techniques, the latter has got little attention. We focus on this latter aspect and present two DWT domain methods to seamlessly stitch tiles of heterogeneous resolutions. The first method is local in that each of the tiles that constitute the view, is subjected to one of the three context-based smoothing functions proposed for horizontal, vertical, and radial smoothing, depending on its localization in the tessellation. These functions are applied at the DWT subband level and followed by an inverse DWT to give a smoothened tile. In the second method, though we assume the same tessellation scenario, the view field is thought to be of a sliding window which may contain parts of the tiles from the heterogeneous tessellation. The window is refined in the DWT domain through mosaicking and smoothing followed by a global inverse DWT. Rather than the traditional sense, the mosaicking employed over here targets the heterogeneous resolution. Perceptually, this second method has shown better results than the first one. The methods have been successfully applied to practical examples of both the texture and its corresponding DEM for seamless 3D terrain visualization.
1. Introduction
The contemporary geobrowsers—like Google Earth, NASA's World Wind, or Microsoft's Virtual Earth—give little importance to individual client characteristics, and with the low-end clients, the performance is far from being satisfactory. In addition, area coverage by these browsers is slack, if not judicious, in the case of the underdeveloped and developing parts of the world as opposed to their developed counterparts. There is a need to reform all these browsers to cater for the diversity of clients through some scalable data structuring. One obvious choice is to create multiple levels of detail (LOD) by representing the shape at different levels of approximation. This is essential for the terrain tessellation adjustment as a function of the view parameters [1]. For LOD, one can rely on the multiresolution nature of the discrete wavelet transform (DWT). It is better to employ some standard state-of-the-art DWT, like the now widely accepted JPEG2000 standard (The ISO/IEC 15444-1 standard.). In fact JPEG2000 is better than the popular pyramidal resolution representation with JPEG or other format closer to normal graphic cards that are of high storage cost: there is a need to store different resolutions. Additional advantages of the JPEG2000, in this context, include capabilities like better compression and progressive data transfer.
Traditionally, tile-based approaches have been favored to render large terrains. The problem, however, arises when the tiles have either been rendered at different resolutions or not photographed in identical luminance or radiometric conditions. To elaborate this we rely on the two snapshot examples of Google Earth, shown in Figure 1. In the first example (Figure 1(a)), where the observer is changing his view to the right, it can be seen that the resolution is not uniform. Usually there are two reasons for this heterogeneity. First is the download latency and second is the nonavailability of proper resolution due to a variety of reasons like area security, data inaccessibility, and the like. The second snapshot (Figure 1(b)), which pertains to the area surrounding the Pakistani capital of Islamabad, suffers from both heterogeneous resolution and aerial photography in nonidentical light conditions. Obviously the photographs have been taken at different times and then joined together to what we see in the snapshot.
In essence, one can safely deduce that even for today's geobrowsers the tessellations are far from being smooth due to varying resolutions or heterogeneous luminance conditions or even both when the tiles have been acquired. Whilst, the traditional focus of the mosaicking community has been the seamless rendering of tiles that may vary in luminance, little attention has been paid to the heterogeneity due to resolution. That is why traditional mosaicking may correct the light difference phenomenon but the underlying tiles may still be hardly seamless if they vary in resolution. In this paper we focus on the resolution part, mainly, as we try to smoothen the tile interfaces to avoid the artifacts like those in Figure 1, for example. Our methods are aimed at rendering texture and DEM tessellations, from JPEG2000-coded tiles, in a scenario where only visible tiles are rendered and the focused ones, out of these, have the highest quality depending on the viewer's distance. As the viewer moves in, the tiles corresponding to the new view must be rendered and gradually refined in quality as the focus is coming near to it. This refinement is additive, as more and more subbands are added to it, at runtime. The main challenge to this strategy is that the tile must be seamlessly stitched for both the texture and the DEM and the boundaries must be diluted enough to prevent popping artifacts. In this paper, although we are more inclined to the texture, the DEM has also been treated as its integral part. We, therefore, present two different methods to look for a seamless tessellation that is composed of heterogeneous resolution tiles. In fact this work is a continuation of our earlier efforts about the synchronous unification of the DEM/texture pair through data hiding [2] for scalable 3D visualization. That work is our inspiration for the LOD aspect, since its scalable character can result in various tile qualities for both the DEM and its texture.
The first method is local in nature and relies on context-based smoothing of the tile boundaries. The smoothing is carried out at the subband level in the DWT domain by employing three different smoothing masks. We assume that, at worst, there can be three possible tile resolutions, namely, high, middle, and low. The lowest-resolution tiles of the panorama are not treated while the highest-resolution tile are smoothed by a radial smoothing function. The rest of the tiles are rendered at mid-level resolution. Of these the left/right neighbors of center are smoothed horizontally, while the above/below neighbors are smoothed vertically. The treated tiles can be joined, after each has been subjected to an inverse DWT, to get a smoother tessellation.
In the second method, we take the change in viewpoint focus, analogous to a window-sliding approach. The worst we expect is that the window may come up to be composed of three different tile qualities with the resultant artifacts at tile interfaces. To dilute these artifacts, we treat the tiles at the subband level, in the DWT domain, by employing operations involving suitable subband-sized composite masks, conceived with smoothing and mosaicking in perspective. The resultant composite subbands are subjected to a global inverse DWT to get the final seamless tessellation.
The rest of the paper is arranged as follows. Section 2 gives a brief literature survey on the subject. The presentation of the proposed methods is the theme of Section 3. Application of our methods to a practical worst case example is being demonstrated in Section 4. Section 5 concludes the paper.
2. State of the Art
The process of mosaicking involves the connection of two or more images to get a new wide-area image with no visible seams. In the case of aerial or satellite photographs, a wide screen-view is synthesized by the proportional combination of a set of images. The mosaic is hence commonly used to increase the view field with pasting successively overlapped images onto the same plane or other structures, like a cylinder or a sphere. In order to be efficient, a mosaicking method should be robust to light change, moving objects, image noise and to some extent rotation and zooming [3]. An integral part of the process is image registration which pertains to the overlaying two or more images of the same scene taken at different times, from different viewpoints or by different sensors. The final information is gained from variety of sources like image fusion, change detection and multichannel image restoration. In this context Zitova and Flusser [4] classify the various approaches according to their nature (area-based and feature-based) and to four basic steps of image registration procedure, namely, feature detection, feature matching, mapping function design and image transformation and resampling. The thrust of the mosaicking methods, in general, is either on the interest point matching or on theoretical corner models. All these, hardly consider the aspect where a resolution image is to be stitched to a considerably lower-resolution image.
Terrain LOD algorithms can be classified [1], on the basis of the hierarchical structure, into four groups, namely, the triangulated irregular networks (TINs), bin-tree hierarchies, bin-tree regions and tiled blocks. The tessellation, in the last category, is carried out with the square tiles of different resolutions as has been done by Wagner [5]. But the process requires seamless stitching at the boundaries. According to Deb et al. [6], Wagner's technique is not suited for the terrains with large height variations and that is why they tweak the technique by having the projection on real-time average height of terrain for a client/server terrain streaming to handle heterogeneous clients. The blending factors are calculated on a per-tile basis because of the use of a regular tile structure, thus, reducing the amount of computation. Special techniques based on mipmaps and clipmaps [7] can be found in the literature. Losasso and Hoppe [1] break the terrains into geometric clipmaps of varying metric sizes which can be used as LODs through a view-centered hierarchy resulting in a simplified spatial and temporal interlevel continuity. A thresholding scheme based on calculated ground sample distances is proposed by Tsai and Chiu [8] with a nested LOD system for efficient seamless visualization of large datasets. In order to remove the T-junctions they have put forward a mesh refinement algorithm. Ueng and Chuang [9] propose a dike structure between two adjacent blocks,for a smooth blending between two meshes of different LOD. This approach is combined by Li et al. [10] with heuristics to dynamically stitch the tile meshes together seamlessly. For the texture part they use high-resolution aerial photos subjected to the similar LOD mechanism as described for the meshes. Larsen and Christensen [11] try to avoid popping for low-end users by exploiting the low-level hardware programmability in order to maintain interactive frame-rates. They claim their work as pioneering as far as a smooth LOD implementation in commodity hardware is concerned.
Little attention has been paid to the texture images which require their own LOD structure. There have been proposals, like texture clipmaps [7], but texture tiling is usually preferred. The multiresolution technique, described by Döllner et al. [12], presents static LOD terrain models, allowing for combination of multiple large-scale textures of different size. The view-dependent texture management technique of Okamoto et al. [13] manages multiresolution textures in multiple caching levels—database, main memory and graphics card memory—which the authors claim to be suitable for hardware with limited resources. The approach of Buchholz and Döllner [14] includes dynamic texture loading for memory management and, combine several textures into atlases for avoiding too much texture switches [15]. Their computationally complex preprocessing part helps them to significantly reduce runtime rendering overhead. Frueh et al. [16] described an approach to create a specialized texture atlas for building facades and supports efficient rendering for virtual flythroughs. The created atlas is static, and different texture resolutions are not considered. Based on the minimum error boundary cut idea of the image quilting algorithm as well as Efros and Freeman [17], Somol and Haindl [18] propose their minimum error path search algorithm. To avoid visible seams,for combining incompatible pieces of texture, they propose to find (possibly irregular) boundaries between the image pieces to minimize the visual error. Based on eccentric image overlapping, the source image is cropped at the prospective interface along the minimum error path and placed over the target background image. The problem is, however, if no good path exists in the error map, visible artifacts may be inevitable. Integer wavelet transform has been applied to DEM and a simple coding algorithm with high efficiency was introduced by Chen and Li [19]. Many references can be found on the subject in the works of Danovaro et al. [20] and Buchholz and Döllner [14]. A survey about 3D interactive rendering by Pajarola and Gobbetti [21] is worth reading.
3. The Smoothing Strategies
In this section we explain the two methods for seamlessly stitching heterogeneous resolution tiles. This heterogeneity is traced back to the concept of the level of detail (LOD). For the LOD we are relying on the multiresolution nature of DWT from the JPEG2000 codec. The reasons for choosing JPEG2000 are its scalability, its wide acceptance as a standard, its support to various wavelet forms for multiresolution, progressive transfer capability and last but not the least is its approximation paradigm for LOD. The various approximations do not differ in size but only in quality which is additive in nature. If each tile is DWTed in the JPEG2000 codec at level  then a level-
then a level- approximate image is the one that is constructed with
approximate image is the one that is constructed with  percent of the total coefficients. These coefficients correspond to the available lowest
percent of the total coefficients. These coefficients correspond to the available lowest  subbands and for the coefficients corresponding to the rest of the
subbands and for the coefficients corresponding to the rest of the  subbands, zeros are stuffed. Subsequent application of
subbands, zeros are stuffed. Subsequent application of  -level inverse DWT yields what is known as the
-level inverse DWT yields what is known as the  -approximate image. For example, level-
-approximate image. For example, level- approximate image is constructed from all the coefficients and level-
approximate image is constructed from all the coefficients and level- approximate image is constructed from
approximate image is constructed from  of the count of the initial coefficients.
of the count of the initial coefficients.
3.1. Scenario
We are assuming a simplistic scenario of a panorama of  tiles given in Figure 2. This use case should represent almost all the possibilities we will have in our application. An individual tile is large enough to circumscribe the field of view if the observer is close enough to require highest visual resolution. If the observer is far off, his view is limited to at least
tiles given in Figure 2. This use case should represent almost all the possibilities we will have in our application. An individual tile is large enough to circumscribe the field of view if the observer is close enough to require highest visual resolution. If the observer is far off, his view is limited to at least  tessellation with all the tiles at their lowest visual resolutions but as soon as he draws closer, further details may be added to the tile of focus and, to some extent, its
tessellation with all the tiles at their lowest visual resolutions but as soon as he draws closer, further details may be added to the tile of focus and, to some extent, its  -neighbors to improve their visual resolution. This leads to variations in the tile qualities of the view tessellation. The tessellation is thus heterogeneous in terms of resolution and a given tile can have one of the three qualities, namely, high, middle and low. The high-quality resolution (H) corresponds to the center which is the viewpoint focus for a given distance to the observer in a flyby process. We are rendering the
-neighbors to improve their visual resolution. This leads to variations in the tile qualities of the view tessellation. The tessellation is thus heterogeneous in terms of resolution and a given tile can have one of the three qualities, namely, high, middle and low. The high-quality resolution (H) corresponds to the center which is the viewpoint focus for a given distance to the observer in a flyby process. We are rendering the  -neighbors of the center with the middle-resolution (M) tiles and the rest, that is, the corners, with low resolution (L). The terms high, low and middle are not static and their extent depends on the distance of observer from the view as well as the time passed after the viewer changed his position. It also depends on the capacities of the media employed, as we may have M and L or just L for poorer conditions. There may be a tessellation having concentric square rings with each successive ring having a different quality [7] but we believe that at any instant one would hardly be dealing with a rendering involving more than three resolutions.
-neighbors of the center with the middle-resolution (M) tiles and the rest, that is, the corners, with low resolution (L). The terms high, low and middle are not static and their extent depends on the distance of observer from the view as well as the time passed after the viewer changed his position. It also depends on the capacities of the media employed, as we may have M and L or just L for poorer conditions. There may be a tessellation having concentric square rings with each successive ring having a different quality [7] but we believe that at any instant one would hardly be dealing with a rendering involving more than three resolutions.
3.2. Shape of the Smoothing Function
Figure 3 depicts the shape of an example smoothing function in the simplest of forms. Note that we are affecting the quality of only a small part on the periphery, of the higher resolution tiles in the view, during a given smoothing process. For any given subband, the smoothing function creates a scalar multiplication mask (over  ) of the size of the subband. This depends on the position of the tile, to which the subband belongs, in the view. for example, for the subbands of a tile having low resolution neighbors on left/right, we may consider the central column of coefficients as the origin in the figure and
) of the size of the subband. This depends on the position of the tile, to which the subband belongs, in the view. for example, for the subbands of a tile having low resolution neighbors on left/right, we may consider the central column of coefficients as the origin in the figure and  may then be the offset from this central column on right or left with
may then be the offset from this central column on right or left with  being half the width of the subband. In a similar fashion, for a tile with up/down neighbors in the view, the origin may be the center row with row offset represented by
being half the width of the subband. In a similar fashion, for a tile with up/down neighbors in the view, the origin may be the center row with row offset represented by  . Finally for a tile in the
. Finally for a tile in the  -neighbor environment, the center of its subband may be the origin and
-neighbor environment, the center of its subband may be the origin and  may be the offset of the polygonal ring of coefficients. The function
may be the offset of the polygonal ring of coefficients. The function  has two parameters,
has two parameters,  and
and  . the parameter
. the parameter  decides where to start the smoothing process in the subband whereas
decides where to start the smoothing process in the subband whereas  denotes the index where it should fall to zero. To have a full smoothing in a subband we must have
denotes the index where it should fall to zero. To have a full smoothing in a subband we must have  and
and  , but to dilute the seam, it is preferable to have
, but to dilute the seam, it is preferable to have  and to not deteriorate too much the subband it is preferable to have
and to not deteriorate too much the subband it is preferable to have  . To not have a strong smoothing between
. To not have a strong smoothing between  and
and  and avoiding the full deterioration of the subband, one can locate
and avoiding the full deterioration of the subband, one can locate  at one quarter of the subband, that is,
at one quarter of the subband, that is,  , where, as already stated,
, where, as already stated,  is roughly half the subband dimension (width, length or radius).
is roughly half the subband dimension (width, length or radius).
In Figure 3 the given function is of the form,

Of special importance is the shape of the fall from  to
to  which may be streamlined to emulate a more sophisticated function, for example, tail of a Gaussian distribution. One such function could be:
which may be streamlined to emulate a more sophisticated function, for example, tail of a Gaussian distribution. One such function could be:

Note that beyond  we shall be dealing with
we shall be dealing with  consecutive integers as
consecutive integers as  ; therefore
; therefore  . One can borrow from sinusoidal functions too and a smoothing function that we tested is given below:
. One can borrow from sinusoidal functions too and a smoothing function that we tested is given below:

There can be many more functions to emulate but due to space limitation we would restrict to the three given in (1)–(3) only.
Let the high, the middle, and the low resolution of our scenario correspond to  ,
,  , and
, and  approximate images, respectively. The quality gap would essentially bring with it the popping artifacts at tile boundaries. To undo that, we are proposing two different DWT domain smoothing methods in the next two sections.
approximate images, respectively. The quality gap would essentially bring with it the popping artifacts at tile boundaries. To undo that, we are proposing two different DWT domain smoothing methods in the next two sections.
3.3. Method I: Smoothing the Tiles before Stitching
In this section we present a wavelet-domain context-dependent smoothing strategy illustrated in Figure 4. At the corners (labeled L) are the  -approximate images obtained from lowest
-approximate images obtained from lowest  subbands with the rest of
subbands with the rest of  subbands being replaced by
subbands being replaced by  s. For the rest of the tiles one can partition their subbands into the following three sets.
s. For the rest of the tiles one can partition their subbands into the following three sets.
-
(i)
The lowest
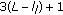 subbands will remain untouched since they represent the lowest rendered quality.
subbands will remain untouched since they represent the lowest rendered quality. -
(ii)
The highest
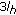 subbands of center tile (H) and
subbands of center tile (H) and 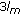 subbands of its
subbands of its 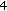 -neighbors (labeled M) are stuffed with
-neighbors (labeled M) are stuffed with  s.
s. -
(iii)
Last are the remaining
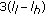 and
and 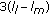 subbands of central tile and its
subbands of central tile and its 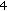 -neighbors, respectively.
-neighbors, respectively.
It is the third set (or its subset thereof) which will be subjected to the DWT domain treatment with three different smoothing functions on each subband individually. These smoothing functions are the following.
-
(1)
The medium-resolution left/right neighbors of center require the horizontal smoothing function.
-
(2)
The medium-resolution above/below neighbors of center need the vertical smoothing function.
-
(3)
The high-resolution center is treated through the radial smoothing function.
The horizontal smoothing mask would have a central band of rows of  's. The thickness of this band depends on the maximum diameter,
's. The thickness of this band depends on the maximum diameter,  , of the view focus. If the subband belongs to the
, of the view focus. If the subband belongs to the  resolution level, then the thickness should be around
resolution level, then the thickness should be around  . Beyond the band of
. Beyond the band of  's, the rows gradually attenuate on both sides approaching
's, the rows gradually attenuate on both sides approaching  at the periphery, complying anyone of the (1)–(3). An example smoothing function, for the horizontal case and loosely based on (1), is described in the appendix in the form of Algorithm 1. Along similar lines we can get a vertical smoothing mask by transposing the horizontal mask for a given subband. An example illustration of horizontal smoothing between two tiles (a high-resolution tile H and a medium-resolution tile M on right) is given in Figure 5.
at the periphery, complying anyone of the (1)–(3). An example smoothing function, for the horizontal case and loosely based on (1), is described in the appendix in the form of Algorithm 1. Along similar lines we can get a vertical smoothing mask by transposing the horizontal mask for a given subband. An example illustration of horizontal smoothing between two tiles (a high-resolution tile H and a medium-resolution tile M on right) is given in Figure 5.
Algorithm 1: Example horizontal smoothing function.
Input: dimensions ( ) of the DWT domain subband and smoothing parameters (
) of the DWT domain subband and smoothing parameters ( )
)
Output: Horizontal  smoothing mask
smoothing mask 
( ) begin
) begin
( ) set
) set 
( ) set the coefficients of the first and last
) set the coefficients of the first and last  rows of
rows of  to
to 
( ) set the coefficients of the
) set the coefficients of the  to
to  rows of
rows of  to
to 
(5) for  do
do
(6) 
(7) for  do
do
(8) 
(9) 
(10) end for
(11) end for
(12) end
The radial smoothing mask is a bit tricky. We would have a center core of  's having a diameter of about
's having a diameter of about  for a the subband of the
for a the subband of the  resolution level. Ideally, this core should be circular with
resolution level. Ideally, this core should be circular with  being its radius, but due to the discrete character of the subband, the shape is at best polygonal. For the sake of simplicity of Algorithm 2 presented in the appendix, we are considering a square core of
being its radius, but due to the discrete character of the subband, the shape is at best polygonal. For the sake of simplicity of Algorithm 2 presented in the appendix, we are considering a square core of  's with dimensions
's with dimensions  . Each ring of coefficients around the core would gradually attenuate approaching
. Each ring of coefficients around the core would gradually attenuate approaching  at the corners (or the
at the corners (or the  ring to be precise) and around
ring to be precise) and around  in the up/down and left/right directions.
in the up/down and left/right directions.
Algorithm 2: Example radial smoothing function.
Input: dimensions ( ) of the DWT domain subband and smoothing parameters (
) of the DWT domain subband and smoothing parameters ( )
)
Output: Radial smoothing square mask  of dimensions (
of dimensions ( )
)
( ) begin
) begin
( ) set
) set 
( ) declare an array
) declare an array  with all elements initialized to
with all elements initialized to 
( ) for
) for  do
do
(5) 
(6) 
(7) end for
(8) declare a  array
array 
(9) for  do
do
(10) for  do
do
(11) if  then
then
(12) 
(13) 
(14) else
(15) 
(16) 
(17) end if
(18) end for
(19) end for
(20) end
After the smoothing treatment of a subset or all of the third group of subbands and inverse DWT, one can have a seamless visualization of the type given in Figure 4. In our application, we are using the same strategy for the DEM to avoid popping effect on elevation data.
3.4. Method II: Sliding Window Analogy to View Field
For method II we introduce a sliding window analogy, as shown in Figure 6, where the red square/window represent our initial point of focus which had been rendered with high-quality resolution, H. Let the focus changes and the window slides to the position represented by the blue square. The new window may have, at the worst, three different resolutions. This situation is illustrated by the  panorama in the right part of Figure 6. Rendering three different resolutions, side by side, will obviously give rise to nonsmooth transitions at the interface of heterogeneous tiles.
panorama in the right part of Figure 6. Rendering three different resolutions, side by side, will obviously give rise to nonsmooth transitions at the interface of heterogeneous tiles.
For a 1D viewpoint displacement from H to M or M to L, whether horizontal or vertical, a smooth transition can be realized by following the scheme given in Figure 7. This figure illustrates the DWT domain, H to M seamless smoothing, in the horizontal direction. For H we have all the subbands available but for the M part we have just level-2 subbands available, and six highest-frequency subbands are missing which will be replaced with zero coefficients. This gives rise to two types of combinations. First, the direct concatenation of nonzero subbands with their counterparts from H. Second, the concatenation of each of the zero subbands with the pretreated corresponding subband of H. The pretreatment involves scalar multiplication with a subband-sized mask generated by one of the functions,  , outlined Section 3.2, with
, outlined Section 3.2, with  being the column index of the subband coefficient. Note that for a vertical transition, column index will have to be replaced with the row index in the function
being the column index of the subband coefficient. Note that for a vertical transition, column index will have to be replaced with the row index in the function  . The resultant concatenated H/M subbands, upon inverse DWT, results the required seamlessly smoothed image.
. The resultant concatenated H/M subbands, upon inverse DWT, results the required seamlessly smoothed image.
Note that we are affecting the quality of only a small part on the periphery of the tile during a given smoothing process. For any given subband, the smoothing function creates a scalar multiplication mask (over  ) of the size of the subband. For example, the H to M horizontal smoothing mask would have a band of columns of
) of the size of the subband. For example, the H to M horizontal smoothing mask would have a band of columns of  's on the left. The thickness of this band depends on the maximum diameter of the view focus. Beyond the band of
's on the left. The thickness of this band depends on the maximum diameter of the view focus. Beyond the band of  's the columns gradually attenuate toward right, approaching
's the columns gradually attenuate toward right, approaching  at the periphery. Along similar lines we can get a vertical smoothing mask for a given subband.
at the periphery. Along similar lines we can get a vertical smoothing mask for a given subband.
In two dimensions, the diagonal transition from H to L is also to be taken into account. One can think of the 2D version as an operation involving either two horizontal 1D smoothings followed by a vertical 1D smoothing, as shown in Figure 8, or two vertical 1D smoothings followed by a horizontal smoothing. Keeping this in view, these operations can be easily carried out in parallel to avoid time delay, thanks to the involvement of subbands and the independence of blocks as envisioned in the JPEG2000 standard. Taking the argument further, since we have three different resolution tiles, for concatenation we may face three subband combinations as follows.
-
(1)
The corresponding subbands of all of the H, M, and L are nonzero implying direct concatenation according to their localization in space.
-
(2)
With zero subbands of L corresponding to nonzero subbands of M and H, we would follow the smoothing strategy described in Figure 8.
-
(3)
For nonzero subbands of H, corresponding to zero subbands of L and M, we would concatenate the former in the pretreated form with the zero subbands keeping in view their localization in space.
But we believe that if one think at the outset about the diagonal transition by starting the smoothing process from those subbands of M and H whose counterparts are zero in L, the overall smoothing may still be commendable. In addition the closest part of H to L can be programmed to be degraded more than the rest of its interfaces during smoothing.
4. Simulation Results
We have applied our smoothing strategies to practical examples provided by IGN (http://www.ign.fr/) France and the results have been encouraging. For the reader we are presenting a representative example of  texture tessellation composed of
texture tessellation composed of  tiles of size
tiles of size  pixels. The corresponding DEM tessellation at our disposal has a size of
pixels. The corresponding DEM tessellation at our disposal has a size of  with each of the nine tiles having
with each of the nine tiles having  coefficients. The texture tiles were transformed at level-
coefficients. The texture tiles were transformed at level- reversible DWT in a standard JPEG2000 encoder whereas the DEM tiles were subjected to reversible level-
reversible DWT in a standard JPEG2000 encoder whereas the DEM tiles were subjected to reversible level- DWT simply. In our example visualization, we are going for a case where the corners are being rendered with level-3 approximate tiles which would mean a rendering with only
DWT simply. In our example visualization, we are going for a case where the corners are being rendered with level-3 approximate tiles which would mean a rendering with only  of the coefficients. The
of the coefficients. The  -neighbors of center have the middle quality of level-2 approximation. For the centre we are taking highest possible quality, that is, level-0. The high-quality gap between three qualities is likely to make the tile boundaries conspicuous. For the purpose of clarity we are taking subset
-neighbors of center have the middle quality of level-2 approximation. For the centre we are taking highest possible quality, that is, level-0. The high-quality gap between three qualities is likely to make the tile boundaries conspicuous. For the purpose of clarity we are taking subset  tessellation comprising of the tile H and its right, below and base diagonal neighbors—eastern, southern and south eastern, to be exact. A texture tessellation with these tiles without any smoothing treatment is shown in Figure 9(a). To observe the boundaries, we have magnified a small
tessellation comprising of the tile H and its right, below and base diagonal neighbors—eastern, southern and south eastern, to be exact. A texture tessellation with these tiles without any smoothing treatment is shown in Figure 9(a). To observe the boundaries, we have magnified a small  area at coordinates
area at coordinates  ), corresponding to the small white square in Figure 9(a), from the tessellation in Figure 9(b). We have deliberately selected a region that contains each of the three (H, M, and L) resolutions and smooth quality. This magnification is only for the purpose of comparison and the magnified portion does not represent the visual effect, we are up to, since the distance, it represents, warrants improved qualities at corners in our strategy. For the treated examples, we will not be showing the whole tessellation but rather displaying the corresponding square region in each tessellation for comparison.
), corresponding to the small white square in Figure 9(a), from the tessellation in Figure 9(b). We have deliberately selected a region that contains each of the three (H, M, and L) resolutions and smooth quality. This magnification is only for the purpose of comparison and the magnified portion does not represent the visual effect, we are up to, since the distance, it represents, warrants improved qualities at corners in our strategy. For the treated examples, we will not be showing the whole tessellation but rather displaying the corresponding square region in each tessellation for comparison.
Let  imply that
imply that  lowest subbands of level-4 DWT decomposition have been avoided during smoothing, for example,
lowest subbands of level-4 DWT decomposition have been avoided during smoothing, for example,  implies that the lowest
implies that the lowest  subbands have not been touched. The tessellations for various smoothing possibilities are illustrated in Figure 10. Based on
subbands have not been touched. The tessellations for various smoothing possibilities are illustrated in Figure 10. Based on  we are defining
we are defining  which corresponds to the center tile and
which corresponds to the center tile and  that corresponds to the 4-neighbors. Note that since the
that corresponds to the 4-neighbors. Note that since the  -neighbors are level-2 approximates, the highest six subbands are already zero. This implies that
-neighbors are level-2 approximates, the highest six subbands are already zero. This implies that  cannot exceed
cannot exceed  . If we do not tamper the lowest four subbands during the horizontal smoothing of left/right neighbors and vertical smoothing of above/below neighbors, then
. If we do not tamper the lowest four subbands during the horizontal smoothing of left/right neighbors and vertical smoothing of above/below neighbors, then  , otherwise
, otherwise  where the only lowest level-4 subband is avoided from smoothing.
where the only lowest level-4 subband is avoided from smoothing.  , which corresponds to the center H, can assume a value of up to
, which corresponds to the center H, can assume a value of up to  and it was observed that the border between the four tiles gradually smoothen as we decrease the value of
and it was observed that the border between the four tiles gradually smoothen as we decrease the value of  since more and more subbands are being involved in the radial smoothing of center. Since we are working on a worst case scenario and we are closer than we should be, the borders do not disappear at all but in the original environment the transition is seamless. When subjected to method II, the resultant tessellation was considerably smooth as can be seen in Figure 11 which represents the detailed square area in the tessellation corresponding to Figure 9(a). The difference is obvious as it is very hard now to differentiate the tile interfaces, even though they have different qualities. The better results of method II are also supported by the PSNR values. The original texture detail (Figure 9(b)) has a PSNR of
since more and more subbands are being involved in the radial smoothing of center. Since we are working on a worst case scenario and we are closer than we should be, the borders do not disappear at all but in the original environment the transition is seamless. When subjected to method II, the resultant tessellation was considerably smooth as can be seen in Figure 11 which represents the detailed square area in the tessellation corresponding to Figure 9(a). The difference is obvious as it is very hard now to differentiate the tile interfaces, even though they have different qualities. The better results of method II are also supported by the PSNR values. The original texture detail (Figure 9(b)) has a PSNR of  dB with respect to the original full-resolution panorama. With method I this value comes down to
dB with respect to the original full-resolution panorama. With method I this value comes down to  dB for the case where
dB for the case where  ,
,  (Figure 10(c)) as against
(Figure 10(c)) as against  dB for method II (Figure 11). The corresponding difference images are shown in Figure 12.
dB for method II (Figure 11). The corresponding difference images are shown in Figure 12.
We now apply, to our example, the two other smoothing functions (Equations (2) and (3)) in liaison with method II. The results are shown in Figure 13. It is evident that the blurring is a bit in excess and the seam is hardly evident. But this has degraded the quality in the vicinity the tile interfaces. This can be judged from the PSNR of these images ( dB and
dB and  dB) as well as their respective differences shown in Figure 14. These results imply that although seam elimination is marginally, the accompanying blur is excessive and the linear form behaves well in this regard. This does not mean that one should entirely ignore the functions. In fact, they are equally effective but further detailed analysis is needed to make them or similar function indispensable. The purpose of this work is to show the way to eliminate the seams using some suitable function tailored to the view environment. The quest for alternatives is open to the user. Therefore, from this point onwards we will be employing the simplest of the potential functions (i.e., the linear one of (1)) for smoothing.
dB) as well as their respective differences shown in Figure 14. These results imply that although seam elimination is marginally, the accompanying blur is excessive and the linear form behaves well in this regard. This does not mean that one should entirely ignore the functions. In fact, they are equally effective but further detailed analysis is needed to make them or similar function indispensable. The purpose of this work is to show the way to eliminate the seams using some suitable function tailored to the view environment. The quest for alternatives is open to the user. Therefore, from this point onwards we will be employing the simplest of the potential functions (i.e., the linear one of (1)) for smoothing.
The DEM data corresponding to the above example is too small and using the same resolutions will not be a good idea, for example, a level-3 approximate tile would require only four coefficients. Still, for the purpose of comparison we are illustrating a  tessellation along the similar lines as the texture in Figure 15. The original, with all tiles at highest-resolution, is given in Figure 15(a). For the sake of comparison, Figure 15(b) shows a tessellation obtained by the simple replication of available coefficients to fill in for the missing coefficients to get the original size. For example, if only level-2 subband (1/16th of the original in size) of M is available, each of its coefficient has to be quadruplicated horizontally as well as vertically to get the original size and fill in for the missing coefficients. In this way, though naive, we subdivide the larger triangles uniformly to get to the original triangle size in the 3D modeling by the DEM. If one uses the concept of approximation, the results for two different resolution combinations are shown in Figures 15(c) and 15(d). After the application of method I to the tessellation of Figures 15(c) and 15(d), we got the tessellations illustrated in Figures 16(a) and 16(b). One observes that the difference is not that evident.
tessellation along the similar lines as the texture in Figure 15. The original, with all tiles at highest-resolution, is given in Figure 15(a). For the sake of comparison, Figure 15(b) shows a tessellation obtained by the simple replication of available coefficients to fill in for the missing coefficients to get the original size. For example, if only level-2 subband (1/16th of the original in size) of M is available, each of its coefficient has to be quadruplicated horizontally as well as vertically to get the original size and fill in for the missing coefficients. In this way, though naive, we subdivide the larger triangles uniformly to get to the original triangle size in the 3D modeling by the DEM. If one uses the concept of approximation, the results for two different resolution combinations are shown in Figures 15(c) and 15(d). After the application of method I to the tessellation of Figures 15(c) and 15(d), we got the tessellations illustrated in Figures 16(a) and 16(b). One observes that the difference is not that evident.
The same is not the case with method II, since the results are far better, as can be seen in Figure 17. Method II has thus an obvious advantage, as far as the DEM stitching is concerned and the results are better than those of method I.
When it comes to 3D, the DEM triangulation results support the arguments given above. For comparison we are showing the 3D triangulation with and without the overlaying of the corresponding texture in Figure 18. As an additional reference, the replication example of Figure 15(b) is shown in the triangulated form in Figure 19. The popping artifacts are conspicuous and obviously this is not we are up to. Things are a bit improved when the level-0, level-2 and level-3 approximation images are tessellated without any treatment, as shown in Figure 20. The artifacts are still visible due to the tile seams, however. Figure 21 shows the 3D view rendered from the heterogeneous tessellation after treatment with method I. The results are not that impressive, as far as the DEM triangulation is concerned. This may probably due to the use of very small tiles, as the  tiles at our disposal may not allow for effective smoothing. But even with this situation, method II gives interesting results, as illustrated in Figure 22. It is evident that the artifacts have been eliminated to a great extent and in fact there are hardly any feeling of unsmooth transition.
tiles at our disposal may not allow for effective smoothing. But even with this situation, method II gives interesting results, as illustrated in Figure 22. It is evident that the artifacts have been eliminated to a great extent and in fact there are hardly any feeling of unsmooth transition.
3D triangulation of the replication example from Figure 15(b)  .
.
5. Conclusion
The results, presented above, have been interesting in the face of the fact that we presented a worst case example tessellation in terms of quality difference as well as DEM size. Whilst the two methods were at par in the case of texture stitching, method II had the edge in the case of DEM. The problem of synchronization may arise if the DEM is different enough to warrant its own LOD. One probable answer to this is the fact that since the LOD is wavelet driven, one can always synchronously unify the DEM texture pairs as explained by Hayat et al. [2] or even adapt the synchronization [22] to exclude some subbands from embedding. One can still argue that the seam elimination has been realized at the expense of blurring the better resolution tile. The counter argument to this is the fact that the resultant blur is temporary and as soon as further resolution information for a given tile arrives, one can employ complement of the mask to restore the lost information.
In our method we are using a regular grid. To increase the performance, we would like to employ an irregular grid depending on the DEM resolution. The well-known T-cracks problem will be avoided by the application of the junction technique of Pajarola and Gobbetti [21]. In the continuation of our work we would like to extensively analyze and optimize the parameters of the functions employed for smoothing. Alongside, a better function needs to be discovered to further improve the stitching. The overhead in terms of the DWT and its inverse has to be quantified and optimization must be proposed for practical applications. The ultimate is its extension to real-time environment, with the emphasis on scalability.
References
Losasso F, Hoppe H: Geometry clipmaps: terrain rendering using nested regular grids. ACM Transactions on Graphics 2004, 23(3):769-776. 10.1145/1015706.1015799
Hayat K, Puech W, Gesquière G: Scalable 3D terrain visualization through reversible JPEG2000-based blind data hiding. IEEE Transactions on Multimedia 2008, 10(7):1261-1276.
Zagrouba E, Barhoumi W, Amri S: An efficient image-mosaicing method based on multifeature matching. Machine Vision and Applications 2009, 20(3):139-162. 10.1007/s00138-007-0114-y
Zitova B, Flusser J: Image registration methods: a survey. Image and Vision Computing 2003, 21(11):977-1000. 10.1016/S0262-8856(03)00137-9
Wagner D: ShaderX2: Shader Programming Tips and Tricks with DirectX 9.0, chapter Terrain Geomorphing in Vertex Shader. Wordware Publishing, Plano, Tex, USA; 2003.
Deb S, Bhattacharjee S, Patidar S, Narayanan PJ: Real-time streaming and rendering of terrains. Proceedings of the 5th Indian Conference Computer Vision, Graphics and Image Processing (ICVGIP '06), 2006, Madurai, India 276-288.
Tanner CC, Migdal CJ, Jones MT: The clipmap: a virtual mipmap. Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '98), 1998, New York, NY, USA 151-158.
Tsai F, Chiu HC: Adaptive level of detail for large terrain visualization. Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences Congress (ISPRS '08), October 2008, Beijing, China XXXVII: 579-584.
Ueng MF, Chuang JH: Terrain rendering with view-dependent LOD caching. Proceedings of the 10th International Conference on Artificial Reality and Tele-Existence (ICAT '00), October 2000 10: 58-65.
Li BY, Liao HS, Chang CH, Chu SL: Visualization for HPC data—large terrain model. Proceedings of the 7th International Conference on High Performance Computing and Grid in Asia Pacific Region (HPCASIA '04), 2004, Washington, DC, USA 280-284.
Larsen B, Christensen NJ: Real-time terrain rendering using smooth hardware optimized level of detail. Journal of Winter School of Computer Graphics 2003, 11(2):282-289.
Döllner J, Baumann K, Hinrichs K: Texturing techniques for terrain visualization. Proceedings of the 11th IEEE Visualization Conference (VIS '00), 2000, Washington, DC, USA 227-234.
Okamoto RM, de Mello FL, Esperança C: Texture management in view dependent application for large 3D terrain visualization. Proceedings of the Spring Simulation Multiconference (SpringSim '08), 2008, New York, NY, USA 641-647.
Buchholz H, Döllner J: View-dependent rendering of multiresolution texture-atlases. Proceedings of the IEEE Visualization Conference, 2005 215-222.
Wloka M: ShaderX3: Advanced Rendering with DirectX and OpenGL, chapter Improved Batching via Texture Atlases. Charles River Media, Hingham, Mass, USA; 2004.
Frueh C, Sammon R, Zakhor A: Automated texture mapping of 3D city models with oblique aerial imagery. Proceedings of the 2nd International Symposium on 3D Data Processing, Visualization, and Transmission (3DPVT '04), 2004, Washington, DC, USA 396-403.
Efros AA, Freeman WT: Image quilting for texture synthesis and transfer. Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '01), 2001, New York, NY, USA 341-346.
Somol P, Haindl M: Novel path search algorithm for image stitching and advanced texture tiling. In Proceedings of the 13th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG '05), February 2005, Plzen, Czech Republic. Edited by: Skala V. University of Western Bohemia; 155-218.
Chen R, Li X: DEM compression based on integer wavelet transform. Geo-Spatial Information Science 2007, 10(2):133-136. 10.1007/s11806-007-0038-8
Danovaro E, Floriani L, Magillo P, Puppo E, Sobrero D: Level-of-detail for data analysis and exploration: a historical overview and some new perspectives. Computers & Graphics 2006, 30(3):334-344. 10.1016/j.cag.2006.02.006
Pajarola R, Gobbetti E: Survey of semi-regular multiresolution models for interactive terrain rendering. The Visual Computer 2007, 23(8):583-605. 10.1007/s00371-007-0163-2
Hayat K, Puech W, Gesquière G: Scalable data hiding for online textured 3D terrain visualization. Proceedings of the IEEE International Conference on Multimedia and Expo (ICME '08) 2008, 217-220.
Acknowledgments
This work is in part supported by the Higher Education Commission (HEC), Pakistan, as well as by VOODDO (2008–2011), a project of ANR and the region of Languedoc Roussillon, France.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hayat, K., Puech, W., Islam, N. et al. Seamless Heterogeneous 3D Tessellation via DWT Domain Smoothing and Mosaicking. EURASIP J. Adv. Signal Process. 2010, 913681 (2010). https://doi.org/10.1155/2010/913681
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/913681



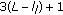 subbands will remain untouched since they represent the lowest rendered quality.
subbands will remain untouched since they represent the lowest rendered quality.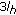 subbands of center tile (H) and
subbands of center tile (H) and 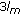 subbands of its
subbands of its 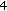 -neighbors (labeled M) are stuffed with
-neighbors (labeled M) are stuffed with  s.
s.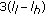 and
and 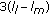 subbands of central tile and its
subbands of central tile and its 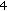 -neighbors, respectively.
-neighbors, respectively.





 . (a) The original (2048 × 2048 pixels) (b) zoomed square of (a)
. (a) The original (2048 × 2048 pixels) (b) zoomed square of (a)
 .
.  ,
,  ,
, 

 ,
,
 .
.


 . (a) exponential (2) (b) cosine (3)
. (a) exponential (2) (b) cosine (3)

 ). (a) Original:
). (a) Original:  (b) Coefficient replication:
(b) Coefficient replication:  (c)
(c)  (d)
(d) 

 . (a)
. (a)  and
and  with
with  (b)
(b)  and
and  with
with 

 . (a)
. (a)  and
and  (b)
(b)  and
and 

 ). (a) 3D triangulation of DEM (b) overlaying the texture
). (a) 3D triangulation of DEM (b) overlaying the texture

 . (a) 3D triangulation (b) overlaying its texture
. (a) 3D triangulation (b) overlaying its texture

 . (a) 3D triangulation (b) overlaying its texture
. (a) 3D triangulation (b) overlaying its texture
 ,
,  . (a) 3D triangulation (b) overlaying its texture
. (a) 3D triangulation (b) overlaying its texture