- Research Article
- Open access
- Published:
Interactions between Uterine EMG at Different Sites Investigated Using Wavelet Analysis: Comparison of Pregnancy and Labor Contractions
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 918012 (2010)
Abstract
This paper describes the use of the Morlet wavelet transform to investigate the difference in the time-frequency plane between uterine EMG signals recorded simultaneously on two different sites on women's abdomen, both during pregnancy and in labor. The methods used are wavelet transform, cross wavelet transform, phase/amplitude correlation, and phase synchronization. We computed the linear relationship and phase synchronization between uterine signals measured during the same contractions at two different sites on data obtained from women during pregnancy and labor. The results show that the Morlet wavelet transform can successfully analyze and quantify the relationship between uterine electrical activities at different sites and could be employed to investigate the evolution of uterine contraction from pregnancy to labor.
1. Introduction
There are many open questions concerning the functioning of the human uterus. One of these open questions concerns exactly how the uterus operates as an organ to perform the very organized act of contracting, in a synchronized way, to expulse a new human into this world. If we do not understand how the uterus works when it is working normally, it is obvious that we will not be able to detect or even prevent problems when it does not work properly leading to child born before time, sometimes with tragic consequences.
Uterine electromyography has been a research subject for many years since the 1950s. It has been proven to be of interest for pregnancy and parturition monitoring [1–4].
Uterine electromyogram recorded externally in women, the so-called electrohysterogram (EHG), has been proven to be representative of uterine contractility. The analysis of this signal may allow the prediction of a preterm labor threat as soon as 28 weeks of gestation (WG) [5].
One of the ways used to understand the functioning of biological systems is the detection of the relationship between signals. Several methods are proposed; it can be done by detecting the amplitude correlation (linear and nonlinear regression…), or the frequency relation (coherence…), or the phase synchronization and the dependency in time-frequency domain.
There have been little studies in the past concerning the application of these methods on EHG signals. One of the most important work was Marque et al. who showed, by using linear correlation coefficient, that the strongest correlation between bursts is located at the low frequency component [6]. The intercorrelation is however a temporal method; it cannot be used to analyze the interplay of various frequency components independently.
Furthermore, classical interrelation measures such as Fourier-based coherence and correlation rely on the stationarity of the measured signals, which is a condition that is rarely fulfilled with real biological signals.
Time frequency distributions (TFDs) were introduced as means of representing signals whose frequency content is varying with time, and for which both time domain representations and frequency domain representations are inadequate to appropriately describe the signal. Many different TFDs of a signal exist, including, but not limited to, the Wigner-Ville distribution (WVD), the spectrogram using a Short Time Fourier Transform (STFT), the wavelet transform (WT), the Hilbert Huang transform (HHT) and other methods that evaluate several parameters with TFD, such as the relationship between the instantaneous frequency (IF) and the TFD's [7]. Recently, alternative tools based on wavelet analysis have been developed and successfully applied to biological signals like EEG/MEG signals [8]. They allow tracking the time course of coherence in nonstationary neuronal signals with good temporal and frequency resolution.
Several approaches have been taken to study the relationship between nonstationary signals in the time-frequency domain. The three main approaches are
-
(1)
multiple window time frequency analysis (MW-TFA) [9],
-
(2)
frequency-dependant correlation coefficient [10],
-
(3)
time varying causal coherence function (TVCCF) based on the multivariate autoregressive model [11].
We chose to use the complex-wavelet analysis because, due to its variable window length, depending on the analyzed frequency band, it does not suppose a particular model of the data. Furthermore, another advantage is the possibility it offers to extract phase information. In addition, the wavelet analysis has been used with success on many types of signals such as EEG signals [12] as well as geophysical time series [13].
In a previous work, we have used the "wavelet coherence" to detect the interaction between the uterine electrical activities [14].
The results has shown the presence of higher coherence at the low frequency with constant phase shift [15]. Another interesting result is the possibility to use wavelet coherence on the whole signal without segmentation of the bursts of contractile activity [14]. However, the wavelet coherence depends on both amplitude and phase of the time series. Therefore, we cannot detect the nature of the relation by using the wavelet coherence.
The aim of this work is to separate the two kinds of information (phase and amplitude) in order to detect the nature of the relation between the uterine bursts in the time-frequency plane. First, we compute the scalogram of two uterine bursts and get their cross-scalogram. We then use two methods to describe phase and amplitude relation. The first method is the wavelet local correlation coefficient (WLCC), which detects the phase correlation. The second one is the cross wavelet coherence function (CWCF), which detects the amplitude correlation. The phase synchronization is described by the wavelet synchronization index, which can reveal the phase synchronization in the time-frequency domain. This index is used to evidence a difference between sets of uterine bursts during pregnancy and labor.
2. Materials And Methods
2.1. EHG Signals
The real EHG signals used in this study are obtained from 10 women: 5 during pregnancy (30–32 week of gestation) and 5 women during labor. The measurements were performed by using a 16-channel multipurpose physiological signal recorder, most commonly used for investigating sleep disorders (Embla A10). We used reusable Ag/AgCl electrodes. The measurements were performed at the Landspitali University hospital in Iceland, following a protocol approved by the relevant ethical committee (VSN 02-0006-V2).
The signals used for this study were the bipolar signals Vb7-Vb8 (Figure 1) corresponding to two channels on the median vertical axis of the uterus. The signal sampling rate was 200 Hz on 16 bits. The recording device has an anti-aliasing filter with a low pass cutoff frequency of 100 Hz and is capable of recording DC. The concurrent tocodynamometer paper trace (tocographic trace) was digitized in order to ease the identification of contractions. The EHG signals were segmented manually to extract segments containing uterine activity bursts. Table 1 resumes the segmentation information about the bursts shown in Figure 1.
(a) Electrode configuration on the woman's abdomen. Vbi represents the derived bipolar signals and ref. the reference electrodes. (b) Two uterine bursts for the same contractions during pregnancy. (c) Two uterine bursts for the same contractions in labor. Both (b) and (c) represent Vb7 (top) and Vb8 (bottom) bipolar signals.
2.2. Wavelet Analysis
The wavelet transform can be used to analyze time series that contain nonstationary power for many different frequencies [16].
The continuous wavelet transform (CWT) can decompose a signal into a set of finite basis functions. Wavelet coefficients  are produced through the convolution of a mother wavelet function
are produced through the convolution of a mother wavelet function  with the analyzed signal
with the analyzed signal  or
or

where  and
and  denote the scale and translation parameters respectively;
denote the scale and translation parameters respectively;  denotes complex conjugation. By adjusting the scale
denotes complex conjugation. By adjusting the scale  , a series of different frequency components in the signal can be extracted. The
, a series of different frequency components in the signal can be extracted. The  is for energy normalization across the different scales. The wavelet transforms, thus projects the information of the time series
is for energy normalization across the different scales. The wavelet transforms, thus projects the information of the time series  on the two dimension space (scale
on the two dimension space (scale  and translation
and translation  ).
).
In this study, we used the complex Morlet wavelet, given by

where  is the wavelet central pulsation. In this paper, we used
is the wavelet central pulsation. In this paper, we used  . Morlet wavelet is a Gaussian–windowed complex sinusoid; the Gaussian's second order exponential decay of the Morlet function gives a good time localization in the time domain [17]. We chose this wavelet as it provides simultaneously the signal amplitude and phase. This property allows us to use the complex Morlet Wavelet transform (cMWT) to investigate the coherence/synchronization between two signals recorded at two different sites simultaneously.
. Morlet wavelet is a Gaussian–windowed complex sinusoid; the Gaussian's second order exponential decay of the Morlet function gives a good time localization in the time domain [17]. We chose this wavelet as it provides simultaneously the signal amplitude and phase. This property allows us to use the complex Morlet Wavelet transform (cMWT) to investigate the coherence/synchronization between two signals recorded at two different sites simultaneously.
Based on cMWT, the wavelet power of a time series  at the time scale space is called the scalogram. It is simply defined as the squared modulus of
at the time scale space is called the scalogram. It is simply defined as the squared modulus of  .
.
Given two time series  and
and  , their cMWT are
, their cMWT are  and
and  , respectively. Their cross-cMWT is defined as
, respectively. Their cross-cMWT is defined as  , where
, where  means complex conjugation. The plot of
means complex conjugation. The plot of  is called cross-scalogram [12]. It provides the means to indicate the coincident events over frequency, for each time in the signals
is called cross-scalogram [12]. It provides the means to indicate the coincident events over frequency, for each time in the signals  and
and  .
.
Cross-scalogram is a measure of the similarity of power, at different frequency bands, for two separate uterine signals. It gives a "direct" estimation of the correlation of two uterine activities in the time–frequency domain. So the estimated values contain bias and noise information. In preliminary work [14], we used the wavelet coherence to describe the relation between our signals in the time-frequency domain. The wavelet coherence computes the relation in phase and amplitude simultaneously. It does not permit to describe separately the relations of amplitude and phase between two uterine electrical activities. As we are interested in identifying the nature of the relation between EHG signals, we choose to use two different methods that focus on separate aspects of the relationship between the signals, namely, the phase and the amplitude.
(i) The first method is the Wavelet local correlation coefficient (WLCC), proposed by [18] and defined as

where Re is the real part of  . WLCC is a tool that describes the phase correlation between two time series in the time-frequency domain.
. WLCC is a tool that describes the phase correlation between two time series in the time-frequency domain.
(ii) The second method is the cross wavelet coherence function (CWCF) which computes the amplitude (intensity) relation between two signals in the time-frequency domain [19]. It is defined as

The values of CWCF range between 0 (no amplitude correlation between X and Y) and 1 (X and Y are totally correlated in amplitude).
The application of these 2 methods on EEG signals has indicated that phase correlation decreases during the transition from interictal stage to ictal stage and that amplitude correlation increases from interictal to ictal [12].
Simultaneously, with CWCF and WLCC, we computed the phase difference between X and Y in the time-frequency plane, defined as

Re is the real part of the cross-cMWT and Im is its imaginary part.
The phase difference is represented by arrows with both methods: WLCC and CWCF. Phase arrows indicate the phase difference of the two bursts being compared. This can also be interpreted as a lead/lag: if the arrows are oriented to the right it means that the two signals are in phase and if they are oriented to the left it means that the signals are in antiphase.
The parameter used for measuring phase synchronization is the relative phase angle between two oscillatory systems. The Morlet wavelet transform acts as a bandpass filter and, at the same time, yields separate values for the instantaneous amplitude  and the phase
and the phase  of a time series signal at a specific frequency. Thus, the wavelet phases of two signals X and Y can be used to determine their instantaneous phase difference in a given frequency band, and to establish a synchronization measure (Wavelet Phase Synchronization: WPS) which quantifies the coupling of phases independently from amplitude effects.
of a time series signal at a specific frequency. Thus, the wavelet phases of two signals X and Y can be used to determine their instantaneous phase difference in a given frequency band, and to establish a synchronization measure (Wavelet Phase Synchronization: WPS) which quantifies the coupling of phases independently from amplitude effects.
The principle of phase synchronization corresponds to a phase locking between two systems defined as

where  and
and  are the unwrapped phases of the signals of the two systems and
are the unwrapped phases of the signals of the two systems and  is a constant. For real noisy data the cyclic relative phase,
is a constant. For real noisy data the cyclic relative phase,  mod
mod  , is preferentially used. Note that according to the above equation, the phase difference has to be calculated from the univariate phase angle. Phase locking is observed if the phase difference remains approximately constant over some time period.
, is preferentially used. Note that according to the above equation, the phase difference has to be calculated from the univariate phase angle. Phase locking is observed if the phase difference remains approximately constant over some time period.
In order to evidence the variation of the strength of phase synchronization between two uterine segment bursts, we used the intensity of the first Fourier mode of the distribution, given by

where  denotes the average over time. The measure of synchronization strength range from 0 to 1. It is also called the synchronization index. As it is the most usual case in neurophysiological signals, in this paper we use
denotes the average over time. The measure of synchronization strength range from 0 to 1. It is also called the synchronization index. As it is the most usual case in neurophysiological signals, in this paper we use  .
.
2.3. Statistical Test
The statistical significance of the results of the two methods WLCC and CWCF was tested using surrogates. By this way, we can be sure that the results obtained are not due to chance and that they correspond to real features present in the signals. Surrogate data are time series that are generated in order to keep particular statistical characteristics of an original time series while destroying all others. They have been used to test for nonlinearity [20] and nonstationarity of time series [21]. A classical approach to construct such time series is phase randomization in the Fourier domain or simulated annealing [20]. We used the iterative amplitude adjusted Fourier transform (IAAFT) method to produce the surrogates in the case of WLCC and bootstraps in the case of CWCF. The choice of the type of surrogates depends on the way the surrogate is resampled in the particular method. We used the bootstraps in the case of CWCF (linear relation) because its resampling is linear, whereas when studying the phase correlation (nonlinear relation) nonlinear resampling is needed and IAAFT is appropriate in this case. In IAAFT, surrogates have the same power spectrum and autocorrelation function as the original time series, but their phases are totally different.
The method we propose to use in this work can be described with the following steps, for WLCC, for example,
-
(1)
compute WLCC between the two original signals
 and
and 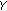 , we obtain WLCCorg,
, we obtain WLCCorg, -
(2)
generate
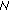 surrogates from signal
surrogates from signal 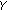 , so we obtained:
, so we obtained: 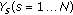 ,
, -
(3)
at each surrogate, calculate WLCC between
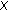 and
and  then: WLCCsurr = WLCC(X, Ys),
then: WLCCsurr = WLCC(X, Ys), -
(4)
the confidence limit for WLCC may be obtained from the tails of the WLCCsurr distribution,
-
(5)
the generated surrogates have the same amplitude information as
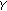 but their phases are randomized. The null hypothesis is that the results related to amplitude information obtained on
but their phases are randomized. The null hypothesis is that the results related to amplitude information obtained on  are the same as those obtained on the surrogates. By rejecting this hypothesis we can be sure (to within 1-p) that the phase information obtained is significant and not due to chance,
are the same as those obtained on the surrogates. By rejecting this hypothesis we can be sure (to within 1-p) that the phase information obtained is significant and not due to chance, -
(6)
"rank test" is used to reject or accept the hypothesis.
In a rank test, [WLCCorg; WLCCsurr (:)] is sorted in increasing order, and the rank index for WLCCorg returned. With a number of surrogates (n_surr = 25 for example), if the rank of WLCCorg is unity or 25, this means that it lies in the tail of the distribution, and the null can be rejected (two-tailed test) with a significance of  (1/(n_surr + 1)). In this paper, the n_surr used was 100. Ranks <5 and > 95 were considered significant and the hypothesis thus rejected (P = .05). The significant values were contoured by thick black lines and arrows are only plotted inside the contoured regions but values that did not test as significant were not plotted on the graphs.
(1/(n_surr + 1)). In this paper, the n_surr used was 100. Ranks <5 and > 95 were considered significant and the hypothesis thus rejected (P = .05). The significant values were contoured by thick black lines and arrows are only plotted inside the contoured regions but values that did not test as significant were not plotted on the graphs.
3. Results
As stated before, wavelet transform is a powerful tool to analyze non-stationary signals [12]. In this section we present the results of applying this powerful tool to analyze the relationship between uterine signals recorded at different sites during the same contractions. All the results were obtained using MATLAB (version 2008b) on a Pentium4 (2 GHz) PC computer. The typical computational costs are 0.12 ms per contraction for scalogram, cross-scalogram and phase synchronization, and 10 min per contraction for WLCC and CWCF with the significance test.
The scalogram displays the frequency content of the EHG signal over time. The difference in its aspect between pregnancy and labor bursts is clear and as shown in Figure 2: in labor (Figures 2(a) and 2(b) right) there are more high-frequency components than during pregnancy (Figures 2(a) and 2(b) left).
In Figure 2 and Figure 3, two EHG data sets are used: Vb7 (denoted by  ) and Vb8 (denoted by
) and Vb8 (denoted by  ). Their MWT are
). Their MWT are  and
and  , respectively. The plot of
, respectively. The plot of  displays the coincident events in the time-frequency domain for the two EHG signals: Figure 2(c) (left) shows the cross-scalogram of the two bursts measured during pregnancy; Figure 2(c) (right) shows the cross-scalogram of the two bursts measured during labor.
displays the coincident events in the time-frequency domain for the two EHG signals: Figure 2(c) (left) shows the cross-scalogram of the two bursts measured during pregnancy; Figure 2(c) (right) shows the cross-scalogram of the two bursts measured during labor.
(a)-(b) Cross wavelet coherence function: amplitude correlation between two bursts. (c)-(d) Wavelet local correlation: phase correlation between two bursts. (Left): pregnancy, (right): labor. The vertical lines indicate the start and the end of the uterine activity extracted from the Topography trace. Inside the thick black line there is significant level of 95% with resampling of Bootstraps (CWCF) and IAFFT (WLCC). The phase difference of cross spectrum is shown by arrow direction (in-phase: arrow pointing right, means Vb7 leads Vb8; antiphase: arrow pointing left, means Vb8 leads Vb7).
The cross-scalogram shows that the highest levels of common power are located during the uterine activity that is, 50s–100s for the pregnancy bursts and 40s–80s for the labor bursts. This common power is therefore clearly due to and related to the contractile activity of the uterus.
Based on Figure 1, the uterine electrical activities occur between 40–100 s for the pregnancy bursts and 40–80 s for the labor bursts (segmented from the Tocographic trace).
The statistical rank test with surrogates is applied to the CWCF and WLCC methods. When the statistical test indicates that the values obtained are significant, the area where these values are located are contoured by a thick black line and any values obtained outside these regions (nonsignificant) are shown as blank. The arrows indicating the phase difference are plotted only inside the regions where the values are found to be significant.
In the case of the signals recorded during pregnancy, we notice a small area between 40 s and 100 s where the method shows significant values in the case of CWCF-amplitude correlation—(Figure 3(a)) and much larger area in the case of WLCC-phase correlation—(Figure 3(c)). In the labor contraction we notice the opposite (between 40 s and 80 s): large areas of significance with CWCF and smaller ones with WLCC.
The comparison between CWCF and WLCC figures indicates that during pregnancy there is more phase correlation than during labor. At the opposite, there is more amplitude correlation during labor than during pregnancy (Figure 3). Some regions of significance can be seen outside the burst ranges that are probably due to noise. This is one of the disadvantages of both methods. The use of wavelet coherence that has great advantages is better in this respect because it can be applied to the whole signal without segmentation.
The results of CWCF are similar to our previous results, with a method that computes the nonlinear amplitude relation between two signals in the time domain, that indicated an increase in the nonlinear correlation coefficient from pregnancy to labor [22].
Concerning the wavelet phase synchronization results, Figure 4 indicates, either during labor or pregnancy, the highest phase synchronization is located at the lower frequencies of the signal. The phase synchronization is higher during pregnancy than during labor, which confirms the results of WLCC presented in Figure 3.
In order to compare quantitatively between pregnancy and labor, the signals were numerically filtered in three frequency bands (0–0.25 Hz; 0.25–0.5 Hz; >0.5 Hz). Then the mean of WPS was computed for each band. By doing this, we aim to evidence for which frequency bands the highest phase synchronization is located. Our previous work indicated that the highest coherence (computed by wavelet coherence) was located at the lower frequencies [14]. We seek to confirm this result. The second aim of this analysis is to investigate the difference in phase synchronization (WPS) between pregnancy and labor bursts in order to find if this method can potentially be used as a tool to classify pregnancy versus labor EHG bursts.
The results in Table 2 correspond to the mean of WPS at different frequency bands calculated on 25 contractions (CTs) for 5 women during pregnancy (30 to 36 WG) and 25 contractions from 5 women during labor (delivery time of 39 to 42 WG). These results indicate that the highest phase synchronization during both pregnancy and during labor is at the low frequencies (0–0.25 Hz) and the results indicate a significance difference (P = .05) in the phase synchronization in the time-frequency plane between pregnancy and labor.
The values indicate also that during labor the location of the high synchronization becomes clearer and that there is more difference between values at the low frequencies and higher ones, while this difference is less clear during pregnancy.
4. Discussion and Conclusion
In this paper, a study based on the Morlet wavelet transform is proposed to analyze the difference between uterine electrical activity bursts recorded from woman during pregnancy and others from women during labor. The wavelet transform, cross wavelet transform, phase correlation, amplitude correlation, and phase synchronization of the two types of uterine signals were described.
The scalogram exhibited the previously observed result: the presence of higher frequency components during labor than during pregnancy.
The cross-scalogram was used to detect where the highest common power was located between the two signals recorded during the same contraction. The highest common powers were found to be at lower frequencies during pregnancy than during labor.
WLCC and CWCF are two tools used to separate the phase and amplitude correlation. We used them in order to detect the nature of the relation between signals, for pregnancy and labor. The results indicate that there is more significant amplitude correlation in labor than during pregnancy and more significant phase correlation during pregnancy than in labor.
Phase synchronization index in the time frequency domain, is then used to describe the phase synchronization between signals. The pregnancy signals were again shown to be more synchronized in phase than the labor signals.
We noted that the results of WLCC and CWCF are similar with the results of the EEG during the transition from preictal to ictal stages, a phase desynchronization and amplitude synchronization. The question can be raised if there are similarities in the underlying physiological interpretation of these phenomena.
Although the cross-scalogram, WLCC, CWCF, and wavelet phase synchronization can describe linear relationship between the two time series, nonlinear interactions between the two time series cannot be revealed by these methods. The next step will be the use of the bicoherence method, which is a powerful tool to detect the nonlinear relation between signals.
We also plan to use signals recorded during pregnancy and labor for the same woman. By studying the time-frequency synchronization longitudinally along the weeks of gestation, we expect to be able to define the parameters related to propagation that are most likely to evidence the change from the no-coherent and inefficient contractions, during normal pregnancy, to the strong and organized contractions of labor. If robust parameters of this type can be found, these methods can be used to predict preterm labor.
References
Wolfs GM, van Leeuwen M: Electromyographic observations on the human uterus during labour. Acta Obstetricia et Gynecologica Scandinavica 1979, 58, supplement 90: 1-61.
Steer CM, Hertsch GJ: Electrical activity of the human uterus in labor; the electrohysterograph. American Journal of Obstetrics and Gynecology 1950, 59(1):25-40.
Planes JG, Morucci JP, Grandjean H, Favretto R: External recording and processing of fast electrical activity of the uterus in human parturition. Medical and Biological Engineering and Computing 1984, 22(6):585-591. 10.1007/BF02443874
Marque C, Duchene JMG, Leclercq S, Panczer GS, Chaumont J: Uterine EHG processing for obstetrical monitoring. IEEE Transactions on Biomedical Engineering 1986, 33(12):1182-1187.
Léman H, Marque C, Gondry J: Use of the electrohysterogram signal for characterization of contractions during pregnancy. IEEE Transactions on Biomedical Engineering 1999, 46(10):1222-1229. 10.1109/10.790499
Marque C, Duchene J: Human abdominal EHG processing for uterine contraction monitoring. In Applied Biosensors. Butterworth, Boston, Mass, USA; 1989:187-226.
Boashash B: Interpreting and estimating the instantaneous frequency of a signal-part 1: fundamentals. Proceedings of the IEEE 1992, 80: 520-538. 10.1109/5.135376
Lachaux J-P, Lutz A, Rudrauf D, Cosmelli D, Le Van Quyen M, Martinerie J, Varela F: Estimating the time-course of coherence between single-trial brain signals: an introduction to wavelet coherence. Neurophysiologie Clinique 2002, 32(3):157-174. 10.1016/S0987-7053(02)00301-5
Xu Y, Haykin S, Racine RJ: Multiple window time-frequency distribution and coherence of EEG using Slepian sequences and Hermite functions. IEEE Transactions on Biomedical Engineering 1999, 46(7):861-866. 10.1109/10.771197
Ansari-Asl K, Bellanger J-J, Bartolomei F, Wendling F, Senhadji L: Time-frequency characterization of interdependencies in nonstationary signals: application to epileptic EEG. IEEE Transactions on Biomedical Engineering 2006, 52(7):1218-1226.
Zhao H, Cupples WA, Ju KH, Chon KH: Time-varying causal coherence function and its application to renal blood pressure and blood flow data. IEEE Transactions on Biomedical Engineering 2007, 54(12):2142-2150.
Li X, Yao X, Fox J, Jefferys JG: Interaction dynamics of neuronal oscillations analysed using wavelet transforms. Journal of Neuroscience Methods 2007, 160(1):178-185. 10.1016/j.jneumeth.2006.08.006
Grinsted A, Moore JC, Jevrejeva S: Application of the cross wavelet transform and wavelet coherence to geophysical times series. Nonlinear Processes in Geophysics 2004, 11(5-6):561-566.
Hassan M, Terrien J, Karlsson B, Marque C: Application of wavelet coherence to the detection of uterine electrical activity synchronization in labor. IRBM 2010, 31(3):182-187. 10.1016/j.irbm.2009.12.004
Hassan M, Terrien J, Karlsson B, Marque C: Coherence and phase relationship analysis of the two main frequency components of EHG, as observed by complex wavelet transform. Proceedings of the World Congress on Medical Physics and Biomedical Engineering, September 2009, Munich, Germany 25(4):2219-2222.
Daubechies I: Wavelet transform, time-frequency localization and signal analysis. IEEE Transactions on Information Theory 1990, 36(5):961-1004. 10.1109/18.57199
Torrence C, Compo GP: A practical guide to wavelet analysis. Bulletin of the American Meteorological Society 1998, 79(1):61-78. 10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2
Buresti LG, Lombardi G: Application of continuous wavelet transforms to the analysis of experimental turbulent velocity signals. In Proceedings of the 1st International Symposium on Turbulence and Shear Flow Phenomena, 1999, Santa Barbara, Calif, USA. Volume 1. Begell House; 762.
Sello S, Bellazzini J: Wavelet cross-correlation analysis of turbulent mixing from large-eddy-simulations. http://arxiv.org/abs/physics/0003029
Schreiber T, Schmitz A: Surrogate time series. Physica D 2000, 142(3-4):346-382. 10.1016/S0167-2789(00)00043-9
Borgnat P, Flandrin P: Stationarization via surrogates. Journal of Statistical Mechanics: Theory and Experiment 2009., 2009(1):
Hassan M, Terrien J, Karlsson B, Marque C: Spatial analysis of uterine EMG signals: evidence of increased in synchronization with term. Proceedings of the IEEE Annual International Conference of the Engineering in Medicine and Biology Society (EMBC '09), 2009 1: 6296-6299.
Acknowledgments
This paper is financed by the Icelandic centre for research RANNÍS and the French National Center for University and School (CNOUS). The authors would like to especially thank Mr. Ásgeir Alexandersson for his help in the acquisition of EHG signals.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hassan, M., Terrien, J., Karlsson, B. et al. Interactions between Uterine EMG at Different Sites Investigated Using Wavelet Analysis: Comparison of Pregnancy and Labor Contractions. EURASIP J. Adv. Signal Process. 2010, 918012 (2010). https://doi.org/10.1155/2010/918012
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/918012

 and
and 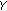 , we obtain WLCCorg,
, we obtain WLCCorg,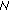 surrogates from signal
surrogates from signal 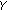 , so we obtained:
, so we obtained: 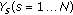 ,
,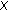 and
and  then: WLCCsurr = WLCC(X, Ys),
then: WLCCsurr = WLCC(X, Ys),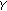 but their phases are randomized. The null hypothesis is that the results related to amplitude information obtained on
but their phases are randomized. The null hypothesis is that the results related to amplitude information obtained on  are the same as those obtained on the surrogates. By rejecting this hypothesis we can be sure (to within 1-p) that the phase information obtained is significant and not due to chance,
are the same as those obtained on the surrogates. By rejecting this hypothesis we can be sure (to within 1-p) that the phase information obtained is significant and not due to chance,

