- Research Article
- Open access
- Published:
Noise and Speckle Reduction in Doppler Blood Flow Spectrograms Using an Adaptive Pulse-Coupled Neural Network
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 918015 (2010)
Abstract
A novel method, called adaptive pulse coupled neural network (AD-PCNN) using a two-stage denoising strategy, is proposed to reduce noise and speckle in the spectrograms of Doppler blood flow signals. AD-PCNN contains an adaptive thresholding PCNN and a threshold decaying PCNN. Firstly, PCNN pulses based on the adaptive threshold filter a part of background noise in the spectrogram while isolating the remained noise and speckles. Subsequently, the speckles and noise of the denoised spectrogram are detected by the pulses generated through the threshold decaying PCNN and then are iteratively removed by the intensity variation to speckle or noise neurons. The relative root mean square (RRMS) error of the maximum frequency extracted from the AD-PCNN spectrogram of the simulated Doppler blood flow signals is decreased 25.2% on average compared to that extracted from the MPWD (matching pursuit with Wigner Distribution) spectrogram, and the RRMS error of the AD-PCNN spectrogram is decreased 10.8% on average compared to MPWD spectrogram. Experimental results of synthetic and clinical signals show that the proposed method is better than the MPWD in improving the accuracy of the spectrograms and their maximum frequency curves.
1. Introduction
The Doppler ultrasound blood flow signal has been extensively used in clinic to diagnose arterial and venous diseases due to its advantage of being noninvasive [1]. The diagnostic indices which are necessary for a clinical judgment are all extracted from the maximum frequency waveform of the Doppler spectrogram, calculated by using short-time Fourier transform (STFT), and are very useful in diagnosing arterial stenosis or other vascular disease by evaluating the vascular resistance [2]. However, two types of noise are present in the Doppler spectrogram. Firstly, there is background noise, arising from additional frequency components, added to the Doppler ultrasound signals. Additionally, the characteristic granular pattern, known as Doppler speckles, of spectrogram is obtained from Fourier transform-based analyzers when the Doppler signal scattered from cells moving within the same velocity resolution cell interferes with each others [3]. Noise and speckle, which are considered as undesirable properties, directly impact on the subjective study of the maximum frequency waveform extracted from the spectrogram, deteriorate the quality and the perceivable resolution of the indices and the features based on the estimated spectrograms and thus lead to inaccuracy in diagnoses of the artery diseases. Therefore, it is preliminary and essential to remove noise and speckles in the spectrogram of the Doppler ultrasound signal.
Discrete wavelet frames (DWFs), which is superior to methods based on standard discrete wavelet transform (DWT), were used to denoise the Doppler ultrasound signal [4]. Here discrete wavelet frame analysis was first applied to obtain the wavelet coefficients of the Doppler signal at multiple scales. Then, these coefficients were processed by a soft thresholding-based denoising algorithm to remove noise in the signal. In order to improve the adaptability of the threshold, a threshold-based wavelet packet denoising method was employed [5]. This approach, which can adaptively select the threshold, preserved useful high frequency components and offered higher signal-to-noise ratio (SNR) compared with straightforward wavelet-based denoising methods. The matching pursuit (MP) method was also used for improving the SNR of Doppler blood flow signals [6]. Using MP, the denoised Doppler signal was reconstructed by iteratively selecting the components approximate to the signal by a given directory while removing the incoherent residue, which was determined as noise, through a decay parameter-based algorithm. The performance of the MP method was better than those of the DWT and WPs (Wavelet Packets) methods for Doppler ultrasound signal denoising [6]. These denoising methods are effective in removing background noise in the Doppler spectrogram. However, they cannot suppress Doppler speckles in the STFT spectrograms due to the fact that background noise is usually random Gaussian distribution while speckle may be modeled by Rayleigh or  distribution [7, 8].
distribution [7, 8].
To alleviate the negative effect of the speckle, two types of speckle-reduction approaches, ensemble averaging and filtering [9], have been developed. Ensemble averaging approach is usually achieved by averaging a series of regular spectrograms produced by a flow phantom. However, physiological changes such as heart rate variation make the synchronization of the required waveforms difficult. Moreover, these uncorrelated images may be sampled at different times, from different views, or with different frequencies for the same target. Therefore, ensemble averaging is complex in clinical implementation. The filtering approaches, which treat the Doppler spectrogram as a grayscale image, offer an alternative for clinical applications, and many adaptive filters have been developed. Filtering approaches eliminate the speckle at each pixel based on the local statistics estimated from the Doppler spectrogram. However, the spatial spectral content of sharp intensity variations, such as edges contained in images, extends to infinity and overlaps with noise. Therefore, filters suppress noise while blurring important information-bearing features and fine image details. Meanwhile these speckle reduction methods become ineffective in filtering Doppler background noise and cause loss of the time-frequency resolution in the STFT spectrograms.
In order to effectively suppress Doppler noise and speckle in the STFT spectrograms, a method, called matching pursuit with Wigner distribution (MPWD), was proposed and has obtained good performance in noise and speckle suppression [10]. Using MPWD, a segmented Doppler ultrasound signal was first decomposed by MP greedy iterations for denoising purpose, and then the Wigner distribution was calculated and averaged during each small interval to reconstruct the spectrogram of the denoised signal for Doppler speckle reduction. Since the time interval is small, the Doppler speckle can be effectively smoothed. Meanwhile, this method may not cause the loss of time-frequency resolution in spectrograms as the interval is small enough, and it also does not require invariant heart rate to produce the very regular spectrograms. However, since MP is a greedy iteration and the Wigner distribution is calculated and averaged based on each small time interval, the MPWD is implemented at a high expense of computing complexity. Moreover, since the decomposition continues until the decay parameter is less than a predefined small value and the averaging interval is empirically selected, the MPWD method cannot completely remove all the background noise, and the adaptability of the method is relatively low.
To compensate for the drawback of the previous techniques, a method, called adaptive Pulse Coupled Neural Network (AD-PCNN), is proposed for noise and speckle reduction in the spectrograms of Doppler blood flow signals, while improving the accuracy of the spectrograms and their maximum frequency curves. PCNN biologically inspired from the visual cortex of mammals was first introduced by Eckhorn in [11] and has been widely used for image denoising [12–17]. The pulse capture characteristics of PCNN determine that the neurons that spatially connected and intensity correlated are tend to pulse together, while Doppler noise or speckle, which is independent and uncorrelated to the signal component, can not capture neighboring neurons or can not be captured by neighboring neurons. Thus each contiguous set of synchronously pulsing neurons indicates a coherent structure of the spectrogram, corresponding to the signal component, and the residue, defined as Doppler noise or speckle, can be identified. However, when conventional PCNN is applied for noise and speckle reduction, present theories cannot explain the relationship between the parameters of PCNN mathematical model and the processing effect. Satisfactory results usually require time-consuming selection of experimental parameters. Meanwhile, in a properly selected parametric model, the number of iteration that determines the denoising effect is evaluated by visual judgment, which decreases the efficiency of PCNN. Various improved PCNN models have developed for noise filtering, such as weighted-linking PCNNs [12], which contains four PCNN models to filter Gaussian and impulse noise in images, and a two-step PCNN impulse noise filter [13], which first determines the noisy pixels and then modifies the intensities of noisy pixels in the image. In addition PCNN was combined with other new techniques such as fuzzy, rough set theory and morphology to depress noises [14–17] meanwhile adaptively determining the PCNN parameters. However the computational complexity is therefore increased. These PCNN denoising approaches are proved to be effective in removing isolated noise while the performance of filtering Gaussian noise is degraded since all pixels in an image are contaminated by Gaussian noise. Therefore, conventional PCNN or existing PCNNs cannot be directly applied to suppress noise and speckles in Doppler spectrogram.
In order to improve the adaptability of parameter selection, decrease the computation redundancy of conventional PCNN algorithm, and to be effective in suppressing noise and speckles in Doppler spectrogram, an adaptive PCNN, which contains an adaptive thresholding PCNN and a threshold decaying PCNN is proposed. The proposed PCNN is greatly simplified compared to conventional PCNN and employs an adaptive threshold, which is defined as the basic intensity of the signal component based on the histogram of the spectrogram. The proposed PCNN is a two-dimensional structure with the same size of the Doppler spectrogram, and each neuron is corresponding to a pixel in the spectrogram. The PCNN pulses based on the adaptive threshold decompose the spectrogram into two parts of neurons, coherent structure which is spatially connected and intensity correlated and incoherent component, indicating the signal and noise or speckle in the spectrogram, respectively. After removing a part of noise from the coherent signal, the rule, the Gaussian distribution of the background noise and the Rayleigh or  distribution of speckle is broken, and the remained noise or speckle is greatly isolated. Subsequently, the firing matrix of the denoised spectrogram, specifying what time a neuron first fires, is calculated by using the threshold decaying PCNN through iterations, and then the target neuron is detected as a speckle or noise if it fires but more than 50% of the neurons in the linking window do not fire [13], indicating that the intensity of the target neuron is sharply variant compared to other neurons in the linking window. Finally, spectrograms are improved by iteratively suppressing the speckles or noise through a median filter [13], while the signal neurons are kept unmodified. Experiment results show that the proposed method can effectively conserve fine detail information, such as edges while removing speckles and noise. Furthermore, the iteration continues until the firing matrix of the threshold decaying PCNN is unchanged any further. Therefore, the iteration time can be adaptively determined.
distribution of speckle is broken, and the remained noise or speckle is greatly isolated. Subsequently, the firing matrix of the denoised spectrogram, specifying what time a neuron first fires, is calculated by using the threshold decaying PCNN through iterations, and then the target neuron is detected as a speckle or noise if it fires but more than 50% of the neurons in the linking window do not fire [13], indicating that the intensity of the target neuron is sharply variant compared to other neurons in the linking window. Finally, spectrograms are improved by iteratively suppressing the speckles or noise through a median filter [13], while the signal neurons are kept unmodified. Experiment results show that the proposed method can effectively conserve fine detail information, such as edges while removing speckles and noise. Furthermore, the iteration continues until the firing matrix of the threshold decaying PCNN is unchanged any further. Therefore, the iteration time can be adaptively determined.
The distinctive elements of the proposed method are as follows. ( ) a two-step PCNN model is proposed for noise and speckle suppression in Doppler spectrogram. Firstly an adaptive threshold, taking advantages of the pulse capture characteristics of PCNN and the histogram statistics of the spectrogram, is employed to filter noise from the signal component in the spectrogram. (
) a two-step PCNN model is proposed for noise and speckle suppression in Doppler spectrogram. Firstly an adaptive threshold, taking advantages of the pulse capture characteristics of PCNN and the histogram statistics of the spectrogram, is employed to filter noise from the signal component in the spectrogram. ( ) After a part of background noise is removed by the adaptive threshold PCNN, the remained noise and speckle are greatly isolated and the rule, that background noise is usually Gaussian distribution and speckle is molded by Rayleigh or
) After a part of background noise is removed by the adaptive threshold PCNN, the remained noise and speckle are greatly isolated and the rule, that background noise is usually Gaussian distribution and speckle is molded by Rayleigh or  distribution, is broken. Therefore the isolated noise and speckle can be effectively suppressed by the proposed threshold decaying PCNN, which first detects noise and speckles and then iteratively suppresses the noise and speckles with a median filter. (
distribution, is broken. Therefore the isolated noise and speckle can be effectively suppressed by the proposed threshold decaying PCNN, which first detects noise and speckles and then iteratively suppresses the noise and speckles with a median filter. ( ) It is the first attempt to reduce noise and speckles for Doppler ultrasound spectrogram by using PCNN algorithm. The indices, the relative root-mean-square (RRMS) errors of the spectrograms, and their maximum frequency curves between the estimated ones and their corresponding theoretical ones are used to evaluate the performance of the proposed method. Furthermore, effective noise and speckle suppression methods, MP and MPWD [10], are compared with the proposed method.
) It is the first attempt to reduce noise and speckles for Doppler ultrasound spectrogram by using PCNN algorithm. The indices, the relative root-mean-square (RRMS) errors of the spectrograms, and their maximum frequency curves between the estimated ones and their corresponding theoretical ones are used to evaluate the performance of the proposed method. Furthermore, effective noise and speckle suppression methods, MP and MPWD [10], are compared with the proposed method.
The remainder of this paper is organized as follows. Section 2 briefly describes the mathematical background of the MPWD and the proposed AD-PCNN noise and speckle reduction methods. Section 3 presents the simulation of the Doppler blood flow signals and experiments on simulated Doppler signals and clinical cases based on two different methods, AD-PCNN and MPWD [10]. Section 4 exhibits experimental results and discussions. Finally, some conclusions are drawn in Section 5.
2. Methods
2.1. MPWD Noise and Speckle Reduction Algorithm
The principle of matching pursuit is to decompose a signal into the linear superposition of the basis function  (
( ) that belongs to a redundant dictionary
) that belongs to a redundant dictionary  . After greedy search a
. After greedy search a  is gained, which best matches the signal structures, and the signal
is gained, which best matches the signal structures, and the signal  can be decomposed into
can be decomposed into

where  is a signal residuum after approximating
is a signal residuum after approximating  in the direction of
in the direction of  . Obviously,
. Obviously,  is orthogonal to
is orthogonal to  , so
, so

To minimize  , we must choose
, we must choose  such that
such that  is maximized, which is the first step of the approximation procedure. It is repeated iteratively into the residual signal obtained. If the decomposition is performed
is maximized, which is the first step of the approximation procedure. It is repeated iteratively into the residual signal obtained. If the decomposition is performed  times,
times,  is decomposed into a sum of
is decomposed into a sum of  atoms
atoms  and of the
and of the  th-order residue
th-order residue  :
:

In the present study, the discrete implementation of a matching pursuit for a Gabor dictionary is employed [18]. It is supposed that the signal is real and have  samples. At any scale
samples. At any scale  , the window function is defined as
, the window function is defined as

where the constant  normalizes the discrete norm of
normalizes the discrete norm of  to 1. For any integer
to 1. For any integer  and
and  , we denote
, we denote  , then the real discrete atoms of matching pursuit implementation with Gabor dictionary are given by
, then the real discrete atoms of matching pursuit implementation with Gabor dictionary are given by

with  is such that
is such that  .
.
MP is an iterative algorithm. When the MP is applied for denosing purpose, the atoms which are best coherent to the dictionary are isolated as the signal, and the residue is defined as noise at each iteration. The decomposition, which is determined by a decay parameter [18], is stopped after extracting the first  coherent structures of the signal. The first
coherent structures of the signal. The first  coherent structures are determined using a decay parameter, denoted by
coherent structures are determined using a decay parameter, denoted by

where  is the residual energy level at the M th iteration. The decomposition is continued until the decay parameter does not reduce any further. At this stage, the selected components represent the coherent structures, and the residue represents the incoherent structures in the signal with respect to the dictionary.
is the residual energy level at the M th iteration. The decomposition is continued until the decay parameter does not reduce any further. At this stage, the selected components represent the coherent structures, and the residue represents the incoherent structures in the signal with respect to the dictionary.
After extracting the first M coherent structures, a time-frequency energy distribution that is free of cross-terms is derived by adding the Wigner distribution of selected atoms

where  is the Wigner distribution of the selected atom
is the Wigner distribution of the selected atom  :
:

In the processing, the Doppler signal is divided into successive small segments, each one has a time interval  . The Wigner distribution in a time interval, estimated from the denoised signal by (7)-(8), is averaged during this time duration for Doppler speckle reduction in the spectrum. Since the time interval
. The Wigner distribution in a time interval, estimated from the denoised signal by (7)-(8), is averaged during this time duration for Doppler speckle reduction in the spectrum. Since the time interval  is small, the Doppler speckle, which arises from the interference with each other of cells moving within the same velocity resolution cell, could be smoothed. Meanwhile, this method may not cause the loss of time-frequency resolution in spectrograms as the
is small, the Doppler speckle, which arises from the interference with each other of cells moving within the same velocity resolution cell, could be smoothed. Meanwhile, this method may not cause the loss of time-frequency resolution in spectrograms as the  is small enough, and it also does not require the invariant heart rate to produce the very regular spectrograms, one of the limitations of the ensemble average speckle suppression method. However, since MP is a greedy iteration and the Winger distribution is calculated and averaged based on each small time interval
is small enough, and it also does not require the invariant heart rate to produce the very regular spectrograms, one of the limitations of the ensemble average speckle suppression method. However, since MP is a greedy iteration and the Winger distribution is calculated and averaged based on each small time interval  , the MPWD is implemented at a high expense of computing complexity. Moreover, since the decomposition continues until the decay parameter is no more than a predefined small value and the averaging interval is empirically selected, the MPWD method cannot completely remove all the background noise.
, the MPWD is implemented at a high expense of computing complexity. Moreover, since the decomposition continues until the decay parameter is no more than a predefined small value and the averaging interval is empirically selected, the MPWD method cannot completely remove all the background noise.
2.2. Adaptive PCNN Noise and Speckle Reduction Algorithm
The adaptive PCNN network model of neuron  is shown in Figure 1(a), where
is shown in Figure 1(a), where  is the feeding,
is the feeding,  is the linking,
is the linking,  is the dynamic threshold,
is the dynamic threshold,  is the internal activity, and
is the internal activity, and  and
and  are the pulse output of the adaptive threshold PCNN and the threshold decaying PCNN, respectively.
are the pulse output of the adaptive threshold PCNN and the threshold decaying PCNN, respectively.
The feeding field  corresponds to the input impulse signal
corresponds to the input impulse signal  :
:

The linking field accepts input from an eight-neuron linking window, shown in Figure 1(b):

where  , which means each neuron is connected in a
, which means each neuron is connected in a  neighboring field and the neighboring field does not include the neuron itself. Therefore the center element of
neighboring field and the neighboring field does not include the neuron itself. Therefore the center element of  is equal to 0, but not 1. The linking inputs are biased and then multiplied with the feeding input to form the internal activity
is equal to 0, but not 1. The linking inputs are biased and then multiplied with the feeding input to form the internal activity  :
:

The pulse generator of the neuron consists of a step-function generator and a threshold signal generator. At each firing step, the neuron output  is set to 1 when the internal activity
is set to 1 when the internal activity  is greater than the threshold
is greater than the threshold  ; otherwise the output
; otherwise the output  is set to 0:
is set to 0:

The threshold of PCNN for removing background noise in the Doppler spectrogram is adaptively defined as the basic intensity of the signal estimated from the histogram of the spectrogram. Suppose the PCNN contains  neurons distributed on
neurons distributed on  intensity levels
intensity levels  , which is normalized into
, which is normalized into  , the intensity histogram of Doppler spectrogram is expressed as
, the intensity histogram of Doppler spectrogram is expressed as

where  indicates the number of the neuron with intensity
indicates the number of the neuron with intensity  and
and  . A Doppler spectrogram contains three elements, which are background, signal, and noise or speckle. Therefore, the three extreme values shown in the intensity histogram of the spectrogram correspond to the basic intensities of these three elements. Consequently, the two extreme values whose intensities are less than 1 in the histogram represent the basic intensity of noise and signal components, respectively,
. A Doppler spectrogram contains three elements, which are background, signal, and noise or speckle. Therefore, the three extreme values shown in the intensity histogram of the spectrogram correspond to the basic intensities of these three elements. Consequently, the two extreme values whose intensities are less than 1 in the histogram represent the basic intensity of noise and signal components, respectively,


where  ,
,  and
and  are the two extreme values on the histogram of the Doppler spectrogram, and
are the two extreme values on the histogram of the Doppler spectrogram, and  and
and  are the intensities corresponding to the two extremes, respectively. The intensity of the signal is lower than that of the noise in the Doppler spectrogram. Therefore, the adaptive threshold for denoising the spectrogram is defined as
are the intensities corresponding to the two extremes, respectively. The intensity of the signal is lower than that of the noise in the Doppler spectrogram. Therefore, the adaptive threshold for denoising the spectrogram is defined as

After filtering a part of background noise from the spectrum, a threshold decaying PCNN is employed to detect and suppress the remained noise and speckles, where the threshold is defined as

where  is the decaying parameter. The firing matrix of the threshold decaying PCNN denotes what time each neuron first fires and is calculated through
is the decaying parameter. The firing matrix of the threshold decaying PCNN denotes what time each neuron first fires and is calculated through  times of iteration:
times of iteration:

The iteration is continued until the firing matrix  does not change any further to adaptively determine the iteration time
does not change any further to adaptively determine the iteration time  .
.
During the firing procedure, the intensity value of each pixel and the status of its neighbors (active or inactive) determine what time a neuron fires. Neurons in the same region or with an approximate  value tend to fire at the same time. When there are pixels whose intensity values are approximate in their linking region, the pulse output of one of them will fire the others in the linking region, and then produce a firing matrix. Obviously, the firing matrix of PCNN includes the information of the image intensity distribution and the geometry of the original image, which makes noise and speckle detection possible.
value tend to fire at the same time. When there are pixels whose intensity values are approximate in their linking region, the pulse output of one of them will fire the others in the linking region, and then produce a firing matrix. Obviously, the firing matrix of PCNN includes the information of the image intensity distribution and the geometry of the original image, which makes noise and speckle detection possible.
When using AD-PCNN for noise and speckle reduction in Doppler spectrogram, in the first step, since the threshold is defined as the basic intensity of the signal, the firing matrix  of the adaptive threshold PCNN separates noise, independent and uncorrelated to the signal components, from the signal neurons, which are spatially connected and intensity correlated and then remove the detected noise. Subsequently, the firing matrix
of the adaptive threshold PCNN separates noise, independent and uncorrelated to the signal components, from the signal neurons, which are spatially connected and intensity correlated and then remove the detected noise. Subsequently, the firing matrix  of the threshold decaying, indicating what time a neuron first fires, is calculated. If the target neuron fires but more than 50% the neurons in the filtering window do not fire, it denotes that the target neuron has sharp intensity fluctuation and can not capture most of the other neurons in the filtering window; therefore, it is detected as noise or speckle. Finally, the noise and speckle pixels are modified to be the median intensity values in the filtering window and are removed. Since the threshold decaying PCNN detects noise and speckle first and performs intensity variation to the noise and speckle only, the fine image details, such as edges, can be well preserved.
of the threshold decaying, indicating what time a neuron first fires, is calculated. If the target neuron fires but more than 50% the neurons in the filtering window do not fire, it denotes that the target neuron has sharp intensity fluctuation and can not capture most of the other neurons in the filtering window; therefore, it is detected as noise or speckle. Finally, the noise and speckle pixels are modified to be the median intensity values in the filtering window and are removed. Since the threshold decaying PCNN detects noise and speckle first and performs intensity variation to the noise and speckle only, the fine image details, such as edges, can be well preserved.
3. Experiments
In the experimental study, simulated and clinical Doppler ultrasound signals are used as test sources. The two algorithms, AD-PCNN and MPWD [10], are used to reduce noise and speckle for the simulated Doppler ultrasound signals with a 1024-point duration. The performance of noise and speckle reduction in Doppler spectrogram based on the AD-PCNN is compared with that based on the MPWD method.
3.1. Simulation Study
A signal model proposed by Mo and Cobbold [19] is used to simulate the one-directional Doppler signal of the carotid artery, by which the performance of the AD-PCNN is evaluated. The maximum frequency waveform used in the simulation is shown in Figure 2, and the details of this simulation model can be found in the work by Mo and cobbold [19]. The sampling frequency is 20 kHz, above the Nyquist rate; the cardiac cycle period is 1000 ms. Thirty realizations of the Doppler signal of the carotid artery are simulated on cardiac cycle basis by changing the random seed used in the model. The prespecified SNRs (SNR = 0 dB, SNR = 5 dB, and SNR = 10 dB) are obtained by adding white Gaussian noise to the simulated Doppler signals.
For the STFT spectrogram, a 10 ms window is normally used in practice because the signal is assumed to be stationary over this segment. The Gaussian window, which produces best compromise between the time and frequency resolution [20], is chosen in the present study for the STFT analysis. The signal  is divided into 100 intervals, each of which has a 10 ms time duration
is divided into 100 intervals, each of which has a 10 ms time duration , and their frequency spectra are calculated respectively,
, and their frequency spectra are calculated respectively,

where  is the window,
is the window,  and
and 
 are the discrete time and frequency, respectively, and
are the discrete time and frequency, respectively, and  is the window length.
is the window length.
A 200-point fast Fourier transform (FFT) is computed for each windowed signal segment. Within one-second cardiac period, 100 spectra are computed. This signal is divided into 100 intervals, each of which has a 10 ms time duration for the MPWD method, in which the Doppler signals are decomposed and denoised according to the decay parameter algorithm [10]. The STFT spectrograms of the original simulated Doppler signals and the MP-based denoised signals, and the MPWD spectrograms calculated by adding and averaging the Wigner distribution of selected atoms, are estimated for comparison. For the proposed AD-PCNN noise and speckle reduction algorithm, Figure 3 shows the coarse structure of such a proposed method, and the detailed algorithm is described below, which can be directly implemented by MATLAB or C language.
-
(1)
The pixel intensity of the original Doppler spectrogram is normalized to
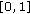 and input to
and input to 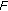 . Initialize
. Initialize 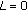 ,
, 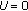 ,
,  ,
,  ,
, 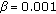 ,
, 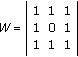 as a weight-matrix of
as a weight-matrix of 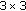 linking field, and
linking field, and 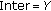 as a temporal matrix. Calculate
as a temporal matrix. Calculate  by (13)–(16).
by (13)–(16). -
(2)
Calculate linking field
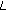 by (10).
by (10). -
(3)
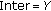 ,
,  , and
, and 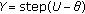 .
. -
(4)
If
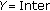 go to (5); else,
go to (5); else,  go back to (3).
go back to (3). -
(5)
 .
. -
(6)
Set
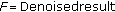 ,
, 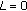 ,
, 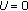 ,
, 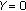 ,
, 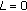 ,
,  , and iteration time
, and iteration time  .
. -
(7)
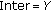 ,
, 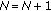 .
. -
(8)
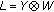 ,
,  ,
, 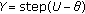 , and
, and 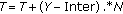 .
. -
(9)
In a filtering window, if the target neuron fires but more than 50% the neurons do not fire, then the target neuron is identified as a speckle or noise [13]. Modify the intensity of the target neuron to be the median intensities of the neurons in the filtering window. Otherwise, keep the target neuron unchanged.
-
(10)
If
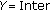 stop, and output the spectrum after noise and speckle reduction; else, go to (7).
stop, and output the spectrum after noise and speckle reduction; else, go to (7).
The maximum frequency waveforms are extracted from the spectrograms. The indices, the RRMS errors of the spectrograms, and their maximum frequency curves between the estimated ones and their corresponding theoretical ones are used to evaluate the performance of the proposed method for noise and speckle suppression in the spectrograms:

where  and
and  are the simulated original signal and the signal after noise and speckle suppression of the length
are the simulated original signal and the signal after noise and speckle suppression of the length  , respectively. The RRMS errors of the spectrogram and their maximum frequency waveform from 30 simulated signals are calculated before and after noise and speckle suppression and are used to compare the performance improvements of the AD-PCNN algorithm to that by MPWD.
, respectively. The RRMS errors of the spectrogram and their maximum frequency waveform from 30 simulated signals are calculated before and after noise and speckle suppression and are used to compare the performance improvements of the AD-PCNN algorithm to that by MPWD.
3.2. Clinical Study
To obtain the clinical Doppler ultrasound signal, a pulsed Doppler unit of HP SONOS 5500 ultrasound imaging system is used in pulse mode, and the applied frequency of the ultrasound is set to 2.7 MHz. The clinical Doppler signals are recorded from a child's aorta by placing sample volume near the center of the aortic arch. The audio Doppler signals are sampled by using an analog-to-digital Sound Blaster Card in a personal computer, and the sampling rate is set to 22.05 kHz. The objective effect and subjective indices of the spectrogram and their maximum frequency waveform are used to compare the performance of the AD-PCNN and the MPWD noise and speckle suppression algorithms.
4. Results and Discussions
Figure 4 presents the STFT, MP, MPWD, and AD-PCNN spectrograms and their maximum frequency waveforms, which are superimposed on the spectrograms with the solid curves, of a simulated original, MP-based and PCNN-based noise and speckle reduced Doppler signals with different noise levels (SNR = 0 dB, 5 dB, and 10 dB), respectively. In Figures 4(f), 4(k), and 4(p), it can be observed that the STFT spectrograms estimated from the signals with different noise levels (SNR = 0 dB, 5 dB, and 10 dB) include a mass of disturbance distributed in whole frequency band. The maximum frequency waveforms extracted from these estimated spectrograms include considerable distortion and illegibility, which implies the difficulty in finding correct indices used for quantification of vascular diseases' severity from the spectrograms. However, compared with the theoretical spectrogram shown in Figure 4(a), the disturbance components in both the MP spectrograms (shown in Figures 4(g), 4(l), and 4(q)) and the MPWD spectrograms (shown in Figures 4(h), 4(m), and 4(r)) have been significantly suppressed because these spectrograms are estimated from the denoised signals by using the MP-based denoising method. But obvious Doppler speckles can be found in the all STFT spectrograms estimated from the signals without added noise (shown in Figure 4(b)), signals added different noise levels (shown in Figures 4(f), 4(k), and 4(p)), and MP-based denoised signals (shown in Figures 4(g), 4(l), and 4(q)). This means that the MP-based denoising algorithm, which can effectively reduce the random noise in Doppler signals, can not suppress the Doppler speckle in the STFT spectrograms. From Figures 4(c), 4(h), 4(m), and 4(r), it can be found that the Doppler speckles in the MPWD spectrograms have been obviously suppressed. However, the MPWD spectrograms inevitably include background noise and discontinuity. Meanwhile, the computing complexity of MPWD is high since MP is a greedy algorithm, and Wigner distribution is calculated and averaged based on each small time interval. The background noise in the PCNN-denoised spectrogram (shown in Figures 4(d), 4(i), 4(n), and 4(s)) has been partly removed, and the remained noise has been greatly isolated so that it can be effectively reduced by using the threshold decaying PCNN. From Figures 4(e), 4(j), 4(o), and 4(t), it is obvious that the Doppler random noise and speckles can be effectively removed by using AD-PCNN. The spectrograms and their maximum frequency waveforms obtained by using the AD-PCNN are much closer to the theoretical one than those by using the MPWD.
The spectrogram and its maximum frequency waveform, which is superimposed on the spectrogram with a solid curve, of a simulated Doppler signal. The theoretical (a), the STFT (b), the MPWD (c), the PCNN denoised (d), and the PCNN noise and speckle reduced (e) versions of the original signal. The STFT versions (f, k, p), the STFT versions after the MP denoising (g, l, q), the MPWD versions (h, m, r), the STFT versions after PCNN denoising (i, n, s), and the PCNN noise and speckle reduced version (j, o, t) of the signals added noise with SNR = 0 dB ( f, g, h, i, j), 5 dB (k, l, m, n, o), and 10 dB (p, q, r, s, t).
Table 1 lists the mean and standard deviation of the RRMS errors of the maximum frequency waveforms extracted from the spectrograms of the 30 independent realizations of Doppler signals with SNR = 0 dB, 5 dB, 10 dB and  based on the MP, the MPWD, and the PCNN-based methods, respectively. From Table 1 it can be concluded that the RRMS errors of the maximum frequency waveforms extracted from the PCNN spectrograms have decreased much more than those before noise and speckle reduction. For example, the RRMS errors of the maximum frequency waveforms of the original STFT are 2.92 and 3.84 times higher than those denoised by using MPWD and AD-PCNN on Doppler signals with SNR = 10 dB, respectively. While the MPWD has presented the RRMS errors of the maximum frequency waveforms
based on the MP, the MPWD, and the PCNN-based methods, respectively. From Table 1 it can be concluded that the RRMS errors of the maximum frequency waveforms extracted from the PCNN spectrograms have decreased much more than those before noise and speckle reduction. For example, the RRMS errors of the maximum frequency waveforms of the original STFT are 2.92 and 3.84 times higher than those denoised by using MPWD and AD-PCNN on Doppler signals with SNR = 10 dB, respectively. While the MPWD has presented the RRMS errors of the maximum frequency waveforms  ,
,  ,
,  and
and  results on Doppler signals with SNR = 0 dB, 5 dB, 10 dB, and
results on Doppler signals with SNR = 0 dB, 5 dB, 10 dB, and  , respectively, the AD-PCNN has presented the RRMS errors 9.68%, 38.10%, 31.58%, and 21.43% decrease compared to MPWD spectra. Table 2 lists the mean and standard deviation of the RRMS errors of the spectrograms of the 30 independent realizations of Doppler signals with SNR = 0 dB, 5 dB, 10 dB, and
, respectively, the AD-PCNN has presented the RRMS errors 9.68%, 38.10%, 31.58%, and 21.43% decrease compared to MPWD spectra. Table 2 lists the mean and standard deviation of the RRMS errors of the spectrograms of the 30 independent realizations of Doppler signals with SNR = 0 dB, 5 dB, 10 dB, and  based on the STFT, the MPWD, and the PCNN methods, respectively. Table 2 indicates that the Doppler noise and speckles in the STFT spectrograms have been greatly suppressed by using MPWD and AD-PCNN. For example, the RRMS errors of the spectrogram of the original STFT are 1.65 and 1.83 times higher than those denoised by using MPWD and AD-PCNN on Doppler signals with SNR = 10 dB, respectively. While the MPWD has presented the RRMS errors of the spectrogram
based on the STFT, the MPWD, and the PCNN methods, respectively. Table 2 indicates that the Doppler noise and speckles in the STFT spectrograms have been greatly suppressed by using MPWD and AD-PCNN. For example, the RRMS errors of the spectrogram of the original STFT are 1.65 and 1.83 times higher than those denoised by using MPWD and AD-PCNN on Doppler signals with SNR = 10 dB, respectively. While the MPWD has presented the RRMS errors of the spectrogram  ,
,  ,
,  and
and  results on Doppler signals with SNR = 0 dB, 5 dB, 10 dB, and
results on Doppler signals with SNR = 0 dB, 5 dB, 10 dB, and  respectively, the AD-PCNN has presented RRMS errors 9.52%, 9.52%, 10.0%, and 10.0% decrease compared to MPWD spectra. It is found that in all cases, the RRMS errors of the maximum frequency waveforms and the spectrograms based on the AD-PCNN method are smaller than those based on the STFT and MPWD, which means that the AD-PCNN spectrograms are much closer to the theoretical ones and contain least extra frequency components and least distortion in the estimated maximum waveforms.
respectively, the AD-PCNN has presented RRMS errors 9.52%, 9.52%, 10.0%, and 10.0% decrease compared to MPWD spectra. It is found that in all cases, the RRMS errors of the maximum frequency waveforms and the spectrograms based on the AD-PCNN method are smaller than those based on the STFT and MPWD, which means that the AD-PCNN spectrograms are much closer to the theoretical ones and contain least extra frequency components and least distortion in the estimated maximum waveforms.
When the MPWD and the AD-PCNN algorithms are applied to process the clinical Doppler ultrasound signals, all of the cases show that the AD-PCNN achieves better performance for suppressing noise and speckles in the spectrograms and smoothing the maximum frequency waveforms. As an illustration, the spectrogram and its maximum frequency waveform of a segment of Doppler ultrasound signal recorded from a child's aortic arch based on the MP, the MPWD, and the AD-PCNN algorithms are shown in Figure 5. From Figure 5(b), we can observe that the MP-denoised spectrogram has fewer additional noise and distortion than the original STFT spectrogram shown in Figure 5(a). The superimposed maximum frequency waveform also confirms that MP achieves a good denoising performance. However, Doppler speckles in the MP spectrogram are obvious. As observed in Figure 5(c), the random noise and Doppler speckles have been suppressed in the spectrogram by using the MPWD method. However, the MPWD spectrogram inevitably includes background noise. From Figure 5(d), it is obvious that the Doppler random noise and speckles are effectively suppressed; meanwhile the superimposed maximum frequency waveform indicates that the AD-PCNN obtains a better noise and speckle reduction performance than MPWD.
The spectrogram and the maximum frequency waveform, which is superimposed on the spectrogram with a solid curve, of a clinical signal. (a) The STFT version of the original signal; (b) the MP denoising version of the original signal; (c) the MPWD version of the original signal; (e) the AD-PCNN version of the original signal.
5. Conclusions
A novel method, AD-PCNN has been proposed to enhance Doppler blood flow spectrograms. First, the Doppler spectrograms are denoised by using the adaptive threshold PCNN, which removes background noise from the coherent component with spatiality vicinity and intensity correlation in the Doppler spectrogram and isolates the remained noise. Then, the firing matrix of the denoised spectrogram, calculated by the threshold decaying PCNN is employed to detect speckles. Finally the improved spectrogram is reconstructed by modifying the speckles to be the median intensity in the filtering window. Results from the experiments on simulation and clinical signals show that the proposed method performs effectively in noise and speckle suppression, improves the accuracy of spectrograms and their maximum frequency curves, and achieves better performance than MPWD algorithm. The RRMS errors of the AD-PCNN spectrograms and the extracted maximum frequency of simulated Doppler blood flow signals are decreased by 10.8% and 25.2% on average when compared to MPWD spectrograms on Doppler signals with various SNRs, respectively.
References
Ozbek SS, Aytac SK, Erden MI, Sanlidilek NU: Intrarenal Doppler findings of upstream renal artery stenosis: a preliminary report. Ultrasound in Medicine and Biology 1993, 19(1):3-12. 10.1016/0301-5629(93)90012-D
Brkljačić B, Mrzljak V, Drinković I, Soldo D, Sabljar-Matovinović M, Hebrang A: Renal vascular resistance in diabetic nephropathy: Duplex Doppler US evaluation. Radiology 1994, 192(2):549-554.
Evans DH, McDicken WN: Doppler Ultrasound: Physics, Instrumentation and Signal Processing. John Wiley & Sons, Chichester, UK; 2000.
Zhang Y, Wang Y, Wang W, Liu B: Doppler ultrasound signal denoising based on wavelet frames. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2001, 48(3):709-716. 10.1109/58.920698
Yu JF, Liu DC: Thresholding-based wavelet packet methods for Doppler ultrasound signal denoising. Proceedings of the 7th IEEE Asian-Pacific conference on Medical and Biological Engineering, 2008, Beijing, China 408-412.
Zhang Y, Wang L, Gao Y, Chen J, Shi X: Noise reduction in Doppler ultrasound signals using an adaptive decomposition algorithm. Medical Engineering and Physics 2007, 29(6):699-707. 10.1016/j.medengphy.2006.08.002
Tuthill TA, Sperry RH, Parker KJ: Deviations from Rayleigh statistics in ultrasonic speckle. Ultrasonic Imaging 1988, 10(2):81-89. 10.1016/0161-7346(88)90051-X
Dutt V, Greenleaf JF: Statistics of the log-compressed echo envelope. Journal of the Acoustical Society of America 1996, 99(6):3817-3825. 10.1121/1.414999
Hoskins PR, Loupas T, McDicken WN: A comparison of three different filters for speckle reduction of doppler spectra. Ultrasound in Medicine and Biology 1990, 16(4):375-389. 10.1016/0301-5629(90)90067-M
Zhang Y, Yu Q, Zhang K, Chen J, Shi X: Doppler blood flow spectrogram enhancement based on the matching pursuit with wigner distribution. DCDIS Series B 2007, 14(S4):48-52.
Eckhorn R, Reitboeck HJ, Arndt M, Dicke PW: Feature linking via synchronization among distributed assemblies: simulation of results from cat cortex. Neural Computation 1990, 2: 293-307. 10.1162/neco.1990.2.3.293
Ji L, Yi Z: A mixed noise image filtering method using weighted-linking PCNNs. Neurocomputing 2008, 71(13-15):2986-3000. 10.1016/j.neucom.2007.04.015
Zhang J, Lu Z, Shi L, Dong J, Shi M: Filtering images contaminated with pep and salt type noise with pulse-coupled neural networks. Science in China. Series F 2005, 48(3):322-334.
Gu X-D, Cheng C-Q, Yu D-H: Noise-reducing of four-level image using PCNN and fuzzy algorithm. Journal of Electronics and Information Technology 2003, 25(12):1585.
Gu X, Zhang L: Morphology open operation in Unit-linking pulse coupled neural network for image processing. Proceeding of International Conference on Signal Processing, 2004, Beijing, China 2: 1597-1600.
Zhang J, Dong J, Shi M: An adaptive method for image filtering with pulse-coupled neural networks. Proceedings of IEEE International Conference on Image Processing (ICIP '05), September 2005 133-136.
Ma Y, Lin D, Zhang B, Xia C: A novel algorithm of image enhancement based on pulse coupled neural network time matrix and rough set. Proceeding of the 4th International Conference on Fuzzy Systems and Knowledge Discovery, 2007, Haikou, China 3: 86-90.
Mallat SG, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993, 41(12):3397-3415. 10.1109/78.258082
Mo LYL, Cobbold RSC: Nonstationary signal simulation model for continuous wave and pulsed Doppler ultrasound. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 1989, 36(5):522-530. 10.1109/58.31796
Zhang Y, Guo Z, Wang W, He S, Lee T, Loew M: A comparison of the wavelet and short-time fourier transforms for Doppler spectral analysis. Medical Engineering and Physics 2003, 25(7):547-557. 10.1016/S1350-4533(03)00052-3
Acknowledgments
This paper was supported by Grant (60861001) from the National Natural Science Foundation of China, Grant (2009CD016) from the Yunnan Natural Science Foundation, Grant (2008YB009) from the Science and Engineering Fund of Yunnan University, and Grant (21132014) from the Young and Middle-aged Backbone Teacher's Supporting Programs of Yunnan University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, H., Zhang, Y. & Xu, D. Noise and Speckle Reduction in Doppler Blood Flow Spectrograms Using an Adaptive Pulse-Coupled Neural Network. EURASIP J. Adv. Signal Process. 2010, 918015 (2010). https://doi.org/10.1155/2010/918015
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/918015


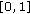 and input to
and input to 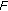 . Initialize
. Initialize 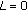 ,
, 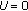 ,
,  ,
,  ,
, 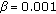 ,
, 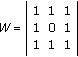 as a weight-matrix of
as a weight-matrix of 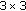 linking field, and
linking field, and 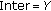 as a temporal matrix. Calculate
as a temporal matrix. Calculate  by (13)–(16).
by (13)–(16).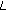 by (10).
by (10).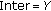 ,
,  , and
, and 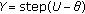 .
.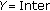 go to (5); else,
go to (5); else,  go back to (3).
go back to (3). .
.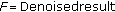 ,
, 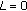 ,
, 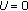 ,
, 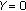 ,
, 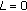 ,
,  , and iteration time
, and iteration time  .
.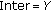 ,
, 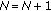 .
.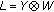 ,
,  ,
, 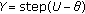 , and
, and 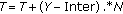 .
.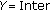 stop, and output the spectrum after noise and speckle reduction; else, go to (7).
stop, and output the spectrum after noise and speckle reduction; else, go to (7).

