- Research Article
- Open access
- Published:
A Relative-Localization Algorithm Using Incomplete Pairwise Distance Measurements for Underwater Applications
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 930327 (2010)
Abstract
The task of localizing underwater assets involves the relative localization of each unit using only pairwise distance measurements, usually obtained from time-of-arrival or time-delay-of-arrival measurements. In the fluctuating underwater environment, a complete set of pair-wise distance measurements can often be difficult to acquire, thus hindering a straightforward closed-form solution in deriving the assets' relative coordinates. An iterative multidimensional scaling approach is presented based upon a weighted-majorization algorithm that tolerates missing or inaccurate distance measurements. Substantial modifications are proposed to optimize the algorithm, while the effects of refractive propagation paths are considered. A parametric study of the algorithm based upon simulation results is shown. An acoustic field-trial was then carried out, presenting field measurements to highlight the practical implementation of this algorithm.
1. Introduction
The capability of reliable underwater modem technology [1, 2] has led to a growing number of emerging underwater applications, presenting with them new possibilities and challenges. One of these applications is the deployment of a cluster of underwater sensors [3], which offers benefits ranging from oil-platform monitoring [4] to ecosystem monitoring, surveillance, and early warning systems for tsunami. A typical application of a sensor deployment generally involves the collection of data and the delivery of these data [5, 6]. In the former, the knowledge of sensor positions may play an important role in aiding the interpretation of the recorded data or in improving the performance of signal processing algorithms such as in array processing [7]. In the latter, where the collected data are sent or relayed to a destination, the estimation of sensor position enables the implementation of more energy and latency efficient routing and channelaccess protocols [8, 9]. Therefore, in situations where the positional information are not available to the sensors prior to deployment, or that it changes after deployment, there exists the motivation to localize the sensors with existing modem capabilities.
The aim of this paper is to present and evaluate an algorithm using the weighted-majorization [10, 11] multidimensional scaling (MDS) approach for the localization of sparsely deployed sensors within the underwater environment. Based on extensive study of sensor localization in the radio frequency domain, the underpinning methodology can be broadly categorised into range-free and rangebased schemes [12]. Range-free schemes are effective in obtaining estimated positions for applications requiring limited accuracies but usually impose constraints on the flexibility of deployment. Range-based schemes are based upon the accurate measurements of Euclidean distances between the sensors, which can be derived from two-way ranging delays, time-of-arrivals, angles-of-arrival, or received signal strength indicator (RSSI). In the underwater environment, RSSI measurements are affected by multipaths and back-scattering especially in a shallow water environment such as in coastal waters or within a busy harbour. Also, acoustic modems generally operate within a frequency band that captures many external sources of noise, varying from shrimps [13] (in tropical waters) to breaking waves in a stormy weather [14], thus contributing to a high and fluctuating level of ambient noise. These factors can potentially lead to inconsistency in RSSI measurements. Similarly, measuring angles-of-arrival to a high accuracy may prove prohibitive unless every node is equipped with the necessary hydrophone array. The viable methods are therefore by using time-of-arrival measurements which require strict synchronization amongst all the nodes or by two-way ranging. The latter method requires no synchronization and operates by measuring the two-way propagation time assuming that the queried modem sends a reply packet after a fixed time-delay.
The task of underwater sensor localization can be considered as a two-step process; first by the localization of the sensors in the 3D Euclidean space with respect to one another using measurements of internode distances only, and then, if necessary, the anchoring of these positions to a reference or geodetic coordinate system. A relatively straightforward method of resolving the sensors' relative locations using only pairwise distance measurements is by metric multidimensional scaling, as a special case where one assumes that the measure of dissimilarities is represented by Euclidean distances, and that a set of coordinates within the relevant dimensions explain the observed distances. This concept has its roots in the field of psychometrics [15], in which an early analytical solution was presented by Torgerson [16] and referred to as classical MDS. In order to apply classical MDS to the problem of sensor localization, all the pairwise distances between the nodes need to be obtained [17]. This implies that every node needs to have acoustic visibility to all the other nodes. Such a requirement may often be difficult to meet in practice, as ranging measurements may be erroneous or unsuccessful between nodes that are further apart, as well as nodes that are partially obstructed (such as by harbour walls) and have no complete visibility to all the other nodes.
The contribution of this article is in addressing the problem of relative localization using incomplete pairwise distance measurements. By applying a robust approach based upon an iterative, weighted, cost-minimization algorithm known as stress-majorization [18, 19], it is shown that a cluster of sensor nodes can be efficiently localized in the absence of complete pairwise distance measurements. The key improvements introduced herein are a robust and effective method of initialization of the algorithm, a parametric study of the proposed approach, and a case-study of its practical application based upon experimental field measurements. The next section relates the contribution of this paper with regard to previous research effort within similar domain. Section 3 presents the analytical formulation of the problem and the algorithm of the proposed approach. In Section 4, simulation results provide a parametric evaluation on the algorithm's performance. Section 5 describes a field trial being conducted with 12 nodes using acoustic time-of-arrival measurements, capturing the issues related to the implementation of this algorithm and verifying the results predicted in the simulation study. Section 6 presents a short discussion on the scope of this article while Section 7 draws the conclusion from this work.
2. Related Work
Sensor localization is an area of active research in both the radio [20–24] and underwater domains [25–29], where various solutions based on different levels of constraints and assumptions on infrastructure availability have been studied. Broader reviews on this subject can be found in [12, 30].
In [23], Patwari et al. applied maximum likelihood estimation techniques to approximate a node's relative location, but the accuracy of the approximations (and the validity of the derived lower Cramer-Rao bounds) depends on having complete pairwise distances for all the nodes and knowledge of the probability distribution underlying the observed data. Although one can assume that the pairwise distances are Gaussian distributed (the validity of which increases with higher signal-to-noise ratios [31]), the requirement of obtaining all pairwise distances may introduce a challenging constraint in practice for the application scenario considered in this article. In [22], Moses et al. also presented a self-localization approach method using a maximum-likelihood estimator, relying on both time-of-arrival measurements and angle-of-arrival measurements. It is also acknowledged that with incomplete data measurements, the maximum likelihood estimator may not yield a unique solution.
In [17], Shang et al. applied classical-MDS by eigenvalue decomposition (EVD) for the localization of nodes using distance measurements. It is demonstrated that closed-form solutions can be obtained without the need for iterative computations, but this is restricted by the condition that global information of pairwise distances in the network needs to be made available to a central processor or to all individual nodes. Ji and Zha [32] applied a majorization-MDS approach for sensor localization, allowing for missing pairwise distances. This removes the requirement for complete pairwise distance measurements. However, a random start configuration is applied for the estimation of the initial point coordinates, and the possible existence of non-linear propagation paths was not discussed. The work is extended by Costa et al. in [33], where arbitrary non-negative weightings can be applied to distance measurements, such that adaptive weightings can be applied to account for different levels of confidence amongst the pairwise distances. The proposed algorithm is decentralised such that each node estimates its local cost function iteratively, then communicates this to their neighbours in order to achieve cost minimization globally across all the nodes. However, there is little emphasis on the method for estimating initial node positions, and the algorithm similarly assumes that the measured distances are an accurate representation of Euclidean distances between the nodes. Also, since the focus is on adaptively choosing neighbours based upon the quality of measurements by allocating the appropriate weightings, the work did not investigate the tolerance of the algorithm to varying levels of missing pairwise measurements.
An experimental study of sensor self-localization in the free-space outdoor environment was conducted using acoustic ranging by Kwon et al. in [34]. In addressing the issue of missing and noisy distance measurements, a weighting function that was coupled with a soft constraint of minimum distances were introduced. The key difference in their approach is in that a gradient descent algorithm was applied in the process of minimization, and that a multiple restart scheme was used to avoid local minima. Separately, an alternative method of addressing missing distances within a 3D environment was studied by Birchfield [35], which iteratively uses a subset of points (up to 4 for 3D) with the highest availability of distance measurements to derive an estimate of local coordinates, until all the coordinates based on relative distances are obtained. Simulation results showed that this can effectively mitigate the need for classical MDS in cases where the condition, that each node has a minimum of  unique distance measurements to nodes that satisfies the same condition, is met, where
unique distance measurements to nodes that satisfies the same condition, is met, where  is the total number of dimensions. This condition is more easily met when the total number of sensors is high compared to the number of dimensions which is usually only up to 3 in a Euclidean space.
is the total number of dimensions. This condition is more easily met when the total number of sensors is high compared to the number of dimensions which is usually only up to 3 in a Euclidean space.
The focus of this work is on a majorization-MDS algorithm for the relative localization of underwater sensors, or nodes, by using only incomplete inter-node distance measurements, given no other a priori information. Central to this approach is the application of classical-MDS using approximated distances in replacement of missing pairwise distances for obtaining the initial estimates of coordinates for the majorization algorithm. This is shown to be effective in avoiding local minima, and mitigates the need for multiple restarts with different sets of random estimates.
3. A Weighted and Iterative Minimization Approach
Iterative majorization, a term coined by Heiser [11], is a minimization method formulated in the field of geometric data representation [10, 18], and can be applied to multidimensional scaling [19, 36]. One of the attractive features of this algorithm is that a non-increasing sequence of function values are yielded, implying a quick and guaranteed convergence. However, it is worth noting that the algorithm does not necessarily converge at the global minimum. On the contrary, the point of convergence would, in most cases, be at a local minimum [37], hence the importance of having an effective approach to find the global minimum when applying this algorithm.
The sensor nodes are assumed to be stationary, or drifting at such a rate that the change in position during localization is negligibly small. Nodes are also assumed to have protocols to broadcast their presence to the other nodes, to perform mutual ranging measurements, and to share their range measurements with the other nodes. This assumption does not reduce the practicality of the algorithm proposed herein. In its simplest form, this can be based on a classical time-division protocol, where nodes broadcast their ID and any known pairwise measurements before performing ranging measurements to any previously unknown nodes, and repeating the process several times. Time-slots can be uniquely allocated based upon each node's unique ID [38], while the slot length is defined in order to mitigate the need for strict time-synchronization across all the nodes. Optimized distributed protocols can be found in [33, 39].
3.1. Problem Formulation
Relative-localization involves calculating a set of relative coordinates in the relevant dimensions of the Euclidean space for all the nodes within a cluster, such that their corresponding pairwise distances closely match the measured pairwise distances. Given  number of sensor nodes, the coordinates of these nodes are represented by an
number of sensor nodes, the coordinates of these nodes are represented by an  matrix X where
matrix X where  is the number of dimensions. The pairwise distance between any two nodes is a function of the set of coordinates
is the number of dimensions. The pairwise distance between any two nodes is a function of the set of coordinates  , and for a Euclidean space can be expressed as
, and for a Euclidean space can be expressed as

where  is the pairwise distance between nodes i and j, calculated using their respective m dimensional coordinates. The elements
is the pairwise distance between nodes i and j, calculated using their respective m dimensional coordinates. The elements  form a symmetrical
form a symmetrical  pairwise distance matrix, D. Similarly, the measured distances between nodes
pairwise distance matrix, D. Similarly, the measured distances between nodes  and
and  ,
,  , form a symmetrical pairwise distance matrix
, form a symmetrical pairwise distance matrix  . The mismatch between the measured distances and those which are calculated for the approximated coordinates
. The mismatch between the measured distances and those which are calculated for the approximated coordinates  can be expressed as
can be expressed as

where  is the weighting for the distance between node
is the weighting for the distance between node  and
and  that corresponds to element (i, j) in both the matrices
that corresponds to element (i, j) in both the matrices  and D. The condition of
and D. The condition of  denotes the elements in the upper triangle of the symmetrical matrices. The weightings are normalized to values between 0 and 1 where a 0 represents a missing distance measurement. The function σ is commonly referred to as the stress function in related literatures [40]. The remaining task is to approximate the coordinates of the nodes,
denotes the elements in the upper triangle of the symmetrical matrices. The weightings are normalized to values between 0 and 1 where a 0 represents a missing distance measurement. The function σ is commonly referred to as the stress function in related literatures [40]. The remaining task is to approximate the coordinates of the nodes,  , such that the value of
, such that the value of  is minimized.
is minimized.
3.2. Classical-MDS
When all the pairwise distance measurements are available, classical-MDS offers a solution without iterative computations. Using the matrix  , the computation steps for classical-MDS [16, 24] are given as follows.
, the computation steps for classical-MDS [16, 24] are given as follows.
-
(1)
Calculate a covariance matrix, Z, from the square of the distance matrix,
 by multiplication with centring matrices, producing a centred matrix
by multiplication with centring matrices, producing a centred matrix  where
where 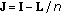 , I is an identity matrix of size
, I is an identity matrix of size  , and L is a square matrix of ones of size n.
, and L is a square matrix of ones of size n. -
(2)
Compute the eigenvalues,
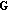 , and eigenvectors, Q, by applying eigen-decomposition on
, and eigenvectors, Q, by applying eigen-decomposition on  .
. -
(3)
The approximated coordinates,
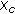 , is then given by
, is then given by 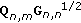 where
where 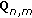 is the first
is the first 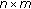 elements of
elements of  , while
, while  is the first
is the first 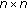 elements of
elements of 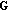 that usually correspond to the non-negative eigenvalues in the diagonal.
that usually correspond to the non-negative eigenvalues in the diagonal.
3.3. Iterative Majorization Initiated by Approximated Classical-MDS
If some of the pairwise range measurements cannot be obtained, for example as a result of obstruction to the line-of-sight, then the measured pairwise distance matrix  will be incomplete (in which the elements
will be incomplete (in which the elements  that correspond to the unavailable measurements are 0). In such cases, the function in (2) can be iteratively minimized by updated approximations of
that correspond to the unavailable measurements are 0). In such cases, the function in (2) can be iteratively minimized by updated approximations of  . This is achieved by using a majorization function that satisfies a chain of inequality towards the stress function, resulting to new approximations of
. This is achieved by using a majorization function that satisfies a chain of inequality towards the stress function, resulting to new approximations of  that yield a smaller value for the stress function. The derivation of the majorization function is well documented in [36]. For the purpose of clarity in describing the proposed modifications, the usual procedures of the algorithm are herein described.
that yield a smaller value for the stress function. The derivation of the majorization function is well documented in [36]. For the purpose of clarity in describing the proposed modifications, the usual procedures of the algorithm are herein described.
-
(1)
Set the weights
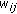 corresponding to the
corresponding to the 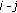 pairwise distances, using 0 for missing measurements and 1 otherwise, or, if a priori knowledge is available to provide indication towards the relative levels of confidence in the measurements, positive ratios of up to 1 are allocated.
pairwise distances, using 0 for missing measurements and 1 otherwise, or, if a priori knowledge is available to provide indication towards the relative levels of confidence in the measurements, positive ratios of up to 1 are allocated. -
(2)
Initialize
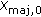 to a set of random coordinates, and the number of iterations,
to a set of random coordinates, and the number of iterations,  , then calculate
, then calculate 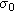 using (2).
using (2). -
(3)
Calculate an update for
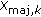 by using the relationship:
by using the relationship: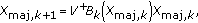 (3)
(3) -
where
 ,
,  is a matrix with elements
is a matrix with elements 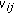 formed from the allocated weightings such that
formed from the allocated weightings such that  if
if 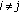 and
and 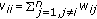 for the diagonal elements. Recall that L is a square matrix of ones of size n.
for the diagonal elements. Recall that L is a square matrix of ones of size n.  contains elements
contains elements  calculated in the following manner:
calculated in the following manner: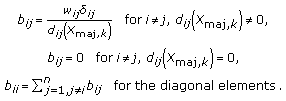 (4)
(4) -
(4)
Calculate s k+1 and repeat from step 3 if
 , where
, where 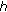 is an arbitrarily small positive constant acting as a threshold beyond which is indicative of a convergence, or if
is an arbitrarily small positive constant acting as a threshold beyond which is indicative of a convergence, or if 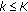 , where
, where 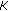 is the maximum number of iterations allowed. Otherwise, the relative locations are given by the coordinates in
is the maximum number of iterations allowed. Otherwise, the relative locations are given by the coordinates in  . The corresponding distance matrix is
. The corresponding distance matrix is  . The value of
. The value of 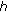 can be set as
can be set as  , such that it is suitably small to indicate that any further iterations yield negligible minimisation of the error parameter s, hence no further improvements to the estimate of relative positions.
, such that it is suitably small to indicate that any further iterations yield negligible minimisation of the error parameter s, hence no further improvements to the estimate of relative positions.
3.4. Algorithm Optimization
A common method to optimise the iterative algorithm in Section 3.3 is to apply multiple restarts (i.e., performing the complete iterative algorithm repetitively) using different sets of random initial coordinates in order to avoid local minima. This may be computationally intensive for embedded processors on deployable nodes, which usually implies greater power consumption. An alternative method is herein proposed for mitigating random restarts, and is shown in Section 4 to have comparable performance but with a significant reduction in computation requirement.
Central to the proposed approach is the observation that, albeit with poor results, classical-MDS can be performed on a distance matrix with missing measurements. One may choose to obtain a relatively inaccurate, but rapid, approximation of the missing measurements by taking the mean of available pairwise distances corresponding to both  and
and  nodes (i.e., mean of available measurements across the rows of
nodes (i.e., mean of available measurements across the rows of  and
and  ). The algorithm of classical-MDS described in Section 3.2 can be applied to
). The algorithm of classical-MDS described in Section 3.2 can be applied to  , but
, but  is set to
is set to  so that
so that  is a set of coordinates in a larger number of dimensions than the Euclidean space. By principle component analysis [41], one then notes that the columns of
is a set of coordinates in a larger number of dimensions than the Euclidean space. By principle component analysis [41], one then notes that the columns of  that have larger values of standard deviations would represent the more principal axes, or dimensions, in the data. It is then possible to discard the dimension with the least standard deviation, recalculate an updated distance matrix, and obtain a new
that have larger values of standard deviations would represent the more principal axes, or dimensions, in the data. It is then possible to discard the dimension with the least standard deviation, recalculate an updated distance matrix, and obtain a new  with a smaller number of dimensions, until the coordinates in 3-dimensional space are obtained. This is applicable because distance measurements corresponding to the Euclidean space are often restricted to within 2 or 3 dimensions, such that
with a smaller number of dimensions, until the coordinates in 3-dimensional space are obtained. This is applicable because distance measurements corresponding to the Euclidean space are often restricted to within 2 or 3 dimensions, such that  . However, the final result is often a few orders of magnitude inferior to the results obtained from iterative majorization with multiple restarts. This is because some useful information in the discarded axes is inevitably lost during dimensionality reduction.
. However, the final result is often a few orders of magnitude inferior to the results obtained from iterative majorization with multiple restarts. This is because some useful information in the discarded axes is inevitably lost during dimensionality reduction.
A more robust approach therefore is to merge this technique with the iterative majorization algorithm, such that the coordinates  can be used as the initial estimates for the iteration. The complete steps are described as follows.
can be used as the initial estimates for the iteration. The complete steps are described as follows.
-
(1)
Obtain rapid approximations of the missing pairwise distances using simple averaging for available measurements corresponding to the pair of nodes, yielding
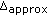 .
. -
(2)
Perform classical-MDS on
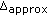 to obtain
to obtain 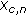 such that the coordinates have
such that the coordinates have  number of dimensions.
number of dimensions. -
(3)
Set
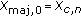 and perform the majorization algorithm in Section 3.3 using the original
and perform the majorization algorithm in Section 3.3 using the original 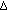 and corresponding weightings.
and corresponding weightings. -
(4)
Upon convergence, calculate a new set of distances,
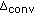 , by using
, by using 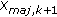 .
. -
(5)
Perform classical-MDS on
 with
with 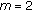 or 3 depending on the desired number of dimensions.
or 3 depending on the desired number of dimensions. -
(6)
Using the obtained
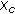 as initial estimates, perform the majorization algorithm to obtain the final coordinates. The corresponding distance matrix is
as initial estimates, perform the majorization algorithm to obtain the final coordinates. The corresponding distance matrix is 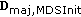 .
.
To distinguish between the two approaches, this approach is named as MDSInit while the random multiple restart approach is named as RandInit. The results from a parametric study comparing MDSInit and RandInit are shown in Section 4.
3.5. Issues Related to Underwater Sound Propagation
There are two issues related to underwater sound propagation that have a direct impact on the measurement of pairwise distances. The first is the estimation of sound velocity. The distances are usually obtained from the time or time-delay-of-arrival measurements using an estimated sound velocity. However, this estimated velocity may contain an error if the sound speed profile is not measured prior to localization of the assets. By making the assumption that the estimated velocity is the velocity at the corresponding depth of the node, the error can be compensated using a simple scaling factor. However, the accurate scaling factor cannot be directly optimized using the implied distances because the actual path of sound propagation is usually greater than the shortest Euclidean internode distance assumed by MDS algorithms, which leads to the second issue.
The refraction experienced by a sound wave is proportional to the gradient of velocity with respect to depth. Although the modelling of the precise path is more involved, it is possible to approximate a relationship between the shortest distance and the non-linear path using the Ray theory [42], which in the underwater environment is applicable for higher frequencies of a few kHz and above. This is applicable for underwater modems that have effective range of up to a few kilometres, hence operating within a relatively high frequency band, typically from 2 to 20 kHz. If the operating environment is assumed to have a depth of not more than 100 m, the velocity gradient can be treated as quasi-constant such that there is no significant fluctuation in the underlying trend [43]. This is usually representative of shallow coastal waters, and may not encapsulate all possible deployment environments for underwater sensor networks. Given this assumption, the non-linear path then becomes an arc of curvature for a circle with a radius r as shown in Figure 1, expressed as (by Snell's law):

where  is the velocity of sound corresponding to the depth of the source, g is the gradient of the velocity variation, and
is the velocity of sound corresponding to the depth of the source, g is the gradient of the velocity variation, and  is the launch angle of the ray. The relationship between the length of the refracted ray, s, and the shortest distance a can be stated as (by trigonometry of an isosceles triangle):
is the launch angle of the ray. The relationship between the length of the refracted ray, s, and the shortest distance a can be stated as (by trigonometry of an isosceles triangle):

As an example, if the ray is horizontally launched by a node at 50 m depth, and the velocity profile has a gradient of 2 ms-1/100 m, the relationship between ( ) and s is shown in Figure 2, indicating that for the assumed environment, the error introduced by sound refraction is mild for ranges under 4000 m. With time-delay-of-arrival measurements, this error is doubled due to the two-way propagation path.
) and s is shown in Figure 2, indicating that for the assumed environment, the error introduced by sound refraction is mild for ranges under 4000 m. With time-delay-of-arrival measurements, this error is doubled due to the two-way propagation path.
Compensating for this error requires the availability of sound velocity profile data during localisation. Figure 2 shows that in very shallow water environments with relatively benign velocity profiles and short ranges (i.e., under 4000 m), the error caused by sound refraction is relatively small (i.e., 0.02% of the range) compared to the ambiguity errors that are potentially introduced by a large percentage of missing pairwise distances (typically in the order of 10 to 20% of range). Another common compensation approach is by using a set of available anchor points of which the precise coordinates, and hence shortest inter-node distances, are used to predict a best-fit velocity profile by matching against ranging measurements. These anchor points are also used for mapping the relative locations onto geo-coordinates by using m-axis vector translations along with  -axis rotations.
-axis rotations.
It must be noted that the nonlinearity of the propagation path is only insignificant in very shallow waters where the variation of sound velocity with respect to depth is small. However, this assumption is no longer valid in deeper waters, and therefore, it is important in such cases to compensate for the associated errors. An effective numerical solution is presented by Berger et al. [44] that evaluate and compensate for the stratification effect of the depth-dependent sound velocity by using only the depth and sound velocity profile information, and allows for noisy (Gaussian) time-of-arrival and depth measurements.
3.6. Weighting Matrix
The weighting matrix can be used to set the level of influence exerted by the corresponding distances in the outcome of the algorithm. Intuitively, the weightings are a representation of confidence in the measured data, and with the appropriate levels that best matches the actual underpinning conditions, one seeks to obtain an optimal weighting matrix that produces the relative locations with the smallest error. A priori data can be used to guide the allocation of weighting. As an example, if a modem is known to produce an error that is proportional to the measured distance, then one would penalise the weighting for a larger distance measurements. Such information can also come from detailed channel modelling for a known environment. Without a priori data, the estimation of an optimal weighting matrix relies heavily on the availability of statistical information that can be extracted from the measured data.
With both time-of-arrival measurements and time-delay-of-arrival measurements, it is possible to obtain multiple measurements, and adjust the weighting based upon the standard deviations of these repetitive measurements, such that data with large standard deviations are allocated smaller weights. This assumes that the error influencing the deviations has a nonzero mean. Otherwise, taking the average of a sufficiently large number of repetitive measurements would give a similarly confident result. In the case of time-of-arrival measurements, the difference between the measurements in opposite directions provides an indicator to the bias in the distance measurement. For the acoustic experiments detailed in Section 5, the wind speed was estimated using the differences in time-of-arrival measurements, and the weighting matrix is adjusted based upon the standard deviations of repetitive measurements.
4. Parametric Simulations
Simulations were carried out in order to obtain a comparison between the initialization approaches. The approach of using MDS and dimensionality reduction to initialize points is named as MDSInit, while RandInit denotes the use of multiple sets of random initial points.
The environment was a 10000  10000
10000  3000 m 3-D space. As the purpose of the simulation is to carry out a parametric and comparative study of the algorithms within a 3-D space, using a very shallow environment (i.e.,
3000 m 3-D space. As the purpose of the simulation is to carry out a parametric and comparative study of the algorithms within a 3-D space, using a very shallow environment (i.e.,  100 m depth) would reduce the dimensionality problem to a 2-D approximation. A number of nodes,
100 m depth) would reduce the dimensionality problem to a 2-D approximation. A number of nodes,  , were randomly placed in this environment with uniform probability on all 3 axes. It is usually desirable for underwater sensors to be deployed on the sea-bed with sensing elements buoyed to known depths. However, given a priori knowledge of sensor depth and a relatively flat sea-bed, the 3-D MDS problem becomes reducible. The random placement of the sensor in the depth dimension simulates the unknown variation of depth amongst the sensors, and can be reasonably assumed to be a superset of the equi-depth and known-depth scenarios.
, were randomly placed in this environment with uniform probability on all 3 axes. It is usually desirable for underwater sensors to be deployed on the sea-bed with sensing elements buoyed to known depths. However, given a priori knowledge of sensor depth and a relatively flat sea-bed, the 3-D MDS problem becomes reducible. The random placement of the sensor in the depth dimension simulates the unknown variation of depth amongst the sensors, and can be reasonably assumed to be a superset of the equi-depth and known-depth scenarios.
The majorization algorithm was performed using both the MDSInit and RandInit approaches. After obtaining the relative coordinates, the inter-node distances were calculated and compared to the inter-node distances from the actual coordinates. The elapsed processing time was also logged. This was then repeated with an increasing percentage of missing pairwise distances. The distances were removed in the order of their magnitude, such that the largest distances are first removed, until the required level is reached. The number of random multiple restart allowed for RandInit is limited to 50, from which the solution with the lowest stress function value was selected. The results are shown in Figures 3–6. It is worth noting that the scale on the  -axis of the figures have been adjusted in order to give a better visual comparison. Any off-the-chart points, with values beyond the maximum on the
-axis of the figures have been adjusted in order to give a better visual comparison. Any off-the-chart points, with values beyond the maximum on the  -axis, are considered to be the point at which the corresponding percentages of missing distances become large enough to contribute to significant performance degradation.
-axis, are considered to be the point at which the corresponding percentages of missing distances become large enough to contribute to significant performance degradation.
Each data-point of the simulation results is obtained by averaging over 10 random geometrical configurations. This relatively small number of random trials contributed to the non-smoothness in the data, but this sufficiently illustrates the trend of relationship between the parameters. Figure 3 shows the result under ideal measurement conditions, while Figure 4 shows the result where the distances are corrupted with Gaussian noise of zero mean and 5 m standard deviation. Both the MDSInit and RandInit approaches are shown to have comparable minimization performance in terms of error from the actual distances, while the MDSInit approach has a lower tolerance to incomplete pairwise distances. Where the distances are corrupted by Gaussian noise (Figure 4(a)), the error performance is dominated by the noise, demonstrating that the error performance is very similar in both approaches. The spikes in the error charts are due to a node's coordinate being resolved inaccurately, hence biasing the average error. As the missing pairwise measurements are those with the furthest distances, this occurred in the random arrangements where a single node was located much further away than the rest of the nodes, hence sharing most of the missing distances. This is verified by the results in Figure 5 obtained using ideal distance measurements, but with distances set to missing in a random manner as opposed to the largest distances. When missing distances are set as missing in a random manner, there is a smaller probability that any one node would suffer a much higher loss of measurements, hence the higher missing pairwise tolerances in both the approaches.
The simulation results also demonstrate that the processing time for the RandInit approach is significantly longer. Where a 50-time multiple restart was applied, the RandInit approach provided consistent error performance and outperformed the MDSInit approach in terms of missing-pairwise tolerance, at the expense of a processing time that is up to 20 times longer. Figure 6 shows that when the number of multiple restarts was reduced to 15, the empirical level at which both the error performance and missing pairwise tolerance is comparable, the processing times were reduced to a level of up to 3 times longer.
5. Acoustic Field Trial
A practical demonstration of the localisation capabilities of a partially interconnected set of sensors was conducted during June 2009. A blustery, humid day was deliberately chosen to provide anisotropic propagation velocity conditions. The sensors were located on an undulating site to provide a 3D topography. This site was chosen to be adjacent to a road and under an airport flight path in order to provide intermittent noise conditions. Finally, high buildings surrounded two sides of the site in order to provide extreme multipath propagation conditions. Photographs of the site and equipment setup are shown in Figure 7.
Twelve microphones were located at positions previously determined using a survey-grade, carrier-phase-tracking global positioning satellites (GPS) receiver, as shown in Figure 8. Five of these microphones were colocated with a projector, whilst a roving projector was manually moved to the remaining seven microphone positions. Each projector was sequentially excited by a Hann weighted, linear frequency modulated sinusoid sweeping the band from 0 Hz to 16 kHz in 5.26 seconds. The receiver consisted of a bilaterally weighted matched filter providing a processing gain of some 46 dB against white noise. However, the coloured traffic-noise environment and blustery conditions typically resulted in a processing gain varying from 20 to 35 dB.
A constant probability of false alarm (CFAR) detector [45, 46] was used to automatically detect the occurrence of the direct-blast originating from the projectors. This consisted of a 30 ms noise-estimation window and a 2 ms signal-estimation window, separated by a guard-band of 1 ms. A 20 dB detection threshold was applied in order to reduce the false alarm rate. A typical matched filter output is shown in Figure 9, this shows that the direct blast is frequently of smaller amplitude than the multipath reverberation from the adjacent buildings and that the reverberation decays as an inverse square law. This is often associated with the adverse propagation conditions in the vicinity of the air-ground interface resulting from wind-shear and thermal profiles and unpredictable phase-changes [47]. A dynamic range of received signal strength in excess of 60 dB was encountered during the experiment.
Both the microphones and projectors have dimensions that are large in terms of wavelengths at the higher operating frequencies and thus become directional. The identification of the direct blast becomes virtually impossible under noise- and reverberation-limited conditions, resulting in a random selection of a multipath, as shown in Figure 10.
Under such circumstances, the approach adopted was to determine the cumulative distribution function and to place more confidence in results with tightly clustered distributions. The zero-mean range estimate ensemble average of the cumulative distribution functions from fifty six available sensor pairs is illustrated in Figure 11. The limit of the shaded area equates to one standard deviation from the mean. It will be noted that the standard deviation of the majority of range estimates is less than 1 m. With a temperature of 2 C, the wind-free sound velocity is estimated as 345 ms-1.
C, the wind-free sound velocity is estimated as 345 ms-1.
The standard deviation of the range estimates may be used to compute a scoring matrix for use within the MDS algorithm, as shown in Figure 12. The value of the scoring matrix is calculated from  , where
, where  and
and  represent the standard deviation of a sensor pair range estimate and the peak standard deviation of all the sensor pair range estimates, respectively. Values of unity are associated with sensor-pairs with a low standard deviation. Where a higher value of standard deviation is encountered, or associated with the random selection of a multipath, a low score is returned and this measurement has less impact on the position estimation algorithm.
represent the standard deviation of a sensor pair range estimate and the peak standard deviation of all the sensor pair range estimates, respectively. Values of unity are associated with sensor-pairs with a low standard deviation. Where a higher value of standard deviation is encountered, or associated with the random selection of a multipath, a low score is returned and this measurement has less impact on the position estimation algorithm.
The range estimates can also provide information about the anisotropic propagation velocities by considering the difference between elements mirrored by the leading diagonal of the range estimation matrix. This may be directly mapped back to wind speed and direction. A display of wind vectors derived from sensor pair measurements is shown in Figure 13. The centre of each cluster of vectors corresponds to the microphone position. The average length of the vectors varies significantly across the site because some microphones were nestling in hollows and were well shielded from the wind, whilst others were mounted on stands of typical height 1 m and placed in positions exposed to prevailing wind conditions.
The averaged wind speed across the sensor field was estimated as 1.94 m/s (7 km/hr) and a heading of 160 degrees. This compares with the meteorological wind speed measured on the day of 19 km/hr from the North East direction, obtained from the nearest weather station at an airport about 12 km away. Therefore, the wind speed on the experimental site varied due to local conditions such as the presence of urban landscapes. The wind speed estimate was obtained from the difference between the time-delay measurements in opposite directions, a method applicable only when using time-of-arrival measurements.
The estimated ranges formed a 12  12 distance matrix,
12 distance matrix,  . The actual distances as surveyed by GPS was stored in matrix
. The actual distances as surveyed by GPS was stored in matrix  and was only used to calculate errors of the final results from the algorithms. The error-per-node was calculated by taking the average of the absolute difference between
and was only used to calculate errors of the final results from the algorithms. The error-per-node was calculated by taking the average of the absolute difference between  and
and  . Both the RandInit and MDSInit algorithms as detailed in Sections 3.3 and 3.4, respectively, were applied on the estimated ranges. The estimated ranges were first processed with a unity weighting matrix such that
. Both the RandInit and MDSInit algorithms as detailed in Sections 3.3 and 3.4, respectively, were applied on the estimated ranges. The estimated ranges were first processed with a unity weighting matrix such that  equals to 1 for available distance entries or 0 otherwise, over an increasing percentage of missing pairwise distances, chosen from the larger distances. This was then repeated with randomly chosen missing pairwise distances. The results are shown in Figures 14 and 15, respectively.
equals to 1 for available distance entries or 0 otherwise, over an increasing percentage of missing pairwise distances, chosen from the larger distances. This was then repeated with randomly chosen missing pairwise distances. The results are shown in Figures 14 and 15, respectively.
It can be observed that the results are comparable with the prediction from the simulation study. The error performance is dominated by external factors such as varying wind conditions and the presence of bursty noise associated with the traffic. Therefore, the error performances of both the RandInit and MDSInit approaches are almost identical. Where the missing distances are set with largest distances, the tolerance to the level of missing distances is significantly lower as the error from the furthest node increases the average error.
The data were then processed by using a nonuniform weighting matrix that was scored in an inversely proportional manner to the standard deviation of the measured data. The results are shown in Figures 16 and 17.
The improvement in error performance from the use of an adjusted weighting matrix is minimal. This is because the algorithm is minimizing the error between the distance matrix of the estimated relative coordinates and the measured distance matrix. Figure 18 shows the final stress values in the MDSInit approach for both uniform weighting and adjusted weightings, demonstrating lower stress values (as expressed in (2)) for the adjusted weightings across all the levels of missing pairwise distances. The lower stress value indicates that the adjusted-weighting yields estimates that better fit the measured distances. Figure 19 shows the individual errors of the pairwise distances with respect to the actual distances, highlighting the fact that the average error per node can be biased due to the failure to resolve the relative location of a small number of nodes in the cluster.
The average wind speed estimate, as shown in Figure 13, can be used to build a compensation matrix for the resolved distances. By using the matrix dot product, the variation in sound velocity experienced by the path between any pair of nodes can be calculated. Figure 20 shows that the error from the actual distances is reduced when the velocity compensation matrix is applied based upon the average value of 1.94 m/s with a 160 degree heading. Both were processed with the MDSInit approach using adjusted weighting. Where all distance measurements are available, the average error per node from actual, GPS-surveyed, distances is 0.2 m. It is worth noting that the GPS survey data has a standard deviation of about 0.05 m, while the co-location of the projector and microphone has an ambiguity of approximately 0.03 m.
For completeness, the relative coordinates are mapped onto the reference coordinate shown in Figure 8. Three anchor points are chosen arbitrarily (nodes 1, 2, and 3) and the coordinate transformation matrix involving a 3-axes translation and a 3-axes rotation is derived using Nelder-Mead minimization [48]. Figure 21 shows the mapped coordinates of the nodes for different percentages of missing largest distances.
Mapped node positions with respect to actual surveyed positions using anchor nodes 1, 2, and 3. Circles are actual surveyed positions, crosses are positions resolved with complete set of pairwise distance, triangle are resolved with 10% largest distance missing, while asterisks are resolved with 20% largest distance missing.
6. Scope of Study
The proposed algorithm inherently seeks the points that best fit the measured distances. In most realistic scenarios, the measured distances will contain some errors from the actual distances. It was shown that compensating the bias in sound velocity using the estimated wind vector reduces the error between the estimated distances and the actual distances. Similarly, in underwater applications where the sound velocity profile is available, the refraction path can be estimated to produce an adjustment matrix for the estimated distances. Also, the actual distances between available anchor nodes can be used to evaluate the reliability of the measured distances. More involved research related to the area of optimising the fit between the estimated and actual distances using information from anchor points can be found in [49, 50].
The relative-localization problem considered in this article is for a cluster of node, but the solution is not necessarily restricted to a single-hop cluster. In a distributed, multi-hop arrangement of underwater nodes, relative-localization is usually reduced to the local positioning of a cluster of nodes with local anchor points, before iteratively optimizing the relative positions between the clusters. Therefore, the incomplete pairwise distance matrix can be considered as an irreducible matrix from a larger, global distance matrix for a distributed network of nodes.
A theoretical analysis on the performance constraints of relative location estimation as a function of the number of links to an anchor node and the total number of unanchored nodes is documented in [51].
Although the acoustic environment in which the experimental trial was conducted was also affected by ambient noise, multipath signal arrivals, and wind distortions, there are, nevertheless, notable differences from the underwater environment. The spectral characteristics of the ambient noise differ between the air-acoustic and the underwater environment. In the experiment, the main sources of ambient noise were from the nearby traffic. In the underwater environment, the performance-limiting ambient noise may originate from various sources local shipping in coastal waters, organisms such as snapping shrimps in tropical waters, and breaking waves. In both cases, the ambient noise would be expected to have non-stationary statistical characteristics. In terms of multipaths, reflections came from the buildings as well as the ground in the experimental environment, whilst in the underwater environment there are sea surface and sea bed reflections as well as multipaths from refractive spreading. The experimental environment is relatively homogeneous, and therefore gave rise to negligible refraction. The same is only valid in a very shallow water environment.
7. Conclusions
A robust approach for relative location estimation is presented, based upon a minimization method known as iterative majorization, which allows the estimation of relative coordinates using an incomplete pairwise distance matrix. An optimized initialization approach is proposed which demonstrated comparable minimization performance while requiring approximately 20 times less computing cycles.
It is shown that for underwater applications, sound refraction can contribute to the error between the measured and actual distances. However, in relatively shallow waters where the sound velocity gradient is benign and for ranges under 4000 m, the difference is likely to be small, but should be taken into account if the sound velocity profile is known.
Simulation study on the proposed approach demonstrated that the tolerance to missing pairwise distance is in the region of 8% to 30% depending on the number of nodes in the cluster and the pattern of missing distances. In cases where the missing pairwise distances are the largest distances, the tolerance is lower compared to randomly missing pairwise distances. This is because the higher loss of pairwise distances at the furthest nodes leads to failure to resolve their positions.
An acoustic field trial was carried out to evaluate the proposed algorithm. The results demonstrated that the application of a weighting function adjusted by the standard deviation of the observed data optimizes the fit between the estimated and measured distances, while the improvement in fit between the estimated and actual distances is much smaller. The estimated distances are then corrected using an estimate of the wind vector to calculate the variation from wind-free sound velocity during the trial. This leads to an observed reduction in the error of the estimated distances. The error performance and tolerance to missing pairwise distances of both approaches, as well as the significant reduction in processing time of the proposed approach are similarly demonstrated with the field trial measurements. Finally, the relative coordinates of the nodes are also mapped onto the reference coordinate of the site, showing good agreement with the actual nodes' positions as surveyed by a carrier-phase-tracking GPS. Although both the simulation and experimental field trial results provided an indication to the practicality and robustness of the proposed algorithm in the context of optimising the process of relative positioning using incomplete distance measurements, it is worth noting that a direct extrapolation to predict its performance in an underwater environment is still constrained by variables that are not herein considered due the fundamental difference between the air-acoustic and the underwater environment.
References
Freitag L, Grund M, Singh S, Johnson M: Acoustic communication in very shallow water: results from the 1999 AUV fest. Proceedings of the IEEE Oceans Conference and Exhibition (OCEANS '00), 2000 3: 2155-2160.
Kilfoyle DB, Baggeroer AB: The state of the art in underwater acoustic telemetry. IEEE Journal of Oceanic Engineering 2000, 25(1):4-27. 10.1109/48.820733
Heidemann J, Ye W, Wills J, Syed A, Yuan L: Research challenges and applications for underwater sensor networking. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '06), 2006 1: 228-235.
Johnston G: Long term underwater positioning technologies for the offshore oil and gas industry. Proceedings of IEEE Oceans Europe (OCEANS '07), June 2007 1-4.
Sozer EM, Stojanovic M, Proakis JG: Underwater acoustic networks. IEEE Journal of Oceanic Engineering 2000, 25(1):72-83. 10.1109/48.820738
Rice J, Green D: Underwater acoustic communications and networks for the us navy's seaweb program. Proceedings of the 2nd International Conference on Sensor Technologies and Applications, August 2008 715-722.
Solomon ISD, Knight AJ, Greening MV: Sonar array signal processing for sparse linear arrays. Proceedings of the 5th International Symposium on Signal Processing and Its Applications (ISSPA '99), August 1999 2: 527-530.
Partan J, Kurose J, Levine BN: A survey of practical issues in underwater networks. Mobile Computing and Communications Review 2007, 11(4):23-33. 10.1145/1347364.1347372
Chitre M, Shahabudeen S, Stojanovic M: Underwater acoustic communications and networking: recent advances and future challenges. Marine Technology Society Journal 2008, 42(1):103-116. 10.4031/002533208786861263
de Leeuw J, Heiser WJ: Convergence of correction matrix algorithms for multidimensional scaling. In Data, Expert, Knowledge and Decisions. Edited by: Gaul W, Schader M. Springer, Berlin, Germany; 1977:329-340.
Heiser WJ: Convergent computation by iterative majorization: theory and applications in multidimensional data analysis. In Recent Advances in Descriptive Multivariate Analysis. Edited by: Krzanowski WJ. Oxford University Press, Oxford, UK; 1995:157-189.
Chandrasekhar V, Seah WKG, Choo YS, Ee HV: Localization in underwater sensor networks—survey and challenges. Proceedings of the 1st ACM International Workshop on Underwater Networks (WUWNet '06), 2006 2006: 33-40.
Chitre M, Potter J, Ong SH: Underwater acoustic channel characterisation for medium-range shallow water communications. Proceedings of the IEEE/MTS Oceans Conference, November 2004 1: 40-45.
Weston DE, Horrigan AA, Thomas SJL, Revie J: Studies of sound transmission fluctuations in shallow coastal water. Philosophical Transactions for the Royal Society of London. Series A 1969, 265(1169):567-606. 10.1098/rsta.1969.0066
Eckart C, Young G: The approximation of one matrix by another of lower rank. Psychometrika 1936, 1(3):211-218. 10.1007/BF02288367
Torgerson WS: Multidimensional scaling: theory and method. Psychometrika 1952, 17: 401-419. 10.1007/BF02288916
Shang Y, Ruml W, Zhang Y, Fromherz MPJ: Localization from mere connectivity. Proceedings of the 4th International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '03), June 2003 201-212.
De Leeuw J: Convergence of the majorization method for multidimensional scaling. Journal of Classification 1988, 5(2):163-180. 10.1007/BF01897162
Groenen PJF: The Majorization Approach to Multidimensional Scaling: Some Problems and Extensions. DSWO Press, Leiden, The Netherlands; 1993.
Bulusu N, Heidemann J, Estrin D: GPS-less low-cost outdoor localization for very small devices. IEEE Personal Communications Magazine 2000, 7(5):28-34. 10.1109/98.878533
Savarese C, Rabaey J, Beutel J: Locationing in distributed ad-hoc wireless sensor networks. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '01), 2001, Salt Lake City, Utah, USA 4: 2037-2040.
Moses RL, Krishnamurthy D, Patterson RM: A self-localization method for wireless sensor networks. EURASIP Journal on Applied Signal Processing 2003, 2003(4):348-358. 10.1155/S1110865703212063
Patwari N, Hero AO III, Perkins M, Correal N, O'Dea RJ: Relative location estimation in wireless sensor networks. IEEE Transactions on Signal Processing 2003, 51(8):2137-2148. 10.1109/TSP.2003.814469
Cheung KW, So HC: A multidimensional scaling framework for mobile location using time-of-arrival measurements. IEEE Transactions on Signal Processing 2005, 53(2):460-470.
Garcia JE: Ad hoc positioning for sensors in underwater acoustic networks. Proceedings of the MTS/IEEE Oceans Conference (OCEANS '04), November 2004 4: 2338-2340.
Zhou Z, Cui J-H, Zhou S: Localization for large-scale underwater sensor networks. University of Connecticut, Computer Science and Engineering, Storrs, Conn, USA; 2006.
Chandrasekhar V, Seah W: An area localization scheme for underwater sensor networks. Proceedings of the MTS/IEEE Oceans Conference (OCEANS '06), May 2007 1-8 .
Cheng W, Teymorian AY, Liran M, Cheng X, Lu X, Lu Z: Underwater localization in sparse 3D acoustic sensor networks. Proceedings of the 27th Conference on Computer Communications (INFOCOM '08), April 2008 236-240.
Erol M, Vieira L, Caruso A, Paparella F, Gerla M, Oktug S: Multi stage underwater sensor localization using mobile beacons. Proceedings of the 2nd International Conference on Sensor Technologies and Applications, (SENSORCOMM '08), August 2008 710-714.
Wang C, Xiao L: Sensor localization under limited measurement capabilities. IEEE Network 2007, 21(3):16-23.
Knapp C, Carter GC: The generalized correlation method for estimation of time delay. IEEE Transactions on Acoustics, Speech, and Signal Processing 1976, 24(4):320-327. 10.1109/TASSP.1976.1162830
Ji X, Zha H: Sensor positioning in wireless ad-hoc sensor networks using multidimensional scaling. Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '04), 2004 4: 2652-2661.
Costa JA, Patwari N, Hero AO III: Distributed weighted-multidimensional scaling for node localization in sensor networks. ACM Transactions on Sensor Networks 2006, 2(1):39-64. 10.1145/1138127.1138129
Kwon YM, Mechitov K, Sundresh S, Kim W, Agha G: Resilient localization for sensor networks in outdoor environments. Proceedings of the 25th International Conference on Distributed Computing Systems (ICSCS '05), June 2005 643-652.
Birchfield ST: Geometric microphone array calibration by multidimensional scaling. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '03), April 2003 5: 157-160.
Borg I, Groenen PJF: Modern Multidimensional Scaling: Theory and Applications, Springer Series in Statistics. Springer, London, UK; 2005.
Fletcher R: Practical Methods of Optimization. Wiley-Interscience, New York, NY, USA; 1987.
Foo KY, Atkins PR, Pointer SA, Tiltman CP: Robust time-division channel access approach for an ad hoc underwater network. Proceedings of the 155th Meeting of the Acoustical Society of America, July 2008 4:
Othman AK: GPS-less localization protocol for underwater acoustic networks. Proceedings of the 5th International Conference on Wireless and Optical Communications Networks (WOCN '08), May 2008 1-6.
Groenen PJF, Heiser WJ, Meulman JJ: Global optimization in least-squares multidimensional scaling by distance smoothing. Journal of Classification 1999, 16(2):225-254. 10.1007/s003579900055
Shlens J: A tutorial on principal component analysis. In Tutorial. Center for Neural Science, New York University, New York, NY, USA; 2009. http://www.snl.salk.edu/~shlens/pca.pdf
Schroeder M: Springer Handbook of Acoustics, T. D. Rossing, Ed.. Springer, London, UK; 2007.
Urick RJ: Principles of Underwater Sound for Engineers. McGraw-Hill, New York, NY, USA; 1975.
Berger CR, Zhou S, Willett P, Liu L: Stratification effect compensation for improved underwater acoustic ranging. IEEE Transactions on Signal Processing 2008, 56(8):3779-3783.
Hansen VG, Ward HR: Detection performance of the cell averaging LOG/CFAR receiver. IEEE Transactions on Aerospace and Electronic Systems 1972, 8(5):648-652.
Nitzberg R: Analysis of the arithmetic mean CFAR normalizer for fluctuating targets. IEEE Transactions on Aerospace and Electronic Systems 1978, 14(1):44-47.
Kurze UJ, Beranek LL: Sound propagation outdoors. In Noise and Vibration Control. Edited by: Beranek LL. Institute of Noise Control Engineering, Washington, DC, USA; 1988.
Nelder JA, Mead R: A simplex method for function minimization. Computer Journal 1965, 7: 308-313.
Chan YT, Ho KC: A simple and efficient estimator for hyperbolic location. IEEE Transactions on Signal Processing 1994, 42(8):1905-1915. 10.1109/78.301830
Chen P-C: A non line-of-sight error mitigation algorithm in location estimation. Proceedings of the IEEE Wireless Communications and Networking Conference, September 1999 1: 316-320.
Shi Q, Kyperountas S, Correal NS, Niu F: Performance analysis of relative location estimation for multihop wireless sensor networks. IEEE Journal on Selected Areas in Communications 2005, 23(4):830-838.
Acknowledgments
The authors thank Mr. Zhaoyang You and Dr. Tim Collins for their contribution and assistance in the carrying out of the field trials.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Foo, K.Y., Atkins, P.R. A Relative-Localization Algorithm Using Incomplete Pairwise Distance Measurements for Underwater Applications. EURASIP J. Adv. Signal Process. 2010, 930327 (2010). https://doi.org/10.1155/2010/930327
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/930327
 by multiplication with centring matrices, producing a centred matrix
by multiplication with centring matrices, producing a centred matrix  where
where 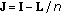 , I is an identity matrix of size
, I is an identity matrix of size  , and L is a square matrix of ones of size n.
, and L is a square matrix of ones of size n.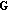 , and eigenvectors, Q, by applying eigen-decomposition on
, and eigenvectors, Q, by applying eigen-decomposition on  .
.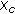 , is then given by
, is then given by 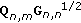 where
where 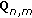 is the first
is the first 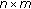 elements of
elements of  , while
, while  is the first
is the first 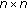 elements of
elements of 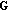 that usually correspond to the non-negative eigenvalues in the diagonal.
that usually correspond to the non-negative eigenvalues in the diagonal.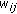 corresponding to the
corresponding to the 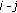 pairwise distances, using 0 for missing measurements and 1 otherwise, or, if a priori knowledge is available to provide indication towards the relative levels of confidence in the measurements, positive ratios of up to 1 are allocated.
pairwise distances, using 0 for missing measurements and 1 otherwise, or, if a priori knowledge is available to provide indication towards the relative levels of confidence in the measurements, positive ratios of up to 1 are allocated.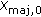 to a set of random coordinates, and the number of iterations,
to a set of random coordinates, and the number of iterations,  , then calculate
, then calculate 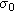 using (2).
using (2).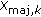 by using the relationship:
by using the relationship: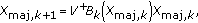
 ,
,  is a matrix with elements
is a matrix with elements 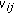 formed from the allocated weightings such that
formed from the allocated weightings such that  if
if 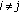 and
and 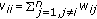 for the diagonal elements. Recall that L is a square matrix of ones of size n.
for the diagonal elements. Recall that L is a square matrix of ones of size n.  contains elements
contains elements  calculated in the following manner:
calculated in the following manner: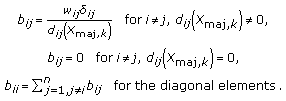
 , where
, where 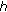 is an arbitrarily small positive constant acting as a threshold beyond which is indicative of a convergence, or if
is an arbitrarily small positive constant acting as a threshold beyond which is indicative of a convergence, or if 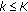 , where
, where 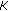 is the maximum number of iterations allowed. Otherwise, the relative locations are given by the coordinates in
is the maximum number of iterations allowed. Otherwise, the relative locations are given by the coordinates in  . The corresponding distance matrix is
. The corresponding distance matrix is  . The value of
. The value of 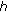 can be set as
can be set as  , such that it is suitably small to indicate that any further iterations yield negligible minimisation of the error parameter s, hence no further improvements to the estimate of relative positions.
, such that it is suitably small to indicate that any further iterations yield negligible minimisation of the error parameter s, hence no further improvements to the estimate of relative positions.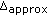 .
.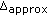 to obtain
to obtain 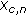 such that the coordinates have
such that the coordinates have  number of dimensions.
number of dimensions.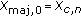 and perform the majorization algorithm in Section 3.3 using the original
and perform the majorization algorithm in Section 3.3 using the original 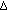 and corresponding weightings.
and corresponding weightings.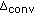 , by using
, by using 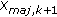 .
. with
with 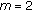 or 3 depending on the desired number of dimensions.
or 3 depending on the desired number of dimensions.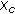 as initial estimates, perform the majorization algorithm to obtain the final coordinates. The corresponding distance matrix is
as initial estimates, perform the majorization algorithm to obtain the final coordinates. The corresponding distance matrix is 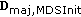 .
.



















