- Research Article
- Open access
- Published:
Time-Frequency Based Channel Estimation for High-Mobility OFDM Systems—Part II: Cooperative Relaying Case
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 973286 (2010)
Abstract
We consider the estimation of time-varying channels for Cooperative Orthogonal Frequency Division Multiplexing (CO-OFDM) systems. In the next generation mobile wireless communication systems, significant Doppler frequency shifts are expected the channel frequency response to vary in time. A time-invariant channel is assumed during the transmission of a symbol in the previous studies on CO-OFDM systems, which is not valid in high mobility cases. Estimation of channel parameters is required at the receiver to improve the performance of the system. We estimate the model parameters of the channel from a time-frequency representation of the received signal. We present two approaches for the CO-OFDM channel estimation problem where in the first approach, individual channels are estimated at the relay and destination whereas in the second one, the cascaded source-relay-destination channel is estimated at the destination. Simulation results show that the individual channel estimation approach has better performance in terms of MSE and BER; however it has higher computational cost compared to the cascaded approach.
1. Introduction
In wireless communication, antenna diversity is intensively used to mitigate fading effects in the recent years. This technique promises significant diversity gain. However due to the size and power limitations of some mobile terminals, antenna diversity may not be practical in some cases (e.g., Wireless Sensor Networks). Cooperative communication [1–3], also referred to as cooperative relaying, has become a popular solution for such cases since it maintains virtual antenna array without utilizing multiple antennas. Single-carrier modulation schemes are usually used in cooperative communication in the case of the flat fading channel [3]. A simple cooperative communication system with a source ( ), a relay (
), a relay ( ), and a destination (
), and a destination ( ) terminal is shown in Figure 1.
) terminal is shown in Figure 1.
In beyond third generation and fourth generation wireless communication systems, fast moving terminals and scatterers are expected to cause the channel to become frequency selective. Orthogonal Frequency Division Multiplexing (OFDM) is a powerful solution for such channels. OFDM has a relatively longer symbol duration than single-carrier systems which makes it very immune to fast channel fading and impulsive noise. However, the overall system performance may be improved by combining the advantages of cooperative communication and OFDM systems (CO-OFDM) when the source terminal has the above-mentioned physical limitations
As in the traditional mobile OFDM systems, large fluctuations of the channel parameters are expected between and during OFDM symbols in CO-OFDM systems, especially when the terminals are mobile. To combat this problem, accurate modeling and estimation of time-varying channels are required. Early channel estimation methods for CO-OFDM assume a time-invariant model for the channel during the transmission of an OFDM symbol, which is not valid for fast-varying environments [4, 5].
A widely used channel model is a linear time-invariant impulse response where the coefficients are complex Gaussian random variables [5]. In this work we present channel estimation techniques for CO-OFDM systems over time-varying channels. We use the parametric channel model [6] employed in MIMO-OFDM system discussed in Part I. We consider two different scenarios similar to [7]: (i)  is estimated at the relay, and
is estimated at the relay, and  is estimated at the destination individually; (ii) the cascaded channel of
is estimated at the destination individually; (ii) the cascaded channel of  and
and  , that is, the equivalent channel impulse response
, that is, the equivalent channel impulse response  is estimated at the destination terminal. Here
is estimated at the destination terminal. Here  denotes the channel response between
denotes the channel response between  and
and  ,
,  denotes the channel response between
denotes the channel response between  and
and  , and
, and  is the equivalent cascaded channel response between
is the equivalent cascaded channel response between  and
and  . Since no channel estimation is performed at the relay, this approach has the advantage in terms of computational requirement over the first one.
. Since no channel estimation is performed at the relay, this approach has the advantage in terms of computational requirement over the first one.
We will show here that the parameters of these individual as well as the cascaded time-varying channels can be obtained by means of time-frequency representations of the channel outputs.
The rest of the paper is organized as follows. In Section 2, we give a brief summary of the parametric channel model and CO-OFDM signal model. Section 3 presents time-frequency channel estimation for CO-OFDM systems via DET. In Section 4, we present computer simulations to illustrate the performance of proposed channel estimation in both scenarios mentioned above. Conclusions are drawn in Section 5.
2. CO-OFDM System Model
2.1. Time-Varying CO-OFDM Channel Model
In this paper, all channels are assumed multipath, fading with long-term path loss, and Doppler frequency shifts. Path loss is proportional to  where
where  is the propagation distance between transmitter and receiver, and
is the propagation distance between transmitter and receiver, and  is the path loss coefficient [8]. Let
is the path loss coefficient [8]. Let  and
and  are defined as relative gain factors of
are defined as relative gain factors of  and
and  links relative to
links relative to  link [7, 9]. Here,
link [7, 9]. Here,  , and
, and  denote the distances of
denote the distances of  ,
,  , and
, and  links, respectively.
links, respectively.
In this study, we use the same time-varying channel model given in Section  .2 of Part I of this series. We show here that the channel parameters between source-to-destination
.2 of Part I of this series. We show here that the channel parameters between source-to-destination  , source-to-relay
, source-to-relay  , relay-to-destination
, relay-to-destination  and the cascaded channel, and source-to-relay-to-destination
and the cascaded channel, and source-to-relay-to-destination  may all be estimated through the spreading function of the channels. Let the channel
may all be estimated through the spreading function of the channels. Let the channel  be given by
be given by

The spreading function corresponding to  is obtained by taking the Fourier transform with respect to
is obtained by taking the Fourier transform with respect to  as
as

where  is the number of transmission paths,
is the number of transmission paths,  represents the Doppler frequency shift,
represents the Doppler frequency shift,  is the relative attenuation, and
is the relative attenuation, and  is the delay in path
is the delay in path  . In beyond 3G wireless mobile communication systems, Doppler frequency shifts become significant and have to be taken into account. The spreading function
. In beyond 3G wireless mobile communication systems, Doppler frequency shifts become significant and have to be taken into account. The spreading function  displays peaks located at the time-frequency positions determined by the delays and the corresponding Doppler frequencies, with
displays peaks located at the time-frequency positions determined by the delays and the corresponding Doppler frequencies, with  as their amplitudes. In this study, we extract the individual as well as the cascaded channel information from the spreading function of the received signals at the relay and at the destination.
as their amplitudes. In this study, we extract the individual as well as the cascaded channel information from the spreading function of the received signals at the relay and at the destination.
The cascaded source-to-relay-to-destination  channel may be represented in terms of the individual channels as follows. Let the
channel may be represented in terms of the individual channels as follows. Let the  and the
and the  channels be given by
channels be given by

The equivalent impulse response of the cascaded  channel may be obtained as follows:
channel may be obtained as follows:

where  stands for convolution. After defining the parameters
stands for convolution. After defining the parameters  ,
,  ,
,  ,
,  , and
, and  , we obtain the impulse response of the cascaded
, we obtain the impulse response of the cascaded  channel as
channel as

In our second approach, instead of estimating the individual channel parameters, we obtain the equivalent  , and
, and  parameters.
parameters.
2.2. CO-OFDM Signal Model
We consider an Amplify-and-Forward (AF) cooperative transmission model where a source sends information to a destination with the assistance of a relay [3, 10]. In this model, all of the terminals are equipped with only one transmit and one receive antenna. To manage cooperative transmission, we consider a special protocol which is originally proposed in [10] and named "Protocol II". According to this protocol, total transmission is divided in two phases. In Phase I, source sends OFDM signal to both relay and destination terminals. Relay terminal amplifies the received signal in the same phase. In Phase II, relay terminal transmits the amplified signal to the destination terminal.
The OFDM symbol transmitted from the source at Phase I is given by

where  ,
,  is the length of the cyclic prefix, and
is the length of the cyclic prefix, and  is the total length of one OFDM symbol. The received signals at relay and destination suffer from time and frequency dispersion of the channels, that is, multipath propagation, fading and Doppler frequency shifts. Thus, the received signals at the relay and destination in Phase I are
is the total length of one OFDM symbol. The received signals at relay and destination suffer from time and frequency dispersion of the channels, that is, multipath propagation, fading and Doppler frequency shifts. Thus, the received signals at the relay and destination in Phase I are

where  and
and  represent the additive white Gaussian channel noise at
represent the additive white Gaussian channel noise at  and
and  channels, respectively. Here
channels, respectively. Here  represents the transmitted OFDM symbol energy. The signal
represents the transmitted OFDM symbol energy. The signal  is amplified by a factor
is amplified by a factor  at the relay and then transmitted to the destination in Phase II. The signal at the output of
at the relay and then transmitted to the destination in Phase II. The signal at the output of  channel, received by the destination terminal, is
channel, received by the destination terminal, is

Now, using the cascaded equivalent of  and
and  from (5), we get
from (5), we get

where  is the response of the
is the response of the  channel to the
channel to the  noise
noise

The receiver at the destination terminal discards the cyclic prefix and demodulates the received signals  and
and  using a
using a  -point DFTs. For example the demodulated signal corresponding to
-point DFTs. For example the demodulated signal corresponding to  is
is

If the Doppler shifts in all  channel paths are negligible,
channel paths are negligible,  for all
for all  , then the channel is almost time-invariant within one OFDM symbol, and
, then the channel is almost time-invariant within one OFDM symbol, and

where  is the frequency response of the almost time-invariant channel and
is the frequency response of the almost time-invariant channel and  is the DFT of the
is the DFT of the  . By estimating the channel frequency response coefficients
. By estimating the channel frequency response coefficients  , data symbols,
, data symbols,  , can be recovered according to (12). Estimation of the channel coefficients is usually achieved by using training symbols
, can be recovered according to (12). Estimation of the channel coefficients is usually achieved by using training symbols  , called pilots inserted between data symbols. Then the transfer function is interpolated from the responses to
, called pilots inserted between data symbols. Then the transfer function is interpolated from the responses to  by using different filtering techniques. This is called Pilot Symbol Assisted (PSA) channel estimation [11].
by using different filtering techniques. This is called Pilot Symbol Assisted (PSA) channel estimation [11].
However, in beyond 3G communication systems, fast moving terminals and scatterers are expected in the environment, causing the Doppler frequency shifts to become significant which makes the above assumption invalid. In this paper, we consider a completely time-varying model for the CO-OFDM channels where the parameters may change during one transmit symbol [12], based on the time-frequency approach.
3. Time-Varying Channel Estimation for CO-OFDM Systems
In this section we consider the estimation procedure of time-varying CO-OFDM channels  ,
,  as well as the cascaded
as well as the cascaded  channels. We approach the channel estimation problem from a time-frequency point of view and employ the channel estimation technique proposed in Part I of this series. Details on the Discrete Evolutionary Transform (DET) that we use here as a time-frequency representation of time-varying CO-OFDM channels may be found in Section
channels. We approach the channel estimation problem from a time-frequency point of view and employ the channel estimation technique proposed in Part I of this series. Details on the Discrete Evolutionary Transform (DET) that we use here as a time-frequency representation of time-varying CO-OFDM channels may be found in Section  of Part I.
of Part I.
The time-varying frequency response or equivalently the spreading function of the individual as well as the cascaded channels may be calculated by means of the DET of the received signal.
We consider two channel estimation approaches for the CO-OFDM system illustrated in Figure 1.
3.1. Individual Channel Estimation Approach
The  channel is estimated at the relay terminal, then the transmitted signal is amplified, and new pilot symbols are inserted for the estimation of
channel is estimated at the relay terminal, then the transmitted signal is amplified, and new pilot symbols are inserted for the estimation of  channel. The pilot symbols that are inserted at the source are effected by the multipath fading nature of the
channel. The pilot symbols that are inserted at the source are effected by the multipath fading nature of the  channel, as such may not be used for the estimation of
channel, as such may not be used for the estimation of  channel. Therefore, we need to insert fresh pilot symbols and extend the length of the OFDM symbol at the relay. The estimated
channel. Therefore, we need to insert fresh pilot symbols and extend the length of the OFDM symbol at the relay. The estimated  channel information is quantized and transmitted to the destination together with the data symbols. Then at the destination terminal, the
channel information is quantized and transmitted to the destination together with the data symbols. Then at the destination terminal, the  channel is estimated and used for the detection. Parameters of both
channel is estimated and used for the detection. Parameters of both  and
and  channel impulse responses are estimated according to the procedure explained in Section
channel impulse responses are estimated according to the procedure explained in Section  of Part I.
of Part I.
3.2. Cascaded Channel Estimation Approach
The relay terminal does not perform any channel estimation. The cascaded  channel is estimated at the destination terminal.
channel is estimated at the destination terminal.
The received signal  can be given in matrix form as
can be given in matrix form as

where

We ignore the additive noise in the sequel to simplify the equations. If the time-varying frequency response of the channel  is known, then
is known, then  may be estimated by
may be estimated by

Calculating the DET of  , we get
, we get

where  is the time-varying kernel of the DET transform. Comparing the above representations of
is the time-varying kernel of the DET transform. Comparing the above representations of  , we require that the kernel is
, we require that the kernel is

Finally, the time-varying channel frequency response for the  th OFDM symbol can be obtained as
th OFDM symbol can be obtained as

Calculation of  in such a way that it satisfies (17) is explained in Section
in such a way that it satisfies (17) is explained in Section  of Part I by using windows that are adapted to the Doppler frequencies.
of Part I by using windows that are adapted to the Doppler frequencies.
According to the above equation, we need the input pilot symbols  to estimate the channel frequency response. Here we consider simple, uniform pilot patterns; however improved patterns may be employed as well [11].
to estimate the channel frequency response. Here we consider simple, uniform pilot patterns; however improved patterns may be employed as well [11].
Equation (18) can be given in matrix form as

where

where  denotes a
denotes a  identity matrix. The above relation is also valid at the preassigned pilot positions
identity matrix. The above relation is also valid at the preassigned pilot positions 

where  and
and  is a decimated version of the
is a decimated version of the  . Note that
. Note that  is again the number of pilots, and
is again the number of pilots, and  is the distance between adjacent pilots. Taking the inverse DFT of
is the distance between adjacent pilots. Taking the inverse DFT of  with respect to
with respect to  and DFT with respect to
and DFT with respect to  , we obtain the subsampled spreading function
, we obtain the subsampled spreading function 

Note that, the evolutionary kernel  can be calculated directly from
can be calculated directly from  , and all unknown channel parameters can be estimated according to (21) and (22) for a time-varying model that does not require any stationarity assumption. Estimated channel parameters are used for the detection at the destination terminal according to the channel equalization algorithm presented in Section
, and all unknown channel parameters can be estimated according to (21) and (22) for a time-varying model that does not require any stationarity assumption. Estimated channel parameters are used for the detection at the destination terminal according to the channel equalization algorithm presented in Section  .2 of Part I.
.2 of Part I.
In the following, we demonstrate the time-frequency channel estimation as well as the detection performance of our approach by means of examples.
4. Experimental Results
In our simulations, a CO-OFDM system scenario with a source, a relay, and a destination terminal is considered with the following parameters: the distances  and
and  are chosen such that the relative gain ratio
are chosen such that the relative gain ratio  takes the values
takes the values  dB, where the path loss coefficient is assumed to be
dB, where the path loss coefficient is assumed to be  [7]. The angle between
[7]. The angle between  and
and  propagation paths is taken as
propagation paths is taken as  . The performance of both individual and cascaded channel estimation approaches is investigated by means of the mean square error (MSE) and the bit error rate (BER) according to varying signal-to-noise ratios. QPSK-coded data symbols
. The performance of both individual and cascaded channel estimation approaches is investigated by means of the mean square error (MSE) and the bit error rate (BER) according to varying signal-to-noise ratios. QPSK-coded data symbols  are modulated onto
are modulated onto  subcarriers to generate one OFDM symbol. 16 equally spaced pilot symbols are inserted into OFDM symbols. The
subcarriers to generate one OFDM symbol. 16 equally spaced pilot symbols are inserted into OFDM symbols. The  ,
,  , and
, and  channels are simulated randomly. For each of these channels, the maximum number of paths is set to
channels are simulated randomly. For each of these channels, the maximum number of paths is set to  where the delays and the attenuations on each path are chosen as independent, normal distributed random variables. Normalized Doppler frequency on each path is fixed to
where the delays and the attenuations on each path are chosen as independent, normal distributed random variables. Normalized Doppler frequency on each path is fixed to  [12].
[12].
The channel output is corrupted by zero-mean AWGN whose SNR is changed between  and
and  dB.
dB.
-
(1)
Individual Channel Estimation Results. The
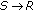 and
and 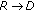 channels are estimated at the corresponding terminals and are available at the destination. Moreover, the
channels are estimated at the corresponding terminals and are available at the destination. Moreover, the  channel is estimated at the destination by using the signal
channel is estimated at the destination by using the signal 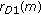 . Then data symbols are detected from the received signals
. Then data symbols are detected from the received signals 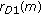 and
and  by using this channel information. Figure 2(a) shows the total MSE of the channel estimations
by using this channel information. Figure 2(a) shows the total MSE of the channel estimations  and
and 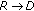 for
for  in dB. We see that we obtain the best channel estimation for
in dB. We see that we obtain the best channel estimation for  dB which corresponds to equal distance between
dB which corresponds to equal distance between 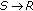 and
and 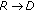 . We give the BER performances at different channel noise levels for
. We give the BER performances at different channel noise levels for 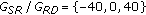 dB in Figure 2(b). We also compare and present our results with the performance of the perfect channel state information (CSI) in the same figure. Similar to the MSE, we have the closest BER performance to the perfect CSI for the case of
dB in Figure 2(b). We also compare and present our results with the performance of the perfect channel state information (CSI) in the same figure. Similar to the MSE, we have the closest BER performance to the perfect CSI for the case of  dB. We observe from this figure that, the "individual approach for 0 dB" has about 5 dB SNR gain over the "individual 40 dB" at BER
dB. We observe from this figure that, the "individual approach for 0 dB" has about 5 dB SNR gain over the "individual 40 dB" at BER 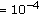 .
. -
(2)
Cascaded Channel Estimation Results: The combined
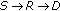 channel is estimated at the destination terminal from
channel is estimated at the destination terminal from  . The
. The  channel is estimated at the destination by using the signal
channel is estimated at the destination by using the signal  . Data symbols are detected from
. Data symbols are detected from 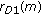 and
and  by using estimated channel parameters. Figure 3(a) shows the MSE of the cascaded
by using estimated channel parameters. Figure 3(a) shows the MSE of the cascaded  channel estimation for
channel estimation for 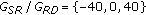 dB. Note that we obtain almost the same estimation performance for
dB. Note that we obtain almost the same estimation performance for 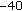 and
and  dB and obtain better results for
dB and obtain better results for 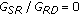 dB as in the individual channel estimation case. We show the BER performance for
dB as in the individual channel estimation case. We show the BER performance for 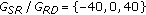 dB, as well as for the perfect CSI case in Figure 3(b). The noise floors in the figures are due to the fact that we do not consider advanced detection techniques for the receiver in our studies. Our main concern is the estimation of the time-varying channel. By using more advanced detection methods, error floors shown in our figures may be reduced.
dB, as well as for the perfect CSI case in Figure 3(b). The noise floors in the figures are due to the fact that we do not consider advanced detection techniques for the receiver in our studies. Our main concern is the estimation of the time-varying channel. By using more advanced detection methods, error floors shown in our figures may be reduced.
Notice that the individual channel estimation approach outperforms the cascaded approach in terms of both MSE and BER as expected, at the expense of twice the computational complexity. This comes from the fact that relay terminal estimates the channel and transmits to the destination with an increased symbol duration due to the insertion of new pilot symbols. In approach two, the relay does not perform any channel estimation; hence the computational burden is reduced. However, the estimated combined channel parameters are not as reliable as in the first approach.
We have also investigated the effect of the number of pilots to the channel estimation performance in both approaches. We show the BER and MSE plots in Figures 4(a) and 4(b), respectively, for  . Notice that increasing the number of pilots improves the BER performance in both approaches especially the cascaded approach.
. Notice that increasing the number of pilots improves the BER performance in both approaches especially the cascaded approach.
The effect of the number of channel paths on the BER is illustrated by a simulation where the number of pilots is taken as  and the SNR =
and the SNR =  dB. The number of paths is changed between
dB. The number of paths is changed between  and
and  , and the BER is presented in Figure 5. Note that both approaches equally suffer from increasing the number of paths.
, and the BER is presented in Figure 5. Note that both approaches equally suffer from increasing the number of paths.
5. Conclusions
In this paper, we present a time-varying channel estimation technique for CO-OFDM systems. We propose two approaches where in the first one, individual channels are estimated at the relay and destination whereas in the second approach, the cascaded source-relay-destination channel is estimated at the destination. We assume that the communication channels are multipath and affected by considerable Doppler frequencies. Simulation results show that the individual channel estimation approach gives better performance than the cascaded approach in terms of both estimation error and the bit error rate. However, in the cascaded channel estimation case, the computational cost is reduced significantly at the expense of decreased performance. We observe that the best performance is achieved when the distances of source-to-relay and relay-to-destination is equal, for both approaches.
References
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Doǧan H: Maximum a posteriori channel estimation for cooperative diversity orthogonal frequency-division multiplexing systems in amplify-and-forward mode. IET Communications 2009, 3(4):501-511. 10.1049/iet-com.2008.0195
Zhang Z, Zhang W, Tellambura C: Cooperative OFDM channel estimation in the presence of frequency offsets. IEEE Transactions on Vehicular Technology 2009, 58(7):3447-3459.
Bello PA: Characterization of randomly time-variant linear channels. IEEE Transactions on Communication Systems 1963, 11: 360-393. 10.1109/TCOM.1963.1088793
Amin O, Gedik B, Uysal M: Channel estimation for amplify-and-forward relaying: Cascaded against disintegrated estimators. IET Communications 2010, 4(10):1207-1216. 10.1049/iet-com.2009.0435
Mark JW, Zhuang W: Wireless Communication and Networking. Prentice Hall, Upper Saddle River, NJ, USA; 2003.
Ochiai H, Mitran P, Tarokh V: Variable-rate two-phase collaborative communication protocols for wireless networks. IEEE Transactions on Information Theory 2006, 52(9):4299-4313.
Nabar RU, Bölcskei H, Kneubühler FW: Fading relay channels: performance limits and space-time signal design. IEEE Journal on Selected Areas in Communications 2004, 22(6):1099-1109. 10.1109/JSAC.2004.830922
Kang SG, Ha YM, Joo EK: A comparative investigation on channel estimation algorithms for OFDM in mobile communications. IEEE Transactions on Broadcasting 2003, 49(2):142-149. 10.1109/TBC.2003.810263
Tang Z, Cannizzaro RC, Leus G, Banelli P: Pilot-assisted time-varying channel estimation for OFDM systems. IEEE Transactions on Signal Processing 2007, 55(5):2226-2238.
Acknowledgment
This work was supported by The Research Fund of The University of Istanbul, project nos. 6904, 2875, and 6687.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Önen, E., Odabaşioğlu, N. & Akan, A. Time-Frequency Based Channel Estimation for High-Mobility OFDM Systems—Part II: Cooperative Relaying Case. EURASIP J. Adv. Signal Process. 2010, 973286 (2010). https://doi.org/10.1155/2010/973286
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/973286

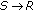 and
and 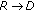 channels are estimated at the corresponding terminals and are available at the destination. Moreover, the
channels are estimated at the corresponding terminals and are available at the destination. Moreover, the  channel is estimated at the destination by using the signal
channel is estimated at the destination by using the signal 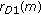 . Then data symbols are detected from the received signals
. Then data symbols are detected from the received signals 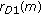 and
and  by using this channel information. Figure
by using this channel information. Figure  and
and 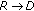 for
for  in dB. We see that we obtain the best channel estimation for
in dB. We see that we obtain the best channel estimation for  dB which corresponds to equal distance between
dB which corresponds to equal distance between 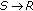 and
and 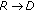 . We give the BER performances at different channel noise levels for
. We give the BER performances at different channel noise levels for 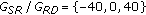 dB in Figure
dB in Figure  dB. We observe from this figure that, the "individual approach for 0 dB" has about 5 dB SNR gain over the "individual 40 dB" at BER
dB. We observe from this figure that, the "individual approach for 0 dB" has about 5 dB SNR gain over the "individual 40 dB" at BER 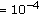 .
.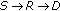 channel is estimated at the destination terminal from
channel is estimated at the destination terminal from  . The
. The  channel is estimated at the destination by using the signal
channel is estimated at the destination by using the signal  . Data symbols are detected from
. Data symbols are detected from 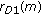 and
and  by using estimated channel parameters. Figure
by using estimated channel parameters. Figure  channel estimation for
channel estimation for 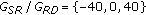 dB. Note that we obtain almost the same estimation performance for
dB. Note that we obtain almost the same estimation performance for 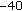 and
and  dB and obtain better results for
dB and obtain better results for 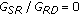 dB as in the individual channel estimation case. We show the BER performance for
dB as in the individual channel estimation case. We show the BER performance for 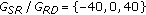 dB, as well as for the perfect CSI case in Figure
dB, as well as for the perfect CSI case in Figure 



 and
and  pilots, and
pilots, and  dB SNR.
dB SNR.