- Research Article
- Open access
- Published:
The Optimal Design of Weighted Order Statistics Filters by Using Support Vector Machines
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 024185 (2006)
Abstract
Support vector machines (SVMs), a classification algorithm for the machine learning community, have been shown to provide higher performance than traditional learning machines. In this paper, the technique of SVMs is introduced into the design of weighted order statistics (WOS) filters. WOS filters are highly effective, in processing digital signals, because they have a simple window structure. However, due to threshold decomposition and stacking property, the development of WOS filters cannot significantly improve both the design complexity and estimation error. This paper proposes a new designing technique which can improve the learning speed and reduce the complexity of designing WOS filters. This technique uses a dichotomous approach to reduce the Boolean functions from 255 levels to two levels, which are separated by an optimal hyperplane. Furthermore, the optimal hyperplane is gotten by using the technique of SVMs. Our proposed method approximates the optimal weighted order statistics filters more rapidly than the adaptive neural filters.
References
Cristianini N, Shawe-Taylor J: An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge University Press, Cambridge, UK; 2000.
Vapnik VN: The Nature of Statistical Learning Theory. Springer, New York, NY, USA; 1995.
Lee Y-J, Mangasarian OL: SSVM: a smooth support vector machine for classification. Computational Optimization and Applications 2001, 20(1):5–22. 10.1023/A:1011215321374
Mangasarian OL: Generalized support vector machines. In Advances in Large Margin Classifiers. Edited by: Smola AJ, Bartlett P, Schölkopf B, Schuurmans C. MIT Press, Cambridge, Mass, USA; 2000:135–146.
Mangasarian OL, Musicant DR: Successive overrelaxation for support vector machines. IEEE Transactions on Neural Networks 1999, 10(5):1032–1037. 10.1109/72.788643
Chapelle O, Haffner P, Vapnik VN: Support vector machines for histogram-based image classification. IEEE Transactions on Neural Networks 1999, 10(5):1055–1064. 10.1109/72.788646
Guo G, Li SZ, Chan KL: Support vector machines for face recognition. Image and Vision Computing 2001, 19(9–10):631–638. 10.1016/S0262-8856(01)00046-4
Drucker H, Wu D, Vapnik VN: Support vector machines for spam categorization. IEEE Transactions on Neural Networks 1999, 10(5):1048–1054. 10.1109/72.788645
Vapnik VN: Statistical Learning Theory. John Wiley & Sons, New York, NY, USA; 1998.
Yang R, Gabbouj M, Yu P-T: Parametric analysis of weighted order statistics filters. IEEE Signal Processing Letters 1994, 1(6):95–98. 10.1109/97.295344
Yu P-T: Some representation properties of stack filters. IEEE Transactions on Signal Processing 1992, 40(9):2261–2266. 10.1109/78.157225
Yu P-T, Chen R-C: Fuzzy stack filters-their definitions, fundamental properties, and application in image processing. IEEE Transactions on Image Processing 1996, 5(6):838–854. 10.1109/83.503903
Yu P-T, Coyle EJ: The classification and associative memory capability of stack filters. IEEE Transactions on Signal Processing 1992, 40(10):2483–2497. 10.1109/78.157291
Yu P-T, Coyle EJ: Convergence behavior and N-roots of stack filters. IEEE Transactions on Acoustics, Speech, and Signal Processing 1990, 38(9):1529–1544. 10.1109/29.60073
Yu P-T, Liao W-H: Weighted order statistics filters-their classification, some properties, and conversion algorithm. IEEE Transactions on Signal Processing 1994, 42(10):2678–2691. 10.1109/78.324733
Chakrabarti C, Lucke LE: VLSI architectures for weighted order statistic (WOS) filters. Signal Processing 2000, 80(8):1419–1433. 10.1016/S0165-1684(00)00046-3
Perry SW, Guan L: Weight assignment for adaptive image restoration by neural networks. IEEE Transactions on Neural Networks 2000, 11(1):156–170. 10.1109/72.822518
Wong H-S, Guan L: A neural learning approach for adaptive image restoration using a fuzzy model-based network architecture. IEEE Transactions on Neural Networks 2001, 12(3):516–531. 10.1109/72.925555
Yin L, Astola J, Neuvo Y: Optimal weighted order statistic filters under the mean absolute error criterion. Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP '91), April 1991, Toronto, Ontario, Canada 4: 2529–2532.
Yin L, Astola J, Neuvo Y: A new class of nonlinear filters-neural filters. IEEE Transactions on Signal Processing 1993, 41(3):1201–1222. 10.1109/78.205724
Yin L, Astola J, Neuvo Y: Adaptive multistage weighted order statistic filters based on the backpropagation algorithm. IEEE Transactions on Signal Processing 1994, 42(2):419–422. 10.1109/78.275617
Wendt PD, Coyle EJ, Gallagher NC: Stack filters. IEEE Transactions on Acoustics, Speech, and Signal Processing 1986, 34(4):898–911. 10.1109/TASSP.1986.1164871
Avedillo MJ, Quintana JM, Rodriguez-Villegas E: Simple parallel weighted order statistic filter implementations. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '02), May 2002 4: 607–610.
Gasteratos A, Andreadis I: A new algorithm for weighted order statistics operations. IEEE Signal Processing Letters 1999, 6(4):84–86. 10.1109/97.752061
Huttunen H, Koivisto P: Training based optimization of weighted order statistic filters under breakdown criteria. Proceedings of the International Conference on Image Processing (ICIP '99), October 1999, Kobe, Japan 4: 172–176.
Koivisto P, Huttunen H: Design of weighted order statistic filters by training-based optimization. Proceedings of the 6th International Symposium on Signal Processing and Its Applications (ISSPA '01), August 2001, Kuala Lumpur, Malaysia 1: 40–43.
Marshall S: New direct design method for weighted order statistic filters. IEE Proceedings - Vision, Image, and Signal Processing 2001, 151(1):1–8.
Yli-Harja O, Astola J, Neuvo Y: Analysis of the properties of median and weighted median filters using threshold logic and stack filter representation. IEEE Transactions on Signal Processing 1991, 39(2):395–410. 10.1109/78.80823
Bertsekas DP: Nonlinear Programming. Athena Scientific, Belmont, Mass, USA; 1999.
Poikonen J, Paasio A: A ranked order filter implementation for parallel analog processing. IEEE Transactions on Circuits and Systems I: Regular Papers 2004, 51(5):974–987. 10.1109/TCSI.2004.827620
Savin CE, Ahmad MO, Swamy MNS:
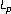 norm design of stack filters. IEEE Transactions on Image Processing 1999, 8(12):1730–1743. 10.1109/83.806619
norm design of stack filters. IEEE Transactions on Image Processing 1999, 8(12):1730–1743. 10.1109/83.806619Schlkopf B, Smola AJ: Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT Press, Cambridge, Mass, USA; 2002.
Gill PE, Murray W, Wright MH: Practical Optimization. Academic Press, London, UK; 1981.
Lee Y-J, Mangasarian OL: RSVM: Reduced Support Vector Machines. Proceedings of the 1st SIAM International Conference on Data Mining, April 2001, Chicago, Ill, USA
Stone M: Cross-validatory choice and assessment of statistical predictions. Journal of the Royal Statistical Society 1974, B36: 111–147.
Yin L, Yang R, Gabbouj M, Neuvo Y: Weighted median filters: a tutorial. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 1996, 43(3):157–192. 10.1109/82.486465
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yao, CC., Yu, PT. The Optimal Design of Weighted Order Statistics Filters by Using Support Vector Machines. EURASIP J. Adv. Signal Process. 2006, 024185 (2006). https://doi.org/10.1155/ASP/2006/24185
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/24185
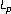 norm design of stack filters. IEEE Transactions on Image Processing 1999, 8(12):1730–1743. 10.1109/83.806619
norm design of stack filters. IEEE Transactions on Image Processing 1999, 8(12):1730–1743. 10.1109/83.806619