- Research Article
- Open access
- Published:
Denoising by Sparse Approximation: Error Bounds Based on Rate-Distortion Theory
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 026318 (2006)
Abstract
If a signal is known to have a sparse representation with respect to a frame, it can be estimated from a noise-corrupted observation
is known to have a sparse representation with respect to a frame, it can be estimated from a noise-corrupted observation by finding the best sparse approximation to
by finding the best sparse approximation to . Removing noise in this manner depends on the frame efficiently representing the signal while it inefficiently represents the noise. The mean-squared error (MSE) of this denoising scheme and the probability that the estimate has the same sparsity pattern as the original signal are analyzed. First an MSE bound that depends on a new bound on approximating a Gaussian signal as a linear combination of elements of an overcomplete dictionary is given. Further analyses are for dictionaries generated randomly according to a spherically-symmetric distribution and signals expressible with single dictionary elements. Easily-computed approximations for the probability of selecting the correct dictionary element and the MSE are given. Asymptotic expressions reveal a critical input signal-to-noise ratio for signal recovery.
. Removing noise in this manner depends on the frame efficiently representing the signal while it inefficiently represents the noise. The mean-squared error (MSE) of this denoising scheme and the probability that the estimate has the same sparsity pattern as the original signal are analyzed. First an MSE bound that depends on a new bound on approximating a Gaussian signal as a linear combination of elements of an overcomplete dictionary is given. Further analyses are for dictionaries generated randomly according to a spherically-symmetric distribution and signals expressible with single dictionary elements. Easily-computed approximations for the probability of selecting the correct dictionary element and the MSE are given. Asymptotic expressions reveal a critical input signal-to-noise ratio for signal recovery.
References
Duffin RJ, Schaeffer AC: A class of nonharmonic Fourier series. Transactions of the American Mathematical Society March 1952, 72: 341–366. 10.1090/S0002-9947-1952-0047179-6
Daubechies I: Ten Lectures on Wavelets. SIAM, Philadelphia, Pa, USA; 1992.
Demmel JW: Applied Numerical Linear Algebra. SIAM, Philadelphia, Pa, USA; 1997.
Donoho DL, Vetterli M, DeVore RA, Daubechies I: Data compression and harmonic analysis. IEEE Transactions on Information Theory 1998, 44(6):2435–2476. 10.1109/18.720544
Gorodnitsky IF, Rao BD: Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Transactions on Signal Processing 1997, 45(3):600–616. 10.1109/78.558475
Malioutov D, Çetin M, Willsky AS: A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Transactions on Signal Processing 2005, 53(8, Part 2):3010–3022.
Donoho DL, Elad M, Temlyakov V: Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Transactions on Information Theory 2006, 52(1):6–18.
Elad M, Bruckstein AM: A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Transactions on Information Theory 2002, 48(9):2558–2567. 10.1109/TIT.2002.801410
Donoho DL, Elad M:Optimally sparse representation in general (nonorthogonal) dictionaries via
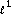 minimization. Proceedings of the National Academy of Sciences 2003, 100(5):2197–2202. 10.1073/pnas.0437847100
minimization. Proceedings of the National Academy of Sciences 2003, 100(5):2197–2202. 10.1073/pnas.0437847100Gribonval R, Nielsen M: Sparse representations in unions of bases. IEEE Transactions on Information Theory 2003, 49(12):3320–3325. 10.1109/TIT.2003.820031
Fuchs J-J: On sparse representations in arbitrary redundant bases. IEEE Transactions on Information Theory 2004, 50(6):1341–1344. 10.1109/TIT.2004.828141
Tropp JA: Greed is good: Algorithmic results for sparse approximation. IEEE Transactions on Information Theory 2004, 50(10):2231–2242. 10.1109/TIT.2004.834793
Donoho DL, Elad M: On the stability of basis pursuit in the presence of noise. submitted to EURASIP Journal on Applied Signal Processing, October 2004
Tropp JA: Just relax: Convex programming methods for subset selection and sparse approximation. In ICES Report 0404. University of Texas at Austin, Austin, Tex, USA; February 2004.
Candès EJ, Romberg J, Tao T: Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory 2006, 52(2):489–509.
Candès EJ, Tao T: Near optimal signal recovery from random projections: Universal encoding strategies? submitted to IEEE Transactions on Information Theory, October 2004
Candès EJ, Romberg J, Tao T: Stable signal recovery from incomplete and inaccurate measurements. In Comput. & Appl. Math. Report 05-12. University of California, Los Angeles, Calif, USA; March 2005.
Fletcher AK, Ramchandran K: Estimation error bounds for frame denoising. Wavelets: Applications in Signal and Image Processing X, August 2003, San Diego, Calif, USA, Proceedings of SPIE 5207: 40–46.
Fletcher AK, Rangan S, Goyal VK, Ramchandran K: Denoising by sparse approximation: Error bounds based on rate-distortion theory. In Electron. Res. Lab. Memo M05/5. University of California, Berkeley, Calif, USA; September 2004.
Fletcher AK: Estimation via sparse approximation: Error bounds and random frame analysis, M.A. thesis. University of California, Berkeley, Calif, USA; May 2005.
Elad M, Zibulevsky M: A probabilistic study of the average performance of basis pursuit. sumitted to in IEEE Transactions on Information Theory, December 2004
Cohen A, D'Ales J-P: Nonlinear approximation of random functions. SIAM Journal on Applied Mathematics 1997, 57(2):518–540. 10.1137/S0036139994279153
DeVore RA: Nonlinear approximation. Acta Numerica 1998, 7: 51–150.
Goodwin MM: Adaptive Signal Models: Theory, Algorithms, and Audio Applications. Kluwer Academic, Boston, Mass, USA; 1998.
Engan K, Aase SO, Husoy JH: Designing frames for matching pursuit algorithms. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '98), May 1998, Seattle, Wash, USA 3: 1817–1820.
Tropp JA, Dhillon IS, Heath RW Jr., Strohmer T: Designing structured tight frames via an alternating projection method. IEEE Transactions on Information Theory 2005, 51(1):188–209.
Davis G: Adaptive nonlinear approximations, M.S. thesis. New York University, New York, NY, USA; September 1994.
Natarajan BK: Sparse approximate solutions to linear systems. SIAM Journal on Computing 1995, 24(2):227–234. 10.1137/S0097539792240406
Golub GH, Van Loan CF: Matrix Computations. 2nd edition. Johns Hopkins University Press, Baltimore, Md, USA; 1989.
Mallat SG, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993, 41(12):3397–3415. 10.1109/78.258082
Chen SS, Donoho DL, Saunders MA: Atomic decomposition by basis pursuit. SIAM Review 2001, 43(1):129–159. 10.1137/S003614450037906X
Gribonval R, Nielsen M: Highly sparse representations from dictionaries are unique and independent of the sparseness measure. In Tech. Rep. R-2003-16. Department of Mathematical Sciences, Aalborg University, Aalborg, Denmark; October 2003.
Gribonval R, Vandergheynst P: On the exponential convergence of matching pursuits in quasi-incoherent dictionaries. In Tech. Rep. 1619. Institut de Recherche en Informatique et Systèmes Aléatoires, Rennes, France; April 2004.
Gribonval R, Nielsen M:Beyond sparsity: Recovering structured representations by
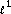 minimization and greedy algorithms—Application to the analysis of sparse underdetermined ICA. In Tech. Rep. 1684. Institut de Recherche en Informatique et Systèmes Aléatoires, Rennes, France; January 2005.
minimization and greedy algorithms—Application to the analysis of sparse underdetermined ICA. In Tech. Rep. 1684. Institut de Recherche en Informatique et Systèmes Aléatoires, Rennes, France; January 2005.Saito N: Simultaneous noise suppression and signal compression using a library of orthonormal bases and the minimum description length criterion. In Wavelets in Geophysics. Edited by: Foufoula-Georgiou E, Kumar P. Academic Press, San Diego, Calif, USA; 1994:299–324. chapter XI
Natarajan BK: Filtering random noise from deterministic signals via data compression. IEEE Transactions on Signal Processing 1995, 43(11):2595–2605. 10.1109/78.482110
Krim H, Tucker D, Mallat S, Donoho DL: On denoising and best signal representation. IEEE Transactions on Information Theory 1999, 45(7):2225–2238. 10.1109/18.796365
Chang SG, Yu B, Vetterli M: Adaptive wavelet thresholding for image denoising and compression. IEEE Transactions on Image Processing 2000, 9(9):1532–1546. 10.1109/83.862633
Liu J, Moulin P: Complexity-regularized image denoising. IEEE Transactions on Image Processing 2001, 10(6):841–851. 10.1109/83.923281
Bergeaud F, Mallat S: Matching pursuit of images. Proceedings of International Conference on Image Processing (ICIP '95), October 1995, Washington, DC, USA 1: 53–56.
Neff R, Zakhor A: Very low bit-rate video coding based on matching pursuits. IEEE Transactions on Circuits and Systems for Video Technology 1997, 7(1):158–171. 10.1109/76.554427
Goyal VK, Vetterli M, Thao NT:Quantized overcomplete expansions in
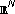 : Analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985
: Analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985Al-Shaykh OK, Miloslavsky E, Nomura T, Neff R, Zakhor A: Video compression using matching pursuits. IEEE Transactions on Circuits and Systems for Video Technology 1999, 9(1):123–143. 10.1109/76.744280
Moschetti F, Granai L, Vandergheynst P, Frossard P: New dictionary and fast atom searching method for matching pursuit representation of displaced frame difference. Proceedings of International Conference on Image Processing (ICIP '02), September 2002, Rochester, NY, USA 3: 685–688.
Conway JH, Hardin RH, Sloane NJA: Packing lines, planes, etc.: Packings in Grassmannian spaces. Experimental Mathematics 1996, 5(2):139–159.
Strohmer T, Heath RW Jr.: Grassmannian frames with applications to coding and communication. Applied and Computational Harmonic Analysis 2003, 14(3):257–275. 10.1016/S1063-5203(03)00023-X
Sloane NJA, Hardin RH, Smith WD, et al.: A library of putatively optimal spherical codes, together with other arrangements which may not be optimal but are especially interesting for some reason. https://doi.org/www.research.att.com/~njas/packings
Gallager RG: Information Theory and Reliable Communication. John Wiley & Sons, New York, NY, USA; 1968.
Andrews GE, Askey R, Roy R: Special Functions, Encyclopedia of Mathematics and Its Applications. Volume 71. Cambridge University Press, Cambridge, Mass, USA; 1999.
Berger T: Rate Distortion Theory: A Mathematical Basis for Data Compression, Information and System Sciences Series. Prentice-Hall, Englewood Cliffs, NJ, USA; 1971.
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Gray RM: Source Coding Theory. Kluwer Academic, Boston, Mass, USA; 1990.
Grimmett GR, Stirzaker DR: Probability and Random Processes. 2nd edition. Oxford University Press, Oxford, UK; 1992.
Conway JH, Hardin RH, Sloane NJA: Packing lines, planes, etc.: Packings in Grassmannian spaces. Experimental Mathematics 1997, 6(2):175. editors' note
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fletcher, A.K., Rangan, S., Goyal, V.K. et al. Denoising by Sparse Approximation: Error Bounds Based on Rate-Distortion Theory. EURASIP J. Adv. Signal Process. 2006, 026318 (2006). https://doi.org/10.1155/ASP/2006/26318
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/26318
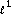 minimization. Proceedings of the National Academy of Sciences 2003, 100(5):2197–2202. 10.1073/pnas.0437847100
minimization. Proceedings of the National Academy of Sciences 2003, 100(5):2197–2202. 10.1073/pnas.0437847100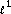 minimization and greedy algorithms—Application to the analysis of sparse underdetermined ICA. In Tech. Rep. 1684. Institut de Recherche en Informatique et Systèmes Aléatoires, Rennes, France; January 2005.
minimization and greedy algorithms—Application to the analysis of sparse underdetermined ICA. In Tech. Rep. 1684. Institut de Recherche en Informatique et Systèmes Aléatoires, Rennes, France; January 2005.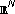 : Analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985
: Analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985