- Research Article
- Open access
- Published:
2D Four-Channel Perfect Reconstruction Filter Bank Realized with the 2D Lattice Filter Structure
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 042672 (2006)
Abstract
A novel orthogonal 2D lattice structure is incorporated into the design of a nonseparable 2D four-channel perfect reconstruction filter bank. The proposed filter bank is obtained by using the polyphase decomposition technique which requires the design of an orthogonal 2D lattice filter. Due to constraint of perfect reconstruction, each stage of this lattice filter bank is simply parameterized by two coefficients. The perfect reconstruction property is satisfied regardless of the actual values of these parameters and of the number of the lattice stages. It is also shown that a separable 2D four-channel perfect reconstruction lattice filter bank can be constructed from the 1D lattice filter and that this is a special case of the proposed 2D lattice filter bank under certain conditions. The perfect reconstruction property of the proposed 2D lattice filter approach is verified by computer simulations.
References
Crochiere RE, Webber SA, Flanagan JL: Digital coding of speech in subbands. Bell System Technical Journal 1976, 55(8):1069–1085.
Vetterli M: Multidimensional subband coding: some theory and algorithms. Signal Processing 1984, 6(2):97–112. 10.1016/0165-1684(84)90012-4
Woods JW, O'neil SD: Subband coding of images. IEEE Transactions on Acoustics, Speech, and Signal Processing 1986, 34(5):1278–1288. 10.1109/TASSP.1986.1164962
Smith MJT, Eddins SL: Analysis/synthesis techniques for subband image coding. IEEE Transactions on Acoustics, Speech, and Signal Processing 1990, 38(8):1446–1456. 10.1109/29.57579
Daubechies I: Orthonormal bases of compactly supported wavelets. Communications on Pure and Applied Mathematics 1988, 41: 909–996. 10.1002/cpa.3160410705
Mallat SG: Multifrequency channel decompositions of images and wavelet models. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(12):2091–2110. 10.1109/29.45554
Galand CR, Nussbaumer HJ: New quadrature mirror filter structures. IEEE Transactions on Acoustics, Speech, and Signal Processing 1984, 32(3):522–531. 10.1109/TASSP.1984.1164356
Jain VK, Crochiere RE: Quadrature mirror filter design in the time domain. IEEE Transactions on Acoustics, Speech, and Signal Processing 1984, 32(2):353–361. 10.1109/TASSP.1984.1164329
Smith MJT, Barnwell TP: Exact reconstruction techniques for tree-structured subband coders. IEEE Transactions on Acoustics, Speech, and Signal Processing 1986, 34(3):434–441. 10.1109/TASSP.1986.1164832
Vaidyanathan PP:Quadrature Mirror Filter banks,
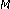 -Band extensions, and PR techniques. IEEE Acoustics, Speech, and Signal Processing Magazine 1987, 4(3):4–20.
-Band extensions, and PR techniques. IEEE Acoustics, Speech, and Signal Processing Magazine 1987, 4(3):4–20.Vaidyanathan PP:Theory and design of M-channel maximally decimated quadrature mirror filters with arbitraryM, having the perfect reconstruction property. IEEE Transactions on Acoustics, Speech, and Signal Processing 1987, 35(4):476–492. 10.1109/TASSP.1987.1165155
Vetterli M, Le Gall DJ: Perfect reconstruction FIR filter banks: some properties and factorizations. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(7):1057–1071. 10.1109/29.32283
Nguyen TQ, Vaidyanathan PP: Two-channel perfect reconstruction FIR QMF structures which yield linear phase analysis and synthesis filters. IEEE Transactions on Acoustics, Speech, and Signal Processing 1990, 38(3):433–446. 10.1109/29.106862
Vaidyanathan PP, Hoang PQ: Lattice structures for optimal design and robust implementation of two-channel perfect-reconstruction QMF banks. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988, 36(1):81–94. 10.1109/29.1491
Akansu AN, Haddad RA: Multiresolution Signal Decomposition: Transforms, Subbands and Wavelets. Academic Press, San Diego, Calif, USA; 1992.
Tay DBH, Kingsbury NG: Flexible design of multidimensional perfect reconstruction FIR 2-band filters using transformations of variables. IEEE Transactions on Image Processing 1993, 2(4):466–480. 10.1109/83.242356
Simoncelli EP, Adelson EH: Non-separable extensions of quadrature mirror filters to multiple dimensions. Proceedings of the IEEE 1990, 78(4):652–664. Special issue on multi-dimensional signal processing 10.1109/5.54805
Bamberger RH, Smith MJT: A filter bank for the directional decomposition of images: theory and design. IEEE Transactions on Signal Processing 1992, 40(4):882–893. 10.1109/78.127960
Ansari R, Lau CL: Two dimensional IIR filters for exact reconstruction in tree-structured sub-band decomposition. Electronics Letters 1987, 23(12):633–634. 10.1049/el:19870453
Ansari R: Efficient IIR and FIR fan filters. IEEE Transactions on Circuits and Systems 1987, 34(8):941–945. 10.1109/TCS.1987.1086224
Chen T, Vaidyanathan PP: Multidimensional multirate filters derived from one dimensional filters. Electronics Letters 1991, 27(3):225–228. 10.1049/el:19910146
Chen T, Vaidyanathan PP: Multidimensional multirate filters and filter banks derived from one-dimensional filters. IEEE Transactions on Signal Processing 1993, 41(5):1749–1765. 10.1109/78.215297
Viscito E, Allebach JP: Design of perfect reconstruction multi-dimensional filter banks using cascaded Smith form matrices. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '88), June 1988, Espoo, Finland 1: 831–834.
Viscito E, Allebach JP: The analysis and design of multidimensional FIR perfect reconstruction filter banks for arbitrary sampling lattices. IEEE Transactions on Circuits and Systems 1991, 38(1):29–41. 10.1109/31.101301
Basu S, Chiang CH: A complete parametrization of 2D nonseparable orthogonal wavelets. Proceedings of IEEE International Symposium on Time-Frequency and Time-Scale Analysis, October 1992, Victoria, BC, Canada 55–58.
Kovacevic J, Vetterli M:Nonseparable multidimensional perfect reconstruction filter banks and wavelet bases for
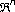 . IEEE Transactions on Information Theory 1992, 38(2):533–555. Special issue on wavelet transform and multiresolution signal analysis 10.1109/18.119722
. IEEE Transactions on Information Theory 1992, 38(2):533–555. Special issue on wavelet transform and multiresolution signal analysis 10.1109/18.119722Kovaceciv J, Vetterli M: Perfect reconstruction filter banks with rational sampling factors. IEEE Transactions on Signal Processing 1993, 41(6):2047–2066. 10.1109/78.218135
Venkataraman S, Levy BC: Nonseparable orthogonal linear phase perfect reconstruction filter banks and their application to image compression. Proceedings of the International Conference on Image Processing (ICIP '94), November 1994, Austin, Tex, USA 334–338.
Gao XQ, Nguyen TQ, Strang G: Theory and lattice structures of complex paraunitary filterbanks with filters of (Hermitian)-symmetry/antisymmetry properties. IEEE Transactions on Signal Processing 2001, 49(5):1028–1043. 10.1109/78.917806
Chan SC: Two-dimensional nonseparable modulated filter banks. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '94), April 1994, Adelaide, Australia 141–144.
Kovacevic J, Vetterli M: Nonseparable two- and three-dimensional wavelets. IEEE Transactions on Signal Processing 1995, 43(5):1269–1273. 10.1109/78.382414
Tran TD, Nguyen TQ:On
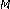 -Channel linear phase FIR Filter banks and application in image compression. IEEE Transactions on Signal Processing 1997, 45(9):2175–2187. 10.1109/78.622942
-Channel linear phase FIR Filter banks and application in image compression. IEEE Transactions on Signal Processing 1997, 45(9):2175–2187. 10.1109/78.622942Huang J, Gu G: A direct approach to the design of QMF banks via frequency domain optimization. IEEE Transactions on Signal Processing 1998, 46(8):2131–2146. 10.1109/78.705424
Evangelista G, Cavaliere S: Frequency warped filter banks and wavelet transform: a discrete-time approach via laguerre expansions. IEEE Transactions on Signal Processing 1998, 46(10):2638–2650. 10.1109/78.720367
Goh CK, Lim YC: An efficient algorithm to design weighted minimax perfect reconstruction quadrature mirror filter banks. IEEE Transactions on Signal Processing 1999, 47(12):3303–3314. 10.1109/78.806074
Labeau F, Vandendorpe L, Macq B: Structures, factorizations and design criteria for oversampled paraunitary filterbanks yielding linear-phase filters. IEEE Transactions on Signal Processing 2000, 48(11):3062–3071. 10.1109/78.875464
Tran TD, Ikehara M, Nguyen TQ: Linear phase paraunitary filter bank with filters of different lengths and its application in image compression. IEEE Transactions on Signal Processing 1999, 47(10):2730–2744. 10.1109/78.790655
Gao X, Nguyen Q, Strang G:On factorization of
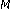 -channel paraunitary filterbanks. IEEE Transactions on Signal Processing 2001, 49(5):1433–1446.
-channel paraunitary filterbanks. IEEE Transactions on Signal Processing 2001, 49(5):1433–1446.Oraintara S, Tran TD, Heller PN, Nguyen TQ:Lattice structure for regular paraunitary linear-phase filterbanks and
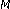 -band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001, 49(11):2659–2672. 10.1109/78.960413
-band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001, 49(11):2659–2672. 10.1109/78.960413Parker SR, Kayran AH: Lattice parameter autoregressive modelling of 2-D fields-Part I: the quarter plane case. IEEE Transactions on Acoustics, Speech, and Signal Processing 1984, 32(4):872–885. 10.1109/TASSP.1984.1164412
Lev-Ari H, Parker SR: Stable and efficient 2-D lattice filters. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '86), April 1986, Tokyo, Japan 695–698.
Sezen S: Application of 2-D lattice filter structures to the subband decomposition problem, M.S. thesis. Boğaziçi University, Istanbul, Turkey; 1998.
Ertuzun A, Kayran AH, Panayirci E: Stable quarter-plane 2-D lattice filters. Electronic Letters 1990, 26(12):806–807. 10.1049/el:19900526
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sezen, S., Ertüzün, A. 2D Four-Channel Perfect Reconstruction Filter Bank Realized with the 2D Lattice Filter Structure. EURASIP J. Adv. Signal Process. 2006, 042672 (2006). https://doi.org/10.1155/ASP/2006/42672
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/42672
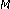 -Band extensions, and PR techniques. IEEE Acoustics, Speech, and Signal Processing Magazine 1987, 4(3):4–20.
-Band extensions, and PR techniques. IEEE Acoustics, Speech, and Signal Processing Magazine 1987, 4(3):4–20.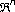 . IEEE Transactions on Information Theory 1992, 38(2):533–555. Special issue on wavelet transform and multiresolution signal analysis 10.1109/18.119722
. IEEE Transactions on Information Theory 1992, 38(2):533–555. Special issue on wavelet transform and multiresolution signal analysis 10.1109/18.119722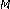 -Channel linear phase FIR Filter banks and application in image compression. IEEE Transactions on Signal Processing 1997, 45(9):2175–2187. 10.1109/78.622942
-Channel linear phase FIR Filter banks and application in image compression. IEEE Transactions on Signal Processing 1997, 45(9):2175–2187. 10.1109/78.622942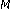 -channel paraunitary filterbanks. IEEE Transactions on Signal Processing 2001, 49(5):1433–1446.
-channel paraunitary filterbanks. IEEE Transactions on Signal Processing 2001, 49(5):1433–1446.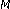 -band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001, 49(11):2659–2672. 10.1109/78.960413
-band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001, 49(11):2659–2672. 10.1109/78.960413