- Research Article
- Open access
- Published:
Quantization Noise Shaping on Arbitrary Frame Expansions
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 053807 (2006)
Abstract
Quantization noise shaping is commonly used in oversampled A/D and D/A converters with uniform sampling. This paper considers quantization noise shaping for arbitrary finite frame expansions based on generalizing the view of first-order classical oversampled noise shaping as a compensation of the quantization error through projections. Two levels of generalization are developed, one a special case of the other, and two different cost models are proposed to evaluate the quantizer structures. Within our framework, the synthesis frame vectors are assumed given, and the computational complexity is in the initial determination of frame vector ordering, carried out off-line as part of the quantizer design. We consider the extension of the results to infinite shift-invariant frames and consider in particular filtering and oversampled filter banks.
References
Daubechies I: Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics. SIAM, Philadelphia, Pa, USA; 1992.
Cvetkovic Z, Vetterli M: Overcomplete expansions and robustness. Proceedings of IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, June 1996, Paris, France 325–328.
Goyal VK, Vetterli M, Thao NT:Quantized overcomplete expansions in
 : analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985
: analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985Thao NT, Vetterli M:Reduction of the MSE in
 -times oversampled A/D conversion
-times oversampled A/D conversion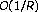 to
to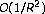 . IEEE Transactions on Signal Processing 1994, 42(1):200–203. 10.1109/78.258137
. IEEE Transactions on Signal Processing 1994, 42(1):200–203. 10.1109/78.258137Benedetto JJ, Powell AM, Yilmaz Ö:Sigma-Delta
 quantization and finite frames. to appear in IEEE Transactions on Information Theory, available at: https://doi.org/www.math.umd.edu/~jjb/ffsd.pdf to appear in IEEE Transactions on Information Theory, available at:
quantization and finite frames. to appear in IEEE Transactions on Information Theory, available at: https://doi.org/www.math.umd.edu/~jjb/ffsd.pdf to appear in IEEE Transactions on Information Theory, available at:Benedetto JJ, Yilmaz Ö, Powell AM: Sigma-delta quantization and finite frames. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '04), May 2004, Montreal, Quebec, Canada 3: 937–940.
Bolcskei H, Hlawatsch F: Noise reduction in oversampled filter banks using predictive quantization. IEEE Transactions on Information Theory 2001, 47(1):155–172. 10.1109/18.904519
Boufounos PT, Oppenheim AV: Quantization noise shaping on arbitrary frame expansion. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '05), March 2005, Philadelphia, Pa, USA 4: 205–208.
Strang G, Nguyen T: Wavelets and Filter Banks. Wellesley-Cambridge Press, Wellesley, Mass, USA; 1996.
Candy JC, Temes GC (Eds): Oversampling Delta-Sigma Data Converters: Theory, Design and Simulation. IEEE Press, New York, NY, USA; 1992.
Cormen TH, Leiserson CE, Rivest RL, Stein C: Introduction to Algorithms. 2nd edition. MIT Press, Cambridge, Mass, USA; 2001.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Boufounos, P.T., Oppenheim, A.V. Quantization Noise Shaping on Arbitrary Frame Expansions. EURASIP J. Adv. Signal Process. 2006, 053807 (2006). https://doi.org/10.1155/ASP/2006/53807
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/53807
 : analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985
: analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998, 44(1):16–31. 10.1109/18.650985 -times oversampled A/D conversion
-times oversampled A/D conversion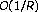 to
to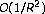 . IEEE Transactions on Signal Processing 1994, 42(1):200–203. 10.1109/78.258137
. IEEE Transactions on Signal Processing 1994, 42(1):200–203. 10.1109/78.258137 quantization and finite frames. to appear in IEEE Transactions on Information Theory, available at:
quantization and finite frames. to appear in IEEE Transactions on Information Theory, available at: