- Research Article
- Open access
- Published:
A Unified Transform for LTI Systems—Presented as a (Generalized) Frame
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 091604 (2006)
Abstract
We present a set of functions in and show it to be a (tight) generalized frame (as presented by G. Kaiser (1994)). The analysis side of the frame operation is called the continuous unified transform. We show that some of the well-known transforms (such as Laplace, Laguerre, Kautz, and Hambo) result by creating different sampling patterns in the transform domain (or, equivalently, choosing a number of subsets of the original frame). Some of these resulting sets turn out to be generalized (tight) frames as well. The work reported here enhances the understanding of the interrelationships between the above-mentioned transforms. Furthermore, the impulse response of every stable finite-dimensional LTI system has a finite representation using the frame we introduce here, with obvious benefits in identification problems.
and show it to be a (tight) generalized frame (as presented by G. Kaiser (1994)). The analysis side of the frame operation is called the continuous unified transform. We show that some of the well-known transforms (such as Laplace, Laguerre, Kautz, and Hambo) result by creating different sampling patterns in the transform domain (or, equivalently, choosing a number of subsets of the original frame). Some of these resulting sets turn out to be generalized (tight) frames as well. The work reported here enhances the understanding of the interrelationships between the above-mentioned transforms. Furthermore, the impulse response of every stable finite-dimensional LTI system has a finite representation using the frame we introduce here, with obvious benefits in identification problems.
References
Heuberger PSC, de Hoog TJ, Van den Hof PMJ, Wahlberg B: Orthonormal basis functions in time and frequency domain: Hambo transform theory. SIAM Journal on Control and Optimization 2003, 42(4):1347–1373. 10.1137/S0363012902405340
Oppenheim AV, Willsky AS, Young IT: Signals and Systems. Prentice-Hall, Englewood Cliffs, NJ, USA; 1983.
Vetterli M, Kovacevic J: Wavelets and Subband Coding. Prentice-Hall, Englewood Cliffs, NJ, USA; 1995.
Mallat S: A Wavelet Tour of Signal Processing. 2nd edition. Academic Press, San Diego, Calif, USA; 1999.
Daubechies I: Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics. SIAM, Philadelphia, Pa, USA; 1992.
Chui CK: An Introduction to Wavelets, Wavelet Analysis and Its Applications. Academic Press, Boston, Mass, USA; 1992.
Christensen O: An Introduction to Frames and Riesz Bases. Birkhäuser, Boston, Mass, USA; 2003.
Kaiser G: A Friendly Guide to Wavelets. Birkhäuser, Boston, Mass, USA; 1994.
Ali ST, Antoine JP, Gazeau JP: Continuous frames in Hilbert space. Annals of Physics 1993, 222(1):1–37. 10.1006/aphy.1993.1016
Viscito E, Allebach JP: The analysis and design of multidimensional FIR perfect reconstruction filter banks for arbitrary sampling lattices. IEEE Transactions on Circuits And Systems—Part I : Fundamental Theory and Applications 1991, 38(1):29–41.
Apostol TM: Mathematical Analysis. 2nd edition. Addison-Wesley, Sydney, Australia; 1974.
Paley REAC, Wiener N: Fourier Transforms in the Complex Domain. American Mathematical Society, New York, NY, USA; 1934.
de Hoog TJ: Rational orthonormal bases and related transforms in linear system modeling, M.S. thesis. Delft University of Technology, Delft, The Netherlands; 2001.
Donoho DL, Stark PB: Uncertainty principles and signal recovery. SIAM Journal on Applied Mathematics 1989, 49(3):906–931. 10.1137/0149053
Donoho DL, Elad M:Optimally sparse representation in general (nonorthogonal) dictionaries via
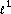 minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100
minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feuer, A., Van den Hof, P.M. & Heuberger, P.S. A Unified Transform for LTI Systems—Presented as a (Generalized) Frame. EURASIP J. Adv. Signal Process. 2006, 091604 (2006). https://doi.org/10.1155/ASP/2006/91604
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/91604
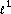 minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100
minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100