- Research
- Open access
- Published:
Statistical resolution limit for the multidimensional harmonic retrieval model: hypothesis test and Cramér-Rao Bound approaches
EURASIP Journal on Advances in Signal Processing volume 2011, Article number: 12 (2011)
Abstract
The statistical resolution limit (SRL), which is defined as the minimal separation between parameters to allow a correct resolvability, is an important statistical tool to quantify the ultimate performance for parametric estimation problems. In this article, we generalize the concept of the SRL to the multidimensional SRL (MSRL) applied to the multidimensional harmonic retrieval model. In this article, we derive the SRL for the so-called multidimensional harmonic retrieval model using a generalization of the previously introduced SRL concepts that we call multidimensional SRL (MSRL). We first derive the MSRL using an hypothesis test approach. This statistical test is shown to be asymptotically an uniformly most powerful test which is the strongest optimality statement that one could expect to obtain. Second, we link the proposed asymptotic MSRL based on the hypothesis test approach to a new extension of the SRL based on the Cramér-Rao Bound approach. Thus, a closed-form expression of the asymptotic MSRL is given and analyzed in the framework of the multidimensional harmonic retrieval model. Particularly, it is proved that the optimal MSRL is obtained for equi-powered sources and/or an equi-distributed number of sensors on each multi-way array.
Introduction
The multidimensional harmonic retrieval problem is an important topic which arises in several applications [1]. The main reason is that the multidimensional harmonic retrieval model is able to handle a large class of applications. For instance, the joint angle and carrier estimation in surveillance radar system [2, 3], the underwater acoustic multisource azimuth and elevation direction finding [4], the 3-D harmonic retrieval problem for wireless channel sounding [5, 6] or the detection and localization of multiple targets in a MIMO radar system [7, 8].
One can find many estimation schemes adapted to the multidimensional harmonic retrieval estimation problem, see, e.g., [1, 2, 4–7, 9, 10]. However, to the best of our knowledge, no work has been done on the resolvability of such a multidimensional model.
The resolvability of closely spaced signals, in terms of parameter of interest, for a given scenario (e.g., for a given signal-to-noise ratio (SNR), for a given number of snapshots and/or for a given number of sensors) is a former and challenging problem which was recently updated by Smith [11], Shahram and Milanfar [12], Liu and Nehorai [13], and Amar and Weiss [14]. More precisely, the concept of statistical resolution limit (SRL), i.e., the minimum distance between two closely spaced signalsa embedded in an additive noise that allows a correct resolvability/parameter estimation, is rising in several applications (especially in problems such as radar, sonar, and spectral analysis [15].)
The concept of the SRL was defined/used in several manners [11–14, 16–24], which could turn in it to a confusing concept. There exist essentially three approaches to define/obtain the SRL. (i) The first is based on the concept of mean null spectrum: assuming, e.g., that two signals are parameterized by the frequencies f1 and f2, the Cox criterion [16] states that these sources are resolved, w.r.t. a given high-resolution estimation algorithm, if the mean null spectrum at each frequency f1and f2is lower than the mean of the null spectrum at the midpoint . Another commonly used criterion, also based on the concept of the mean null spectrum, is the Sharman and Durrani criterion [17], which states that two sources are resolved if the second derivative of the mean of the null spectrum at the midpoint
. Another commonly used criterion, also based on the concept of the mean null spectrum, is the Sharman and Durrani criterion [17], which states that two sources are resolved if the second derivative of the mean of the null spectrum at the midpoint is negative. It is clear that the SRL based on the mean null spectrum is relevant to a specific high-resolution algorithm (for some applications of these criteria one can see [16–19] and references therein.) (ii) The second approach is based on detection theory: the main idea is to use a hypothesis test to decide if one or two closely spaced signals are present in the set of the observations. Then, the challenge herein is to link the minimum separation, between two sources (e.g., in terms of frequencies) that is detectable at a given SNR, to the probability of false alarm, Pfa and/or to the probability of detection Pd. In this spirit, Sharman and Milanfar [12] have considered the problem of distinguishing whether the observed signal contains one or two frequencies at a given SNR using the generalized likelihood ratio test (GLRT). The authors have derived the SRL expressions w.r.t. Pfa and Pd in the case of real received signals, and unequal and unknown amplitudes and phases. In [13], Liu and Nehorai have defined a statistical angular resolution limit using the asymptotic equivalence (in terms of number of observations) of the GLRT. The challenge was to determine the minimum angular separation, in the case of complex received signals, which allows to resolve two sources knowing the direction of arrivals (DOAs) of one of them for a given Pfa and a given Pd. Recently, Amar and Weiss [14] have proposed to determine the SRL of complex sinusoids with nearby frequencies using the Bayesian approach for a given correct decision probability. (iii) The third approach is based on a estimation accuracy criteria independent of the estimation algorithm. Since the Cramér-Rao Bound (CRB) expresses a lower bound on the covariance matrix of any unbiased estimator, then it expresses also the ultimate estimation accuracy [25, 26]. Consequently, it could be used to describe/obtain the SRL. In this context, one distinguishes two main criteria for the SRL based on the CRB: (1) the first one was introduced by Lee [20] and states that: two signals are said to be resolvable w.r.t. the frequencies if the maximum standard deviation is less than twice the difference between f1and f2. Assuming that the CRB is a tight bound (under mild/weak conditions), the standard deviation,
is negative. It is clear that the SRL based on the mean null spectrum is relevant to a specific high-resolution algorithm (for some applications of these criteria one can see [16–19] and references therein.) (ii) The second approach is based on detection theory: the main idea is to use a hypothesis test to decide if one or two closely spaced signals are present in the set of the observations. Then, the challenge herein is to link the minimum separation, between two sources (e.g., in terms of frequencies) that is detectable at a given SNR, to the probability of false alarm, Pfa and/or to the probability of detection Pd. In this spirit, Sharman and Milanfar [12] have considered the problem of distinguishing whether the observed signal contains one or two frequencies at a given SNR using the generalized likelihood ratio test (GLRT). The authors have derived the SRL expressions w.r.t. Pfa and Pd in the case of real received signals, and unequal and unknown amplitudes and phases. In [13], Liu and Nehorai have defined a statistical angular resolution limit using the asymptotic equivalence (in terms of number of observations) of the GLRT. The challenge was to determine the minimum angular separation, in the case of complex received signals, which allows to resolve two sources knowing the direction of arrivals (DOAs) of one of them for a given Pfa and a given Pd. Recently, Amar and Weiss [14] have proposed to determine the SRL of complex sinusoids with nearby frequencies using the Bayesian approach for a given correct decision probability. (iii) The third approach is based on a estimation accuracy criteria independent of the estimation algorithm. Since the Cramér-Rao Bound (CRB) expresses a lower bound on the covariance matrix of any unbiased estimator, then it expresses also the ultimate estimation accuracy [25, 26]. Consequently, it could be used to describe/obtain the SRL. In this context, one distinguishes two main criteria for the SRL based on the CRB: (1) the first one was introduced by Lee [20] and states that: two signals are said to be resolvable w.r.t. the frequencies if the maximum standard deviation is less than twice the difference between f1and f2. Assuming that the CRB is a tight bound (under mild/weak conditions), the standard deviation,  and
and  , of an unbiased estimator
, of an unbiased estimator  is given by
is given by  and
and  , respectively. Consequently, the SRL is defined, in the Lee criterion sense, as 2max
, respectively. Consequently, the SRL is defined, in the Lee criterion sense, as 2max  . One can find some results and applications in [20, 21] where this criterion is used to derive a matrix-based expression (i.e., without analytic inversion of the Fisher information matrix) of the SRL for the frequency estimates in the case of the conditional and unconditional signal source models. On the other hand, Dilaveroglu [22] has derived a closed-form expression of the frequency resolution for the real and complex conditional signal source models. However, one can note that the coupling between the parameters, CRB(f1, f2) (i.e., the CRB for the cross parameters f1 and f2), is ignored by this latter criterion. (2) To extend this, Smith [11] has proposed the following criterion: two signals are resolvable w.r.t. the frequencies if the difference between the frequencies, δ
f
, is greater than the standard deviation of the DOA difference estimation. Since, the standard deviation can be approximated by the CRB, then, the SRL, in the Smith criterion sense, is defined as the limit of δ
f
for which
. One can find some results and applications in [20, 21] where this criterion is used to derive a matrix-based expression (i.e., without analytic inversion of the Fisher information matrix) of the SRL for the frequency estimates in the case of the conditional and unconditional signal source models. On the other hand, Dilaveroglu [22] has derived a closed-form expression of the frequency resolution for the real and complex conditional signal source models. However, one can note that the coupling between the parameters, CRB(f1, f2) (i.e., the CRB for the cross parameters f1 and f2), is ignored by this latter criterion. (2) To extend this, Smith [11] has proposed the following criterion: two signals are resolvable w.r.t. the frequencies if the difference between the frequencies, δ
f
, is greater than the standard deviation of the DOA difference estimation. Since, the standard deviation can be approximated by the CRB, then, the SRL, in the Smith criterion sense, is defined as the limit of δ
f
for which  is achieved. This means that, the SRL is obtained by solving the following implicit equation
is achieved. This means that, the SRL is obtained by solving the following implicit equation

In [11, 23], Smith has derived the SRL for two closely spaced sources in terms of DOA, each one modeled by one complex pole. In [24], Delmas and Abeida have derived the SRL based on the Smith criterion for DOA of discrete sources under QPSK, BPSK, and MSK model assumptions. More recently, Kusuma and Goyal [27] have derived the SRL based on the Smith criterion in sampling estimation problems involving a powersum series.
It is important to note that all the criteria listed before take into account only one parameter of interest per signal. Consequently, all the criteria listed before cannot be applied to the aforementioned the multidimensional harmonic model. To the best of our knowledge, no results are available on the SRL for multiple parameters of interest per signal. The goal of this article is to fill this lack by proposing and deriving the so-called MSRL for the multidimensional harmonic retrieval model.
More precisely, in this article, the MSRL for multiple parameters of interest per signal using a hypothesis test is derived. This choice is motivated by the following arguments: (i) the hypothesis test approach is not specific to a certain high-resolution algorithm (unlike the mean null spectrum approach), (ii) in this article, we link the asymptotic MSRL based on the hypothesis test approach to a new extension of the MSRL based on the CRB approach. Furthermore, we show that the MSRL based on the CRB approach is equivalent to the MSRL based on the hypothesis test approach for a fixed couple (Pfa, Pd), and (iii) the hypothesis test is shown to be asymptotically an uniformly most powerful test which is the strongest statement of optimality that one could expect to obtain [28].
The article is organized as follows. We first begin by introducing the multidimensional harmonic model, in section "Model setup". Then, based on this model, we obtain the MSRL based on the hypothesis test and on the CRB approach. The link between theses two MSRLs is also described in section "Determination of the MSRL for two sources" followed by the derivation of the MSRL closed-form expression, where, as a by product the exact closed-form expressions of the CRB for the multidimensional retrieval model is derived (note that to the best of our knowledge, no exact closed-form expressions of the CRB for such model is available in the literature). Furthermore, theoretical and numerical analyses are given in the same section. Finally, conclusions are given.
Glossary of notation
The following notations are used through the article. Column vectors, matrices, and multi-way arrays are represented by lower-case bold letters (a, ...), upper-case bold letters (A, ...) and bold calligraphic letters  , whereas
, whereas
-
ℝ and ℂ denote the body of real and complex values, respectively,
-
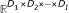 and
and 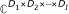 denote the real and complex multi-way arrays (also called tensors) body of dimension D1 × D2 × ⋯ ×D
I
, respectively,
denote the real and complex multi-way arrays (also called tensors) body of dimension D1 × D2 × ⋯ ×D
I
, respectively, -
j = the complex number
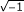 .
. -
I Q = the identity matrix of dimension Q,
-
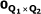 = the Q1 × Q2 matrix filled by zeros,
= the Q1 × Q2 matrix filled by zeros, -
[a] i = the i th element of the vector a,
-
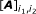 = the i1th row and the i2th column element of the matrix A,
= the i1th row and the i2th column element of the matrix A, -
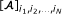 = the (i1, i2, ..., i
N
)th entry of the multi-way array
= the (i1, i2, ..., i
N
)th entry of the multi-way array 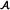 ,
, -
[A]i,p:q= the row vector containing the (q - p + 1) elements [A]i,k, where k = p, ..., q,
-
[A]p:q,k= the column vector containing the (q - p + 1) elements [A]i,k, where i = p, ..., q,
-
the derivative of vector a w.r.t. to vector b is defined as follows:
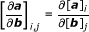 ,
, -
AT = the transpose of the matrix A,
-
A* = the complex conjugate of the matrix A,
-
AH = (A*)T,
-
tr {A} = the trace of the matrix A,
-
det {A} = the determinant of the matrix A,
-
ℜ{a} = the real part of the complex number a,
-
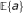 = the expectation of the random variable a,
= the expectation of the random variable a, -
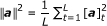 denotes the normalized norm of the vector a(in which L is the size of a),
denotes the normalized norm of the vector a(in which L is the size of a), -
sgn (a) = 1 if a ≥ 0 and -1 otherwise.
-
diag(a) is the diagonal operator which forms a diagonal matrix containing the vector a on its diagonal,
-
vec(.) is the vec-operator stacking the columns of a matrix on top of each other,
-
⊙ stands for the Hadamard product,
-
⊗ stands for the Kronecker product,
-
○ denotes the multi-way array outer-product (recall that for a given multi-way arrays
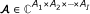 and
and 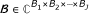 , the result of the outer-product of
, the result of the outer-product of 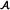 and
and  denoted by
denoted by 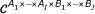 is given by
is given by 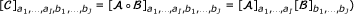 .
.
Model setup
In this section, we introduce the multidimensional harmonic retrieval model in the multi-way array form (also known as tensor form[29]). Then, we use the PARAFAC (PARallel FACtor) decomposition to obtain a vector form of the observation model. This vector form will be used to derive the closed-form expression of the MSRL.
Let us consider a multidimensional harmonic model consisting of the superposition of two harmonics each one of dimension P contaminated by an additive noise. Thus, the observation model is given as follows [8, 9, 26, 30–32]:

where  ,
,  , and
, and  denote the noisy observation, the noiseless observation, and the noise multi-way array at the t th snapshot, respectively. The number of snapshots and the number of sensors on each array are denoted by L and (N1, ...,N
P
), respectively. The noiseless observation multi-way array can be written as followsb[26, 30–32]:
denote the noisy observation, the noiseless observation, and the noise multi-way array at the t th snapshot, respectively. The number of snapshots and the number of sensors on each array are denoted by L and (N1, ...,N
P
), respectively. The noiseless observation multi-way array can be written as followsb[26, 30–32]:

where  and s
m
(t) denote the m th frequency viewed along the p th dimension or array and the m th complex signal source, respectively. Furthermore, the signal source is given by
and s
m
(t) denote the m th frequency viewed along the p th dimension or array and the m th complex signal source, respectively. Furthermore, the signal source is given by  where α
m
(t) and ϕ
m
(t) denote the real positive amplitude and the phase for the m th signal source at the t th snapshot, respectively.
where α
m
(t) and ϕ
m
(t) denote the real positive amplitude and the phase for the m th signal source at the t th snapshot, respectively.
Since,

where a(.) is a Vandermonde vector defined as

then, the multi-way array  follows a PARAFAC decomposition [7, 33]. Consequently, the noiseless observation multi-way array can be rewritten as follows:
follows a PARAFAC decomposition [7, 33]. Consequently, the noiseless observation multi-way array can be rewritten as follows:

First, let us vectorize the noiseless observation as follows:

Thus, the full noise-free observation vector is given by

Second, and in the same way, we define y, the noisy observation vector, and n, the noise vector, by the concatenation of the proper multi-way array's entries, i.e.,

Consequently, in the following, we will consider the observation model in (5). Furthermore, the unknown parameter vector is given by

where ω denotes the unknown parameter vector of interest, i.e., containing all the unknown frequencies

in which

whereas ρ contains the unknown nuisance/unwanted parameters vector, i.e., characterizing the noise covariance matrix and/or amplitude and phase of each source (e.g., in the case of a covariance noise matrix equal to 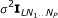 and unknown deterministic amplitudes and phases, the unknown nuisance/unwanted parameters vector ρ is given by ρ= [α1(1) ⋯ α2(L)ϕ1(1) ⋯ ϕ2(L)σ2]T.
and unknown deterministic amplitudes and phases, the unknown nuisance/unwanted parameters vector ρ is given by ρ= [α1(1) ⋯ α2(L)ϕ1(1) ⋯ ϕ2(L)σ2]T.
In the following, we conduct a hypothesis test formulation on the observation model (5) to derive our MSRL expression in the case of two sources.
Determination of the MSRL for two sources
Hypothesis test formulation
Resolving two closely spaced sources, with respect to their parameters of interest, can be formulated as a binary hypothesis test [12–14] (for the special case of P = 1). To determine the MSRL (i.e., P ≥ 1), let us consider the hypothesis  which represents the case where the two emitted signal sources are combined into one signal, i.e., the two sources have the same parameters (this hypothesis is described by
which represents the case where the two emitted signal sources are combined into one signal, i.e., the two sources have the same parameters (this hypothesis is described by  , whereas the hypothesis
, whereas the hypothesis  embodies the situation where the two signals are resolvable (the latter hypothesis is described by ∃p ∈ [1 ... P], such that
embodies the situation where the two signals are resolvable (the latter hypothesis is described by ∃p ∈ [1 ... P], such that  ). Consequently, one can formulate the hypothesis test, as a simple one-sided binary hypothesis test as follows:
). Consequently, one can formulate the hypothesis test, as a simple one-sided binary hypothesis test as follows:

where the parameter δ is the so-called MSRL which indicates us in which hypothesis our observation model belongs. Thus, the question addressed below is how can we define the MSRL δ such that all the P parameters of interest are taken into account? A natural idea is that δ reflects a distance between the P parameters of interest. Let the MSRL denotes the l1 normc between two sets containing the parameters of interest of each source (which is the naturally used norm, since in the mono-parameter frequency case that we extend here, the SRL is defined as δ = f1 - f2[13, 14, 34]). Meaning that, if we denote these sets as C1 and C2 where  , m = 1,2, thus, δ can be defined as
, m = 1,2, thus, δ can be defined as

First, note that the proposed MSRL describes well the hypothesis test (8) (i.e., δ = 0 means that the two emitted signal sources are combined into one signal and δ ≠ 0 the two signals are resolvable). Second, since the MSRL δ is unknown, it is impossible to design an optimal detector in the Neyman-Pearson sense. Alternatively, the GLRT [28, 35] is a well-known approach appropriate to solve such a problem. To conduct the GLRT on (8), one has to express the probability density function (pdf) of (5) w.r.t. δ. Assuming (without loss of generality) that  , one can notice that ξ is known if and only if δ and
, one can notice that ξ is known if and only if δ and  are fixed (i.e., there is a one to one mapping between δ, ϑ, and ξ). Consequently, the pdf of (5) can be described as p(y|δ,ϑ). Now, we are ready to conduct the GLRT for this problem:
are fixed (i.e., there is a one to one mapping between δ, ϑ, and ξ). Consequently, the pdf of (5) can be described as p(y|δ,ϑ). Now, we are ready to conduct the GLRT for this problem:

where  ,
,  , and
, and  denote the maximum likelihood estimates (MLE) of δ under
denote the maximum likelihood estimates (MLE) of δ under  , the MLE of ϑ under
, the MLE of ϑ under  and the MLE of ϑ under
and the MLE of ϑ under  , respectively, and where ς' denotes the test threshold. From (10), one obtains
, respectively, and where ς' denotes the test threshold. From (10), one obtains

in which Ln denotes the natural logarithm.
Asymptotic equivalence of the MSRL
Finding the analytical expression of T
G
(y) in (11) is not tractable. This is mainly due to the fact that the derivation of  is impossible since from (2) one obtains a multimodal likelihood function [36]. Consequently, in the following, and as ind[13], we consider the asymptotic case (in terms of the number of snapshots). In [35, eq (6C.1)], it has been proven that, for a large number of snapshots, the statistic T
G
(y) follows a chi-square pdf under
is impossible since from (2) one obtains a multimodal likelihood function [36]. Consequently, in the following, and as ind[13], we consider the asymptotic case (in terms of the number of snapshots). In [35, eq (6C.1)], it has been proven that, for a large number of snapshots, the statistic T
G
(y) follows a chi-square pdf under  and
and  given by
given by

where  and
and  denote the central chi-square and the noncentral chi-square pdf with one degree of freedom, respectively. Pfa and Pd are, respectively, the probability of false alarm and the probability of detection of the test (8). In the following, CRB(δ) denotes the CRB for the parameter δ where the unknown vector parameter is given by [δ ϑT]T. Consequently, assuming that CRB(δ) exists (under
denote the central chi-square and the noncentral chi-square pdf with one degree of freedom, respectively. Pfa and Pd are, respectively, the probability of false alarm and the probability of detection of the test (8). In the following, CRB(δ) denotes the CRB for the parameter δ where the unknown vector parameter is given by [δ ϑT]T. Consequently, assuming that CRB(δ) exists (under  and
and  ), is well defined (see section "MSRL closed-form expression" for the necessarye and sufficient conditions) and is a tight bound (i.e., achievable under quite general/weak conditions [36, 37]), thus the noncentral parameter κ'(Pfa, Pd) is given by [[35], p. 239]
), is well defined (see section "MSRL closed-form expression" for the necessarye and sufficient conditions) and is a tight bound (i.e., achievable under quite general/weak conditions [36, 37]), thus the noncentral parameter κ'(Pfa, Pd) is given by [[35], p. 239]

On the other hand, one can notice that the noncentral parameter κ'(Pfa, Pd) can be determined numerically by the choice of Pfa and Pd[13, 28] as the solution of

in which  and
and  are the inverse of the right tail of the
are the inverse of the right tail of the  and
and  pdf starting at the value ϖ. Finally, from (13) and (14) one obtainsf
pdf starting at the value ϖ. Finally, from (13) and (14) one obtainsf

where  is the so-called translation factor [13] which is determined for a given probability of false alarm and probability of detection (see Figure 1 for the behavior of the translation factor versus Pfa and Pd).
is the so-called translation factor [13] which is determined for a given probability of false alarm and probability of detection (see Figure 1 for the behavior of the translation factor versus Pfa and Pd).
Result 1: The asymptotic MSRL for model (5) in the case of P parameters of interest per signal (P ≥ 1) is given by δ which is the solution of the following equation:

where Adirect denotes the contribution of the parameters of interest belonging to the same dimension as follows

and where Across is the contribution of the cross terms between distinct dimension given by

in which  .
.
Proof see Appendix 1.
Remark 1: It is worth noting that the hypothesis test (8) is a binary one-sided test and that the MLE used is an unconstrained estimator. Thus, one can deduce that the GLRT, used to derive the asymptotic MSRL [13, 35]: (i) is the asymptotically uniformly most powerful test among all invariant statistical tests, and (ii) has an asymptotic constant false-alarm rate (CFAR). Which is, in the asymptotic case, considered as the strongest statement of optimality that one could expect to obtain [28].
-
Existence of the MSRL: It is natural to assume that the CRB is a non-increasing (i.e., decreasing or constant) function on ℝ+ w.r.t. δ since it is more difficult to estimate two closely spaced signals than two largely-spaced ones. In the same time the left hand side of (15) is a monotonically increasing function w.r.t. δ on ℝ+. Thus for a fixed couple (Pfa, Pd), the solution of the implicit equation given by (15) always exists. However, theoretically, there is no assurance that the solution of equation (15) is unique.
-
Note that, in practical situation, the case where CRB(δ) is not a function of δ is important since in this case, CRB(δ) is constant w.r.t. δ and thus the solution of (15) exists and is unique (see section "MSRL closed-form expression").
In the following section, we study the explicit effect of this so-called translation factor.
The relationship between the MSRL based on the CRB and the hypothesis test approaches
In this section, we link the asymptotic MSRL (derived using the hypothesis test approach, see Result 1) to a new proposed extension of the SRL based on the Smith criterion [11]. First, we recall that the Smith criterion defines the SRL in the case of P = 1 only. Then, we extend this criterion to P ≥ 1 (i.e., the case of the multidimensional harmonic model). Finally, we link the MSRL based on the hypothesis test approach (see Result 1) to the MSRL based on the CRB approach (i.e., the extended SRL based on the Smith criterion).
The Smith criterion: Since the CRB expresses a lower bound on the covariance matrix of any unbiased estimator, then it expresses also the ultimate estimation accuracy. In this context, Smith proposed the following criterion for the case of two source signals parameterized each one by only one frequency [11]: two signals are resolvable if the difference between their frequency,  , is greater than the standard deviation of the frequency difference estimation. Since, the standard deviation can be approximated by the CRB, then, the SRL, in the Smith criterion sense, is defined as the limit of
, is greater than the standard deviation of the frequency difference estimation. Since, the standard deviation can be approximated by the CRB, then, the SRL, in the Smith criterion sense, is defined as the limit of  for which
for which  is achieved. This means that, the SRL is the solution of the following implicit equation
is achieved. This means that, the SRL is the solution of the following implicit equation

The extension of the Smith criterion to the case of P ≥ 1: Based on the above framework, a straightforward extension of the Smith criterion to the case of P ≥ 1 for the multidimensional harmonic model is as follows: two multidimensional harmonic retrieval signals are resolvable if the distance between C1and C2, is greater than the standard deviation of the δCRBestimation. Consequently, assuming that the CRB exists and is well defined, the MSRL δCRB is given as the solution of the following implicit equation

Comparison and link between the MSRL based on the CRB approach and the MSRL based on the hypothesis test approach: The MSRL based on the hypothesis test approach is given as the solution of

whereas the MSRL based on the CRB approach is given as the solution of (17). Consequently, one has the following result:
Result 2: Upon to a translation factor, the asymptotic MSRL based on the hypothesis test approach (i.e., using the binary one-sided hypothesis test given in (8)) is equivalent to the proposed MSRL based on the CRB approach (i.e., using the extension of the Smith criterion). Consequently, the criterion given in (17) is equivalent to an asymptotically uniformly most powerful test among all invariant statistical tests for κ(Pfa, Pd) = 1 (see Figure 2 for the values of (Pfa, Pd) such that κ (Pfa, Pd) = 1).
The following section is dedicated to the analytical computation of closed-form expression of the MSRL. In section "Assumptions," we introduce the assumptions used to compute the MSRL in the case of a Gaussian random noise and orthogonal waveforms. Then, we derive non matrix closed-form expressions of the CRB (note that to the best of our knowledge, no closed-form expressions of the CRB for such model is available in the literature). In "MSRL derivation" and thanks to these expressions, the MSRL wil be deduced using (16). Finally, the MSRL analysis is given.
MSRL closed-form expression
in section "Determination of the MSRL for two sources" we have defined the general model of the multidimensional harmonic model. To derive a closed-form expression of the MSRL, we need more assumptions on the covariance noise matrix and/or on the signal sources.
Assumptions
-
The noise is assumed to be a complex circular white Gaussian random process i.i.d. with zero-mean and unknown variance
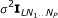 .
. -
We consider a multidimensional harmonic model due to the superposition of two harmonics each of them of dimension P ≥ 1. Furthermore, for sake of simplicity and clarity, the sources have been assumed known and orthogonal (e.g., [7, 38]). In this case, the unknown parameter vector is fixed and does not grow with the number of snapshots. Consequently, the CRB is an achievable bound [36].
-
Each parameter of interest w.r.t. to the first signal,
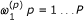 , can be as close as possible to the parameter of interest w.r.t. to the second signal
, can be as close as possible to the parameter of interest w.r.t. to the second signal 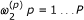 , but not equal. This is not really a restrictive assumption, since in most applications, having two or more identical parameters of interest is a zero probability event [[9], p. 53].
, but not equal. This is not really a restrictive assumption, since in most applications, having two or more identical parameters of interest is a zero probability event [[9], p. 53].
Under these assumptions, the joint probability density function of the noisy observations y for a given unknown deterministic parameter vector ξ is as follows:

where  . The multidimensional harmonic retrieval model with known sources is considered herein, and thus, the parameter vector is given by
. The multidimensional harmonic retrieval model with known sources is considered herein, and thus, the parameter vector is given by

where

in which

CRB for the multidimensional harmonic model with orthogonal known signal sources
The Fisher information matrix (FIM) of the noisy observations y w.r.t. a parameter vector ξ is given by [39]

For a complex circular Gaussian observation model, the (i th, k th) element of the FIM for the parameter vector ξ is given by [34]

Consequently, one can state the following lemma.
Lemma 1: The FIM for the sum of two P-order harmonic models with orthogonal known sources, has a block diagonal structure and is given by

where, the (2P) × (2P) matrix F ω is also a block diagonal matrix given by

in which Δ = diag {||α1||2 ,||α2||2} where

and

Proof see Appendix 2.
After some calculation and using Lemma 1, one can state the following result.
Result 3: The closed-form expressions of the CRB for the sum of two P-order harmonic models with orthogonal known signal sources are given by

where  denotes the SNR of the m th source and where
denotes the SNR of the m th source and where

Furthermore, the cross-terms are given by

where

Proof see Appendix 3.
MSRL derivation
Using the previous result, one obtains the unique solution of (16), thus, the MSRL for model (1) is given by the following result:
Result 4: The MSRL for the sum of P-order harmonic models with orthogonal known signal sources, is given by

where the so-called extended SNR is given by  .
.
Proof see Appendix 4.
Numerical analysis
Taking advantage of the latter result, one can analyze the MSRL given by (26):
-
First, from Figure 3 note that the numerical solution of the MSRL based on (12) is in good agreement with the analytical expression of the MSRL (23), which validate the closed-form expression given in (23). On the other hand, one can notice that, for Pd = 0.37 and Pfa = 0.1 the MSRL based on the CRB is exactly equal to the MSRL based on hypothesis test approach derived in the asymptotic case. From the case Pd = 0.49 and Pfa = 0.3 or/and Pd = 0.32 and Pfa = 0.1, one can notice the influence of the translation factor κ(Pfa, Pd) on the MSRL.
-
The MSRLg is
 which is consistent with some previous results for the case P = 1 (e.g., [12, 14, 24]).
which is consistent with some previous results for the case P = 1 (e.g., [12, 14, 24]). -
From (26) and for a large number of sensors N1 = N2 = ⋯ = N P = N ≫ 1, one obtains a simple expression
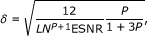
meaning that, the SRL is  .
.
-
Furthermore, since P ≥ 1, one has
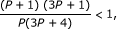
and consequently, the ratio between the MSRL of a multidimensional harmonic retrieval with P parameters of interest, denoted by δ P and the MSRL of a multidimensional harmonic retrieval with P + 1 parameters of interest, denoted by δP+1, is given by

meaning that the MSRL for P + 1 parameters of interest is less than the one for P parameters of interest (see Figure 4). This, can be explained by the estimation additional parameter and also by an increase of the received noisy data thanks to the additional dimension. One should note that this property is proved theoretically thanks to (27) using the assumption of an equal and large number of sensors. However, from Figure 4 we notice that, in practice, this can be verified even for a small number of sensors (e.g., in Figure 4 one has 3 ≤ N p ≤ 5 for p = 3, ..., 6).
-
Furthermore, since

one can note that, the SRL is lower bounded by  .
.
-
One can address the problem of finding the optimal distribution of power sources making the SRL the smallest as possible (s.t. the constraint of constant total source power). In this issue, one can state the following corollary: Corollary 1: The optimal power's source distribution that ensures the smallest MSRL is obtained only for the equi-powered sources case.
Proof see Appendix 5.
This result was observed numerically for P = 1 in [12] (see Figure 5 for the multidimensional harmonic model). Moreover, it has been shown also by simulation for the case P = 1 that the so-called maximum likelihood breakdown (i.e., when the mean square error of the MLE increases rapidly) occurs at higher SNR in the case of different power signal sources than in the case of equi-powered signal sources [40]. The authors explained it by the fact that one source grabs most of the total power, then, this latter will be estimated more accurately, whereas the second one, will take an arbitrary parameter estimation which represents an outlier.
-
In the same way, let us consider the problem of the optimal placement of the sensorshN1, ...,NP , making the minimum MSRL s.t. the constraint that the total number of sensors is constant (i.e.,
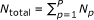 in which we suppose that Ntotal is a multiple of P).
in which we suppose that Ntotal is a multiple of P).
Corollary 2: If the total number of sensors Ntotal, is a multiple of P, then an optimal placement of the sensors that ensure the lowest MSRL is (see Figure 6 and 7)

Proof see Appendix 6.
Remark 3: Note that, in the case where Ntotal is not a multiple of P, one expects that the optimal MSRL is given in the case where the sensors distribution approaches the equi-sensors distribution situation given in corollary 3. Figure 7 confirms that (in the case of P = 3, N1 = 8 and a total number of sensors N = 22). From Figure 7, one can notice that the optimal distribution of the number of sensors corresponds to N2 = N3 = 7 and N1 = 8 which is the nearest situation to the equi-sensors distribution.
Conclusion
In this article, we have derived the MSRL for the multidimensional harmonic retrieval model. Toward this end, we have extended the concept of SRL to multiple parameters of interest per signal. First, we have used a hypothesis test approach. The applied test is shown to be asymptotically an uniformly most powerful test which is the strongest statement of optimality that one could hope to obtain. Second, we have linked the asymptotic MSRL based on the hypothesis test approach to a new extension of the SRL based on the Cramér-Rao bound approach. Using the Cramér-Rao bound and a proper change of variable formula, closed-form expression of the MSRL are given.
Finally, note that the concept of the MSRL can be used to optimize, for example, the waveform and/or the array geometry for a specific problem.
Appendix 1
The proof of Result 1
Appendix 1.1: In this appendix, we derive the MSRL using the l1 norm.
From CRB(ξ) where ξ= [ωTρT]T in which  , one can deduce
, one can deduce  where
where  in which
in which  . Thanks to the Jacobian matrix given by
. Thanks to the Jacobian matrix given by

where h = [g1g2 ... g
P
]T ⊗ [1 - 1]T, in which  and A = [0 I]. Using the change of variable formula
and A = [0 I]. Using the change of variable formula

one has

Consequently, after some calculus, one obtains

where  and where
and where  Finally using (30) one obtains (16)
Finally using (30) one obtains (16)
Appendix 1.2: In this part, we derive the MSRL using the lk norm for a given integer k ≥ 1. The aim of this part is to support the endnote a, which stays that using the l1 norm computing the MSRL using the l1 norm is for the calculation convenience.
Once again, from CRB(ξ), one can deduce  where
where  in which the distance between C1 and C2 using the l
k
norm is given by δ(k) ≜ k-norm
in which the distance between C1 and C2 using the l
k
norm is given by δ(k) ≜ k-norm  and where
and where  . The Jacobian matrix is given by
. The Jacobian matrix is given by

where h
k
= [1 - 1]T ⊗ [g1(k)g2(k) ... g
P
(k)]T, in which  and A = [0I]. Since |x| k can be written as
and A = [0I]. Since |x| k can be written as  . Thus, for × ≠ 0, one has
. Thus, for × ≠ 0, one has

Again, using the change of variable formula (29), one has

Consequently, after some calculus, one obtains

where  and where
and where  .
.
Consequently, note that resolving analytically the implicit equation (32) w.r.t. δ(k) is intractable (aside from some special cases). Whereas, resolving analytically the implicit equation (30) can be tedious but feasible (see section "MSRL closed form expression").
Furthermore, denoting g p (1) = g p , Across(1) ≜ Across and Adirect(1) ≜ Adirect and using (32) one obtains (16).
Appendix 2
Proof of Lemma 1
From (20) one can note the well-known property that the model signal parameters are decoupled from the noise variance [42]. Consequently, the block-diagonal structure in (21) is self-evident.
Now, let us prove (22). From (4), one obtains

where

Thus,

where s m = [s m (1) ... s m (L)]T. Using the distributivity of the Hermitian operator over the Kronecker product and the mixed-product property of the Kronecker product [43] and assuming, without loss of generality that p' < p, one obtains

On the other hand, one has

whereas

Finally, assuming known orthogonal wavefronts [38] (i.e.,  ) and replacing (35) and (34) into (33), one obtains
) and replacing (35) and (34) into (33), one obtains

where α m = [α m (1) ... α m (L)] for m ∈ {1, 2}: Consequently, using (36), F ω can be expressed as a block diagonal matrix

where each P × P block J m is defined by

where

Consequently, from (37) and (38) one obtains (22).
Appendix 3
Proof of Result 3
Using (22) one obtains

where  . In the following, we give a closed-form expression of G-1. One can notice that the matrix G has a particular structure such that it can be rewritten as the sum of a diagonal matrix and of a rank-one matrix: G = Q + γγT where
. In the following, we give a closed-form expression of G-1. One can notice that the matrix G has a particular structure such that it can be rewritten as the sum of a diagonal matrix and of a rank-one matrix: G = Q + γγT where  and
and  Thanks to this particular structure, an analytical inverse of G can easily be obtained. Indeed, using the matrix inversion lemma
Thanks to this particular structure, an analytical inverse of G can easily be obtained. Indeed, using the matrix inversion lemma

A straightforward calculus leads to the following results,

and

Consequently, replacing (41) and (42) into (40), one obtains

where  . Finally, replacing (43) into (39) one finishes the proof.
. Finally, replacing (43) into (39) one finishes the proof.
Appendix 4
Proof of Result 4
Using Results 1 and 3, one has

and

Consequently, replacing (44) and (45) into (16), one finishes the proof.
Appendix 5
Proof of Corollary 1
In this appendix, we minimize the MSRL under the constraint SNR1 + SNR2 = SNRtotal (where SNRtotal is a real fixed value). Since, the term  is independent from SNR1 and SNR2, minimizing δ is equivalent to minimize
is independent from SNR1 and SNR2, minimizing δ is equivalent to minimize  where
where

Using the method of Lagrange multipliers, the problem is as follows:

Thus, the Lagrange function is given by  where λ denotes the so-called Lagrange multiplier. A simple derivation leads to,
where λ denotes the so-called Lagrange multiplier. A simple derivation leads to,



Consequently, from (46) and (47), one obtains SNR1 = SNR1. Using (48), one obtains  . Using the constraint SNR1 + SNR2 = SNRtotal one deduces corollary 1.
. Using the constraint SNR1 + SNR2 = SNRtotal one deduces corollary 1.
Appendix 6
Minimizing δ w.r.t. N1, ..., N
P
is equivalent to minimizing the function  , where N= [N1 ... N
P
]T. However, since the numbers of sensors on each array, N1, ..., N
P
, are integers, the derivation of f(N) w.r.t. N is meaningless. Consequently, let us define the function
, where N= [N1 ... N
P
]T. However, since the numbers of sensors on each array, N1, ..., N
P
, are integers, the derivation of f(N) w.r.t. N is meaningless. Consequently, let us define the function  exactly as f (.) where the set of definition is ℝ P instead of ℕ P . Consequently,
exactly as f (.) where the set of definition is ℝ P instead of ℕ P . Consequently,

in which  are real (continuous) variables.
are real (continuous) variables.
Using the method of Lagrange multipliers, the problem is as follows:

where  is a real positive constant value. Thus, the Lagrange function is given by
is a real positive constant value. Thus, the Lagrange function is given by  where λ denotes the Lagrange multiplier. For a sufficient number of sensors, the Lagrange function can be approximated by
where λ denotes the Lagrange multiplier. For a sufficient number of sensors, the Lagrange function can be approximated by

where  . A simple derivation leads to,
. A simple derivation leads to,

This system of equations seems hard to solve. However, an obvious solution is given by  and
and  in which
in which  . Since,
. Since,  , thus the trivial solution is given by
, thus the trivial solution is given by  . Consequently, if
. Consequently, if  is a multiple of P then, the solution of minimizing the function
is a multiple of P then, the solution of minimizing the function  in ℝ P coincides the solution of minimizing the function f(N) in ℕ P . Thus, the optimal placement minimizing the MSRL is
in ℝ P coincides the solution of minimizing the function f(N) in ℕ P . Thus, the optimal placement minimizing the MSRL is  . This conclude the proof.
. This conclude the proof.
Endnotes
aThe notion of distance and closely spaced signals used in the following, is w.r.t. to the metric space (d, C), where d : C × C → ℝ in which d and C denote a metric and the set of the parameters of interest, respectively. bSee [2–9] for some practical examples for the multidimensional harmonic retrieval model. cThis study can be straightforwardly extended to other norms. The choice of the l1 is motivated by its calculation convenience (see the derivation of Result 1 and Appendix 1). Furthermore, since the MSRL is considered to be small (this assumption can be argued by the fact that the high-resolution algorithms have asymptotically an infinite resolving power [44]), thus all continuous p-norms are similar to (i.e., looks like) the l1 norm. More importantly, in a finite dimensional vector space, all continuous p-norms are equivalent [[45], p. 53], thus the choice of a specific norm is free. dNote that, due to the specific definition of the SRL in [13] (i.e., using the same notation as in [13],  and the restrictive assumption in [13] (u1 and u2 belong to the same plan), the SRL as defined in [13] cannot be used in the multidimensional harmonic context. eOne of the necessary conditions regardless the noise pdf is that
and the restrictive assumption in [13] (u1 and u2 belong to the same plan), the SRL as defined in [13] cannot be used in the multidimensional harmonic context. eOne of the necessary conditions regardless the noise pdf is that  . Meaning that each parameter of interest w.r.t. to the first signal
. Meaning that each parameter of interest w.r.t. to the first signal  can be as close as possible to the parameter of interest w.r.t. to the second signal
can be as close as possible to the parameter of interest w.r.t. to the second signal  , but not equal. This is not really a restrictive assumptions, since in most applications, having two or more identical parameters of interest is a zero probability event [[9], p. 53]. fNote that applying (15) for P = 1 and for κ(Pfa, Pd) = 1, one obtains the Smith criterion [11]. gWhere O(.) denotes the Landau notation [46]. hOne should note, that we assumed a uniform linear multi-array, and the problem is to find the optimal distribution of the number of sensors on each array. The more general case, i.e., where the optimization problem considers the non linearity of the multi-way array, is beyond the scope of the problem addressed herein.
, but not equal. This is not really a restrictive assumptions, since in most applications, having two or more identical parameters of interest is a zero probability event [[9], p. 53]. fNote that applying (15) for P = 1 and for κ(Pfa, Pd) = 1, one obtains the Smith criterion [11]. gWhere O(.) denotes the Landau notation [46]. hOne should note, that we assumed a uniform linear multi-array, and the problem is to find the optimal distribution of the number of sensors on each array. The more general case, i.e., where the optimization problem considers the non linearity of the multi-way array, is beyond the scope of the problem addressed herein.
Abbreviations
- CRB:
-
Cramér-Rao Bound
- DOAs:
-
direction of arrivals
- FIM:
-
Fisher information matrix
- GLRT:
-
generalized likelihood ratio test
- MLE:
-
maximum likelihood estimates
- MSRL:
-
multidimensional SRL
- PARAFAC:
-
PARallel FACtor
- pdf:
-
probability density function
- SNR:
-
signal-to-noise ratio
- SRL:
-
statistical resolution limit.
References
Jiang T, Sidiropoulos N, ten Berge J: Almost-sure identifiability of multidimensional harmonic retrieval. IEEE Trans. Signal Processing 2001,49(9):1849-1859. 10.1109/78.942615
Vanpoucke F: Algorithms and Architectures for Adaptive Array Signal Processing. Universiteit Leuven, Leuven, Belgium: Ph. D. dissertation; 1995.
Haardt M, Nossek J: 3-D unitary ESPRIT for joint 2-D angle and carrier estimation. Proc. of IEEE Int. Conf. Acoust., Speech, Signal Processing, Munich, Germany 1997, 1: 255-258.
Wong K, Zoltowski M: Uni-vector-sensor ESPRIT for multisource azimuth, elevation, and polarization estimation. IEEE Trans. Antennas Propagat 1997,45(10):1467-1474. 10.1109/8.633852
Mokios K, Sidiropoulos N, Pesavento M, Mecklenbrauker C: On 3-D harmonic retrieval for wireless channel sounding. Proc. of IEEE Int. Conf. Acoust., Speech, Signal Processing, Philadelphia, USA 2004, 2: 89-92.
Schneider C, Trautwein U, Wirnitzer W, Thoma R: Performance verification of MIMO concepts using multi-dimensional channel sounding. Proc. EUSIPCO, Florence, Italy 2006.
Nion D, Sidiropoulos N: A PARAFAC-based technique for detection and localization of multiple targets in a MIMO radar system. Proc. of IEEE Int. Conf. Acoust., Speech, Signal Processing, Taipei, Taiwan 2009.
Nion D, Sidiropoulos D: Tensor algebra and multi-dimensional harmonic retrieval in signal processing for MIMO radar. IEEE Trans. Signal Processing 2010, 58: 5693-5705.
Gershman A, Sidiropoulos N: Space-time processing for MIMO communications. New York: Wiley; 2005.
Boyer R: Decoupled root-MUSIC algorithm for multidimensional harmonic retrieval. Proc. IEEE Int. Work. Signal Processing, Wireless Communications, Recife, Brazil 2008, 16-20.
Smith ST: Statistical resolution limits and the complexified Cramér Rao bound. IEEE Trans. Signal Processing 2005, 53: 1597-1609.
Shahram M, Milanfar P: On the resolvability of sinusoids with nearby frequencies in the presence of noise. IEEE Trans. Signal Processing 2005,53(7):2579-2585.
Liu Z, Nehorai A: Statistical angular resolution limit for point sources. IEEE Trans. Signal Processing 2007,55(11):5521-5527.
Amar A, Weiss A: Fundamental limitations on the resolution of deterministic signals. IEEE Trans. Signal Processing 2008,56(11):5309-5318.
VanTrees HL: Detection, Estimation and Modulation Theory. Volume 1. New York: Wiley; 1968.
Cox H: Resolving power and sensitivity to mismatch of optimum array processors. J Acoust Soc Am 1973,54(3):771-785. 10.1121/1.1913659
Sharman K, Durrani T: Resolving power of signal subspace methods for fnite data lengths. Proc. of IEEE Int. Conf. Acoust., Speech, Signal Processing, Florida, USA 1995, 1501-1504.
Kaveh M, Barabell A: The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves in noise. Proc. ASSP Workshop on Spectrum Estimation and Modeling 1986,34(2):331-341.
Abeidam H, Delmas J-P: Statistical performance of MUSIC-like algorithms in resolving noncircular sources. IEEE Trans. Signal Processing 2008,56(6):4317-4329.
Lee HB: The Cramér-Rao bound on frequency estimates of signals closely spaced in frequency. IEEE Trans. Signal Processing 1992,40(6):1507-1517. 10.1109/78.139253
The Cramér-Rao bound on frequency estimates of signals closely spaced in frequency (unconditional case) IEEE Trans. Signal Processing 1994,42(6):1569-1572. 10.1109/78.286979
Dilaveroglu E: Nonmatrix Cramér-Rao bound expressions for high-resolution frequency estimators. IEEE Trans. Signal Processing 1998,46(2):463-474. 10.1109/78.655430
Smith ST: Accuracy and resolution bounds for adaptive sensor array processing. Proceedings in the ninth IEEE SP Workshop on Statistical Signal and Array Processing 1998, 37-40.
Delmas J-P, Abeida H: Statistical resolution limits of DOA for discrete sources. Proc. of IEEE Int. Conf. Acoust., Speech, Signal Processing, Toulouse, France 2006, 4: 889-892.
Liu X, Sidiropoulos N: Cramér-Rao lower bounds for low-rank decomposition of multidimensional arrays. IEEE Trans. Signal Processing 2002, 49: 2074-2086.
Boyer R: Deterministic asymptotic Cramér-Rao bound for the multidimensional harmonic model. Signal Processing 2008, 88: 2869-2877. 10.1016/j.sigpro.2008.06.011
Kusuma J, Goyal V: On the accuracy and resolution of powersum-based sampling methods. IEEE Trans. Signal Processing 2009,57(1):182-193.
Scharf LL: Statistical Signal Processing: Detection, Estimation, and Time Series Analysis. Reading: Addison Wesley; 1991.
Westin C: A Tensor Framework For Multidimensional Signal Processing. Citeseer. 1994.
Haardt M, Nossek J: Simultaneous Schur decomposition of several nonsymmetric matrices to achieve automatic pairing in multidimensional harmonic retrieval problems. IEEE Trans. Signal Processing 1998,46(1):161-169. 10.1109/78.651206
Roemer F, Haardt M, Galdo GD: Higher order SVD based subspace estimation to improve multi-dimensional parameter estimation algorithms. Proc. IEEE Int. Conf. Signals, Systems, and Computers Work 2007.
Pesavento M, Mecklenbrauker C, Bohme J: Multidimensional rank reduction estimator for parametric MIMO channel models. EURASIP Journal on Applied Signal Processing 2004, 9: 1354-1363.
Harshman R: Foundations of the PARAFAC procedure: Models and conditions for an "explanatory" multi-modal factor analysis. UCLA Working Papers in Phonetics. 1970.
Stoica P, Moses R: Spectral Analysis of Signals. NJ: Prentice Hall; 2005.
Kay SM: Fundamentals of Statistical Signal Processing: Detection Theory. Volume 2. NJ: Prentice Hall; 1998.
Ottersten B, Viberg M, Stoica P, Nehorai A: Exact and large sample maximum likelihood techniques for parameter estimation and detection in array processing. In Radar Array Processing. Volume ch 4. Edited by: Haykin S, Litva J, Shepherd TJ. Berlin: Springer-Verlag; 1993:99-151.
Renaux A, Forster P, Chaumette E, Larzabal P: On the high SNR conditional maximum-likelihood estimator full statistical characterization. IEEE Trans. Signal Processing 2006,12(54):4840-4843.
Li J, Compton RT: Maximum likelihood angle estimation for signals with known waveforms. IEEE Trans. Signal Processing 1993, 41: 2850-2862. 10.1109/78.236507
Cramér H: Mathematical Methods of Statistics. New York: Princeton University, Press; 1946.
Abramovich Y, Johnson B, Spencer N: Statistical nonidentifiability of close emitters: Maximum-likelihood estimation breakdown. EUSIPCO, Glasgow, Scotland 2009.
El Korso MN, Boyer R, Renaux A, Marcos S: Statistical resolution limit for multiple signals and parameters of interest. Proc. of IEEE Int. Conf. Acoust., Speech, Signal Processing, Dallas, TX 2010.
Kay SM: Fundamentals of Statistical Signal Processing. Volume 1. NJ: Prentice Hall; 1993.
Petersen KB, Pedersen MS:The matrix cookbook. ver. nov. 14, 2008 [http://matrixcookbook.com]
VanTrees HL: Detection, Estimation and Modulation theory: Optimum Array Processing. Volume 4. New York: Wiley; 2002.
Golub GH, Loan CFV: Matrix Computations. London: Johns Hopkins; 1989.
Cormen T, Leiserson C, Rivest R: Introduction to algorithms. The MIT press; 1990.
Acknowledgements
This project is funded by region Île de France and Digiteo Research Park. This work has been partially presented in communication [41].
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
El Korso, M.N., Boyer, R., Renaux, A. et al. Statistical resolution limit for the multidimensional harmonic retrieval model: hypothesis test and Cramér-Rao Bound approaches. EURASIP J. Adv. Signal Process. 2011, 12 (2011). https://doi.org/10.1186/1687-6180-2011-12
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-12
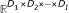 and
and 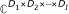 denote the real and complex multi-way arrays (also called tensors) body of dimension D1 × D2 ×
denote the real and complex multi-way arrays (also called tensors) body of dimension D1 × D2 × 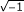 .
.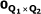 = the Q1 × Q2 matrix filled by zeros,
= the Q1 × Q2 matrix filled by zeros,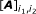 = the i1th row and the i2th column element of the matrix A,
= the i1th row and the i2th column element of the matrix A,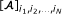 = the (i1, i2, ..., i
N
)th entry of the multi-way array
= the (i1, i2, ..., i
N
)th entry of the multi-way array 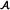 ,
,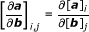 ,
,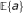 = the expectation of the random variable a,
= the expectation of the random variable a,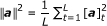 denotes the normalized norm of the vector a(in which L is the size of a),
denotes the normalized norm of the vector a(in which L is the size of a),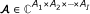 and
and 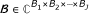 , the result of the outer-product of
, the result of the outer-product of  denoted by
denoted by 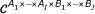 is given by
is given by 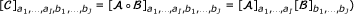 .
.

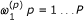 , can be as close as possible to the parameter of interest w.r.t. to the second signal
, can be as close as possible to the parameter of interest w.r.t. to the second signal 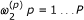 , but not equal. This is not really a restrictive assumption, since in most applications, having two or more identical parameters of interest is a zero probability event [[
, but not equal. This is not really a restrictive assumption, since in most applications, having two or more identical parameters of interest is a zero probability event [[
 which is consistent with some previous results for the case P = 1 (e.g., [
which is consistent with some previous results for the case P = 1 (e.g., [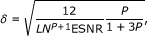
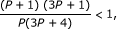



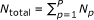 in which we suppose that Ntotal is a multiple of P).
in which we suppose that Ntotal is a multiple of P).
 as predicted by (28).
as predicted by (28).