- Research
- Open access
- Published:
Joint fundamental frequency and order estimation using optimal filtering
EURASIP Journal on Advances in Signal Processing volume 2011, Article number: 13 (2011)
Abstract
In this paper, the problem of jointly estimating the number of harmonics and the fundamental frequency of periodic signals is considered. We show how this problem can be solved using a number of methods that either are or can be interpreted as filtering methods in combination with a statistical model selection criterion. The methods in question are the classical comb filtering method, a maximum likelihood method, and some filtering methods based on optimal filtering that have recently been proposed, while the model selection criterion is derived herein from the maximum a posteriori principle. The asymptotic properties of the optimal filtering methods are analyzed and an order-recursive efficient implementation is derived. Finally, the estimators have been compared in computer simulations that show that the optimal filtering methods perform well under various conditions. It has previously been demonstrated that the optimal filtering methods perform extremely well with respect to fundamental frequency estimation under adverse conditions, and this fact, combined with the new results on model order estimation and efficient implementation, suggests that these methods form an appealing alternative to classical methods for analyzing multi-pitch signals.
Introduction
Periodic signals can be characterized by a sum of sinusoids, each parametrized by an amplitude, a phase, and a frequency. The frequency of each of these sinusoids, sometimes referred to as harmonics, is an integer multiple of a fundamental frequency. When observed, such signals are commonly corrupted by observation noise, and the problem of estimating the fundamental frequency from such observed signals is referred to as fundamental frequency, or pitch, estimation. Some signals contain many such periodic signals, in which case the problem is referred to as multi-pitch estimation, although this is somewhat of an abuse of terminology, albeit a common one, as the word pitch is a perceptual quality, defined more specifically for acoustical signals as "that attribute of auditory sensation in terms of which sounds may be ordered on a musical scale" [1]. In most cases, the fundamental frequency and pitch are related in a simple manner and the terms are, therefore, often used synonymously. The problem under investigation here is that of estimating the fundamental frequencies of periodic signals in noise. It occurs in many speech and audio applications, where it plays an important role in the characterization of such signals, but also in radar and sonar. Many different methods have been invented throughout the years to solve this problem, with some examples being the following: linear prediction [2], correlation [3–7], subspace methods [8–10], frequency fitting [11], maximum likelihood [12–16], cepstral methods [17], Bayesian estimation [18–20], and comb filtering [21–23]. Note that several of the listed methods can be interpreted in several ways, as we will also see examples of in this paper. For a general overview of pitch estimation methods, we refer the interested reader to [24].
The scope of this paper is filtering methods with application to estimation of the fundamental frequencies of multiple periodic signals in noise. First, we state the problem mathematically in Sect. II and introduce some useful notation and results after which we present, in Sect. III, some classical methods for solving the aforementioned problem. These are intimately related to the methods under consideration in this paper. Then, we present our optimal filter designs in Sect. IV. This work has recently been published by the authors [16, 25]. These designs are generalizations of Capon's classical optimal beamformer and are not novel to this paper, but the key aspects of this paper are based on them. The resulting filters are signal-adaptive and optimal in the sense that they minimize the output power while passing the harmonics of a periodic signal undistorted, and they have been demonstrated to have excellent performance for parameter estimation under adverse conditions [16]. Especially their ability to reject interfering periodic components is remarkable and important as it leads to a natural decoupling of the fundamental frequency estimation problem for multiple sources, a problem that otherwise involves multi-dimensional non-linear optimization. However, also the resulting filters' ability to adapt to the noise statistics without prior knowledge of these is worth noting. We also note that the filter designs along with related methods have been proven to work well for enhancement and separation of periodic signals [26]. After the presentation of the filters, an analysis of the properties of the optimal filtering methods follows in Sect. V which reveals some valuable insights. It should be noted that the first part of this analysis appeared also in [25], in a very brief form, but we here repeat it for completeness along with some additional details and information. It was shown in [9] that it is not only necessary for a fundamental frequency estimator to be optimal to also estimate the number of harmonics, but it is in fact also necessary to avoid ambiguities in the cost functions, something that is often the cause of spurious estimates at rational values of the fundamental frequency for single pitch estimation. In Sect. VI, we derive an order estimation criterion specifically for the signal model used through this paper, and, in Section VII, we show how to use this criterion in combination with the filtering methods. This order estimation criterion is based on the maximum a posteriori principle following [27]. Compared to traditional methods such as the comb filtering method [23] and maximum likelihood methods [12, 16], the optimal filtering methods suffer from a high complexity, requiring that operations of cubic complexity be performed for each candidate fundamental frequency and order. Indeed, this complexity may be prohibitive for many applications and to address this, we derive an exact order-recursive fast implementation of the optimal filtering methods in Sect. VIII. Finally, we present some numerical results in Sect. IX, comparing the performance of the estimators to other state-of-the-art estimators before concluding on our work in Sect. X.
Preliminaries
A signal containing a number of periodic components, termed sources, consists of multiple sets of complex sinusoids having frequencies that are integer multiples of a set of fundamental frequencies, {ω k }, and additive noise. Such a signal can be written for n = 0, ..., N - 1 as

where  is the complex-valued amplitude of the l th harmonic of the source, indexed by k, and e
k
(n) is the noise associated with the k th source which is assumed to be zero-mean and complex. The complex-valued amplitude is composed of a real, non-zero amplitude A
k, l
> 0 and a phase ϕ
k, l
. The number of sinusoids, L
k
, is referred to as the order of the model and is often considered known in the literature. However, this is often not the case for speech and audio signals, where the number of harmonics can be observed to vary over time. Furthermore, for some signals, the frequencies of the harmonics will not be exact integer multiples of the fundamental. There exists several modified signal models for dealing with this (e.g., [24, 28–32]), but this is beyond the scope of this paper and we will defer from any further discussion of this.
is the complex-valued amplitude of the l th harmonic of the source, indexed by k, and e
k
(n) is the noise associated with the k th source which is assumed to be zero-mean and complex. The complex-valued amplitude is composed of a real, non-zero amplitude A
k, l
> 0 and a phase ϕ
k, l
. The number of sinusoids, L
k
, is referred to as the order of the model and is often considered known in the literature. However, this is often not the case for speech and audio signals, where the number of harmonics can be observed to vary over time. Furthermore, for some signals, the frequencies of the harmonics will not be exact integer multiples of the fundamental. There exists several modified signal models for dealing with this (e.g., [24, 28–32]), but this is beyond the scope of this paper and we will defer from any further discussion of this.
We refer to signals of the form (1) as multi-pitch signals and the model as the multi-pitch model. The special case with K = 1 is referred to as a single-pitch signal. The methods under consideration can generally be applied to multi-pitch signals (and will be in the experiments), but when we wish to emphasize that the derivations strictly speaking only hold for single-pitch signal, those will be based on x k (n) and related quantities. It should be noted that even if a recording is only of a single instrument, the signal may still be multi-pitch as only a few instruments are monophonic. Room reverberation may also cause the observed signal to consist of several different tones at a particular time instance.
We define a sub-vector as consisting of M, with M ≤ N (we will introduce more strict bounds later), time-reversed samples of the observed signal, as

where (·)T denotes the transpose, and similarly for the sources x
k
(n) and the noise e
k
(n). Next, we define a Vandermonde matrix  , which is constructed from a set of L
k
harmonics, each defined as
, which is constructed from a set of L
k
harmonics, each defined as

leading to the matrix

and a vector containing the corresponding complex amplitudes as  . Introducing the following matrix
. Introducing the following matrix

the vectorized model in (1) can be expressed as


It can be seen that the complex amplitudes can be thought of as being time-varying, i.e., a k(n) = D n a k. Note that it is also possible to define the signal model such that the Vandermonde matrix is time-varying.
In the remainder of the text, we will make extensive use of the covariance matrix of the sub-vectors. Let E {·} and (·)H denote the statistical expectation operator and the conjugate transpose, respectively. The covariance matrix is then defined as

and similarly we define R k for x k(n). Assuming that the various sources are statistically independent, the covariance matrix of the observed signal can be written as


where the matrix P k is the covariance matrix of the amplitudes, which is defined as

For statistically independent and uniformly distributed phases (on the interval (-π, π]), this matrix reduces to the following (see [33]):

with diag (·) being an operator that generates a diagonal matrix from a vector. Furthermore, Q
k
is the covariance matrix of the noise e
k
( n ), i.e.,  . The sample covariance matrix, defined as
. The sample covariance matrix, defined as

is used as an estimate of the covariance matrix. It should be stressed that for  to be invertible, we require that
to be invertible, we require that  . Throughout the text, we generally assume that M is chosen proportionally to N, something that is essential to the consistency of the proposed estimators.
. Throughout the text, we generally assume that M is chosen proportionally to N, something that is essential to the consistency of the proposed estimators.
Classical methods
Comb filter
One of the oldest methods for pitch estimation is the comb filtering method [21, 22], which is based on the following ideas. Mathematically, we can express periodicity as x(n) ≈ x(n - D) where D is the repetition or pitch period. From this observation it follows that we can measure the extent to which a certain waveform is periodic using a metric on the error e(n), defined as e(n) = x(n) - αx(n - D). The Z-transform of this is E(z) = X(z)(1 - αz-D ). This shows that the matching of a signal with a delayed version of itself can be seen as a filtering process, where the output of the filter is the modeling error e(n). This can of course also be seen as a prediction problem, only the unknowns are not just the filter coefficient α but also the lag D. If the pitch period is exactly D, the output error is just the observation noise. Usually, however, the comb filter is not used in this form as it is restricted to integer pitch periods and is rather inefficient in several ways. Instead, one can derive more efficient methods based on notch filters [23]. Notch filters are filters that cancel out, or, more correctly, attenuate signal components at certain frequencies. Periodic signals can be comprised of a number of harmonics, for which reason we use L k such filters having notches at frequencies {ψ i }. Such a filter can be factorized into the following form

i.e., consisting of a polynomial that has zeros on the unit circle at angles corresponding to the desired frequencies. From this, one can define a polynomial  where 0 < ρ < 1 is a parameter that leads to poles located inside the unit circle at the same angles as the zeros of P(z) but at a distance of ρ from the origin. ρ is typically in the range 0.95-0.995 [23]. For our purposes, the desired frequencies are given by ψ
l
= ω
k
l, where ω
k
is considered an unknown parameter. As a consequence, the zeros of (14) are distributed uniformly on the unit circle in the z-plane. By combining P(z) and P(ρ-1z), we obtain the following filter:
where 0 < ρ < 1 is a parameter that leads to poles located inside the unit circle at the same angles as the zeros of P(z) but at a distance of ρ from the origin. ρ is typically in the range 0.95-0.995 [23]. For our purposes, the desired frequencies are given by ψ
l
= ω
k
l, where ω
k
is considered an unknown parameter. As a consequence, the zeros of (14) are distributed uniformly on the unit circle in the z-plane. By combining P(z) and P(ρ-1z), we obtain the following filter:

where {β l } are the complex filter coefficients that result from expanding (14). This filter can be used by filtering the observed signal x(n) for various candidate fundamental frequencies to obtain the filtered signal e(n) where the harmonics have been attenuated. This can also be expressed as E(z) = X(z)H(z) which results in the following difference function:

By imposing a metric on e(n) and considering the fundamental frequency to be an unknown parameter, we obtain the estimator

from which ρ can also be found in a similar manner as done in [23], if desired. In [23], this is performed in a recursive manner given an initial fundamental frequency estimate, leading to a computationally efficient scheme that can be used for either suppressing or extracting the periodic signal from the noisy signal.
Maximum likelihood estimator
Perhaps the most commonly used methodology in estimators is maximum likelihood. Interestingly, the maximum likelihood estimator for white Gaussian noise can also be interpreted as a filtering method when applied to the pitch estimation problem. First, we will briefly present the maximum likelihood pitch estimator. For an observed signal x
k
with M=N (note that we have omitted the dependency on n for this special case)consisting of white Gaussian noise and one source, the log-likelihood function ln  is given by
is given by

By maximizing (18), the maximum likelihood estimates of ω
k
, a k, and,  are obtained. The expression can be seen to depend on the unknown noise variance
are obtained. The expression can be seen to depend on the unknown noise variance  and the amplitudes a k, both of which are of no interest to us here. To eliminate this dependency, we proceed as follows. Given ω
k
and L
k
, the maximum likelihood estimate of the amplitudes is obtained as
and the amplitudes a k, both of which are of no interest to us here. To eliminate this dependency, we proceed as follows. Given ω
k
and L
k
, the maximum likelihood estimate of the amplitudes is obtained as

and the noise variance as

The matrix Π Z in (20) is the projection matrix which can be approximated as

This is essentially because the columns of Z k are complex sinusoids that are asymptotically orthogonal. Using this approximation, the noise variance estimate can be simplified significantly, i.e.,

which leaves us with a log-likelihood function that depends only on the fundamental frequency. We can now express the maximum likelihood pitch estimator as


Curiously, the last expression can be rewritten into a different form that leads to a familiar estimator:


which shows that harmonic summation methods [12, 34] are in fact approximate maximum likelihood methods under certain conditions. We note that it can be seen from these derivations that, under the aforementioned conditions, the minimization of the 2-norm leads to the maximum likelihood estimates. Since the fundamental frequency is a nonlinear parameter, this approach is sometimes referred to as the nonlinear least-squares (NLS) method.
Next, we will show that the approximate maximum likelihood estimator can also be seen as a filtering method. First, we introduce the output signal yk, l(n) of the l th filter for the k th source having coefficients hk, l(n) as

with hk, lbeing a vector containing the filter coefficients of the l th filter, i.e.,

The output power of the l th filter can be expressed in terms of the covariance matrix R k as


The total output power of all the filters is thus given by


where H
k
is a filterbank matrix containing the individual filters, i.e.,  and Tr[·] denotes the trace. The problem at hand is then to choose or design a filter or a filterbank. Suppose we construct the filters from finite length complex sinusoids as
and Tr[·] denotes the trace. The problem at hand is then to choose or design a filter or a filterbank. Suppose we construct the filters from finite length complex sinusoids as

which is the same as the vector z(ω k l) defined earlier. The matrix H k is therefore also identical to the Vandermonde matrix Z k. Then, we may express the total output power of the filterbank as


This shows that by replacing the expectation operator by a finite sum over the realizations x k(n), we get the approximate maximum likelihood estimator, only we average over the sub-vectors x k(n). By using only one sub-vector of length N, leaving us with just a single observed sub-vector, the method becomes asymptotically equivalent (in N) to the NLS method and, therefore, the maximum likelihood method for white Gaussian noise. For more on the relation between various spectral estimators and filterbank methods, we refer the interested reader to [33, 35].
Optimal filter designs
We will now delve further into signal-adaptive and optimal filters and in doing so we will make use of the notation and definitions of the previous section. Two desirable properties of a filterbank for our application is that the individual filters pass power undistorted at specific frequencies, here integer multiples of the fundamental frequency, while minimizing the power at all other frequencies. This problem can be stated mathematically as the following quadratic constrained optimization problem:

Here, I is the L k × L k identity matrix. The matrix constraints specify that the Fourier transforms of the filterbank should have unit gain at the l th harmonic frequency and zero for the others. Using the method of Lagrange multipliers, we obtain that the filter bank matrix H k solving (36) is (see [16] for details)

which is a data and fundamental frequency dependent filter bank. It can be used to estimate the fundamental frequency by evaluating the output power of the filterbank for a set of candidate fundamental frequencies, i.e.,

Suppose that instead of designing a filterbank, we design a single filter for the k th source, h k that passes the signal undistorted at the harmonic frequencies while otherwise minimizing the output power. This problem can be stated mathematically as


The single filter in (39) is designed subject to L k constraints, whereas the filterbank design problem in (36) is stated using number of constraints for each filter. In solving for the optimal filter, we proceed as before by using the Lagrange multiplier method, whereby we get the optimal filter expressed in terms of the covariance matrix and the (unknown) Vandermonde matrix Z k, i.e.,

where 1 = [1 ... 1]T. The output power of this filter can then be expressed as

By maximizing the output power, we can obtain an estimate of the fundamental frequency as

Properties
We will now relate the two filter design methods and the associated estimators in (38) and (42). Comparing the optimal filters in (37) and (40), two facts can be established. First, the two cost functions are generally different as


with equality only  when is diagonal. Second, the two methods are clearly related in some way as the single filter can be expressed in terms of the filterbank, i.e., h
k
= H k 1. To quantify under which circumstances
when is diagonal. Second, the two methods are clearly related in some way as the single filter can be expressed in terms of the filterbank, i.e., h
k
= H k 1. To quantify under which circumstances  is diagonal and thus when the methods are equivalent, we will analyze the properties of
is diagonal and thus when the methods are equivalent, we will analyze the properties of  , which figures in both estimators. More specifically, we analyze the asymptotic properties of the expression, i.e.,
, which figures in both estimators. More specifically, we analyze the asymptotic properties of the expression, i.e.,

where M has been introduced to ensure convergence. We here assume M to be chosen proportional to N, so asymptotic analysis based on M going towards infinity simply means that we let the number of observations tend to infinity. For simplicity, we will in the following derivations assume that the power spectral density of x(n) is finite and non-zero. Although this is strictly speaking not the case for our signal model, the analysis will nonetheless provide some insights into the properties of the filtering methods. The limit in (45) can be rewritten as (see [25] for more details on this subtlety)

which leads to the problem of determining the inner limit. To do this, we make use of the asymptotic equivalence of Toeplitz and circulant matrices. For a given Toeplitz matrix, here R, we can construct an asymptotically equivalent circulant M × M matrix C in the sense that [36]

where ||·||F is the Frobenius norm and the limit is taken over the dimensions of C and R. The conditions under which this was derived in [36] apply to the noise covariance matrix when the stochastic components are generated by a moving average or a stable auto-regressive process. More specifically, the auto-correlation sequence has to be absolutely summable. The result also applies to the deterministic signal components as Z k P k Z k is asymptotically the EVD of the covariance matrix of Z k a k (except for a scaling) and circulant. A circulant matrix C has the eigenvalue decomposition C = UΓUH where U is the Fourier matrix. Thus, the complex sinusoids in Z k are asymptotically eigenvectors of R. Therefore, the limit is (see [36, 37])

with Φx(ω) being the power spectral density of x(n). Similarly, an expression for the inverse of R can be obtained as C-1 = UΓ-1UH (again, see [36] for details). We now arrive at the following (see also [37] and [38]):

This shows that the expression in (42) asymptotically tends to the following:

and similarly for the filterbank formulation:

We conclude that the methods are asymptotically equivalent, but may be different for finite M and N. In [25], the two approaches were also reported to have similar performance although the output power estimates deviate. An interesting consequence of the analysis in this section is that the methods based on optimal filtering yield results that are asymptotically equivalent to those obtained using the NLS method.
The two methods based on optimal filtering involve the inverse covariance matrix and we will now analyze the properties of the estimators further by first finding a closed-form expression for the inverse of the covariance matrix based on the covariance matrix model. For the single-pitch case, the covariance matrix model is


and, for simplicity, we will use this model in the following. A variation of the matrix inversion lemma provides us with a useful closed-form expression of the inverse covariance matrix model, i.e.,

Note that  exists for a set of sinusoids having distinct frequencies and non-zero amplitudes and so does the inverse noise covariance matrix
exists for a set of sinusoids having distinct frequencies and non-zero amplitudes and so does the inverse noise covariance matrix  as long as the noise has non-zero variance.
as long as the noise has non-zero variance.
Proceeding in our analysis, we evaluate the expression for a candidate fundamental frequency resulting in a Vandermonde matrix that we denote  . Based on this definition, we get the following expression:
. Based on this definition, we get the following expression:


As before, we normalize this matrix to analyze its behavior as M grows, i.e.,

Noting that  , we obtain
, we obtain

Furthermore, by substituting  by Z k, i.e., by evaluating the expression for the true fundamental frequency, we get
by Z k, i.e., by evaluating the expression for the true fundamental frequency, we get

This shows that the expression tends to the zero matrix as M approaches infinity for the true fundamental frequency. The cost functions of the two optimal filtering approaches in (50) and (51) therefore can be thought of as tending towards infinity.
Because the autocorrelation sequence of the noise processes e k (n) can safely be assumed to be absolutely summable and have a smooth and non-zero power spectral density Φek(ω) the results of [36, 38] can be applied directly to determine following limit:

For the white noise case, the noise covariance matrix is diagonal, i.e.,  . The inverse of the covariance matrix model is then
. The inverse of the covariance matrix model is then

Next, we note that asymptotically, the complex sinusoids in the columns of Z k are orthogonal, i.e.,

Therefore, for large M (and thus N), the inverse covariance matrix can be approximated as

It can be observed that the remaining inverse matrix involves two diagonal matrices that can be rewritten as


which leads to the inverse

Finally, we arrive at the following expression, which is an asymptotic approximation of the inverse of the matrix covariance model:

Interestingly, it can be seen that the inverse covariance matrix asymptotically exhibits a similar structure to that of the covariance matrix model.
Order estimation
We will now consider the problem of finding the model order L k . This problem is a special case of the general model selection problem, where the models under consideration are nested as the simple models are special cases of the more complicated models. Many methods for dealing with this problem have been investigated over the years, but the most common ones for order selection are the Akaike information criterion (AIC) [39] and the minimum description length criterion (MDL) [40] (see also [41]). Herein, we derive a model order selection criterion using the asymptotic MAP approach of [27, 42] (see also [43]), a method that penalizes linear and nonlinear parameters differently. We will do this for the single-pitch case, but the principles can be used for multi-pitch signals too. First, we introduce a candidate model index set

and the candidate models  with m ∈ ℤq. We will here consider the problem of estimating the number of harmonics for a single source from a single-pitch signal x k. In the following, f(·) denotes probability density function (PDF) of the argument (with the usual abuse of notation).
with m ∈ ℤq. We will here consider the problem of estimating the number of harmonics for a single source from a single-pitch signal x k. In the following, f(·) denotes probability density function (PDF) of the argument (with the usual abuse of notation).
The principle of MAP-based model selection can be explained as follows: Choose the model that maximizes the a posteriori probability  of the model given the observation x k. This can be stated mathematically as
of the model given the observation x k. This can be stated mathematically as


Noting that the probability of x k, i.e., f (x k), is constant once x
k
has been observed and assuming that all the models are equally probable  , the MAP model selection criterion reduces to
, the MAP model selection criterion reduces to

which is the likelihood function when seen as a function of ℳk. The various candidate models depend on a number of unknown parameters, in our case amplitudes, phases and fundamental frequency, that we here denote θ k . To eliminate this dependency, we seek to integrate those parameters out, i.e.,

However, simple analytic expression for this integral does not generally exist, especially so for complicated nonlinear models such as the one used here. We must therefore seek another, possibly approximate, way of evaluating this integral. One such way is numerical integration, but we will here instead follow the Laplace integration method as proposed in [27, 42].
The first step is as follows. Define g(θ
k
) as the integrand in (71), i.e., g(θ
k
) = f (x k|θ
k
, ℳm) f (θ
k
|ℳm). Next, let  be the mode of g(θ
k
), i.e., the MAP estimate. Using a Taylor expansion of g(θ
k
) in
be the mode of g(θ
k
), i.e., the MAP estimate. Using a Taylor expansion of g(θ
k
) in  , the integrand in (71) can be approximated as
, the integrand in (71) can be approximated as

where  the Hessian of the logarithm of g(θ
k
) evaluated in
the Hessian of the logarithm of g(θ
k
) evaluated in  , i.e.,
, i.e.,

Note that the Taylor expansion of the function in (72) is of a real function in real parameters, even if the likelihood function is for complex quantities. The above results in the following simplified expression for (71):

The integral involved in this expression involves a quadratic expression that is much simpler than the highly nonlinear one in (71). It can be shown to be

where |·| is the matrix determinant and D k the number of parameters in θ k . The expression in (71) can now be written as [27, 42] (see also [43])

Next, assuming a vague prior on the parameters given the model, i.e., on f(θ
k
|ℳm), g(θ
k
) reduces to a likelihood function and  to the maximum likelihood estimate. Note that this will also be the case for large N, as the MAP estimate will then converge to the maximum likelihood estimate. In that case, the Hessian matrix reduces to
to the maximum likelihood estimate. Note that this will also be the case for large N, as the MAP estimate will then converge to the maximum likelihood estimate. In that case, the Hessian matrix reduces to

which is sometimes referred to as the observed information matrix. This matrix is related to the Fisher information matrix in the following way: it is evaluated in  instead of the true parameters and no expectation is taken. However, it was shown in [43] that (77) can be used as an approximation (for large N) of the Fisher information matrix, and, hence, also vice versa, leading to the following approximation:
instead of the true parameters and no expectation is taken. However, it was shown in [43] that (77) can be used as an approximation (for large N) of the Fisher information matrix, and, hence, also vice versa, leading to the following approximation:

The benefit of using (78) over (77) is that the former is readily available in the literature for many models, something that also is the case for our model [9].
Taking the logarithm of the right-hand side of (76) and sticking to the tradition of ignoring terms of order  and
and  (which are negligible for large N), we get that under the aforementioned conditions, (70) can be written as
(which are negligible for large N), we get that under the aforementioned conditions, (70) can be written as

which can be used for determining which models is the most likely explanation for the observed signal. Now we will derive a criterion for selecting the model order of the single-pitch model and detecting the presence of a periodic source.
Based on the Fisher information matrix as derived in [9], we introduce the normalization matrix (see [43])

where I is an 2L k × 2L k identity matrix. The diagonal terms are due to the fundamental frequency and the L k amplitudes and phases, respectively. The determinant of the Hessian in (79) can be written as

By observing that  and taking the logarithm, we obtain the following expression:
and taking the logarithm, we obtain the following expression:



Assuming that the observation noise is white and Gaussian distributed, the log-likelihood function in (79) depends only on the term  where
where  is replaced by an estimate for each candidate order L
k
. We denote this estimate as
is replaced by an estimate for each candidate order L
k
. We denote this estimate as  . Finally, substituting (84) into (79), the following simple and useful expression for selecting the model order is obtained:
. Finally, substituting (84) into (79), the following simple and useful expression for selecting the model order is obtained:

Note that for low N, the inclusion of the term  may lead to more accurate results. To determine whether any harmonics are present at all, i.e., performing pitch detection, the above cost function should be compared to the log-likelihood of the zero order model, meaning that no harmonics are present if
may lead to more accurate results. To determine whether any harmonics are present at all, i.e., performing pitch detection, the above cost function should be compared to the log-likelihood of the zero order model, meaning that no harmonics are present if

where, in this case,  is simply the variance of the observed signal. The rule in (86) is essentially a pitch detection rule as it detects the presence of a pitch. It can be seen that both (85) and (86) require the determination of the noise variance for each candidate model order. The criterion in (85) reflects the tradeoff between the variance of the residual and the complexity of the model. For example, for a high model order, the estimated variance will be low, but the number of parameters will be high. Conversely, for a low model order, there are only few parameters but a high variance residual.
is simply the variance of the observed signal. The rule in (86) is essentially a pitch detection rule as it detects the presence of a pitch. It can be seen that both (85) and (86) require the determination of the noise variance for each candidate model order. The criterion in (85) reflects the tradeoff between the variance of the residual and the complexity of the model. For example, for a high model order, the estimated variance will be low, but the number of parameters will be high. Conversely, for a low model order, there are only few parameters but a high variance residual.
Variance estimation
As we have seen, the order selection criterion requires that the noise variance is estimated, and we will now show how to use these filters for estimating the variance of the signal by filtering out the harmonics. We will do this based on the filterbank design. First, we define an estimate of the noise obtained from x(n) as

which we will refer to as the residual. Moreover, y k (n) is the sum of the input signal filtered by the filterbank, i.e.,


where h k (m) is the sum over the impulse responses of the filters of the filterbank. From the relation between the single filter design and the filterbank design, it is now clear that when used this way, the two approaches lead to the same output signal y k (n). This also offers some insights into the difference between the designs in (36) and (39). More specifically, the difference is in the way the output power is measured, where (36) is based on the assumption that the power is additive over the filters, i.e., that the output signals are uncorrelated. We can now write the noise estimate as


where g k = [(1 - h k (0)) - h k (1) ⋯ - h k (M - 1)]H is the modified filter. From the noise estimate, we can then estimate the noise variance for the L k th order model as


This expression is, however, not very convenient for a number of reasons: A notable property of the estimator in (42) is that it does not require the calculation of the filter and that the output power expression in (41) is simpler than the expression for the optimal filter in (40). To use (93) directly, we would first have to calculate the optimal filter using (40), then calculate the modified filter g k, before evaluating (93). Instead, we simplify the evaluation of (93) by defining the modified filter as g k = b1- h k where, as defined earlier,

Next, we use this definition to rewrite the variance estimate as


The first term can be identified to equal the variance of the observed signal x(n), i.e.,  , and
, and  we know from (41). Writing out the cross-terms
we know from (41). Writing out the cross-terms  using (40) yields
using (40) yields


Furthermore, it can easily be verified that  , from which it can be concluded that
, from which it can be concluded that


Therefore, the variance estimate can be expressed as

where  is simply the variance of the observed signal. The variance estimate in (101) involves the same expression as in the fundamental frequency estimation criterion in (42), which means that the same expression can be used for estimating the model order and the fundamental frequency, i.e., the approach allows for joint estimation of the model order and the fundamental frequency. The variance estimate in (101) also shows that the same filter that maximizes the output power minimizes the variance of the residual. A more conventional variance estimate could be formed by first finding the frequency using, e.g., (42) and then finding the amplitudes of the signal model using (weighted) least-squares [38] to obtain a noise variance estimate. Since the discussed procedure uses the same information in finding the fundamental frequency and the noise variance, it is superior to the least-squares approach in terms of computational complexity. Note that for finite filter lengths, the output of the filters considered here are generally "power levels" and not power spectral densities (see [44]), which is consistent with our use of the filters for estimating the variance. Asymptotically, the filters do comprise power spectral density estimates [25].
is simply the variance of the observed signal. The variance estimate in (101) involves the same expression as in the fundamental frequency estimation criterion in (42), which means that the same expression can be used for estimating the model order and the fundamental frequency, i.e., the approach allows for joint estimation of the model order and the fundamental frequency. The variance estimate in (101) also shows that the same filter that maximizes the output power minimizes the variance of the residual. A more conventional variance estimate could be formed by first finding the frequency using, e.g., (42) and then finding the amplitudes of the signal model using (weighted) least-squares [38] to obtain a noise variance estimate. Since the discussed procedure uses the same information in finding the fundamental frequency and the noise variance, it is superior to the least-squares approach in terms of computational complexity. Note that for finite filter lengths, the output of the filters considered here are generally "power levels" and not power spectral densities (see [44]), which is consistent with our use of the filters for estimating the variance. Asymptotically, the filters do comprise power spectral density estimates [25].
By inserting (101) in (85), the model order can be determined using the MAP criterion for a given fundamental frequency. By combining the variance estimate in (101) with (85), we obtain the following fundamental frequency estimator for the case of unknown model orders (for L k > 0):

where the model order is also estimated in the process. To determine whether any harmonics are present at all, the criterion in (86) can be used.
Order-recursive implementation
Both the filterbank method and the single filter method require the calculation of the following matrix for every combination of candidate fundamental frequencies and orders:

where  denotes the inverse matrix for an order L
k
model. The respective cost function are formed from (103) as either the trace or the sum of all elements of this matrix. Since this requires a matrix inversion of cubic complexity for each pair, there is a considerable computational burden of using these methods. We will now present an efficient implementation of the matrix inversion in (103). The methods also require that the inverse covariance matrix be calculated, but this is less of a concern for two reasons. Firstly, it is calculated only once per segment, and, secondly, many standard methods exist for updating the matrix inverse over time (see, e.g., [45]).
denotes the inverse matrix for an order L
k
model. The respective cost function are formed from (103) as either the trace or the sum of all elements of this matrix. Since this requires a matrix inversion of cubic complexity for each pair, there is a considerable computational burden of using these methods. We will now present an efficient implementation of the matrix inversion in (103). The methods also require that the inverse covariance matrix be calculated, but this is less of a concern for two reasons. Firstly, it is calculated only once per segment, and, secondly, many standard methods exist for updating the matrix inverse over time (see, e.g., [45]).
The fast implementation that we will now proceed to derive, is based on the matrix inversion lemma, and is basically a recursion over the model order. To apply the matrix inversion lemma to the calculation of (103), we first define the matrix composed of vectors corresponding to the L k - 1 first harmonics of the full matrix Z k as

and a vector containing the last harmonic L k as

Using these definitions, we can now rewrite (103) as


Next, define the scalar quantity

which is real and positive since R-1 is positive-definite and Hermitian, and the vector

We can now express the matrix in (103) in terms of the order (L
k
- 1) matrix  , and
, and  as
as

This can be rewritten as follows:


This shows that once  is known,
is known,  can be obtained in a simple way. To use this result to calculate the cost functions for the estimators (38) and (42) for a model order L
k
, we proceed as follows. For a given ω
k
, calculate the order 1 inverse matrix as
can be obtained in a simple way. To use this result to calculate the cost functions for the estimators (38) and (42) for a model order L
k
, we proceed as follows. For a given ω
k
, calculate the order 1 inverse matrix as

and then for l = 2, ..., L k calculate the quantities needed to update the inverse matrix, i.e.,






using which the estimators in (38) and (42) along with the variance estimate in (101) can easily be implemented. In assessing the efficiency of the proposed recursion, we will use the following assumptions:
-
Matrix-vector product: the computation of Ax where
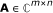 and
and 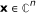 requires
requires 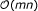 operations.
operations. -
Matrix-matrix product: the computation of AB where
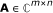 and
and 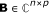 requires
requires 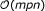 operations.
operations. -
Matrix inversion: the computation of A-1 where
 requires
requires 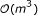 operations.
operations.
The number of operations required to calculate the matrix inverse in (103) is determined by the filter length M and the number of harmonics L
k
. This leads to a complexity of  for the direction implementation of (103). On the other hand, an update (from the (l - 1)th order model to the l th order model) in the order-recursive implementation requires
for the direction implementation of (103). On the other hand, an update (from the (l - 1)th order model to the l th order model) in the order-recursive implementation requires  operations with l = 1, ..., L
k
. For the case where only the cost for an order L
k
model needs to be calculated, the saving is negligible. On the other hand, if the order is unknown and the cost function has to be calculated for a wide range of orders, e.g., L
k
= 1, 2, ..., only a single update is required as the information from prior iterations are simply reused. At this point it should also be noted that the filter length and thus the covariance matrix size is generally much larger than the model order, i.e., M ≫ L
k
. In Figure 1, the approximate complexities of the respective implementations are depicted for M = 50.
operations with l = 1, ..., L
k
. For the case where only the cost for an order L
k
model needs to be calculated, the saving is negligible. On the other hand, if the order is unknown and the cost function has to be calculated for a wide range of orders, e.g., L
k
= 1, 2, ..., only a single update is required as the information from prior iterations are simply reused. At this point it should also be noted that the filter length and thus the covariance matrix size is generally much larger than the model order, i.e., M ≫ L
k
. In Figure 1, the approximate complexities of the respective implementations are depicted for M = 50.
It should be stressed that this order recursive implementation is exact as no approximations are involved, meaning that it implements exactly the matrix inversion in (103). We note in passing that, as usual, all the inner products involving complex sinusoids of different frequencies can be calculated efficiently using FFTs.
Experimental results
First, we will provide an illustrative example of what the derived optimal filters may look like. In Figure 2, an example of such filters are given with the magnitude response of the optimal filterbank and the single filter being shown for white Gaussian noise with ω1 = 1.2566 and L1 = 3. It should be stressed that for a non-diagonal R, i.e., when the observed signal contains sinusoids and/or colored noise, the resulting filters can look radically different.
We will now evaluate the statistical performance of the proposed scheme. In doing so, we will compare to some other methods based on well-established estimation theoretical approaches that are able to jointly estimate the fundamental frequency and the order, namely a subspace method, the MUSIC method of [9], and the NLS method [16]. The NLS method in combination with the criterion (85) yields both a maximum likelihood fundamental frequency estimate and a MAP order estimate (see [27] for details) and it is asymptotically a filtering method as described in Sect. III. More specifically, noise variance estimates are obtained using (20) after which the order estimation criterion is applied. For a finite number of samples, however, the exact NLS used here is superior to the filtering method of Sect. III. We remark that the NLS, MUSIC and optimal filtering methods under consideration here are comparable in terms of computational efficiency as they all have cubic complexity, involving either inverses of matrices, matrix-matrix products or eigenvalue decompositions of matrices. Additionally, we also compare to the performance of the comb filtering method described in Sect. III combined with the criterion (85). We will here focus on their application to order estimation, investigating the performance of the estimators given the fundamental frequency. The reason for this is simply that the high-resolution estimation capabilities of the proposed method, MUSIC and NLS for the fundamental frequency estimation problem for both single- and multi-pitch signals are already well-documented in [9, 16, 25], and there is little reason to repeat those experiments here. We note that the NLS method reduces to a linear least-squares method when the fundamental frequency is given, but the joint estimator is still nonlinear. The statistical order estimation criterion in (85) was derived based on x k, i.e., a single-pitch model, and none of the methods considered in this paper take additional sources into account in an explicit manner. Since one cannot generally assume that only a single periodic source is present, we will test the methods for a multi-pitch signal containing two sources, namely the signal of interest and an interfering periodic source that is considered to be of no interest to us. However, we will use all the methods as if only one source is present, thereby testing the robustness of the respective methods. In the experiments the following additional conditions were used: a periodic signal was generated using (1) with a fundamental frequency of ω1 = 0.8170, L1 = 5 and A l = 1 ∀l along with an interfering periodic source having the same number of harmonics and amplitude distribution but with ω2 = 1.2. For each test condition, 1000 Monte Carlo iterations were run. In the first experiment, we will investigate the performance as a function of the pseudo signal-to-noise (PSNR) as defined in [9]. Note that this PSNR is higher than the usual SNR, meaning that the conditions are more noisy than they may appear at first sight. The performance of the estimators has been evaluated for N = 200 observed samples with a covariance matrix size/filter length of M = 50. The results are shown in Figure 3 in terms of the percentage of correctly estimated orders. Similarly, the performance is investigated as a function of N with M = N/4 in the second experiment for PSNR = 40 dB, i.e., the filter length is set proportionally to the number of samples. Note that the NLS method operates on the entire length N signal and thus does not depend on M. This experiment thus reveals not only the dependency of the performance on the number of observed samples but also on the filter length. The results are shown in Figure 4. Similarly, it is interesting to investigate the importance of the number of unknown parameters relative to the number of samples. Consequently, an experiment has been carried out to do exactly this with the results being shown in Figure 5. The signals were generated as before with N = 400 for PSNR = 40 dB with M = N/ 4 while L k was varied from 1 to 10. In the final experiment, the N is kept fixed while the filter length M is varied with PSNR = 40 dB. In the process, the covariance matrix of MUSIC is varied too. The results can be seen in Figure 6.
From the figures, it can be observed that the proposed method shows good performance for high PSNRs and N with the percentage approaching 100%. Furthermore, it can also be observed that the filter length should not be chosen too low or too close to N/2. As expected, the proposed method generally also exhibits better performance than the comb filtering approach. That the NLS, comb filtering, and optimal filtering methods all perform well for high PSNRs and N confirms that the MAP order estimation criterion indeed works well, as all of them are based on this criterion. The subspace method, MUSIC, appears not to work at all, and there is a simple explanation for this: the presence of a second interfering source has not been taken into account in any of the methods, and for MUSIC, this turns out to be a critical problem; indeed, the one source assumption leads to an incorrect noise subspace estimate. At this point, it should be stressed that it is possible to take multiple sources into account in MUSIC at the cost of an increased computational complexity [10, 16]. While the method based on optimal filtering appears to sometimes exhibit slightly worse performance than NLS in terms of estimating the model order, it generally outperforms both MUSIC and the NLS with respect to fundamental frequency estimation under adverse conditions, in particular when multiple periodic sources are present at the same time [16], something that happens frequently in audio signals. That is, unless the NLS approach is modified to either iteratively estimate the parameters of the individual sources using expectation maximization (EM) like iterations or is modified to incorporate the presence of multiple sources in the cost function [16]. The latter approach is to be avoided as it requires multi-dimensional nonlinear optimization. Overall, it can be concluded that the optimal filtering methods form an intriguing alternative for joint fundamental frequency and order estimation, especially so for multi-pitch signals.
Summary
A number of filtering methods for fundamental frequency estimation have been considered in this paper, namely the classical comb filtering and maximum likelihood methods along with some more recent methods based on optimal filtering. The latter approaches are generalizations of Capon's classical optimal beamformer. These methods have recently been demonstrated to show great potential for high-resolution pitch estimation. In this paper, we have extended these methods to account for an unknown number of harmonics, a quantity also known as the model order, by deriving a model-specific order estimation criterion based on the maximum a posteriori principle. This has led to joint fundamental frequency and order estimators that can be applied in situations where the model order cannot be known a priori or may change over time, as is the case in speech and audio signals. Additionally, some new analyses of the optimal filtering methods and their properties have been provided. Moreover, a computationally efficient order-recursive implementation that is much faster than a direct implementation has been proposed. Finally, the optimal filtering methods have been demonstrated, in computer simulations, to have good performance in terms of the percentage of correctly estimated model orders when multiple sources are present.
Abbreviations
- AIC:
-
Akaike information criterion
- EM:
-
expectation maximization
- MDL:
-
minimum description length criterion
- NLS:
-
nonlinear least-squares
- PDF:
-
probability density function
- PSNR:
-
pseudo signal-to-noise.
References
American Standards Association (ASA): Acoustical Terminology. SI, 1-1960, New York 1960.
Chan KW, So HC: Accurate frequency estimation for real harmonic sinusoids. IEEE Signal Process Lett 2004,11(7):609-612. 10.1109/LSP.2004.830115
Ross M, Shaffer H, Cohen A, Freudberg R, Manley H: Average magnitude difference function pitch extractor. IEEE Trans Acoust Speech Signal Process 1974,22(5):353-362. 10.1109/TASSP.1974.1162598
Rabiner L: On the use of autocorrelation analysis for pitch detection. IEEE Trans Acoust Speech Signal Process 1977,25(1):24-33. 10.1109/TASSP.1977.1162905
Medan Y, Yair E, Chazan D: Super resolution pitch determination of speech signals. IEEE Trans Signal Process 1991,39(1):40-48. 10.1109/78.80763
de Cheveigné A, Kawahara H: YIN, a fundamental frequency estimator for speech and music. J Acoust Soc Am 2002,111(4):1917-1930. 10.1121/1.1458024
Talkin D: A robust algorithm for pitch tracking (RAPT). In Speech Coding and Synthesis. Volume Chap. 5. Edited by: Kleijn WB, KK Paliwal. Elsevier Science B.V., New York; 1995:495-518.
Christensen MG, Jensen SH, Andersen SV, Jakobsson A: Subspace-based fundamental frequency estimation. Proceedings of the European Signal Processing Conference 2004, 637-640.
Christensen MG, Jakobsson A, Jensen SH: Joint high-resolution fundamental frequency and order estimation. IEEE Trans Audio Speech Lang Process 2007,15(5):1635-1644.
Christensen MG, Jakobsson A, Jensen SH: Fundamental frequency estimation using the shift-invariance property. Record of the Asilomar Conference on Signals, Systems, and Computers 2007, 631-635.
Li H, Stoica P, Li J: Computationally efficient parameter estimation for harmonic sinusoidal signals. Signal Process 2000, 80: 1937-1944. 10.1016/S0165-1684(00)00103-1
Noll M: Pitch determination of human speech by harmonic product spectrum, the harmonic sum, and a maximum likelihood estimate. Proceedings of the Symposium on Computer Processing Communications 1969, 779-797.
Quinn BG, Thomson PJ: Estimating the frequency of a periodic function. Biometrika 1991,78(1):65-74. 10.1093/biomet/78.1.65
Kundu D, Nandi S: A note on estimating the fundamental frequency of a periodic function. Elsevier Signal Process 2004, 84: 653-661.
Lavielle M, Lévy-Leduc C: Semiparametric estimation of the frequency of unknown periodic functions and its application to laser vibrometry signals. IEEE Trans Signal Process 2005,53(7):2306-2314.
Christensen MG, Stoica P, Jakobsson A, Jensen SH: Multi-pitch estimation. Signal Process 2008,88(4):972-983. 10.1016/j.sigpro.2007.10.014
Noll AM: Cepstrum pitch determination. J Acoust Soc Am 1967,41(2):293-309. 10.1121/1.1910339
Cemgil AT, Kappen HJ, Barber D: A generative model for music transcription. IEEE Trans Audio Speech Lang Process 2006,14(2):679-694.
Cemgil AT: Bayesian music transcription. Ph.D. dissertation, Nijmegen University; 2004.
Godsill S, Davy M: Bayesian harmonic models for musical pitch estimation and analysis. Proceedings of the IEEE International Conference on Acoust., Speech, Signal Processing 2002, 2: 1769-1772.
Moorer J: The optimum comb method of pitch period analysis of continuous digitized speech. IEEE Trans Acoust Speech Signal Process 1974,22(5):330-338. 10.1109/TASSP.1974.1162596
Lim J, Oppenheim A, Braida L: Evaluation of an adaptive comb filtering method for enhancing speech degraded by white noise addition. IEEE Trans Acoust Speech Signal Process 1978,26(4):354-358. 10.1109/TASSP.1978.1163117
Nehorai A, Porat B: Adaptive comb filtering for harmonic signal enhancement. IEEE Trans Acoust Speech Signal Process 1986,34(5):1124-1138. 10.1109/TASSP.1986.1164952
Christensen MG, Jakobsson A: Multi-Pitch Estimation. Synthesis Lectures on Speech & Audio Processing. Volume 5. Morgan & Claypool Publishers, San Rafael, CA; 2009.
Christensen MG, Jensen JH, Jakobsson A, Jensen SH: On optimal filter designs for fundamental frequency estimation. IEEE Signal Process Lett 2008, 15: 745-748.
Christensen MG, Jakobsson A: Optimal filter designs for separating and enhancing periodic signals. IEEE Trans Signal Process 2010,58(12):5969-5983.
Djuric PM: Asymptotic MAP criteria for model selection. IEEE Trans Signal Process 1998, 46: 2726-2735. 10.1109/78.720374
Godsill S, Davy M: Bayesian computational models for inharmonicity in musical instruments. Proceedings of IEEE Workshop on Applications of Signal Processing to Audio and Acoustics 2005, 283-286.
Davy M, Godsill S, Idier J: Bayesian analysis of western tonal music. J Acoust Soc Am 2006,119(4):2498-2517. 10.1121/1.2168548
Christensen MG, Vera-Candeas P, Somasundaram SD, Jakobsson A: Robust subspace-based fundamental frequency estimation. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing 2008, 101-104.
George EB, Smith MJT: Speech analysis/synthesis and modification using an analysis-by-synthesis/overlap-add sinusoidal model. IEEE Trans Speech Audio Process 1997,5(5):389-406. 10.1109/89.622558
George EB, Smith MJT: Generalized overlap-add sinusoidal modeling applied to quasi-harmonic tone synthesis. Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics 1993, 165-168.
Stoica P, Moses R: Spectral Analysis of Signals. Pearson Prentice Hall, Upper Saddle River, NJ; 2005.
Hermes DJ: Measurement of pitch by subharmonic summation. J Acoust Soc Am 1988,83(1):257-264. 10.1121/1.396427
Stoica P, Jakobsson A, Li J: Matched-filterbank interpretation of some spectral estimators. Signal Process 1998,66(1):45-59. 10.1016/S0165-1684(97)00239-9
Gray RM: Toeplitz and circulant matrices: a review. Found. Trends Commun Inf Theory 2006,2(3):155-239.
Hannan EJ, Wahlberg B: Convergence rates for inverse Toeplitz matrix forms. J Multivar Anal 1989, 31: 127-135. 10.1016/0047-259X(89)90055-9
Stoica P, Li H, Li J: Amplitude estimation of sinusoidal signals: survey, new results and an application. IEEE Trans Signal Process 2000,48(2):338-352. 10.1109/78.823962
Akaike H: A new look at the statistical model identification. IEEE Trans Autom Control 1974, 19: 716-723. 10.1109/TAC.1974.1100705
Rissanen J: Modeling by shortest data description. Automatica 1978, 14: 468-478.
Schwarz G: Estimating the dimension of a model. Ann Stat 1978, 6: 461-464. 10.1214/aos/1176344136
Djuric PM: A model selection rule for sinusoids in white Gaussian noise. IEEE Trans Signal Process 1996,44(7):1744-1751. 10.1109/78.510621
Stoica P, Selen Y: Model-order selection: a review of information criterion rules. IEEE Signal Process Mag 2004,21(4):36-47. 10.1109/MSP.2004.1311138
Lagunas MA, Santamaria ME, Gasull A, Moreno A: Maximum likelihood filters in spectral estimation problems. Elsevier Signal Process 1986,10(1):19-34.
Haykin S: Adaptive Filter Theory. 3rd edition. Prentice-Hall, Upper Saddle River, NJ; 1996.
Acknowledgements
A. Jakobsson is funded by Carl Trygger's Foundation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Christensen, M.G., Højvang, J.L., Jakobsson, A. et al. Joint fundamental frequency and order estimation using optimal filtering. EURASIP J. Adv. Signal Process. 2011, 13 (2011). https://doi.org/10.1186/1687-6180-2011-13
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-13
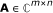 and
and 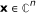 requires
requires 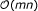 operations.
operations.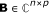 requires
requires 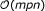 operations.
operations. requires
requires 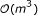 operations.
operations.




