- Research
- Open access
- Published:
Chaotic signal reconstruction with application to noise radar system
EURASIP Journal on Advances in Signal Processing volume 2011, Article number: 2 (2011)
Abstract
Chaotic signals are potentially attractive in engineering applications, most of which require an accurate estimation of the actual chaotic signal from a noisy background. In this article, we present an improved symbolic dynamics-based method (ISDM) for accurate estimating the initial condition of chaotic signal corrupted by noise. Then, a new method, called piecewise estimation method (PEM), for chaotic signal reconstruction based on ISDM is proposed. The reconstruction performance using PEM is much better than that using the existing initial condition estimation methods. Next, PEM is applied in a noncoherent reception noise radar scheme and an improved noncoherent reception scheme is given. The simulation results show that the improved noncoherent scheme has better correlation performance and range resolution especially at low signal-to-noise ratios (SNRs).
Introduction
Recently, there has been a growing amount of interest in chaotic signal estimation, which has been applied in the field of radar and communication [1–8]. In order to exploit chaotic signals in engineering applications, there is a need of robust and efficient algorithms for reconstructing signals in the presence of noise. Initial condition estimation is an important way to reconstruct the chaotic signal, because the certain chaotic signal will be obtained once the initial condition value is estimated exactly.
Initial condition estimation has been investigated by many researchers and a variety of algorithms have been proposed for estimating chaotic signal [8–16]. "Halving method" (HM) [10] and "extend halving method" (EHM) [12] have low computational complexity, but either HM or EHM is only useful for some special maps. "Symbolic dynamics-based method" (SDM) [11] and "extend symbolic dynamics method" (ESDM) [8] have very low computational complexity and they are useful for general chaotic maps. However, because they rely heavily on the accurate symbolic sequence, thus the estimation is not always accurate.
In order to get an accurate method for usual chaotic maps, in this article, we present a new method called improved symbolic dynamics-based method (ISDM), for initial condition estimation. It makes full use of the initial condition sensitivity of chaos to get an accurate estimation value. Initial condition sensitivity means that the two chaotic signals with nearby initial condition will exponentially diverge from each other. Thus, we notice that only the estimation value which is the closest to the true value can make the smallest difference between estimation signal and the observation signal. Based on this, the improved SDM is given. In improved SDM, an approximate estimation value is first got by SDM. Different from SDM, an interval whose center point is the approximate estimation value is defined according to the estimation error of SDM, and we let the value in the interval, which can make the smallest estimation error between the estimation signal and the observation signal, be the initial condition value.
Next, a new method called piecewise estimation method (PEM), for chaotic signal reconstruction is presented based on improved SDM. PEM can further enhance the signal reconstruction performance. Since the initial condition of chaotic signal cannot be estimated exactly in noise, and a small error in the initial condition will make the reconstruction signal exponentially diverge from true signal. So only using the initial condition method for chaotic signal reconstruction may not obtain the satisfying performance especially at low SNR. However, chaotic sequence still can be predicted by small error when the sequence length is smaller than the embedding dimension according to the CAO method [17]. Thus, in the PEM, the whole signal is first divided into several appropriate small parts; then estimate initial condition of every part, respectively, and simultaneously using improved SDM; finally, joint the estimated signal of every part to reconstruct the estimated signal. The reconstruction performance is better than that using the existing initial condition method.
Then the chaotic signal reconstruction is applied in the noncoherent reception noise radar scheme which is proposed by Venkatasubramanian [1]. In [1], the correlation processing reference signal is reconstructed using the existing initial condition estimation. However, after our research, we find that the correlation performance is not so well especially at low SNR. So the PEM for reconstruction the transmitted signal is used and we offer an improved noncoherent reception noise radar scheme. In this scheme, it has the better correlation performance and better range resolution especially at low SNR. What is more, it can also achieve a similar performance as the ideal coherent scheme. In this improved noncoherent scheme, both the delayed transmission reference signal and the synchronization circuit which is necessary and difficult to be realized in coherent scheme [18] are not required.
This article is organized as follows. In "Initial condition estimation of chaotic signal based on SDM," we present the improved SDM and compare its performance with the other methods. Followed by PEM based on the improved SDM to reconstruct the estimation signal, the improved noncoherent reception noise radar system based on PEM is presented. Simulation results show that improved noncoherent scheme has better range resolution and it has nearly the same effect as that of the ideal coherent reception scheme. Brief conclusion of this article is drawn finally.
Initial condition estimation of chaotic signal based on SDM
In this section, at the beginning the main idea of symbolic dynamics-based method (SDM) is given. Then a new method for initial condition estimation for chaotic signal is proposed and its performance is also shown.
SDM
Since our research is based on SDM for initial condition estimation, we give a brief introduction for SDM.
Let E = {E0, E1,...,Eq-1}be a finite disjoint partition of phase space M,  , E
i
⋂ E
j
= Ø, for i ≠ j. Assuming that the phase point x(n) is in the i th element of the partition at time n. s(n) = i(i ∈ {0,1,...q-1}) is an assigned symbol. Then, any orbit can be encoded as a string S = {s(0), s(1),...s(n),...}, which is called a symbolic sequence. The above coding naturally determines a mapping ψ from M to the space of symbolic sequence.
, E
i
⋂ E
j
= Ø, for i ≠ j. Assuming that the phase point x(n) is in the i th element of the partition at time n. s(n) = i(i ∈ {0,1,...q-1}) is an assigned symbol. Then, any orbit can be encoded as a string S = {s(0), s(1),...s(n),...}, which is called a symbolic sequence. The above coding naturally determines a mapping ψ from M to the space of symbolic sequence.

where fn denotes the n-fold composition, f-nis the n th order inverse function of f and f-n(Es(n)) is the set of points that map to set Es(n)after n iterations. A sequence S is admissible if there exits at least one initial condition x(0) such that ψ(x(0)) = S. The SDM using the following equation for estimation initial condition:

where η is a point in the domain of  , S = {s(0), s(1),..., s(n),...s(N-1)} (s(n) = i, i ∈ {0,1,2,...}) is a symbolic sequence obtained from the its measurement sequence. An illustration example for understanding this is the Logistic map f(x) = μx(1-x), (|x| ≤ 1, 0 ≤ μ ≤ 4). The enerating partition consists of two parts: E0 = [0,0.5) and E1 = [0.5,1]. Then, the symbolic sequence is obtained according to
, S = {s(0), s(1),..., s(n),...s(N-1)} (s(n) = i, i ∈ {0,1,2,...}) is a symbolic sequence obtained from the its measurement sequence. An illustration example for understanding this is the Logistic map f(x) = μx(1-x), (|x| ≤ 1, 0 ≤ μ ≤ 4). The enerating partition consists of two parts: E0 = [0,0.5) and E1 = [0.5,1]. Then, the symbolic sequence is obtained according to

The two inverse mapping are given by:

Then, the initial condition of Logistic map can be estimated using Equation 2.
SDM has low computational complexity and it is useful for general chaotic map. However, SDM cannot get the exact initial condition value and the estimation error is about 1/2 N[11]. Since chaotic signal is very sensitive to initial condition and a small error in initial condition can make large difference as the iteration grows. So a more accurate method for estimating the initial condition is needed.
ISDM
In this part, an ISDM is proposed based on chaotic initial sensitivity character.
Though SDM cannot get the exact estimation, the idea of SDM still can be used to get an approximate estimation, and the estimation error is about 1/2 N[11]. In our article, a more accurate estimation can be got based on the chaotic initial condition sensitivity. The chaotic initial condition sensitivity means the two signals with nearby initial condition will exponentially diverge from each other. Thus, the estimation signal error has a close relationship to the initial condition error. So the initial condition could be obtained indirectly by computing the error between the observation signal and the signal generated by the initial condition in a special interval.
Based on this, in this article, a uniform search with M sampling points over the interval  is made, where
is made, where  is the estimation value using Equation 2. Then estimation value is got in l by the rule that which can make the minimum difference between the estimation signal and the observation signal. This can be illustrated in Equation 5.
is the estimation value using Equation 2. Then estimation value is got in l by the rule that which can make the minimum difference between the estimation signal and the observation signal. This can be illustrated in Equation 5.

where inf(f(x)) denotes the infimum of f(x),  , y(x(0), N) is the obtained signal and it consists of chaotic signal and additive noise,
, y(x(0), N) is the obtained signal and it consists of chaotic signal and additive noise,  is the estimation signal, N is the length of the sequence.
is the estimation signal, N is the length of the sequence.
The step of improved SDM is summarized as follows.
-
(1)
Compute the suboptimal value
 by Equation 2 according to the observation signal.
by Equation 2 according to the observation signal. -
(2)
A uniform search over the interval
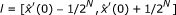 is made, where i = 1,2...M and M is the total sampling number in l.
is made, where i = 1,2...M and M is the total sampling number in l. -
(3)
The initial condition estimation is obtained by picking up the special value which can make the minimum difference between the estimation signal and the obtained signal using Equation 5.
Simulation analysis of initial condition estimation
To validate the accuracy of the improved SDM, we do experiments on the Logistic map and Chebyshev map.
The Logistic map is described as f(x) = μx(1-x), (|x| ≤ 1, 0 ≤ μ ≤ 4).
The Chebyshev map is described as f(x) = cos(k cos-1(x)), (|x| ≤ 1).
Cramer-Rao lower bound (CRLB) for both of the maps is computed by Equation 6 quoted from [19].

where λ is the Lyapunov number and  is the noise power.
is the noise power.
For the Logistic map, let μ = 4, x(0) = 0.6534, M = 1000, and N = 10. The comparison of CRLB which is computed by Equation 6, the proposed method, SDM, and HM [10] are shown in Figure 1.
For the Chebyshev map, let k = 4, x0 = 0.3411, M = 1000, and N = 10. The comparison of CRLB which is computed by Equation 6 in [20], the proposed method and SDM is shown in Figure 2.
Figures 1 and 2 indicate that the proposed method is more accurate especially at low SNR. Here, we should know the proposed method cannot be obtained at arbitrary low SNR. The performance of estimators for chaotic systems tends to degrade quite suddenly as the SNR decreases below some threshold SNR (SNRth) [18, 21]. When the SNR is below SNRth, which means the entropy of the chaotic signal exceeds the channel capacity, the initial condition estimation performance is not well. In the improved SDM, using Equation 7 which is obtained from [21], we can get SNRth which is nearly 8.67 dB in the Logistic map in experiment 1. By the same way we obtain SNRth is nearly 6.54 dB in the Chebyshev map in experiment 2. In this article, the SNR is given more than SNRth. We can see from Figures 1 and 2, every estimation method nearly reaches the CRLB when the SNR is much more than SNRth. When the SNR is close to SNRth, the estimation error becomes worse. But when the SNR is low (a little more than SNRth), the estimation performance of the proposed method is better than the existing methods shown in Figures 1 and 2, because it makes full use of the initial condition sensitivity of chaos.

where α is the parameter in the chaotic map (for Chebyshev map α = k and for Logistic map α = μ), SNRth is the threshold SNR,  is the noise power, N is the length of chaotic sequence and λ is the Lyapunov number.
is the noise power, N is the length of chaotic sequence and λ is the Lyapunov number.
PEM
In this section, the PEM (the schematic diagram is shown in Figure 3) is proposed. It is a more accurate way to reconstruct the estimated signal.
The aim of using the PEM is to improve the signal reconstruction accuracy. In engineering, the initial condition may not be estimated perfectly accurately, and "the extreme sensitivity of a chaotic system's steady state response to small changes in its initial conditions makes long term prediction of the evolution of such a system difficult, if not impossible" [20]. Thus, the chaotic signal reconstruction for long sequence may not reach the ideal effect only using the initial condition estimation method. However, chaos also has the deterministic characteristic, and it can be predicted in short time according to CAO method [17]. Thus, if the sequence of the chaotic signal is short, even if there is a change in the initial condition, the error between the reconstructed signal and the real signal is small. So dividing the whole received signal into several appropriate small parts can improve the signal estimation accuracy. The remaining question is how to define the length of the small part.
Define the length of the small part is different for different chaotic maps, but the way is almost the same. Here, we use the Logistic map as an example to illustrate it. First, we see Figure 4 which shows the relationship between the sequence length and the initial condition estimation error of the improved SDM for Logistic map. It is clear that the initial condition error does not decrease much when the sequence length is more than a certain number (in Figure 4, the certain number is 8 when SNR = 20 dB) at certain SNR. We know that if the initial condition is fixed, the sequence reconstruction error becomes bigger when the sequence length increases. So if the sequence length is more than 8, the reconstruction error is more than that of the sequence with length 8 at SNR = 20 dB. Thus, we only need to compute the reconstruction error of the sequence with the length 1-8. After computation and comparing, we find that when the sequence length is 7, the reconstruction error is the smallest. So, we let the length of every small part is 7 for the Logistic map at SNR = 20 dB.
The main idea of PEM is: first divide the received signal into several appropriate small parts; then estimate the initial condition of every part, respectively, and simultaneously using the improved SDM; finally, joint the estimated signal of every part to reconstruct the estimated signal. The schematic diagram of the PEM is given in Figure 3.
To validate the analysis above, Figures 5, 6, and 7 show the signal reconstructed by the method in this article, the signal reconstructed by HM and by ESDM, respectively. We can see clearly that the reconstruction error of using the PEM in this article is the smallest. One reason is it divides the long sequence into small part. The other reason is the improved SDM is used in every small part to enhance the initial condition estimation accuracy.
Chaotic signal reconstructed by HM in [10]at SNR = 10 dB, the chaotic map is the Logistic map, the mean error of the reconstructed signal is 0.6841.
Chaotic signal reconstructed by ESDM in [7]at SNR = 10 dB, the chaotic map is the Logistic map, the mean error of the reconstructed signal is 0.6646.
Improved noncoherent reception noise radar scheme
In this section, an improved noncoherent reception noise radar scheme is given, and its better range resolution is also shown.
The noise radar scheme is shown in Figure 8. In Figure 8, in the right red dashed line frame, the coherent method is shown as the conventional way while in the left red dashed line frame the noncoherent method which is proposed by Venkatasubramanian [1] is shown. X(t) is the transmitted signal generated by noise source and X(t-Tr) is the returned signal from the target with Tr = 2R/c and R is the distance from the radar. The main difference between the coherent system and the noncoherent system is that, the latter using the reconstructed transmitted signal X'(t-Td) but not the transmitted signal X(t-Td) delayed by the delay lines, to correlate with the returned signal (Td is the delayed time by the delay lines). This can avoid some difficult problems, such as maintaining a distortion-free line and getting accurate synchronization of the transmitted signal [1].
In this article, we do further research in noncoherent reception noise radar scheme, and the improving point is on the transmitted signal reconstruction. The transmitted signal reconstruction in [1] is just using the existing initial condition estimation method. But here, the transmitted signal reconstruction is using PEM. In doing so, the reconstruction error is much smaller than that caused by just using the existing initial condition estimation method especially at low SNR. The reason is that: dividing the whole received signal into several small parts enhances the reconstruction accuracy; using the improved SDM decreases the initial condition estimation error in every divided part.
In order to illustrate the effect of the improved scheme, we use the correlation processing performance to show the advance, since the target range resolution can be obtained from it. Let us consider a radar transmitted signal X(t). Denote the received signal by Y(t). Furthermore, we consider a point target located at the range R along the radar line of sight. Then, the received signal can be written as

where Tr = 2R/c is the round-trip delay time, n(t) is the white Gauss noise. The correlation of the reconstruction signal X'(t) and received signals Y(t) can be written as

where Tint is the available correlation time. In the noiseless case, the maximum value |R(τ)| is at the point τ = Tr Let us analyze the expected value of Equation 9 as

Since the emitted signal X(t) is the chaotic signal, thus the reconstructed signal X'(t) and the noise n(t) are independent processes. Then the second term in Equation 10 is equal to zero and we obtain

Since the autocorrelation function's maximum is at τ = 0, the delay time T r can be estimated as the position of the maximum as

Thus, we can obtain the target range resolution form Tr by R = cTr/2.
The correlation simulation is given next. Let a stationary target 30 m from the radar. Let X(t) be chaotic signal generated by the Chebyshev map, and the SNR is 40, 20, 10 dB, respectively. The signal bandwidth is 200 MHz, the sampling frequency is 1 GMHz and the pulse length is 1 μs. In order to show the criterion, the correlation processing performance using the traditional ideal coherent way with no noise is shown in Figure 9 first. Then, the correlation processing performance using the PEM in this article is shown in Figure 10, and the correlation processing performance using the existing initial condition estimation method as [1] described is shown in Figure 11.
Correlation sum over chaotic signal samples, the reference signal is the reconstructed signal which is obtained using the existing initial condition method as Ref. [1]. (A) SNR = 40 dB; (B) SNR = 20 dB; (C) SNR = 10 dB.
When using the method in this article, the correlation performance has nearly the same effect as that using the traditional ideal coherent way, and the peak value of the correlation function is clear even at low SNR. We can get the estimated delay time Tr easily using Equation 12 and the range resolution can be obtained by R = Trc/2. The range resolution of the two methods is shown in Table 1. We can see from Table 1 that every method can get an approximate resolution at high SNR, but the method in this article has advantage at low SNR.
Conclusion
In this article, we developed an improved SDM for accurate estimating the initial condition of chaotic signal in noise. A new method called PEM is then given. The PEM develops a new way to reconstruct the chaotic signal.
Based on the PEM, an improved noncoherent reception noise radar system is developed. It uses the reconstructed signal to correlate with the received signal. The simulation results show that improved noncoherent scheme has better correlation performance and range resolution than just using the existing initial condition estimation method. It has nearly the same effect as that of the ideal coherent reception scheme, and its realization is cheaper and easier than the coherent reception scheme since the delayed transmission reference signal and the synchronization circuits are not required.
Abbreviations
- CRLB:
-
Cramer-Rao lower bound
- EHM:
-
extend halving method
- ESDM:
-
extend symbolic dynamics method
- HM:
-
Halving method
- ISDM:
-
improved symbolic dynamics-based method
- PEM:
-
piecewise estimation method
- SNR:
-
signal-to-noise ratios
- SDM:
-
symbolic dynamics-based method.
References
Venkatasubramanian V, Leung H: A novel chaos-based high-resolution imaging technique and its application to through-the-wall imaging. IEEE Signal Process Lett 2005,12(7):528-531.
Leung H, H Yu, Murali K: Ergodic chaos-based communication schemes. Phys Rev E 2002,66(9):036203(1)-036203(8).
Huang PD, Pi YM, Zhao ZQ: Weak GPS signal acquisition algorithm based on chaotic oscillator. EURASIP J Adv Signal Process
Leung H, Shanmugam S, Xie N, Wang SC: An ergodic approach for chaotic signal estimation at low SNR with application to ultra-wide-band communication. IEEE Trans Signal Process 2006,54(5):1091-1103.
Ghosh D: Adaptive scheme for synchronization-based multiparameter estimation from a single chaotic time series and its applications. Phys Rev E 2008,78(5):056211(1)-056211(5).
Hu JF, Guo JB: Breaking a chaotic secure communication scheme. CHAOS 2008, 18: 01321(1)-01321(7).
Yu LF, Zhao Y, Ni RR, Li T: Improved adaptive LSB steganography based on chaos and genetic algorithm. EURASIP J Adv Signal Process
Wang K, et al.: Symbolic vector dynamics approach to initial condition and control parameters estimation of coupled map lattices. IEEE Trans Circ Syst I 2008,55(4):1116-1124.
Kay S: Asymptotic maximum likelihood estimator performance for chaotic signals in noise. IEEE Trans Signal Process 1995,43(4):1009-1012.
Kay S, Nagesha V: Methods for chaotic signal estimation. IEEE Trans Signal Process 1995,43(8):2013-2016. 10.1109/78.403367
Ling C, Wu X, Sun S: A general efficient method for chaotic signal estimation. IEEE Trans Signal Process 2008,47(5):1424-1428.
Wang S, Yip P, Leung H: Estimating initial conditions of noisy chaotic signals generated by piecewise linear Markov maps using itineraries. IEEE Trans Signal Process 1999,47(12):3289-3302. 10.1109/78.806073
Lu F, Xu D, Wen G: Estimation of initial conditions and parameters of a chaotic evolution process from a short time series. CHAOS 2004,14(4):1050-1055. 10.1063/1.1811548
Jorg S, Thomas S: Symbolic dynamics for processing chaotic signals--I: noise reduction of chaotic sequences. IEEE Trans Circ Syst I Fundam Theory Appl 2001,48(11):1269-1282. 10.1109/81.964416
Jorg S, Thomas S: Symbolic dynamics for processing chaotic signals--II: communication and coding. IEEE Trans Circ Syst I Fundam Theory Appl 2001,48(11):1283-1295. 10.1109/81.964417
Wang K, Pei WJ, He ZY, Cheung YM: Estimating initial conditions in coupled map lattices from noisy time series using symbolic vector dynamics. Phys Lett A 2007,367(6):316-321.
Cao L: Practical method for determining the minimum embedding dimension of a scalar time series. Physica D 1997,110(12):43-50.
Drake DF, Williams DB: Linear, random representations of chaos. IEEE Trans Signal Process 2007,55(4):1379-1389.
Eisencraft M, Baccala LA: The Cramer-Rao bound for initial conditions estimation of chaotic orbits. Chaos, Solitons Frac 2008,38(10):132-139.
Drake DF, Williams DB: On error function selection for the analysis of nonlinear time series. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, vol. V, San Francisco, CA 1992, 329-332.
Hen H, Merhav N: On the threshold effect in the estimation of chaotic sequences. IEEE Trans Inf Theory 2004,50(10):2894-2904.
Flores BC, Solis E, Thomas G: Assessment of chaos-based FM signals for range-Doppler imaging. IEEE Proc Radar Sonar Navig 2003,150(4):3-15.
Qiao S, Shi ZG, Chen KS: A new architecture of UWB radar utilizing microwave chaotic signals and chaos synchronization. Prog Electromag Res 2007, 75: 225-237.
Acknowledgements
The authors would like to thank the suggestions of the anonymous reviewers. And the authors would like to thank the support of Defense Pre-research Fund (9140A07011609DZ0216), the Fundamental Research Funds for the Central Universities (ZYGX2009J011, ZYGX2009J015, ZYGX2010J015, 103.1.2-E022050205).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, L., Hu, J., He, Z. et al. Chaotic signal reconstruction with application to noise radar system. EURASIP J. Adv. Signal Process. 2011, 2 (2011). https://doi.org/10.1186/1687-6180-2011-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-2
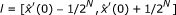 is made, where i = 1,2...M and M is the total sampling number in l.
is made, where i = 1,2...M and M is the total sampling number in l.









