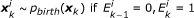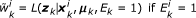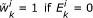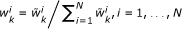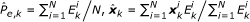- Research
- Open access
- Published:
Track-before-detect procedures for detection of extended object
EURASIP Journal on Advances in Signal Processing volume 2011, Article number: 35 (2011)
Abstract
In this article, we present a particle filter (PF)-based track-before-detect (PF TBD) procedure for detection of extended objects whose shape is modeled by an ellipse. By incorporating of an existence variable and the target shape parameters into the state vector, the proposed algorithm performs joint estimation of the target presence/absence, trajectory and shape parameters under unknown nuisance parameters (target power and noise variance). Simulation results show that the proposed algorithm has good detection and tracking capabilities for extended objects.
Introduction
Most target tracking algorithms assume a single point positional measurement corresponding to a target at each scan. However, high resolution sensors are able to supply the measurements of target extent in one or more dimensions. For example, a high-resolution radar provides a useful measure of down-range extent given a reasonable signal-to-noise ratio (SNR). The possibility to additionally make use of the high-resolution measurements is referred as extended object tracking [1]. Estimation of the object shape parameters is especially important for track maintenance [2] and for the object type classification.
More recent approaches to tracking extended targets have been investigated by assuming that the measurements of target extent are available [1–5]. However, the measurements of extended targets provided by the high resolution sensor are inaccurate in a low SNR environment since those are obtained by threshold-based decisions made on the raw measurement at each scan. Ristic et al. [3] investigated the influence of extent measurement accuracy on the estimation accuracy of target shape parameters, and demonstrated that the estimation of target shape parameters is unbelievable when the measurement of extended targets is not available. An alternative approach, referred as track-before-detect (TBD), consists of using raw, unthresholded sensor data. TBD-based procedures jointly process several consecutive scans and, relying on a target kinematics, jointly declare the presence of a target and, eventually, its track, and show superior detection performance over the conventional methods. In previously developed TBD algorithms, the target is assumed to be a point target [6–18]. Recently extension of TBD method for tracking extended targets has been considered in [19], by modeling the target extent as a spatial probability distribution.
In this study, an ellipsoidal model of target shape proposed in [1–3] is adopted. The elliptical model is convenient as down-range and cross-range extent vary smoothly with orientation relative to the line-of-sight (LOS) between the observer and the target. The considered problem consists of both detection and estimation of state and size parameters of an extended target in the TBD framework. By incorporating of a binary target existence variable and the target shape parameters into the state vector, we have proposed a particle filter (PF)-based TBD (PF TBD) method for joint detection and estimation of an extended target state and size parameters. The proposed method is investigated under unknown nuisance parameters (target power and noise variance). The detection and tracking performances of the proposed algorithm are studied with respect to different system settings.
The article is organized as follows. 'Target and measurement models' section introduces target and measurement models. The PF TBD algorithm is presented under unknown nuisance parameters (target power and noise variance) in 'PF TBD procedures' section. The performance assessment of the proposed algorithm is the object of 'Simulation and results' section. 'Conclusion' section contains some concluding remarks.
Target and measurement models
Extended target model and state dynamics
In this article, we are concerned with an extended object moving on the x-y plane, whose shape can be modeled by an ellipse. Figure 1 illustrates a typical scenario of interest. Similarly to [2], we assume that the ratio of minor and major axes of the ellipse is fixed and known for the targets of interest to simplify the exposition. Thus, only the single parameter of target length ℓ is required. Our goal is to estimate the joint kinematic-feature state vector:  , where [x y]
k
and
, where [x y]
k
and  denote position and velocity of the centre of an extended target, respectively; ℓ
k
denotes the target length. We assume that the target centroid moves according to a constant velocity model:
denote position and velocity of the centre of an extended target, respectively; ℓ
k
denotes the target length. We assume that the target centroid moves according to a constant velocity model:

where ΔT is the time interval between successive scans and v k is a zero-mean Gaussian noise vector with covariance cov[v k ] = Q = diag(q x , q y , qℓ), where q x and q y are the usual acceleration noise variances for the constant velocity model. A small, non-zero value for qℓ allows for some adjustment of the target length estimate.
The target down-range extent L(ϕ(x)) is given by (omitting the frame subscript k)

where ϕ(x) is the angle between the major axis of the ellipse and the target-observer LOS. If the target ellipse is oriented so that its major axis is parallel to its velocity vector then the down-range target extent L(ϕ(x)) can be written as

Thus, L(ϕ(x)) depends only on the target length ℓ and its orientation with respect to the LOS.
Furthermore, to indicate the presence or absence of a target, the random variable modeled by a two-state Markov chain, i.e., E k ∈ {0,1}, is used [14–16], where E k = 1 means the target is present and E k = 0 means the target is absent. The Markov transition matrix is defined as

Pb = Pr{ E k = 1| Ek-1= 0} is the probability of transition from absent to present, i.e., 'birth of the target', and Pd = Pr{ E k = 0| Ek-1= 1} is the probability of transition from present to absent, i.e., 'death of the target'.
Measurement model
The measurements are the reflected power on range-azimuth domain. The range and azimuth domains are divided into Nr and Na cells, respectively. The resolutions of range and azimuth are Δr and Δa. Let Ω ≡ {1, ..., Nr} and S ≡ {1, ..., Na - 1} denote the set of resolution cell in range and azimuth domain, respectively. According to 'Extended target model and state dynamics' subsection, the set of range cell containing useful target echoes can be expressed as

where  and ⌈X⌉ rounds the elements of X to the nearest integers towards infinity. Let
and ⌈X⌉ rounds the elements of X to the nearest integers towards infinity. Let  , where
, where  is the total number of the range cell occupied by the down-range target extent, depending on the target state, target length, and the range resolution. Thus, ΩT = {m1,..., m
R
} ∈ Ω. The azimuth cell containing target echoes is
is the total number of the range cell occupied by the down-range target extent, depending on the target state, target length, and the range resolution. Thus, ΩT = {m1,..., m
R
} ∈ Ω. The azimuth cell containing target echoes is  . At each scan k, the power measurement
. At each scan k, the power measurement  is given by
is given by


where Ω/ΩT denotes the difference between Ω and ΩT.  is an exponential distribution noise with variance σ2.
is an exponential distribution noise with variance σ2.  is the unknown target power in one range cell. The SNR is defined as
is the unknown target power in one range cell. The SNR is defined as  . Note that this measurement is highly nonlinear with the target state.
. Note that this measurement is highly nonlinear with the target state.
Each pixel  follows an exponential distribution
follows an exponential distribution

if only noise exists or a non-central chi-square distribution with two degrees of freedom

if the cell containing target echoes, where I0 is the zero-order modified Bessel function; μ
k
= σ2 when E
k
= 0 and  when E
k
= 1, denotes the nuisance parameters. Assuming that all the pixels of z
k
are independent, the likelihood function of z
k
is given by
when E
k
= 1, denotes the nuisance parameters. Assuming that all the pixels of z
k
are independent, the likelihood function of z
k
is given by

if no target exists or

if the target is present, where  when E
k
= 1. The likelihood ratio can be written as
when E
k
= 1. The likelihood ratio can be written as


PF TBD procedures
From a Bayesian perspective, a complete solution of the above problem is that given the set of unthresholded range-azimuth data maps up to the k th scan, Zk = (z1, ..., z
k
) and prior PDF pbirth(x
k
), determines the posterior PDF p(x
k
, E
k
|Zk). Due to the highly nonlinear relationship couples the measurement with the target state we resort to PF TBD procedures. The algorithm outlined here is similar to the work of [15, 16] but the target state is augmented by the target length ℓ and does not include the unknown target power. The reason is that the unknown target power is a variable based on the point target assumption in [15, 16]. However, as we discussed in 'Target and measurement models' section, the extended target echoes occupy the multi range cells depending on the down-range extent and the range resolution (recall Equation 5). Thus, not only the unknown target power  is variable but also the number of unknown target power R is variable. It is difficult to use the PF to estimate them simultaneously. Therefore, we consider maximum likelihood (ML) estimates of the unknown nuisance parameters
is variable but also the number of unknown target power R is variable. It is difficult to use the PF to estimate them simultaneously. Therefore, we consider maximum likelihood (ML) estimates of the unknown nuisance parameters  . We first give an algorithm description of the PF TBD.
. We first give an algorithm description of the PF TBD.
At k-1 th time step, given the hybrid state of the particles  , the PF TBD algorithm is given as follows:
, the PF TBD algorithm is given as follows:
-
(1)
Generate the new hybrid state (x k , E k ) i, i = 1, ..., N:
-
(a)
Generate the new existence variable
 on the basis of
on the basis of 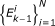 and
and 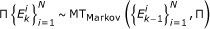
-
(b)
Generate the new target state
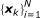 :
:
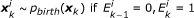
-
(2)
Calculate the weights:
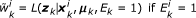
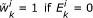
-
(3)
Normalize the weights:
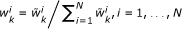
-
(4)
Resample:

-
(5)
Calculate the probability of the target existence and the MMSE estimate of the target state:
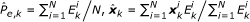
For the unknown nuisance parameters μ k , we assume they as an unknown deterministic parameters and derive ML estimates. The logarithm of the likelihood function can be written as

Where M = NrNa is the total number of the range-azimuth cells;  is the summation of all pixels; ΩT is the range cells occupied by the down-range target extent; nT is the azimuth cell occupied by the target. We evaluate the partial derivatives of the logarithm likelihood function as
is the summation of all pixels; ΩT is the range cells occupied by the down-range target extent; nT is the azimuth cell occupied by the target. We evaluate the partial derivatives of the logarithm likelihood function as



where  is the first-order modified Bessel Function. Equating (15) and (16) to zero, we obtain
is the first-order modified Bessel Function. Equating (15) and (16) to zero, we obtain


Substituting (18) and (19) into (17), and equating (17) to zero, we obtain

By solving equation (18) to (20) jointly, we can find the ML estimates of the unknown parameters 
Simulation and results
In our simulation, the radar is located at the origin and the system parameter is ΔT = 0.1s, Δa = 1°, Δr = 5 m, Nr = 3000, and Na = 60. The total number of scan simulated is 30, and a target appears at scan k = 6 at initial location [9520 9040] m with a constant velocity of [-507 -390] m/s towards the radar and disappears at scan k = 21. The target length is ℓ = 20 m and the target may occupy as much as four range cells depending on its orientation. The acceleration noise variances were set to q x = q y = 1, qℓ = 10-2. Figure 2 shows the target trajectory in x-y plane.
The filter parameters are used as follow. The number of particles is N = 8000. The prior PDF pbirth(x
k
) is assumed as uniform distribution: [x, y] ~ U[8000, 10000],  , and ℓ ~U[0, 60]. The probability of birth and death required by the Markov transition matrix are pb = pd = 0.1.
, and ℓ ~U[0, 60]. The probability of birth and death required by the Markov transition matrix are pb = pd = 0.1.
The average probabilities of target existence of the proposed algorithm with respect to different SNR are plotted in Figure 3. For each SNR, the target present is declared if the probability of existence is higher than where there is only noise. Figure 3 demonstrates that the proposed algorithm detect the extended targets with an average SNR as low as 3 dB, on average. However, it can be seen from Figure 3 that the more SNR is low, the more the detection delay is serious. For example, the target present is declared immediately at k = 6 for SNR = 12 dB, but for SNR = 3 the target present is declared till k = 11. It is means that the detection delay is 5 scans when SNR declines from 12 to 3 dB. Due to TBD-based procedures integrate all information over time, k ≥ 6 frames had been used to jointly process for the batch methods like dynamic programming based TBD (or Viterbi-like TBD) [6–8], the detection delay for the recursive method like PF TBD, therefore, reflects that frames are needed to detect the targets for different SNR.
Figures 4 and 5 show the tracking performance in terms of root mean square error (RMSE) in position and length, respectively. The position RMSE was calculated according to

where x
k
and y
k
are the true target position at time k,  , and
, and  are the estimated target position at time k of simulation I and I is the number of Monte-Carlo simulations. The length RMSE is given similarly:
are the estimated target position at time k of simulation I and I is the number of Monte-Carlo simulations. The length RMSE is given similarly:

It is shown that consistent estimates of the target position and length are calculated by the filter, with higher SNR providing better position and length estimates in Figures 4 and 5. However, considering the resolution of range is Δr = 5 m, the position RMSE is greater than one resolution cell of range even for SNR = 12 dB. The reason is that estimation of the target position is the position of the centre of the extended target (see 'Extended target model and state dynamics' subsection), while the length of target is unknown and needs to be estimated.
Conclusions
In this article, we have investigated the PF TBD procedures for detection of the extended targets whose shape is modeled aby an ellipse. An existence variable is incorporated into the state vector to determine the presence of an extended target in the data. The target shape parameters are also included in the state vector to be estimated. Due to the highly nonlinear relationship couples the measurements of target extent with the target state, we have proposed a PF TBD method for joint estimation of the target presence/absence, trajectory, and length under unknown nuisance parameters (target power and noise variance). Simulation results show that the proposed algorithm has good detection and tracking capabilities for the extended targets even for low SNR, i.e., 3 dB.
Abbreviations
- LOS:
-
line-of-sight
- ML:
-
maximum likelihood
- PF:
-
particle filter
- PF TBD:
-
particle filter-based track-before-detect
- RMSE:
-
root mean square error
- SNR:
-
signal-to-noise ratio
- TBD:
-
track-before-detect.
References
Angelova D, Mihaylova L: Extended object tracking using Monte Carlo methods. IEEE Trans Signal Process 2008,56(2):825-832.
Salmond D, Parr M: Track maintenance using measurements of target extent. IEE Proc Radar Sonar Navig 2003,150(6):389-395. 10.1049/ip-rsn:20030933
Ristic B, Salmond D: A study of a nonlinear filtering problem for tracking an extended target. Proceedings of 7th International Conference on Information Fusion 2004, 503-509.
Gilholm K, Salmond D: Spatial distribution model for tracking extended objects. IEE Proc Radar Sonar Navig 2005,152(5):364-371. 10.1049/ip-rsn:20045114
Salmond D, Gordon N: Group and extended object tracking. Proc SPIE 1999., 3809:
Barniv Y: Dynamic programming solution for detecting dim moving targets. IEEE Trans Aerosp Electron Syst 1985, 21: 144-156.
Pohlig SC: An algorithm for detection of moving optical targets. IEEE Trans Aerosp Electron Syst 1989,25(1):56-63. 10.1109/7.18661
Carlson BD, Evans ED, Wilson SL: Search radar detection and track with the Hough Transform, Part I: system concept. IEEE Trans Aerosp Electron Syst 1994,30(1):102-108. 10.1109/7.250410
Wallace WR: The use of track-before-detect in pulse-Doppler radar. Proceedings of International Conference on Radar 2002, 315-319.
Johnstom LA, Krishnamurthy V: Performance analysis of a dynamic programming track before detect algorithm. IEEE Trans Aerosp Electron Syst 2002,38(1):228-242. 10.1109/7.993242
Tonissen SM, Evans RJ: Performance of dynamic programming techniques for track-before-detect. IEEE Trans Aerosp Electron Syst 1996,32(4):1440-1451. 10.1109/7.543865
Buzzi S, Lops M, Venturino L: Track-before-detect procedures for early detection of moving target from airborne radars. IEEE Trans Aerosp Electron Syst 2005,41(3):937-954. 10.1109/TAES.2005.1541440
Buzzi S, Lops M, Ferri M: Track-before-detect procedures in a multi-target environment. IEEE Trans Aerosp Electron Syst 2008,44(3):1135-1148.
Salmond DJ, Birch H: A particle filter for track-before-detect. Proceedings of American Control Conference 2001, 5: 3755-3760.
Rollason M, Salmond D: A particle filter for track-before-detect of a target with unknown amplitude. Ref Target Track Algorithms Appl 2001, 1: 14/1-14/4.
Rutten MG, Gordon NJ, Maskell S: Recursive track-before-detect with target amplitude fluctuations. IEE Proc Radar Sonar Navig 2005,152(5):345-322. 10.1049/ip-rsn:20045041
Boers Y, Driessen H: Multitarget particle filter track before detect application. IEE Proc Radar Sonar Navig 2004,151(6):351-357. 10.1049/ip-rsn:20040841
Guo H, Ji HB, Wu B: A novel track-before-detect algorithm for weak target. Proceedings of 2009 International Workshop on Information Security Applications, Qingdao, China 2009, 39-42.
Boers Y, Driessen H, Torstensson J, Trieb M, Karlsson R, Gustafsson F: Track-before-detect algorithm for tracking extended targets. IEE Proc Radar Sonar Navig 2006,153(4):345-351. 10.1049/ip-rsn:20050123
Acknowledegments
This work was supported by the Aero Science Foundation of China, Project 20090180001
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fan, L., Zhang, X. & Shi, J. Track-before-detect procedures for detection of extended object. EURASIP J. Adv. Signal Process. 2011, 35 (2011). https://doi.org/10.1186/1687-6180-2011-35
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-35

 on the basis of
on the basis of 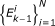 and
and 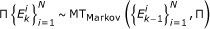
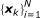 :
: