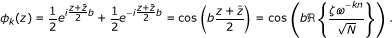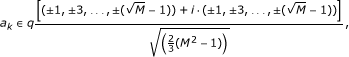- Research
- Open access
- Published:
On the EVM computation of arbitrary clipped multi-carrier signals
EURASIP Journal on Advances in Signal Processing volume 2011, Article number: 36 (2011)
Abstract
A common figure of merit in multi-carrier systems is the error vector magnitude (EVM). A method for EVM computation of a multi-carrier signal without any underlying model (e.g., the Gaussianity assumption) was proposed in a previous work of the authors. However, it addressed only the case of identical constellations and power loadings in all tones. In practice, however, the constellation and power loading may vary among the tones (e.g., boosted pilots, waterfilling and zero guard bands). Here the earlier approach is generalized in such a way that it is able to accommodate for an accurate analytical EVM computation in the cases of power loading and different constellations for different tones. Moreover, the derivation is valid for a general magnitude clipping function, so that any realistic clipper can be plugged in.
1 Introduction
The use of multi-carrier (MC) communication schemes (e.g., OFDM, DMT, etc.) is very common nowadays due to its ability to cope well with channel interference while keeping the receiver complexity low, the ease of spectral mask shaping and high spectral efficiency. However, one of MC scheme's greatest drawbacks is the high peak-to-average power ratio (PAPR) caused by various degrees of coherent summation in the signal generation using IFFT [1]. Thus, systems utilizing MC communications must work with a large back-off in the high-power amplifier (HPA), which reduces both the efficiency of the HPA and the average power transmitted, or risk clipping. Based on the understanding that clipping is a nonlinear operation causing both in-band and out-of-band spectral noise and thus is an undesirable operation, methods for reducing the PAPR were devised. For a survey see [1–4]. Most of the power reduction methods are either statistical in nature--that is they do not guarantee PAPR limits, or iterative--in which required PAPR limits are easier to meet at the expense of computational complexity. Hence, while it is understood that the amount of clipping should be minimized, due to practical system limitations clipping cannot be entirely eliminated, but rather be set on a compromise level. Therefore, evaluating the performance of MC systems with clipping becomes relevant.
Two prominent criteria for evaluating the performance of a MC system are its capacity [5–7], and the system's error probability [8, 9]. However, in engineering practice, the most popular measure is the error vector magnitude (EVM). The EVM is a figure of merit for in-band distortion, which does not only quantifies the distortion but in some cases can attribute impairments to various system components [10]. Due to its popularity and troubleshooting capabilities, the EVM has become a mandatory part of a few communication standards, e.g. [[11], Tables 165, 172].
In [12] the authors express the EVM of an OFDM signal impaired by clipping without relying on the Gaussianity assumption and show that the EVM can be expressed with an arbitrary precision as a power series of the number of tones with constellation-dependent coefficients. It is also shown that for some specific constellations the EVM can be calculated via easy to use expressions without the need for a power series expansion. However, these computations fit the case of MC signals with an identical constellation for all tones and no power loading. Yet, real world signal utilize both different constellations for different tones and power loading. Some of the tones are zeroed due to spectral mask considerations, while some tones are boosted (e.g., pilot tones) to allow better channel tracking. A waterfilling solution in high SNR MIMO OFDM or in DMT also requires adjusting power and thus constellation to each tone individually. In this paper we address the issue of various constellations and power loading in the MC signal as well as the effect of an arbitrary magnitude clipping response by giving an analytical expression in the form of a power series for computing the EVM of the generalized case.
Analysis of clipped signals usually relies on the Gaussianity assumption [5]. However, this assumption is not always valid, especially for a mix of BPSK and QAM constellations. Hence, in order to evaluate the performance of such systems one must resort to numerical evaluations. This work allows to accurately compute the EVM of clipped signals for any constellation mixture and clipping function without the need to redo the numerical evaluation for each desired scenario.
The paper is organized as follows. In Section 2 the system model used in this work is introduced. Theorem 3.1 in Section 3 presents the main result of this work. In Section 4 we present simulation results and compare them to the theoretical results about EVM derived in this work.
2 System model
The system model discussed in this work is depicted in Figure 1. The vector a= [a0, a1,..., aN-1] T denotes the N data symbols vector in the form of constellation points, e.g., a∈ {+1, -1} N for BPSK. The vector x= [x0, x1,..., xN-1] T denotes the time domain discrete time signal and is obtained by applying the inverse discrete Fourier transform on a:

The vector y denotes the vector x after clipping operation. Two clipping functions we will specifically address are the SSPA clipper [13]:

and the soft clipper (which is a special case of the SSPA clipper for p ≫ 1):

where c is the clipping level. The noise vector w denotes an AWGN with variance  and is independent of a.
and is independent of a.  is the noisy clipped discrete time domain signal and
is the noisy clipped discrete time domain signal and  is the data symbols vector reconstructed from the clipped and noisy signal. For this system we define the EVM as
is the data symbols vector reconstructed from the clipped and noisy signal. For this system we define the EVM as

Assuming the constellation energy  is known and the noise variance is known, we need to calculate the error power
is known and the noise variance is known, we need to calculate the error power  to be able to evaluate the EVM. By virtue of Parseval's theorem, we have
to be able to evaluate the EVM. By virtue of Parseval's theorem, we have

Hence, it immediately follows that

The EVM contribution due to clipping can thus be calculated by computing the quantity  for every 0 ≤ n ≤ N - 1. Obviously, for scenaria with large channel noise we can allow more signal distortion due to clipping as long as it is negligible relative to the channel noise.
for every 0 ≤ n ≤ N - 1. Obviously, for scenaria with large channel noise we can allow more signal distortion due to clipping as long as it is negligible relative to the channel noise.
3 EVM computation
In this section we present the main result. Let f(|x n |) = f(r) be the energy of the clipped portion of the sample x n , and let us decompose the symbols vector a of length N into three groups:
-
N B groups of BPSK symbols. The symbols of each group, of size N r , are drawn from a constellation with energy
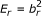 for 1 ≤ r ≤ N
B
.
for 1 ≤ r ≤ N
B
. -
N Q groups of QAM symbols. The symbols of each group, of size N s , are drawn from a constellation of size Ms, with constellation coefficients ν s,lm (which are the series expansion coefficients of a function of the constellation -see Appendix A for details.) and energy
 for 1 ≤ s ≤ N
Q
. For example, for QPSK of the form
for 1 ≤ s ≤ N
Q
. For example, for QPSK of the form  ,
, 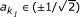 we have νs,11= -1/4, νs,22= -1/64, and for 16QAM of the form
we have νs,11= -1/4, νs,22= -1/64, and for 16QAM of the form  ,
, 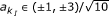 we have νs,11= -1/4 and νs,22= -17/1600.
we have νs,11= -1/4 and νs,22= -17/1600. -
N Z zero tones.
Clearly N B + N Q + N Z = N. Then, the following quantities are defined:

and

In addition, let  and
and  .
.
Theorem 3.1. The term in (6) can be calculated as follows:
in (6) can be calculated as follows:

where m q (c) depend on the clipping level, the constellations, power loading and symbol length. In particular, m0(c)and m1(c) can be calculated as follows:


Proof. See Appendix A. □
4 Simulation results and discussion
4.1 The Gaussian approximation
A common method for analyzing the EVM of an OFDM signal uses the central limit theorem (CLT). By invoking the CLT x
n
are assumed to be distributed complex normally, i.e.  , and thus |x
n
| ~ Rayleigh(σ). Hence, the EVM can be computed in a straightforward method:
, and thus |x
n
| ~ Rayleigh(σ). Hence, the EVM can be computed in a straightforward method:

where f(r) = f(|x n |)is the clipping function in polar coordinates. In this work, when the results are compared to the Gaussian approximation it is assumed that σ2 = 1.
4.2 Simulation results
In the following examples two cases of magnitude clipping functions are considered. The SSPA clipper, for which

and the soft clipper, for which  , where the operation()+ denotes taking only the positive part. The soft clipper is a special case of the SSPA clipper for p → ∞, which can be practically achieved with p > 100. In the following simulations p = 200 was chosen. Figure 2a demonstrates the EVM versus clipping level for the mixture of 64 BPSK modulated tones, 320 16QAM modulated tones and 128 zero tones, all randomly spread across the symbol. That is, N
B
= 1, Nr = 1= 64, N
Q
= 1, Ns = 1= 320, ν1,11 = -1/4 and ν1,22 = -17/1600. In this figure all constellation energies are normalized to unity (i.e. b
r
= q
s
= 1). Figure 2b demonstrates the EVM versus clipping level for the mixture of 128 BPSK modulated tones with constellation energy boosted by 3 dB, 128 QPSK modulated tones and 256 16QAM modulated tones (the two latter constellations are with unity constellation energy). Namely, for Figure 2b, the simulation parameters are N
B
= 1, Nr = 1= 128,
, where the operation()+ denotes taking only the positive part. The soft clipper is a special case of the SSPA clipper for p → ∞, which can be practically achieved with p > 100. In the following simulations p = 200 was chosen. Figure 2a demonstrates the EVM versus clipping level for the mixture of 64 BPSK modulated tones, 320 16QAM modulated tones and 128 zero tones, all randomly spread across the symbol. That is, N
B
= 1, Nr = 1= 64, N
Q
= 1, Ns = 1= 320, ν1,11 = -1/4 and ν1,22 = -17/1600. In this figure all constellation energies are normalized to unity (i.e. b
r
= q
s
= 1). Figure 2b demonstrates the EVM versus clipping level for the mixture of 128 BPSK modulated tones with constellation energy boosted by 3 dB, 128 QPSK modulated tones and 256 16QAM modulated tones (the two latter constellations are with unity constellation energy). Namely, for Figure 2b, the simulation parameters are N
B
= 1, Nr = 1= 128,  , and N
Q
= 2 with Ns = 1= 128, ν1,11 = -1/4, ν1,22 = -1/64, q1 = 1 and Ns = 2= 256, ν2,11 = -1/4, ν2,22 = -17/1600, q2 = 1.
, and N
Q
= 2 with Ns = 1= 128, ν1,11 = -1/4, ν1,22 = -1/64, q1 = 1 and Ns = 2= 256, ν2,11 = -1/4, ν2,22 = -17/1600, q2 = 1.
It can be clearly seen that as the mixture becomes more diverse in tone constellations and power loading, the mixed signal's EVM diverges from the Gaussian model. Additionally, as can be expected, the less linear the clipping function, the higher the EVM is. It can be also seen that the analytical computation coincides perfectly with the simulation.
5 Summary
In this paper we present a method for computing the EVM of a MC signal with power loading and various constellations on various tones that is impaired by clipping. This computation does not rely on any underlying model for the signal (such as the Gaussianity assumption), making it accurate for any mixture of tone constellations and power loading. A comparison between the simulated and theoretical EVM results shows a perfect match between the two. The main result of this work can be also used with any arbitrary magnitude clipping function for achieving more realistic results for practical uses.
Appendix A Proof of the EVM computation equation
We define the energy of the clipped portion of the signal as  . Any clipping function can be represented as a superposition of its effect on the signal's magnitude (AM/AM) and its effect on the signal's phase (AM/PM). The AM/AM function can be further represented in terms of |x
n
|. Thus, f can be defined as
. Any clipping function can be represented as a superposition of its effect on the signal's magnitude (AM/AM) and its effect on the signal's phase (AM/PM). The AM/AM function can be further represented in terms of |x
n
|. Thus, f can be defined as  , where
, where  is the polar coordinates representation. We wish to calculate
is the polar coordinates representation. We wish to calculate  any 0 ≤ n ≤ N -1. We start by representing
any 0 ≤ n ≤ N -1. We start by representing  by its inverse Fourier transform:
by its inverse Fourier transform:

where  is the Fourier transform of
is the Fourier transform of  :
:


where J0 is the Bessel function of the first kind and zeroth order. Furthermore, x n can be written explicitly as a sum of its real and imaginary parts as follows:

Thus, we can substitute (16) into(13) and rewrite  as
as

Denoting

and using the fact that a k are independent, we can write:

Therefore, according to(15)

We now proceed to calculate the term  of (20) by expanding to a power series the term
of (20) by expanding to a power series the term  and then taking the exponent of the series. Unlike [12], if a
k
are not identically distributed then ϕ
k
must be computed for every k, or alternatively for every type of constellation and then combined together. We rewrite the arguments of ϕ
k
as follows:
and then taking the exponent of the series. Unlike [12], if a
k
are not identically distributed then ϕ
k
must be computed for every k, or alternatively for every type of constellation and then combined together. We rewrite the arguments of ϕ
k
as follows:

where ζ = ω1 + iω2,  is the complex conjugate of ζ and ω = exp(2πi/N). Denoting
is the complex conjugate of ζ and ω = exp(2πi/N). Denoting  we can write ϕ
k
as follows:
we can write ϕ
k
as follows:

as in(18). We expand In ϕ k as a power series:

where we choose the representation  . We further assume that the data symbols vector a contains p ≤ N distinct groups of N
ι
,1 ≤ ι ≤ p symbols, where each group is drawn from the set of BPSK, QAM or zero constellation points with an average constellation energy of E
ι
,1 ≤ ι ≤ p. That is, groups of symbols are distinguished by the constellation type and by the average constellation energy. Hence, we have
. We further assume that the data symbols vector a contains p ≤ N distinct groups of N
ι
,1 ≤ ι ≤ p symbols, where each group is drawn from the set of BPSK, QAM or zero constellation points with an average constellation energy of E
ι
,1 ≤ ι ≤ p. That is, groups of symbols are distinguished by the constellation type and by the average constellation energy. Hence, we have

Now we proceed to compute In ϕ k for each type of constellation:
-
a k = 0: This option is usually used to generate guard bands [11]. For this option ϕ k = 1, and hence ln ϕ k = 0.
-
BPSK (a k = ±b = b · {±1}): First, it is noted that a k are drawn from a BPSK constellation with energy Ebpsk = b2. Next, we compute ln
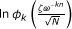 for a group of 1 ≤ Nbpsk ≤ N bins. Now, using the fact that a
k
are equi-probable we have
for a group of 1 ≤ Nbpsk ≤ N bins. Now, using the fact that a
k
are equi-probable we have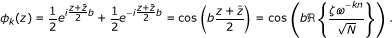 (25)
(25)
By Maclauren's series expansion we have

where ν2 = -1, ν4 = -2, ν6 = -16, etc. Now,

Using

-
(27)
becomes
 (29)
(29)
where N|2ns, -j ≤ s ≤ j and n ∈ [0, ..., N -1]. Next we compute the first two terms of (29), that is for j = 1,2, as it is assumed these terms yield sufficient accuracy. The cases of  require special attention. However, as the impact of the slightly different analytical expression for the above four cases relative to all other n is negligible for practical values of N (e.g., N ≥ 128) these cases will be neglected and treated equally as the rest of the BPSK tones.
require special attention. However, as the impact of the slightly different analytical expression for the above four cases relative to all other n is negligible for practical values of N (e.g., N ≥ 128) these cases will be neglected and treated equally as the rest of the BPSK tones.
-j = 1: If n ≠ 0, N/2 then the term  in (29) contains only the term s = 0, so
in (29) contains only the term s = 0, so

-j = 2: If n ≠ 0, N/4, N/2,3N/4 then the only possible term in the sum is s = 0, thus the sum is

Going back to (29)and substituting the above expressions, we find the following:

-
M-QAM: The QAM constellation points are drawn from the set
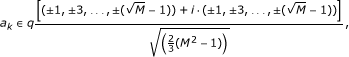 (33)
(33)
i.e. the QAM constellation is symmetric and the constellation energy is EQAM = q2. Symmetric QAM constellations satisfy ν00 = 0, ν20 = ν02 = 0, and ν11< 0. In addition, in all the symmetric cases ν
lm
= 0 if l+ m is odd. We proceed by computing the expansion of 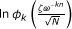 for a group of 1 ≤ NQAM ≤ N bins.
for a group of 1 ≤ NQAM ≤ N bins.
For the sake of simplicity, the expansion coefficients ν
lm
here are for the unity energy constellation, hence the expansion coefficients of ln ϕ are ql+m ν
lm
. For example, for QPSK of the form  ,
, 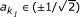 we have ν11 = -1/4, ν22 = -1/64, and for 16QAM of the form
we have ν11 = -1/4, ν22 = -1/64, and for 16QAM of the form  ,
, 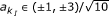 we have ν11 = -1/4 and ν22 = -17/1600.
we have ν11 = -1/4 and ν22 = -17/1600.
Then, similar to the BPSK case, we have

We next decompose the symbols vector a of length N into three groups:
-
N B groups of BPSK symbols. The symbols of each group, of size N r , are drawn from a constellation of energy
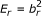 for 1 ≤ r ≤ N
B
.
for 1 ≤ r ≤ N
B
. -
N Q groups of QAM symbols. The symbols of each group, of size N s , are drawn from a constellation of size M s (that is, the coefficients ν lm are constellation dependent and are denoted as ν s,lm )and energy
 for 1 ≤ s ≤ N
Q
.
for 1 ≤ s ≤ N
Q
. -
N Z zero tones.
Obviously, N B + N Q + N Z = N.
Following(24),the expansions of In ϕ k of all groups are summed:

Denoting  and
and  we have
we have

Now, using ex = 1+ x + ⋯ we have

Following (20), we multiply (37) by  and integrate over ℝ2. First, we pass to polar coordinates u,θ (i.e. ζ = u exp (iθ)), and observe that all the terms
and integrate over ℝ2. First, we pass to polar coordinates u,θ (i.e. ζ = u exp (iθ)), and observe that all the terms  with l ≠ m vanish (since the integral of cos ((l-m)θ) is zero). Therefore, we are left with
with l ≠ m vanish (since the integral of cos ((l-m)θ) is zero). Therefore, we are left with

Using [14,(6.631)] we arrive at

Using the identities  and
and  and summing up N times (20), we get
and summing up N times (20), we get

Denoting  and
and  , (40) can be rewritten as
, (40) can be rewritten as

and following (9) we have

and

Abbreviations
- CLT:
-
central limit theorem
- EVM:
-
error vector magnitude
- HPA:
-
high-power amplifier
- MC:
-
multi-carrier
- PAPR:
-
peak-to-average power ratio.
References
Litsyn S: Peak Power Control in Multicarrier Communications. Cambridge University Press, Cambridge; 2007.
Han SH, Lee JH: An overview of peak-to-average power ratio reduction techniques for multicarrier transmission. IEEE Wireless Commun Mag 2005, 12: 56-65. 10.1109/MWC.2005.1421929
Jiang T, Wu Y: An overview: peak-to-average power ratio reduction techniques for OFDM signals. IEEE Trans Broadcast 2008,54(2):257-268.
Tellado J: Multicarrier Modulation with Low PAR. Kluwer Academic Publishers, Dordrecht; 2000.
Ochiai H, Imai H: Performance analysis of deliberately clipped ofdm signals. IEEE Trans Commun 2002,50(1):89-101. 10.1109/26.975762
Peng F, Ryan WE: On the capacity of clipped ofdm channels. ISIT2006, Seattle, USA, 9-14 July2006 2006.
Raich R, Qian H, Zhou G: Optimization of SNDR for amplitude-limited nonlinearities. IEEE Trans Commun 2005,53(11):1964-1972. 10.1109/TCOMM.2005.857141
Bahai A, Singh M, Goldsmith A, Saltzberg B: A new approach for evaluating clipping distortion in multicarrier systems. IEEE J Sel Areas Commun 2002,20(5):1037-1046. 10.1109/JSAC.2002.1007384
Nikopour H, Jamali S: On the performance of OFDM systems over a Cartesian clipping channel: a theoretical approach. IEEE Trans Wireless Commun 2004,3(6):2083-2096. 10.1109/TWC.2004.837425
Cutler B: Effects of physical layer impairments on ofdm systems. RF Design May 2002, 36-44.
IEEE standard for local and metropolitan area networks, part 16: Air interface for fixed broadband wireless access systems IEEE, Technical Report 2004.
Kotzer I, Har-Nevo S, Sodin S, Litsyn S: An analytical approach to the calculation of EVM in clipped multi-carrier signals., in press.
Rapp C: Effects of hpa-nonlinearity on a 4-dpsk/ofdm-signal for a digital sound broadcasting system. Second European Conference on Satellite Communications, 22-24.10.91, Liege, Belgium 1991, 179-184.
Gradshteyn I, Ryzhik I: Table of Integrals, Series and Products. Elsevier, Amsterdam; 2007.
Acknowledgement
The authors would like to thank Eyal Verbin for his contribution to this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kotzer, I., Litsyn, S. On the EVM computation of arbitrary clipped multi-carrier signals. EURASIP J. Adv. Signal Process. 2011, 36 (2011). https://doi.org/10.1186/1687-6180-2011-36
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-36

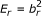 for 1 ≤ r ≤ N
B
.
for 1 ≤ r ≤ N
B
. for 1 ≤ s ≤ N
Q
. For example, for QPSK of the form
for 1 ≤ s ≤ N
Q
. For example, for QPSK of the form