- Research
- Open access
- Published:
Image denoising by a direct variational minimization
EURASIP Journal on Advances in Signal Processing volume 2011, Article number: 8 (2011)
Abstract
In this article we introduce a novel method for the image de-noising which combines a mathematically well-posdenes of the variational modeling with the efficiency of a patch-based approach in the field of image processing. It based on a direct minimization of an energy functional containing a minimal surface regularizer that uses fractional gradient. The minimization is obtained on every predefined patch of the image, independently. By doing so, we avoid the use of an artificial time PDE model with its inherent problems of finding optimal stopping time, as well as the optimal time step. Moreover, we control the level of image smoothing on each patch (and thus on the whole image) by adapting the Lagrange multiplier using the information on the level of discontinuities on a particular patch, which we obtain by pre-processing. In order to reduce the average number of vectors in the approximation generator and still to obtain the minimal degradation, we combine a Ritz variational method for the actual minimization on a patch, and a complementary fractional variational principle. Thus, the proposed method becomes computationally feasible and applicable for practical purposes. We confirm our claims with experimental results, by comparing the proposed method with a couple of PDE-based methods, where we get significantly better denoising results specially on the oscillatory regions.
1. Introduction
Since the work of Perona and Malik [1], PDE methods have been used for image processing, especially for denoising and stabilizing edges (see [1, 2]). They were the first to replace an isotropic diffusion expressed through a linear heat equation with an anisotropic diffusion. Diffusion, in generally, is associated with an energy dissipating process. This process seeks the minima of an energy functional. For example, the well known total variation (TV) minimization model [3, 4] is obtained in the case when the energy functional is equal to the TV norm of the image. Although these methods have been demonstrated to be able to achieve a good trade-off between the noise removal and the edge preservation, the resulting image in the presence of the noise often has a "blocky" look.
It is caused by the use of a second-order PDE modeling methods. In order to reduce the "blocky effect", while preserving sharp jump discontinuities, many other nonlinear filters have been suggested in the literature (see [5–9]). In [5], You and Kaveh proposed a class of fourth-order PDEs that are obtained by the minimization of a functional given as an increasing function of the edge detector Δu . Since the second-order derivatives are zero if the image intensity function is planar, the class of fourth-order PDEs will evolve and settle down to a planar image, if the image support is infinite. This is important, since piecewise planar images look more natural than the step images which are stationary points of the particular nonconvex energy functional [5], whose minimization (after the application of gradient descent) leads to the second-order diffusion. The problem with the use of fourth-order equations is that it tends to leave the image with isolated black and white speckles (so called "speckle effect") which may be characterized as pixels whose intensity values are either much larger or much smaller than those of the neighboring pixels as it is explained in [5]. Recently, fractional order PDEs have been studied and applied to the problem of image denoising. Bai and Feng in [10] proposed the use of nonlinear anisotropic fractional diffusion equation based on the Euler-Lagrange (EL) equation of a cost functional which is an increasing function of the absolute value of fractional gradient of the image intensity function. They managed to interpolate between second- and fourth-order nonlinear anisotropic diffusion equation to obtain a more natural images.
Nevertheless, only in a very limited number of simple cases, EL PDE that corresponds to the target energy functional can be analytically solved [11, 12]. Thus, in all related works, the actual minimization is conducted by the transition from an elliptic EL PDE, to a parabolic PDE with the artificial time. By doing so, a sort of low (in a general case nonlinear) filtering process [13] on a particular image is introduced. This process smoothes the image more and more in time. As a consequence, the problem of obtaining the optimal stopping time of a process emerges since the filtering can easily over-smooth the useful image features (edges, etc.). A similar problem appears with the choice of the optimal time step. Actually, a parabolic PDE model is obtained from the particular EL equation in the limiting process (ϕ-ϕ0)/λ → 0 as λ → 0, where ϕ0 is the noisy image, and λ is a Lagrange multiplier (see [11] or [13]). The role of λ, as the trade of between image smoothness and preservation of image features is lost: it becomes just a time step in the filtering process. The second problem related to the conventional PDE approach is that it is applied on a global image, so that the local image features are not sufficiently taken into account. In recent times, in the fields of Image Analysis, Processing and Synthesis, patch-based techniques emerged and meet with success. Defined as local square neighborhoods of image pixels, patches are very simple objects to work with, but they have the intrinsic ability to catch large-scale structures and textures present in natural images. Some recent image denoising methods are patch-based, such as "Non-Local Means" algorithm [14], and some of its derivatives [15, 16].
In this work, we present a novel variational, and at the same time patch-based image smoothing method, which combines a mathematically well-posdenes of the variational modeling with the efficiency of a patch-based approach. More-over, the proposed method is based on the direct variational minimization of the appropriate energy functional, which (as in [10]) involves fractional gradient. By doing so, we avoid problems of finding the optimal stopping time and the optimal time step. The role of λ is sustained and the actual minimization is conducted till it converges (with respect to the predefined error bound of the particular optimization method). We note that patch-based approach is also convenient to make the proposed direct variational method computationally feasible and applicable on real images. Actually, if working with the whole image, one needs a huge approximation bases1, which is not computationally feasible. According to this, we proceed as follows: The image is divided into relatively small overlap-ping patches, and the energy functional is minimized on each particular patch independently by using a direct variational minimization. As patches should not be to small, in order to capture enough relevant image features, the computational load would be still unacceptable for any real application if one calculates the minimizer in the whole orthonormal basis of the particular patch. There-fore, we approximate the true minimizer by using the Ritz variational method with a specially chosen trial functions [17]. In the sequel we call the set of those functions: the approximation generator. For that purpose, we derive the complementary fractional variational principle (CFVP) [17] for the corresponding energy functional. The CFVP gives us the explicit upper bound for the L2 norm of the approximation error. Next, we proceeded with spatial discretization of the continuous model, i.e., we make transition from the continuous image to pixels.
Every discrete patch is analyzed in the chosen discrete over-complete dictionary (same for every patch) that has the sparsity property in the class of discrete images of interest. In this work, we use a simple discrete cosine transform (DCT) over-complete dictionary which possess a sparsity property in the class of images (see [18]). The elements of the actual approximation generator for a particular patch, are chosen to be those with the largest K ≪ N projections 〈ϕ0, ψ n 〉, where N is size of the orthonormal basis and ϕ0 is observed noisy image, so that the upper error bound obtained by a spatially discretized CFVP is below the predefined threshold. Thus, the computational load is additionally rapidly reduced, making the method applicable for practical purposes. Moreover, as we conduct the minimization of the target functional on each patch separately, we use different values for the Lagrange multiplier for each patch. The choice is based on the measure of nonsmoothness of the signal present on that particular patch which is obtained by an appropriate pre-processing. Thus, we obtain additional stronger regularization on the uniform and weaker regularization on the oscillatory patches, which significantly improves resulting image quality. It is an additional adaptive feature of the proposed method which is not applicable to anisotropic diffusion PDE modeling. Actually, for that purpose anisotropic diffusion uses only an appropriate edge stopping function (in our case "mini-mal surface"), which is also included in the proposed model. We also note that we use the functional that contains gradient of a fractional order, in order to gain all benefits of fractional approach (see [10]), in comparison to the classical gradient method or the methods of higher order, as it is previously explained.
The article is organized as follows: In Sect. 2, the basic facts about the fractional order anisotropic [1, 10] diffusion, for image smoothing are mentioned. We emphasise the link between the energy functional and the actual parabolic PDE derived from its EL equation. In Sects. 3.1 and 3.2, we derive the CFVP for the energy functional with the fractional "minimal surface" regularizer. In Sect. 3.3, we use the spatially discretized model to obtain denoising on a single image patch, while in Sect. 3.4 we generalize this approach to obtain denoising of the whole image. In Sect. 4, we present experimental results and compare the proposed method with several anisotropic diffusion methods, and show that the proposed method better preserves image features, especially oscillatory regions. The conclusions are given in Sect. 5.
2. Fractional order anisotropic diffusion
In order to give an insight in the PDE approach to anisotropic image smoothing, which we tend to improve, we recall the derivation of the PDE used in [10]. We consider the following energy functional

with the Lagrangian

where ϕ0 is the initial noisy image. We assume that ϑ is the "minimal surface" edge stoping function ϑ (s) = (1 + s2)1/2 (see [13]) and λ is the Lagrange multiplier, i.e., a regularization weight. For the sake of simplicity, the image is defined to be the function on the whole space ℝ2 (as, for example in [19]). Thus, (2.2) is the functional which we will minimize by a patch-based direct variational minimization (PBDVM).
Denote by  the fractional gradient of order γ > 0 acting on an admissible scalar field ϕ: The partial fractional derivative operators
the fractional gradient of order γ > 0 acting on an admissible scalar field ϕ: The partial fractional derivative operators  and
and  of order γ act as
of order γ act as

where ξ = (ξ1, ξ2), and  is the Fourier-Plancherel transform operator. For the set of admissible functions ϕ, we chose Hγ (ℝ2), γ > 0. It is defined as
is the Fourier-Plancherel transform operator. For the set of admissible functions ϕ, we chose Hγ (ℝ2), γ > 0. It is defined as

Note that  and
and  exist for every ϕ ∈ Hγ(ℝ2) and belong to L2(ℝ2) due to (2.3) and the fact that
exist for every ϕ ∈ Hγ(ℝ2) and belong to L2(ℝ2) due to (2.3) and the fact that  . We also recall that the space Hγ(ℝ2), γ > 0 is dense in L2(ℝ2). This follows from the fact that
. We also recall that the space Hγ(ℝ2), γ > 0 is dense in L2(ℝ2). This follows from the fact that  is dense in L2(ℝ2). The density implies the existence of the adjoint operators
is dense in L2(ℝ2). The density implies the existence of the adjoint operators  and
and  , for
, for  and
and  , defined on Hγ(ℝ2). This can be easily shown by using the property
, defined on Hγ(ℝ2). This can be easily shown by using the property  implying that
implying that  (and similarly for
(and similarly for  ). Consequently, the fractional divergence
). Consequently, the fractional divergence  is well defined for u = (u1, u2) ∈ (Hγ(ℝ2))2.
is well defined for u = (u1, u2) ∈ (Hγ(ℝ2))2.
The Gateaux derivative of a functional J at ϕ in the direction η is defined as  . Condition J'(ϕ, η) = 0, for admissible functions η, gives the EL equation for (2.1). This is written as
. Condition J'(ϕ, η) = 0, for admissible functions η, gives the EL equation for (2.1). This is written as

As it is almost always infeasible to solve (2.4) directly [11, 12], the problem is solving by the introduction of the artificial time t ≥ 0. Let ϕ (·, 0) = ϕ0 and consider the right hand side of (2.4) as the discretization of ϕ t . Using the time step λ in the limiting process (ϕ - ϕ0)/λ → 0 as λ → 0, it follows that (2.4) becomes a fractional order anisotropic diffusion proposed in [10],

As it is mentioned in Sect. 1, one is able to smooth the homogenous regions of the image and leave the most of the useful features, due to the anisotropic property of the edge stopping function (see [13]). Moreover, the use of the fractional gradient provides a natural interpolation between the second- and the fourth-order diffusion equations [5, 10].
3. Patch-based direct variational minimization
Fractional anisotropic diffusion, as well as all other diffusion PDE models, has a problem of finding the optimal stopping time, as well as the optimal time step (for more details, see for example [11]). Moreover, as it is designed to be applied on a global image, it does not possess the benefits of the patch-based approach. It means that it can not model the local image features such as textures and oscillatory regions of the image such efficiently as the patch-based methods. We propose the novel PBDVM of the energy functional (2.1), which deals with those problems, as it is mentioned in Sect. 1. For that purpose, we divide image into overlapping patches, perform discretization of the continuous model and use a Ritz variational method for finding the minimizer of (2.1) on every particular patch of the image. Ritz variational method (we consider discretized version) for the particular discretized patch of the image of format N = M × M is based on representing the minimizer of the functional (2.1) in some fixed basis  of ℝN . Minimizer is represented in the form
of ℝN . Minimizer is represented in the form  , replaced in (2.1). Thus, one has to find
, replaced in (2.1). Thus, one has to find  , α = (α1,..., α
N
). Our intention is to find as small as possible approximation generator and still obtain satisfactory approximation. For that purposes, we use the generator
, α = (α1,..., α
N
). Our intention is to find as small as possible approximation generator and still obtain satisfactory approximation. For that purposes, we use the generator  of the space ℝN , with the size D much larger (at least several times) than N (D ≫ N), which additionally possess the sparsity property in the space of image patches of the particular class of images under consideration. It means that any patch which belongs to an image from that particular class, can be represented in
of the space ℝN , with the size D much larger (at least several times) than N (D ≫ N), which additionally possess the sparsity property in the space of image patches of the particular class of images under consideration. It means that any patch which belongs to an image from that particular class, can be represented in  with a small number of nonzero coefficient
with a small number of nonzero coefficient  , i.e., that ||α* ||0 ≪ N, where || · ||0 stands for l0 norm (see [18] for more details). In the sequel we call the approximation generator that possess sparsity property "over-complete dictionary" and its elements "atoms". It is common in the literature (see [18]). As a particular over-complete dictionary in our experiment in Section 4, we use DCT over-complete dictionary which has the sparsity property for a broad class of images (we can say almost all used in real applications). Note that the representation in the over-complete dictionary is not unique. In addition, we deliver the CFVP for the functional (2.1). This gives the L2 upper bound of the approximation error. In applications, in Sect. 3.3, we use the discretized version of that estimate (which gives the l2 approximation error bound) in order to find as small as possible approximation generator with sufficiently small approximation error for every patch. The procedure of finding the desired approximation generator, and the usage of CFVP for that purpose are explained in details in Sect. 3.3. Applying the proposed procedure, we significantly reduce the number of parameters for which we search the minimum of the target functional using the Ritz method and thus significantly reduce the computational complexity. The computational complexity is of order O(PN3) for minimization in the whole orthonormal bases of size N, which is not computationally feasible in real applications. It is reduced to
, i.e., that ||α* ||0 ≪ N, where || · ||0 stands for l0 norm (see [18] for more details). In the sequel we call the approximation generator that possess sparsity property "over-complete dictionary" and its elements "atoms". It is common in the literature (see [18]). As a particular over-complete dictionary in our experiment in Section 4, we use DCT over-complete dictionary which has the sparsity property for a broad class of images (we can say almost all used in real applications). Note that the representation in the over-complete dictionary is not unique. In addition, we deliver the CFVP for the functional (2.1). This gives the L2 upper bound of the approximation error. In applications, in Sect. 3.3, we use the discretized version of that estimate (which gives the l2 approximation error bound) in order to find as small as possible approximation generator with sufficiently small approximation error for every patch. The procedure of finding the desired approximation generator, and the usage of CFVP for that purpose are explained in details in Sect. 3.3. Applying the proposed procedure, we significantly reduce the number of parameters for which we search the minimum of the target functional using the Ritz method and thus significantly reduce the computational complexity. The computational complexity is of order O(PN3) for minimization in the whole orthonormal bases of size N, which is not computationally feasible in real applications. It is reduced to  when using the proposed CFVP, where
when using the proposed CFVP, where  is the average size of the approximation generator (averaged for all patches) and P is the overall number of overlapped patches. It is the consequence of the fact that Newton-based optimization methods that we use to obtain α*, uses the inversion of the Hessian of the target function and the order of complexity for the inversion of n × n matrix is O(n3).
is the average size of the approximation generator (averaged for all patches) and P is the overall number of overlapped patches. It is the consequence of the fact that Newton-based optimization methods that we use to obtain α*, uses the inversion of the Hessian of the target function and the order of complexity for the inversion of n × n matrix is O(n3).
3.1. Existence of the CFVP for the target energy functional
To formulate CFVP, we proceed by derivation of the canonical Hamiltonian equations. We introduce a new variable (generalized impulse) as

Now from the EL equation (2.4), we have the first canonical equation

As  , it follows
, it follows

and consequently

From (3.3) and (3.4) now follows the second canonical equation

where |u| < 1 is satisfied by definition (see (3.3)).
We briefly introduce some terms which will be used in the sequel. We denote  , and its adjoint operator
, and its adjoint operator  , so that
, so that

for admissible ϕ ∈ Hγ (ℝ2) and u ∈ (Hγ (ℝ2))2.
We define the potential I (u, ϕ) as

where we use (3.6)2. The functional W is defined as

where H (u, ϕ) = u · Tϕ - L (ϕ, Tϕ) is Hamiltonian.
Now, we have
Proposition 1. Assuming the existence and the uniqueness of the minimizer for the functional (2.1), there exists a complementary variational principal for (2.1).
Proof:
In terms of the theory presented in [17] (see [17], p. 94), the canonical equations for the boundary value problem (for which we seek the complementary principle) can be derived using (3.2) and (3.5) as

where

Theorem 5.3.1, p. 95. [17] states that sufficient conditions for I (u, ϕ) to be a convex-concave saddle functional (equivalently for a complementary principle) are that W is strictly convex in u and is concave in ϕ. Since W is differentiable on its domain, it is equivalent to say that W u = f1 (u) is strictly monotone and that W ϕ = f2 (ϕ) is anti-monotone. It is clear that f2 is anti-monotone, as

Next, we show that f1 (u) is strictly monotone. By the mean value theorem, there holds

where δ u = u - v, and w = v + εδ u, for some ε ∈ (0, 1).
Since

it follows that

for all |w| < 1 and δ u ≠ 0. This implies that f1 (u) is strictly monotone. The proof is completed. □
3.2. The L2 bound of the approximation error
From the fact that W (u, ϕ.) = F1 (u) + F2 (ϕ.), where  and
and  , and (3.10), it follows that
, and (3.10), it follows that

Now, (3.7) and (3.15) imply that

We denote

in which the terms J and G are primal and dual functionals, respectively, and

Note that I u = 0 and I ϕ = 0 are equivalent to Tϕ = W u (u, ϕ) = f1(u) and T * u = W ϕ (u, ϕ) = f2 (ϕ), respectively, i.e., (3.5) or (3.2) are satisfied, respectively.
Let (u1, ϕ1) ∈ Ω1. Then

From (3.16) and (u1, ϕ1) ∈ Ω1 (i.e., (3.5) is satisfied) we have

By substituting (3.19) into (3.20), we get

Note that E (ϕ) = λJ (ϕ) and that the minimizer ϕ* for J (ϕ) is also the minimizer for E (ϕ), so that J is actually a primal functional.
We also derive the relation for the dual functional. As (u2, ϕ2) ∈ Ω2 implies (3.2), i.e.,  , replacing into (3.16), we get
, replacing into (3.16), we get

Next we derive a bound on the L2 norm of the approximation error of (2.1). We state it as:
Proposition 2. The L2 norm of the approximation error  , where
, where  is approximate, and ϕ true minimizer of the functional J (ϕ) given by (3.21), has an upper bound:
is approximate, and ϕ true minimizer of the functional J (ϕ) given by (3.21), has an upper bound:

Proof:
Proposition (1) actually states that I(u, ϕ) has a saddle point, i.e., that for (u1, ϕ1) ∈ Ω1 and (u2, ϕ2) ∈ Ω2, so we have

Next we determine the second variation for J. The second partial derivatives are

so it holds that

This implies

Now, for ξ = ϕ + t(ϕ1 - ϕ), for some t ∈ (0, 1), from (3.24) and (3.27) we have

which completes the proof. □
3.3. Spatial discretization of the continuous model and the single patch denoising procedure
We proceed with the spatial discretization of the continuous model. It involves discretization of the primal and the dual energy functionals given by (3.21) and (3.22), respectively, and the inequality (3.23). We consider the discretized patch ϕ obtained from the fixed continuous L × L patch (which is cropped from the original image) by using the uniform M × M greed as ϕ (p, l) = ϕ (p Δx, l Δy), for p, l ∈ {0, 1,⋯, M - 1} = I, where Δx = Δy = L/M. In order to apply DFT transform, we actually impose a periodicity assumption, i.e., the continuous patch is defined on the rectangular domain Π ⊂ ℝ2, where Π = [a, b]2, b-a = L, and it is periodically prolonged on the whole ℝ2. For the spatial discretization (and thus approximation) of  and
and  , the fractional central differences [10] are used as follows:
, the fractional central differences [10] are used as follows:


where ω1, ω2 ∈ {0, 1, ⋯, M - 1} are DFT frequencies that correspond to the spatial coordinate x and y, respectively, and F is DFT operator.
Operator  has the form
has the form  , where
, where

is a diagonal matrix.
The adjoint operator  of
of  is expressed [10] by
is expressed [10] by

Similarly,

where

The relations (3.29)-(3.34) are used for the actual spatial discretization of the whole problem described by (3.21), (3.22), and (3.23). We thus get the following spatially discretized relations:


where  , including the estimate
, including the estimate

which correspond to the continuous relations (3.21), (3.22), and (3.23), respectively.
In the actual denoising procedure, we will also use the discretized version of the relation (3.1):

For a particular discretized M × M patch ϕ, we proceed with the single patch denoising procedure as follows. We chose the over-complete dictionary  as the fixed approximation generator (see [18]), where D ≫ N, for N = M 2. (We use the DFT over-complete dictionary in our experiments.) We analyze observed noisy patch ϕ0 in
as the fixed approximation generator (see [18]), where D ≫ N, for N = M 2. (We use the DFT over-complete dictionary in our experiments.) We analyze observed noisy patch ϕ0 in  . As noisy patch ϕ0 and atoms ψ
n
are M × M matrices, when we analyze ϕ0 by making the projections 〈ϕ0, ψ
n
〉, we use the classical l2 scalar product in ℝN. Here we present real matrices ϕ0 and ψ
n
as vectors of length N. Then we take the predefined K number (K ≪ N) of those atoms ψ
i
from
. As noisy patch ϕ0 and atoms ψ
n
are M × M matrices, when we analyze ϕ0 by making the projections 〈ϕ0, ψ
n
〉, we use the classical l2 scalar product in ℝN. Here we present real matrices ϕ0 and ψ
n
as vectors of length N. Then we take the predefined K number (K ≪ N) of those atoms ψ
i
from  with the largest projections |〈ϕ0, ψ
i
〉|, thus fixing the subspace where the approximation belongs. Next, we proceed with the Ritz method. We minimize (3.35) with respect to α = (α1,⋯, α
K
), Where we impose the approximate solution as
with the largest projections |〈ϕ0, ψ
i
〉|, thus fixing the subspace where the approximation belongs. Next, we proceed with the Ritz method. We minimize (3.35) with respect to α = (α1,⋯, α
K
), Where we impose the approximate solution as  . Actually, as
. Actually, as  and the terms can be calculated a priori (the same holds for
and the terms can be calculated a priori (the same holds for  ), the functional (3.35) becomes the function
), the functional (3.35) becomes the function  . In this way we get the unconstrained nonlinear optimization problem. As both, the gradient
. In this way we get the unconstrained nonlinear optimization problem. As both, the gradient  and the Hessian
and the Hessian  are defined and bounded, we apply classical Newton line search nonlinear optimization method to obtain the numerical solution for the minimizer α* of
are defined and bounded, we apply classical Newton line search nonlinear optimization method to obtain the numerical solution for the minimizer α* of  . We start from the initial α0 = (〈ϕ0, ψ1〉⋯〈ϕ0, ψ
K
〉), in order to be initially as close as possible to α*. This is reasonable since the assumption is that the additive Gaussian noise, superposed with the image, has a not so big variance. When we find
. We start from the initial α0 = (〈ϕ0, ψ1〉⋯〈ϕ0, ψ
K
〉), in order to be initially as close as possible to α*. This is reasonable since the assumption is that the additive Gaussian noise, superposed with the image, has a not so big variance. When we find  , we calculate û using the relation (3.38). Using the estimate (3.37), we obtain the l2 upper bound for the approximation error induced by the simple shrinkage procedure4. If it is above the predefined threshold ε, the approximation error could be greater than ε. So we add next m ≤ K vectors
, we calculate û using the relation (3.38). Using the estimate (3.37), we obtain the l2 upper bound for the approximation error induced by the simple shrinkage procedure4. If it is above the predefined threshold ε, the approximation error could be greater than ε. So we add next m ≤ K vectors  , with the next m largest values of |〈ϕ0, ψ
i
〉| in the approximation generator of that particular patch. Then we set
, with the next m largest values of |〈ϕ0, ψ
i
〉| in the approximation generator of that particular patch. Then we set  , where we obtained ϕold in the previous step. We optimize
, where we obtained ϕold in the previous step. We optimize  with respect to (αK+1, ..., αK+m) and get new, suboptimal, approximate
with respect to (αK+1, ..., αK+m) and get new, suboptimal, approximate  5. We continue with adding vectors as previously explained, until l2 upper bound for the approximation error becomes lower than ε. Experimental results presented in the next section show that the introduction of CFVP makes the method computationally feasible as the average number of coefficients
5. We continue with adding vectors as previously explained, until l2 upper bound for the approximation error becomes lower than ε. Experimental results presented in the next section show that the introduction of CFVP makes the method computationally feasible as the average number of coefficients  (by averaging on all patches) that we have to optimize, for the satisfactory approximation error obtained for every patch, is much (several times) smaller then N.
(by averaging on all patches) that we have to optimize, for the satisfactory approximation error obtained for every patch, is much (several times) smaller then N.
3.4. Generalization from a single patch to the whole image denoising
In order to effectively apply patch-based approach to the whole image denoising, but also eliminate the border effects that would emerge, we formulate the overlapped patch approach. We actually consider the generalized minimization task

where  is reconstructed patch of size N = M × M with coordinates i and j, with coefficients α
ij
, and λ
ij
are Lagrange multipliers for ij th patch. The terms ϕ0 and ϕ represent the noisy and the target image, respectively, and Ψ is some fixed basis for ℝN, or over-complete dictionary for space of patches of size M × M We denote
is reconstructed patch of size N = M × M with coordinates i and j, with coefficients α
ij
, and λ
ij
are Lagrange multipliers for ij th patch. The terms ϕ0 and ϕ represent the noisy and the target image, respectively, and Ψ is some fixed basis for ℝN, or over-complete dictionary for space of patches of size M × M We denote  . So it holds that
. So it holds that  , where
, where  are fixed. The operator R
ij
presents the matrix that crops the ij th patch from the image. The third and the second term in (3.39) correspond to the sum of the patch square errors and the regularization terms, respectively. For fixed ij th patch,
are fixed. The operator R
ij
presents the matrix that crops the ij th patch from the image. The third and the second term in (3.39) correspond to the sum of the patch square errors and the regularization terms, respectively. For fixed ij th patch,  actually corresponds to the discretized version of the primal functional (2.1), and thus to (3.35), defined on the ij th patch. The first term in (3.39) is the log-likelihood global force, that does not allow the target image (i.e., minimizer) to differ substantially from the original noisy image. The level of that proximity can be controlled using μ ≥ 0.
actually corresponds to the discretized version of the primal functional (2.1), and thus to (3.35), defined on the ij th patch. The first term in (3.39) is the log-likelihood global force, that does not allow the target image (i.e., minimizer) to differ substantially from the original noisy image. The level of that proximity can be controlled using μ ≥ 0.
Instead of minimizing (3.39) simultaneously for all α ij and ϕ, we perform two step modal approach, thus obtaining the suboptimal solution. First, we optimize α ij for fixed ϕ = ϕ0, and then optimize ϕ for previously determine α ij . In the first step we obtain

for all ij th patches separately. Thus, we proceed with the single patch de-noising procedure, where we fix over-complete dictionary Ψ, obtaining  for each ij th patch independently, where
for each ij th patch independently, where  is defined by (3.35), and it is described in details in the previous section. In the second step, by set-ting α
ij
= α
ij
*, we obtain
is defined by (3.35), and it is described in details in the previous section. In the second step, by set-ting α
ij
= α
ij
*, we obtain

which we solve for ϕ and obtain the close form solution [18]:

which is the final denoising result. Our additional goal is to use different values of λ for every patch, based on information on the level of its smoothness, in order to obtain better edge preservation. We extract that information by performing the synthesis of the auxiliary patch ϕ
pp
in the subspace of ℝN , generated by  obtained by taking first
obtained by taking first  atoms ψ
i
with largest 〈ϕ0, ψ
j
〉, where ϕ0 is original noisy patch and is fixed. If we denote c
j
=〈ϕ0, ψ
j
〉, for
atoms ψ
i
with largest 〈ϕ0, ψ
j
〉, where ϕ0 is original noisy patch and is fixed. If we denote c
j
=〈ϕ0, ψ
j
〉, for  , the synthesized auxiliary patch ϕ
pp
is given using the pseudo inverse of the matrix
, the synthesized auxiliary patch ϕ
pp
is given using the pseudo inverse of the matrix  containing the elements
containing the elements  as the column vectors:
as the column vectors:

This pre-processing can be interpreted as a simple shrinkage of the noisy patch, which "cuts off" some amount of noise, but without significant degradation of important image features. Next we calculate the modulus of gradient |∇ϕ pp | of the auxiliary patch ϕ pp using (3.29) and (3.30). If it is below the predefined, empirically chosen threshold T1, we consider the region predominantly homogeneous, and set λ = λ1, where predefined λ1 is large. If it is between T1 and T2, we set λ = λ2 for some medium λ2. Finally, if it is above T2, we set λ = λ3 for some small λ3. By doing so, we smooth more intensively homogeneous, and less intensively oscillatory regions of the target image.
4. Experimental results
Experimental results of this section are obtained by applying the proposed method on real images. All test images of size 512 × 512, were corrupted with the white Gaussian additive white noise of various standard deviation σ. We compare the proposed method with the several anisotropic diffusion methods. One is the classical Perona-Malik [1] anisotropic diffusion, on which we refer as baseline algorithm 1. The second one is the method proposed by Bai and Feng (also mentioned in Sect. 1) which is reported to give good results in pre-serving edges. We refer to it as the baseline algorithm 2. The third one is the method proposed by Cao and Yin [20], which belongs to the class of parabolic-hyperbolic equations applied to image smoothing. It is also reported to have very good edge preservation results. We refer to it as the baseline algorithm 3. The fourth one is the recent nonlocal diffusion proposed by Guidotti and Lambers [21]. For the first three baseline algorithms, the edge stoping function was set to ϑ(s) = (1+ s2)1/2, as it is also used in the proposed model. We use the PSNR as the objective measure of the denoising quality, as it is widespread throughout the image processing community. As PSNR is proved to be inconsistent with the human eye perception, we also use more profound structural similarity index measure (SSIM) [22] to additionally validate the proposed method, in comparison to the baseline algorithms. The resulting images for the baseline algorithms was chosen so that the best PSNR is reached, as it is usually done in the literature. Results presented show that the proposed method significantly outperform all baseline methods in the means of both, the PSNR and the SSIM measure. We have to mention that in the actual exploitation the referent, i.e., original image is not available. Thus, one has to fix the number of iterations of the used diffusion algorithm. This possibly causes the stronger over-smoothing effect on the target image. So the actual result would be even more in favor of the proposed method.
In Figure 1a,b,c, original test images are presented, while the corresponding noisy images are presented in Figure 2a,b,c, for σ = 20. We tested the proposed algorithm on "Barbara", "Fishing boat", and "Bicycle" test images, with three different values of Gaussian white noise standard deviation σ.
In Figure 3, processing results on the "Barbara" test image are presented for σ = 20. Results for the baseline algorithms 1, 2, 3, and 4 are presented in Figure 3a,b,c,d, respectively, while the processing result of the proposed method is presented in Figure 3e. The same algorithm order and settings, but for different test images is presented on Figures 4 ("Fishing boat") and 5 ("Bicycle"). For all the experiments, the order of the fractional gradient in the baseline method 2 and the proposed algorithm was set to be γ = 1.8, as it is the best reported in [10]. For all the experiments, parameter λ for the baseline algorithm 3 was set to λ = 20 which is the best reported in [20], while the parameter τ was set to τ = 0:1. Also, for all the experiments, for the baseline method 4, parameters c and "where set to c = 1.0, and ε = 0.6, respectively, which are the best reported in [21]. It can be seen visually (Figures 3, 4, and 5), that the proposed method gives much better edge preservation on the oscillatory regions compared to the baseline methods. At the same time, on the homogeneous region, noise is also better removed. The values of PSNR and SSIM are consistent with the visual results, as it can be seen from Tables 1, 2, and 3.
In Table 1, processing results are given for the proposed, and the baseline methods obtained on the "Barbara" test image for three different values of σ. Similar results are given in Tables 2 and 3, for "Fishing boat" and "Bicycle" test images, respectively. It can be seen that the values of PSNR and SSIM are consistent with the visual results, and that the proposed method significantly outperforms all baseline methods in the means of PSNR and specially SSIM measure. In Tables 2 and 3, similar results are given for "Fishing boat" and "Bicycle" test images, respectively. The same can be concluded as for the "Barbara" test image.
The upper l2 bound for the patch approximation error for all experiments was set to ε = 0.05. The patch size was fixed to n × n = 8 × 8 = 64, so it was the size of the orthonormal DCT basis. For all the experiments, we use 1/4 overlapped patches. We denote by  the average size of the approximation generators chosen from the atoms of the overcomplicate DCT dictionary, so that ||δ ϕ||2 < ε. As explained in the previous section, for the fix patch, we first take some predefined initial number of atoms K. In all experiments we set K = 5. If the upper bound (obtained by (3.37)) for ||δϕ||2 is greater than ε, we add additional m = 3 atoms, optimize coefficients, and continue until we obtain ||δ ϕ||2 < ε, as it is explained in the previous section. For all experiments,
the average size of the approximation generators chosen from the atoms of the overcomplicate DCT dictionary, so that ||δ ϕ||2 < ε. As explained in the previous section, for the fix patch, we first take some predefined initial number of atoms K. In all experiments we set K = 5. If the upper bound (obtained by (3.37)) for ||δϕ||2 is greater than ε, we add additional m = 3 atoms, optimize coefficients, and continue until we obtain ||δ ϕ||2 < ε, as it is explained in the previous section. For all experiments,  was obtained several times smaller then the size of the orthonormal DCT basis. For the "Barbara" test image, we obtain
was obtained several times smaller then the size of the orthonormal DCT basis. For the "Barbara" test image, we obtain  . For the "Fishing boat" test image, we obtain
. For the "Fishing boat" test image, we obtain  , and for the "Bicycle" test image,
, and for the "Bicycle" test image,  . This makes the proposed method considerably faster and thus computationally much more efficient, than it would be the case if one uses the whole orthonormal DCT basis. For all experiments,
. This makes the proposed method considerably faster and thus computationally much more efficient, than it would be the case if one uses the whole orthonormal DCT basis. For all experiments,  used for obtaining the ancillary patch was fixed on
used for obtaining the ancillary patch was fixed on  . Also, for all experiments, we set the thresholds and the corresponding Lagrange multipliers (explained in the previous section) on the following values:T1 = 0.003 and T2 = 0.01, and ¸ λ1 = 3.7, ¸ λ2 = 2.3, and ¸ λ2 = 0.8, respectively.
. Also, for all experiments, we set the thresholds and the corresponding Lagrange multipliers (explained in the previous section) on the following values:T1 = 0.003 and T2 = 0.01, and ¸ λ1 = 3.7, ¸ λ2 = 2.3, and ¸ λ2 = 0.8, respectively.
In Figure 6, enlargements of the processing results for the "Barbara" test image are presented. The enlargements for the baseline algorithms 1, 2, 3, and 4 are presented in Figure 6a,b,c,d, respectively, while the enlargement for the proposed method is presented in Figure 6e. As it can be seen, the proposed method has saved stripes on Barbaras kerchief, much more efficiently than the baseline algorithms. The similar can be concluded for Figure 7, where the enlargements of the processing results for the "Bicycle" test image are presented in the same order as in Figure 6. Again, it can be seen that the highly oscillatory regions (strips of the various thickness in the right upper corner) are much better preserved in the case of the proposed algorithm, than in the case of baseline algorithms.
5. Conclusion
In this article we introduce a novel patch-based method for image denoising. It is based on a direct minimization of the appropriate energy functional containing a "minimal surface" regularizer with the fractional gradient. We use the Ritz variational method to approximate the true minimizer of the target energy functional on a particular patch. In order to reduce the average number of vectors in the approximation generator, we deliver the CFVP for the target functional. After the spatial discretization, we obtain the l2 upper bound for the approximation error introduced by a simple shrinkage procedure, where we take the generator vectors from the DCT over-complete dictionary. Thus, we manage to significantly reduce computational load and make the method applicable. Moreover, we control the level of image smoothing on each patch (and thus on the whole image) by adapting the Lagrange multiplier using the information on the level of discontinuities present on a particular patch, which we obtain by pre-processing. We have compared the proposed method with the several anisotropic diffusion methods, and obtained significantly better results in the means of the objective PSNR, SSIM measures, as well as the subjective, visual results. In the future work, as we have manage to minimize the energy functional directly, we will try to introduce a group symmetry approach directly into the variational problem, similarly as it was done in the geometric PDE approach [12].
End notes
-
1.
For example, for 512 × 512 images it would be of size 5122 = 262144.
-
2.
In the framework of theory presented in [17], it holds that σ = 0, for all values of γ > 0.
-
3.
In the means of Gateaux derivatives (see [17]).
-
4.
By a simple shrinkage procedure, we consider disposing in synthesis all the other N - K elements of the frame
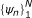 , with lower values for 〈ϕ0, ψ
n
〉.
, with lower values for 〈ϕ0, ψ
n
〉. -
5.
It is suboptimal, as it is not obtained by simultaneous minimization for all α i in the representation.
Abbreviations
- CFVP:
-
complementary fractional variational principle
- DCT:
-
discrete cosine transform
- PBDVM:
-
patch-based direct variational minimization
- SSIM:
-
structural similarity index measure.
References
Perona P, Malik J: Scale-space and edge detection using anisotropic diffusion. IEEE Trans Pattern Anal Mach Intell 1990, 12: 629-639. 10.1109/34.56205
Catte F, Lions PL, Morel JM, Coll T: Image selective smooting and edge detection by nonlinear diffusion. SIAM J Numer Anal 1992, 29: 182-193. 10.1137/0729012
Rudin LI, Osher S, Fatemi E: Nonlinear total variation based noise removal algorithms. Phys D 1992, 60: 259-268. 10.1016/0167-2789(92)90242-F
Vogel C, Oman M: Iterative methods for total variation denoising. SIAM J Sci Stat Comput 1996, 17: 227-238. 10.1137/0917016
You YL, Kaveh M: Fourth-order partial differential equation for noise removal. IEEE Trans Image Process 2000, 9: 1723-1730. 10.1109/83.869184
Lysaker M, Lundervold A, Tai XC: Noise removal using fourth-order partial differential equation with aplication to medical magnetic resonance images in space and time. IEEE Trans Image Process 2003, 12: 1579-1590. 10.1109/TIP.2003.819229
Chambole A, Lions PL: Image recovery via total variation minimization and related problems. Numer Math 1997, 76: 167-188. 10.1007/s002110050258
Blomgren P, Mulet P, Chan TF, Wong CK: Total variation image restoration: numerical methods and extensions. Proc Int Conf Image Process 1997, 3: 384-387.
Chan TF, Marquina A, Mulet P: High order total variation-based image restoration. SIAM J Sci Comput 2000, 22: 503-516. 10.1137/S1064827598344169
Bai J, Chu Feng X: Fractional order anisotropic difusion for image denoising. IEEE Trans Image Process 2007, 16: 2492-2502.
Didas S, Weickert J, Burgeth B: Properties of higher order nonlinear diffusion filtering. J Math Imaging Vis 2009, 35: 208-226. 10.1007/s10851-009-0166-x
Sapiro G: Geometric partial differential equations and image analysis. Cambridge University Press, Cambridge; 2001.
Aubert Gilles, Kornprobst Pierre: Mathematical Problems in Image Processing, Partial Differential Equations and the Calculus of Variation. 2nd edition. Springer, New York; 2006.
Buades A, Coll B, Morel JM: A non-local algorithm for image denoising. IEEE CVPR 6065 2005.
Azzabou N, Paragios N, Guichard F, Cao F: Variable bandwidth image denoising using image-based noise models. IEEE CVPR 2007.
Boulanger J, Kervrann C, Bouthemy P: Space-time adaptation for patch-based image sequence restoration. IEEE PAMI 2007,29(6):10961102.
Arthurs AM: Complementary Variational Principles. 2nd edition. Clarendon Press, Oxford; 1980.
Elad M, Aharon M: Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans Image Process 2006,15(12):3362.
Didas S, Burgeth B, Imiya A, Weickert J: Regularity and Scale Space Properties of Fractional High Order Linear Filtering. Volume 3459. Lecture Notes in Computer Science Springer, Berlin; 2005:13-25.
Cao Y, Yin J, Liu G, Li M: A class of nonlinear parabolic-hyperbolic equations applied to image restoration. Nonlinear Anal Real World Appl 2010,11(1):253-261. 10.1016/j.nonrwa.2008.11.004
Guidotti P, Lambers JV: Two new nonlinear nonlocal diffusion s for noise reduction. J Math Imaging Vis 2009, 33: 2537.
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP: Image quality assessment: from error to structural similarity. IEEE Trans Image Process 2004,13(4):600-612. 10.1109/TIP.2003.819861
Acknowledgements
This research work has been supported by the "Serbian Ministry of Science and Technology" and it has been realized as a part of 174005, 174024, III44003, and TR32035 projects.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Janev, M., Atanacković, T., Pilipović, S. et al. Image denoising by a direct variational minimization. EURASIP J. Adv. Signal Process. 2011, 8 (2011). https://doi.org/10.1186/1687-6180-2011-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2011-8







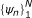 , with lower values for 〈ϕ0, ψ
n
〉.
, with lower values for 〈ϕ0, ψ
n
〉.