- Research
- Open access
- Published:
Informed spectral analysis: audio signal parameter estimation using side information
EURASIP Journal on Advances in Signal Processing volume 2013, Article number: 178 (2013)
Abstract
Parametric models are of great interest for representing and manipulating sounds. However, the quality of the resulting signals depends on the precision of the parameters. When the signals are available, these parameters can be estimated, but the presence of noise decreases the resulting precision of the estimation. Furthermore, the Cramér-Rao bound shows the minimal error reachable with the best estimator, which can be insufficient for demanding applications. These limitations can be overcome by using the coding approach which consists in directly transmitting the parameters with the best precision using the minimal bitrate. However, this approach does not take advantage of the information provided by the estimation from the signal and may require a larger bitrate and a loss of compatibility with existing file formats. The purpose of this article is to propose a compromised approach, called the 'informed approach,’ which combines analysis with (coded) side information in order to increase the precision of parameter estimation using a lower bitrate than pure coding approaches, the audio signal being known. Thus, the analysis problem is presented in a coder/decoder configuration where the side information is computed and inaudibly embedded into the mixture signal at the coder. At the decoder, the extra information is extracted and is used to assist the analysis process. This study proposes applying this approach to audio spectral analysis using sinusoidal modeling which is a well-known model with practical applications and where theoretical bounds have been calculated. This work aims at uncovering new approaches for audio quality-based applications. It provides a solution for challenging problems like active listening of music, source separation, and realistic sound transformations.
1 Introduction
Active listening aims at enabling the listener to modify the music in real time while it is played. This makes produced music, fixed on some support, more lively. The modifications can be, for example, audio effects (time stretching, pitch shifting, etc.) on any of the sound sources (vocal or instrumental tracks) present in the musical mix.
To perform these sound transformations with a very high quality, sinusoidal modeling[1, 2] is well suited. However, this parametric model requires a very precise analysis step in order to estimate the sound parameters accurately.
For simple sounds, i.e., monophonic with a high signal-to-noise ratio (SNR), state-of-the-art estimators such as the spectral reassignment[3] or the derivative method[4] are sufficient. But this is rarely the case for more complex audio signals, like the final mix of the music.
Indeed, theoretical limitations for the best estimators exist and are given by the Cramér-Rao bound (CRB) which corresponds to the minimal error variance reachable with an unbiased estimator. This bound indicates that despite efforts to enhance the analysis methods, the maximal quality is bounded and can be insufficient for complex audio signals and demanding applications such as as active listening of music.
However, digital multi-track audio recording techniques are now widely used by recording studios and make available - for the producer - the isolated audio signals which compose the mix. This allows the estimation of audio parameters with a high accuracy when the signals are not disturbed by other sound sources (interferers). Furthermore, music creators sometimes use pure synthetic sounds (e.g., MIDI expander or virtual instruments) where the exact audio signal parameters can be known.
The coding approach consists in transmitting the parameters of the signal using a minimal amount of information. The sinusoidal model has interesting sparsity properties for representing sound signals and allows efficient audio coding[5, 6]. Furthermore, this model which corresponds to the deterministic part of sounds is used by MPEG-SSC[7] and MPEG-HILN[8] and obtains a high perceptual quality using about 24 kbps per source. The major drawback with this approach is the loss of compatibility with legacy digital audio formats. For the purpose of compatibility, one can embed the coded parameters in the digital audio file, using watermarking techniques. However, the pure coding approach will not take advantage of the information provided by a classic estimator which could intuitively be used to reduce the resulting coding bitrate.
When collaborating with the music producers and aiming at enabling active listening for the consumer, we are then in a situation where we can have access to many audio tracks - simpler signals, thus with more accurate parameters - prior to the mixing stage of the music production, whereas for compatibility reasons, we will have to deal with the final mix - much more complex - as a standard digital audio file.
So, on the one hand, the classic estimation approach deals with the standard digital audio file of the mix but produces parameters of insufficient quality. But, on the other hand, the coding of the isolated sound sources often requires the introduction of a new audio format and does not take advantage of estimation from the transmitted mix.
In this article, we propose an alternative approach called 'informed analysis’ for parameter estimation which consists in combining a classic estimator with side information. In recent years, the informed approach was successfully introduced[9] and applied to audio source separation. The proposed methods[10, 11] also called informed source separation (ISS) provide a practical solution to underdetermined (where the number of observed mixtures is smaller than the number of sources) audio source separation which remains challenging in the blind case.
Using this approach, extra information is extracted and coded using the original separated source signals assumed to be known before the creation of the mixture signal which is sent to the decoder. At the decoder where the source signals are unknown, the analysis process is assisted by the transmitted extra information. To ensure the compatibility with existing audio formats, the extra information is inaudibly embedded into the analyzed mixture signal itself using a large bandwidth watermarking approach[12].
In spite of promising audio listening results, ISS techniques are specific to the source separation problem and the resulting quality of existing approaches remains limited by the oracle estimator (e.g., Wiener filtering). Furthermore, these approaches do not estimate directly the audio signal parameters which can be of great interest for audio transformations and cannot yet master the audio quality by defining a target distortion measure (e.g., SNR) according to the rate-distortion theory.
In this article, we introduce a generalized framework which can be applied to any parameter estimation problem and which is not limited to audio applications. The method proposed in this article is applied to audio sinusoidal modeling and reaches the desired target quality by combining a classic estimator with minimal extra information. Thus, we both improve the precision of classic spectral analysis which is theoretically limited by the CRB and we improve the efficiency of distortion-rate optimal quantization (used for lossy compression), thanks to the information provided by the classic analysis. Moreover, the resynthesis of the sound sources from their parameters (without transformation) results in a source separation technique.
This work is an extension of previously published conference papers[13, 14]. Firstly, it proposes a generalization and a complete theoretical framework which can be applied to any informed analysis problem for an optimal combination of estimation and coding. Secondly, it provides more advanced simulations and more detailed calculations about the informed approach applied to the sinusoidal model. Thirdly, it provides more advanced source separation results using the proposed technique (realistic mixture composed of six sources). Finally, the mask computation technique used by the source separation method was enhanced since[14] and uses long-term sinusoidal modeling to minimize the overall bitrate.
This article is organized as follows. The informed analysis framework is described in Section 2. It is applied to the spectral analysis for the sinusoidal model in Section 3. In Section 4, we propose an implementation of an ISS -like system which estimates the isolated source parameters. Finally, results and future work are discussed in Section 5.
2 Generalized informed analysis framework
Due to limitations of the blind or the semi-blind approach for challenging estimation problems like audio source separation, recent methods have considered the usage of side information to improve the resulting quality for practical applications[9, 10]. In this section, we propose to generalize this idea to any estimation problem where model parameters have to be estimated from a perturbed observed signal. Thus, the problem of parameter estimation using side information is formulated and solved using the proposed method.
2.1 Problem formulation
First consider a real signal s which is a function of a deterministic parameter p (which can be a real vector) combined with noise b resulting from a stochastic process. Thus, the observed signal can be expressed as follows:
where μ is the function which models the observed signal. The classic estimation problem consists in recovering the parameter p from the observed signal s with the minimal error. The resulting estimation using a classic estimator denoted is a stochastic process due to the presence of b; thus, we have
where ε corresponds to the error of estimation. The Cramér-Rao bound defines the minimal variance for the best unbiased estimator (which verifies); thus, we have
Here, F denotes the Fisher matrix which can be expressed as the second derivative of the log-likelihood function expressed as
where E[·] and V[·], respectively, are the expectation and variance operators and f(s;p) is the probability density function of s which depends on the p value. The inequality (3) means that the minimal error variance is bounded for the best estimator. Thus, if we aim at reaching a target variance V target ≤ CRB, according to (3), the unique solution for a given model f(s;p) is to use side information.
2.2 Informed approach for parameter estimation
Now we assume a configuration (see Figure1) similar to existing ISS techniques[10] where p is exactly known before the signal s is synthesized according to (1). The informed approach for a given analysis problem consists in minimizing both the resulting error of estimation and the bitrate of the side information.
At the coder, the minimal extra information denoted is computed from p according to V
target using the parameter I
σ
which depends on the estimator precision. At the decoder,
is computed from p according to V
target using the parameter I
σ
which depends on the estimator precision. At the decoder, is combined with estimation to obtain which verifies. For an unbiased estimator, we can notice that the variance is equal to the mean squared error:.
is combined with estimation to obtain which verifies. For an unbiased estimator, we can notice that the variance is equal to the mean squared error:.
To describe the proposed method based on this configuration, we consider first the estimation of a scalar parameter p in Section 2.2.1. In Section 2.2.2, the proposed method is generalized to the estimation of a ν-dimensional vector parameter.
2.2.1 Single-parameter informed analysis
Suppose we have to estimate a real parameter p ∈ [0,1). p is related to the signal s which is created according to (1) from the parameter p including the noise. The information needed to recover p based on the estimate obtained from s is extracted as follows: firstly, we define the d-bit fixed-point binary coding application and the decoding application. C = (C
1,C
2,…,C
d
) denotes the representation of p and is the d-bit fixed-point value of p. The coding and decoding applications correspond to a uniform scalar quantizer with a quantization step Δ = 2-d. The bit precision d can be deduced from the target average distortion which can be the mean squared error resulting from uniform quantization. In practice, the design of the quantizer depends on the choice of the distortion measure. This point is discussed for the vector quantization case in Section 2.2.2 and is detailed for a specific application in Section 3.3.
the decoding application. C = (C
1,C
2,…,C
d
) denotes the representation of p and is the d-bit fixed-point value of p. The coding and decoding applications correspond to a uniform scalar quantizer with a quantization step Δ = 2-d. The bit precision d can be deduced from the target average distortion which can be the mean squared error resulting from uniform quantization. In practice, the design of the quantizer depends on the choice of the distortion measure. This point is discussed for the vector quantization case in Section 2.2.2 and is detailed for a specific application in Section 3.3.
Secondly, I σ is defined as the most significant bit (MSB) of the upper bound of the estimator confidence interval (CI) and corresponds to the boundary between the reliable and the unreliable part of each estimation. In practice, I σ is estimated for a significant number of occurrences over using the estimator for a given noise probability density function. In this case, we assume that the noise can be measured or simulated. Otherwise, I σ can also be estimated iteratively[14] as proposed for the application described in Section 4. According to the Figure2 which results from the reassignment method applied to a signal combined with a white Gaussian noise (see[13] for the experiment details), can be separated respectively in a reliable part (the useful information provided by the classic estimator) and an unreliable part as we have
Thus, can be exactly recovered from any estimated value using :
:
which satisfies. Thus, the extra information denoted is defined as the part of situated between indices I
σ
- 1 and d (the unreliable part). The additional bit value is required for the error correction process based on the binary substitution mechanism which is applied in Algorithm 1. The informed estimation denoted is finally recovered from any taking advantage of
is defined as the part of situated between indices I
σ
- 1 and d (the unreliable part). The additional bit value is required for the error correction process based on the binary substitution mechanism which is applied in Algorithm 1. The informed estimation denoted is finally recovered from any taking advantage of using Algorithm 1, where ' inc’ and ' dec’ stand, respectively, for incrementing and decrementing the binary representation. In this algorithm, we chose the MATLAB notation where C(i) denotes C
i
and C(i:j) denotes the vector C
i
,C
i+1,…,C
j
. Firstly, Algorithm 1 substitutes the unreliable part of with where l = min(d,d-I
σ
+ 2) corresponds to the length of vector
using Algorithm 1, where ' inc’ and ' dec’ stand, respectively, for incrementing and decrementing the binary representation. In this algorithm, we chose the MATLAB notation where C(i) denotes C
i
and C(i:j) denotes the vector C
i
,C
i+1,…,C
j
. Firstly, Algorithm 1 substitutes the unreliable part of with where l = min(d,d-I
σ
+ 2) corresponds to the length of vector . Secondly, the bit value at position I
σ
- 1 is compared to which tests if the substitution process is sufficient for error correction. When the values are different, a complementary arithmetic operation is required to solve eventual matching exception problems of the binary representation due to the carry mechanism. In this case, the binary representation of is separated into two parts denoted C
ante and C
post which are used to compute two possible candidates denoted p
+ and p
-. The one which is the closest to is chosen as the error-corrected value.
. Secondly, the bit value at position I
σ
- 1 is compared to which tests if the substitution process is sufficient for error correction. When the values are different, a complementary arithmetic operation is required to solve eventual matching exception problems of the binary representation due to the carry mechanism. In this case, the binary representation of is separated into two parts denoted C
ante and C
post which are used to compute two possible candidates denoted p
+ and p
-. The one which is the closest to is chosen as the error-corrected value.
Algorithm 1 Error correction of using


For audio applications, I
σ
can also be estimated directly from the mixture using a noise estimation method (e.g.,[15]) or can be deduced using d and the length of . In other cases, it has to be transmitted as extra information using a maximum of ⌈log2(d)⌉ bits. Here, ⌈.⌉ denotes the ceiling function.
. In other cases, it has to be transmitted as extra information using a maximum of ⌈log2(d)⌉ bits. Here, ⌈.⌉ denotes the ceiling function.
In the considered configuration, the exact value of is assumed to be different at the coder and at the decoder. This configuration is particularly realistic when the observed signal depends on the transmitted extra information used for the error correction itself. This is the case for ISS methods which use watermarking where estimated values depend on the embedded extra information. In this particular configuration, a closed-loop differential predictive coder[16] cannot be used. Single-parameter informed analysis is applied to sinusoidal model parameters estimation described in Section 3.2.
2.2.2 Generalization to vector parameter informed analysis
Consider now that we have to estimate P ∈ [0,1)ν, a ν-dimensional real vector. As we aim at minimizing both the bitrate and the resulting error, P has to be an entropy-constrained vector quantized first according to the rate-distortion theory[17] to obtain.
Thus, for a target maximal average distortion, the Shannon theorem tells us that there exists a code of minimal rate. The rate-distortion problem can be formulated as a minimization of the following unconstrained Lagrangian cost function:
where λ is the Lagrangian multiplier. The solution to this optimization problem defines the rate-distortion function R(D) which is defined as the lower bound for the bitrate required to code with the maximal average distortion D. A computational solution consists in using the generalized Lloyd algorithm for entropy-constrained vector quantization proposed by Chou et al. in[18]. The resulting optimal quantizer is almost uniform according to the rate-distortion theory[17] and can be combined with variable-length entropy coding (e.g.,[19]).
After the entropy-constrained optimal quantization, the extra information used to recover from any estimated has to be computed. As each component vector P i can have a different contribution for the overall distortion D, it results to a variable relative precision over each vector component (resulting from the vector quantizer design). According to[16], the optimal entropy-constrained vector quantizer is a uniform quantizer for each dimension, where a different bit budget d i can be allocated to each vector component. This bit budget can easily be deduced from the relative accuracy over each component resulting from the vector quantizer design. Thus, the technique proposed for single-parameter informed analysis can be applied on each separated component P i . The overall generalized vector parameter informed analysis can be summarized as follows, respectively, for the coder and the decoder:
-
Coder
-
Synthesize s from P according to observation model (1).
-
Perform entropy-constrained vector quantization of P using[18] (or an equivalent method) for a given target distortion D target.
-
Define the reliable and the unreliable part for each component P i using a given estimator and compute.
-
Transmit s and
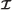 to the decoder using separated communication channels where
to the decoder using separated communication channels where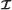 can be coded using entropy coding.
can be coded using entropy coding.
-
-
Decoder
-
Estimate from s.
-
Perform entropy-constrained vector quantization of using[18] for the given target distortion D target.
-
Apply error correction using Algorithm 1 for each component P i using. Each component can be recovered if a prefix code or a separator word was chosen at the coder.
-
The proposed generalized informed analysis method for signal parameter estimation is applied to the sinusoidal model described in the next section.
3 Informed spectral analysis
The sinusoidal model involves a complete analysis/transformation/synthesis chain which is common for most audio applications. This model is particularly suitable for representing the deterministic part of sounds which is perceptually the most important[6]. The quality of synthesized signals strongly depends on the accuracy of the estimated parameters of each sinusoidal component.
3.1 Sinusoidal modeling of sound signals
As mentioned by Fourier’s theorem, any periodic signal can be decomposed in a sum of sinusoids with various amplitude and harmonically related frequencies. In its more generalized expression, we consider a sum of time-varying complex sinusoids (the partials). We also consider a residual signal denoted r(t) which results from the modeling approximation using a finite number L of sinusoidal components and an eventual additive observation noise. The resulting model can be written as
where j 2 = -1. Here, a(t) and denote, respectively, the time-varying (non-stationary) amplitude and initial phase (for t = 0). The phase parameter depends on the time-varying frequency denoted ω(t) which corresponds to its instantaneous first derivative:.
3.1.1 Parameter estimation
As proposed in[20], efficient estimators for sinusoidal model parameters may be derived from the short-time Fourier transform (STFT) of the observed signal. STFT-based methods are preceded by peak detection and noise thresholding in the magnitude spectrum before the sinusoidal parameters are estimated[21]. For each spectral peak, the signal model is reduced to only one partial (L = 1) where the influence of the other partials is neglected (in the general case when L > 1). For a local analysis frame centered around time 0 using the stationary model, the signal can be expressed as
where a 0, ω 0, and ϕ 0 are the instantaneous parameters. The stationary model considered here is sufficient for most of the sounds where parameters are slowly varying. Thus, the parameters are assumed constant for a short analysis frame[22].
3.1.2 The reassignment method
The reassignment method, first proposed by Kodera et al.[23, 24], was generalized by Auger and Flandrin[3] for time and frequency. This method enhances the resolution in time and in frequency of classic STFT methods. Let us consider first the STFT of signal s:
This involves an analysis window w, band-limited in such a way that for any frequency corresponding to one specific partial (corresponding to a local maximum in the magnitude spectrum), the influence of the other partials can be neglected. We use the zero-centered (symmetric) Hann window of duration N, defined on the [-N/2;+N/2] interval according to
By considering (10), one can easily derive
thus,
where ℜ(z) and ℑ(z) correspond, respectively, to the real and the imaginary part of the complex scalar z. Here, denotes the STFT of signal s using the first time derivative of the analysis window w. The estimates of the frequency, amplitude, and phase parameters can respectively be expressed for a partial l corresponding to a local maximum m of the (discrete) magnitude spectrum at the (discrete) frequency ω m :
and
where W(ω) is the spectrum of the analysis window w:
In the case of the Hann window, we have
where is the spectrum of the rectangular window,, and F s is the sampling frequency. The reassignment method is among the best STFT-based methods in terms of efficiency and estimation precision[4, 25]. High-resolution methods[26] improve the frequency resolution, but not the estimation precision, always limited by the CRB (see Figure3).
3.1.3 Theoretical bounds
When evaluating the performance of an estimator in the presence of noise and in terms of the variance of the estimation error, an interesting element to compare with is the CRB which is defined as the limit to the best possible performance achievable by an unbiased estimator given a data set. For the model of (9), for the three model parameters, these bounds have been derived, e.g., by Zhou et al.[27]. We will consider the asymptotic version (for a large and a high number of observations) of the corresponding bound.
Djurić and Kay[28] have shown that the CRB depends on the time n 0 which corresponds to time 0 in (9) and at which the parameters are estimated. The optimal choice in terms of lower bounds is to set n 0 at the center of the frame since the CRB depends on
Thus, in the stationary case, the lower bound for the amplitude a, frequency ω, and phase ϕ are[27]
The precision of the estimation of each sinusoid is limited by this CRB, at least without using additional information. As shown in Figure3, the variance of the error obtained with the reassignment method is close to the CRB. However, for practical problems, this resulting quality can be insufficient and may require enhancement using complementary information as it is proposed in the next section.
3.2 Informed approach in the scalar case
Informed analysis consists of a two-step analysis. Firstly, extra information is extracted during a coder step using the knowledge about the distribution of the estimation error resulting from a classic (not informed) analysis. Secondly, the same estimator is applied to an altered version of the same signal (e.g., mixing with other sounds plus addition of noise) and the errors are systematically corrected using the previously extracted information. This approach assumes that the reference parameters are exactly known at the coder step before the alteration of the signal. In this section, the informed analysis framework which was described in a general case in Section 2 is respectively applied to scalar and vector informed sinusoidal parameter estimation in the following sections.
In this section, all parameters of the sinusoidal model described in (9) are considered separately. Thus, the single-parameter informed analysis method described in Section 2.2.1 is applied to sinusoidal model parameter estimation using the reassignment method.
3.2.1 Simulation
For the experiment where the results are presented in Figure3, we consider a discrete-time signal s with sampling rate F s = 44.1 kHz consisting of one complex exponential (L = 1) generated according to (8) with an amplitude a 0 = 1 and mixed with white Gaussian noise of variance σ 2. The SNR is given in decibels by. To make the parameters independent of the sampling frequency, in the remaining part of this paper, we normalize ω by F s . The analysis frames we consider are of odd length N = 2H + 1 = 513 samples (the duration, in seconds, of the analysis window being T = N/F s ), with the estimation time 0 set at their center. The computation uses the fast Fourier transform based on (10) where the continuous integral turns into a discrete summation over N values, with an index from -H to +H.
Thus, Figure3 compares the variances of the errors obtained from the estimation of each sinusoidal parameter using the classic reassignment method and the 5-bit informed version. The informed reassignment method combines the estimation obtained using the classic reassignment method with Algorithm 1.
The results are also compared with the CRB and informed lower bound (ILB) which are the theoretical best performances, respectively, for the classic and the informed approach. The defined ILB assumes that the resulting error is divided by 2 (and the variance per 22) for each informing bit. Thus, the ILB can be defined as a function of the existing CRB and the number of informing bits denoted i as
This bound is not reached in practice because each informed bit can be identical to the one estimated using the classic approach. Thus, in our experiment, the variance of each 5-bit informed estimated parameter seems to be situated approximately in the middle between the CRB and the ILB.
3.3 Informed approach in the vector case
In this section, each parameter of the sinusoidal model described in (9) is grouped in a vector. We consider now that we have to estimate P = (a,ω,ϕ) a vector of. As a, ω, and ϕ have different physical meaning, they require a different relative accuracy in order to minimize a defined distortion measure.
3.3.1 Principles
Firstly, P is optimally vector-quantized using entropy-constrained unrestricted spherical quantization (ECUSQ)[29] which minimizes the weighted mean square error (WMSE) between synthesized signals according to (9). The ECUSQ method was shown to obtain similar performance to that of the method described in[18] applied to spherical quantization with a better computational complexity (not iterative). Furthermore, this technique designs the quantizer from the probability density function over each parameter component and does not require a codebook at the decoder.
The overall bit budget d allocated component and results in a variable bitrate for a fixed target entropy H t which depends on the target maximal average distortion D (e.g., if a ≈ 0, we need to allocate bits neither to phase nor to frequency). The relationship between the rate R = ⌈H t ⌉ and the average distortion is detailed in Section 3.3.2. The function which returns the number of bits allocated to each vector component of P for a given overall bit budget d is ⌈log2 γ⌉, where γ is the point density function given by ECUSQ.
Secondly, informed spectral analysis is applied separately on each vector component of P which can be processed as in the single-parameter case. The coding application uses a simple concatenation and is written as
Thus, the final extra information is.
For the decoding process, the relative bit allocation e, f, and g for each parameter is required to apply the error correction. As[29] shows that the optimal quantizer of a depends on H t and the optimal quantizer of ϕ and ω depends on the value of the amplitude, then a is informed first to obtain using. Thus, f and g can be calculated from using ECUSQ in order to apply the error correction on ϕ and ω using and. This point is more detailed in the next section.
3.3.2 Quantization
According to the rate-distortion theory[17], it is possible to calculate the minimal rate of information required to obtain a defined target quality.
Firstly, we define the average distortion D chosen to be the expected value of the distortion function δ between the synthesized signals using the reference and quantized parameters which can be expressed as
As a distortion function δ, we choose the weighted squared error which depends on the ground difference between the signals synthesized on a short analysis frame. Thus, (25) corresponds to the WMSE between the signals s and. This is expressed as a function of the sinusoidal model defined at (9) for a local frame analysis of length N:
where and n = ν,…,ν + N - 1. Here, w denotes the analysis window assumed to be evenly symmetric and which defines the considered signal segment. According to[29], the distortion (25) is minimal for ν = -(N-1)/2. This is the assumption for the remainder of this article. Using the Taylor expansion of the cos function and the approximation, (26) can be expressed as (see details in the Appendix)
Thus, which corresponds to the distortion over a quantization cell with lengths Δ a ,Δ ω ,Δ ϕ can be deduced from (26) by applying the expectation operation as
where f A,Ω,Φ(a,ω,ϕ) denotes the joint probability density function of each source parameter represented by random variables A, Ω, and Φ. Using the approximation (42), can be expressed as a function of quantization step denoted Δ assumed to be constant over each quantization cell (using the high resolution assumption). A high rate approximation of (25) can be obtained by averaging the distortion over all quantization cells of indices ι a , ι ω , and ι ϕ taken in their corresponding alphabet I a ,I ω ,I ϕ :
where p(ι a ,ι ω ,ι ϕ ) is the probability of the cell with quantization indices (ι a , ι ω , ι ϕ ),, and γ = Δ-1 is the so-called quantization point density function which gives the total number of quantization levels when it is integrated over a region.
Now we aim at defining the quantization point density functions which minimize D for a target entropy denoted H t which corresponds to the theoretical minimal amount of information required to code one sinusoidal component.
Using the high rate assumption, the joint entropy can be approximated as follows:
So finally, we have to minimize the following criterion using the method of Lagrange multiplier:
where and we obtain (see[29])
with
where e = exp(1) and; thus, we deduce
which corresponds to the ECUSQ optimal vector quantizer design. This result provides the relative accuracy of each parameter for the target entropy H t . By substituting (35), (36), and (37) in (29), we obtain the corresponding theoretical minimal distortion reachable with ECUSQ:
Here, D ECUSQ is obtained for a target entropy H t which corresponds in practice approximately to the average amount of bits required for the coding of one sinusoidal component. Using the proposed informed analysis framework for vector informed analysis, we can reduce this distortion with a classic estimator using the same bit budget. As shown in the next section, the resulting distortion depends on the initial SNR of the analyzed mixture signal.
3.3.3 Simulation
For this experiment we generated 10,000 random signals composed of one exponential sinusoid according to (9) and combined with a white Gaussian noise of different variance in order to result a SNR in the range of [-20 dB, 50 dB]. Amplitude and frequency parameters are generated according to Rayleigh probability density functions, respectively, of parameters σ a = 0.2 and σ ω = π/11. The phase parameter follows the uniform probability density function U(0,2π). For analysis, we use the Hann window of length N = 1,023 with estimation set at this center. The target entropy H t is calculated from ECUSQ quantized[29] for a target SNR set respectively at 45 dB and at 100 dB. I σ is estimated using the knowledge about the fixed initial SNR uniformly quantized with 4 bits on the [-20 dB, SNRtarget] interval.
For results, Figure4a,b shows the reached average SNR using informed spectral analysis and Figure4c,d shows the corresponding average number of bits of extra information used for the analysis of each sinusoidal component. The presented measures are expressed as functions of the initial SNR simulated with a white Gaussian noise. These figures show that informed analysis can be used to master the resulting target audio quality. We observe that the amount of transmitted information decreases when the effective resulting error is lower using the classic estimator (here, the reassignment method described in Section 3.1.2). As shown in Figure4c, the required amount of extra information is zero when the classic estimator reaches the target SNR in Figure4a, an average bitrate of 0 kbps is reached for an initial SNR greater than 20 dB due to the expectation operation applied over 10,000 random signals). Thus, the proposed informed analysis method achieves to reach any fixed target SNR taking benefit of the classic estimator. Furthermore, the transmitted data is optimally allocated to each sinusoidal parameter using the vector quantized design described in Section 3.3.2.
4 Application to isolated source parameter estimation from a monophonic mixture
As explained in Section 3, the estimation obtained with a classic estimator applied on a simple signal (composed of one source) is more accurate than when it is applied on complex sounds (e.g., polyphonic mixture with several sources plus noise). When the separated source signals are available before the mixing process, this particular configuration can be exploited using the informed analysis framework described previously.
4.1 Method overview
We propose here (see Figure5) an ISS technique based on a coder/decoder configuration where the original discrete source signals s k [n] are assumed to be exactly known at the coder. The reference sinusoidal parameters of each source signal denoted P k are estimated from isolated s k [n] using a classic estimator before the mixing process. The necessary information needed to recover P k from x[n] using a classic estimator is estimated and inaudibly embedded into the mixture using watermarking[30]. As described in Figure5, the embedded side information depends on the resulting watermarked mixture itself denoted x W[n]. Thus, it is computed using an iterative update process detailed in Section 4.7. At the decoder, the embedded information is extracted and is combined with the same classic estimator according to the informed analysis framework detailed in Section 2.
4.2 Sound source model and parameter estimation
Consider a discrete instantaneous single-channel discrete mixture signal composed of K sources which can be expressed as follows:
where r[n] is the residual signal. Source signals s k [n] are decomposed as a sum of L real sinusoidal components[1] for each local analysis frame written as
which corresponds to the real part of (9) where a, ω, and ϕ, respectively, are the amplitude, frequency, and phase parameters assumed to be locally constant. For the analysis process, the instantaneous parameters are estimated using a classic frame-based estimator.
As discussed in[13] (see Section 2), efficient estimators like the spectral reassignment or the derivative method[4] are suitable for informed spectral analysis. In fact, these estimators almost reach the theoretical bounds and minimize the bitrate required to code the extra information.
4.3 Source mask computation and coding
In order to estimate separately the sinusoidal parameters of each source signal, the discrete spectrogram has to be clustered. Thus, the time-frequency activation mask of each source signal s k has to be known before the estimation of sinusoidal parameter step (which is often preceded by a peak detection step in the magnitude spectrum). This issue is solved using long-term sinusoidal modeling[31] of the reference parameters at the coder which allows to code the entire mask with a negligible bitrate, thanks to the informed estimation of sinusoidal parameters.
Long-term sinusoidal modeling consists in estimating the trajectory of each partial by associating the instantaneous sinusoidal components estimated between adjacent analysis frames. This task is completed using a partial tracking algorithm[31] which estimates instantaneous partials both at frame and at frame. Thus, each partial at frame is associated with the most probable one (the closest from the prediction) at frame which verifies given threshold conditions (a maximal distance threshold is fixed). Using a partial tracking algorithm, a new partial trajectory is created (partial birth) for each isolated estimated component (not associated to an existing partial trajectory). The end of a partial trajectory (partial death) is reached when no instantaneous sinusoidal component can be associated to an existing partial.
As a partial tracking algorithm applied on each isolated source signal provides different results than when it is applied to the mixture, information about the reference partials has to be transmitted. An efficient solution consists in coding the partials of each source signal (computed from the reference sinusoidal parameters) as a triplet where corresponds to the first discrete frequency index corresponding to the birth of the partial. α and β correspond to the time frame indices which, respectively, are the birth and the death of the considered partial. Thus, each frequency index can be coded using ⌈log2(N/2)⌉ bits where N is the STFT length. Each frame index is coded using ⌈log2(T)⌉ where T is the total number of analysis frames.
As the estimated sinusoidal parameters are reliable at the decoder using informed spectral analysis, the exact trajectory of each partial is recovered at each instant. Thus, the mask at frame is computed using the predicted parameters from the corrected partials at frame. This process is applied for each partial until the last frame index is reached (coded as β in the triplet).
In our implementation, we use a simplified predictor where amplitude and frequency parameters are assumed constant between two adjacent frames. As a threshold, the difference between the estimated and the predicted frequency should not exceed 10%. In our experiments, we use 23-ms-long 50% overlapped frames at a sampling rate F s = 44.1 kHz. As shown in Section 4.7, the resulting bitrate depends on the number of sinusoidal components and is negligible compared to the entire extra information bitrate.
4.4 Watermarking process
The technique presented in[30] is used to inaudibly embed the extra information computed previously. It is inspired from quantization index modulation (QIM)[12] and is based on a modified discrete cosine transform (MDCT) coefficient quantization. We choose this method for its large embedding capacity, higher than 200 kbits/s and for its high perceptual resulting quality. Furthermore,[30] ensures that the exact embedded information is recovered at the decoder and can be used for real-time processing with STFT-based analysis. However, this technique is not robust to lossy audio compression and must be used with lossless or uncompressed audio format (e.g., FLAC, AIFF, WAVE).
4.5 Implementation details
The entire method summarized in Figure5a,b can be implemented according to Algorithms 2 and 3, respectively, for the coder and the decoder. The results obtained with our implementation are detailed and discussed in Section 4.7.
Algorithm 2 Coder

Algorithm 3 Decoder

4.6 Computational complexity
The proposed algorithm depends on the number of sources K, the STFT length N, and the number of non-negligible sinusoidal components denoted M which depends on the parameter quantization step. In the proposed implementation, the maximal value of M was limited to 50 by analysis frame. We also consider the number λ of iteration used at the coder to update the value of I σ and which require the analysis of the watermarked mixture created at a previous iteration.
We detail in Table1 the run-time complexity expressed in units of time for both the coder and the decoder. These complexities correspond to the worst-case scenario using the 'big O’ notation where λ < K < M < N. In the proposed notation, we postulate that all arithmetic operations require exactly one unit of time to be executed. The complexity of the watermarking method is not taken into account in this calculation. Table1 reveals that the encoder is more expensive than the decoder in terms of run-time complexity due to the iterative process and the (K + λ)-fold STFT used for the reference parameter estimation and the information extraction which dominate the execution time.
4.7 Experiments and results
In this section, we apply the isolated source parameter estimation system described in Section 4 to a musical piece mixture composed of six source signals: a female singing voice, two guitars, a drum, a bass, and a synthesizer keyboard. The reference parameters P k,l are estimated first at the coder from isolated source signals. According to the desired target quality, the reference parameters are quantized and partials are constructed in order to compute the time-frequency mask of each source. Finally, the extra information composed of the coded mask and the computed information resulting from the informed spectral analysis algorithm is inaudibly embedded into the resulting mixture signal using watermarking. After the coding process, a decoding verification is applied on the watermarked signal in order to check if the I σ parameter of each component was correctly estimated for decoding. Otherwise, I σ is updated with a new estimated lower value and the coding process is reiterated. As explained in Section 2.2.1 for single-parameter estimation, a lower value of I σ increases the amount of transmitted extra information; however, it ensures that each informed parameter reaches the target precision. In practice, the final watermarked mixture was reached after less than three iterations.
Figures6 and7 compare the practical resulting bitrate used to reach the target SNR which is computed between the resulting signals and the references signals (synthesized using P k,l ). These figures describe the exact SNR reached using the proposed method. However, when the size of the extra information exceeds the watermark capacity, the results are obtained with a simulated mixture using the maximal watermarking bandwidth. These figures compare the results obtained with the classic (not informed) approach (represented with a red circle), the pure coding approach using the ECUSQ optimal quantizer, and the informed approach which combines estimation and coding. The results obtained using these three different approaches can be explained as follows:
-
The classic (not informed) result is obtained using the reassignment estimator and uses a bitrate equal to 0 kbps.
-
Using the pure coding approach, the theoretical ECUSQ curve corresponds to D ECUSQ which is computed according to (38) under the assumption that each sinusoidal component is coded using the same target entropy denoted H t . Thus, this curve indicates the number of non-negligible (with a quantized amplitude higher than zero) sinusoidal components resulting from the quantization process. This number increases with the target quality and the mismatch of the source signal with the sinusoidal model. The practical ECUSQ curve corresponds to the real bitbrate which was used to reach the target SNR. This bitrate differs from the theoretical curve due to the high rate assumption and the mismatch between the theoretical and the practical distribution over source signal parameters (used to design the vector quantizer).
-
Using the informed approach, we compute two curves which show the bitrate required by the time-frequency mask with the proposed method. When the number of non-negligible components increases, the bitrate used to code the mask increases (e.g., drum which mismatches the sinusoidal model).
The resulting bitrate presented in Figures6 and7 strongly depends on the number of non-negligible sinusoidal components which increases according to the resulting SNR. According to Figures6 and7, informed analysis requires a lower bitrate than the ECUSQ method alone when the signal mixture is available. However, this benefit decreases when the target SNR is too high due to a large number of sinusoidal components which cannot be efficiently analyzed using the classic estimator. Moreover, as shown in Figure6 for a realistic application on the entire mixture with a limited watermarking capacity, informed analysis offers a gain of more than 15 dB for the SNR. The practical results which use the maximal quality simultaneously for all source signals using entire watermark capacity are available online for listeninga.
5 Conclusions
The informed approach for model parameter estimation was described in a theoretical and a practical framework. Firstly, we proposed a general method which can be applied to any signal parameter estimation problem. Secondly, the proposed method was applied to sinusoidal model parameter estimation of isolated source signals from a monaural sound mixture. The resulting quality and bitrate were compared with those of the classic estimation approach and the pure coding approach using ECUSQ which was shown optimal for WMSE distortion. The results show a significant benefit of the proposed approach which successfully takes advantage of a classic estimation using side information coded with a lower bitrate than theoretically required to reach a target quality. Furthermore, we showed that this approach can be combined with a watermarking technique to inaudibly embed the required extra information into the analyzed signal itself. Thus, it allows the implementation of realistic applications where the signal parameters are required with a target precision. However, the practical experiments show limitations of this approach for high target precision where the efficiency of extra information coding should be improved.
Future works will consist in proposing applications with more adapted models (e.g., sound transients and noise) and a more efficient coding scheme for the side information (e.g., entropy coding) to reduce the resulting bitrate. Also, considering a perceptual distortion measure should be a better choice for audio listening applications which do not require a fine precision of the imperceptible signal parameters. This should result in bitrates comparable to those of existing ISS techniques.
Endnote
a Sound results are available online for listening athttp://www.labri.fr/perso/fourer/publi/JASP13.
Appendix
Average distortion between two sinusoidal signals
Let the weighted square error between two sinusoidal signals s and be expressed according to (26) as
Using the second order of the Taylor series expansion at 0 of the cosine function, we can approximate. Thus, (41) can be expressed as
with.
Using the approximation, we obtain
Now we aim at calculating the expectation over a quantization cell with lengths Δ a ,Δ ω ,Δ ϕ . This can be expressed as a function of the joint probability density function f A,Ω,Φ(a,ω,ϕ) of the sinusoïdal parameters included into a quantization cell:
Under the high rate assumptions, f A,Ω,Φ(a,ω,ϕ) is approximately constant over each quantization cell. Thus, each quantized value is located in the center of the quantization intervals.
Thus, can be approximated using (42) as
This result is used for the calculation of (29).
Abbreviations
- CI:
-
Confidence interval
- CRB:
-
Cramér-Rao bound
- ECUSQ:
-
Entropy-constrained unrestricted spherical quantization
- ILB:
-
Informed lower bound
- ISS:
-
Informed source separation
- MDCT:
-
Modified discrete cosine transform
- MSB:
-
Most significant bit
- QIM:
-
Quantization index modulation
- SNR:
-
Signal-to-noise ratio
- STFT:
-
Short-time fourier transform
- WMSE:
-
Weighted mean square error.
References
McAulay R, Quatieri T: Speech analysis/synthesis based on a sinusoidal representation. IEEE Trans. Acoust., Speech, Signal Process 1986, 34(4):744-754. 10.1109/TASSP.1986.1164910
Smith J, Serra X: PARSHL: an analysis/synthesis program for non-harmonic sounds based on a sinusoidal representation. In International Computer Music Conference. Urbana: IEEE; 1987:290-297.
Auger F, Flandrin P: Improving the black readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process 1995, 43(5):1068-1089. 10.1109/78.382394
Marchand S, Depalle P: Generalization of the derivative analysis method to non-stationary sinusoidal modeling. In Proceedings of the Digital Audio Effects Conference (DAFx’08). Espoo: DAFx; 2008:281-288.
Hamdy K, Ali M, Tewfi A: Low bit rate high quality audio coding with combined harmonic and wavelet representations. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’96), vol. 2. Atlanta: IEEE; 1996:1045-1048.
Verma T, Meng T: A 6kbps to 85kbps scalable audio coder. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’00), vol. 2. Istanbul: IEEE; 2000:877-880.
Schuijers E, Oomen W, Brinker B, Breebaart J: Advances in parametric coding for high-quality audio. In Proceedings of the 114th Convention of the Audio Engineering Society (AES). Amsterdam: AES; 2003:201-204.
Purnhagen H, Meine N: HILN – the MPEG-4 parametric audio coding tools. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’00). Istanbul: IEEE; 2000:201-204.
Knuth KH: Informed source separation: a Bayesian tutorial. In Proceedings of the IEEE European Signal Processing Conference (EUSIPCO’05),. Istanbul: IEEE; 2005.
Parvaix M, Girin L, Brossier JM: A watermarking-based method for single-channel audio source separation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’09). Taipei: IEEE; 2009:101-104.
Parvaix M, Girin L: Informed source separation of underdetermined instantaneous stereo mixtures using source index embedding. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’10). Dallas: IEEE; 2010:245-248.
Chen B, Wornell G: Quantization index modulation: a class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inf. Theory 2001, 47(4):1423-1443. 10.1109/18.923725
Marchand S, Fourer D: Breaking the bounds: introducing informed spectral analysis. In Proceedings of the Digital Audio Effects Conference (DAFx’10). Graz: DAFx; 2010:359-366.
Fourer D, Marchand S: Informed spectral analysis for isolated audio source parameters estimation. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA’11). New Paltz: IEEE; 2011:57-60.
Meurisse G, Hanna P, Marchand S: A new analysis method for sinusoids+noise spectral models. In Proceedings of the Digital Audio Effects Conference (DAFx’06). Montreal: DAFx; 2006:139-144.
Gersho A, Gray RM: Vector Quantization and Signal Compression. Norwell: Kluwer; 1991.
Gray RM: Source Coding Theory. Norwell: Kluwer; 1989.
Chou PA, Lookabaugh T, Gray RM: Entropy-constrained vector quantization. IEEE Trans. Acoust., Speech Signal Process 1989, 37: 31-42.
Huffman D: A method for the construction of minimum-redundancy codes. Proc. IRE 1952, 40(9):1098-1101.
Keiler D, Marchand S: Survey on extraction of sinusoids in stationary sounds. In Proceedings of the Digital Audio Effects Conference (DAFx’02). Hamburg: DAFx; 2002:51-58.
Yeh C, Roebel A: Adaptive noise level estimation. In Proceedings of the Digital Audio Effects Conference (DAFX’06). Montréal: DAFx; 2006.
Girin L, Marchand S, di Martino J, Robel A, Peeters G: Comparing the order of a polynomial phase model for the synthesis of quasi-harmonic audio signals. In Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA’03). New Paltz: IEEE; 2003:193-196.
Kodera K, de Villedary C, Gendrin R: A new method for the numerical analysis of non-stationary signals. Phys. Earth Planetary Inter 1976, 12: 142-150. 10.1016/0031-9201(76)90044-3
Kodera K, Gendrin R, de Villedary C: Analysis of time-varying signals with small BT values. IEEE Trans. Acoust. Speech Signal Process 1978, 26: 64-76. 10.1109/TASSP.1978.1163047
Betser M, Collen P, Richard G, David B: Estimation of frequency for AM/FM models using the phase vocoder framework. IEEE Trans. Signal Process 2008, 56(2):505-517.
Badeau R, David B, Richard G: High-resolution spectral analysis of mixtures of complex exponentials modulated by polynomials. IEEE Trans. Signal Process 2006, 54(4):1341-1350.
Zhou G, Giannakis G, Swami A: On polynomial phase signal with time-varying amplitudes. IEEE Trans. Signal Process 1996, 44(4):848-860. 10.1109/78.492538
Djurić PM, Kay SM: Parameter estimation of chirp signals. IEEE Trans. Acoust., Speech Signal Process 1990, 38(12):2118-2126. 10.1109/29.61538
Korten P, Jensen J, Heusdens R: High-resolution spherical quantization of sinusoidal parameters. IEEE Trans. Audio Speech Lang. Process 2007, 15(3):966-981.
Pinel J, Girin L, Baras C, Parvaix M: A high-capacity watermarking technique for audio signals based on MDCT-domain quantization. In International Congress on Acoustics. St Malo: ICA; 2010.
Lagrange M, Marchand S, Rault JB: Using linear prediction to enhance the tracking of partials. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’04), vol. 4. Montreal: IEEE; 2004:241-244.
Acknowledgements
Thanks go to J. Pinel for his implementation of the QIM-based watermarking method detailed in[30]. This research was partly supported by the French ANR DReaM project (ANR-09-CORD-006).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fourer, D., Marchand, S. Informed spectral analysis: audio signal parameter estimation using side information. EURASIP J. Adv. Signal Process. 2013, 178 (2013). https://doi.org/10.1186/1687-6180-2013-178
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2013-178


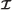 to the decoder using separated communication channels where
to the decoder using separated communication channels where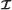 can be coded using entropy coding.
can be coded using entropy coding.



