- Review
- Open access
- Published:
Survey of hyperspectral image denoising methods based on tensor decompositions
EURASIP Journal on Advances in Signal Processing volume 2013, Article number: 186 (2013)
Abstract
A hyperspectral image (HSI) is always modeled as a three-dimensional tensor, with the first two dimensions indicating the spatial domain and the third dimension indicating the spectral domain. The classical matrix-based denoising methods require to rearrange the tensor into a matrix, then filter noise in the column space, and finally rebuild the tensor. To avoid the rearranging and rebuilding steps, the tensor-based denoising methods can be used to process the HSI directly by employing multilinear algebra. This paper presents a survey on three newly proposed HSI denoising methods and shows their performances in reducing noise. The first method is the Multiway Wiener Filter (MWF), which is an extension of the Wiener filter to data tensors, based on the TUCKER3 decomposition. The second one is the PARAFAC filter, which removes noise by truncating the lower rank K of the PARAFAC decomposition. And the third one is the combination of multidimensional wavelet packet transform (MWPT) and MWF (MWPT-MWF), which models each coefficient set as a tensor and then filters each tensor by applying MWF. MWPT-MWF has been proposed to preserve rare signals in the denoising process, which cannot be preserved well by using the MWF or PARAFAC filters. A real-world HYDICE HSI data is used in the experiments to assess these three tensor-based denoising methods, and the performances of each method are analyzed in two aspects: signal-to-noise ratio and improvement of subsequent target detection results.
1 Review
1.1 Introduction
Hyperspectral images (HSI) attract more and more interest in recent years in different domains, such as geography, agriculture, and military [1–3]. They use the HSI to do the target detection [4] or classification [5] to find objects or materials of interest on the ground. Unfortunately, in the capturing procedure, the HSI is usually impaired by several types of noise, such as thermal noise [6], photonic noise [7], and strip noise [8]. Therefore, denoising methods [9–13] have become a critical step for improving the subsequent target detection and classification in remote sensing imaging applications [14].
In HSI processing, images are modeled as a three-dimensional tensor, i.e., two spatial dimensions and one spectral dimension. The classical denoising methods [15–18] rearrange the HSI into a matrix whose columns contain the spectral signatures of all the pixels, then estimate the signal subspace by methods based on the analysis of second-order statistics, and finally rebuild the original HSI structure after processing.
Since matrix-based techniques cannot take advantage of spectra in hyperspectral images, therefore, in order to treat the HSI as a whole entity, some new techniques were developed. For example, an HSI was treated as a hypercube in order to take into account the correlation among different bands [19, 20], tensor-algebra was brought to jointly analyze the 3D HSI, etc. In this paper, we mainly focus on the problem of applying tensor algebra in reducing noise in HSIs. Unlike the matrix-based denoising methods which are based on matrix algebra, the newly proposed tensor-based denosing methods utilize multilinear algebra to analyze the HSI tensor directly. It is well known that SVD (singular value decomposition) is important for matrix analysis. Similarly, there are two important tensor decompositions: TUCKER3 and PARAFAC. These two decompositions play significant roles in analyzing tensors. Therefore, in this paper, we focus on comparative methods based on multilinear algebra for sake of coherence with the recently developed method which combines multidimensional wavelet packet transform and TUCKER3 decomposition: The three methods involve a tensor decomposition either TUCKER3 or PARAFAC.
TUCKER3 decomposition, also known as lower rank-(K 1,…,K N ) tensor approximation (LRTA-(K 1,…,K N )), has been firstly used as multimode PCA, which uses the first K n PCA components in mode n, n=1,…,N, to restore the multidimensional signal. The LRTA-(K 1,…,K N ) has been employed for seismic wave separation [21], face recognition [22], and color image denoising [23]. Although the LRTA-(K 1,…,K N ) can obtain good results in denoising, it is not an optimal solution for filtering noise in the aspect of the mean squared error (MSE). The multidimensional Wiener filter (MWF) has been proposed to overcome this drawback of LRTA-(K 1,…,K N ) [24]. MWF calculates the filter in each mode under the criterion of minimizing the MSE between the desired signal and the estimated signal, therefore it can been understood as an optimal LRTA-(K 1,…,K N ). Moreover, MWF can also be understood as an extension of the classical matrix-based Wiener filter to the tensor model by using multilinear algebra tools. MWF has been used in seismic wave denoising [24] and HSI denoising [12, 25], and obtained good results. Recently, a statistical criteria has been adapted to estimate the rank of signal subspace in each mode [13], which makes MWF an automatic method to reduce noise in the data.
Apart from TUCKER3, the PARAFAC [26] decomposition, also known as CANDECOMP [27], is another way to decompose a tensor into lower rank factors. Distinguishing from TUCKER3, PARAFAC decomposes a tensor into a sum of rank-one tensors and only one rank K needs to be estimated for the tensor. Moreover, the PARAFAC decomposition is unique when the rank K is greater than one, whereas TUCKER3 cannot be. PARAFAC decomposition has recently been applied to chemical sciences [28], array processing [29], telecommunications [30], and HSI denoising [14]. As a comparison of MWF, reference [31] shows the potential of PARAFAC in the HSI denoising. However, there is not an efficient way to estimate the rank of PARAFAC, which constrains it in automaticdenoising.
In a HSI, a rare signal is the one that is represented by only a few number of pixels, while the abundant signal is the one that contains a large number of pixels compared to a rare signal [17]. MWF and PARAFAC treat a HSI as a whole entity in the denoising operation; therefore, the abundant signals and the rare signals are processed together, which inhibits a drawback: the rare signals may be unintentionally removed. In fact, the energy of the rare signal is so weak compared to that of the abundant signal that the estimated signal subspace cannot include the rare signal, and as a result, the rare signal is removed. MWPT-MWF (multidimensional wavelet packet transform (MWPT) with multiway Wiener filter) has been proposed to overcome this drawback of MWF and PARAFAC [32]. Instead of treating the HSI as a whole entity, MWPT-MWF firstly decomposes the HSI into several coefficient sets, also called components, by employing MWPT, therefore the abundant signal and the rare signal can be separated. After this step, each component is filtered by MWF automatically. Because the rare signal and the abundant signal are separated into different components, the signal subspace in each component can be estimated more exactly.
The goal of this paper is to present a survey of the tensor-based denoising methods applied in filtering the HSI. Some recent simulations and comparative results on a real-world HYDICE HSI are also presented. The reminder of this paper is organized as follows: Section 1.2 briefly introduces some basic knowledge about multilinear algebra. Section 1.3 introduces the signal model used in this paper. Sections 1.4, 1.5, and 1.6 present the recently proposed denoising methods MWF, PARAFAC, and MWPT-MWF, respectively. Section 1.7 supplies some comparative denoising and detection results. And finally, Section 2 concludes this paper.
1.2 Basics on tensor tools and multilinear algebra
1.2.1 Tensor model
A multiway signal is also called tensor. A tensor is a multidimensional array, , in which indicates the real mainfold, and N is the number of dimensions. The elements in this tensor can be expressed as , with i
1=1,…,I
1; i
2=1,…,I
2;⋯ ; i
N
=1,…,I
N
. The n-th dimension of this tensor is called n-mode. In particular, tensor  is called a rank-one tensor when it can be written as the outer product of N vectors [33]:
is called a rank-one tensor when it can be written as the outer product of N vectors [33]:
where ∘ indicates the outer product [34].
1.2.2 Multilinear algebra tools
1.2.2.0 n-mode unfolding
denotes the n-mode unfolding matrix of a tensor , where M
n
=I
n+1…I
1
I
N
…I
n−1. The columns of X
n
are the I
n
-dimensional vectors obtained from  by varying index i
n
while keeping the other indices fixed. Here, we define the n-mode rank K
n
as the n-mode unfolding matrix rank, i.e., K
n
=rank (X
n
).
by varying index i
n
while keeping the other indices fixed. Here, we define the n-mode rank K
n
as the n-mode unfolding matrix rank, i.e., K
n
=rank (X
n
).
1.2.2.0 n-mode product
The n-mode product is defined as the product between a data tensor and a matrix in mode n. This n-mode product is denoted by
whose entries are given by
where .
1.3 Problem formulation and signal modeling
A noisy HSI is modeled as a tensor resulting from a pure HSI impaired by an additive noise . The tensor  can be expressed as:
can be expressed as:
In this paper, we assume that the noise  is zero-mean white Gaussian noise and independent from the signal
is zero-mean white Gaussian noise and independent from the signal  . The aim of this paper was to estimate the desired signal
. The aim of this paper was to estimate the desired signal  from the noisy HSI
from the noisy HSI  .
.
1.4 Multiway Wiener filtering
1.4.1 Denoising model
MWF provides an estimate of the desired signal  from data tensor
from data tensor  by using a three-dimensional filtering, which can be expressed as follows [35]:
by using a three-dimensional filtering, which can be expressed as follows [35]:
From the signal processing point of view, the n-mode product is a n-mode filtering of  ; therefore, H
n
is named as n-mode filter.
; therefore, H
n
is named as n-mode filter.
In order to obtain the optimal n-mode filters {H
n
, n=1,2,3}, the usually used criterion is the mean squared error (MSE) between the estimated signal and the desired signal  :
:
Then, the optimal n-mode filters are the ones which can minimize the MSE given in (6).
1.4.2 Calculation of H n
To minimize the MSE given in (6) with respect to n-mode filters {H n , n=1,2,3}, the derivation is employed and the calculation details are presented in [24]. By setting the derivation of the MSE to zero, the expression of the optimal n-mode filter H n is [24]:
where is a matrix containing the K n orthonormal basis vectors of the signal subspace in the column space of the n-mode unfolding matrix R n , and
in which and are the K n largest eigenvalues of matrices and respectively, where
with
where p 1≠n, p 2≠n, p 1,p 2=1,2,3 and ⊗ defines the Kronecker product. Moreover, is equal to the I n −K n smallest eigenvalues of . However, in the practice, the I n −K n smallest eigenvalues are generally different. Hence, can be estimated by:
1.4.3 Estimation of K n
Being used in the computation of the n-mode filter H n , expression (7) requires the unknown K n value, i.e., the number of largest eigenvalues of the covariance matrix of , for n=1, 2, 3. Choosing a small K n makes that some signals are lost whereas choosing a large K n makes that noise is included after restoration. For this case, the optimal K n should be estimated to yield an optimum restoration. Akaike information criterion (AIC) is a criterion used to measure the information lost; therefore, it is employed in MWF to determine the optimal rank K n [13]. For mode n, the AIC can be expressed as:
where are the eigenvalues of , M n is the column number of and k n changes in the range of {1,…,I n −1}. The estimated n-mode rank K n is the value of k n which minimizes AIC criterion.
1.4.4 ALS algorithm
To jointly find n-mode filters {H n , n=1,2,3} that minimize (6), an Alternating Least Square (ALS) algorithm [13] is necessary. Owing to this procedure, any filter along a given mode depends on the filters along all other modes. The steps of this algorithm can be summarized as presented here.
-
1.
Input: Data tensor
-
2.
Initialization k=0:
. Where is the I n ×I n identity matrix.
-
3.
ALS loop: Repeat until convergence, that is, for example, while
-
(a)
Estimation of K n , n=1,2,3,
-
(b)
Estimation of for n=1,2,3.
-
(i)
.
p,q=1,2,3, p,q≠n and p<q
-
(ii)
subject to
-
(i)
-
(c)
Multidimensional Wiener filtering .(d)
.
-
(a)
-
4.
Output: Estimated signal tensor , where k c is the convergence iteration index.
As the calculation of n-mode filter H n in step 33b utilizes the filters in other modes {H i , 1≤i≤3andi≠n}, it shows that the MWF considers the relationships between elements in all modes of the data set.
1.5 PARAFAC filtering
1.5.1 Denoising model
Since the decomposition by TUCKER3 model is not unique and needs to estimate the rank K
n
in each mode, another tensor decomposition model PARAFAC was recently introduced to reduce noise in  [14]. Different from TUCKER3 model, PARAFAC model can decompose a tensor
[14]. Different from TUCKER3 model, PARAFAC model can decompose a tensor  uniquely into a sum of rank-one tensors:
uniquely into a sum of rank-one tensors:
where is the decomposition error. Under the assumption that signal can be expressed by finite rank PARAFAC factorization, the estimate of the desired signal  can be expressed by the PARAFAC model:
can be expressed by the PARAFAC model:
where  is a identity tensor, and , n=1,2,3. In order to obtain the optimal A
n
, the error between and
is a identity tensor, and , n=1,2,3. In order to obtain the optimal A
n
, the error between and  should be minimized:
should be minimized:
Nonetheless, it is worth noting that the criterion of PARAFAC is the squared error between the estimate and the noisy HSI  , while that of MWF is the mean squared error between the estimate and the desired signal
, while that of MWF is the mean squared error between the estimate and the desired signal  (see (6)). For a given rank K, minimizing (17) means removing as little signal as possible in the denoising process.
(see (6)). For a given rank K, minimizing (17) means removing as little signal as possible in the denoising process.
1.5.2 Calculation of A n
To obtain A n in each mode, the error given in (17) should be minimized:
where is the n-mode unfolding matrix of in (16):
where p,q=1,2,3 and p≠q≠n. By substituting (19) into (18), we can obtain
Obviously, the estimation of A n needs information of A p and A q , which are not known. In this situation, an ALS algorithm should be employed to calculate the optimal A n .
1.5.3 PARAFAC ALS algorithm
To jointly estimate A n , a ‘PARAFAC ALS’ algorithm is introduced and its steps are listed as follows:
-
1.
Input:
Data tensor
 .
. -
2.
Initialization:
Set k=0 and e k =0. Randomly initialize , n=1,2,3.
-
3.
Loop:
-
(a)
Estimate
-
(b)
Compute
-
(c)
, if |e k+1-e k |>e and k is less than the maximum number of iteration, and then go back to step 33a. Otherwise, break the loop.
-
(i)
-
(ii)
-
(iii)
-
(i)
-
(a)
-
4.
Output:
Return , n=1,2,3.
1.5.4 Rank estimation
As described in Section 1.5.1, PARAFAC filtering is an algorithm which minimizes e(A 1,A 2,A 3) in (17) under a given rank K. In other words, it is assumed that the rank K is known in PARAFAC filtering. Unfortunately, the rank K is generally unknown in practice; therefore, an algorithm used to estimate K is presented in this section. The details are as follows:
-
1.
Input: Data tensor

-
2.
Initialization:
Set i=1. Set rank-searching-set K-SCOPE.
-
3.
Loop:
-
(a)
Set K=K-SCOPE[i].
-
(b)
Do PARAFAC decomposition: .
-
(c)
At n=1,2,3, calculate the covariance matrix C n of , the n-mode unfolding matrix of .
-
(d)
If
-
(i)
, , where c i,i is the diagonal elements of C n .
-
(ii)
-
(i)
these two conditions are satisfied for all n=1,2,3 at the same time, break the loop. Otherwise, .
-
(a)
-
4.
Output:
Return the rank K.
1.6 MWPT-MWF
1.6.1 Denoising model
MWF and PARAFAC treat  as an entire entity in the denoising process. This works well when there are only abundant signals or the rare signals can be neglected. However, in the situation where the rare signals cannot be neglected, such as the target detection, MWF and PARAFAC might remove rare signals in the denoising process.
as an entire entity in the denoising process. This works well when there are only abundant signals or the rare signals can be neglected. However, in the situation where the rare signals cannot be neglected, such as the target detection, MWF and PARAFAC might remove rare signals in the denoising process.
MWPT-MWF has been proposed to preserve rare signals in the denoising process and hence improve the denoising performance. In MWPT-MWF,  is estimated by minimizing MSE between the desired signal
is estimated by minimizing MSE between the desired signal  and its estimate :
and its estimate :
Nevertheless, unlike MWF or PARAFAC, MWPT-MWF reduces noise by jointly filtering the wavelet packet coefficient set. The details of MWPT-MWF will be described in the following subsections.
1.6.2 Multidimensional wavelet packet transform
The multidimensional wavelet packet transform (MWPT) can be written in tensor form as:
and the reconstruction can be written as:
where indicate the wavelet packet transform matrices. When the transform level vector is l=[ l 1,l 2,l 3]T, where l n ≥0 denotes the wavelet packet transform level in mode n, the coefficient tensor , which is also called a component in this paper, of scale m=[m 1,m 2,m 3], where , can be extracted by
and the corresponding inverse process is
where the extraction operator is defined as
where 0 1 is a zero matrix with size and 0 2 is a zero matrix with size .
1.6.3 Multiway Wiener filter in multidimensional wavelet packet domain
After the MWPT, abundant and rare signals can be separated into different components; therefore, the signal subspace of each component can be estimated more accurately than that of the entire dataset. Furthermore, a better estimation of the signal subspace can improve the performance of MWF in each component. However, the denoising criterion of MWPT-MWF is the minimization of the MSE between  and but not the component and its estimate; therefore, this subsection proves the ability of MWPT-MWF in minimizing the MSE between
and but not the component and its estimate; therefore, this subsection proves the ability of MWPT-MWF in minimizing the MSE between  and , which is defined in (21). By performing MWPT to tensor
and , which is defined in (21). By performing MWPT to tensor  ,
,  and
and  in expression (4), we obtain
in expression (4), we obtain
The coefficient tensor of each part:
and the coefficient tensor of the estimate :
Extracting the components of each frequency , and from , and respectively by using (24), we obtain
From Parseval’s theorem, the following expression can be obtained:
which means that minimizing the MSE between  and its estimate is equivalent to minimizing the MSE between and for each m. If is estimated by Tucker3 decomposition of :
and its estimate is equivalent to minimizing the MSE between and for each m. If is estimated by Tucker3 decomposition of :
then H 1,m ,H 2,m ,H 3,m are the n-mode filters of the multiway Wiener filter aforementioned in Section 1.4. After estimating for each m, we obtain by concatenating . Furthermore, the estimate can be obtained by inverse MWPT:
1.6.4 Best transform level and basis selection
In MWPT-MWF, several parameters should be determined, as presented here.
-
1.
Level of transform: the performance of the algorithm is affected by the level of transform, which depends on the size of tensor
 . The maximum level can be calculated by (36)
. The maximum level can be calculated by (36)where ⌈·⌉ rounds a number upward to its nearest integer, and the constant 5 is subtracted from to make sure there are enough elements in each mode so that the transform is meaningful.
Then, the set of possible transform levels can be expressed as:
(37)where {·} denotes a set.
-
2.
Basis of transform: there are many wavelet bases designed for different cases. For the simplicity of expression, we define
(38)to denote the set of possible wavelet bases, where N W is the number of wavelets in this set.
The best transform level and basis should minimize the MSE or risk [36], whose equivalent form for each component can be expressed as:
Then, the best transform level and basis can be selected by
While selecting the optimal l,w depends on  which is generally unknown. To overcome this drawback, an alternative solution should be found. Denoting by the estimate of at the d-th ALS loop aforementioned in Section 1.4.4 and noticing that, when is minimized, is the optimal estimate of obtained by MWF, and at the same time, is minimized according to Section 1.4.2. Therefore, (40) can be replaced by
which is generally unknown. To overcome this drawback, an alternative solution should be found. Denoting by the estimate of at the d-th ALS loop aforementioned in Section 1.4.4 and noticing that, when is minimized, is the optimal estimate of obtained by MWF, and at the same time, is minimized according to Section 1.4.2. Therefore, (40) can be replaced by
where
1.6.5 Summary of the MWPT-MWF
The proposed algorithm, which is denoted by MWPT-MWF, can be summarized as presented here.
-
1.
Input:
Data tensor
 .
. -
2.
Initialization:
Set , and the risk threshold ε.
-
3.
Loop:
For each l 1,l 2,l 3∈L and w∈W. Loop l 1,l 2,l 3 and w:
-
(a)
Decompose the whitened data
 by MWPT: .
by MWPT: . -
(b)
Extract component from by (24), for m=[m 1,m 2,m 3]T, where , k=1,2,3.
-
(c)
Filter component by MWF: .
-
(d)
Calculate the risk . If reaches a fixed threshold ε, return the optimal l 1,l 2,l 3,w and .
-
(a)
-
4.
Output: Concatenate to obtain and perform inverse MWPT: .
1.7 Experimental results
In this section, we use a real-world high spatial resolution image acquired by HYperspectral Digital Imagery Collection Experiment (HYDICE). The HYDICE image contains 65 rows, 100 columns, and 160 spectral bands, and is modeled as a 65×100×160 tensor in this paper. Six targets of interest are selected in the image as shown in the ground-truth map in Figure 1 and the corresponding mask is shown in Figure 2. The spectral signatures of these six targets are presented in Figure 3. These six targets are chosen because they have different spectral signatures and sizes, so that the denoising and target detection performance on different target sizes can be evaluated.
White Gaussian noise is added into the HSI with signal-to-noise ratio (SNR) ranged from 15 to 30 dB (with a step of 5 dB) to reproduce different simulation scenarios. MWF, PARAFAC, and MWPT-MWF are used to reduce noise in the HSI. The rank-searching-set of PARAFAC is set as [51,101,151,201], and wavelet db3 is selected to do MWPT with transform levels [ l 1,l 2,l 3]=[ 1,1,0].
1.7.1 Denoising performance evaluation and comparison
To present the denoising results intuitively, Figure 4 shows the target spectral signatures of the noisy HSI and the HSI denoised by MWF, PARAFAC, and MWPT-MWF, respectively. By comparing the four sub-figures in Figure 4, it is evident that denoising is a necessary procedure to restore the target spectral signatures. Moreover, we can see that there still exists more noise in Figure 4b than Figure 4c and Figure 4d. Especially, the spectral signatures of targets 1, 3, and 5 are almost mixed together in Figure 4b. Figure 4c and Figure 4d are much better, at least the residual noise is small after denoising. However, the spectral signatures are changed more greatly after denoising by PARAFAC than by MWPT-MWF, which can be seen obviously from the signatures of targets 5 and 6. In Figure 4c, the signatures of targets 5 and 1 are almost overlapped, while in Figure 4d, these two signatures can be distinguished easily.
To compare the performances of MWF, PARAFAC, and MWPT-MWF, the SNR of the image after denoising, also named as SNR output, is defined as below [12]:
If SNROUTPUT is greater than SNRINPUT, we can conclude that the algorithm improves the SNR of the image.
The SNROUTPUT values obtained when SNRINPUT is varying from 15 to 30 dB by different denoising methods are shown in Table 1. It is obvious that MWPT-MWF outperforms the other two denoising methods significantly. When the SNRINPUT is low, from 15 to 25 dB in Table 1, the denoising result of PARAFAC is better than that of MWF. But when the SNRINPUT is high, from 25 to 30 dB, the performance of MWF is slightly better than that of PARAFAC. Moreover, it is worth noting that all of these three methods can improve the SNR significantly. When the SNRINPUT is 15 dB, the SNROUTPUT after denoising is 30 dB maximum by MWPT-MWF and 24 dB minimum by MWF. The denoising results shown in Table 1 give the experimental evidence of the benefits derived from the denoising procedure.
1.7.2 Target detection performance evaluation and comparison
In the last subsection, we have compared the denoising performances of different methods in the aspect of SNROUTPUT. However, sometimes SNROUTPUT cannot reflect the denoising performance we want, especially when we consider preserving small targets in the HSI while removing noise. Hence, in this subsection, we compare the target detection performance after denoising by MWF, PARAFAC, and MWPT-MWF.
Spectral Angle Mapper (SAM) detector [37] is used in the experiment to detect targets in the HSI. As SAM does not require the characterization of the background, it can avoid the inaccuracy of the comparison result caused by the noise covariance matrix estimation error. The SAM detector can be expressed as
where s is the reference spectrum and x is the pixel spectrum.
To assess the performances of detection, the probability of detection (Pd) is defined as
and the probability of false alarm (Pfa) is defined as
where n s is the number of spectral signatures, N i the number of pixels with spectral signature i, the number of correctly detected pixels, and the number of false-alarm pixels.
Figures 5, 6, and 7 are the target detection results after denoising by MWF, PARAFAC, and MWPT-MWF, respectively, in the noise environment SNRINPUT=15dB. In the images, the black pixel indicates no-target, the green the correct-detection, the red the false alarm, and the blue the missed target. From Figure 5, which shows the detection result after denoising by MWF, we can see that all of the three small targets (targets 1, 3, and 5) are missed in the detection. Moreover, most of the pixels of target 5 are also missed. The detection result after denoising by PARAFAC, in Figure 6, is slightly better than that by MWF, but all of the small targets are also lost in the detection. MWPT-MWF shows its capability of preserving small targets in Figure 7, in which two of the three small targets are detected correctly. Apart from preserving small targets, MWPT-MWF can also improve the detection performance of the large-size-small-energy target 6, which is obvious by comparing Figures 5, 6, and 7.
To evaluate the detection performance in different noise environments, Table 2 shows the Pd values versus SNRINPUT of different denoising methods with SNRINPUT ranged from 15 to 30 dB.
It is obvious that the detection result after denoising by MWPT-MWF outperforms the two other methods. By comparing Table 2 with Table 1, we can understand that the denoising process can improve the target detection performance.
2 Conclusion
In this paper, a survey has been presented on three recently proposed tensor filtering methods: MWF, PARAFAC, and MWPT-MWF. They utilize multilinear algebra in analyzing a multidimensional data cube to jointly filter it in each mode.
The MWF extends the classical Wiener filter to the multidimensional case by using the TUCKER3 decomposition while minimizing the MSE between the desired signal tensor and the estimated signal tensor. As the filter in one mode relies on the filters in the other modes, the ALS algorithm is used to jointly calculate the MWF filters. In the filtering process, the signal subspace rank in mode n needs to be known to remove the noise in the orthogonal complement subspace of the signal subspace. For this reason, the AIC algorithm is taken to estimate the rank in mode n, which implies that the MWF can reduce noise automatically.
The PARAFAC filtering method was proposed to reduce the number of rank values to be estimated. As aforementioned, the rank in each mode must be estimated in MWF, while only one rank must be estimated in PARAFAC filtering. Moreover, the low-rank PARAFAC decomposition is unique for rank values higher than one, whereas the TUCKER3 decomposition is not. However, there is not an efficient way to estimate the PARAFAC rank automatically. Though we have shown a rank estimation method in this paper, it is a time-consuming brute force searching way.
The MWF and PARAFAC were proposed to process the HSI as a whole entity, but this may remove the small targets in an HSI in the denoising process. Distinguishing from MWF and PARAFAC, MWPT-MWF firstly transforms the HSI into different wavelet packet sets, also called components in this paper, and then filters each component as a whole entity. As the small targets are separated from the large ones, the former can be well preserved in the denoising process.
A real-world HYDICE HSI is used in the comparative study. Quantitative and visual evaluation of the three methods is shown. From the experimental results, we can conclude that MWPT-MWF is a suitable tool for denoising especially when there exist small targets in the HSI.
References
Kotwal K, Chaudhuri S: Visualization of hyperspectral images using bilateral filtering. IEEE Trans. Geosci. Remote Sens 2010, 48(5):2308-2316.
Lewis S, Hudak A, Ottmar R, Robichaud P, Lentile L, Hood S, Cronan J, Morgan P: Using hyperspectral imagery to estimate forest floor consumption from wildfire in boreal forests of Alaska, USA. Int. J. Wildland Fire 2011, 20(2):255-271. 10.1071/WF09081
Tiwari K, Arora M, Singh D: An assessment of independent component analysis for detection of military targets from hyperspectral images. Int. J. Appl. Earth Obs. Geoinf 2011, 13(5):730-740. 10.1016/j.jag.2011.03.007
Veracini T, Matteoli S, Diani M, Corsini G: Nonparametric framework for detecting spectral anomalies in hyperspectral images. IEEE Geosci. Remote Sens. Lett 2011, 8(4):666-670.
Prasad S, Li W, Fowler JE, Bruce LM: Information fusion in the redundant-wavelet-transform domain for noise-robust hyperspectral classification. IEEE Trans. Geosci. Remote Sens 2012, 50(9):3474-3486.
Kerekes J, Baum J: Full-spectrum spectral imaging system analytical model. IEEE Trans. Geosci. Remote Sens 2005, 43(3):571-580.
Uss ML, Vozel B, Lukin VV, Chehdi K: Local signal-dependent noise variance estimation from hyperspectral textural images. IEEE J. Sel. Topics Signal Process 2011, 5(3):469-486.
Acito N, Diani M, Corsini G: Subspace-based striping noise reduction in hyperspectral images. IEEE Trans. Geosci. Remote Sens 2011, 49(4):1325-1342.
Shao L, Yan R, Li X, Liu Y: From heuristic optimization to dictionary learning: a review and comprehensive comparaison of image denoising algorithms. IEEE Trans. Cybernet. 2013. in press.
Yan R, Shao L, Liu Y: Nonlocal hierarchical dictionary learning using wavelets for image denoising. IEEE Trans. Image Process 2013, 22(12):4689-4698.
Yan R, Shao L, Cvetković S, Klijn J: Improved nonlocal means based on pre-classification and invariant block matching. J. Display Technol 2012, 8(4):212-218.
Letexier D, Bourennane S: Noise removal from hyperspectral images by multidimensional filtering. IEEE Trans. Geosci. Remote Sens 2008, 46(7):2061-2069.
Renard N, Bourennane S: Improvement of target detection methods by multiway filtering. IEEE Trans. Geosci. Remote Sens 2008, 46(8):2407-2417.
Liu X, Bourennane S, Fossati C: Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis. IEEE Trans. Geosci. Remote Sens 2012, 50(10):3717-3724.
Richards JA: Remote sensing digital image analysis: an introduction. Berlin Heidelberg: Springer; 2012.
Chein IC, Qian D: Estimation of number of spectrally distinct signal sources in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens 2004, 42(3):608-619. 10.1109/TGRS.2003.819189
Kuybeda O, Malah D, Barzohar M, Rank estimation and redundancy reduction of high-dimensional noisy signals with preservation of rare vectors: IEEE Trans. Signal Process. 2007, 55(12):5579-5592.
Acito N, Diani M, Corsini G: A new algorithm for robust estimation of the signal subspace in hyperspectral images in the presence of rare signal components. IEEE Trans. Geosci. Remote Sens 2009, 47(11):3844-3856.
Martin-Herrero J: Anisotropic diffusion in the hypercube. IEEE Trans. Geosci. Remote Sens 2007, 45(5):1386-1398.
Mendez-Rial R, Calvino-Cancela M, Martin-Herrero J: Accurate implementation of anisotropic diffusion in the hypercube. IEEE Geosci. Remote Sens. Lett 2010, 7(4):870-874.
Le Bihan N, Ginolhac G: Three-mode data set analysis using higher order subspace method: application to sonar and seismo-acoustic signal processing. Signal Process 2004, 84(5):919-942. 10.1016/j.sigpro.2004.02.003
Vasilescu MAO, Terzopoulos D: Multilinear image analysis for facial recognition. In International Association of Pattern Recognition (IAPR). Quebec City; August 2002:511-514.
Muti D, Bourennane S: Multidimensional signal processing using lower-rank tensor approximation. In IEEE ICASSP. Hongkong; 6–10 April 2003:457-60.
Muti D, Bourennane S: Multidimensional filtering based on a tensor approach. Signal Process 2005, 85(12):2338-2353. 10.1016/j.sigpro.2004.11.029
Letexier D, Bourennane S, Talon J: Nonorthogonal tensor matricization for hyperspectral image filtering. IEEE Geosci. Remote Sens. Lett 2008, 5: 3-7.
Harshman RA, Lundy ME: The PARAFAC model for three-way factor analysis and multidimensional scaling. In Research methods for multimode data analysis. New York: Praeger; 1984:122-215.
Carroll JD, Chang JJ: Analysis of individual differences in multidimensional scaling via an N-way generalization of Eckart-Young decomposition. Psychometrika 1970, 35(3):283-319. 10.1007/BF02310791
Smilde A, Bro R, Geladi P: Multi-way analysis: applications in the chemical sciences. Hoboken: Wiley; 2005.
Guo X, Miron S, Brie D, Zhu S, Liao X: A CANDECOMP/PARAFAC perspective on uniqueness of DOA estimation using a vector sensor array. IEEE Trans. Signal Process 2011, 59(7):3475-3481.
De Almeida AL, Favier G, Mota JCM: PARAFAC-based unified tensor modeling for wireless communication systems with application to blind multiuser equalization. Signal Process 2007, 87(2):337-351. 10.1016/j.sigpro.2005.12.014
Liu X, Bourennane S, Fossati C: Nonwhite noise reduction in hyperspectral images. IEEE Geosci. Remote Sens. Lett 2012, 9(3):368-372.
Lin T, Bourennane S: Hyperspectral image processing by jointly filtering wavelet component tensor. IEEE Trans. Geosci. Remote Sens 2013, 51(6):3529-3541.
Kolda TG, Bader BW: Tensor decompositions and applications. SIAM Rev 2009, 51(3):455-500. 10.1137/07070111X
Cichocki A, Zdunek R, Phan A, Amari S: Nonnegative matrix and tensor factorizations: applications to exploratory multi-way data analysis and blind source separation. Hoboken: Wiley; 2009.
Muti D, Bourennane S, Marot J: Lower-rank tensor approximation and multiway, filtering. SIAM J. Matrix Anal. Appl 2008, 30(3):1172-1204. 10.1137/060653263
Donoho D, Johnstone I: Ideal denoising in an orthonormal basis chosen from a library of bases. Comptes Rendus de l’Academie des Sciences-Serie I-Mathematique 1994, 319(12):1317-1322.
Jin X, Paswaters S, Cline H: A comparative study of target detection algorithms for hyperspectral imagery. In SPIE Defense, Security, and Sensing. Orlando, FL; 13–17 April 2009.
Acknowledgements
The authors would like to thank the reviewers for their careful reading and helpful comments which improve the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, T., Bourennane, S. Survey of hyperspectral image denoising methods based on tensor decompositions. EURASIP J. Adv. Signal Process. 2013, 186 (2013). https://doi.org/10.1186/1687-6180-2013-186
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2013-186
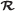
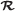 .
.
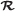 . The maximum level can be calculated by
. The maximum level can be calculated by  .
.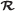 by MWPT: .
by MWPT: .





