Skip to main content

Advertisement

EURASIP Journal on Advances in Signal Processing
EURASIP Journal on Advances in Signal Processing Cover Image
We’d like to understand how you use our websites in order to improve them. Register your interest.
Download PDF

Low-rank filter and detector for multidimensional data based on an alternative unfolding HOSVD: application to polarimetric STAP

EURASIP Journal on Advances in Signal Processing volume 2014, Article number: 119 (2014) Cite this article

Abstract

This paper proposes an extension of the higher order singular value decomposition (HOSVD), namely the alternative unfolding HOSVD (AU-HOSVD), in order to exploit the correlated information in multidimensional data. We show that the properties of the AU-HOSVD are proven to be the same as those for HOSVD: the orthogonality and the low-rank (LR) decomposition. We next derive LR filters and LR detectors based on AU-HOSVD for multidimensional data composed of one LR structure contribution. Finally, we apply our new LR filters and LR detectors in polarimetric space-time adaptive processing (STAP). In STAP, it is well known that the response of the background is correlated in time and space and has a LR structure in space-time. Therefore, our approach based on AU-HOSVD seems to be appropriate when a dimension (like polarimetry in this paper) is added. Simulations based on signal-to-interferenceplus-noise ratio (SINR) losses, probability of detection (Pd), and probability of false alarm (Pfa) show the interest of our approach: LR filters and LR detectors which can be obtained only from AU-HOSVD outperform the vectorial approach and those obtained from a single HOSVD.

1 Introduction

In signal processing, more and more applications deal with multidimensional data, whereas most of the signal processing algorithms are derived based on one- or two-dimensional models. Consequently, multidimensional data have to be folded as vector or matrix to be processed. These operations are not lossless since they involve a loss of structure. Several issues may arise from this loss: decrease of performances and lack of robustness (see for instance [1]). The multilinear algebra [2, 3] provides a good framework to exploit these data by preserving the structure information. In this context, data are represented as multidimensional arrays called tensor. However, generalizing matrix-based algorithms to the multilinear algebra framework is not a trivial task. In particular, some multilinear tools do not retain all the properties of the vectorial and matrix tools. Let us consider the case of the singular value decomposition (SVD). The SVD decomposes a matrix into a sum of rank-1 matrices and has uniqueness and orthonormality properties. There is no single multilinear extension of the SVD, with exactly the same properties as the SVD. Depending on which properties are preserved, several extensions of the SVD have been introduced.

On one hand, CANDECOMP/PARAFAC (CP) [4] decomposes a tensor as a sum of rank-1 tensors, preserving the definition of rank. Due to its properties of identifiability and uniqueness, this decomposition is relevant for multiple parameter estimation. CP was first introduced in the signal processing community for direction of arrival (DOA) estimation [5, 6]. New decompositions were then derived from CP. For example, in [7, 8], a decomposition based on a constrained CP model is applied to multiple-input multiple-output (MIMO) wireless communication system. These decompositions share a common issue for some applications: they are not orthogonal.

On the other hand, the higher order singular value decomposition (HOSVD) [3, 9] decomposes a tensor as a product of a core tensor and a unitary matrix for each dimension of the tensor. This decomposition relies on matrix unfoldings. In general, HOSVD does not have the properties of identifiability and uniqueness. The model provided by HOSVD is defined up to a rotation. It implies that HOSVD cannot be used for multiple parameters estimation unlike CP. Orthogonality properties of HOSVD allow to extend the low-rank methods such as [10, 11]. These methods are based on the ranks of the different matrix unfoldings, called p-ranks [2, 12, 13]. HOSVD has been successfully applied in many fields such as image processing [14], sonar and seismo-acoustic [15], ESPRIT [16], ICA [17], and video compression [18].

HOSVD is based on the classic tensor unfolding and in particular on the matrix of left singular vectors. This unfolding transforms a tensor into a matrix in order to highlight one dimension. In other words, HOSVD only considers simple information, which is the information contained in each dimension taken separately. The correlated information, which is the information contained in a combination of dimensions, is neglected. In [19], a new decomposition, PARATREEa, based on the sequential unfolding SVD (SUSVD) was proposed. This decomposition considers some correlated information, using the right matrix of the singular vectors. This approach can be improved, to consider any type of correlated information. Consequently, we propose to develop a new set of orthogonal decompositions which will be called alternative unfolding HOSVD (AU-HOSVD). In this paper, we will define this new operator and study its main properties, especially the extension of the low-rank approximation. We will show the link between AU-HOSVD and HOSVD.

Based on this new decomposition, we derive new low-rank (LR) filters and LR detectors for multidimensional data containing a target embedded in an interference. We assume that the interference is the sum of two noises: a white Gaussian noise and a low-rank structured one. In order to illustrate the interest of these new LR filters and LR detectors, we will consider the multidimensional space-time adaptive processing (STAP). STAP is a technique used in airborne phased array radar to detect moving target embedded in an interference background such as jamming (jammers are not considered in this paper) or strong ground clutter [20] plus a white Gaussian noise (resulting from the sensor noise). While conventional radars are capable of detecting targets both in the time domain related to target range and in the frequency domain related to target velocity, STAP uses an additional domain (space) related to the target angular localization. From the Brennan rule [21], STAP clutter is shown to have a low-rank structureb. That means that the clutter response in STAP is correlated in time and space. Therefore, if we add a dimension, the LR filter and LR detector based on HOSVD will not be interesting. In this paper, we show the interest of our new LR filters and LR detectors based on AU-HOSVD in a particular case of multidimensional STAP: polarimetric STAP [22]. In this polarimetric configuration, each element transmits and receives in both H and V polarizations, resulting in three polarimetric channels (HH, VV, HV/VH). The dimension of the data model is then three. Simulations based on signal-to-interference-plus-noise ratio (SINR) losses [20], probability of detection (Pd), and probability of false alarm (Pfa) show the interest of our approach: LR filters and LR detectors which are obtained using AU-HOSVD outperform the vectorial approach and those obtained from HOSVD in the general polarimetry model (the channels HH and VV are not completely correlated). We believe that these results could be extended to more generalized multidimensional STAP systems like MIMO-STAP [23–26].

The paper is organized as follows. Section 2 gives a brief overview of the basic multilinear algebra tools. In particular, the HOSVD and its main properties are presented. In Section 3, the AU-HOSVD and its properties are derived. Section 4 is devoted to the derivation of the LR filters and LR detectors based on AU-HOSVD. Finally, in Section 5, these new tools are applied to the case of polarimetric STAP.

The following convention is adopted: scalars are denoted as italic letters, vectors as lowercase boldface letters, matrices as boldface capitals, and tensors as boldface calligraphic letters. We use the superscripts H for Hermitian transposition and ∗ for complex conjugation. The expectation is denoted by E[.], and the Frobenius norm is denoted ∥.∥.

2 Some basic multilinear algebra tools

This section contains the main multilinear algebra tools used in this paper. Let , ℬ∈ C I 1 × … × I P , be two P th-order tensors and h i 1 … i P , b i 1 … i P their elements.

2.1 Basic operators of multilinear algebra

Unfoldings In this paper, three existing unfoldings are used; for a general definition of tensor unfolding, we refer the reader to [2].

  • Vector: vec transforms a tensor into a vector, vec(ℋ)∈ C I 1 I 2 … I P . We denote v e c−1, the inverse operator.

  • Matrix: this operator transforms the tensor 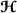into a matrix [ ℋ ] p ∈ C I p × I 1 … I p − 1 I p + 1 … I P , p=1…P. For example, [ ℋ ] 1 ∈ C I 1 × I 2 … I P . This transformation allows to enhance simple information (i.e., information contained in one dimension of the tensor).

  • Square matrix: this operator transforms a 2P th-order tensor R∈ C I 1 × I 2 … × I P × I 1 × I 2 … × I P into a square matrix, SqMat(R)∈ C I 1 … I P × I 1 … I P . S q M a t−1 is the inverse operator.

    The inverse operators always exist. However, the way the tensor was unfolded must be known.

    Products

  • The scalar product <ℋ,ℬ> of two tensors is defined as

    < ℋ , ℬ > = ∑ i 1 ∑ i 2 … ∑ i P b i 1 i 2 … i P ∗ h i 1 i 2 … i P = vec ( ℬ ) H vec ( ℋ ) .
    (1)

    It is the usual Hermitian scalar product in linear spaces [12, 27].

  • Let E∈ C J n × I n be a matrix, the n-mode product between E and a tensor 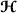is defined as

    G = ℋ × n E ∈ C I 1 × … × J n × … × I P ⇔ ( G ) i 1 … j n … i P = ∑ i n h i 1 … i n … i P e j n i n ⇔ [ G ] n = E [ ℋ ] n .
    (2)

  • The outer product between and , E=ℋ∘ℬ∈ C I 1 × … × I P × I 1 × … × I P is defined as

    e i 1 … i P i 1 … i P = h i 1 … i P . b i 1 … i P .
    (3)

Tensor ranks There are two concepts of rank for tensors:

  • The tensor rank: it is defined as the minimum number of rank-1 tensors (for example a P th-order rank-1 tensor can be written as the outer product of P vectors) necessary to obtain the considered tensor.

  • The p-ranks: they are defined as the ranks of the unfoldings, r p =rank [ ℋ ] p .

2.2 Higher order singular value decomposition

This subsection recalls the main results on the HOSVD used in this paper.

Theorem 2.1

The higher order singular value decomposition (HOSVD) is a particular case of Tucker decomposition [9] with orthogonality properties. HOSVD decomposes a tensor as follows [3]:

ℋ=K × 1 U ( 1 ) … × P U ( P ) ,
(4)

where ∀n, U ( n ) ∈ C I n × I n is an orthonormal matrix and K∈ C I 1 × … × I P is the core tensor, which satisfies the all-orthogonality conditions [3]. The matrix U(n) is given by the singular value decomposition of the n-dimension unfolding, [ ℋ ] n = U ( n ) Σ ( n ) V ( n ) H . Using classical unfolding, the HOSVD only considers the simple information.

Remark Let ℋ∈ C I 1 × I 2 … × I P × I 1 × I 2 … × I P be a 2P th-order Hermitian tensor, i.e., h i 1 , … , i p , j 1 , … , j p = h j 1 , … , j p , i 1 , … , i p ∗ . The HOSVD of is written as [16]

ℋ=K × 1 U ( 1 ) … × P U ( P ) × P + 1 U ( 1 ) ∗ … × 2 P U ( P ) ∗ .
(5)

The following result permits to compute a tensor approximation of lower p-ranks.

Proposition 2.1(Low-rank approximation)

Let us introduce ℋ= ℋ c + ℋ 0 . ℋ c is a (r1,…,r P ) low-rank tensor where r k <I k , for k=1,…,P. An approximation of ℋ 0 is given by [15, 27]:

ℋ 0 ≈ℋ × 1 U 0 ( 1 ) U 0 ( 1 ) H … × P U 0 ( P ) U 0 ( P ) H ,
(6)

with U 0 ( n ) = u r n + 1 ( n ) … u I n ( n ) .

It is well known that this solution is not optimal in the sense of least squares. However, it is a correct approximation in most cases [16, 27] and it is easy to implement. That is why iterative algorithms will not be used in this paper.

2.3 Covariance tensor and estimation

Definition Let Z∈ C I 1 × … × I P be a random P th-order tensor, and the covariance tensor R∈ C I 1 × … × I P × I 1 … × I P is defined as [28]

R=E Z ∘ Z ∗ .
(7)

Sample covariance matrix Let z∈ C I 1 … I P be a zero-mean Gaussian random vector and R∈ C I 1 … I P × I 1 … I P its covariance matrix. Let z k be K observations of z. The sample covariance matrix (SCM), R ̂ , is written as follows:

R ̂ = 1 K ∑ k = 1 K z k z k H .
(8)

Sample covariance tensor Let Z k ∈ C I 1 × … × I P be K observations of . By analogy with the SCM, R ̂ ∈ C I 1 … × I P × I 1 … × I P , the sample covariance tensor (SCT) is defined as [16]

R ̂ = 1 K ∑ k = 1 K Z k ∘ Z k ∗ .
(9)

Remark If we denote z=vec(Z), then

R=SqMat(R).
(10)

3 Alternative unfolding HOSVD

Due to proposition 2.1, it is possible to design LR filters based on HOSVD. This approach does not work when all p-ranks are full (i.e., r p =I p , p=1…P), since no projection could be done. However, the data may still have a LR structure. This is the case of correlated data where one or more ranks relative to a group of dimensions are deficient. Tensor decompositions allowing to exploit this kind of structure have not been promoted. To fill this gap, we propose to introduce a new tool which will be able to extract this kind of information. This section contains the main contribution of this paper: the derivation of the AU-HOSVD and its principal properties.

3.1 Generalization of standard operators

Notation of indices In order to consider correlated information, we introduce a new notation for the indices of a tensor. We consider ℋ∈ C I 1 × … × I P , a P th-order tensor. We denote A={1,…,P} the set of the dimensions and A 1 ,…, A L , L subsets of which define a partition of . In other words, A 1 ,…, A L satisfy the following conditions:

  • A 1 ∪…∪ A L =A

  • They are pairwise disjoint, i.e.,

    ∀i≠j, A i ∩ A j =∅.

Moreover C I 1 … I P is denoted C I A . For example, when A 1 ={1,2} and A 2 ={3,4}, C I A 1 × I A 2 means C I 1 I 2 × I 3 I 4 .

A generalization of unfolding in matrices In order to build our new decomposition, we need a generalized unfolding, adapted from [2]. This operator allows to unfold a tensor into a matrix whose dimensions could be any combination A l of the tensor dimensions. It is denoted as [ . ] A l , and it transforms into a matrix [ ℋ ] A l ∈ C I A l × I A ∖ A l .

A new unfolding in tensors We denote as Reshape the operator which transforms a tensor into a tensor Reshape(ℋ, A 1 ,…, A L )∈ C I A 1 × … × I A L and Reshape−1 the inverse operator.

A new tensor product The n-mode product allows to multiply a tensor with a matrix along one dimension. We propose to extend the n-mode product to multiply a tensor with a matrix along several dimensions, combined in A l . Let D∈ C I A l × I A l be a square matrix. This new product, called multimode product, is defined as

ℬ=ℋ × A l D⇔ [ ℬ ] A l =D [ ℋ ] A l .
(11)

The following proposition shows the link between multimode product and n-mode product.

Proposition 3.1(Link between n -mode product and multimode product).

Let ℋ∈ C I 1 × … × I P be a P th-order tensor, A 1 ,…, A L be a partition of , and D∈ C I A l × I A l be a square matrix. Then, the following equality is verified:

Reshape ( ℋ × A l D , A 1 , … , A L ) = Reshape ( ℋ , A 1 , … , A L ) × l D
(12)

Proof 3.1

The proof of Theorem 3.1 relies on the following straightforward result:

∀ l ∈ [ 1 , L ] , [ ℋ ] A l = [ Reshape ( ℋ , A 1 , … , A L ) ] l .

This leads to [ ℬ ] A l = [ Reshape ( ℬ , A 1 , … , A L ) ] l and [ ℋ ] A l = [ Reshape ( ℋ , A 1 , … , A L ) ] l . Applying these two results on (11), we obtain

Reshape ( ℬ , A 1 , … , A L ) l = D [ Reshape ( ℋ , A 1 , … , A L ) ] l .
(13)

From Equation 2, Equation 13 is equivalent to

Reshape ( ℬ , A 1 , … , Reshape ( ℋ , A 1 , … , A L ) × l A L ) D .

Finally, one has

Reshape ( ℋ × A l D , A 1 , … , A L ) = Reshape ( ℋ , A 1 , … , A L ) × l D .

Remark Thanks to the previous proposition and the commutative property of n-mode product, multimode product is also commutative.

3.2 AU-HOSVD

With the new tools presented in the previous subsection, we are now able to introduce the AU-HOSVD. This is the purpose of the following theorem.

Theorem 3.1(Alternative unfolding HOSVD).

Let ℋ∈ C I 1 × … × I P and A 1 … A L a partition of . Then, may be decomposed as follows:

ℋ= K A 1 / … / A L × A 1 U ( A 1 ) … × A L U ( A L ) ,
(14)

where

  • l∈ [ 1,L], U ( A l ) ∈ C A l × A l is unitary. The matrix U ( A l ) is given by the singular value decomposition of the A l -dimension unfolding, [ ℋ ] A l = U ( A l ) Σ ( A l ) V ( A l ) H .

  • K A 1 / … / A L ∈ C I 1 × … × I P

    is the core tensor. It has the same properties as the HOSVD core tensor.

Notice that there are several ways to decompose a tensor with the AU-HOSVD. Each choice of the A 1 ,…, A L gives a different decomposition. For a P th-order tensor, the number of different AU-HOSVD is given by the Bell number, B P :

B 1 = 1 B P + 1 = ∑ k = 1 P P k B k .

The AU-HOSVD associated to the partition A 1 ,…, A L is denoted AU-HOSVD A 1 , … , A L .

Proof 3.2.

First, let us consider A 1 ,…, A L , a partition of . Reshape(ℋ, A 1 … A L ) is a L th-order tensor and may be decomposed using the HOSVD:

Reshape ( ℋ , A 1 , … , A L ) = K × 1 U ( 1 ) … × L U ( L ) ,
(15)

where the matrix U(l) is given by the singular value decomposition of the l-dimension unfolding, [ Reshape ( ℋ , A 1 , … , A L ) ] l = [ ℋ ] A l = U ( l ) Σ ( l ) V ( l ) H .

Since the matrices U(l)’s are unitary, Equation 15 is equivalent to

Reshape ( ℋ , A 1 , … , A L ) × 1 U ( 1 ) H … × L U ( L ) H = K .
(16)

Then, using proposition 3.1, the following equality is true:

Reshape ( ℋ , A 1 , … , A L ) × 1 U ( 1 ) H … × L U ( L ) H = Reshape ℋ × A 1 U ( 1 ) H … × A L U ( L ) H , A 1 , … , A L ,
(17)

which leads to

Reshape ℋ × A 1 U ( 1 ) H … × A L U ( L ) H , A 1 , … , A L = K .
(18)

Finally, the operator Reshape−1 is applied

ℋ = Reshap e − 1 ( K , A 1 , … , A L ) × A 1 U ( 1 ) … × A L U ( L ) ,
(19)

which concludes the proof.

Example For a third-order tensor ℋ∈ C I 1 × I 2 × I 3 with A 1 ={1,3}, A 2 ={2}, the AU-HOSVD will be written as follows:

ℋ = K A 1 / A 2 × A 1 U ( A 1 ) × A 2 U ( A 2 ) ,
(20)

with K A 1 / A 2 ∈ C I 1 × I 2 × I 3 , U ( A 1 ) ∈ C I 1 I 3 × I 1 I 3 and U ( A 2 ) ∈ C I 2 × I 2 .

Remark Let ℋ∈ C I 1 × I 2 … × I P × I 1 × I 2 … × I P be a 2P th-order Hermitian tensor. We consider 2L subsets of {I1,…,I P ,I1,…,I P } such as

  • A 1 ,…, A L

    and A L + 1 ,…, A 2 L are two partitions of {I1,…,I P }

  • l∈ [ 1,L],

    A l = A l + L

Under these conditions, the AU-HOSVD of is written:

ℋ = K A 1 / … / A 2 L × A 1 U ( A 1 ) … × A L U ( A L ) × A L + 1 U ( A 1 ) ∗ … × A 2 L U ( A L ) ∗ .

As discussed previously, the main motivation for introducing the new AU-HOSVD is to extract the correlated information when processing the low-rank decomposition. This is the purpose of the following proposition.

Proposition 3.2(Low-rank approximation).

Let , ℋ c , ℋ 0 be three P th-order tensors such that

ℋ= ℋ c + ℋ 0 ,
(21)

where ℋ c is a r A 1 , … , r A L low-rank tensorc r A l = rank [ ℋ c ] A l . Then, ℋ 0 is approximated by

ℋ 0 ≈ℋ × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H
(22)

where U 0 ( A 1 ) , …, U 0 ( A L ) minimize the following criterion:

U 0 ( A 1 ) , … , U 0 ( A L ) = argmin ℋ 0 − ℋ × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H 2 .
(23)

In this paper, the matrices U 0 ( A L ) ’s are given by truncation of the matrices U ( A l ) ’s obtained by the AU-HOSVD A 1 , … , A L of : U 0 ( A l ) = u r A l + 1 ( A l ) … u A l ( A l ) . This solution is not optimal in the sense of least squares but is easy to implement. However, thanks to the strong link with HOSVD, it should be a correct approximation. That is why iterative algorithms for AU-HOSVD will not be investigated in this paper.

Proof 3.3.

By applying Reshape to Equation 21, one obtains

Reshape ( ℋ , A 1 , … , A L ) = Reshape ( ℋ c , A 1 , … , A L ) + Reshape ( ℋ 0 , A 1 , … , A L ) .

Then, Reshape ℋ c , A 1 , … , A L is a r A 1 , … , r A L low-rank tensor where r A l = rank Reshape ℋ c , A 1 , … , A L l . Proposition 2.1 can now be applied, and this leads to

Reshape ( ℋ 0 , A 1 , … , A L ) ≈ Reshape ( ℋ , A 1 , … , A L ) × 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × L U 0 ( A L ) U 0 ( A L ) H .

Finally, applying R e s h a p e−1 to the previous equation leads to the end of the proof:

ℋ 0 ≈ ℋ × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H .

Discussion on choice of partition and complexity As mentioned previously, the total number of AU-HOSVD for a P th-order tensor is equal to B P . Since this number could become significant, it is important to have a procedure to find good partitions for the AU-HOSVD computation. We propose a two-step procedure. Since the AU-HOSVD has been developed for LR reduction, the most important criterion is to choose the partitions which emphasize deficient ranks. For some applications, it is possible to use a priori knowledge to select some partitions as will be shown in Section 5 for polarimetric STAP. Next, another step is needed if several partitions induce an AU-HOSVD with a deficient rank. At this point, we propose to maximize a criterion (see Section 5.3 for examples) over the remaining partitions.

Concerning the complexity, the number of operation necessary to compute the HOSVD of a P th-order tensor is equal to 4 ∏ p I p ∑ p I p [3]. Similarly, the complexity of the AU-HOSVD is equal to 4 ∏ p I p ∑ l I A l .

4 Low-rank filter and detector for multidimensional data based on the alternative unfolding HOSVD

We propose in this section to apply this new decomposition to derive a tensorial LR filter and a tensorial LR detector for multidimensional data. We consider the case of a P-dimensional data composed of a target described by its steering tensor and two additive noises: and . We assume that we have K secondary data X k containing only the additive noises. This configuration could be summarized as follows:

X = α S + C + N
(24)
X k = C k + N k k ∈ [ 1 , K ] .
(25)

where X, X k ,C, C k ,N, N k ∈ C I 1 × … × I P . We assume that N, N k ∼CN 0 , σ 2 SqMa t − 1 I I 1 … I p and C, C k ∼CN(0, R c ) SqMa t − 1 I I 1 … I p , R c ∈ C I 1 × … × I P × I 1 × … × I P . These notations mean vec(N),vec( N k )∼CN(0, σ 2 I I 1 … I p ) and vec(C),vec( C k )∼CN(0,SqMat( R c )). We denote R= R c + σ 2 SqMa t − 1 ( I I 1 … I p ) the covariance tensor of the total interference. We assume in the following that the additive noise (and hence also C k ) has a low-rank structure.

4.1 LR filters

Proposition 4.1(Optimal tensor filter).

The optimal tensor filter, , is defined as the filter which maximizes the SINR output

SINR out = | < W , S > | 2 vec ( W ) H SqMat ( R ) vec ( W ) .
(26)

It is given by the following expression:

W opt =ve c − 1 SqMat ( R ) − 1 vec ( S ) .
(27)

Proof 4.1.

See Appendix 1.

In practical cases, is unknown. Hence, we propose an adaptive version:

W ̂ opt =ve c − 1 SqMat ( R ̂ ) − 1 vec ( S ) ,
(28)

where R ̂ is the estimation of given by the SCT from Equation 9. This filter is equivalent to the vector filter. In order to reach correct performance [29], K=2I1…I P secondary data are necessary. As with the vectorial approach, it is interesting to use the low-rank structure of to reduce this number K.

Proposition 4.2(Low-rank tensor filter).

Let A 1 ,…, A L be a partition of {1,…,P}. The low-rank tensor filter associated to AU-HOSVD A 1 , … , A L , which removes the low-rank noise , is given by

W lr ( A 1 , … , A P ) = S × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H
(29)
y= < W A 1 , … , A P , X > .
(30)

The matrices U 0 ( A L ) ’s are given by truncation of the matrices U ( A l ) ’s obtained by the AU-HOSVD A 1 , … , A L of : U 0 ( A l ) = u r A l + 1 ( A l ) … u A l ( A l ) .

For a P-dimensional configuration, B P filters will be obtained.

Proof 4.2.

See Appendix 2.

In its adaptive version, denoted W ̂ lr ( A 1 / … / A L ) , the matrices U 0 ( A 1 ) ,…, U 0 ( A L ) are replaced by their estimates U ̂ 0 ( A 1 ) ,…, U ̂ 0 ( A L ) .

The number of secondary data necessary to reach classical performance is not known. In the vectorial case, the performance of LR filter depends on the deficient rank [10, 11]. It will be similar for the LR tensor filters. This implies that the choice of the partition A 1 ,…, A L is critical.

4.2 LR detectors

In a detection point of view, the problem can also be stated as the following binary hypothesis test:

H 0 : X = C + N , X k = C k + N k , k ∈ [ 1 , K ] H 1 : X = α S + C + N , X k = C k + N k , k ∈ [ 1 , K ] .
(31)

Proposition 4.3(Low-rank tensor detector).

Let A 1 ,…, A L be a partition of {1,…,P}. The low-rank tensor detector associated to AU-HOSVD A 1 , … , A L , which removes the low-rank noise and performs the generalized likelihood ratio test (GLRT), is given by

Λ A 1 … A L = | < S A 1 … A L , X A 1 … A L > | 2 < S A 1 … A L , S A 1 … A L > < X A 1 … A L , X A 1 … A L >
(32)

where

X A 1 … A L = X × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H S A 1 … A L = S × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H
(33)

The matrices U 0 ( A L ) ’s are given by truncation of the matrices U ( A l ) ’s obtained by the AU-HOSVD A 1 , … , A L of : U 0 ( A l ) = u r A l + 1 ( A l ) … u A l ( A l ) .

Proof 4.3.

See Appendix 3.

In its adaptive version, denoted as Λ ̂ A 1 … A L , the matrices U 0 ( A 1 ) ,…, U 0 ( A L ) are replaced by their estimates U ̂ 0 ( A 1 ) ,…, U ̂ 0 ( A L ) .

4.3 Particular case

When the partition A 1 ={1,…,P} is chosen, the filter and the detector obtained by the AU-HOSVD are equal to the vectorial one. In other words, it is equivalent to apply the operator vec on Equations 24 and 25 and use the vectorial method. We denote m=I1…I P , x=vec(X) and s=vec(S). We obtain the basis of the orthogonal clutter subspace U0 by taking the last (m−r) columns of U which is computed by the SVD of SqMat(R)=UΣ V H . From this basis, the low-rank filter is then equal to [10, 11]:

w lr = U 0 U 0 H s,
(34)
y lr =|< w lr ,x>|.
(35)

In its adaptive version, denoted w ̂ lr , the matrix U0 is replaced by its estimate U 0 ̂ .

Similarly, the detector is equal to the low-rank normalized matched filter proposed in [30, 31]:

Λ LR-NMF = s H U 0 U 0 H x 2 s H U 0 U 0 H s x H U 0 U 0 H x .
(36)

In its adaptive version, denoted Λ ̂ LR-NMF , the matrix U0 is replaced by its estimate U ̂ 0 .

5 Application to polarimetric STAP

5.1 Model

We propose to apply the LR filters and the LR detectors derived in the previous section to polarimetric STAP. STAP is applied to airborne radar in order to detect moving targets [20]. Typically, the radar receiver consists of an array of N antenna elements processing M pulses in a coherent processing interval. In polarimetric configuration, each element transmits and receives in both H and V polarizations, resulting in three polarimetric channels (HH, VV, HV/VH). The number of dimensions of polarimetric STAP data is then equal to three: N antenna, M pulses, and three polarimetric channels.

We are in the data configuration proposed in Equations 24 and 25 which is recalled in the following equations:

X=αS+C+N
(37)
X k = C k + N k k∈[1,K],
(38)

where X, X k ∈ C M × N × 3 . The steering tensor and the responses of the background and C k , called clutter in STAP, are obtained from the model proposed in [22]. and N k , which arise from the electrical components of the radar, are distributed as a white Gaussian noise.

The steering tensor, , is formed as follows:

S(θ,v)=ve c − 1 s HH ( θ , v ) α VV s HH ( θ , v ) α VH s HH ( θ , v ) ,
(39)

where sHH(θ,v) is the 2D steering vector [20], characterized by the angle of arrival (AOA) θ and the speed v of the target. αVV and αVH are two complex coefficients. These coefficients are assumed to be known. This is the case when the detection process concerns a particular target (surface, double-bounds, volume, …). The covariance tensor, denoted as R∈ C M × N × 3 × M × N × 3 , of the two noises (C+N and C k + N k ) is given by

R=SqMa t − 1 R pc + σ 2 I 3 MN ,
(40)

where σ2 is the power of the white noise. R p c is built as follows:

R pc = R c ρ γ VV R c 0 ρ ∗ γ VV R c γ VV R c 0 0 0 γ VH R c ,
(41)

where R c ∈ C MN × MN is the covariance matrix of the HH channel clutter, built as the 2D clutter, which is known to have a LR structure [20]. γVV and γVH are two coefficients relative to the nature of the ground, and ρ is the correlation coefficient between the channels HH and VV. Due to the structure of R p c , the low-rank structure of the clutter is preserved.

In the following subsection, we discuss about the choice of partitions in this particular context.

5.2 Choice of partition

For polarimetric STAP, we have P=3 and A={1,2,3}: B3=5 LR filters and LR detectors are obtained. The different choices of partition are presented in Table 1. All filters and detectors are computed with the AU-HOSVD. Nevertheless, the first two partitions are particular cases. When A 1 ={1,2,3}, the algorithms are equal to the vectorial one as mentioned in Section 4.3. When A 1 ={1}, A 2 ={2}, A 3 ={3}, we obtain the same LR filter and LR detector as those given by the HOSVD. The ranks relative to the LR filters and LR detectors are described in the following:

Table 1 Description of the LR filters and LR detectors provided by AU-HOSVD for polarimetric STAP
Full size table

  • The rank r1 is the spatial rank, and the rank r2 is the temporal rank. They depend on radar parameters, and in most cases, they are not deficient.

  • r3 could be deficient depending on the nature of the data and especially on the correlation coefficient ρ between the polarimetric channels.

  • r12 is the same as the 2D low-rank vector case and can be calculated by the Brennan’s rule [21].

  • r123 is deficient and is linked to r3 and r12.

  • r13 and r23 could be deficient and depends on r1, r2 and r3.

5.3 Performance criteria

In order to evaluate the performance of our LR filters, we evaluate the SINR loss defined as follows [20]:

ρ loss = SINR out SINR max ,
(42)

where S I N R o u t is the SINR at the output of the LR tensor STAP filter and S I N R m a x the SINR at the output of the optimal filter W opt . The S I N R o u t is maximum when W= W opt =ve c − 1 SqMat ( R ) − 1 vec ( S ) . After some developments, the SINR loss is equal to [1]

ρ loss = | ( vec ( W lr ) H vec ( S ) ) | 2 vec ( W lr ) H SqMat ( R ) vec ( W lr ) vec ( S ) H SqMat ( R ) − 1 vec ( S ) .
(43)

For the moment, as the analytical formulation of the SINR loss for the tensorial approach is not available, it will be evaluated using Monte Carlo simulations.

In order to evaluate the performance of our LR detectors, we use the probability of false alarm (Pfa) and probability of detection (Pd):

Pfa=Pr Λ ̂ A 1 … A L > η / H 0
(44)
Pd=Pr Λ ̂ A 1 … A L > η / H 1 ,
(45)

where η is the detector threshold. Since there is no analytical formulation for Pfa and Pd (for the adaptive version) even in the vectorial case, Monte Carlo simulations are used to evaluate them.

5.4 Simulations

Parameters The simulations are performed with the following parameters. The target is characterized by an angle of arrival (AOA) of θ=0° and a speed of v=10 m s −1, a case where the 2D STAP is known to be inefficient because the target is close to the clutter ridge. The radar receiver contains N=8 sensors processing M=8 pulses. The platform speed V, is equal to 100 m s −1. For the clutter, we consider two cases: ρ=1, i.e., the channels HH and VV are entirely correlated and ρ=0.5. The SNR is equal to 45 dB and the clutter-to-noise ratio (CNR) to 40 dB. r1, r2, r3, and r12 can be calculated based on the radar configuration. r13 depends on the value of ρ. r123 and r23 are estimated according to the singular values of the different unfoldings of . The results are presented in Table 2. All Monte-Carlo simulations are performed with N r e a =1,000 samples, except the probability of false alarm where N r e a =100.

Table 2 Summary of the value of the ranks for the two scenarios: ρ=1 , ρ=0.5
Full size table

Results on SINR losses Figures 1 and 2 show the SINR losses for each filter as a function of K. SINR losses are obtained from Monte-Carlo simulations using Equation 43. On both figures, the SINR loss of the 2D STAP is plotted for comparison. The well-known result is obtained: the SINR loss reaches −3 dB when K=2r12=30, and it tends to 0 dB as K increases. Similarly, the SINR loss of W ̂ lr ( 1 , 2 , 3 ) reaches −3 dB when K=2r123 (60 for ρ=1 and 90 for ρ=0.5). When ρ=1, all LR filters achieve reasonable performance since all ranks, except r1 and r2, are deficient. W ̂ lr ( 1 / 2 / 3 ) , W ̂ lr ( 1 / 2 , 3 ) , and W ̂ lr ( 1 , 3 / 2 ) , which can only be obtained by AU-HOSVD, outperform W ̂ lr ( 1 , 2 , 3 ) and the 2D STAP for a small number of secondary data. This situation is more realistic since the assumption of homogeneity of the data is no longer true when K is too large. W ̂ lr ( 1 , 2 / 3 ) has poor performance in this scenario.

Figure 1
figure1

SINR losses versus K for ρ=1 , CNR=40 dB. Target located at position (θ=0°,v=10 m s−1).

Full size image
Figure 2
figure2

SINR losses versus K for ρ=0.5 , CNR=40 dB. Target located at position (θ=0°,v=10 m s−1).

Full size image

When ρ=0.5, W ̂ lr ( 1 , 2 / 3 ) outperforms W ̂ lr ( 1 , 2 , 3 ) and the 2D STAP regardless of the number of secondary data. This corresponds to a more realistic scenario, since the channels HH and VV are not entirely correlated. W ̂ lr ( 1 / 2 / 3 ) , W ̂ lr ( 1 / 2 , 3 ) , and W ̂ lr ( 1 , 3 / 2 ) do not have acceptable performance. This is explained by the fact that all ranks pertaining to these filters are full and no projection can be done as mentioned at the end of Section 3. These filters (for ρ=0.5) will not be studied in the rest of the simulations.

Figures 3 and 4 show the SINR loss as a function of the CNR for K=2r12=30 secondary data. They show that our filters are more robust than the vectorial one for polarimetric STAP configuration.

Figure 3
figure3

SINR losses versus CNR for ρ=1 , K=30 , N rea =1,000 . Target located at (θ=0°,v=10 m s−1).

Full size image
Figure 4
figure4

SINR losses versus CNR for ρ=0.5 , K=30 , N rea =1,000 . Target located at (θ=0°,v=10 m s−1).

Full size image

Figures 5 and 6 show the SINR loss as a function of the target velocity for K=180. For both cases, the 2D STAP achieves the expected performance. For ρ=1, the difference in polarimetric properties between the target and the clutter is exploited by our filters, since r3 is deficient. When the target is in the clutter ridge, the SINR loss is higher (especially for W ̂ lr ( 1 / 2 / 3 ) , W ̂ lr ( 1 / 2 , 3 ) , and W ̂ lr ( 1 , 3 / 2 ) ) than the 2D LR STAP filter. By contrast, when ρ=0.5, the 2D LR STAP filter outperforms W ̂ lr ( 1 , 2 / 3 ) W ̂ lr ( 1 , 2 , 3 ) (in the context of large K), since r3 is full.

Figure 5
figure5

SINR losses versus target velocity for ρ=1 , CNR=40 dB, K=180 , N r e a =1,000. Target located at θ=0°.

Full size image
Figure 6
figure6

SINR losses versus target velocity for ρ=0.5 , CNR=40 dB, K=180 , N rea =1,000 . Target located at θ=0°.

Full size image

Results on Pfa and Pd The Pfa as a function of threshold is presented in Figures 7 and 8. The probability of detection as a function of SNR is presented in Figures 9 and 10 for K=30. The thresholds are chosen in order to have a PfA of 10−2 according to Figures 7 and 8. When ρ=1, Λ ̂ lr ( 1 / 2 / 3 ) , Λ ̂ lr ( 1 / 2 , 3 ) , and Λ ̂ lr ( 1 , 3 / 2 ) , which can only be obtained by AU-HOSVD, outperform Λ ̂ lr ( 1 , 2 , 3 ) and the 2D STAP LRNMF. For instance, Pd is equal to 90% when the SNR is equal to 15 dB for Λ ̂ lr ( 1 / 2 / 3 ) , Λ ̂ lr ( 1 / 2 , 3 ) , and Λ ̂ lr ( 1 , 3 / 2 ) ; 20 dB for the 2D STAP LRNMF; and 33 dB for Λ ̂ lr ( 1 , 2 , 3 ) . When ρ=0.5, Λ ̂ lr ( 1 , 2 / 3 ) outperforms Λ ̂ lr ( 1 , 2 , 3 ) and the 2D STAP LRNMF. For instance, Pd is equal to 90% when the SNR is equal to 16 dB for Λ ̂ lr ( 1 , 2 / 3 ) , 20 dB for the 2D STAP LRNMF, and 54 dB for Λ ̂ lr ( 1 , 2 , 3 ) .

Figure 7
figure7

Pfa versus threshold for ρ=1 , K=30 , CNR=40 dB, N rea =100 .

Full size image
Figure 8
figure8

Pfa versus threshold for ρ=0.5 , K=30 , CNR=40 dB, N rea =100 .

Full size image
Figure 9
figure9

Pd versus SNR for ρ=1 , K=30 , CNR=40 dB, Pfa=10−2, N rea =1,000 . Target located at position (θ=0°, v=10 m s −1).

Full size image
Figure 10
figure10

Pd versus SNR for ρ=0.5 , K=30 , CNR=40 dB, Pfa=10−2, N rea =1,000 . Target located at position (θ=0°,v=10 m s −1).

Full size image

The results on Pd confirm the results on SINR loss concerning the most efficient partition for the two scenarios. In particular, it shows that the best results are provided by the filters and detectors which can only be obtained with the AU-HOSVD.

6 Conclusion

In this paper, we introduced a new multilinear decomposition: the AU-HOSVD. This new decomposition generalizes the HOSVD and highlights the correlated data in a multidimensional set. We showed that the properties of the AU-HOSVD are proven to be the same as those for HOSVD: the orthogonality and the LR decomposition. We have also derived LR filters and LR detectors based on AU-HOSVD for multidimensional data containing one LR structure contribution. Finally, we applied our new LR filters and LR detectors to polarimetric space-time adaptive processing (STAP) where the dimension of the problem is three and the contribution of the background is correlated in time and space. Simulations based on signal-to-interference-plus-noise ratio (SINR) losses, probability of detection (Pd), and probability of false alarm (Pfa) showed the interest of our approach: LR filters and LR detectors which can be obtained only from AU-HOSVD outperformed the vectorial approach and those obtained from HOSVD in the general polarimetry physic model (where the channels HH and VV are not completely correlated). The main future work concerns the application of the LR filters and LR detectors developed from the AU-HOSVD for the general system of MIMO-STAP [23–26].

Endnotes

a This new decomposition has similarity with the block term decomposition introduced in [13, 32] and [33], which proposes to unify HOSVD and CP.

b Using this assumption, a low-rank vector STAP filter can be derived based on the projector onto the subspace orthogonal to the clutter (see [10, 11, 34] for more details).

c This definition of rank is directly extended from the definition of p-ranks.

Appendices

Appendix 1

Proof of Proposition 4.1

By analogy with the vector case [35], we derive the optimal filter W opt , which maximizes the output S I N R o u t :

SINR out = | < W opt , S > | 2 vec ( W opt ) H SqMat ( R ) vec ( W opt ) .
(46)

Then,

< W opt , S > 2 = vec W opt H vec ( S ) 2 = vec ( W opt ) H SqMat ( R ) 1 2 SqMat ( R ) − 1 2 vec ( S ) 2 = < SqMat ( R ) 1 2 ( H ) vec ( W opt ) , SqMat ( R ) − 1 2 vec ( S ) > 2
(47)

By Cauchy-Schwarz inequality, (47) is maximum when SqMat ( R ) 1 2 ( H ) vec( W opt )=SqMat ( R ) − 1 2 vec(S) and vec( W opt )=SqMat ( R ) − 1 vec(S). We replace W opt in (46):

x ` SINR = vec ( S ) H SqMat ( R ) − 1 vec ( S ) 2 vec ( S ) H SqMat ( R ) − 1 SqMat ( R ) SqMat ( R ) − 1 vec ( S ) = vec ( S ) H SqMat ( R ) − 1 vec ( S ) = SINR max
(48)

Appendix 2

Proof of Proposition 4.2

We propose to derive the low-rank tensor filter as follows:

  • First, the covariance tensorR is decomposed with the AU-HOSVD:

    R = K A 1 / … / A 2 L × A 1 U ( A 1 ) … × A L U ( A L ) × A L + 1 U ( A 1 ) ∗ … × A 2 L U ( A L ) ∗ .
    (49)
  • r A 1

    , …, r A L r A l = rank R A l are estimated.

  • Each U ( A l ) is truncated to obtain U 0 ( A l ) = u r A l + 1 ( A l ) , … , u A l ( A l ) .

  • Proposition 3.2, with ℋ=X, ℋ c =C and ℋ 0 =αS+N is applied in order to remove the LR contribution:

    X × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H ≈αS+N.
    (50)

  • The problem is then to filter 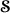which is corrupted by a white noise . The filter given by (27) is applied with R= I I 1 … I p :

    y= < S , X × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H > .
    (51)

  • Finally, the output filter is rewritten:

    W lr ( A 1 , … , A P ) = S × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H
    (52)
    y = | < W A 1 , … , A P , X > | .
    (53)

Appendix 3

Proof of Proposition 4.3

To prove Proposition 4.3, let us recall the hypothesis test:

H 0 : X = C + N , X k = C k + N k , k ∈ [ 1 , K ] H 1 : X = α S + C + N , X k = C k + N k , k ∈ [ 1 , K ] .
(54)

  • Using Proposition 3.2, the data are preprocessed in order to remove the LR contribution. We denote A 1 … A L = × A 1 U 0 ( A 1 ) U 0 ( A 1 ) H … × A L U 0 ( A L ) U 0 ( A L ) H . The hypothesis test becomes

    H 0 : X A 1 … A L = N A 1 … A L , X k , A 1 … A L = N k , A 1 … A L H 1 : X A 1 … A L = α S A 1 … A L + N A 1 … A L , X k , A 1 … A L = N k , A 1 … A L .
    (55)

  • Then, the operator vec is applied, which leads to

    H 0 : vec X A 1 … A L = vec N A 1 … A L , vec X k , A 1 … A L = vec N k , A 1 … A L H 1 : vec X A 1 … A L = αvec S A 1 … A L + vec N A 1 … A L , vec X k , A 1 … A L = vec N k , A 1 … A L
    (56)

    where vec N A 1 … A L ,vec N k , A 1 … A L ∼CN 0 , σ 2 I I 1 … I p .

  • The problem is then to detect a signal vec( S A 1 … A L ) corrupted by a white noise vec( N A 1 … A L ). Since α and σ are unknown, the adaptive normalized matched filter introduced in [30] can be applied:

    Λ A 1 … A L = | < vec S A 1 … A L , vec X A 1 … A L > | 2 < vec S A 1 … A L , vec S A 1 … A L > < vec X A 1 … A L , vec X A 1 … A L > .
    (57)

  • Finally, the proposition is proven by applying the operator v e c−1.

References

  1. 1.

    Boizard M, Ginolhac G, Pascal F, Forster P: A new tool for multidimensional low-rank STAP filter: cross HOSVDs. In Proceedings of EUSIPCO. Bucharest,, Romania; September 2012.

  2. 2.

    Kolda T, Bader B: Tensor decompositions and applications. SIAM Rev 2009, 51: 455-500. 10.1137/07070111X

  3. 3.

    Lathauwer LD, Moor BD, Vandewalle J: A multilinear singular value decomposition. SIAM J. Matrix Anal. Apl 2000, 24(4):1253-1278.

  4. 4.

    Harshman RA: Foundation of the PARAFAC procedure: model and conditions for an explanatory multi-mode factor analysis. UCLA Working Pap. Phon 1970, 16: 1-84.

  5. 5.

    Sidiropoulos ND, Bro R, Giannakis GB: Parallel factor analysis in sensor array processing. IEEE Trans. Proc. Sig. Proc 2000, 48(8):2377-2388. 10.1109/78.852018

  6. 6.

    Sidiropoulos ND, Bro R, Giannakis GB: Blind PARAFAC receivers for DS-CDMA systems. IEEE Trans. Proc. Sig. Proc 2000, 48(3):810-823. 10.1109/78.824675

  7. 7.

    de Almeida ALF, Favier G, Mota JCM: Constrained Tucker-3 model for blind beamforming. Elsevier Signal Process 2009, 89: 1240-1244. 10.1016/j.sigpro.2008.11.016

  8. 8.

    Favier G, da Costa MN, de Almeida ALF, Romano JMT: Tensor space time (TST) coding for MIMO wireless communication systems. Elsevier Signal Process 2012, 92: 1079-1092. 10.1016/j.sigpro.2011.10.021

  9. 9.

    Tucker LR: Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31: 279-311. 10.1007/BF02289464

  10. 10.

    Kirsteins I, Tufts D: Adaptive detection using a low rank approximation to a data matrix. IEEE Trans. Aero. Elec. Syst 1994, 30: 55-67. 10.1109/7.250406

  11. 11.

    Haimovich A: Asymptotic distribution of the conditional signal-to-noise ratio in an eigenanalysis-based adaptive array. IEEE Trans. Aero. Elec. Syst 1997, 33: 988-997.

  12. 12.

    Comon P: Tensors : a brief introduction. IEEE Signal Process. Mag 2014, 31(3):44-53.

  13. 13.

    Lathauwer LD: Decompositions of a higher-order tensor in block terms- part I: lemmas for partitioned matrices. SIAM J. Matrix Anal. Apl 2008, 30(3):1022-1032. 10.1137/060661685

  14. 14.

    Muti D, Bourennane S: Multidimensional filtering based on a tensor approach. Elsevier Signal Process 2005, 85: 2338-2353. 10.1016/j.sigpro.2004.11.029

  15. 15.

    Bihan NL, Ginolhac G: Three-mode data set analysis using higher order subspace method: application to sonar and seismo-acoustic signal processing. Elsevier Signal Process 2004, 84(5):919-942. 10.1016/j.sigpro.2004.02.003

  16. 16.

    Haardt M, Roemer F, Galdo GD: Higher-order SVD-based subspace estimation to improve the parameter estimation accuracy in multidimensionnal harmonic retrieval problems. IEEE Trans. Proc. Sig. Proc 2008, 56(7):3198-3213.

  17. 17.

    Lathauwer LD, Moor BD, Vandewalle J: Independent component analysis and (simultaneous) third-order tensor diagonalization. IEEE Trans. Sig. Proc 2001, 49: 2262-2271. 10.1109/78.950782

  18. 18.

    Vasilescu MAO, Terzopoulos D: Multilinear subspace analysis of image ensembles. Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition June 2003.

  19. 19.

    Salmi J, Richter A, Koivunen V: Sequential unfolding SVD for tensors with applications in array signal processing. IEEE Trans. Sig. Proc 2009, 57(12):4719-4733.

  20. 20.

    Ward J: Space-time adaptive processing for airborne radar. Technical report Lincoln Lab., MIT, Lexington, Mass., USA (December 1994)

  21. 21.

    Brennan LE, Staudaher FM: Subclutter visibility demonstration. Technical report RL-TR-92-21, Adaptive Sensors Incorporated (March 1992)

  22. 22.

    Showman G, Melvin W, Belenkii M: Performance evaluation of two polarimetric STAP architectures. Proc. of the IEEE Int. Radar Conf May 2003, 59-65.

  23. 23.

    Mecca VF, Ramakrishnan D, Krolik JL: MIMO radar space-time adaptive processing for multipath clutter mitigation. Fourth IEEE Workshop On Sensor Array and Multichannel Processing, 2006 July 2006, 249-253.

  24. 24.

    Chen CY, Vaidyanathan PP: A subspace method for MIMO radar space-time adaptive processing. In IEEE International Conference on ICASSP 2007. Honolulu, Hawaii, USA; 2007:925-928.

  25. 25.

    Chen CY, Vaidyanathani PP: MIMO radar space-time adaptive processing using prolate spheroidal wave functions. IEEE Trans. Sig. Proc 2008, 56(2):623-635.

  26. 26.

    Fa R, de Lamare RC, Clarke P: Reduced-rank STAP for MIMO radar based on joint iterative optimization of knowledge-aided adaptive filters. 2009 Conference Record of the Forty-Third Asilomar Conference On Signals, Systems and Computers 496-500.

  27. 27.

    Lathauwer LD, Moor BD, Vandewalle J: On the best rank-1 and rank- ( r1, r2,..., r n ) approximation and applications of higher-order tensors. SIAM J. Matrix Anal. Apl 2000, 21(4):1324-1342. 10.1137/S0895479898346995

  28. 28.

    Miron S, Bihan NL, Mars J: Vector-sensor MUSIC for polarized seismic sources localization. EURASIP J. Adv. Signal Process 2005, 2005: 74-84. 10.1155/ASP.2005.74

  29. 29.

    Reed IS, Mallett JD, Brennan LE: Rapid convergence rate in adaptive arrays. IEEE Trans. Aero. Elec. Syst 1974, AES-10(6):853-863.

  30. 30.

    Scharf LL, Friedlander B: Matched subspace detector. IEEE Trans. Sig. Proc 1994, 42(8):2146-2157. 10.1109/78.301849

  31. 31.

    Rangaswamy M, Lin FC, Gerlach KR: Robust adaptive signal processing methods for heterogeneous radar clutter scenarios. Elsevier Signal Process 84: 2004.

  32. 32.

    Lathauwer LD: Decompositions of a higher-order tensor in block terms- part II definitions and uniqueness. SIAM J. Matrix Anal. Apl 2008, 30(3):1033-1066. 10.1137/070690729

  33. 33.

    Lathauwer LD, Nion D: Decompositions of a higher-order tensor in block terms - part III: alternating least squares algorithms. SIAM J. Matrix Anal. Apl 2008, 30(3):1067-1083. 10.1137/070690730

  34. 34.

    Ginolhac G, Forster P, Pascal F, Ovarlez JP: Performance of two low-rank STAP filters in a heterogeneous noise. IEEE Trans. Signal Process 2013, 61: 57-61.

  35. 35.

    Brennan LE, Reed LS: Theory of adaptive radar. IEEE Trans. Aero. Elec. Syst 1973, 9(2):237-252.

Download references

Author information

Affiliations

  1. SATIE, ENS Cachan, 61, av President Wilson, Cachan, 94230, France
    • Maxime Boizard
    •  & Philippe Forster
  2. SONDRA, Supelec, 3 rue Joliot-Curie, Gif-sur-Yvette, 91192, France
    • Maxime Boizard
    •  & Fréderic Pascal
  3. LISTIC - Polytech Annecy-Chambéry, 5, chemin de Bellevue, Annecy le Vieux, 74944, France
    • Guillaume Ginolhac
Authors
  1. Maxime Boizard
    View author publications
    You can also search for this author in
  2. Guillaume Ginolhac
    View author publications
    You can also search for this author in
  3. Fréderic Pascal
    View author publications
    You can also search for this author in
  4. Philippe Forster
    View author publications
    You can also search for this author in

Corresponding author

Correspondence to Maxime Boizard.

Additional information

Competing interests

The authors declare that they have no competing interests.

Authors’ original submitted files for images

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Boizard, M., Ginolhac, G., Pascal, F. et al. Low-rank filter and detector for multidimensional data based on an alternative unfolding HOSVD: application to polarimetric STAP. EURASIP J. Adv. Signal Process. 2014, 119 (2014). https://doi.org/10.1186/1687-6180-2014-119

Download citation

Keywords

  • Multilinear algebra
  • HOSVD
  • Low-rank approximation
  • STAP
  • Low-rank filter
  • Low-rank detector