Digital image watermarking: its formal model, fundamental properties and possible attacks

Hussain Nyeem; Wageeh Boles; Colin Boyd

doi:10.1186/1687-6180-2014-135

Research
Open Access

Digital image watermarking: its formal model, fundamental properties and possible attacks

Hussain Nyeem¹Email author,
Wageeh Boles² and
Colin Boyd^{2, 3}

EURASIP Journal on Advances in Signal Processing20142014:135

https://doi.org/10.1186/1687-6180-2014-135

Received: 6 November 2013
Accepted: 6 August 2014
Published: 29 August 2014

Abstract

While formal definitions and security proofs are well established in some fields like cryptography and steganography, they are not as evident in digital watermarking research. A systematic development of watermarking schemes is desirable, but at present, their development is usually informal, ad hoc, and omits the complete realization of application scenarios. This practice not only hinders the choice and use of a suitable scheme for a watermarking application, but also leads to debate about the state-of-the-art for different watermarking applications. With a view to the systematic development of watermarking schemes, we present a formal generic model for digital image watermarking. Considering possible inputs, outputs, and component functions, the initial construction of a basic watermarking model is developed further to incorporate the use of keys. On the basis of our proposed model, fundamental watermarking properties are defined and their importance exemplified for different image applications. We also define a set of possible attacks using our model showing different winning scenarios depending on the adversary capabilities. It is envisaged that with a proper consideration of watermarking properties and adversary actions in different image applications, use of the proposed model would allow a unified treatment of all practically meaningful variants of watermarking schemes.

Keywords

Digital watermarking
Data protection
Image watermarking
Watermarking model

1 Introduction

Digital watermarking - a data hiding technology - has already justified its suitability for different multimedia applications. Watermarking generally operates on different digital media or cover objects (e.g., image, audio, video) and is considered to have three major components [1, 2]: watermark generation, embedding, and detection. Watermark generation yields the desired watermark, which can optionally depend on some keys. The generated watermark is embedded into the cover object by the watermark embedding, sometimes based on an embedding key. During detection, the embedded watermark in a cover object is extracted and verified. The basic realization of watermarking may be valid for other multimedia applications; however, we restrict our attention in this paper only to the digital image applications.

An image watermarking application may have different objectives, which determine the necessary watermarking properties for that application. Those objectives can be classified into two types: (i) security objectives (i.e., to achieve certain security properties such as integrity of the watermarked image) and (ii) non-security objectives (e.g., annotation for an efficient image-database management). Achieving these objectives requires determining and considering the necessary properties of the individual watermarking components. The watermark generation and embedding properties generally include visibility, blindness, embedding capacity, and perceptual similarity. Similarly, blindness, robustness, error probability, etc are studied for watermark detection. (We formally define these properties later in section 4. Until then, inverted commas are used to refer to them for their abstract meaning.) A general consideration of these properties, however, is more than difficult for the diverse requirements of the applications. Consequently, without a proper consideration of the properties and the application scenarios, various watermarking schemes are being developed and evaluated.

Proper consideration of watermarking properties and application scenarios, on the other hand, is highly critical for the development and use of a watermarking scheme. A loose consideration of the properties may affect the overall watermarking performance. Similarly, an improper realization of an application scenario may leave security vulnerabilities. For example, if the development (i.e., design and evaluation) of a scheme is motivated by the high embedding capacity and high perceptual similarity requirements (and thus ignores the other properties), the scheme may eventually require high embedding time. On the other hand, in an image content authentication application, if the scenario is not considered properly (e.g., a watermark is generated without considering the required properties such as ‘collision resistance’ property), the scheme can have security flaws and may not be reliable in practice [3]. Therefore, a systematic development of watermarking schemes is essential.

A systematic development means to have mathematical formalism and operation determination for watermarking schemes. Here, operation determination helps identify the objectives and properties of a watermarking scheme with their explicit consideration for an application scenario, and mathematical formalism is used to specify them. An informal study of watermarking is easier to grasp first, but its formal study is desirable since formalism has several benefits: (i) the potential to provide rigorous analysis of the required watermarking properties, (ii) the completeness for resolving ambiguities and misconceptions, and (iii) the readiness for supporting a computer-aided fashion of analysis.

However, the present development of watermarking schemes is rather informal, ad hoc, and usually omits the realization of the application scenarios as mentioned above. This practice not only hinders watermarking applications from choosing a suitable scheme, but also leads to debate about the state-of-the-art for different watermarking applications. Addressing this problem requires a complete generic model with well-defined properties of digital watermarking as a basis for its formal study. Since watermarking may also need to achieve various security properties (along with any non-security objectives), the expected adversary capabilities must also be considered.

In support of a systematic development (i.e., design and evaluation) of the watermarking schemes, in this paper, we aim at developing a formal generic model of digital image watermarking. A generic and formally defined watermarking model gives the big picture of watermarking and helps identify all of its possible variants for different (image, video, etc.) applications. In other words, by determining the required (watermarking) inputs, outputs, and properties for different objectives, this model helps characterize a watermarking scheme. Using the proposed model, we seek to define a set of watermarking properties based on the application requirements. The proposed model also helps thorough analysis of watermarking schemes. An incomplete model here may lead to an inadequate computational analysis of a scheme resulting in various technical flaws and protocol weaknesses, which can be exploited later by an adversary. To this end, we also study a set of possible attacks to show the winning conditions for an adversary in different scenarios.

This paper is organized as follows: Section 2 reviews the relevant literature addressing the need for a formal generic watermarking model. Section 3 presents the construction of a formal generic watermarking model. In section 4, the systematic definition of necessary properties are given with examples to demonstrate their technical use in digital image applications. Section 5 explains different security aspects of the model providing with the common attack models. The conclusions are given in section 6.

2 Related work

The construction of an appropriate general model is a fundamental need for watermarking as discussed in previous section. However, only a few relevant research covers the adjoining fields of steganography and data-hiding [1, 4–15]. In this section, we briefly review different models proposed for watermarking (or its adjoining fields) and thoroughly consider a set of selected criteria to study them. Considering objectives, inputs-outputs, component functions, and underlying theory, we briefly overview those models below. We also summarize our findings in Table 1.

Table 1

Summary of the models used in relevant studies

Models in use	Objectives	Inputs and outputs	Component functions	Underlying theory	Limitations
Jian and Koch et al. [5]	To describe digital watermarking schemes	Original data	Embedding (bit-carrier selector, bit-noise generator, bit-carrier modifier)	Steganography	Limited consideration of the inputs, outputs, component-functions, and watermarking properties for image applications
		Watermarked data	Extraction (bit-carrier selector, bit-pattern matching)	Spread-spectrum communications	Limited to spread-spectrum communication-based watermarking schemes
		Degraded data (as a copy of watermarked data)		Signal processing
		Identification code (as watermark)
O’Sullivan et al. [8]	To determine the optimal hiding strategy, where watermarking is considered as a game between an attacker and information hider	Input and output data (e.g., images, audio, etc as a vector)	Encoder	Information theory	Limited consideration of the image application scenarios, inputs, outputs, component-functions, and watermarking properties
		Message (as watermark)	Decoder	Steganography
Cox et al. [11]	To examine the similarities between watermarking and traditional communication models	Cover data (as a vector)	Perceptual distance function	Spread-spectrum communications	Limited consideration of image application scenarios (e.g., that use only spread-spectrum-based schemes), inputs, outputs, component functions, and watermarking properties
		Watermark message	Encoding function
		Watermarked cover data	Extraction function
			Mixing function
Petitcolas et al. [4]	To illustrate a simplified case of watermarking concept	Mark (as fingerpring or watermark)	Embedding	Information hiding	Limited consideration of inputs, outputs, and components
		Stego image	Recovery		May not be useful to study image watermarking schemes rigorously
		Marked image
Cohen and Lapidoth [9]	To compute the coding capacity of the watermarking game for a Gaussian cover text and squared mean error distortions	Cover text	Encoder	Game theory	Limited consideration of inputs, outputs, and components
		Message	Decoder	Information theory	Watermarking is considered as a game in a copyright application scenario
		Stego-text
		Secret key
Adelsbach et al. [12]	To analyse security of watermarking schemes against protocol attacks (e.g., copy, ambiguity attacks)	Unwatermarked object	Key generation	Cryptography	Limited consideration of inputs, outputs, and components
		Watermarked object	Embedding		Application scenarios are limited to dispute resolving protocols
		Watermark	Detection
		Key
Barni et al. [13]	To provide a general security framework for robust watermark	Original content	Embedding (feature extraction and mixing, watermark generation)	Information theory	The concept of fair and unfair attacks may not be realistic
		Watermark	Decoding	Cryptography	Limited consideration of inputs, outputs, and components (e.g., what original content includes)
		Watermarked content		Signal processing
		Key (for embedding and detection)
Li et al. [1]	To illustrate the formulation of the security definitions and the attacker models	Original and watermarked work (as a vector)	Watermark generation	Data hiding	Limited consideration of inputs and outputs
		Watermark (as bit sequence)	Watermark embedding	Cryptography	The model represents only a simplified case of watermarking
			Watermark detector	Signal processing
			Perceptual distance function
Moulin and O’Sullivan [15]	To evaluate hiding capacity in an optimal attack context (as a data-hiding game)	Host-data (image, audio, video, etc.)	Encoder	Information theory	Limited consideration of inputs, outputs, and component functions (e.g., inputs and outputs are not conventional for watermarking)
		Message	Decoder	Data-hiding
		Side information		Game theory
		Composite data (contains hidden message)
Mittelholzer [6]	To characterize embedding process and attacked stego image (for analyzing secrecy and robustness in terms of mutual information)	Cover data	Stego encoder	Information theory	Limited consideration of inputs, outputs, and component functions
		Key	Stego channel	Steganography	More related to steganography schemes
		Secret message	Stego decoder
Cachin [10]	To quantify steganographic security	Cover text	Key generation	Information theory	Limited consideration of inputs, outputs, and component functions
		Stego text	Embedding	Steganography	More related to steganography schemes
		Secret key	Extraction		Limited to the passive attack scenarios
Adelsbach et al. [7]	To formalize robustness considered as a core security property, of watermarking	Cover data	Key generation	Cryptography	Limited consideration of inputs, outputs, and component functions
		Stego data	Embedding	Limited to robust watermarking schemes
		Watermark	Detection
		Key (for embedding and detection)
		Secret parameter (used as key generation input)

Jian and Koch [5] presented a model for the abstraction of digital watermarking schemes. From the steganography and spread spectrum communication concepts, that model provides a common basis for performance evaluation of some earlier schemes. However, the inputs and outputs are incomplete for a general watermarking scenario. For example, a watermark is not clearly defined and considered as an identification code using bit-noise - the bit-stream of noise-like signals. Therefore, analyzing various security issues (e.g., vector quantization attacks [16] arising from an input image independent watermark generation), and abstraction of new schemes (which are not spread-spectrum communication based) may require a further development of that model.

In the prominent work [4], Petitcolas et al. illustrated a digital watermark embedding and recovery model from an information-hiding viewpoint. To give an overview of the technique, a simplified data-hiding scenario is considered, and thus, any formal definition of the inputs, outputs, and component functions are omitted. The model, therefore, remains limited to describe a watermarking scheme in a more complete sense. For example, how the watermarking key and/or the mark (which represents either a fingerprint - hidden serial number, or a watermark - hidden copyright message) is chosen/generated needs to be explicitly defined.

In order to analyse watermarking as a classical communication system for digital multimedia data, Cox et al. [11] presented a generic communication model of watermarking. In that model, individual vectors generalize cover data and distortion. Distortion is assumed to be additive, and a real valued function is considered to measure perceptual distance between content vectors. That model is suitable to describe an optimal embedding scheme that embeds a watermark with its largest possible size (in bits) to offer the highest possible detection ability. There may be some variants of such an embedding scheme (depending upon different watermarking properties like ‘blindness’, ‘robustness’, etc). that can also be described using that model (by defining the functions in different ways). However, that model may not help to define and analyse an image watermarking scheme completely, because of its limited consideration of the inputs, outputs, and/or use of keys, in some application scenarios (e.g., authentication, tampering detection and recovery, etc.).

Mittelholzer [6] demonstrated a theoretical model to define a case of the embedding process and malicious modification, of a stego message. The embedding process considers hiding a secret stego message (as watermark), and thus mainly aims at achieving confidentiality and robustness properties in terms of mutual information. That model provides a theoretical basis for designing some watermarking schemes, for example, where the cover images have statistically Gaussian components. The model, however, may not be able to address many other watermarking properties due to limited considerations of the inputs, outputs and component functions. For example, the ‘blindness’ property that helps determine the requirements of other inputs (different from the input image and watermark), which are not considered in the model.

Following a thorough security analysis, Li et al. [1] referred to a general watermarking model. Unlike many other models, that model considers the basic component functions more completely using the signal processing paradigm. It also allows a more structured approach to define various threat models. However, the model still has limited specifications of the inputs and outputs of its components. For example, a watermarking scheme may have other inputs (in addition to the input image and other multimedia signal referred to as work) to generate the watermark, which are not present in the model. As a result, it represents only a simplified case of watermarking and may not help realize the overall scenarios completely for the security or other watermarking requirements.

Barni et al. [13] presented a watermarking model to generally tackle the security analysis using an attack classification inspired by cryptographic models. Their model includes two main functions: watermark embedding and decoding. The embedding function has three steps: feature extraction from the original content, watermark generation from the message using a key, and feature mixing with the watermark. The decoding function decodes the hidden message from watermarked version using a decoding key. This realization indeed presents a basic watermarking application scenario. However, a more complete set of inputs and outputs, and the separation of functions (for example, separating watermark generation from embedding, and message decoding from watermark detection) may help describe a watermarking scheme with more insights for a broader application scenario. Besides, although modelling the watermark as a game is compelling for the security analysis, the concept of fair and unfair attacks may not be realistic.

Watermarking has also been studied [8, 9, 14, 15] using the formal concepts of game theory and information theory. O’Sullivan et al. [8] suggested watermarking can be defined as a game played between an information hider and an adversary. The attacker and information hider scenarios are further studied for watermarking [9, 14]. Later, Moulin and O’Sullivan [15] formalized a distortion function, watermarking code, and attack channel. The main limitation of the models used to demonstrate the game scenarios in those studies is that they only represent a set of cases of watermarking. Such an approach of defining a model can help address particular problems for an application, but may not be able to represent the overall watermarking scenario (which is required to develop a unified watermarking theory). In other studies [7, 12], watermarking models are used as an abstraction of security proofs.

The different models, discussed so far, are mainly established for different digital media and to individually describe and analyse different watermarking schemes. In other words, those models are not general in the sense that neither of them would be sufficient to study most of the digital image watermarking schemes available in the literature. Some of them are influenced by the underlying concept of steganography [5, 6, 8, 10], cryptography [1, 7, 12, 13], information theory [6, 8–10, 15], or spread-spectrum communication [11]. In many cases [4–7, 12, 13], a key is used but their respective properties are not clearly defined, especially in achieving a specific security property. Watermark generation and its general inputs-outputs are not considered in most of them [4–7, 12]. A few researchers [5–7, 11] define necessary properties for their model, while others do not. All the above-mentioned models are mainly motivated by the ‘robust’ watermarking scenarios (e.g., copyright protection), where unauthorized removal is of core interest. Moreover, the models studied so far are mostly incomplete to be a generic model in terms of (i) considering the inputs, outputs, and basic components, (ii) defining necessary properties, and/or (iii) realizing the application scenarios. We therefore conclude that despite having a basic need for it, a formal generic image watermarking model is still lacking.

In our earlier work [2], we introduced a formal generic watermarking model for image applications addressing a gap in watermarking literature. We explored the need for the watermarking model and showed some uses of the model to define a few watermarking properties and attacks. In another follow-up work [3], we have also presented the use of the model in describing and analysing security of specific watermarking schemes, where we have shown how these schemes are violating the systematic definition of security. This paper, however, aims at incorporating further clarification and improvements on the constructions and definitions of the model and its uses. We consider here a relatively complete set of fundamental properties and wide range of application scenarios for digital images. With the aid of some practical examples, we also show the uses of the properties addressing a few hidden assumptions in current practice. Further, the set of expected adversaries are reconsidered to show how they can win with a particular attack. In the following sections, the main contributions are presented in three parts: (i) a formal watermarking model (section 3), (ii) definitions and uses of fundamental properties (section 4), and (iii) possible attacks on the watermarking security (section 5).

3 A formal generic watermarking model

There are a number of benefits of a formal generic watermarking model. As discussed in section 1, a formal watermarking model is the first step towards conceptualizing, systematic development, and evaluation of the watermarking schemes. It helps avoid any confusion and misconceptions by defining the necessary inputs, outputs, and component functions of a watermarking scheme. The watermarking schemes described using a formal model offer the readiness for implementation and computer-aided fashion of analysis. The required properties and design criteria of a watermarking application can also be defined by the model, which helps characterize a watermarking scheme for the application. The model also provides a means for defining attack models and thus for carrying out a rigorous analysis of a watermarking scheme. Moreover, a formal watermarking model creates a common platform for all possible watermarking schemes. Such a platform is expected not only to give a designer sufficient flexibility to describe any watermarking scheme, but also to help others understand the scheme in a systematic way.

In this section, we present a construction of a formal generic watermarking model in two stages, namely the basic model and the key-based model. The challenge here is to consider a ‘complete’ set of watermarking inputs, outputs, and component functions in general from their specific information domains and function families. However, the problem can be reduced to a watermarking application(s), where a set of ‘possible’ inputs, outputs and component functions can be defined in general to capture the fundamental properties of prominent schemes proposed today for the application(s). We therefore narrow down our scope to only the watermarking applications in digital images, and start constructing a basic model with considering the possible watermarking inputs, outputs, component functions used in the applications. Later, a key-based model is developed by incorporating keys to the basic model for completeness. This would allow a designer to achieve any required security properties (e.g., authentication, confidentiality) and to employ any suitable cryptographic technique as a building block in a watermarking scheme.

3.1 Construction of a basic model

A basic model, as it implies, is expected to represent a basic scenario for the image watermarking applications. We firstly identify the fundamental components and their possible inputs and outputs of a watermarking scheme. Irrespective of the system and security requirements, a watermarking scheme can have three fundamental components as mentioned in section 1 and shown in Figure 1. In order for their systematic definition, we consider three functions: watermark generation, G (·), embedding, E (·), and detection, D (·), and define their possible inputs and outputs as shown in Table 2. The primary roles of these functions in an image watermarking application are described below. To denote different data (e.g., inputs and outputs) within this context, in what follows, plain letters indicate the original versions, and respective single-bar letters and tilde letters indicate their watermarked and estimated versions accordingly.

Figure 1
**Fundamental components of (digital) image watermarking: (a) watermark generation, (b) watermark embedding, and (c) watermark detection.**

Table 2

Components of a basic watermarking model

Components	Inputs	Outputs
Watermark	Image data, i	Watermark, w
generation, G(·)
	Message, m
	Other image data,
	(j:j≠i)
Watermark	Image data, i	Watermarked image data, ī
embedding, E(·)
	Watermark, w
Watermark	Watermarked image	$\{\begin{array}{l} Estimated imagedata, ĩ \\ Estimated message, \tilde{m} \\ Estimated other image data, \tilde{j} \end{array}$
detection, D(·)	data, ī
	Image data, i
	Watermark, w	or, failure, ⊥

Watermark generation, G(·)

This function generates a suitable watermark according to the watermarking objectives in an application. In a simple data-hiding application, a watermark can be the embedding-data (e.g., message, m, other image data, j) itself (along with any side information). In an advanced application, a watermark may require to have certain properties (depending upon the watermarking objectives). For example, in a copyright protection application, a watermark may need to be ‘robust’ against certain processing techniques and/or attacks. (We will discuss the ‘robustness’ property in detail in section 4.5). Failure to consider those properties may result in technical flaws and security vulnerabilities. Although watermark generation is mainly constrained by the required properties, it starts with necessary inputs and their properties. For an image application, the generation function, G(·), can take image data, i, and message, m and/or other image data, j as input, and outputs a watermark, w.

Watermark embedding, E(·)

As the data-hiding component, watermark embedding function considers where and how to embed the watermark satisfying various requirements of the cover objects (here, digital images). For example, ‘perceptual similarity’ requirements (that control which pixels can be modified to what extent) of medical images may limit the embedding region [17]. (We will discuss the ‘perceptual similarity’ property in detail in section 4.1.) There are different domains (e.g., spatial, transform) for embedding, which are computed directly from an input image. Embedding types may also be different (e.g., invisible, invertible or reversible, blind, etc. - will be discussed in section 4). Irrespective of the embedding region, domain and type, however, an embedding function E(·) can take a watermark, w and the original image data, i as input to output the watermarked image data, ī.

Watermark detection D(·)

This function helps make an objective decision (e.g., to declare whether the content is authentic) and/or initiate further actions (e.g., to extract the embedded data, to engage and retain users of the watermarked objects). In different application scenarios, the additional tasks may vary and depend on the binary decision (i.e, pass or fail). The basic idea is that D(·) extracts the embedded watermark and regenerates another version of the watermark, from the inputs. If the regenerated version matches the extracted version, a pass signal is returned. (The pass signal is considered to pass the parameters such as the valid watermark, the estimated image data, etc. to its dependent module that performs the additional tasks, which will be shown later in Figure 2.) Otherwise, a failure is output. The main constraints for this function thus can be the minimum error probabilities (e.g., false negative/positive rates) and computation time. Like the functions, G(·) and E(·), the internal design of D(·) can also vary, but it generally takes watermarked image data, ī, original image data, i and a watermark, w to yield either an estimated image data, ĩ, message

\tilde{m}

and other image data,

\tilde{j}

, or a failure, ⊥.

Figure 2
**Key-based digital watermarking model: (a) watermark encoding and (b) watermark decoding.**

Thus, a basic watermarking scheme for digital images can be defined as a 6-tuple

(I, M, W, G, E, D)

such that

(i)
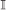, the image data space, is a set of tuples with value in the positive integers $Z^{+} = {| a | \geq 0 : a \in Z}$ . Each tuple is a set of coordinates, (x,y) for 2D space, or (x,y,z) for 3D space with $x, y, z \in Z^{+}$ . An element of image data space is called an image of a×b size for 2D space, and of a×b×c for 3D space, where a,b,c ∈ Z ⁺ and x={1,2,3⋯a}, y={1,2,3⋯b}, and z={1,2,3⋯c}. I,J,Ī, and ĩ are the subsets of 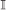, where
- I is the set of original unwatermarked image data;
- J is the set of other image data used for watermark generation and J∩I=ϕ;
- ī is the set of watermarked image data;
- ĩ is the set of estimated original image data;
- $\tilde{j}$
  is the set of estimated other image data.
(ii)

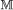is the plaintext space, and $W = {\{0, 1\}}^{+}$ is the watermark space. A message is a string of plaintext symbols. $M \subset M$ is the set of original messages, and $W \subset W$ is the set of original watermarks. $\tilde{M} \subset M$ and $\tilde{W} \subset W$ are the sets of respective estimates.
(iii)

G is a function G:I×M×J→W that is used for watermark generation.
(iv)

E is a function E:I×W→Ī that is used for watermark embedding.
(v)

D is a function $D : Ī \times I \times W \to Ĩ \times \tilde{M} \times \tilde{J} \cup \{⊥\}$ that is used for watermark detection, where ⊥ indicates a failure.
(vi)

a watermark w is valid if and only if it is obtained from valid inputs, (i,m,j) using the valid watermark generation function, G(·) such that, G(i,m,j)=w. Similarly, a watermarked image, ī ∈ Ī is valid if and only if E(i,w)=ī for valid inputs, (i,w) ∈ I×W. More formally, we can define a digital image watermarking scheme to be complete, if the following is true: for all (i,m,j) ∈ I×M×J there exists $(ĩ, \tilde{m}, \tilde{j}) \in Ĩ \times \tilde{M} \times \tilde{J}$ , where $ĩ \approx i, \tilde{j} \approx j$ , such that $D (E (i, G (i, m, j)), i, G (i, m, j)) = (ĩ, \tilde{m}, \tilde{j})$ . Here, the symbol ‘ ≈’ denotes the perceptual similarity between two images. For example, ĩ≈i implies that the perceptual content of i and ĩ are ‘sufficiently’ similar to each other. (For more complete definition of perceptual similarity property, see Definition 4.1.

It is worth noting here that we consider the original (unwatermarked) version of an image as the input image for the watermarking functions. In most cases, original images are used for watermarking. However, there may be cases where a (valid) watermarked version of an image can be used as an input image. For example, to update/re-embed a watermark in an existing watermarked image, one may need to use the present (or any earlier) watermarked version, rather than using the original image. It depends upon the application scenario which version of images are to be used (and how any restrictions on using them should be dealt with). However, this variation (in input image versions) can be studied as a special case of the proposed model, where the model may accept either an original image or its existing watermarked versions as an input. Therefore, we consider the fundamental scenario for the proposed model, where an (original) image is watermarked for the first time.

The construction of the above basic model is suitable for realizing a basic watermarking scenario, but it may not be sufficient to capture the recent watermarking advances. Although study of a complete watermarking model is still lacking, many advances are evident [18–22] in the present watermarking context. For example, the concepts of using keys and deploying cryptographic techniques are prominent in addressing different levels of security in various application scenarios such as content/owner authentication and copy control. Such developments help obtain the combined benefits from the fusion of data hiding and cryptographic techniques.

3.2 Towards a complete watermarking model

To adopt and generalize the use of keys, we extend the basic scenario to a key-based scenario. We assume two individual keys, generation key, g and embedding key, e for G and E, respectively. Although in our basic construction, for simplicity, D(·) is considered to perform the detection and extraction tasks inherently, this should naturally be split into separate functions for security reasons. We, therefore, separate the computation of extraction from D(·) using an additional function X(·), which we call the extraction function. Thus, an individual detection key, d and extraction key, x can be used as shown in Figure 3. These two functions, D(·) and X(·) can be further defined as sub-functions of watermark decoding (to resemble our earlier construction) as shown in Table 3. The other two functions, G(·) and E(·) can similarly be the sub-functions of watermark encoding. Figure 2 illustrates the watermark encoding and decoding processes.

Figure 3
**Deploying keys in the detection function of our basic model.**

Table 3

Components of a key-based watermarking model

Components		Inputs	Outputs
Key generation, K e y(·)		Image data, i	Generation key, g
		Message, m	Embedding key, e
		Other image data, (j:j≠i)	Detection key, d
			Extraction key, x
Watermark encoding	Generation, G(·)	Generation key, g	Watermark, w
		Image data, i
		Message, m
		Other image data, (j:j≠i)
	Embedding, E(·)	Embedding-key, e	Watermarked image-data, ī
		Image-data, i
		Watermark, w
Watermark decoding	Detection, D(·)	Detection-key, d	$\{\begin{array}{l} Estimated image data, ĩ \\ Estimated watermark, \tilde{w} \end{array}$
		Watermarked image data, ī
		Image data, i	or, failure, ⊥
		Watermark, w
	Extraction, X(·)	Extraction key, x	$\{\begin{array}{l} Estimated message, \tilde{m} \\ Estimated other image data, \tilde{j} \end{array}$
		Watermarked image data, $\bar{w}$
		Image data, i	or, failure, ⊥
		Estimated watermark, $\tilde{w}$

We note here that the outputs $(ĩ, \tilde{w})$ of D(·) and $(\tilde{m}, \tilde{j})$ of X(·) can be an exact estimate of their original versions respectively for a non-blind decoder (see Definition 4.3 for ‘blindness’ property). Here, exact estimates of (m,j) are obtainable at X(·) from an exact estimate of w as D(·) outputs. For a blind decoder, to get an exact estimate of the input image, original information (that is compromised for embedding) is required by D(·). This requirement leads to the construction of E as an invertible (or reversible) function, a major recent watermarking trend. (We discuss the ‘invertibility’ or ‘reversibility’ property later in section 4.4.) Further, how exactly ĩ, $\tilde{w}$ , $\tilde{m}$ and $\tilde{j}$ can be produced depends on how much error is allowed in their estimation - an error in estimating $\tilde{w}$ at D(·) propagates through to yielding $\tilde{m}$ and $\tilde{j}$ at X(·). However, $\tilde{w}$ and $\tilde{m}$ are defined as bit strings, and for any decoder (blind or non-blind), they should be an exact estimate except for a few bit errors that can be handled by error correction codes.Further, as shown in Figure 2b, the detection function in the watermark decoding invokes the extraction function, once the detection is completed. We note here that the detection function is executed independently and may only output a pass or fail signal depending upon the existence of a valid watermark. This also means that the extraction is not always required (depending upon the applications such as image content authentication). However, the extraction function can be performed after the detection, when required for the applications like image annotation, since extraction of the information carried by the watermark will make sense, only if the image is passed by the detection (e.g., ensuring the authenticity or integrity of the watermarked image).

We, therefore, develop the construction of a basic watermarking model (for digital images) further to incorporate the use of keys. We define here a key-based watermarking scheme as a 8-tuple

(I, M, W, K, G, E, D, X)

such that

(i)

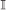I,J,Ī,Ĩ, and $\tilde{j}$ are subsets of . Definition for the image-data space, , the plain text space, 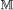, the watermark space, , and their respective subsets are the same as defined in the basic model of section 3.1.
(ii)

K is the set of all keys and a key is a sequence of m binary bits, where $m \in Z^{+}$ . Sets of watermark generation keys, K _g, embedding keys, K _e, extraction keys, K _x, and decoding keys, K _d are subsets of K (i.e., K _g⊂K, K _e⊂K, K _x⊂K, and K _d⊂K).
(iii)

G={G _g|g ∈ K _g} is a family of functions G _g:I×M×J→W that is used for watermark generation.
(iv)

E={E _e|e ∈ K _e} is a family of functions E _e:I×W→Ī that is used for watermark embedding.
(v)

D={D _d|d ∈ K _d} is a family of functions $D_{d} : Ī \times I \times W \to Ĩ \times \tilde{W} \cup \{⊥\}$ that is used for watermark detection.
(vi)

X={X _x|x ∈ K _x} is a family of functions $X_{x} : Ī \times I \times \tilde{W} \to \tilde{M} \times \tilde{J} \cup \{⊥\}$ that is used for watermark extraction.
(vii)

For each key, g ∈ K _g and e ∈ K _e there exists d ∈ K _d and x ∈ K _x respectively i.e., for all (i,m,j) ∈ I×M×J, there exists $(ĩ, \tilde{w}) \in Ĩ \times \tilde{W} | ĩ \approx i$ such that $D_{d} (E_{e} (i, G_{g} (i, m, j)), i, G_{g} (i, m, j)) = (ĩ, \tilde{w})$ , and for all $\tilde{w} \in \tilde{W}$ , there exists $(\tilde{m}, \tilde{j}) \in \tilde{M} \times \tilde{J} | \tilde{J} \approx j$ such that $X_{x} (E_{e} (i, G_{g} (i, m, j)), i, \tilde{w}) = (\tilde{m}, \tilde{j})$ .

At this point, we stress the properties of the keys that can differentiate between private and public watermarking schemes. We define a watermarking scheme as a private key (or simply private or symmetric) scheme if d=e, and x=g (i.e., if d and x can at least be easily computed from e and g, respectively). Otherwise, we call it a public key (or simply public or asymmetric) scheme if d≠e and x≠g, and if computing d and x from e and g is ‘computationally infeasible’ in practice respectively. The phrase ‘computationally infeasible’ follows the standard definition in cryptography. Here, d and x are the private keys and e and g are the public keys. Similar to the watermarking keys, watermarking itself has many properties that may lead to its many practically meaningful variants for different applications. Before discussing these properties, and defining them in section 4, we present below a comparative study in support of our above model.

3.3 A comparative study

In comparison with the summary of existing models (Table 1), we summarize the features of our proposed model in Table 4.

Table 4

Summary of the proposed model

Model in use	Objectives	Inputs & outputs	Component functions	Underlying theory	Limitations
Proposed	To provide a means for the systematic development, and thus to develop a unified and more realistic theory, of digital image watermarking	Image-data (with different properties, e.g., original, watermarked, etc, see Figure 2)	Key generation	Digital image and signal processing	May not be suitable for studying steganography schemes
		Watermark	Watermark generation	Cryptography
		Message	Watermark embedding
		Key (for each function)	Watermark detection
			Watermark extraction

As discussed in section 2, a common limitation is the narrow focus on a particular type of data hiding, steganography or watermarking scenario with different objectives, in developing a watermarking model. This leads to considering a simplified set of inputs, outputs and component functions. Although such a simplified and generalized model helps realize the application scenarios of some relevant schemes, in the formal watermarking context, they are incomplete and thus need to be re-defined to be used as a general model for image applications.

Our model addresses the major limitations of relevant models for studying image watermarking schemes. We believe that the proposed model is a first step towards a formalized conception of image watermarking, and allows a unified treatment of all its practically meaningful variants. Considering this, we also define a set of fundamental properties in following sections using our model to further strengthen the watermarking theory in the image application context.

4 Fundamental watermarking properties

Defining the properties of watermarking plays an important role in the systematic development of various schemes. For example, in developing a new scheme, the watermarking objectives determine a set of criteria (as discussed in section 1). Each criterion can be expressed in terms of the minimum requirements for a relevant watermarking property. In the design phase, those requirements help characterize the scheme (e.g., by setting constraints for the construction of watermarking functions). In the evaluation phase, measuring (with a suite of tests) how those requirements are fulfilled gives merit to the scheme. The relative importance of each property, thus, can be determined based on the application requirements. This also means that the interpretation and significance of watermarking properties can vary with the application. These properties, in practice, can be interpreted in terms of the inputs and outputs of watermarking components, use of keys, etc. They can also be mutually dependent, which requires a trade-off among the improvements in the properties [23] for an application.

In the image watermarking context, a number of defining properties (considering their relative importance) are studied below: perceptual similarity, visibility, blindness, invertibility, robustness, embedding capacity, error probabilities, and security. In the following sections, we formally define these properties using the developed watermarking model (section 3) and show how they can be interpreted and used in a real application scenario. To simplify reading, from now on, the notations are used without explicitly giving their domains. For example, ‘for all a,b,c,⋯’ will be used to mean ‘for all (a,b,c,⋯) ∈ A×B×C⋯’.

4.1 Perceptual similarity

The perceptual similarity (or imperceptibility) is one of the most important properties for the image applications. Since embedding distortion is inevitable, E exploits the (relatively) redundant information of an image intelligently for a minimum of visual artefacts. In almost any image application, therefore, keeping a watermarked image perceptually similar to the original image becomes an important criterion. Perceptual similarity means the perceptual contents of the two images are ‘sufficiently’ similar to each other, (and thus it is mainly studied for the invisible watermarking schemes; the ‘visibility’ property is discussed below). The requirements for this property may vary with the application scenario. In order to ease the problem of dealing with these varying requirements, we now define the perceptual similarity property using a quantitative approach.

Definition 4.1(Perceptual similarity).

Any two images, i₁ and i₂, are said to be (d,t)perceptually similar, if d_j(i₁,i₂)≤t_j for all similarity measures d_j ∈ d≡{d₁,d₂,⋯,d_n} and thresholds t_j ∈ t≡{t₁,t₂,⋯,t_n}.

Various measures are used to quantify the requirements for the perceptual similarity. For example, correlation quality (CQ), signal to noise ratio (SNR), peak or weighted SNR (PSNR or WPSNR), mean square error (MSE), structural similarity index (SSIM), mean or weighted SSIM (MSSIM or WSSIM), normalized cross-correlation (NCC), etc. However, no globally agreed and effective measures for visual quality currently exist [24]. In addition, not all the measures give the similar estimation. Therefore, we define perceptual similarity by defining a similarity measure, which is a set of n-suitable measures that help quantify the perceptual distance between two images. Now, we define two images to be perceptually similar (or imperceptible) for an acceptable value returned by all suitable measures defined for similarity.

As an example to use the above definition, we may consider two measures (i.e., n=2): PSNR and MSSIM, for the similarity measure, d such that d₁=PSNR and d₂=MSSIM. The given thresholds are t₁=60 (dB) and t₂=0.995. Two images i₁ and i₂ are said to be perceptually similar if both d₁(i₁,i₂)≥60 and d₂(i₁,i₂)≥0.995 are satisfied.

4.2 Visibility

A visible watermarking scheme deliberately inserts a watermark such that it appears noticeably on the watermarked image to show some necessary information such as company logo, icon, or courtesy. However, in order that the watermark does not become so strongly pronounced that it takes over the main image, the level of visibility can be controlled, for example, by a parameter α. Visible watermarks are important in recognition and support of possessing a digital image. In contrast, an invisible watermark is embedded by keeping the perceptual content of the watermarked images similar to that of the original images to address security problems in different application scenarios. Therefore, there are schemes which are either visible or invisible based on the appearance of watermark on the watermarked images.

Definition 4.2(Visibility).

A watermarking scheme is called visible or perceptible, if E(·) embeds a given watermark, w, into an image, i, such that the w appears at least noticeably in ī. That is, |E_e(i,w)−i|=α w for all i, w. Here, α is weight factor that controls the degree of visibility.

A watermarking scheme is called invisible or imperceptible, if E(·) embeds w into i such that the ī is perceptually similar to the original image, i. That is E_e(i,w)≈i for all i, w.

Although the visibility and perceptual similarity properties share some perceptual aspects of a watermarked image, they need not be confused with each other. As stated in Definition 4.1, the perceptual similarity property determines if an original image and its watermarked version remain ‘perceptually’ the same. On the other hand, Definition 4.2 states that a visible watermark appears on a watermarked image with a predefined degree of visibility, α, and thus strictly speaking for the visible watermarking, the watermarked image is not perceptually similar to the original image. Perceptual similarity property is thus studied for the invisible watermarking schemes

An invisible watermarking scheme usually differs from a visible watermarking scheme, not only in the visibility factor, but also in their embedding processes. Invisible embedding of a watermark aims at keeping the perceptual difference (resulting from the embedding distortion) at a ‘minimum’ level such that the watermarked and original images remain perceptually the same. Their perceptual similarity is verified by quantifying the perceptual difference using similarity measures. The commonly used similarity measures do not indicate any subjective quality degradation, rather they quantify the overall perceptual difference either by their local (e.g., block-wise or kernel-based) or global (e.g., whole image based) operations. As a result, the defined perceptual similarity does not directly indicate whether a watermarking scheme is visible or invisible. However, for an invisible watermarking scheme, the quantified perceptual difference between an original image and its watermarked version would naturally be much lower than that for a visible watermarking scheme.

In short, an invisible scheme may be considered a variant of visible watermarking with a ‘negligible’ (i.e., approaching zero) α, and having an additional (and even more strict) perceptual similarity requirement. Visible watermarking is present in a few applications such as video broadcasting. However, recent research is mainly focussed on invisible watermarking with a high perceptual similarity in various image applications [25–41].

4.3 Blindness

Another important watermarking property is blindness that helps characterize a scheme to be blind, non-blind, or semi-blind. The term blindness (or oblivious) is generally used in cryptography to define a detection process independent of any side information. More specifically, blindness is used to define a computational property of information retrieval (e.g., to define the computational independence on the original information or its derivatives to retrieve the required information). Similarly, blindness defines the detection and extraction process in digital watermarking, although there is no complete definition for a watermarking scheme to be blind or non-blind.

As a requirement for blindness, some schemes consider that no original input image and the information derived from the input image should be required, whereas other schemes consider only avoiding the original input requirement during the detection. Although schemes in both categories are often considered as blind, with a more strict blindness requirement, the schemes in the latter category may eventually fail to achieve the overall design requirements in an image application (e.g., image authentication). Additionally, confusion arises when a scheme is defined as semi-blind. Sometimes, it is considered that if the detection and extraction processes can operate objectively without the original image and its derived information, but still require the original watermark, then the scheme can be semi-blind.

Cox et al. [42] informally defined a blind or oblivious watermark detector in such a way that the detector does not require access to the original (i.e., unwatermarked) image, or some information derived from the original image. Otherwise, the detector is called non-blind or informed. However, their definition is not sufficient to realize three different cases associated with the blindness property. We define here (Definition 4.3) watermarking blindness to distinguish the dependency of D(·) and X(·) on any of the original input data that is used in G(·) and E(·), and thereby distinguish three different cases of this watermarking property.

Definition 4.3(Blindness).

A watermarking scheme is called blind ( or oblivious ) if both D(·) and X(·) are independent of the original image, i and watermark, w. Formally, for all images i₁,i₂ and watermarks w₁,w₂, hold both

\begin{array}{lcr} D_{d} (ī, i_{1}, w_{1}) = D_{d} (ī, i_{2}, w_{2}) \\ and X_{x} (ī, i_{1}, \tilde{w}) = X_{x} (ī, i_{2}, \tilde{w}) . \end{array}

A watermarking scheme is called semi-blind if either one of D(·) and X(·) is independent of i and/or w. Thus, for semi-blind watermarking, for all images i₁,i₂ and watermarks w₁,w₂ either

\begin{array}{lcr} D_{d} (ī, i_{1}, w_{1}) = D_{d} (ī, i_{2}, w_{2}) \\ and X_{x} (ī, i, \tilde{w}) \neq X_{x} (ī, i_{1}, \tilde{w}) \end{array}

or

\begin{array}{lcr} D_{d} (ī, i, w) \neq D_{d} (ī, i_{1}, w_{1}) \\ and X_{x} (ī, i_{1}, \tilde{w}) = X_{x} (ī, i_{2}, \tilde{w}) . \end{array}

Otherwise, a watermarking scheme is called non-blind ( or non-oblivious or informed ) if both of D(·) and X(·) are dependent on i and/or w. Thus, for all images i,i₁ and watermarks w,w₁, hold both

\begin{array}{lcr} D_{d} (ī, i, w) \neq D_{d} (ī, i_{1}, w_{1}) \\ and X_{x} (ī, i, \tilde{w}) \neq X_{x} (ī, i_{1}, \tilde{w}) . \end{array}

We note here that strictly speaking, the detection function D(·) and the extraction function X(·) must have all three inputs: ī, i, and w. However, for instances of blind and semi-blind watermarking, some inputs (e.g., i and w) are not used in D(·) and X(·), and thus, they can be optionally omitted.

It can also be noted that the blindness property, as defined in Definition 4.3 in terms of the watermark detection and extraction functions, can also be considered for the watermark generation function. A non-blind (ie, an original image dependent) G can be helpful in resisting copy attacks (that aims at counterfeiting the D(·) for any invalid modifications, or invalid watermarked images; see section 5.1.6 for the definition of copy attack). The blindness for D is also important, where availability of the original image, watermark or other side information at D(·) can thwart watermarking objectives. Blind and non-blind watermarking schemes are sometimes confused with private and public watermarking, respectively. However, we insist on defining a watermarking scheme to be private and public in terms of their keys (as defined in section 3.2) to avoid any confusion.

4.4 Invertibility

Invertibility (or reversibility or losslessness) is a computational property of watermarking. The meaning of this property is quite intuitive; however, we expect that defining invertibility in the current context would help realize its mutual relation with other properties. In an image application, invertibility is expected to restore any watermarked images to their original versions, where no embedding distortion is allowed in the original image. Such a watermarking criterion motivates construction of an invertible E that helps D(·) to reproduce an original image from the watermarked image [30, 32, 34, 38, 39, 43–60]. Here, we define an invertible watermarking scheme such that it allows inverse computation of E(·) during detection.

Definition 4.4(Invertibility)

A watermarking scheme is invertible ( or reversible or lossless) if the inverse of E is computationally feasible to compute and is used in D to estimate an exact original image, i, from the respective watermarked image, ī. Otherwise, the scheme is called non-invertible watermarking scheme.

From the above definition, if E_e(i,w)=ī, then for an invertible watermarking scheme, $E_{e}^{- 1}$ the detection must exist and satisfy $E_{e}^{- 1} (ī) = (i, w)$ . Therefore, such watermarking schemes can be either blind or a semi-blind (according to Definition 4.3). Since, in image applications, an invertible watermarking scheme is mainly designed to reverse the effect of embedding on the original image, the embedding function is only considered to define invertibility of the scheme. However, the concept of an invertible function can also be extended for X, if an invertible G(·) is computationally feasible.

4.5 Robustness

Robustness in watermarking is often confused with its meaning from cryptography [61]. A main reason is probably that watermarking has to consider some spatial or perceptual properties (e.g., perceptual similarity, visibility). Several attempts have been made to informally define the robustness property of watermarking. For example, Piper and Safavi-Naini [62] considered a watermarking scheme as robust if it can successfully detect the watermark in the ‘processed’ images. The strength of this definition depends on how the ‘processed’ image is defined. In contrast, Cox et al. [42] referred to robustness as the ability to detect the watermark after common signal processing techniques. More specifically, robustness can be defined as the degree of resistance of a watermarking scheme to modifications of the host signal due to either common signal processing techniques or operations devised specifically in order to render the watermark undetectable [63]. In summary, watermarking robustness has to deal with (i) defining a set of processing techniques, and (ii) the detection ability for the ‘processed’ images.

We now formalize the concept of watermarking robustness in terms of the processed images and the detection ability. Firstly, a set of processing techniques (i.e., various operations/transforms) is defined below to define a ‘processed’ image for an application. Here, the same set of processing techniques may not be valid for different watermarking applications, and thus a general consideration of the techniques may not be always useful. Secondly, a detection condition is defined as that which determines the detection ability, for the set of ‘processed’ images.

Definition 4.5(Processed image).

A processed image is an image that is not essentially perceptually similar to its original, but a certain amount of distortion, δ is incurred by a processing technique, p ∈ P. That is, if any image, $l \in I$ is processed by p then, for the processed image, p(l) the following is true: p(l)=l+δ. Here, P is the set of applicable processing techniques for an application such that $P \subset P$ , where is the space of processing techniques.

It is worth noting that, in our earlier work [2, 61], we aimed at avoiding any confusion between the robustness and security properties and considered that a processed image is not perceptually similar to its unprocessed version. That consideration was based on the assumption that only an adversary may want to process a valid watermarked image to achieve the perceptual similarity requirements. However, that assumption is not always valid in practice. For example, a watermarked image can be processed such as by lossless compression and file-format conversion, with the required perceptual similarity property (not only maliciously, but also intentionally as a system requirement). We, therefore, revise our earlier consideration for Definition 4.5 such that a processed image is not necessarily perceptually similar to its unprocessed version. We believe that this revision does not conflict with our earlier intention to avoid the confusion between robustness and security properties

With the Definition 4.5, now we may wish to define the detection condition for the robustness property. Suppose a processing technique, p ∈ P, causes distortion to a watermarked image, ī. As defined in our proposed model, D_d(·) accepts with the property $D_{d} (p (ī), i, w) = (ĩ, \tilde{w}) \cup ⊥$ for all p(ī),i,w|p(ī) ∈ Ī. Here, the pass that returns with $(ĩ, \tilde{w})$ and the failure, ⊥ can be used to define two potential variants, robust and fragile respectively, of watermarking schemes for different P. Another variant, semi-fragile watermarking scheme can also be defined considering a suitable subset of P. Thus, we define the robustness property in Definition 4.6 considering detection ability at three different levels

Definition 4.6(Robustness).

A watermarking scheme is defined for the following levels of robustness:

Robust. A watermarking scheme is called robust if $D_{d} (p (ī), i, w) = (ĩ, \tilde{w})$ for all p ∈ P.

Fragile. A watermarking scheme is called fragile if D_d(p(ī),i,w)=⊥ for all p ∈ P.

Semi-fragile. A watermarking scheme is called semi-fragile if $D_{d} (p (ī), i, w) = (ĩ, \tilde{w})$ for all p ∈ P₁ and D_d(p(ī),i,w) = ⊥ for all p ∈ (P∖P₁), where P₁⊂P.

As stated in Definition 4.6, a successful detection (i.e., D_d(·)≠⊥) is the basic criterion for a watermarking scheme to be robust to p ∈ P. However, there is no absolute robustness for watermarking, since taking all known/available processing techniques into consideration (for robustness) is not realistic. It is therefore reasonable to identify only the set of applicable processing techniques for the robustness requirements in an application (like knowing the set of potential adversaries for the security requirements in an application, see section 4.8 below). As Definition 4.6 suggests, we also stress that one must have an explicit consideration on P for design and evaluation of a watermarking scheme in a particular application scenario.

When we consider P (the set of applicable processing techniques), we may notice that different processing techniques (e.g., compression, de-noising) have different parameters (e.g., compression ratio, down sampling rate, type and rank of filter). These parameter settings give different strengths to a processing technique. Therefore, it is worth noting that considering a technique, p, means that p is defined with its all required parameter settings. The technique with other settings thus remains outside of P.

4.6 Embedding capacity

Embedding capacity (or simply capacity) is an important, and may be the most-studied, property for watermarking schemes. A lot of studies have reported recently on improving this property maintaining the required perceptual similarity in different ways [30, 32, 38, 39, 50–59]. A number of ways to estimate the steganographic/watermarking embedding capacity by using information theoretic and perceptual model-based methods and detection theory are also present in the literature [64–70]. Capacity estimation is a fundamental problem of steganography [69], where the question is how much data can safely be hidden without being detected? However, in watermarking, the primary constraint for the capacity is its mutual dependence on a few other properties (e.g., perceptual similarity, robustness) rather than the detection problem as in steganography. Therefore, we define watermarking capacity on the basis of perceptual similarity of (i,ī), for which the scheme works objectively (e.g., without a failure).

Definition 4.7(Embedding capacity).

Watermarking embedding capacity for an image, i is the maximum size of any watermark, w=G_g(i,m,j) for all m and j, to be embedded in i, such that E_e(i,w)≈i, $D_{d} (E_{e} (i, w), i, w) = (ĩ, \tilde{w})$ , and there exists $\tilde{m}, \tilde{j} | \tilde{j} \approx j$ such that $X_{x} (E_{e} (i, w), i, \tilde{w}) = (\tilde{m}, \tilde{j})$ .

Definition 4.7 suggests that to know the capacity of a watermarking scheme for an image, one needs to know how many bits can be embedded in the image with achieving the perceptual similarity and error probability (e.g., successful detection) requirements. This capacity estimation method may vary with the type of watermarking schemes. Although several attempts have already been made [64–70] to know the capacity bound as mentioned above, developing a general method for capacity estimation of each type of watermarking schemes could still be interesting. This may also help solve other capacity-related problems like the capacity control [50]

In image applications, embedding capacity is usually expressed as a ratio, bit-per-pixel (bpp). According to Definition 4.7, if the watermarking embedding capacity is n-bit, and the size of watermark is m-bit (i.e., w={1,0}^m), then the necessary condition for an invisible watermarking scheme is m<n. This condition suggests that there can be a hidden assumption of recursive embedding in developing an invisible scheme - if the required capacity is not achievable in first run of E(·), the remaining bits can be re-embedded recursively. That assumption may severely affect the performance of a watermarking scheme in practice, and thus needs to be explicitly stated, if applicable.

4.7 Error probability

Error probability is an important property that helps determine the reliability of a watermarking scheme in practice. Some of the important and commonly used measures of error probability are bit error rate (BER), false-positive rate (FPR), false-negative rate (FNR). However, this property is often disregarded in developing a watermarking scheme, assuming a reliable (operating) environment where communication errors are ‘negligible’ and can be managed, for example, by using a suitable error correction code. This assumption is useful to simplify the application scenarios, but for some applications (e.g., proof of ownership), this property needs to be studied explicitly.

For example, BER can be considered to evaluate the performance of the functions D(·) and X(·) in obtaining $(ĩ, \tilde{w})$ and $(\tilde{m}, \tilde{j})$ respectively. (Here, BER follows its standard definition in communication system.) In our proposed model, we defined D(·) in such a way that the absence of a valid watermark, w in a watermarked image, ī outputs a detection failure. Otherwise, D(·) returns $(ĩ, \tilde{w})$ , which indicates that the input image is watermarked. Following this, we define the false positive and false negative for our model below.

Definition 4.8(False positive and false negative)

A watermarking detection in a normal condition is said to be a false positive if D_d(i,w)≠⊥ for some i. Conversely, a watermarking detection is a false negative if D_d(ī,i,w)=⊥ for some ī. Here, the normal condition allows the scheme to run with all of its valid inputs, outputs and functions.

Irrespective of application scenarios, ideally, a zero FNR and FPR represents a reliable detection. Particularly, a watermarking scheme can be of no use if a scheme is unable to detect a valid watermark in normal condition of operation. Achieving a zero FNR and FPR in practice, however, may not be realistic for many reasons like communication errors. So, it is reasonable here to define a highly accurate detection for an application scenario in terms of a very low probability (e.g., in the order of 10⁻⁶) of detection failure.

However, error probability may be confused with other watermarking properties. Other properties (e.g., security, robustness, perceptual similarity) may also deal with errors, which can be of different types; for example, bit-errors (often termed as distortion) in a valid watermarked/unwatermarked image, which can be incurred maliciously, unintentionally, or as a system requirement, may also cause a detection failure. Further, we note that the function E(·) itself utilize the error signal, e.g., exploiting the redundant bit planes of an image, for embedding. This embedding error can be considered as a system requirement and thus can be addressed in terms of perceptual similarity requirement. Specifically, while error probability measures can be used to determine the system error rate for the reliability of a watermarking scheme, the other perceptual errors (ie, distortion) can be studied in terms of the security, robustness and perceptual similarity properties.

4.8 Security

Security property of watermarking schemes as a whole may be far from easy to conceptualize (and may not be always necessary in practice) [71–73]. Two main possible reasons are (i) application-dependent properties and (ii) the confusion between security and robustness requirements. In practice, different image applications may require different levels of security. Some applications do not need to be secure at all since there is no ultimate benefit in circumvention of watermarking objectives. For example, where a watermark is used only to add value in which they are embedded rather than to restrict uses for some device control applications [42]. Therefore, these types of watermarks do not need to be secure against any hostile attacks, although they still need to be robust against common processing techniques used in those applications. (This is how we defined the robustness property in Definition 4.6.) Although the requirements for robustness and security properties of a watermarking scheme may overlap [61], they need to be considered separately. For security properties, in contrast to robustness, all possible attacks that an adversary may attempt with in a particular scenario are to be studied.

Definition 4.9(Security)

A watermarking scheme is called –secure if the scheme retains the security against the attack ( ie, if it is ‘hard’ to succeed with the set of adversary actions mounted by the attack ).

An application-specific analytical approach is often considered to study watermarking security [3, 16, 74–80]. In a broad sense, this practice suggests that the security property can be studied for two main types of watermarking schemes: robust and fragile. However, instead of focusing on a specific type of watermarking schemes, in this paper (section 5), we are more interested in studying the general scenarios of a set of possible attacks in an abstract level for image applications. The main idea is to demonstrate how an adversary of different capabilities may win with different conditions. We call this a win condition. Knowing the inputs, outputs and the win conditions would eventually help visualize the possible attacks in an application. (With that visualization, conducting an application-specific security analysis can be easier and more efficient). Here, we consider that identifying the set of attacks in a specific application and defining them in the model are the first steps to defining the watermarking security.

5 Attacks on the watermarking security

In the watermarking context, an attack can be roughly defined as any malicious attempt to perform unauthorized embedding, removal, or detection of a (valid or invalid) watermark. An adversary that makes such attempts can be of different capabilities (e.g., can have different inputs, and access to the watermarking functions). In practice, it is quite reasonable to assume the capabilities of expected adversaries in modelling attacks. For example, an adversary knowing nothing may assume an image is watermarked and may want to remove the watermark by applying a distortion attack (see Definition 5.4). Having access to the embedding function, an adversary can also find and exploit the weakness of the detection function in applying different active attacks including elimination and masking attacks, (see Definition 5.1 and Definition 5.3, respectively). Further, more difficult security problems arise if the adversary has both embedding and detection functions and knows how they work

Attacks on the watermarking security can be mainly divided in two categories [42]: (i) active (i.e., unauthorized embedding and unauthorized removal) and (ii) passive (i.e., unauthorized detection). An active attack attempts to alter the watermarking resources or to affect their operation, whereas a passive attack, without doing that, attempts to know or exploit watermarking information. Some active attacks that circumvent the scheme directly are often referred to as system or protocol attacks. We define different attacks below using our model. Depending on which inputs are available to the adversary, however, there may be different flavours of the definitions. In what follows, the original (valid) watermark is defined as w₀ ∈ W to distinguish it from other modified versions in an attack. Any other new notations will be defined accordingly.

5.1 Active attacks

5.1.1 Elimination attack

In an elimination attack, an adversary tries to output an image that is perceptually similar to the watermarked image, but will never be detected as containing the watermark. Thus, the attacked watermarked image cannot be considered to contain a watermark at all. It is important to consider that eliminating the watermark does not necessarily mean reconstructing (or inverting) the watermarked image [42]. Rather, the adversary may output a new image that is perceptually similar to the watermarked image.

Definition 5.1(Elimination attack).

Input. Watermarked image, i=E_e(i,w₀), where w₀ ∈ W

Output. Attacked image, i_a ∈ Ĩ such that i_a≈ī

Win condition. D_d(i_a,i,w)=⊥ for all w

Here, for a stronger adversary, the input can also include w₀ and the adversary can have access to E_e(·).

5.1.2 Collusion attack

In a collusion attack, an adversary obtains several copies of a watermarked image, each with a different (or same) watermark to obtain a close approximation of the watermarked image and thereby produces a copy with no watermark.

Definition 5.2(Collusion attack)

Input. n copies ( where n≥2) of watermarked image, $\bar{i_{j}} = E_{e} (i, w_{j})$ , where j={1,⋯,n}

Output. i_a ∈ Ĩ such that

i_{a} \approx \bar{i_{j}}

Win condition. D_d(i_a,i,w)=⊥ for all w

As in Definition 5.2, for example, an adversary has n copies (where n≥2) of watermarked image, $\bar{i_{j}} = E_{e} (i, w_{j})$ , where j={1,⋯,n}. In the form of an elimination attack, the adversary outputs i_a ∈ Ĩ such that $i_{a} \approx \bar{i_{j}}$ , and wins if for all w, D_d(i_a,i,w)=⊥.

5.1.3 Masking attack

Masking of a watermark means that the attacked watermarked image can still have the watermark, which is, however, undetectable by existing detectors. More sophisticated detectors might be able to detect it.

Let an adversary have a watermarked image, ī=E_e(i,w₀), where w₀ ∈ W. Here, the adversary aims to output i_a ∈ Ī such that i_a≈ī. The adversary wins if D_d(i_a,i,w₀)=⊥ but there exists w≠w₀ such that D_d(i_a,i,w)≠⊥, as defined in Definition 5.3.

Definition 5.3(Masking attack).

Input. A watermarked image, ī=E_e(i,w₀), where w₀ ∈ W

Output. i_a ∈ Ī such that i_a≈ī

Win condition. D_d(i_a,i,w₀)=⊥, but there exists w≠w₀ such that D_d(i_a,i,w)≠⊥

5.1.4 Distortion attack

In some masking attacks, an adversary applies some processing techniques uniformly over the watermarked image or some part of it, in order to degrade the watermark, so that the embedded watermark becomes undetectable or unreadable. This subclass of masking attack has special merit in image processing and is referred to as distortion attack. De-noising attacks and synchronization attacks are two common attacks in this category.

Given a watermarked image, ī=E_e(i,w₀), an adversary applies a processing technique, q ∈ Q uniformly over the whole ī, or selected object/region of ī, and outputs q(ī). According to Definition 5.4, the adversary wins if D_d(q(ī),i,w₀)=⊥ but there exists w≠w₀ such that D_d(q(ī),i,w)≠⊥. Q is the set of applicable processing techniques such that $Q \subset P$ .

Definition 5.4(Distortion attack).

Input. A watermarked image, ī=E_e(i,w₀), and a processing technique, q ∈ Q, where Q is the set of applicable processing techniques such that

Q \subset P

Output. A processed image, q(ī)

Win condition. D_d(q(ī),i,w₀)=⊥ but there exists w≠w₀ such that D_d(q(ī),i,w) ≠ ⊥

5.1.5 Forgery attack

In a forgery attack, an adversary outputs an invalid watermarked image in the form of unauthorized embedding. An adversary with the ability to perform unauthorized embedding can be presumed able to cause the detector to falsely authenticate an invalid watermarked image.

Given access to E_e(·), an adversary chooses a new unwatermarked image, i_a ∈ I and a new watermark, w_a ∈ W to output the watermarked image, $\bar{i_{a}} \in Ī$ . As in Definition 5.5, the adversary wins with the output $(\bar{i_{a}}, i_{a})$ if there exists w_a ∈ W such that $D_{d} (\bar{i_{a}}, i_{a}, w_{a}) \neq ⊥$ , and also, possibly, there exists $\tilde{w_{a}} \in \tilde{W}$ such that $X_{x} (\bar{i_{a}}, i_{a}, \tilde{w_{a}}) \neq ⊥$

Definition 5.5(Forgery attack).

Input. A new unwatermarked image, i_a ∈ I, a new watermark, w_a ∈ W, and the access to E_e(·)

Output. A new watermarked image,

\bar{i_{a}}

Win condition. There exists w_a ∈ W such that

D_{d} (\bar{i_{a}}, i_{a}, w_{a}) \neq ⊥

This attack is accomplished in two parts. During the first part, the adversary has access to E_e(·). In the second part, the adversary has to output a forgery, which is different from all the outputs from E_e(·) in the first part. A stronger adversary may also have access to G_g(·) to obtain w_a (and possibly, choose m and j), and thus to output $\bar{i_{a}} = E_{e} (i_{a}, G_{g} (i_{a}, m, j))$ that makes the adversary more likely to win, specially over X_x(·).

5.1.6 Copy attack

In a copy attack, an adversary outputs an invalid watermarked image as in a forgery attack. However, the adversary copies a watermark from one valid watermarked image into another to falsely authenticate an invalid watermarked image. In principle, an adversary initially tries to estimate the unwatermarked image from its watermarked version and then estimates the original watermark from the estimated unwatermarked image and the original watermarked image. Finally, the estimated watermark is embedded to a new unwatermarked image to get a forged watermarked copy.

Suppose an adversary is given a valid watermarked image, $ī = E_{e} (i, w_{0})$ and the access to E_e(·). The adversary obtains the estimated original watermark, $\tilde{w_{0}}$ , and chooses an unwatermarked image, i_a to output a new watermarked image, $\bar{i_{a}} = E_{e} (i_{a}, \tilde{w_{0}})$ . Finally, as given in Definition 5.6, the adversary wins with output $(\bar{i_{a}}, i_{a})$ if there exists $\tilde{w_{0}} \in W$ such that $D_{d} (\bar{i_{a}}, i_{a}, \tilde{w_{0}}) \neq ⊥$ . Also possibly, there exists $\tilde{\tilde{w_{0}}} \in \tilde{W}$ such that $X_{x} (\bar{i_{a}}, i_{a}, \tilde{\tilde{w_{0}}}) \neq ⊥$ , where $\tilde{\tilde{w_{0}}}$ is the estimate of $\tilde{w_{0}}$

Definition 5.6(Copy attack).

Input. A valid watermarked image, ī=E_e(i,w₀), a new unwatermarked image, i_a ∈ I, and the access to E_e

Output. A new watermarked image,

\bar{i_{a}} = E_{e} (i_{a}, \tilde{w_{0}})

Win condition. There exists

\tilde{w_{0}} \in W

such that

D_{d} (\bar{i_{a}}, i_{a}, \tilde{w_{0}}) \neq ⊥

, where

\tilde{\tilde{w_{0}}}

is the estimate of

\tilde{w_{0}}

An adversary can win with the copy attack if the original watermark, w₀ is independent of the image, i such that w₀=G_g(m,j). In addition, obtaining $\tilde{w_{0}}$ from ĩ and ī can be easier for the adversary if the watermark embedding is simply additive. such that, $\tilde{w_{0}} ≅ |ī - ĩ|$ . Thus, without having an access to G_g, the adversary can find $\tilde{w_{0}}$ and output a forged watermarked image, $\bar{i_{a}}$ .

5.1.7 Ambiguity attack

In a successful ambiguity attack, an adversary outputs a forgery, where a valid watermarked image is forged (i.e., illegally watermarked) with a chosen watermark. The output forgery later can be verified as valid for the chosen (not for the originally embedded) watermark. Therefore, unlike a copy or forgery attack, it has a direct impact on the scheme.

Suppose a valid watermarked image, ī and access to E_e(·) are given to an adversary. An ambiguity attack outputs a new watermarked image, $\bar{i_{a}} = E_{e} (ī, w_{a})$ and the adversary wins if there exists w_a ∈ W such that $D_{d} (\bar{i_{a}}, ī, w_{a}) \neq ⊥$ (Definition 5.7). Also possibly, there exists $(\tilde{w_{a}}) \in \tilde{W}$ such that $X_{x} (\bar{i_{a}}, ī, \tilde{w_{a}}) \neq ⊥$ . Similar to forgery attack, a stronger adversary may have access to G_g(·) to obtain w_a=G_g(i,m,j)|i=ī

Definition 5.7(Ambiguity attack).

Input. Valid watermarked image, ī and the access to E_e(·)

Output. A new watermarked image,

\bar{i_{a}} = E_{e} (ī, w_{a})

Win condition. There exists w_a ∈ W such that

D_{d} (\bar{i_{a}}, ī, w_{a}) \neq ⊥

5.1.8 Scrambling attack

The objective of an adversary in applying a scrambling attack is similar to that of masking attack (i.e., to falsify the detection of a valid watermarked image). However, in this attack, the samples of a watermarked image are scrambled prior to being presenting to the detector and subsequently descrambled. The type of scrambling can be a simple sample permutation or a more sophisticated pseudo-random scrambling [42]. A well-known scrambling attack is the mosaic attack, in which an image is broken into many small rectangular patches, each too small for reliable watermark detection. These image segments are then displayed in a table such that the segment edges are adjacent. The resulting table of small images is perceptually identical to the image prior to subdivision.

Definition 5.8(Scrambling attack)

Input. A watermarked image, ī=E_e(i,w₀), where w₀ ∈ W, and the access to ‘suitable’ scrambling and descrambling functions

Output. An image, $\bar{i_{a}} \in Ī$ from scrambling the samples of ī ∈ Ī ( before detection, and descrambles back to ī ∈ Ī after detection)

Win condition D_d(i_a,i,w₀)=⊥ but there exists w≠w₀ such that D_d(i_a,i,w)≠⊥

Given input to an adversary includes a watermarked image, ī=E_e(i,w₀), where w₀ ∈ W. The adversary outputs an image, $\bar{i_{a}} \in Ī$ from scrambling the samples of ī ∈ Ī before detection, and descrambles back to ī after detection such that i_a≈ī. The adversary wins with a suitable scrambler and descrambler, if D_d(i_a,i,w₀)=⊥ but there exists w≠w₀ such that D_d(i_a,i,w)≠⊥, as in Definition 5.8.

5.2 Passive attacks

Passive attacks can have different objectives such as detecting the presence of a valid watermark or knowing the associated information being carried by it. As mentioned in the beginning of this section, unlike active attacks, passive attacks do not attempt to alter the watermarking resources. However, a passive attack aims at knowing or exploiting the watermarking information and can have different level of consequences depending upon what it tries to achieve. We, therefore, define three different levels for the passive attacks considering their different objectives. We name these levels (to classify the passive attacks in each level) as comprehensive detection attack, incisive detection attack, and detection only attack.

In a comprehensive detection attack, an adversary wins by achieving all the three levels of target given in Definition 5.9. Similarly, to win an incisive detection attack, an adversary achieves the first two levels of target but fails to achieve target level 3. In the basic form of passive attack, a detection-only attack, an adversary wins only with the target level 1

Definition 5.9(Passive attacks).

Level 1. (Detection only). An adversary only detects the presence of valid watermark, w ∈ W in a watermarked image, ī ∈ Ī.

Level 2. (Incisive detection). An adversary distinguishes the watermark, w ∈ W from that of other watermarked image( s), $\bar{l} \in Ī | \bar{l} \neq ī$ .

Level 3. (Comprehensive detection). An adversary obtains information at least partially (e.g., the message, m ∈ M and other image data, j ∈ J, etc.) that the valid watermark, w ∈ W carries, without modifying the watermarked image, ī ∈ Ī.

6 Conclusions

The study of digital watermarking is by no means new [81, 82]. Although it has received tremendous attention in different applications, formal concept in their systematic developments are yet to be established. Addressing the gap, in this paper, we have presented our work in three main parts: (i) a formal watermarking model (section 3), (ii) definitions and uses of fundamental properties (section 4), and (iii) possible attacks on the watermarking security (section 5).

We have presented a formal generic watermarking model for digital image applications. Due to the high application variant properties of watermarking, we have focused on the image applications. We believe that our models can usefully be extended to other applications later. We determined a set of possible inputs, outputs and component functions by studying the watermarking schemes proposed for different image applications. Thereby, we have initially constructed a basic watermarking model and later extended the model to a key-based model for completeness. Using the proposed model with suitable inputs, outputs and functional properties, all possible variants of digital image watermarking schemes can be characterized and described (for example, to carry out the necessary computational analyses).

In addition, we have highlighted and defined a set of properties of watermarking with their practical interpretation in different image applications. Particularly, we defined the robustness and security properties of watermarking using the sets of (signal and image based) processing techniques and possible attacks, respectively. Although robustness can be interpreted as a security property, w believe our definition helps avoid any potential confusion between them in the signal and image processing contexts. Some other properties, such as computational complexity and cost, are important; however, in this paper, we have considered mainly those properties which can have varying interpretation with the application. Thus, addressing some hidden assumptions and associated confusions, we have presented the necessary corrections and clarifications with examples.

We have also defined a set of possible attacks with their win conditions using our model. Knowing the inputs, outputs and win conditions helps one to visualize the necessary models of possible attacks, and thus helps conduct an application-specific security analysis more efficiently. Depending upon the application scenario and available data (e.g., watermarked image, watermark) and tools (e.g., embedding function), they can be defined for a stronger or weaker adversary. However, we mainly focused on a weaker adversary (as a notion of stronger security requirements) by classifying them into two categories: active and passive. Some active attacks, known as system attacks, aim at the protocols of the schemes. Two prominent system attacks, ambiguity and scrambling attacks, in addition to the common active attacks, are also defined. For passive attacks, we have defined three different levels (ie, detection-only, incisive detection and comprehensive detection attacks) to define the win conditions for an adversary. With all these attack definitions, we have shown how an adversary of different capabilities may win with different conditions.

As a final remark, we believe that the contributions presented in this paper are a first step towards a unified and intuitive theory for digital image watermarking. We also believe that the proposed model allows a unified treatment of all practically meaningful variants of digital image watermarking. Further, our considerations, definitions, and discussions on the fundamental defining properties and attacks can help to understand them while avoiding some potential confusions and taking a step forward towards the systematic development of watermarking schemes. We have supported our thesis with meaningful examples, necessary explanations, and comparative studies. The following, however, could be interesting topics for future research: (i) further development and a quantitative analysis of the proposed model; (ii) developing complete attack models (using the proposed model) and (iii) defining security levels (in terms of possible attacks), for different image (and other media such as audio and video) applications.

Declarations

Authors’ Affiliations

(1)

Department of Electronics and Communication Engineering, Khulna University of Engineering and Technology (KUET), Khulna, 9203, Bangladesh

(2)

School of Electrical Eng. & Computer Science, Queensland University of Technology (QUT), Brisbane, QLD, 4001, Australia

(3)

Department of Telematics, Norwegian University of Science and Technology (NTNU), Trondheim, 7491, Norway

References

Li Q, Memon N, Sencar HT: Security issues in watermarking applications - a deeper look. In Proceedings of MCPS. ACM,, New York; 2007:23-28.Google Scholar
Nyeem H, Boles W, Boyd C: Developing a digital image watermarking model. In Proceedings of DICTA. IEEE,, Piscataway; 2011:468-473.Google Scholar
Nyeem H, Boles W, Boyd C: Counterfeiting attacks on block-wise dependent fragile watermarking schemes. In Proceedings of the 6th International Conference on Security of Information and Networks. ACM,, New York; 2013:86-93.Google Scholar
Petitcolas FAP, Anderson RJ, Kuhn MG: Information hiding - a survey. Proc. IEEE 1999, 87: 1062-1078. 10.1109/5.771065View ArticleGoogle Scholar
Jian Z, Koch E: A generic digital watermarking model. Comput. Graph 1998, 22(4):397-403. 10.1016/S0097-8493(98)00029-6View ArticleGoogle Scholar
Mittelholzer T: An information-theoretic approach to steganography and watermarking. In Proceedings of Information Hiding. Springer,, Heidelberg; 2000:1-16.View ArticleGoogle Scholar
Adelsbach A, Katzenbeisser S, Sadeghi A-R: A computational model for watermark robustness. In Proceedings of Information Hiding. LNCS. Springer, Heidelberg,; 2007:145-160.View ArticleGoogle Scholar
O’Sullivan JA, Moulin P, Ettinger JM: Information theoretic analysis of steganography. In Proceedings of the International Symposium on Information Theory. IEEE,, Piscataway; 1998.Google Scholar
Cohen AS, Lapidoth A: The Gaussian watermarking game. IEEE Trans. Inform. Theor 2002, 48(6):1639-1667. 10.1109/TIT.2002.1003844MathSciNetView ArticleMATHGoogle Scholar
Cachin C: An information-theoretic model for steganography. Inform. Comput 2004, 192(1):41-56. 10.1016/j.ic.2004.02.003MathSciNetView ArticleMATHGoogle Scholar
Cox IJ, Miller ML, McKellips AL: Watermarking as communications with side information. Proc. IEEE 1999, 87: 1127-1141. 10.1109/5.771068View ArticleGoogle Scholar
Adelsbach A, Katzenbeisser S, Veith H: Watermarking schemes provably secure against copy and ambiguity attacks. In Proceedings of Workshop on Digital Rights Management. ACM,, New York; 2003:111-119.Google Scholar
Barni M, Bartolini F, Furon T: A general framework for robust watermarking security. Signal Process 2003, 83(10):2069-2084. 10.1016/S0165-1684(03)00168-3View ArticleMATHGoogle Scholar
Moulin P, Mihcak MK, Lin G-I: An information-theoretic model for image watermarking and data hiding. In Proceedings of ICIP. IEEE,, Piscataway; 2000:667-670.Google Scholar
Moulin P, O’Sullivan JA: Information-theoretic analysis of information hiding. IEEE Trans. Inform. Theor 2003, 49(3):563-593. 10.1109/TIT.2002.808134MathSciNetView ArticleMATHGoogle Scholar
Holliman M, Memon N: Counterfeiting attacks on oblivious block-wise independent invisible watermarking schemes. IEEE Trans. Image Process 2000, 9: 432-441. 10.1109/83.826780View ArticleGoogle Scholar
Nyeem H, Boles W, Boyd C: Utilizing least significant bit-planes of RONI pixels for medical image watermarking. In Proceedings of DICTA. IEEE,, Piscataway; 2013:1-8.Google Scholar
Barreto PSLM, Kim HY, Rijmen V: Toward secure public-key blockwise fragile authentication watermarking. In Proceedings of Vision, Image and Signal Processing. IEEE,, Piscataway; 2002:57-62.Google Scholar
Dai HK, Yeh CT: Content-based image watermarking via public-key cryptosystems. In Proceedings of ICCSA. Springer,, Heidelberg; 2007:937-950.Google Scholar
Fridrich J, Baldoza AC, Simard RJ: Robust digital watermarking based on key-dependent basis functions. In Proceedings of IH. Springer,, Heidelberg; 1998:143-57.Google Scholar
Wong PW, Memon N: Secret and public key image watermarking schemes for image authentication and ownership verification. IEEE Trans. Image Process 2001, 10: 1593-1601. 10.1109/83.951543View ArticleMATHGoogle Scholar
Yu-Wen D, Zi L, Li W: A multipurpose public-key cryptosystem based image watermarking. In Proceedings of WiCOM. IEEE,, Piscataway; 2008:1-4.Google Scholar
Fridrich J, Goljan M: Comparing robustness of watermarking techniques. In Proceedings of SPIE. SPIE,, Bellingham; 1999:214-225.Google Scholar
Tefas A, Nikolaidis N, Pitas I: Image watermarking: techniques and applications. In The Essential Guide to Image Processing (Second Edition). Edited by: Al B. Academic Press,, Boston; 2009:597-648.View ArticleGoogle Scholar
Chen B, Wornell GW: Quantization index modulation: a class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inform. Theor 2001, 47(4):1423-1443. 10.1109/18.923725MathSciNetView ArticleMATHGoogle Scholar
Barni M, Bartolini F, Piva A: Improved wavelet-based watermarking through pixel-wise masking. IEEE Trans. Image Process 2001, 10(5):783-791. 10.1109/83.918570View ArticleMATHGoogle Scholar
Lin C-Y, Wu M, Bloom JA, Cox IJ, Miller ML, Lui YM: Rotation, scale, and translation resilient watermarking for images. IEEE Trans. Image Process 2001, 10(5):767-782. 10.1109/83.918569View ArticleMATHGoogle Scholar
P Chassery J-M, Macq B, Bas: Geometrically invariant watermarking using feature points. IEEE Trans. Image Process 2002, 11(9):1014-1028. 10.1109/TIP.2002.801587View ArticleMATHGoogle Scholar
Luo L, Chen Z, Chen M, Zeng X, Xiong Z: Reversible image watermarking using interpolation technique. IEEE Trans. Inform. Forensics Secur 2010, 5(1):187-193.View ArticleGoogle Scholar
Lin C-C, Tai W-L, Chang C-C: Multilevel reversible data hiding based on histogram modification of difference images. Pattern Recogn 2008, 41(12):3582-3591. 10.1016/j.patcog.2008.05.015View ArticleMATHGoogle Scholar
Deng C, Gao X, Li X, Tao D: A local Tchebichef moments-based robust image watermarking. Signal Process 2009, 89(8):1531-1539. 10.1016/j.sigpro.2009.02.005View ArticleMATHGoogle Scholar
Guo X, Zhuang T-G: A region-based lossless watermarking scheme for enhancing security of medical data. J. Digit. Imag 2009, 22(Compendex):53-64.View ArticleGoogle Scholar
Nikolaidis N, Pitas I: Robust image watermarking in the spatial domain. Signal Process 1998, 66(3):385-403. 10.1016/S0165-1684(98)00017-6View ArticleMATHGoogle Scholar
Pan W, Coatrieux G, Cuppens N, Cuppens F, Roux C: An additive and lossless watermarking method based on invariant image approximation and haar wavelet transform. In Proceedings of EMBC. IEEE,, Piscataway; 2010:4740-4743.Google Scholar
Qi X, Qi J: A robust content-based digital image watermarking scheme. Signal Process 2007, 87(6):1264-1280. 10.1016/j.sigpro.2006.11.002View ArticleMATHGoogle Scholar
Rey C, Dugelay J-L: Blind detection of malicious alterations on still images using robust watermarks. In Proceedings of the Seminar on Secure Images and Image Authentication. IET,, Hertsfordshire; 2000:7-11.View ArticleGoogle Scholar
Shih FY, Wu Y-T: Robust watermarking and compression for medical images based on genetic algorithms. Inform. Sci 2005, 175(3):200-216. 10.1016/j.ins.2005.01.013View ArticleGoogle Scholar
Tsai P, Hu Y-C, Yeh H-L: Reversible image hiding scheme using predictive coding and histogram shifting. Signal Process 2009, 89(6):1129-1143. 10.1016/j.sigpro.2008.12.017View ArticleMATHGoogle Scholar
Lee S, Yoo CD, Kalker T: Reversible image watermarking based on integer-to-integer wavelet transform. IEEE Trans. Inform. Forensics Secur 2007, 2(3):321-330.View ArticleGoogle Scholar
Luo H, Yu F-X, Chen H, Huang Z-L, Li H, Wang P-H: Reversible data hiding based on block median preservation. Inform. Sci 2011, 181(2):308-328. 10.1016/j.ins.2010.09.022View ArticleGoogle Scholar
Nyeem H, Boles W, Boyd C: A review of medical image watermarking requirements for teleradiology. J. Digit. Imag 2013, 26(2):326-343. doi:10.1007/s10278-012-9527-x 10.1007/s10278-012-9527-xView ArticleGoogle Scholar
Cox I, Miller M, Bloom J, Fridrich J, Kalker T: Digital Watermarking and, Steganography. Elsevier, Burlington; 2007.Google Scholar
Fridrich J, Goljan M, Du R: Lossless data embedding-new paradigm in digital watermarking. EURASIP J. Appl. Signal Process 2002, 2002: 185-196. 10.1155/S1110865702000537View ArticleMATHGoogle Scholar
De Vleeschouwer C, Delaigle J-F, Macq B: Circular interpretation of bijective transformations in lossless watermarking for media asset management. IEEE Trans. Multimedia 2003, 5(1):97-105. 10.1109/TMM.2003.809729View ArticleGoogle Scholar
Celik MU, Sharma G, Tekalp AM, Saber E: Lossless generalized-LSB data embedding. IEEE Trans. Image Process 2005, 14(2):253-266.View ArticleGoogle Scholar
Tian J: Reversible data embedding using a difference expansion. IEEE Trans. Circ. Syst. Video Tech 2003, 13(8):890-896. 10.1109/TCSVT.2003.815962View ArticleGoogle Scholar
Ni Z, Shi Y-Q, Ansari N, Su W: Reversible data hiding. IEEE Trans. Circ. Syst. Video Tech 2006, 16(3):354-362.View ArticleGoogle Scholar
Alattar AM: Reversible watermark using the difference expansion of a generalized integer transform. IEEE Trans. Image Process 2004, 13(8):1147-1156. 10.1109/TIP.2004.828418MathSciNetView ArticleGoogle Scholar
Kamstra L, Heijmans HJ: Reversible data embedding into images using wavelet techniques and sorting. IEEE Trans. Image Process 2005, 14(12):2082-2090.MathSciNetView ArticleGoogle Scholar
Caciula I, Coltuc D: Capacity control of reversible watermarking by two-thresholds embedding. In Proceedings of WIFS. IEEE,, Piscataway; 2012:223-227.Google Scholar
Kim HJ, Sachnev V, Shi YQ, Nam J, Choo H-G: A novel difference expansion transform for reversible data embedding. IEEE Trans. Informa. Forensics Secur 2008, 3(3):456-465.View ArticleGoogle Scholar
Hu Y, Lee H-K, Li J: DE-based reversible data hiding with improved overflow location map. IEEE Trans. Circ. Syst. Video Tech 2009, 19(2):250-260.View ArticleGoogle Scholar
Kim K-S, Lee M-J, Lee H-Y, Lee H-K: Reversible data hiding exploiting spatial correlation between sub-sampled images. Pattern Recognit 2009, 42(11):3083-3096. 10.1016/j.patcog.2009.04.004View ArticleMATHGoogle Scholar
Sachnev V, Kim HJ, Nam J, Suresh S, Shi YQ: Reversible watermarking algorithm using sorting and prediction. IEEE Trans. Circ. Syst. Video Tech 2009, 19: 989-999.View ArticleGoogle Scholar
Thodi DM, Rodríguez JJ: Expansion embedding techniques for reversible watermarking. IEEE Trans. Image Process 2007, 16(3):721-730.MathSciNetView ArticleGoogle Scholar
Li X, Yang B, Zeng T: Efficient reversible watermarking based on adaptive prediction-error expansion and pixel selection. IEEE Trans. Image Process 2011, 20(12):3524-3533.MathSciNetView ArticleGoogle Scholar
Coltuc D, Bolon P, Chassery JM: Fragile and robust watermarking by histogram specification. Proceedings of SPIE: Security and Watermarking of Multimedia Contents IV 701-710.Google Scholar
Zhao Z, Luo H, Lu Z-M, Pan J-S: Reversible data hiding based on multilevel histogram modification and sequential recovery. AEU-Int J. Electron. Commun 2011, 65(10):814-826. 10.1016/j.aeue.2011.01.014View ArticleGoogle Scholar
Coatrieux G, Montagner J, Huang H, Roux C: Mixed reversible and RONI watermarking for medical image reliability protection. In Proceedings of EMBC. IEEE,, Piscataway; 2007:5653-5656.Google Scholar
Coatrieux G, Le Guillou C, Cauvin JM, Roux C: Reversible watermarking for knowledge digest embedding and reliability control in medical images. IEEE Trans. Inform. Tech. Biomed 2009, 13(2):158-165.View ArticleGoogle Scholar
Nyeem H, Boles W, Boyd C: On the robustness and security of digital image watermarking. In Proceedings of ICIEV. IEEE,, Piscataway; 2012:1136-1141.Google Scholar
Piper A, Safavi-Naini R: How to compare image watermarking algorithms. Trans. Data Hiding Multimedia Secur 2009, 5510: 1-28. SpringerMATHGoogle Scholar
Tefas A, Nikolaidis N, Pitas I: Image Watermarking: Techniques and, Applications (Chapter 22). Academic Press, Boston; 2009.View ArticleGoogle Scholar
Zhang F, Zhang H: Digital watermarking capacity analysis in wavelet domain. In Proceedings of ICSP’04. IEEE,, Piscataway; 2004:2278-2281.Google Scholar
Yu N, Cao L, Fang W, Li X: Practical analysis of watermarking capacity. Proceedings of the International Conference on Communication Technology 1872-1877.Google Scholar
Wong PHW, Au OC: A capacity estimation technique for JPEG-to-JPEG image watermarking. IEEE Trans. Circ. Syst. Video Tech 2003, 13(8):746-752. 10.1109/TCSVT.2003.815949View ArticleGoogle Scholar
Barni M, Bartolini F, De Rosa A, Piva A: Capacity of full frame DCT image watermarks. IEEE Trans. Image Process 2000, 9(8):1450-1455. 10.1109/83.855442View ArticleGoogle Scholar
Moulin P, Mihcak MK: A framework for evaluating the data-hiding capacity of image sources. IEEE Trans. Image Process 2002, 11(9):1029-1042. 10.1109/TIP.2002.802512View ArticleGoogle Scholar
Harmsen JJ, Pearlman WA: Capacity of steganographic channels. IEEE Trans. Inform. Theory 2009, 55: 1775-1792.MathSciNetView ArticleGoogle Scholar
Kalker T, Willems FM: Capacity bounds and constructions for reversible data-hiding. In Proceedings of the International Conference on Digital Signal Processing, vol. 1. IEEE,, Piscataway; 2002:71-76.Google Scholar
Cayre F, Fontaine C, Furon T: Watermarking security: theory and practice. IEEE Trans. Signal Process 2005, 53(10):3976-3987.MathSciNetView ArticleGoogle Scholar
Kalker T: Considerations on watermarking security. In Proceedings of Multimedia Signal Processing Workshop. IEEE,, Piscataway; 2001:201-206.Google Scholar
Voloshynovskiy S, Pereira S, Iquise V, Pun T: Attack modelling: towards a second generation watermarking benchmark. Signal Process 2001, 81(6):1177-1214. 10.1016/S0165-1684(01)00039-1View ArticleMATHGoogle Scholar
Fridrich J: Security of fragile authentication watermarks with localization. In Proceedings of SPIE- Security and Watermarking of Multimedia Contents, vol. 4675. SPIE; 2002:691-700.Google Scholar
Braci S, Boyer R, Delpha C: Security evaluation of informed watermarking schemes. In Proceedings of ICIP. IEEE; 2009:117-120.Google Scholar
Craver SA, Katzenbeisser S: Security analysis of public key watermarking schemes. In Proceedings of Int. Symposium on Optical Science and Technology. SPIE,, Bellingham; 2001:172-182.Google Scholar
Wang J, Liu G, Lian S: Security analysis of content-based watermarking authentication framework. In Proceedings of MINES, vol. 1. IEEE,, Piscataway; 2009:483-487.Google Scholar
Loukhaoukha K, Chouinard JY: Security of ownership watermarking of digital images based on singular value decomposition. J. Electron. Imag 2010, 19(1):013007-013007. 10.1117/1.3327935View ArticleGoogle Scholar
Xiaomeng C, Jie S, Jianguo Z, Huang HK: Evaluation of security algorithms used for security processing on DICOM images. In Proceedings of SPIE- Medical Imaging: PACS and Imaging Informatics, vol. 5748. SPIE,, Bellingham; 2005:548-56.Google Scholar
Li Q, Memon N: Practical security of non-invertible watermarking schemes. In Proceedings of ICIP. IEEE,, Piscataway; 2007:445-448.Google Scholar
Cox IJ, Miller ML: The first 50 years of electronic watermarking. EURASIP J. Appl. Signal Process 2002, 2002(1):126-132.View ArticleMATHGoogle Scholar
Hartung F, Kutter M: Multimedia watermarking techniques. Proc. IEEE 1999, 87: 1079-1107. 10.1109/5.771066View ArticleGoogle Scholar

Copyright

This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.