- Research
- Open access
- Published:
Canonical polyadic decomposition of third-order semi-nonnegative semi-symmetric tensors using LU and QR matrix factorizations
EURASIP Journal on Advances in Signal Processing volume 2014, Article number: 150 (2014)
Abstract
Semi-symmetric three-way arrays are essential tools in blind source separation (BSS) particularly in independent component analysis (ICA). These arrays can be built by resorting to higher order statistics of the data. The canonical polyadic (CP) decomposition of such semi-symmetric three-way arrays allows us to identify the so-called mixing matrix, which contains the information about the intensities of some latent source signals present in the observation channels. In addition, in many applications, such as the magnetic resonance spectroscopy (MRS), the columns of the mixing matrix are viewed as relative concentrations of the spectra of the chemical components. Therefore, the two loading matrices of the three-way array, which are equal to the mixing matrix, are nonnegative. Most existing CP algorithms handle the symmetry and the nonnegativity separately. Up to now, very few of them consider both the semi-nonnegativity and the semi-symmetry structure of the three-way array. Nevertheless, like all the methods based on line search, trust region strategies, and alternating optimization, they appear to be dependent on initialization, requiring in practice a multi-initialization procedure. In order to overcome this drawback, we propose two new methods, called and , to solve the problem of CP decomposition of semi-nonnegative semi-symmetric three-way arrays. Firstly, we rewrite the constrained optimization problem as an unconstrained one. In fact, the nonnegativity constraint of the two symmetric modes is ensured by means of a square change of variable. Secondly, a Jacobi-like optimization procedure is adopted because of its good convergence property. More precisely, the two new methods use LU and QR matrix factorizations, respectively, which consist in formulating high-dimensional optimization problems into several sequential polynomial and rational subproblems. By using both LU and QR matrix factorizations, we aim at studying the influence of the used matrix factorization. Numerical experiments on simulated arrays emphasize the advantages of the proposed methods especially the one based on LU factorization, in the presence of high-variance model error and of degeneracies such as bottlenecks. A BSS application on MRS data confirms the validity and improvement of the proposed methods.
Introduction
Higher order (HO) arrays, commonly called tensors, play an important role in numerous applications, such as chemometrics [1], telecommunications [2], and biomedical signal processing [3]. They can be seen as HO extensions of vectors (one-way arrays) and matrices (two-way arrays). In many practical situations, the available data measurements cannot be arranged into a tensor form directly, that is to say, the observation diversity is insufficient either in time or frequency. However, if the latent data satisfies the statistical independence assumption, which is reasonable in many applications, meaningful HO arrays can be built by resorting to HO statistics (HOS) of the data [4]. In this instance, the HO arrays are partially symmetric or Hermitian due to the special algebraic structure of the basic HOS, such as moments and cumulants. In independent component analysis (ICA), the latent physical phenomena which are assumed to be statistically independent can be revealed by decomposing the HO array into factors. There exists several ways to decompose a given HO array, such as the Tucker model [5, 6]. Among the existing reliable HO array decomposition models, the canonical polyadic (CP) decomposition model has attracted much attention. Indeed, its uniqueness can be ensured under the sufficient conditions established by Kruskal [7]. In addition, unlike the HO singular value decomposition (HOSVD) [6], the CP model does not impose any orthogonality constraint on its factors.
Theoretically, a polyadic decomposition exactly fits an array by a sum of rank-one terms [8]. A CP decomposition is defined as a polyadic decomposition with a minimal number of rank-one terms which are needed to exactly fit a given HO array. Currently, the CP decomposition is gaining importance in several applications, for example, in exploratory data analysis [9], sensor array processing [10], telecommunications [11, 12], ICA [13], and in multiple-input multiple-output radar systems [14]. A multitude of methods were developed to compute the CP decomposition. They include the iterative alternating least squares (ALS) procedure [15], which gains popularity due to its simplicity of implementation and low numerical complexity. Uschmajew proved the local convergence property of ALS under some conditions [16]. However, this convergence can be slow. Therefore, an enhanced line search (ELS) procedure was proposed by Rajih et al. [17] to cope with the slow convergence problem of ALS. Other approaches were also proposed, such as the conjugate gradient algorithm [18] and joint eigenvalue decomposition-based algorithms [19, 20], to cite a few. Some HO arrays enjoy certain properties, such as i) symmetry and ii) nonnegativity, which cannot be simply handled by the aforementioned general CP decomposition methods. Therefore, special CP models become more and more important.
The first special form of the CP model for three-way arrays that are symmetric in two modes brings the concept of individual differences in scaling (INDSCAL) analysis [21]. On one hand, INDSCAL analysis has been studied as a way of multiple factor analysis [22] with applications to chemometrics, psychology, and marketing research. On the other hand, in the domain of signal processing, and more particularly in blind source separation (BSS), the INDSCAL analysis is widely known as the joint diagonalization of a set of matrices by congruence (JDC). During the past two decades, many successful JDC methods have been proposed, such as Yeredor’s alternating columns and diagonal center (ACDC) algorithm [23], the joint approximate diagonalization (JAD) algorithm proposed by Cardoso and Souloumiac [24], the fast Frobenius diagonalization (FFDIAG) algorithm proposed by Ziehe et al. [25], Afsari’s LUJ1D algorithm [26], and many others [27–33]. A recent survey of JDC can be found in [34]. The second special form of CP model is defined when all the factors in the CP decomposition are constrained to be nonnegative, commonly known as nonnegative tensor factorization (NTF). NTF can be regarded as the extension of nonnegative matrix factorization (NMF) [35] to higher orders. In many applications, the physical properties are inherently nonnegative, such as chemistry [1] and fluorescence spectroscopy [36, 37]. In those applications, the results are only meaningful if the nonnegativity constraint is satisfied. Various methods for computing NTF and also NMF can be found in [38, 39].
So far, the CP model with both the symmetry and nonnegativity constraints has not received much attention. Coloigner et al. proposed a family of algorithms based on line search and trust region strategies [40]. Wang et al. developed an alternating minimization scheme [41]. Those methods appear to depend on initialization, and therefore in practice require a multi-initialization procedure, leading to an increase of numerical complexity. In this paper, we propose to fit the CP model of a three-way array by imposing both the semi-nonnegativity and the semi-symmetry constraints. More precisely, we impose a nonnegativity constraint on the two symmetric modes of the INDSCAL model, which leads to the semi-nonnegative INDSCAL model or equivalently the CP decomposition of semi-nonnegative semi-symmetric three-way arrays. Such a model is often encountered in ICA problems where a nonnegative mixing matrix is frequently considered. For example, in magnetic resonance spectroscopy (MRS), the columns of the mixing matrix represent the positive concentrations of the source metabolites. Then, the three-way array built by stacking the matrix slices of a cumulant array is both nonnegative and symmetric in two modes. In such a case, the semi-nonnegative INDSCAL problem is equivalent to the JDC problem subject to a nonnegativity constraint on the joint transformation matrix. We propose two new algorithms to solve the semi-nonnegative INDSCAL problem, called and . Firstly, we rewrite the constrained optimization problem as an unconstrained one. Actually, the nonnegativity constraint is ensured by means of a square change of variable. Secondly, we propose two Jacobi-like approaches using LU and QR matrix factorizations, respectively, which consist in formulating high-dimensional optimization problems into several sequential polynomial and rational subproblems. By using both LU and QR matrix factorizations, we aim at studying the influence of the used matrix factorization. Numerical experiments highlight the advantages of the proposed methods especially , in the case of dealing with high-variance model error and with degeneracies such as bottlenecks. A BSS application on MRS signals confirms the validity and improvement of the proposed methods. A part of this work has been recently presented at the 8th IEEE Sensor Array and Multichannel Signal Processing Workshop [42].
The rest of the paper is organized as follows. After the presentation of some notations, the ‘Multilinear algebra prerequisites and problem statement’ section introduces some basic definitions of the multilinear algebra then gives the semi-nonnegative INDSCAL problem formulation. In the ‘Methods’ section, we describe the proposed algorithms in detail and also provide an analysis of the numerical complexities. The ‘Simulation results’ section shows the computer simulation results. Finally, we conclude the paper.
Multilinear algebra prerequisites and problem statement
Notations
The following notations are used throughout this paper.  and
and  denote the set of real-valued (N1 × N2 × ⋯ × N
i
) arrays and the set of nonnegative real-valued (N1 × N2 × ⋯ × N
i
) arrays, respectively. Vectors, matrices, and HO arrays are denoted by bold lowercase letters (a, b, ⋯), bold uppercase letters (A, B, ⋯) and bold calligraphic letters (
denote the set of real-valued (N1 × N2 × ⋯ × N
i
) arrays and the set of nonnegative real-valued (N1 × N2 × ⋯ × N
i
) arrays, respectively. Vectors, matrices, and HO arrays are denoted by bold lowercase letters (a, b, ⋯), bold uppercase letters (A, B, ⋯) and bold calligraphic letters ( ,
,  , ⋯), respectively. The (i,j)-th entry of a matrix A is symbolized by Ai,j. Sometimes, the MATLAB®; column/row notation is adopted to indicate submatrices of a given matrix or subarrays of a HO array. Also, a
i
denotes the i-th column vector of matrix A. ⊡ denotes the Hadamard product (element-wise product), and . ⊙ denotes the Khatri-Rao product. A♯ denotes the pseudo inverse of A. The superscripts -1, T, and -T stand for the inverse, the transpose, and the inverse after transpose operators, respectively. The (N × N) identity matrix is denoted by I
N
. 0
N
stands for N-dimensional vectors of zeros. |a| denotes the absolute value of a. ∥A∥
F
and stand for the Frobenius norm and determinant of matrix A, respectively. diag(A) returns a matrix comprising only the diagonal elements of A. Diag(b) is the diagonal matrix whose diagonal elements are given by the vector b. off(A) vanishes the diagonal components of the input matrix A. vec(A) reshapes a matrix A into a column vector by stacking its columns vertically.
, ⋯), respectively. The (i,j)-th entry of a matrix A is symbolized by Ai,j. Sometimes, the MATLAB®; column/row notation is adopted to indicate submatrices of a given matrix or subarrays of a HO array. Also, a
i
denotes the i-th column vector of matrix A. ⊡ denotes the Hadamard product (element-wise product), and . ⊙ denotes the Khatri-Rao product. A♯ denotes the pseudo inverse of A. The superscripts -1, T, and -T stand for the inverse, the transpose, and the inverse after transpose operators, respectively. The (N × N) identity matrix is denoted by I
N
. 0
N
stands for N-dimensional vectors of zeros. |a| denotes the absolute value of a. ∥A∥
F
and stand for the Frobenius norm and determinant of matrix A, respectively. diag(A) returns a matrix comprising only the diagonal elements of A. Diag(b) is the diagonal matrix whose diagonal elements are given by the vector b. off(A) vanishes the diagonal components of the input matrix A. vec(A) reshapes a matrix A into a column vector by stacking its columns vertically.
Definitions and problem formulation
Now we introduce some basic definitions in multilinear algebra which are necessary for the problem formulation.
Definition 1.
The outer product of three vectors  is a three-way array of
is a three-way array of  whose elements are defined by .
whose elements are defined by .
Definition 2.
Each three-way array  expressed as the outer product of three vectors is a rank-1 three-way array.
expressed as the outer product of three vectors is a rank-1 three-way array.
More generally, the rank of a three-way array is defined as follows:
Definition 3.
The rank of an array  , denoted by , is the minimal number of rank-1 arrays belonging to
, denoted by , is the minimal number of rank-1 arrays belonging to  that yield
that yield  in a linear combination.
in a linear combination.
Despite the similarity between the definition of the tensor rank and its matrix counterpart, the rank of a three-way array may exceed its dimensions [4].
Definition 4.
A three-way array slice is a two-dimensional section (fragment) of a three-way array, obtained by fixing one of the three indices [38].
For example, the k-th frontal slice of a three-way array  can be denoted by using MATLAB notation, and sometimes it is also denoted by C(k).
can be denoted by using MATLAB notation, and sometimes it is also denoted by C(k).
The low-rank INDSCAL model of a three-way array is defined as follows:
Definition 5.
For a given P, corresponding to the number of rank-1 terms, the INDSCAL model of a three-way array  can be expressed as:
can be expressed as:
where the three-way array  represents the model residual.
represents the model residual.
The notation refers to the INDSCAL decomposition (1) of  with the associated loading matrices
with the associated loading matrices  and . If and only if the residual
and . If and only if the residual  is a null tensor, we have an exact INDSCAL decomposition.
is a null tensor, we have an exact INDSCAL decomposition.
An exact INDSCAL decomposition is considered to be essentially unique when it is only subject to scale and permutation indeterminacies. It means that an INDSCAL decomposition is insensitive to a scaling of the three vectors a p , a p , and d p provided that the product of the three scale numbers is equal to 1, and an arbitrary permutation of the rank-1 terms. A necessary and sufficient uniqueness condition for the INDSCAL model was established by Afsari [43].
The INDSCAL model can also be described by using the frontal slices of  :
:
where D(k) is a diagonal matrix whose diagonal contains the elements of the k-th row of D, and .
In this paper, we propose to fit the INDSCAL model of three-way arrays while imposing nonnegativity constraints on both equal loading matrices A. It will be referred to as the semi-nonnegative INDSCAL model, as follows:
Problem 1.
Given  and an integer P, find a semi-nonnegative INDSCAL model of , subject to the (N × P) matrix A having nonnegative components.
and an integer P, find a semi-nonnegative INDSCAL model of , subject to the (N × P) matrix A having nonnegative components.
The semi-nonnegative INDSCAL problem is equivalent to the JDC problem subject to the nonnegativity constraint on the joint transformation matrix. In this paper, we mainly focus on the case of square nonnegative joint transformation matrix, for which N = P. The case of N > P will be discussed briefly in the next section. Therefore, the problem that we tackle in this paper is defined as follows:
Problem 2.
Given a three-way array
 with K symmetric frontal slices
with K symmetric frontal slices
 , find a (N × N) joint transformation matrix
A
and K diagonal matrices
D
(k)
of dimension (N × N) such that:
, find a (N × N) joint transformation matrix
A
and K diagonal matrices
D
(k)
of dimension (N × N) such that:
by minimizing the residual term V(k) in a least-squares sense, subject to A having nonnegative components.
JDC cost functions
If the residual array  is a realization of a Gaussian random array, it is logical to fit the INDSCAL model by the following direct least square (DLS) criterion [23, 44]:
is a realization of a Gaussian random array, it is logical to fit the INDSCAL model by the following direct least square (DLS) criterion [23, 44]:
and to minimize (4) with respect to A and D. Note that, in the field of ICA, only the loading matrix A is of interest since it corresponds to the mixing matrix of several latent source signals. The minimization of (4) with respect to D, when A is fixed, was given by Yeredor in [23]:
When A is orthogonal, we can replace D(k) by in (4). Then, the extra parameter D can be eliminated and the minimization of (4) is equivalent to minimizing the following indirect least square (IDLS) criterion [45, 46]:
In some cases such as in ICA, the orthogonality assumption of A can be satisfied by using a spatial whitening procedure [47]. However, it is known that the whitening procedure may introduce additional errors. Therefore, many algorithms propose to relax the orthogonality constraint by introducing the following cost function [25, 31]:
Frequently, the minimization of criterion (7) is performed on a matrix instead of A for simplicity, and Z is called the joint diagonalizer. To use this criterion, the matrix A (or Z) should be properly constrained in order to avoid the trivial zero solution and/or degenerate solutions [34].
Besides the criterions (4) and (7), Afsari [26] presented a new cost function, which is invariant to column scaling of A. Pham proposed an information theoretic criterion [48], which requires each matrix C(k) to be positive definite. Tichavský and Yeredor gave a special weighted least square criterion [49].
Methods
Problem reformulation
Existing semi-nonnegative INDSCAL algorithms are based on the minimization of the cost function (4) [40, 41]. They are able to achieve a better estimation of A than ACDC when the data satisfies the semi-nonnegative INDSCAL model at the cost of a higher computational complexity. We propose to use criterion (7) based on elementary factorizations of A due to the fast convergence property of this kind of procedures. Generally, it is quite difficult to impose the nonnegativity constraint on A while computing its inverse A-1 by minimizing (7). Let us consider the structure of with the following assumptions:
①  is nonsingular;
is nonsingular;
②  does not contain zero entries.
does not contain zero entries.
Then, each frontal slice of  is nonsingular and its inverse can be expressed as follows:
is nonsingular and its inverse can be expressed as follows:
We use C(k,-1) to denote for simplicity. Eq. 8 shows that C(k,-1) also preserves the jointly diagonalizable structure. Furthermore, instead of A-1, A serves as the joint diagonalizer. Then, A can be estimated by minimizing the following modified criterion based on (7):
By such a manipulation, most algorithms based on criterion (7) can now estimate A directly. However, none of them can guarantee the nonnegativity of A. In order to impose the nonnegativity constraint on A, we resort to use a square change of variable which was introduced by Chu et al. [50] for NMF, next adopted by Royer et al. for NTF [37] and by Coloigner et al. for semi-nonnegative INDSCAL [40]:
where  . Then, problem 2 can be reformulated as follows:
. Then, problem 2 can be reformulated as follows:
Problem 3.
Given
 , find the square nonnegative loading matrix
such that
B
minimizes the following cost function:
, find the square nonnegative loading matrix
such that
B
minimizes the following cost function:
LU and QR parameterizations of B
In order to minimize (11), one may consider a gradient-like approach. However, the performance of this kind of method is sensitive to the initial guess and to the search step size. In addition, the calculation of gradient of (11) with respect to B is computationally expensive due to the existence of the Hadamard product. Other algorithms, using Jacobi-like procedures [25, 26, 31], parameterize A as a product of several special elementary matrices and estimate each elementary matrix successively. We propose to follow such a minimization scheme.
Now let us recall the following definitions and lemmas:
Definition 6.
A unit upper (or lower) triangular matrix is an upper (or lower, respectively) triangular matrix whose main diagonal elements are equal to 1.
Definition 7.
An elementary upper (or lower) triangular matrix with parameters {i,j,ui,j} and i<j is a unit upper (or lower, respectively) triangular matrix whose non-diagonal elements are zeros except the (i,j)-th entry, which is equal to ui,j.
U(i,j)(ui,j) with 1 ≤ i < j ≤ N denotes an elementary upper triangular matrix:
Similarly, L(i,j)(ℓi,j) with 1 ≤ j < i ≤ N corresponds to an elementary lower triangular matrix.
Definition 8.
A Givens rotation matrix with parameters {i,j,θi,j} and i < j is equal to an identity matrix except for the (i,i)-th, (j,j)-th, (i,j)-th, and (j,i)-th entries, which are equal to , , , and , respectively.
Q(i,j)(θi,j) with 1 ≤ i < j ≤ N indicates the corresponding Givens rotation matrix:
Lemma 1.
Any (N × N) unit lower triangular matrix L whose (i,j)-th component is ℓi,j(i > j) can be factorized as the following product of N (N-1)/2 elementary lower triangular matrices [51, Chapter 3]:
where the two sets of indices and are defined by and for the sake of convenience. Similarly, any (N × N) unit upper triangular matrix U whose (i,j)-th component is equal to u i,j (i < j) can be factorized as a product of elementary upper triangular matrices as follows:
where and are two sets of indices, defined by and .
Lemma 2.
Any (N × N) orthonormal matrix Q can be factorized as the following product of N (N-1)/2 Givens rotation matrices [52, Chapter 14]:
where and are defined in Lemma 1.
For any nonsingular matrix  , the LU matrix factorization decomposes it as B= L U Λ Π, where
, the LU matrix factorization decomposes it as B= L U Λ Π, where  is a unit lower triangular matrix,
is a unit lower triangular matrix,  is a unit upper triangular matrix,
is a unit upper triangular matrix,  is a diagonal matrix, and
is a diagonal matrix, and  is a permutation matrix. B also admits the QR matrix factorization as B= Q R Λ, where
is a permutation matrix. B also admits the QR matrix factorization as B= Q R Λ, where  is an orthonormal matrix,
is an orthonormal matrix,  is a unit upper triangular matrix, and
is a unit upper triangular matrix, and  is a diagonal matrix. Due to the indeterminacies of the JDC problem, the global minimum of (11), say B, can be expressed as B= L U and B= Q R without loss of generality. Moreover, by incorporating Lemma 1 and Lemma 2, we obtain the two following elementary factorizations of B:
is a diagonal matrix. Due to the indeterminacies of the JDC problem, the global minimum of (11), say B, can be expressed as B= L U and B= Q R without loss of generality. Moreover, by incorporating Lemma 1 and Lemma 2, we obtain the two following elementary factorizations of B:
As a consequence, the minimization of (11) with respect to B is converted to the estimate of N (N-1) parameters: ℓi,j and ui,j for the LU decomposition (17), or θi,j and ui,j for the QR decomposition (18). Instead of simultaneously computing the N(N-1) parameters, we propose two Jacobi-like procedures which perform N(N-1) sequential optimizations. This yields two new algorithms: i) the first algorithm based on (17), named , estimates each ℓi,j and ui,j successively, and ii) the second one based on (18), called , estimates each θi,j and ui,j sequentially.
Now, the difficulty is how to estimate four kinds of parameter, namely L(i,j)(ℓi,j) and U(i,j)(ui,j) for , and Q(i,j)(θi,j) and U(i,j)(ui,j) for . Two points should be noted here: i) L(i,j)(ℓi,j) and U(i,j)(ui,j) belong to the same category of matrices; therefore, they can be estimated by the same algorithmic procedure just with an emphasis on the relation between the i and j indices (i < j for U(i,j)(ui,j) and j < i for L(i,j)(ℓi,j)); ii) for both and algorithms, the procedure of estimating U(i,j)(ui,j) is identical. Consequently, the principal problem is reduced to estimating two kinds of parameters, namely U(i,j)(ui,j) and Q(i,j)(θi,j).
Minimization with respect to the elementary upper triangular matrix U(i,j)(ui,j)
In this section, we minimize (11) with respect to U(i,j)(ui,j) with 1 ≤ i < j ≤ N. Let and denote the current estimate of A and B before estimating the parameter ui,j, respectively. Let and stand for and updated by U(i,j)(ui,j), respectively. Furthermore, the update of is defined as follows:
In order to compute the parameter ui,j, a typical way is to minimize the criterion (11) with respect to ui,j by replacing matrix by . For the sake of convenience, we denote J (ui,j) instead of . Then, J(ui,j) can be expressed as follows:
The expression of the Hadamard square of the update is shown in the following proposition:
Proposition 1.
can be expressed as a function of u i,j as follows:
where and denote the i-th and j-th columns of , respectively, and e j is the j-th column of the identity matrix I N .
Inserting (21) into the cost function (20), we have:
where , , , and are a (N × N) constant matrix, a (N × 1) constant column vector, a (1 × N) constant row vector, and a constant scalar, respectively. The term ① in (22) transforms the j-th column and the j-th row of . The term ② in (22) is a zero matrix except its j-th column containing non-zero elements, while the term ③ contains non-zero entries only on its j-th row. The term ④ is a zero matrix except its (j,j)-th component being non-zero. In addition, is a (N × N) symmetric matrix. Hence, (22) shows that only the j-th column and j-th row of involve the parameter ui,j, while the other elements remain constant. Therefore, the minimization of the cost function (20) is equivalent to minimizing the sum of the squares of the j-th columns of except their (j,j)-th elements with k ∈ {1,⋯,K}. The required elements of can be expressed by the following proposition.
Proposition 2.
The elements of the j-th column except the (j,j)-th entry of is a second-degree polynomial function in u i,j as follows, for every value n different of j:
where and are the (n,i)-th and (n,j)-th components of matrix , respectively, and is the n-th element of vector .
The proof of this proposition is straightforward. Indeed, we can show that the elements of the j-th column except the (j,j)-th entry of the term ① in (22) can be expressed by with 1 ≤ n ≤ N and n ≠ j, and those elements of the term ② in (22) are equal to with 1 ≤ n ≤ N and n ≠ j. The sum of these elements directly leads to (23). The terms ③ and ④ do not need to be considered, since they do not affect the off-diagonal elements in the j-th column. Proposition 2 shows that the minimization of the cost function (20) can be expressed in the following compact matrix form:
where is a (3 × 3) symmetric coefficient matrix. E(k) is a ((N - 1) × 3) matrix defined as follows: the first column contains the i-th column of without the j-th element, the second column contains vector without the j-th entry, and the third column contains the j-th column of without the j-th component. is a three-dimensional parameter vector.
Equation (24) shows that J(ui,j) is a fourth-degree polynomial function. The global minimum ui,j can be obtained by computing the roots of its derivative and selecting the one yielding the smallest value of (24). Once the optimal ui,j is computed, is updated by (19) and the joint diagonalizer is updated by computing . Then, the same procedure is repeated to compute the next ui,j with another (i,j) index.
The minimization of (11) with respect to the elementary lower triangular matrix L(i,j)(ℓi,j) with 1 ≤ j < i ≤ N can be computed in the same way. Proposition 2 is also valid for the parameter ℓi,j when 1 ≤ j < i ≤ N. The detailed derivation is omitted here. The processing of all the N (N - 1) parameters ui,j and ℓi,j is called a LU sweep. In addition, for estimating L(i,j)(ℓi,j), the (i,j) index obeys the following order:
Regarding U(i,j)(ui,j), the (i,j) index varies according to the following sequence:
The proposed algorithm is comprised of several LU sweeps.
Minimization with respect to the Givens rotation matrix Q(i,j)(θi,j)
Now we minimize (11) with respect to Q(i,j) (θi,j) with 1 ≤ i < j ≤ N. By abuse of notation, in this section, we continue to use and to denote the current estimate of A and B, respectively, before estimating the parameter θi,j. Also, let and stand for and updated by Q(i,j)(θi,j), respectively. The update of is defined as follows:
Similarly, for computing the parameter θi,j, we can minimize the criterion (11) with respect to θi,j by replacing matrix by . We denote J(θi,j) instead of for convenience purpose. Then, J(θi,j) can be expressed as follows:
The Hadamard square of the update now can be rewritten as shown in the following proposition.
Proposition 3.
can be written as a function of θ i,j as follows:
where and denote the i-th and j-th columns of , respectively, and e i and e j are the i-th and j-th columns of the identity matrix I N , respectively.
Inserting (29) into the cost function (28), we obtain:
where , , , and are a (N × N) constant matrix, a (N × 1) constant column vector, a (1 × N) constant row vector, and a constant scalar, respectively. The term ① in (30) transforms the i-th and j-th columns and the i-th and j-th rows of . The term ② in (30) is a zero matrix except its i-th and j-th columns containing non-zero elements, while the term ③ contains non-zero entries only on its i-th and j-th rows. The term ④ is a zero matrix except its (i,i)-th, (j,j)-th, (i,j)-th, and (j,i)-th components being non-zero. is a (N × N) symmetric matrix. Hence, (30) shows that only the i-th and j-th columns and the i-th and j-th rows of involve the parameter θi,j, while the other components remain constant. It is noteworthy that the (i,j)-th and (j,i)-th components are twice affected by the transformation. Considering the symmetry of , we propose to minimize the sum of the squares of the (i,j)-th entries of the K matrices , instead of minimizing all the off-diagonal entries. Although minimizing this quantity is not equivalent to minimizing the global cost function (28), such a simplified minimization scheme is commonly adopted in many algorithms, such as [20, 31]. We denote this local minimization by . The (i,j)-th component of is expressed in the following proposition.
Proposition 4.
The (i,j)-th entry of can be expressed as a function of θ i,j as follows:
where , , , and are the (i,i)-th, (j,j)-th, (i,j)-th, and (j,i)-th components of matrix , respectively. and are the i-th and j-th elements of vector with q ∈ {1,2}, respectively.
It is straightforward to show that the (i,j)-th entry of the term ① in (30) can be expressed by , the (i,j)-th element of the term ② is , the (i,j)-th component of the term ③ is equal to , and that of the term ④ is . Then, Proposition 4 can be proved.
In order to simplify the notation of (31), we resort to the Weierstrass change of variable: . Then, we obtain:
By substituting (32) into (31), we obtain an alternative expression of the (i,j)-th entry of which is described in the following proposition. Then, the minimization of transforms to .
Proposition 5.
The (i,j)-th entry of can be expressed by a rational function of t i,j as follows:
where , , , , and .
Eq. 33 easily shows that the sum of the squares of the (i,j)-th entries of the K matrices , is a rational function in ti,j, namely , where the degrees of the numerator and the denominator are 8 and 8, respectively. can be expressed in the following compact matrix form:
where is a (5 × 5) symmetric coefficient matrix, is a five-dimensional vector, and τi,j is a five-dimensional parameter vector defined as follows:
The global minimum ti,j can be obtained by computing the roots of its derivative and selecting the one yielding the smallest value of . Once ti,j is obtained, θi,j can be computed from the inverse tangent function . It is noteworthy that the found θi,j cannot guarantee to decrease the actual cost function (28). If θi,j leads to an increase of (28), we reset θi,j= 0. Otherwise, is updated as described in (27) and the joint diagonalizer is updated by computing . The same procedure will be repeated to compute θi,j with the next (i,j) index. The order of the (i,j) indices is defined in Eq. 26. The processing of all the N(N - 1)/2 parameters θi,j and also the other N(N - 1)/2 parameters ui,j is called a QR sweep. Several QR sweeps yield the proposed algorithm.
Both of the and algorithms can be stopped when the value of cost function (11) or its relative change between two successive sweeps fall below a fixed small positive threshold. Such a stopping criterion is guaranteed to be met since the cost function is non-increasing in each Jacobi-like sweep.
Practical issues
In practice, we observe that if each frontal slice of the three-way array  is almost exactly jointly diagonalizable due to a high signal-to-noise ratio (SNR), the classical non-constrained JDC methods can also give a nonnegative A with high probability. In this situation, the explicit nonnegativity constraint could be unnecessary and could increase the computational burden. Therefore, we propose to relax the nonnegativity constraint by directly decomposing A into elementary LU and QR forms, respectively, instead of using the decompositions of B as follows:
is almost exactly jointly diagonalizable due to a high signal-to-noise ratio (SNR), the classical non-constrained JDC methods can also give a nonnegative A with high probability. In this situation, the explicit nonnegativity constraint could be unnecessary and could increase the computational burden. Therefore, we propose to relax the nonnegativity constraint by directly decomposing A into elementary LU and QR forms, respectively, instead of using the decompositions of B as follows:
where the index sets , , , and are defined in Lemma 1. By inserting (36) and (37) into the cost function (9), the ways of estimating the two sets of parameters {ℓi,j,ui,j} and {θi,j,ui,j} are identical to those of Afsari’s LUJ1D and QRJ1D methods [26], respectively. Therefore, in practice, in order to give an automatically SNR-adaptive method, for , in each Jacobi-like iteration, we suggest to compute ui,j by LUJ1D first. If all the elements in the j-th column of have the same sign ε, the update is adopted. Otherwise, ui,j is computed by minimizing (20) and is updated by computing (21). Each ℓi,j is computed similarly. Furthermore, the proposed and QRJ1D are combined in the same manner.
Afsari reported in [26] that if the rows of matrices (k ∈ {1,⋯,K}) are not balanced in their norms, the computation of the parameter could be inaccurate. In order to cope with this effect, we apply Afsari’s row balancing scheme every few sweeps. Such a scheme updates each by and by using a diagonal matrix  , whose diagonal elements are defined as follows:
, whose diagonal elements are defined as follows:
where denotes the n-th row of .
In ICA, when a non-square matrix  with N>P is encountered, the invertibility assumption of the frontal slices C(k) does not hold. In this situation, we can compress A by means of a nonnegative matrix
with N>P is encountered, the invertibility assumption of the frontal slices C(k) does not hold. In this situation, we can compress A by means of a nonnegative matrix  such that the resulting matrix is a nonnegative square matrix. Then, the and algorithms can be used to compute the compressed loading matrix . W+ can be computed by using the nonnegative compression algorithm (NN-COMP) that we proposed in [53]. More precisely, given a realization of an observation vector, we obtain the square root of the covariance matrix, denoted by
such that the resulting matrix is a nonnegative square matrix. Then, the and algorithms can be used to compute the compressed loading matrix . W+ can be computed by using the nonnegative compression algorithm (NN-COMP) that we proposed in [53]. More precisely, given a realization of an observation vector, we obtain the square root of the covariance matrix, denoted by  . The classical prewhitening matrix is computed by
. The classical prewhitening matrix is computed by  where ♯ denotes the pseudo inverse operator [47]. Then, the NN-COMP algorithm computes a linear transformation matrix
where ♯ denotes the pseudo inverse operator [47]. Then, the NN-COMP algorithm computes a linear transformation matrix  such that W+ = Ψ W has nonnegative components. Once is estimated, the original matrix A is obtained as follows:
such that W+ = Ψ W has nonnegative components. Once is estimated, the original matrix A is obtained as follows:
It should be noted that generally A does not need to be computed in such an ICA problem, since the sources can be estimated directly by means of .
Numerical complexity
The numerical complexities of and are analyzed in terms of the number of floating point operations (flops). A flop is defined as a multiplication followed by an addition. In practice, only the number of multiplications, required to identify the loading matrix  from a three-way array
from a three-way array  , is considered, which does not affect the order of magnitude of the numerical complexity.
, is considered, which does not affect the order of magnitude of the numerical complexity.
For both algorithms, the inverses C(k,-1) (k ∈ {1,⋯,K}) of the frontal slices of  cost N3K flops, the initialization of requires 2N3K flops, and at each sweep, the calculation of parameters ui,j needs N(N-1)(5N2+12N-8)K/2 flops. In addition, in the case of the algorithm, the calculation cost of , , and , with k ∈ {1,⋯,K}, is N (N-1)(4N + (4 N + 1) K) flops, and the numerical complexity of computing the parameters ℓi,j is equal to that of ui,j. Regarding the algorithm, for each sweep, the complexity of calculating the parameters θi,j is equal to N(N-1)(5N2+ 3 N + 29)K/2 flops, and the estimation of , , and , with k ∈ {1,⋯,K}, costs N (N - 1)(5 N + (12 N + 20) K/2) flops. In practice, the proposed and techniques are combined with LUJ1D and QRJ1D [26], respectively, leading to the magnitude of global numerical complexities of and being between and . A recent nonnegative JDC method called [41] is also based on a square change of variable and LU matrix factorization. It minimizes the cost function (4) with respect to A and D alternately, leading to a higher numerical complexity. By means of the reformulation of the cost function, the proposed methods avoid the estimation of D, therefore achieving a lower complexity compared to . The explicit expressions of the overall complexity of , , and [41], as well as those of four classical JDC algorithms, namely ACDC [23], FFDIAG [25], LUJ1D [26], and QRJ1D [26], are listed in Table 1. One can notice that numerical complexities of the proposed and methods are at most one order of magnitude higher than those of the four JDC algorithms and still lower than that of . Moreover, is less computationally expensive than .
cost N3K flops, the initialization of requires 2N3K flops, and at each sweep, the calculation of parameters ui,j needs N(N-1)(5N2+12N-8)K/2 flops. In addition, in the case of the algorithm, the calculation cost of , , and , with k ∈ {1,⋯,K}, is N (N-1)(4N + (4 N + 1) K) flops, and the numerical complexity of computing the parameters ℓi,j is equal to that of ui,j. Regarding the algorithm, for each sweep, the complexity of calculating the parameters θi,j is equal to N(N-1)(5N2+ 3 N + 29)K/2 flops, and the estimation of , , and , with k ∈ {1,⋯,K}, costs N (N - 1)(5 N + (12 N + 20) K/2) flops. In practice, the proposed and techniques are combined with LUJ1D and QRJ1D [26], respectively, leading to the magnitude of global numerical complexities of and being between and . A recent nonnegative JDC method called [41] is also based on a square change of variable and LU matrix factorization. It minimizes the cost function (4) with respect to A and D alternately, leading to a higher numerical complexity. By means of the reformulation of the cost function, the proposed methods avoid the estimation of D, therefore achieving a lower complexity compared to . The explicit expressions of the overall complexity of , , and [41], as well as those of four classical JDC algorithms, namely ACDC [23], FFDIAG [25], LUJ1D [26], and QRJ1D [26], are listed in Table 1. One can notice that numerical complexities of the proposed and methods are at most one order of magnitude higher than those of the four JDC algorithms and still lower than that of . Moreover, is less computationally expensive than .
Simulation results
This section is twofold. In the first part, the performance of the proposed and algorithms is evaluated with simulated semi-nonnegative semi-symmetric three-way arrays  . Several experiments are designed to study the convergence property, the influence of SNR, the impact of the third dimension K of
. Several experiments are designed to study the convergence property, the influence of SNR, the impact of the third dimension K of  , the effect of the coherence of the loading matrix D, and the influence of the condition number of the diagonal matrices D(k). We also evaluate the proposed methods for estimating a non-square matrix A. The proposed algorithms are compared with four classical nonorthogonal JDC methods, namely ACDC [23], FFDIAG [25], LUJ1D [26], QRJ1D [26], and the nonnegative JDC method [41]. In the second part, the source separation ability of the proposed algorithms is studied through a BSS application. In this context, the and are used to jointly diagonalize several matrix slices of the fourth-order cumulant array [40] of the observations and compared with several classical ICA [47, 54, 55] and NMF [56] methods.
, the effect of the coherence of the loading matrix D, and the influence of the condition number of the diagonal matrices D(k). We also evaluate the proposed methods for estimating a non-square matrix A. The proposed algorithms are compared with four classical nonorthogonal JDC methods, namely ACDC [23], FFDIAG [25], LUJ1D [26], QRJ1D [26], and the nonnegative JDC method [41]. In the second part, the source separation ability of the proposed algorithms is studied through a BSS application. In this context, the and are used to jointly diagonalize several matrix slices of the fourth-order cumulant array [40] of the observations and compared with several classical ICA [47, 54, 55] and NMF [56] methods.
Simulated semi-nonnegative INDSCAL model
The synthetic semi-nonnegative semi-symmetric three-way array  of rank N is generated randomly according to the semi-nonnegative INDSCAL model (3). When used without further specification, all the algorithms are manipulated under the following conditions:
of rank N is generated randomly according to the semi-nonnegative INDSCAL model (3). When used without further specification, all the algorithms are manipulated under the following conditions:
-
i)
Model generation: The loading matrix
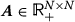 is randomly drawn from a uniform distribution on the interval [ 0,1]. The loading matrix
is randomly drawn from a uniform distribution on the interval [ 0,1]. The loading matrix 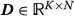 is drawn from a Gaussian distribution with a mean of 1 and a deviation of 0.5. The pure array
is drawn from a Gaussian distribution with a mean of 1 and a deviation of 0.5. The pure array  is perturbed by a residual INDSCAL noise array
is perturbed by a residual INDSCAL noise array  . The loading matrices of
. The loading matrices of  are drawn from a zero-mean unit-variance Gaussian distribution. The resulting noisy three-way array can be written as follows: (40)
are drawn from a zero-mean unit-variance Gaussian distribution. The resulting noisy three-way array can be written as follows: (40)where σ N is a scalar controlling the noise level. Then, the SNR is defined by .
-
ii)
Initialization: In each Monte Carlo trial, all the algorithms are initialized by a same random matrix whose components obey the uniform distribution over [ 0,1].
-
iii)
Afsari’s row balancing scheme: The LUJ1D, QRJ1D, , and algorithms perform the row balancing scheme once per run of five sweeps.
-
iv)
Stopping criterion: All the algorithms stop either when the relative error of the corresponding criterion between two successive sweeps is less than 10-5 or when the number of sweeps exceeds 200. A sweep of ACDC includes a full AC phase and a DCphase.
-
v)
Performance measurement: The performance is measured by means of the error between the true loading matrix A and the estimate , the numerical complexity, and the CPU time. We define the following scale-invariant and permutation-invariant distance [40]:
(41)where a n and are the n-th column of A and the n′-th column of , respectively. is defined recursively by , and where . In addition, is defined as the pseudo-distance between two vectors [13]:
(42)The criterion (41) is an upper bound of the optimal permutation-invariant criterion. It avoids the burdensome computation of all the permutations. A small value of (41) means a good performance in the sense that is close to A.
-
vi)
Test environment: The simulations are carried out in Matlab v7.14 on Mac OS X and run on Intel Quad-Core CPU 2.8 GHz with 32 GB memory. Moreover, we repeat all the experiments with 500 Monte Carlo trials.
Convergence
In this experiment, the convergences of the and algorithms are compared to those of ACDC, FFDIAG, LUJ1D, QRJ1D, and . The dimensions of the three-way array  are set to N = 5 and K = 15. The performance is assessed under three SNR conditions: SNR = - 5, 10, and 25 dB, respectively. Figure 1 shows the convergence curves measured in terms of the cost function as a function of sweeps. It shows that FFDIAG, LUJ1D, and QRJ1D exhibit fast convergence behavior. They converge in less than 20 sweeps. decreases the cost function (4) quasi-linearly. ACDC and do not converge in a maximum of 200 sweeps. The proposed algorithm converges in about 100 sweeps when SNR =25 dB and SNR =10 dB, and it converges in about 40 sweeps when SNR =-5 dB. Regarding , it reduces the cost function (11) to the values relatively higher than those achieved by and converges in about 50 sweeps whatever the SNR is. It seems that FFDIAG, LUJ1D, and QRJ1D achieve the fastest convergence rate. It should be noted that while an algorithm may converge to a point in which the value of the cost function is close to zero, such a point could be a local minimum far from the desired matrix A as shown in Figure 2. The top picture in Figure 2 shows the convergence curves measured in terms of the estimating error as a function of sweeps when SNR=25 dB. It shows that the solutions of FFDIAG, LUJ1D, and QRJ1D are still far from optimum. ACDC and give better estimations of A than the previous three methods. The best results are achieved by the proposed and methods. The middle picture in Figure 2 displays the convergence curves when SNR=10 dB. It can be observed that ACDC converges to a local minimum which is not the global one and that the performance of the proposed methods is still better than that of the five other algorithms. For a low SNR =-5 dB, as shown in the bottom picture in Figure 2, both the methods based on alternating optimization, namely ACDC and , converge to local minima which are less desirable. The proposed algorithms are always able to converge to better results than the classical methods. The average numerical complexities and CPU time of all the algorithms over Monte Carlo trials are shown in Table 2. It is observed that FFDIAG, LUJ1D, and QRJ1D require a small amount of calculations, whereas requires a large amount of calculations. The proposed just costs a bit more flops and CPU time than ACDC, but it is still much more efficient. Concerning the algorithm, it is more costly than , with a comparable performance. We can then conclude that offers the best performance/complexity compromise in these experiments.
are set to N = 5 and K = 15. The performance is assessed under three SNR conditions: SNR = - 5, 10, and 25 dB, respectively. Figure 1 shows the convergence curves measured in terms of the cost function as a function of sweeps. It shows that FFDIAG, LUJ1D, and QRJ1D exhibit fast convergence behavior. They converge in less than 20 sweeps. decreases the cost function (4) quasi-linearly. ACDC and do not converge in a maximum of 200 sweeps. The proposed algorithm converges in about 100 sweeps when SNR =25 dB and SNR =10 dB, and it converges in about 40 sweeps when SNR =-5 dB. Regarding , it reduces the cost function (11) to the values relatively higher than those achieved by and converges in about 50 sweeps whatever the SNR is. It seems that FFDIAG, LUJ1D, and QRJ1D achieve the fastest convergence rate. It should be noted that while an algorithm may converge to a point in which the value of the cost function is close to zero, such a point could be a local minimum far from the desired matrix A as shown in Figure 2. The top picture in Figure 2 shows the convergence curves measured in terms of the estimating error as a function of sweeps when SNR=25 dB. It shows that the solutions of FFDIAG, LUJ1D, and QRJ1D are still far from optimum. ACDC and give better estimations of A than the previous three methods. The best results are achieved by the proposed and methods. The middle picture in Figure 2 displays the convergence curves when SNR=10 dB. It can be observed that ACDC converges to a local minimum which is not the global one and that the performance of the proposed methods is still better than that of the five other algorithms. For a low SNR =-5 dB, as shown in the bottom picture in Figure 2, both the methods based on alternating optimization, namely ACDC and , converge to local minima which are less desirable. The proposed algorithms are always able to converge to better results than the classical methods. The average numerical complexities and CPU time of all the algorithms over Monte Carlo trials are shown in Table 2. It is observed that FFDIAG, LUJ1D, and QRJ1D require a small amount of calculations, whereas requires a large amount of calculations. The proposed just costs a bit more flops and CPU time than ACDC, but it is still much more efficient. Concerning the algorithm, it is more costly than , with a comparable performance. We can then conclude that offers the best performance/complexity compromise in these experiments.
Effect of SNR
In this section, we study the behaviors of the seven algorithms as a function of SNR. The dimensions of the three-way array are set to N = 5 and K = 15. We repeat the experiments with SNR ranging from -30 to 50 dB with a step of 2 dB. The top picture in Figure 3 depicts the average curves of of the seven algorithms as a function of SNR. The obtained results show that the performance of all the methods increases as SNR grows. For the unconstrained methods, generally, ACDC performs better than FFDIAG, LUJ1D, and QRJ1D. The nonnegativity constraint obviously helps , , and to improve the results for lower SNR values. The performance of ACDC and remains stable for higher SNR values due to the small number of available sweeps and the lack of good initializations. Generally, the proposed and algorithms outperform the others when SNR is between -20 and 30 dB and perform similar to FFDIAG, LUJ1D, and QRJ1D when SNR is above 45 dB. The average numerical complexity and CPU time at each SNR level of all the methods in this experiment are shown in the bottom of Figure 3. It shows that the proposed methods achieve better estimations of A and cost less flops and CPU time than . The gives the best performance/complexity trade-off for all the considered SNR values.
Effect of dimension K
In ICA, the third dimension K of the three-way array  corresponds to the number of covariance matrices at different lags, or the number of matrix slices derived from a cumulant array. In this section, we study the influence of K on the performance of the seven algorithms. The first and second dimensions of are set to N = 5. The SNR value is fixed to 10 dB. We repeat the experiment with K ranging from 3 to 55. The top picture in Figure 4 shows the average curves of of all the algorithms as a function of K. For the five existing methods, ACDC, , FFDIAG, LUJ1D, and QRJ1D, their performance is quite stable with respect to K. The performance of the proposed methods progresses as K increases and then practically stabilizes for high values of K. It indicates that after some point (e.g., K ≥ 20), the additional information brought by an increase of K does not further improve the results. The proposed and algorithms maintain competitive advantages through all the K values. The two images in the bottom of Figure 4 present the average numerical complexity and CPU time of all the algorithms in this experiment, respectively. It shows that the numerical complexity of and is between that of ACDC and . The and methods seem to be the most effective algorithms compared to the other methods.
corresponds to the number of covariance matrices at different lags, or the number of matrix slices derived from a cumulant array. In this section, we study the influence of K on the performance of the seven algorithms. The first and second dimensions of are set to N = 5. The SNR value is fixed to 10 dB. We repeat the experiment with K ranging from 3 to 55. The top picture in Figure 4 shows the average curves of of all the algorithms as a function of K. For the five existing methods, ACDC, , FFDIAG, LUJ1D, and QRJ1D, their performance is quite stable with respect to K. The performance of the proposed methods progresses as K increases and then practically stabilizes for high values of K. It indicates that after some point (e.g., K ≥ 20), the additional information brought by an increase of K does not further improve the results. The proposed and algorithms maintain competitive advantages through all the K values. The two images in the bottom of Figure 4 present the average numerical complexity and CPU time of all the algorithms in this experiment, respectively. It shows that the numerical complexity of and is between that of ACDC and . The and methods seem to be the most effective algorithms compared to the other methods.
JDC performance versus dimension K . The first and second dimensions of and the SNR value are set to N=5 and SNR=10 dB, respectively. Top: the average error evolution of all the algorithms as a function of dimension K. Bottom: the average numerical complexities (left) and the CPU time (right) of all the algorithms, respectively.
Effect of coherence of D
In this experiment, the effect of the coherence of the third loading matrix D of the three-way array is evaluated. Let d n and d m denote the n-th and m-th columns of D, respectively. The angle ψn,m between d n and d m can be derived by using the following Euclidean dot product formula . Then, the coherence ρ of D is defined as the maximum absolute cosine of angle ψn,m between the columns of D as follows:
The quantity ρ is also known as the modulus of uniqueness of JDC [43]. By its definition (43), ρ falls in the range of [ 0,1]. The JDC problem is considered to be ill-conditioned when ρ is close to 1. Such an ill-conditioned problem can be met in ICA when A has nearly collinear column vectors. For example, in order to perform ICA, provided that all the sources are non-Gaussian, which is often the case in practice, we can build a three-way array  by stacking the matrix slices of the fourth-order cumulant array of the observation data. Then, the loading matrix D can be expressed as follows:
by stacking the matrix slices of the fourth-order cumulant array of the observation data. Then, the loading matrix D can be expressed as follows:
where is a (N × N) diagonal matrix with being the fourth-order cumulant of the n-th source, n ∈ {1,⋯,N}, and where ⊙ denotes the Khatri-Rao product. It can be observed that the coherence of the columns of A will influence the coherence of the matrix D. In the following test, the dimensions of the three-way array are set to N = 5 and K = 15. The SNR value is fixed to 10 dB. In order to control ρ, firstly, we randomly generate an orthogonal matrix  so that ρ = 0 by orthogonalizing a (15×5) random matrix. Secondly, we rotate its five columns such that all the internal angles between any columns are equal to a predefined value ψ. Therefore, ρ is only controlled by the angle ψ and equals to . We repeat the experiment with the angle ψ ranging from 0 to π/2 with a step of π/60. A small ψ value means a large ρ value. The top picture in Figure 5 displays the average curves of of all the algorithms as a function of ψ. It shows that the nonnegativity constrained methods , , and , outperform the unconstrained ones ACDC, FFDIAG, LUJ1D, and QRJ1D. The proposed algorithms are more efficient, particularly when the coherence level is high. The average numerical complexity and CPU time displayed in the bottom of Figure 5 indicate that the algorithm provides the best performance/complexity compromise, while the algorithm is also competitive with regard to .
so that ρ = 0 by orthogonalizing a (15×5) random matrix. Secondly, we rotate its five columns such that all the internal angles between any columns are equal to a predefined value ψ. Therefore, ρ is only controlled by the angle ψ and equals to . We repeat the experiment with the angle ψ ranging from 0 to π/2 with a step of π/60. A small ψ value means a large ρ value. The top picture in Figure 5 displays the average curves of of all the algorithms as a function of ψ. It shows that the nonnegativity constrained methods , , and , outperform the unconstrained ones ACDC, FFDIAG, LUJ1D, and QRJ1D. The proposed algorithms are more efficient, particularly when the coherence level is high. The average numerical complexity and CPU time displayed in the bottom of Figure 5 indicate that the algorithm provides the best performance/complexity compromise, while the algorithm is also competitive with regard to .
JDC performance versus coherence. The dimensions of and the SNR value are set to N = 5, K = 15, and SNR=10 dB, respectively. Top: the average error evolution of all the algorithms as a function of internal angle ψ between any two columns of D. Bottom: the average numerical complexities (left) and the CPU time (right) of all the algorithms, respectively.
Effect of condition number of D (k)
When the JDC problem is considered, a diagonal matrix D(k) could contain some diagonal elements which, despite being non-zero, are many orders of magnitude lower than some other elements, leading to an ill-conditioned matrix C(k). For the proposed methods, the inverse of such a matrix C(k) would contain numerical errors. In this experiment, we study the performance of the seven algorithms as a function of the condition number of one of the diagonal matrices D(k). The dimensions of the three-way array are set to N = 5 and K = 15. The SNR value is set to 10 dB. We vary the condition number of the first diagonal matrix D(1) from 1 to 1,000 by fixing the ratio of its largest diagonal element to its smallest diagonal element. The top picture in Figure 6 displays the average curves of the estimating error of the seven algorithms as a function of the condition number of D(1). The results reveal that a highly ill-conditioned diagonal matrix D(1) has a clear negative effect on the estimation accuracy of all the algorithms. The nonnegativity constrained methods , , and outperform the classical algorithms ACDC, FFDIAG, LUJ1D, and QRJ1D whatever the condition number is. The proposed and algorithms maintain advantages when the condition number is less than 100. Regarding the cases of larger condition numbers, is more superior since it does not need to invert the highly ill-conditioned matrix. It is worthy pointing out that in practice, we can choose these sufficiently well-conditioned matrices C(k) for the proposed methods, whose condition numbers are below a predefined threshold. In addition, a weighted cost function for which weights would depend on the condition number of each matrix can be considered. On the other hand, the performance of the classical methods can also be improved by choosing a particular subset of available matrices [57] and by properly weighting the cost functions [49]. In order to give a fair comparison, all the algorithms operate on the same set of matrices in all the experiments of this paper. In addition, the average numerical complexity and CPU time at each condition number of all the methods in this experiment are shown in the bottom of Figure 6. It shows that the proposed methods give the best performance/complexity trade-off compared to whatever the condition number is.
JDC performance versus condition number. The dimensions of and the SNR value are set to N = 5, K = 15, and SNR=10 dB, respectively. Top: the average error evolution of all the algorithms as a function of the condition number of one of the diagonal matrices D(k). Bottom: the average numerical complexities (left) and the CPU time (right) of all the algorithms, respectively.
Test with a non-square matrix A
As described in the section of practical issues, when a non-square matrix  with N>P is met in ICA, we propose to compress it by a nonnegative compression matrix
with N>P is met in ICA, we propose to compress it by a nonnegative compression matrix  [53], such that the resulting matrix is a (P × P) nonnegative square matrix. Then, the proposed methods can be applied to estimate . Similar to the classical prewhitening, the nonnegative compression step could introduce numerical errors. In this experiment, we compare our methods to ACDC and through a simulated ICA model. The latter algorithms can directly estimate a non-square matrix A from the fourth-order cumulant matrix slices. The ICA model is established as follows:
[53], such that the resulting matrix is a (P × P) nonnegative square matrix. Then, the proposed methods can be applied to estimate . Similar to the classical prewhitening, the nonnegative compression step could introduce numerical errors. In this experiment, we compare our methods to ACDC and through a simulated ICA model. The latter algorithms can directly estimate a non-square matrix A from the fourth-order cumulant matrix slices. The ICA model is established as follows:
where is the (N × 1) observation vector, is the (3 × 1) zero-mean unit-variance source vector whose elements are independently drawn from a uniform distribution over , is the (N × 1) zero-mean unit-variance Gaussian noise vector, and A is the (N × 3) nonnegative mixing matrix whose components are independently drawn from a uniform distribution over [ 0,1]. In this context, the SNR is defined by:
For the proposed and algorithms, the given realization of {x[f] } is compressed by means of a matrix  computed using the method proposed in [53], leading to a three-dimensional vector . We compute the fourth-order cumulant array of and choose the first three matrix slices in order to build a three-way array. Hence, and decompose a (3×3×3) array. Once the compressed mixing matrix is estimated, the original mixing matrix is obtained by Eq. 39. Regarding ACDC and , the fourth-order cumulant array of {x[f] } is directly computed without compression. We apply ACDC and on two three-way arrays with different third dimensions. The first array of dimension (N × N × 3) is built by choosing the first three matrix slices from the fourth-order cumulant array, while the second array of dimension (N × N× N) is built using the first N matrix slices. We study the impact of the number of observations N on the performance of the JDC algorithms, by varying N from 4 to 24. The SNR value is fixed to 5 dB. The number of samples used to estimate the cumulants is set to 103. Figure 7 shows the average curves of the estimating error of all the algorithms as a function of N. As it can be seen, when N ≤ 15, the larger the value of N, the more accurate estimation of A is achieved. When N > 15, the further increase of N does not bring significant improvement in terms of the estimation accuracy. ACDC and give better results when the array with a larger third dimension is considered. Their results on (N × N × N) arrays outperform the proposed methods when N = 4. also gives the best estimation on (N × N × N) arrays with N = 5. It suggests that the numerical errors introduced by the compression step limit the performance of the proposed methods when only a small number of observation is available. Such a negative effect can be partially compensated by using a large number of observations, since the proposed and methods maintain the highest performance in terms of estimation accuracy when N≥6. The performance ACDC and can be further improved by using a (N × N ×N2) array, which contains all the N2 fourth-order cumulant matrix slices. However, it leads to a higher numerical complexity especially for a large value of N. Regarding the proposed and methods, their performance can also be improved by using all the nine matrix slices of the fourth-order cumulant array of the compressed observation vector. Nevertheless, the experimental result has already shown that by using only a small number of matrix slices, and can maintain lower numerical complexities than ACDC and , while achieving better estimation results, when a large value of N is considered. Therefore, despite the negative influence of the nonnegative compression, the proposed methods still offer a good performance/complexity compromise to estimate a non-square matrix A.
computed using the method proposed in [53], leading to a three-dimensional vector . We compute the fourth-order cumulant array of and choose the first three matrix slices in order to build a three-way array. Hence, and decompose a (3×3×3) array. Once the compressed mixing matrix is estimated, the original mixing matrix is obtained by Eq. 39. Regarding ACDC and , the fourth-order cumulant array of {x[f] } is directly computed without compression. We apply ACDC and on two three-way arrays with different third dimensions. The first array of dimension (N × N × 3) is built by choosing the first three matrix slices from the fourth-order cumulant array, while the second array of dimension (N × N× N) is built using the first N matrix slices. We study the impact of the number of observations N on the performance of the JDC algorithms, by varying N from 4 to 24. The SNR value is fixed to 5 dB. The number of samples used to estimate the cumulants is set to 103. Figure 7 shows the average curves of the estimating error of all the algorithms as a function of N. As it can be seen, when N ≤ 15, the larger the value of N, the more accurate estimation of A is achieved. When N > 15, the further increase of N does not bring significant improvement in terms of the estimation accuracy. ACDC and give better results when the array with a larger third dimension is considered. Their results on (N × N × N) arrays outperform the proposed methods when N = 4. also gives the best estimation on (N × N × N) arrays with N = 5. It suggests that the numerical errors introduced by the compression step limit the performance of the proposed methods when only a small number of observation is available. Such a negative effect can be partially compensated by using a large number of observations, since the proposed and methods maintain the highest performance in terms of estimation accuracy when N≥6. The performance ACDC and can be further improved by using a (N × N ×N2) array, which contains all the N2 fourth-order cumulant matrix slices. However, it leads to a higher numerical complexity especially for a large value of N. Regarding the proposed and methods, their performance can also be improved by using all the nine matrix slices of the fourth-order cumulant array of the compressed observation vector. Nevertheless, the experimental result has already shown that by using only a small number of matrix slices, and can maintain lower numerical complexities than ACDC and , while achieving better estimation results, when a large value of N is considered. Therefore, despite the negative influence of the nonnegative compression, the proposed methods still offer a good performance/complexity compromise to estimate a non-square matrix A.
JDC performance on an ICA model versus number of observations. The number of sources P and the SNR value are set to P = 3 and SNR = 5 dB, respectively. Top: the average error evolution of all the algorithms as a function of the number of observations N. Bottom: the average numerical complexities (left) and the CPU time (right) of all the algorithms, respectively.
BSS application on MRS data
In this section, we aim to illustrate the potential capability of the proposed and algorithms for solving a real-life BSS problem by an application carried on simulated MRS data.
MRS is a powerful non-invasive analytical technique for analyzing the chemical content of MR-visible nuclei and therefore enjoys particular advantages for assessing metabolism. The chemical property of each nucleus determines the frequency at which it appears in the MR spectrum, giving rise to peaks corresponding to specific metabolites [58]. Therefore, the MRS observation spectra can be modeled as the mixture of the spectrum of each constitutional source metabolite. More specifically, it can be written as the noisy linear instantaneous mixing model described in Eq. 45, where  is the MRS observation vector,
is the MRS observation vector,  is the source vector representing the statistically quasi-independent source metabolites,
is the source vector representing the statistically quasi-independent source metabolites,  is the instrumental noise vector, and
is the instrumental noise vector, and  is the nonnegative mixing matrix containing the positive concentrations of the source metabolites. SNR is defined as in Eq. 46. In this experiment, two simulated MRS source metabolites {s1[f] } and {s2[f] }, namely the Choline (Cho) and Myo-inositol (Ins) (see Figure 8b), are generated by Lorentzian and Gaussian functions [59]. Each of the sources contains 103 samples. The observation vector x[f] is generated according to (45). The components of the (N×2) mixing matrix A are randomly drawn from a uniform distribution. The additive noise ν[f] is modeled as a zero-mean unit-variance Gaussian vector. The ICA methods based on the proposed and algorithms, namely -ICA and -ICA, consist of four steps: i) compressing {x[f] } by means of a matrix
is the nonnegative mixing matrix containing the positive concentrations of the source metabolites. SNR is defined as in Eq. 46. In this experiment, two simulated MRS source metabolites {s1[f] } and {s2[f] }, namely the Choline (Cho) and Myo-inositol (Ins) (see Figure 8b), are generated by Lorentzian and Gaussian functions [59]. Each of the sources contains 103 samples. The observation vector x[f] is generated according to (45). The components of the (N×2) mixing matrix A are randomly drawn from a uniform distribution. The additive noise ν[f] is modeled as a zero-mean unit-variance Gaussian vector. The ICA methods based on the proposed and algorithms, namely -ICA and -ICA, consist of four steps: i) compressing {x[f] } by means of a matrix  [53], ii) estimating the fourth-order cumulant array of the compressed observations and stacking all the cumulant matrix slices in a three-way array, iii) decomposing the resulting three-way array by means of and , respectively, and iv) reconstructing the sources. The -ICA and -ICA are compared to four state-of-the-art BSS algorithms, namely two efficient ICA methods CoM 2[54] and SOBI [47], the nonnegative ICA (NNICA) method with a line search along the geodesic [55], and the NMF method [56] based on alternating nonnegativity least squares. The performance is assessed by means of the error between the true source s[f] and its estimate , the numerical complexity, and the CPU time. To find out the detailed analysis of the numerical complexity of the classical ICA algorithms, the reader can refer to the book chapter [60]. Figure 8 shows an example of the separation results of all the methods with N = 32 observations and a SNR of 10 dB. Regarding CoM 2, SOBI, NNICA, and NMF, there are some obvious disturbances presented in the estimated metabolites. As far as -ICA and -ICA are concerned, the estimated source metabolites are quasi-perfect. Furthermore, the comprehensive performance of all the methods will be studied by the following experiments with 200 independent Monte Carlo trials.
[53], ii) estimating the fourth-order cumulant array of the compressed observations and stacking all the cumulant matrix slices in a three-way array, iii) decomposing the resulting three-way array by means of and , respectively, and iv) reconstructing the sources. The -ICA and -ICA are compared to four state-of-the-art BSS algorithms, namely two efficient ICA methods CoM 2[54] and SOBI [47], the nonnegative ICA (NNICA) method with a line search along the geodesic [55], and the NMF method [56] based on alternating nonnegativity least squares. The performance is assessed by means of the error between the true source s[f] and its estimate , the numerical complexity, and the CPU time. To find out the detailed analysis of the numerical complexity of the classical ICA algorithms, the reader can refer to the book chapter [60]. Figure 8 shows an example of the separation results of all the methods with N = 32 observations and a SNR of 10 dB. Regarding CoM 2, SOBI, NNICA, and NMF, there are some obvious disturbances presented in the estimated metabolites. As far as -ICA and -ICA are concerned, the estimated source metabolites are quasi-perfect. Furthermore, the comprehensive performance of all the methods will be studied by the following experiments with 200 independent Monte Carlo trials.
BSS results on MRS data. An example of the results of blind separation of two simulated MRS metabolites. The number of observations N is set to 32, and the SNR value is 10 dB. (a) Cho and Ins source metabolites. (b) Two of the observations. (c-h) Separated metabolites by -ICA, -ICA, CoM 2, SOBI, NNICA, and NMF, respectively.
In the first experiment, the effect of the number of observations N is evaluated. The SNR is fixed to 10 dB. The six methods are compared with N ranging from 4 to 116 with a step of 4. The average curves of error as a function of N are shown in the left image of Figure 9. It can be seen that the estimating errors of all the methods improve as N increases. It suggests that in noisy BSS contexts, using more sensors often yields better results. The proposed -ICA and -ICA methods maintain the competitive advantages. The average curves of the numerical complexities of this experiment are shown in the bottom left picture of Figure 9. We can notice that the numerical complexities of all the methods increase with N. The complexities of -ICA and -ICA seem identical in the logarithmic scaled plot, which is because theoretically their complexities are mainly dominated by the computation of the nonnegative compression step and of the cumulants. Indeed, -ICA is more computationally efficient than -ICA in the step of CP decomposition of the cumulant array. This can be verified by the average CPU time of those methods, shown in the bottom right image of Figure 9. We can observe that -ICA is slower than CoM 2, but it is faster than NNICA, SOBI, and NMF.
BSS performance on MRS data versus the number of observations. Average results of blind separation of two simulated MRS metabolites. The SNR value is set to 10 dB. Left: the average error evolution of all the algorithms as a function of the number of observations. Right: the average numerical complexities (top) and the CPU time (bottom) of all the algorithms, respectively.
In the second experiment, we study the influence of SNR on the performance of the six methods. The number of observations N is set to 32. SNR is varied from 0 to 50 dB with a step of 2 dB. The average curves of the estimating error as well as those of the numerical complexities and CPU time as a function of SNR of all the six methods are shown in Figure 10. The proposed -ICA and -ICA methods provide the best estimation results with moderate computational complexities and CPU time. Generally speaking, the -ICA algorithm offers the best performance/complexity trade-off in this BSS experimental context.
BSS performance on MRS data versus SNR. Average results of blind separation of two simulated MRS metabolites. The number of observations is set to N=32. Left: the average error evolution of all the algorithms as a function of SNR. Right: the average numerical complexities (top) and the CPU time (bottom) of all the algorithms, respectively.
Conclusions
We have proposed two methods, called and , in order to achieve the CP decomposition of semi-nonnegative semi-symmetric three-way arrays. The nonnegativity constraint is imposed on the two symmetric modes of three-way arrays by means of a square change of variable, giving rise to an unconstrained joint diagonalization by congruence problem. Therefore, the nonnegative loading matrix can be estimated by computing the joint diagonalizer. We consider the elementary LU and QR parameterizations of the Hadamard square root of the nonnegative joint diagonalizer, leading to two Jacobilike optimization procedures. In each Jacobi-like iteration, the optimization is formulated into a minimization of a polynomial or rational function with respect to only one parameter. In addition, the numerical complexity for each algorithm has been analyzed.
The performance of the proposed and algorithms is evaluated with simulated semi-nonnegative semi-symmetric three-way arrays. Four classical nonorthogonal JDC methods without nonnegativity constraints including ACDC [23], FFDIAG [25], LUJ1D [26], and QRJ1D [26] and one nonnegative JDC method [41] are tested as reference methods. The performance is assessed in terms of the matrix estimation accuracy, the numerical complexity, and the CPU time. The convergence property, the influence of SNR, the impact of dimension, the effect of coherence, and the influence of condition number are extensively studied by Monte Carlo experiments. The obtained results show that the proposed algorithms offer better estimation accuracy by means of exploiting the nonnegativity a priori. The algorithm provides the best performance/complexity compromise.
The proposed algorithms are suitable tools for solving the ICA problems where a nonnegative mixing matrix is considered, such as in MRS. In this case, the three-way array built by stacking the matrix slices of a HO cumulant array fulfills the semi-nonnegative semi-symmetric structure. We proposed two ICA methods, namely -ICA and -ICA, based on CP decomposition of the fourth-order cumulant array using and , respectively. The source separation ability of the proposed algorithms is verified through a BSS application carried out on simulated MRS data. The -ICA and -ICA are compared to one NMF method [56], one nonnegative ICA method [55], and two classical ICA methods, namely CoM 2[54] and SOBI [47]. The performance is comprehensively studied as a function of the number of observations and of SNR. The experimental results demonstrate the improvement of the proposed methods in terms of the source estimation accuracy and also show that exploiting the two a priori of the data, namely the nonnegativity of the mixing matrix and the statistical independence of the sources, allows us to achieve better estimation results. The -ICA algorithm provides the best performance/complexity trade-off.
References
Smilde A, Bro R, Geladi P: Multi-way Analysis: Applications in the Chemical Sciences. Wiley, West Sussex; 2004.
de Almeida ALF, Favier G, Ximenes LR: Space-time-frequency (STF) MIMO communication systems with blind receiver based on a generalized PARATUCK2 model. IEEE Trans. Signal Process 2013, 61(8):1895-1909.
De Vos M, Vergult A, De Lathauwer L, De Clercq W, Van Huffel S, Dupont P, Palmini A, Van Paesschen W: Canonical decomposition of ictal scalp EEG reliably detects the seizure onset zone. Neuroimage 2007, 37(3):844-854. 10.1016/j.neuroimage.2007.04.041
Comon P, Luciani X, de Almeida ALF: Tensor decompositions, alternating least squares and other tales. J. Chemometr 2009, 23: 393-405. 10.1002/cem.1236
Tucker LR: Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31(3):279-311. 10.1007/BF02289464
De Lathauwer L, De Moor B, Vandewalle J: A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl 2000, 21(4):1253-1278. 10.1137/S0895479896305696
Kruskal JB: Three-way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Lin. Algebra Appl 1977, 18(2):98-138.
Hitchcock FL: The expression of a tensor or a polyadic as a sum of products. J. Math. Phys 1927, 6(1):164-189.
Kroonenberg PM: Applied Multiway Data Analysis. Wiley, Hoboken; 2008.
Sidiropoulos ND, Bro R, Giannakis GB: Parallel factor analysis in sensor array processing. IEEE Trans. Signal Process 2000, 48(8):2377-2388. 10.1109/78.852018
de Almeida ALF, Favier G, Motab JCM: PARAFAC-based unified tensor modeling for wireless communication systems with application to blind multiuser equalization. Signal Process 2007, 87(2):337-351. 10.1016/j.sigpro.2005.12.014
de Almeida ALF, Favier G: Double Khatri-Rao space-time-frequency coding using semi-blind PARAFAC based receiver. IEEE Signal Process. Lett 2013, 20(5):471-474.
Albera L, Ferréol A, Comon P, Chevalier P: Blind identification of overcomplete mixtures of sources (BIOME). Lin. Algebra Appl 2004, 391: 3-30.
Röemer F, Haardt M: Tensor-based channel estimation and iterative refinements for two-way relaying with multiple antennas and spatial reuse. IEEE Trans. Signal Process 2010, 58(11):5720-5735.
Harshman RA, Lundy ME: PARAFAC: parallel factor analysis. Comput. Stat. Data Anal 1994, 18(1):39-72. 10.1016/0167-9473(94)90132-5
Uschmajew A: Local convergence of the alternating least squares algorithm for canonical tensor approximation. SIAM. J. Matrix Anal. Appl 2012, 33(2):639-652. 10.1137/110843587
Rajih M, Comon P, Harshman RA: Enhanced line search: a novel method to accelerate PARAFAC. SIAM J. Matrix Anal. Appl 2008, 30(3):1128-1147. 10.1137/06065577
Acar E, Dunlavy DM, Kolda TG: A scalable optimization approach for fitting canonical tensor decompositions. J. Chemometr 2011, 25(2):67-86. 10.1002/cem.1335
Röemer F, Haardt M: A semi-algebraic framework for approximate CP decompositions via simultaneous matrix diagonalizations (SECSI). Signal Process 2013, 93(9):2722-2738. 10.1016/j.sigpro.2013.02.016
Luciani X, Albera L: Canonical polyadic decomposition based on joint eigenvalue decomposition. Chemometr. Intell. Lab 2014, 132: 152-167.
Carroll JD, Chang J-J: Analysis of individual differences in multidimensional scaling via an n-way generalization of Eckart-Young decomposition. Psychometrika 1970, 35(3):283-319. 10.1007/BF02310791
Husson F, Pagés J: INDSCAL model: geometrical interpretation and methodology. Comput. Stat. Data Anal 2006, 50(2):358-378. 10.1016/j.csda.2004.08.005
Yeredor A: Non-orthogonal joint diagonalization in the least-squares sense with application in blind source separation. IEEE Trans. Signal Process 2002, 50(7):1545-1553. 10.1109/TSP.2002.1011195
Cardoso JF, Souloumiac A: Jacobi angles for simultaneous diagonalization. SIAM J. Matrix Anal. Appl 1996, 17: 161-164. 10.1137/S0895479893259546
Ziehe A, Laskov P, Nolte G, Muller K-R: A fast algorithm for joint diagonalization with non-orthogonal transformations and its application to blind source separation. J. Mach. Learn. Res 2004, 5: 777-800.
Afsari B: Simple LU and QR based non-orthogonal matrix joint diagonalization. In ICA 2006, Springer LNCS 3889. Charleston, SC, USA; 5–8 March 2006.
Van der Veen AJ: Joint diagonalization via subspace fitting techniques. In Proc. ICASSP ‘01. Salt Lake, City, UT; 7–11 May 2001:2773-2776.
Yeredor A: On using exact joint diagonalization for noniterative approximate joint diagonalization. IEEE Signal Process. Lett 2005, 12(9):645-648.
Vollgraf R, Obermayer K: Quadratic optimization for simultaneous matrix diagonalization. IEEE Trans. Signal Process 2006, 54(9):3270-3278.
Li XL, Zhang XD: Nonorthogonal joint diagonalization free of degenerate solution. IEEE Trans. Signal Process 2007, 55(5):1803-1814.
Souloumiac A: Nonorthogonal joint diagonalization by combining Givens and hyperbolic rotations. IEEE Trans. Signal Process 2009, 57(6):2222-2231.
Xu XF, Feng DZ, Zheng WX: A fast algorithm for nonunitary joint diagonalization and its application to blind source separation. IEEE Trans. Signal Process 2011, 59(7):3457-3463.
Chabriel G, Barrère J: A direct algorithm for nonorthogonal approximate joint diagonalization. IEEE Trans. Signal Process 2012, 60(1):39-47.
Chabriel G, Kleinsteuber M, Moreau E, Shen H, Tichavský P, Yeredor A: Joint matrices decompositions and blind source separation: A survey of methods, identification, and applications. IEEE Signal Process. Mag 2014, 31(3):34-43.
Lee DD, Seung HS: Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401(6755):788-791. 10.1038/44565
Zhang Q, Wang H, Plemmons RJ, Pauca VP: Tensor methods for hyperspectral data analysis: a space object material identification study. J. Opt. Soc. Am. A. Opt. Image Sci. Vis 2008, 25(12):3001-3012. 10.1364/JOSAA.25.003001
Royer J-P, Thirion-Moreau N, Comon P: Computing the polyadic decomposition of nonnegative third order tensors. Signal Process 2011, 91(9):2159-2171. 10.1016/j.sigpro.2011.03.006
Cichocki A, Zdunek R, Phan AH, Amari S: Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory Multi-way Data Analysis and Blind Source Separation. Wiley, West Sussex; 2009.
Zhou GX, Cichocki A, Zhao Q, Xie SL: Nonnegative matrix and tensor factorizations : an algorithmic perspective. IEEE Signal Process. Mag 2014, 31(3):54-65.
Coloigner J, Karfoul A, Albera L, Comon P: Line search and trust region strategies for canonical decomposition of semi-nonnegative semi-symmetric 3rd order tensors. Lin. Algebra Appl 2014, 450(1):334-374.
Wang L, Albera L, Kachenoura A, Shu HZ, Senhadji L: Nonnegative joint diagonalization by congruence based on LU matrix factorization. IEEE Signal Process. Lett 2013, 20(8):807-810.
Wang L, Albera L, Kachenoura A, Shu HZ, Senhadji L: CP decomposition of semi-nonnegative semi-symmetric tensors based on QR matrix factorization. In SAM’14, Proceedings of the Eighth IEEE Sensor Array and Multichannel Signal Processing Workshop. A Coruna, Spain; 22–25 June 2014:449-452.
Afsari B: Sensitivity analysis for the problem of matrix joint diagonalization. SIAM J. Matrix Anal. Appl 2008, 30(3):1148-1171. 10.1137/060655997
Wax M, Sheinvald J: A least-squares approach to joint diagonalization. IEEE Signal Process. Lett 1997, 4(2):52-53.
Dégerine S, Kane E: A comparative study of approximate joint diagonalization algorithms for blind source separation in presence of additive noise. IEEE Trans. Signal Process 2007, 55(6):3022-3031.
Fadaili EM, Thirion-Moreau N, Moreau E: Nonorthogonal joint diagonalization/zero diagonalization for source separation based on time-frequency distributions. IEEE Trans. Signal Process 2007, 55(5):1673-1687.
Belouchrani A, Abed-Meraim K, Cardoso JF, Moulines E: A blind source separation technique using second-order statistics. IEEE Trans. Signal Process 1997, 45(2):434-444. 10.1109/78.554307
Pham DT: Joint approximate diagonalization of positive definite Hermitian matrices. SIAM J. Matrix Anal. Appl 2001, 22: 1837-1848.
Tichavský P, Yeredor A: Fast approximate joint diagonalization incorporating weight matrices. IEEE Trans. Signal Process 2009, 57(3):878-891.
Chu M, Diele F, Plemmons R, Ragni S: Optimality computation and interpretation of nonnegative matrix factorizations. Technical report, Wake Forest University 2004
Meyer CD: Matrix Analysis and Applied Linear Algebra. SIAM, Philadelphia; 2000.
Vaidyanathan PP: Multirate Systems and Filter Banks. PTR Prentice Hall, United States; 1993.
Wang L, Kachenoura A, Albera L, Karfoul A, Shu HZ, Senhadji L: Nonnegative compression for semi-nonnegative independent component analysis. In SAM’14, Proceedings of the Eighth IEEE Sensor Array and Multichannel Signal Processing Workshop. A Coruna, Spain; 22–25 June 2014:81-84.
Comon P: Independent component analysis, a new concept? Signal Process 1994, 36(3):287-314. 10.1016/0165-1684(94)90029-9
Plumbley MD: Algorithms for nonnegative independent component analysis. IEEE Trans. Neural Netw 2003, 14(3):534-543. 10.1109/TNN.2003.810616
Kim H, Park H: Nonnegative matrix factorization based on alternating nonnegativity constrained least squares and active set method. SIAM J. Matrix Anal. Appl 2008, 30(2):713-730. 10.1137/07069239X
De Lathauwer: Algebraic methods after prewhitening. In Handbook of Blind Source Separation, ed. by P Comon, C Jutten,. Elsevier, Oxford; 2010:155-177. Chap. 5
Befroy DE, Shulman GI: Magnetic resonance spectroscopy studies of human metabolism. Diabetes 2011, 60(5):1361-1369. 10.2337/db09-0916
Moussaoui S: Séparation de sources non-négatives: application au traitement des signaux de spectroscopie. PhD thesis, Université Henri Poincaré, (2005)
Albera L, Comon P, Parra LC, Karfoul A, Kachenoura A, Senhadji L: Biomedical applications. In Handbook of Blind Source Separation ed. by P Comon, C Jutten,. Elsevier, Oxford; 2010:737-777. Chap. 18
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, L., Albera, L., Kachenoura, A. et al. Canonical polyadic decomposition of third-order semi-nonnegative semi-symmetric tensors using LU and QR matrix factorizations. EURASIP J. Adv. Signal Process. 2014, 150 (2014). https://doi.org/10.1186/1687-6180-2014-150
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2014-150
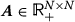 is randomly drawn from a uniform distribution on the interval [ 0,1]. The loading matrix
is randomly drawn from a uniform distribution on the interval [ 0,1]. The loading matrix 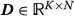 is drawn from a Gaussian distribution with a mean of 1 and a deviation of 0.5. The pure array
is drawn from a Gaussian distribution with a mean of 1 and a deviation of 0.5. The pure array  is perturbed by a residual INDSCAL noise array
is perturbed by a residual INDSCAL noise array  . The loading matrices of
. The loading matrices of  are drawn from a zero-mean unit-variance Gaussian distribution. The resulting noisy three-way array can be written as follows:
are drawn from a zero-mean unit-variance Gaussian distribution. The resulting noisy three-way array can be written as follows: 








