- Research
- Open access
- Published:
On the statistical convergence of bias in mode-based Kalman filter for switched systems
EURASIP Journal on Advances in Signal Processing volume 2018, Article number: 71 (2018)
Abstract
Many physical and engineered systems (e.g., smart grid, autonomous vehicles, and robotic systems) that are observed and controlled over a communication/cyber infrastructure can be efficiently modeled as stochastic hybrid systems (SHS). This paper quantifies the bias of a mode-based Kalman filter commonly used for state estimation in SHS. The main approach involves modeling the bias dynamics as a transformed switched system and the transitions across modes are abstracted via arbitrary switching signals. This general model effectively captures a wide range of SHS systems where the modes may follow deterministic, Markovian, or guard condition based transitions. By leveraging techniques developed to analyze the stability of switched systems, we derive conditions for statistical convergence of the bias in a mode-based Kalman filter in the presence of mode mismatch errors. Developed upon the foundations of Lyapunov theory, we demonstrate a linear matrix inequality condition that guarantees asymptotic stability of the corresponding autonomous switched system irrespective of the choice of mode mismatch probability. Furthermore, we obtain the range of mode mismatch probabilities that assures bounded input bounded output stability of the bias dynamics for both stable and unstable SHS. Using numerical simulations of a smart grid with network topology errors, we verify and validate the theoretical results and demonstrate the potency of using the analysis in critical infrastructures.
1 Introduction
Stochastic hybrid systems (SHS) represent a class of dynamical systems that experience interactions of both discrete and continuous dynamics with uncertainty. The uncertainty can be modeled in continuous dynamics, discrete state transitions, or both. In most cases, the evolution of continuous state is described via stochastic differential/difference equation (SDE) whereas the discrete state evolves depending on the application. Typical examples include random process (such as Markov chain) and guard conditions (i.e., the discrete state transitions depend on the continuous state). The first type of SHS has been applied in modeling of biochemical processes [1, 2], manufacturing processes [3], and communication networks [4]. The second type of SHS, also known as state-dependent SHS, finds application in flight management systems [5, 6]. For more complex systems such as a microgrid [7], the transitions of discrete state may be governed by both random processes and guard conditions.
1.1 Motivating example: impact of smart grid network topology error
Our conventional power grid is transitioning to a “smart grid” with the addition of renewable energy source (e.g., photovoltaics (PV)), advanced metering and sensing infrastructure, electric vehicles, and controllable loads [7]. A conceptual small-scale smart grid model is shown in Fig. 1. This toy model includes a bank of PV panels, electricity grid, home loads, and electric vehicles. S1, S2, S3, and S4 are switches whose status determine the network topology. In practice, S2 can be switched OFF when people unplug their electric vehicles and S1, S3, and S4 can be switched ON or OFF based on power demand and the weather. To aid state estimation in a smart grid, there are typically two types of data collected [8]:
-
1
Status data for switches, breakers, and communication links. Status data defines the real-time network topology of the grid.
-
2
Analog data such as bus voltage, power flow, and reactance. Analog data is used to determine the voltage profile at different nodes of the power grid.
In general, a smart grid can be formally modeled as an SHS with each switch status determining a specific network topology (discrete state) and continuous state capturing the analog parameter dynamics. A typical estimator for the continuous dynamics is a mode-based Kalman filter [9–17] which relies on mode information. Discrete mode information may be obtained from status data entered by human operators or sensor measurements or estimated based on measurements. These approaches are error prone due to human errors, missing data, communication, or estimation errors. Consequently, errors in status data result in network topology errors which eventually lead to performance degradation in a mode-based Kalman filter. In this work, we explore the impact of discrete state estimation error (or inaccurate information) on the quality of continuous state estimation derived via a mode-based Kalman filter.
1.2 Related work
State estimation in SHS has attracted research interest for decades. Kalman filter-based solutions dominate the arena. For one category of SHS where both discrete and continuous states are observable and the discrete state transitions are independent with continuous state, mode-based Kalman filter can be applied as a minimum mean square error (MMSE) estimator [10–12]. Matei et al. [13] proposes a Kalman filter-based MMSE estimator for SHS with observation of continuous state and delayed measurement of discrete state. Matei and Baras [14] expand their results to the case of delayed observations of both continuous and discrete states. In general SHS applications, discrete state may not be directly observable [12, 15–21]. In this case, the optimal estimator is obtained from a weighted sum of a bank of Kalman filters with each matched to a possible mode. Therefore, it requires exponentially increasing memory and computing time. A couple of hybrid estimation algorithms have been proposed for Markov jump linear system (MJLS), such as interacting multiple model (IMM) algorithm [19] and multiple model adaptive estimation (MMAE) algorithm [20, 21]. Seah and Hwang [15] and Liu et al. [16] extend the IMM algorithm to state-dependent SHS. Note that all the abovementioned algorithms require online computation with a bank of Kalman filters and they suffer from high computational complexity. Zhang and Natarajan [17]and Hofbaur et al. [18] decrease the complexity by formulating the mode estimation as a problem of belief-state update and using only one Kalman filter corresponding to estimated mode for continuous state estimation.
As the preceding discussion suggests, Kalman filter plays an essential role in most of the estimation algorithms for SHS. When the discrete states are known, Kalman filter is an optimal estimator; when the discrete states are not available, the optimal estimator is obtained from a bank of Kalman filters. In practice, there are cases that we have information on the discrete states but the information is not accurate as discussed in the motivating example. In this situation, one approach is to implement a bank of Kalman filters at the cost of the exponentially increasing memory and computing time. Another option is to treat the known discrete state as the true state and conduct estimation via only one Kalman filter. This Kalman filter is optimal if there is no mode mismatch. In case of a mode mismatch, the resulting estimator will be biased. Review of the recent literature reveals that there is limited prior work that considers the bias of a mode-based Kalman filter in SHS estimation. For non-hybrid scenarios, Kalman filter is proved to be an unbiased estimator. Therefore, multiple papers have analyzed the performance of Kalman filters by only focusing on error covariance [22–30]. Specifically, [22–28, 30] consider dynamical system with missing measures, intermittent observations, random delays, and packet dropouts and they follow the similar approach of deriving a bound for the critical probability of missing observation that ensures the convergence of error covariance. Another work [31] considers an estimation problem where the model for the Kalman filter is mismatched with the true system. Unlike the previous mentioned papers, [31] studies the residual of Kalman filter and derives mean and covariance of the Kalman filter residual without analyzing its convergence behavior. In terms of estimation strategies for SHS, there have been several prior efforts [32–35]. Their analysis is based on MMAE algorithm and the IMM approach. Hwang et al. [32] first consider the problem of quantifying performance of a hybrid estimation algorithm and derive the condition for exponential convergence of the estimator in terms of detection delay and sojourn time [33]. In [34, 35], the authors extend their research on evaluating the stability of IMM algorithm and they focus on the mean and covariance of the Kalman filter residual. However, the existing research efforts have not explored the relationship between mode mismatch error and SHS estimation. It is not known as to how discrete state estimation error influences the performance of a mode-based Kalman filter. How sensitive is the convergence of bias in a mode-based Kalman filter to errors in discrete state knowledge? Is there a critical region within which the error dynamics in a mode-based Kalman filter will converge? These are the fundamental unanswered questions that our work seeks to address.
1.3 Contributions
In this paper, we study the statistical convergence of the bias dynamics in a mode-based Kalman filter in the presence of mode mismatch errors. To our best knowledge, our work is the first attempt to quantify the influence of inaccurate mode information on continuous state estimation process. Specifically, we consider a linear SHS framework that finds application in many practical system, e.g., smart grid and aircraft management system. In our previous work [36], we derived the dynamics of bias that results from mode mismatch errors for a specific model of SHS with two discrete states. Additionally, the discrete state transitions were modeled via independent and identically distributed (i.i.d) binary Bernoulli random variables. For this specific system, we derived the sufficient condition for statistical convergence of bias. In contrast to the conference paper, the assumptions of two modes and i.i.d. Bernoulli transitions are relaxed in this work. The extension is not trivial because for SHS with two modes, there is only one error mode for a given discrete state. Therefore, in this work, we take a fresh perspective and propose to use a transformed switched system to describe the bias dynamics. The convergence of the bias is then mapped to the stability of the transformed switched system. The SHS model considered in this paper is general and can be applied to many practical systems. The novelty of this work lies in modeling the bias dynamics as a transformed switched system enabling us to exploit techniques developed for stability analysis of switched system to our problem of interest. Specifically, the stability analysis involves two stages. First, we consider stability of the corresponding autonomous switched system and derive sufficient and necessary conditions that guarantee asymptotic stability. Second, we investigate the bounded input bounded output stability and acquire a tolerant region on probability of mode mismatch errors that guarantees the convergence of the bias dynamics. The boundedness of the input is related to the stability of the original SHS and we consider both stable and unstable cases. Finally, the theoretical results are verified and validated using numerical simulations of a smart grid with network topology errors. Theoretical and numerical results help us identify the fidelity required in discrete state knowledge in order to meet the performance requirements of continuous state estimates.
The rest of the paper is organized as follows: The system model, mode-based Kalman filter, and its performance metrics are introduced in Section 2. In Section 3, we derive the bias dynamics and the model of a transformed system that fully captures the bias evolution. The stability analysis for the transformed system is discussed in Section 4. The stability conditions and tolerant region for mode mismatch error are also derived as the main results in Section 4. Two experiments are conducted, and the simulation results are presented in Section 4. We conclude this work and discuss future directions in Section 6.
2 Preliminaries
2.1 Notations
We use normal face to define scalars; bold face to define vectors (lower case) and matrices (upper case); I and 0 denote identity matrix and zero-vector, respectively. \({\mathbb {R}}\) denote the space of real number. For any set, |·| denotes the numbers of elements in the set. ρ(·) denotes the spectral radius of any square matrix. ∥·∥ represents 2-norm of a matrix or a vector. [·]′ and [·]−1 denote transpose and inverse of a matrix, respectively. For any vector u, u[i] denotes ith element of the vector. For a symmetric matrix A, A≻0 denotes that A is positive definite and A≺0 indicates that A is negative definite. \({\mathbb {E}}(\cdot)\) represents expectation and \({\mathbb {P}}(\cdot)\) represents probability measure.
2.2 System model
We consider a discrete-time autonomous linear SHS. Mathematically, the continuous state \({\mathbf {x}}_{k} \in \mathbb {R}^{n}\) and measurement \({\mathbf {y}}_{k} \in \mathbb {R}^{m}\) are related via the following equations:
Here, \({{q}}_{k} \in {\mathcal {Q}}\) represents the discrete state at time k, which is sometimes referred to as the mode. Without loss of generality, we define \({\mathcal {Q}} = \left \{1,2,3,\ldots,d\right \}\). For each qk, the corresponding \(\phantom {\dot {i}\!}{\mathbf {A}}_{{{q}}_{k}}\) is an n-by-n matrix, \(\phantom {\dot {i}\!}{\mathbf {B}}_{{{q}}_{k}}\) is an n-by-p matrix, and \(\phantom {\dot {i}\!}{\mathbf {C}}_{{{q}}_{k}}\) is a m-by-n matrix. Regarding the system model, we have the following assumptions:
-
1
\({\mathbf {w}}_{k} \sim \mathcal {N}(\mathbf {0},{\mathbf {Q}})\) and \({\mathbf {v}}_{k} \sim \mathcal {N}(\mathbf {0},{\mathbf {R}})\) are mutually independent white Gaussian capturing model and measurement uncertainty, respectively.
-
2
The initial distribution of the continuous state follows a Gaussian distribution
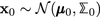 . The discrete state has a unique initial mode \({{q}}_{0} \in {\mathcal {Q}}\).
. The discrete state has a unique initial mode \({{q}}_{0} \in {\mathcal {Q}}\). -
3
For all \({{q}}_{k} \in {\mathcal {Q}}\), \(\left ({\mathbf {A}}_{{{q}}_{k}},{\mathbf {B}}_{{{q}}_{k}} {\mathbf {Q}} {\mathbf {B}}^{\prime }_{{{q}}_{k}}\right)\) is controllable and \(\phantom {\dot {i}\!}\left ({\mathbf {C}}_{{{q}}_{k}},{\mathbf {A}}_{{{q}}_{k}}\right)\) is observable.
In this paper, we consider a generalized SHS model without restricting ourselves to any specific type of discrete state transitions. At a higher level, the generalized SHS can be astracted as a switched system with arbitrary switching. This allows us to neglect specific details of the discrete state behavior and instead incorporate all possible switching patterns [37]. With this connection between switched system and the generalized SHS model in mind, we confine ourselves to the convention of switched systems with arbitrary switching signals throughout the remainder of this paper.
As an illustrative example, we consider a toy smart grid setup inspired by [7, 38]. The system consists of three components—main distribution grid, local power network, and electrical loads. The discrete status for each component is:
-
Local power network—On: 1, Failure mode: 0;
-
Distribution grid (G)—Connected: 1, Disconnected: 0;
-
Electrical loads (D)—Connected: 1, Disconnected: 0.
The corresponding power generation and power consumption dynamics are given below:
-
Grid power: If the micro grid is connected to the main electricity grid (G=1), the grid power PG has the following dynamics: \({\dot {P}_{G}} = k_{G} {P_{G}} + \sigma _{G} dW\), where kG is a proportional coefficient and σG is a variation parameter [7]. If G=0, both kG and σG are close to 0. dW denotes Wiener process.
-
Electrical loads: Electrical loads can be modeled via a stochastic differential equation. We use Uhlenbeck-Ornstein model to describe electricity loads [38]. Let \({\dot {P}_{D}} = \alpha (m - {P_{D}}) dt + \sigma _{D} dW\). Here, we assume m=0. α represents a tracking coefficient. σD is a variation coefficient, and dW denotes Wiener process.
Therefore, the continuous state in this smart grid system can be defined as x=[PG,PD]′ with corresponding state equation as:
By discretizing the state space with a sampling period of τ, we get a discrete-time SHS:
where
and
Here, the index k corresponds to the time instant kτ. The discrete state space is defined by combination of different status of L, G, and D. Consequently, the value of parameters kG,α, σG, and σD are determined by different discrete states. The measurement equation corresponds to
We will provide more details on this smart grid model in Section 5.2.
2.3 Mode-based Kalman filter
The goal of a mode-based Kalman filter is to estimate xk based on knowledge of discrete states \({\hat {q}}_{k}\) and measurements yk until time k. Note that the known mode \({\hat {q}}_{k}\) can be inconsistent with the true mode qk resulting in a mode mismatch error. Denote the measurement sequence and known mode sequence up to time k as ysk=(y1,⋯,yk) and \({\hat {\mathbf {q}}^{s}}_{k} = ({\hat {q}}_{1}, \cdots, {\hat {q}}_{k})\), respectively. The mode-based Kalman filter equations for switched system in (1) are given in Algorithm 1.

Here, \({\mathbf {K}}_{{\hat {q}}_{i},i}\) is the Kalman gain related to mode \({\hat {q}}_{i}\). xk|k is the estimate of xk, and we denote it as \({\hat {\mathbf {x}}}_{k}\). If the estimator has full knowledge of the actual mode, i.e., \({\hat {\mathbf {q}}^{s}}_{k} = {\mathbf {q}^{s}_{k}}\), then the mode-based Kalman filter has been proven to be an unbiased minimum mean square error estimator. However, \({\hat {\mathbf {q}}^{s}}_{k} = {\mathbf {q}^{s}_{k}}\) does not always hold in practice. As a consequence, the inconsistency between \({\mathbf {q}^{s}_{k}}\) and \({\hat {\mathbf {q}}^{s}}_{k}\) results in a bias in the mode-based Kalman filter estimate. In the following, we will first derive the formulation of bias dynamics and then discuss its statistical convergence.
2.4 Bias dynamics in the presence of mode mismatch
In general, the bias is defined as the difference between the estimator and the actual value of a state. However, for a mode-based Kalman filter, both \({\hat {\mathbf {x}}}_{k}\) and xk are random variables which result in the bias being a random variable. Therefore, we define the bias to be the difference between means of estimator and the true state, i.e., \({\mathbf {e}}_{k} = {\mathbb {E}}({\hat {\mathbf {x}}}_{k}) - {\mathbb {E}}({\mathbf {x}}_{k})\). In other words, we capture the difference between \({\hat {\mathbf {x}}}_{k}\) and xk in a mean sense via ek. This metric is similar to those considered in [31, 32]. Based on Algorithm 1, we derive the bias dynamics in a Kalman filter due to mismatch between \({\mathbf {q}^{s}_{k}}\) and \({\hat {\mathbf {q}}^{s}}_{k}\).
Theorem 1
Given the actual mode sequence \({\mathbf {q}^{s}_{k}} = ({{q}}_{1}, \cdots, {{q}}_{k})\) and estimated mode sequence \({\hat {\mathbf {q}}^{s}}_{k} = ({\hat {q}}_{1}, \cdots, {\hat {q}}_{k})\), the bias dynamics in a mode-based Kalman filter corresponds to:
Proof
The expectation of xk is:
The stochasticity of the estimate \({\hat {\mathbf {x}}}_{k}\) comes from the randomness in the measurements. Therefore, we can write the mean of \({\hat {\mathbf {x}}}_{k}\) as:
From the definition of bias ek, we have:
Substituting for \({\mathbb {E}}({\hat {\mathbf {x}}}_{k-1}) = {\mathbf {e}}_{k-1} + {\mathbb {E}}({\mathbf {x}}_{k-1})\), we get:
□
For the sake of compactness in notation, we introduce t and i to denote actual mode and estimated mode at time k. That is, \({\mathsf {t}} = {{q}}_{k} \in {\mathcal {Q}}\) and \({\mathsf {i}} = {\hat {q}}_{k} \in {\mathcal {Q}}\). It needs to be noted that t and i are indeed time-variant random variables. With this, the evolution of ek can be rewritten as:
For each mode i, let Ki be the steady state Kalman gain. Since we assume that Q and R are the same for all modes \({\mathsf {i}} \in {\mathcal {Q}}\), the Kalman gain Ki,k will converge to the corresponding steady Kalman gain Ki quickly [9]. Therefore, the update of ek can be approximately written as:
Denote Λi=Ai−KiCiAi, Γi,t=At−KiCtAt, when t=i, Γi,t=Λi. In general,
In the following sections, we will model the evolution of ek as a transformed switched system and further leverage results in stability analysis for switched systems to derive our main results.
3 Transformed switched system
So far, we have derived the dynamics of the bias in a mode-based Kalman filter. In Eq. (7), the bias evolves based on matrices Λi and Γi,t. As defined in the previous section, i and t are random variables that represent estimated and true mode at time k. In general, for an SHS with discrete state space \({\mathcal {Q}} = \{ 1,2, \cdots, d \}\), if the actual state is t, there are d−1 mode mismatch errors that could happen. Intuitively, we want to derive the evolution of ek as a stochastic equation based on the probabilistic event of mode mismatch occurrence. In the following, we will formally model this random process by introducing two sequences of random variables, {Θt}t=1t=d and {Ξt}t=1t=d as:
with \(\sum _{{\mathsf {i}} = 1}^{d} {\lambda }_{{\mathsf {i}},{\mathsf {t}}} = 1\). For a given t, Θt is a random variable on the outcome space {Λ1,⋯,Λd} and all the events Θt=Λ1, ⋯, Θt=Λd are mutually exclusive. The probability λi,t can be interpreted as the probability that the estimated mode is i while the true mode is t. It is worth mentioning that in realistic applications, the probability of mode mismatch may not only be a function of i and t but can also be correlated across time or across modes. Similarly, a random variable Ξt is defined as:
Note that the probabilities are the same as Θt for the same t. With Θt and Ξt, we can rewrite Eq. (7) as:
From Eq. (8), \(\{ {\mathbf {e}}_{k} \}_{k=0}^{\infty }\) is a stochastic process for a given initial value e0. The process ek is bounded with probability 1 if and only if \({\mathbb {E}}({\mathbf {e}}_{k})\) is bounded [23]. Therefore, we consider convergence in mean, i.e., \(\lim \limits _{k \rightarrow \infty } {\mathbb {E}}({\mathbf {e}}_{k}) < \infty \). According to the tower rule, we have \({\mathbb {E}}({\mathbf {e}}_{k}) = {\mathbb {E}}({\mathbb {E}}({\mathbf {e}}_{k}|{\mathbf {e}}_{k-1}))\), where the outer expectation is taken over ek−1 and the inner expectation is taken over the random variables Θt and Ξt. Therefore,
Recall that a discrete-time switched system is defined on the hybrid space of continuous and discrete state spaces. The dynamics of \({\mathbb {E}}({\mathbf {e}}_{k})\) in Eq. (9) follows the structure of the system in (1). That is, the evolution of \({\mathbb {E}}({\mathbf {e}}_{k})\) is linearly dependant on the previous \({\mathbb {E}}\left ({\mathbf {e}}_{k-1}\right)\) and the current mode t (which by definition is the actual discrete state in the original system). Therefore, we propose to define a transformed switched system to describe (9) as:
where the continuous state \({\mathbf {x}^{*}}_{k} = {\mathbb {E}}({\mathbf {e}}_{k})\) and \({\mathbf {u}}_{k} = {\mathbb {E}}({\mathbf {x}}_{k})\) can be treated as an external input. We use the same notation qk to denote the discrete state since it follows the same transitions in both the original system and the transformed switched system. The system matrices are:
Our goal is to find conditions under which \({\mathbb {E}}({\mathbf {e}}_{k})\) converges. With the transformed switched system (10), this problem is equivalent to analyze the stability of x∗k. As stated, we abstract the discrete state transitions in (1) as arbitrary switching between each linear subsystem. Therefore, the goal is to find conditions such that the switched system (10) with arbitrary switching signal is statistically stable. Additionally, since the system matrices \(\phantom {\dot {i}\!}{\mathbf {F}}_{{{q}}_{k}}\) and \(\phantom {\dot {i}\!}{\mathbf {G}}_{{{q}}_{k}}\) depend on the probability of mode mismatch \(\phantom {\dot {i}\!}{\lambda }_{{\mathsf {i}},{{q}}_{k}}\), the impact of \(\phantom {\dot {i}\!}{\lambda }_{{\mathsf {i}},{{q}}_{k}}\) on the stability of (10) also needs to be investigated. In the following, we will first review and summarize the progress that has been made regarding the stability for switched systems and then derive convergence conditions for stability of (10).
4 Main results
As with general linear systems, numerous concepts of stability have been defined for switched systems. In this paper, we use the definition of asymptotic stability for switched systems.
Definition 1
The switched system (10) is asymptotically stable if there exists some δ>0 such that ∥x∗0∥<δ implies ∀k,∥x∗k∥<ε\(\left (\!or \lim \limits _{k \rightarrow \infty } {\left \|{{\mathbf {x}^{*}}_{k}}\right \|} = 0\right)\) for all solutions x∗k of the system.
Remark 1
A switched system is marginally stable if it is neither asymptotically stable nor unstable.
Note that asymptotic stability gives a stronger condition for \(\lim \limits _{k \rightarrow \infty } {\left \|{{\mathbf {x}^{*}}_{k}}\right \|} < \infty \) since it not only requires convergence but requires convergence to the origin. The definition of marginal stability implies that the state trajectory is bounded but not necessarily convergent, which is equivalent to \(\lim \limits _{k \rightarrow \infty } {\left \|{{\mathbf {x}^{*}}_{k}}\right \|} < \infty \). Therefore, conditions for asymptotic stability are sufficient to guarantee \(\lim \limits _{k \rightarrow \infty } {\left \|{{\mathbf {x}^{*}}_{k}}\right \|} < \infty \). Also, because asymptotic stability is closely related to the stability of the corresponding autonomous system, it is typical to consider the stability of the autonomous system first. For the transformed switched system in (10), the corresponding autonomous system is:
Among the existing research works, there are primarily two approaches to address the stability of the autonomous switched system in (11). One approach involves solving the generalized/joint spectral radius (JSR) of a bounded set of matrices [39]. As proved in [40], testing whether the JSR of a bounded set of matrices is less than or equal to 1 is computationally undecidable. While the exact computation of JSR is Turing-undecidable in general, the approximation of JSR is an active area of research. The other approach is primarily built on the well-known Lyapunov theory. Specifically, it has been proved that the existence of a common quadratic Lyapunov function (CQLF) provides a sufficient condition for the asymptotic stability of the switched system in (11) which also implies the JSR of the bounded set of matrices is less than 1. Therefore, without dwelling on the approaches that involve approximations of JSR, our main results are built on Lyapunov theory. The analysis procedure is summarized in Fig. 2.
We use  to denote the subsystem corresponding to mode q. The autonomous switched system (11) switches between
to denote the subsystem corresponding to mode q. The autonomous switched system (11) switches between  for all q. The following lemma is introduced in [41].
for all q. The following lemma is introduced in [41].
Lemma 1
The switched system (11) is asymptotically stable under arbitrary switching signal if:
(i). \({\rho ({{\mathbf {F}}_{{{q}}}})} < 1, \forall {{q}} \in {\mathcal {Q}}\);
(ii). \(\exists \mathbf {P} = \mathbf {P}^{\prime } {\succ } 0, \quad {\mathbf {F}}^{\prime }_{{q}} \mathbf {P} {\mathbf {F}}_{{q}} - \mathbf {P} {\prec } 0\).
Condition (i) in Lemma 1 implies asymptotic stability of every subsystem  and condition (ii) is the existence of common Lyapunov quadratic function (CQLF). Also, it is worth pointing out that the stability for each subsystem does not imply asymptotic stability of the switched system [42]. The converse does not always hold either. As discussed in [43], by choosing the switching signal carefully, the switched system can be made asymptotically stable even though the subsystem is not. In the following, we first study conditions such that
and condition (ii) is the existence of common Lyapunov quadratic function (CQLF). Also, it is worth pointing out that the stability for each subsystem does not imply asymptotic stability of the switched system [42]. The converse does not always hold either. As discussed in [43], by choosing the switching signal carefully, the switched system can be made asymptotically stable even though the subsystem is not. In the following, we first study conditions such that
holds, i.e., each subsystem is asymptotically stable.
4.1 Stability of subsystem
By definition, Fq is composed of convex combination of matrices as:
The task of checking spectral radius of summation of matrices is not trivial in general. If two matrices are commutable, i.e., AB=BA, then ρ(A+B)≤ρ(A)+ρ(B) [44]. If all the matrices are non-negative (element-wise), [45] proves that spectral radius is strictly convex. But all the mentioned results cannot be extended to general cases. Therefore, directly checking the spectral radius is not feasible. An alternative approach is built on Lyapunov theory which demonstrates the relationship between a quadratic Lyapunov function (QLF) and the spectral radius of system matrices.
Lemma 2
The following statements are equivalent:
(i) if there exists a positive definite matrix P such that \({\mathbf {F}}_{{q}}^{\prime } \mathbf {P} {\mathbf {F}}_{{q}} - \mathbf {P} {\prec } 0\);
(ii) ρ(Fq)<1;
(iii) the subsystem  is asymptotically stable.
is asymptotically stable.
We first illustrate a property related to the spectral radius of Λi in the following lemma.
Lemma 3
For a switched system defined in (1), if \(({\mathbf {A}}_{\mathsf {i}},{\mathbf {B}}_{\mathsf {i}} {\mathbf {Q}} {\mathbf {B}}^{\prime }_{\mathsf {i}})\) is controllable and (Ci,Ai) is observable for all \({\mathsf {i}} \in {\mathcal {Q}}\), then \(\forall {\mathsf {i}} \in {\mathcal {Q}}\), ρ(Λi)<1.
Proof
From the definition,
For any Kalman filter, the observer gain corresponding to mode i is defined as \(\mathbf {L}_{{\mathsf {i}}} = {\mathbf {A}}_{\mathsf {i}} {\mathbf {M}}_{\mathsf {i}} {\mathbf {C}}^{\prime }_{\mathsf {i}} {{\left ({\mathbf {C}}_{\mathsf {i}}{\mathbf {M}}_{\mathsf {i}} {\mathbf {C}}^{\prime }_{\mathsf {i}} + {\mathbf {R}}\right)}^{-1}}\). Here, Mi is the steady error covariance related to steady Kalman gain Ki. Given that \(\left ({\mathbf {A}}_{\mathsf {i}},{\mathbf {B}}_{\mathsf {i}} {\mathbf {Q}} {\mathbf {B}}^{\prime }_{\mathsf {i}}\right)\) is controllable and (Ci,Ai) is observable for all \({\mathsf {i}} \in {\mathcal {Q}}\), the closed-loop dynamics Ai−LiCi is stable. That is,
Rewrite it as:
From commutativity property of spectral radius,
□
With the fact that all the matrices Λi are stable, we have the following theorem.
Lemma 4
If there is only one λi,q>0 for each \({{q}} \in {\mathcal {Q}}\), then the subsystem  is asymptotically stable for all \({{q}} \in {\mathcal {Q}}\).
is asymptotically stable for all \({{q}} \in {\mathcal {Q}}\).
Proof
Let kq be the index indicating the non-zero \({\lambda }_{k_{{q}}, {{q}}}\) for each \({{q}} \in {\mathcal {Q}}\); note that kq also takes value in \({\mathcal {Q}}\). Based on the property of random variable Ξt discussed in Section 3, \({\lambda }_{k_{{q}}, {{q}}} = 1\). Therefore, we have
From Lemma 3, it is straightforward to conclude that \({\rho ({{\mathbf {F}}_{{q}}})} = {\rho ({{\boldsymbol {\Lambda }}_{k_{{q}}}})} < 1, \forall {{q}} \in {\mathcal {Q}}\). According to Lemma 2, all the subsystems  are asymptotically stable. □
are asymptotically stable. □
Following the notation in proof of Lemma 4, we use kq to denote the index indicating the non-zero \({\lambda }_{k_{{q}}, {{q}}}\) for each \({{q}} \in {\mathcal {Q}}\). Note that kq is not necessarily equal to q. As ρ(Λq)<1 for all q, even though the probability of mode mismatch between q and mode kq is 1 (i.e., the mode mismatches always happen), all the subsystems  are still stable. The physical interpretation behind the result seems inconsistent. However, this result is only related to the stability of the autonomous subsystem but not the complete switched system. In fact, if we take a close look at our system in (10), the choice of \({\lambda }_{k_{{q}},{{q}}}\) will have impact on the input matrix Gq. We will discuss this result in Section 4.3.
are still stable. The physical interpretation behind the result seems inconsistent. However, this result is only related to the stability of the autonomous subsystem but not the complete switched system. In fact, if we take a close look at our system in (10), the choice of \({\lambda }_{k_{{q}},{{q}}}\) will have impact on the input matrix Gq. We will discuss this result in Section 4.3.
Lemma 4 gives a non-trivial condition such that the stability of each subsystem  is guaranteed. However, the condition that only one λi,q>0 is not generally realistic since it eliminates the randomness associated with errors. The next theorem is built on the concept of CQLF and it is applicable for broader choices of λi,q.
is guaranteed. However, the condition that only one λi,q>0 is not generally realistic since it eliminates the randomness associated with errors. The next theorem is built on the concept of CQLF and it is applicable for broader choices of λi,q.
Theorem 2
If for all \({\mathsf {i}} \in {\mathcal {Q}}\), Λi share a common quadratic Lyapunov function. That is, if there exists a positive definite matrix \(\mathbf {P} \in {\mathbb {R}}^{n \times n}\) such that
then every subsystem  \(\forall {{q}} \in {\mathcal {Q}}\) is asymptotically stable for all choices of λi,q.
\(\forall {{q}} \in {\mathcal {Q}}\) is asymptotically stable for all choices of λi,q.
Proof
(a) is due to the fact that P is positive definite and (b) is a result of Schur decomposition. According to Lemma 2, in order to prove  is asymptotically stable for all q, we need to find if there exists some positive definite matrix Pq for each q such that \(\mathbf {P}_{{q}} - {\mathbf {F}}_{{q}} \mathbf {P}_{{q}} {\mathbf {F}}^{\prime }_{{q}} {\succ } 0\).
is asymptotically stable for all q, we need to find if there exists some positive definite matrix Pq for each q such that \(\mathbf {P}_{{q}} - {\mathbf {F}}_{{q}} \mathbf {P}_{{q}} {\mathbf {F}}^{\prime }_{{q}} {\succ } 0\).
Since \(\mathbf {P} - {\boldsymbol {\Lambda }}_{\mathsf {i}} \mathbf {P} {\boldsymbol {\Lambda }}^{\prime }_{\mathsf {i}} {\succ } 0\), therefore, \(\mathbf {P} - {\lambda }_{{\mathsf {i}},{{q}}}^{2} {\boldsymbol {\Lambda }}_{\mathsf {i}} \mathbf {P} {\boldsymbol {\Lambda }}^{\prime }_{\mathsf {i}} {\succ } 0\) for 0≤λi,q≤1. For all \({{q}} \in {\mathcal {Q}}\), we have:
By taking Pq=P, we proved that there exists positive definite matrix Pq for each q such that \(\mathbf {P}_{{q}} - {\mathbf {F}}_{{q}} \mathbf {P}_{{q}} {\mathbf {F}}^{\prime }_{{q}} {\succ } 0\). Therefore, every subsystem  \(\forall {{q}} \in {\mathcal {Q}}\) is asymptotically stable for all choices of λi,q. □
\(\forall {{q}} \in {\mathcal {Q}}\) is asymptotically stable for all choices of λi,q. □
As presented in Lemma 1, there are two conditions that can guarantee the stability of the autonomous switched system. Condition (i) is related to the stability of each subsystem and we have developed Lemma 4 and Theorem 2 determine ρ(Fq)<1 for all \({{q}} \in {\mathcal {Q}}\). To complete the stability analysis for switched autonomous system in (11), we will study conditions such that constraint (ii) in Lemma 1 is satisfied in the following subsection.
4.2 Stability of switched autonomous systems
We have introduced the concept of CQLF in Lemma 1. For stability analysis and CQLF conditions, [46] provides an excellent survey on the progress that have been made in this research area. In general, determining algebraic conditions (on the subsystems’ state matrices) for the existence of a CQLF remains an open task. For switched system with only two modes, [47] derives a necessary and sufficient condition for the existence of a CQLF for a second-order (two dimensional) continuous-time switched system with two modes while a similar approach is proposed in [41] by considering a discrete-time system. Their approach is based on the stability of the matrix pencil constructed using the state matrices corresponding to the two modes. While the matrix pencil presents a different perspective on the CQLF existence problem, it also lacks an analytical solution.
In this work, the switched system in (11) contains unknown variable λi,q in the subsystem matrices Fq. Due to the unknown values in Fq and lack of algebraic solutions, we cannot directly solve the LMI conditions nor derive constraints on λi,q such that the existence of CQLF for Fq is guaranteed. In the following, we propose to establish a relationship between the existence of CQLF for Λi and Fq and then obtain conditions for stability of switched system (11) regardless of the choice of λi,q.
Theorem 3
If there exists a CQLF for \({\boldsymbol {\Lambda }}_{\mathsf {i}}, \forall {\mathsf {i}} \in {\mathcal {Q}}\), then there exists a CQLF for \({\mathbf {F}}_{{q}}, \forall {{q}} \in {\mathcal {Q}}\). As a consequence, the switched system (11) is asymptotically stable under arbitrary switching signal.
Proof
We will use the similar approach as shown in the proof of Theorem 2. If there exists a CQLF for Λi, we know that there exists a positive definite matrix \(\mathbf {P} \in {\mathbb {R}}^{n \times n}\) such that
As a result of Theorem 2, for all \({{q}} \in {\mathcal {Q}}\), we have
Therefore, there exists a CQLF for \({\mathbf {F}}_{{q}}, \forall {{q}} \in {\mathcal {Q}}\). From Lemma 1, the switched system (11) is asymptotically stable under arbitrary switching signal. □
The condition derived in Theorem 3 is only based on all the matrices Λi which can be determined given the system matrix. The LMI condition can be easily checked in practice via an LMI solver alleviating the lack of an analytical solution. As illustrated in Fig. 2, we have completed the discussion for the stability of autonomous switched system (11) thus far. In the following, we will consider stability of the complete transformed switched system (10) including the input term.
4.3 Bounded-input bounded-output (BIBO) stability
For the transformed switched system in (10), we introduce the notion of BIBO stability that has been defined in [48].
Definition 2
The system in (10) is BIBO stable if there exists a positive constant η such that for any essentially bounded input signal u, the continuous state x∗ satisfies
According to this definition, an input signal cannot be amplified by a factor greater than some finite constant η after passing through the system if the system is BIBO stable. It has been proven that if the corresponding autonomous switched system (11) is asymptotically stable, then the input-output system (10) is BIBO stable provided the input matrix Gq is uniformly bounded in time for all q [49]. This in fact is the case when the system switches between a finite family of matrices. In our transformed switched system, the input signal uk=xk, where xk is the continuous state of original system (1). Therefore, depending on the stability of (1), uk can be either bounded or unbounded. Therefore, we should consider two different scenarios based on the boundedness of uk in the following discussions.
Scenario 1: Original system in (1) is not asymptotically stable
If the original system in (1) is unstable, then supk≥0∥uk∥= supk≥0∥xk∥=∞. Since uk is an n-dimensional vector, when uk is unbounded, at least one of the elements in the vector is unbounded. We refer to those elements as unstable components and these components are collected in the set \({\mathcal {I}}\):
For this situation, if the columns of Gq corresponding to those unstable components of uk are 0, then the boundedness of supj≥0,q∥Gquj∥ is guaranteed. The process of finding the stable region for each probability of mode mismatch error is summarized in Algorithm 2:

Generally, λi,q=1 for i=q should always be a solution of Algorithm 2 because of Λi=Γi,q for i=q. Furthermore, this condition along with the result of Lemma 4 indicate that λi,q=1 for i=q not only guarantees stability of subsystem but also BIBO stability of the switched system in (10). By definition, λi,q represents the probability that true mode is q while estimated mode is i. λi,q=1 for i=q meaning that there is no mode mismatch error. Therefore, the convergence of x∗k (i.e., the bias generated from mode-based Kalman filter) is reasonable. Besides the trivial solution, Algorithm 2 also gives a less conservative result. For those unstable components in the original SHS, if the difference of Λi−Γi,q at the column corresponding to the unstable components are all 0, the mode-based Kalman filter is still tolerant of the mode mismatch between i and q.
Scenario 2: Original system in (1) is asymptotically stable
If the original system in (1) is asymptotically stable, then the continuous state xk (i.e., uk in the transformed switched system) is bounded. Since linear transformations of a vector is a bounded operator in Euclidean space, for a bounded vector u, Gu is bounded. For this situation, we are interested in minimizing the upper bound of ∥x∗k∥. From the definition of BIBO stability, we can write
where η and supj≥0∥uj∥ are fixed constant for a given system and Gq is related to the unknown variable λi,q. The equality in (a) holds if and only if each row of Gq is linearly dependent of uk for all q,k. In this framework, we seek to address the following questions:
(1) Given the probability of mode mismatch is \({\mathcal {P}}\), i.e., \(\sum _{\substack {{\mathsf {i}} = 1 \\ {\mathsf {i}} \neq {{q}}}}^{d} {\lambda }_{{\mathsf {i}},{{q}}} = {\mathcal {P}}, \forall {{q}}\), what is the lowest upper bound of ∥x∗k∥?
(2) Given a certain upper bound \({\mathcal {B}}\) of ∥x∗k∥, what is the largest tolerant region for mode mismatch probability \({\mathcal {P}}\) that will guarantee that \({\mathcal {B}}\) is achievable?
The following theorem is developed to answer the first question.
Theorem 4
Given the probability of mode mismatch \({\mathcal {P}} \neq 0\) and the original system in (1) is asymptotically stable, the lowest upper bound of ∥x∗k∥ that can be achieved is:
Proof
From the definition of Gq,
With the constraint that \(\sum _{\substack {{\mathsf {i}} = 1 \\ {\mathsf {i}} \neq {{q}}}}^{d} {\lambda }_{{\mathsf {i}},{{q}}} = {\mathcal {P}}\), we have:
From Eq. (14), we have the lowest bound of ∥x∗k∥ as a function of ∥Gq∥. Given the constraint on mode mismatch probability and results of (15) and (16), we get the lowest upper bound of ∥x∗k∥ that can be reached is:
□
To assist in the analysis for the second question, we first define an auxiliary function \({\phi }: {\mathbb {R}}^{d-1} \rightarrow {\mathbb {R}}\) as:
where \(\mathbf {S}_{i,{{q}}} \in {\mathbb {R}}^{n \times n}\) is a series of known matrices for a given q. The following lemma illustrates the convexity of this function.
Lemma 5
ϕ(υ) is a convex function respect to υ.
Proof
In order prove that ϕ(υ) is a convex function respect to υ, we want to show that for all \({\pmb {\upsilon }}, {\pmb {\nu }} \in {\mathbb {R}}^{d-1}\), and θ with 0≤θ≤1, ϕ(θυ+(1−θ)ν)≤θϕ(υ)+(1−θ)ϕ(ν). We have
Therefore ϕ(υ) is a convex function on υ. □
Recall that the second question is to derive the largest tolerant region for mode mismatch probability \({\mathcal {P}}\) such that an upper bound \({\mathcal {B}}\) of ∥x∗k∥ is achievable. In other words, we need to solve for λi,q such that \(\sum _{\substack {{\mathsf {i}} = 1 \\ {\mathsf {i}} \neq {{q}}}}^{d} {\lambda }_{{\mathsf {i}},{{q}}} = {\mathcal {P}}\) and \({\left \|{{\mathbf {x}^{*}}_{k}}\right \|} \leq {\mathcal {B}}\) holds. Based on Eq. (14), we have
Use the auxiliary function and define \({\pmb {\lambda }} \in {\mathbb {R}}^{d-1}\) and Si,q=Λi−Γi,q. We can write the left-hand side of (17) as:
Since ϕ(λ) is convex in λ, a non-negative bound \({\mathcal {B}}\) is achievable by taking λ[i]=0 for all i. To seek a λ such that
we will use triangle inequality to approximate ϕ(λ) and get a more conservative condition. Since
with ∥Si,q∥ is known for all i and q. The condition
is a 1st degree polynomial inequality with d−1 variables, and this can provide a feasible region for each λi,q on the d−1 dimensions space.
The discussion of BIBO stability completes the convergent analysis of bias dynamics in a mode-based Kalman filter. Both stable and unstable original SHS have been taken into consideration. For an unstable system, we can still stabilize the bias dynamics by specifically choosing the probability λi,q. For an asymptotically stable system, we addressed two important questions regarding the minimization of the upper bound for the bias.
5 Experimental results
In this section, we conduct two experiments to verify our main results in Section 4. We first consider a second-order switched system with two discrete states. Then, we illustrate the value of the theoretical results on a small scale smart grid set up.
5.1 Example 1: Switched system with two discrete states
Consider a switched system with two discrete states \({\mathcal {Q}} = \{1,2\}\). The continuous state is a two-dimensional vector. Define matrices A, B, and C as:
Let the system noise be \({\mathbf {w}}_{k} \sim \mathcal {N}(\mathbf {0},{\mathbf {Q}})\) and measurement noise be \({\mathbf {v}}_{k} \sim \mathcal {N}(\mathbf {0},{\mathbf {R}})\), where Q=0.5×I and R=0.3×I. In this system setting, \(\left ({\mathbf {A}}_{1},{\mathbf {B}}_{1} {\mathbf {Q}} {\mathbf {B}}_{1}^{\prime }\right)\) and \(\left ({\mathbf {A}}_{2},{\mathbf {B}}_{2} {\mathbf {Q}} {\mathbf {B}}_{2}^{\prime }\right)\) are both controllable and (C1,A1) and (C2,A2) are observable. The corresponding Λi and Γi,t are calculated as follows:
For this setup, we get ∥Λ1∥=0.3373<1, ∥Λ2∥=0.0209<1. Therefore, for any choice of λi,t, we have
By solving the feasibility of two LMIs that defined in (13), the result shows that Λ1 and Λ2 share a CQLF. Based on Theorem 3, there exists a CQLF for F1 and F2 with any choice of λ1,1,λ1,2,λ2,1,λ2,2. Therefore, the switched system composed with  and
and  is asymptotically stable under arbitrary switching signal.
is asymptotically stable under arbitrary switching signal.
The next step is to study the boundedness of uk (i.e., xk of the original system). The boundedness of xk can be checked by the existence of CQLF between A1 and A2. With a similar LMI condition, it shows that the original system is asymptotically stable. Therefore, the bias dynamics in the mode-based Kalman filter should be BIBO stable with upper bounds derived in (14).
Figures 3 and 4 are the experiment results over N=5000 Monte-Carlo simulation for two different switching signals. For each switching signal, two different probabilities of mode-mismatch error λ1,2 and λ2,1 were considered. In both Figs. 3 and 4, we plot the theoretical bias performance in line with squares. The theoretical bias is obtained via Eq. (9). The actual bias dynamics (difference of \({\mathbb {E}}({\hat {\mathbf {x}}}_{k})\) and \({\mathbb {E}}({\mathbf {x}}_{k})\)) from Monte-Carlo simulation is presented using dashed line with triangles. Since we have verified that the bias evolution should always converge with any switching signal, all the above experiments also validate this result.
In Fig. 5, the line with squares shows the maximum value for norm of bias over Monte-Carlo simulation given that probability of mode mismatch is \({\mathcal {P}}\). The dashed line is the upper bound calculated using Theorem 4. In Fig. 6, we seek to address question (2) proposed in the last section. That is, we want to achieve a certain upper bound \({\mathcal {B}} = 0.3\) for the bias dynamics. By solving Eq. (18), the maximum probability of mode mismatch is λ1,2=λ2,1=0.154554. Figure 6 shows the actual and theoretical bias evolution with mode mismatch error λ1,2=λ2,1=0.154554. We can conclude that the target bound has been achieved.
5.2 Example 2: Smart grid
A classic example of a cyber-physical system that can be modeled in the SHS framework is a smart grid. We have defined the system model in Section 2.2. For this case study, the status of components L, G and D and the grid parameters are defined in Table 1. Based on system settings, kG, α, σG and σD completely determine the system matrices Aq and Bq. Let Cq=I for all modes. Define the noise as \({\mathbf {w}}_{k} \sim \mathcal {N}(\mathbf {0},{\mathbf {Q}})\) and \({\mathbf {v}}_{k} \sim \mathcal {N}(\mathbf {0},{\mathbf {R}})\) with Q=2×I and R=I. With this system setting, we get ∥Λ1∥=0.9817, ∥Λ2∥=0.8837, and ∥Λ3∥=0.8611. Therefore, similar as (19), we have ρ(F1), ρ(F2), and ρ(F3)<1 for all choices of λi,t. The next step is to solve the LMI conditions on Λ1, Λ2, and Λ3 and the results shows that Λ1, Λ2, and Λ3 share a CQLF. Based on Theorem 3, the switched system composed with  ,
,  , and
, and  is asymptotically stable under arbitrary switching signal. In order to check the boundedness of input uk, we solve for the CQLF for A1, A2, and A3. In this case, the result reveals that the original SHS is not stable (falls into scenario 1 in Section 4.3). Therefore, we are able to use Algorithm 2 to derive the stable region of each λi,q. In this system, the unstable component is: \({\mathcal {I}} = \{ 1 \}\), i.e., only the first element is unstable. Based on Algorithm 2, we need to calculate Ti,q and find out the corresponding elements on column 1 of each matrix. We get:
is asymptotically stable under arbitrary switching signal. In order to check the boundedness of input uk, we solve for the CQLF for A1, A2, and A3. In this case, the result reveals that the original SHS is not stable (falls into scenario 1 in Section 4.3). Therefore, we are able to use Algorithm 2 to derive the stable region of each λi,q. In this system, the unstable component is: \({\mathcal {I}} = \{ 1 \}\), i.e., only the first element is unstable. Based on Algorithm 2, we need to calculate Ti,q and find out the corresponding elements on column 1 of each matrix. We get:
It can be observed that the first column in T2,3 and T3,2 are 0. Therefore, the mode-based Kalman filter can be tolerant on mode mismatch error between mode 2 and mode 3. The stable region for each λ is:
Note that the condition that \({\sum }_{{\mathsf {i}} = 1}^{3} {\lambda }_{{\mathsf {i}},{{q}}} = 1\) should also hold for every q. Figure 7 shows a Monte-Carlo simulation for two different λ settings. For Setting I, we use λ2,1=λ3,1=λ1,2=λ1,3=0,λ3,2=0.4,λ2,3=0.7 where all the λs are within the stable region. The simulation results for Setting I are shown in lines with squares and triangles with left y-axis. Specifically, the line with squares is the theoretical bias derived using the bias evolution Eq. (10) while the line with triangles shows the bias in a mode-based Kalman filter via Monte-Carlo simulation. We can conclude that when all the λs are in stable region, the bias of the mode-based Kalman filter is convergent and bounded. For Setting II, we use λ2,1=λ3,1=λ1,2=0.1,λ1,3=0,λ3,2=0.3,λ2,3=0.2 in which λ2,1, λ3,1, and λ1,2 are outside the stable region. The solid line and the dashed line with right y-axis present the results for theoretical bias and actual bias generated in a mode-based Kalman filter via Monte-Carlo simulation. Note that the y-axis on the right is \(\log \left ({\left \|{{\mathbf {x}}^{*}_{k}}\right \|}\right)\) since the actual \({\left \|{{\mathbf {x}}^{*}_{k}}\right \|}\) explodes rapidly. As this system does not have tolerance between mode 1,2 and mode 1,3, even a small probability of error (i.e., 0.1 in this case) will result in rapid explosion in the bias dynamics.
6 Conclusions and future work
In this work, we consider the open research problem of quantifying the impact of mode-mismatch errors on the performance of a mode-based Kalman filter. The problem itself is appropriate to describe network topology errors in a smart grid or other cyber-physical systems. The main technique proposed involves modeling the bias dynamics in the Kalman filter as a transformed switched system. Abstracting the discrete state transitions as arbitrary switching signals not only broaden the application space but also provides us tools from switched system stability analysis to study the statistical convergence of the bias. As part of our future work, we intend to consider generalizing the model of mismatch events as time-variant correlated Bernoulli random processes and study the impact on bias convergence.
Abbreviations
- BIBO:
-
Bounded-input bounded output
- CQLF:
-
Common Lyapunov quadratic function
- IMM:
-
Interacting multiple model
- LMI:
-
Linear matrix inequality
- MJLS:
-
Markov jump linear system
- MMAE:
-
Multiple model adaptive estimation
- MMSE:
-
Minimum mean square error
- MSE:
-
Mean squared error
- PV:
-
Photovoltaics
- QLF:
-
Quadratic Lyapunov function
- SHS:
-
Stochastic hybrid system
References
J. Hu, W. -C. Wu, S Sastry, Modeling subtilin production in Bacillus subtilis using stochastic hybrid systems (Springer, Berlin, 2004).
A. Singh, J. P. Hespanha, Stochastic hybrid systems for studying biochemical processes. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 368(1930), 4995–5011 (2010). https://doi.org/10.1098/rsta.2010.0211.
M. K. Ghosh, A. Arapostathis, S. I. Marcus, Optimal control of switching diffusions with application to flexible manufacturing systems. SIAM J. Control. Optim. 31(5), 1183–1204 (1993). https://doi.org/10.1137/0331056.
J. P. Hespanha, Stochastic hybrid systems: application to communication networks. (R. Alur, G. J. Pappas, eds.) (Springer, Berlin, 2004).
W. Glover, J. Lygeros, A stochastic hybrid model for air traffic control simulation (Springer, Berlin, 2004).
M. Prandini, J. Hu, in Decision and Control, 2008. CDC 2008. 47th IEEE Conference On. Application of reachability analysis for stochastic hybrid systems to aircraft conflict prediction, (2008), pp. 4036–4041. https://doi.org/10.1109/CDC.2008.4739248.
M. Střelec, K. Macek, A. Abate, in 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe). Modeling and simulation of a microgrid as a stochastic hybrid system, (2012), pp. 1–9. https://doi.org/10.1109/ISGTEurope.2012.6465655.
Y. Huang, M. Esmalifalak, Y. Cheng, H. Li, K. A. Campbell, Z. Han, Adaptive quickest estimation algorithm for smart grid network topology error. IEEE Syst. J. 8(2), 430–440 (2014). https://doi.org/10.1109/JSYST.2013.2260678.
G. Welch, G. Bishop, An introduction to the Kalman filter. Technical report, (Chapel Hill, 1995).
H. J. Chizeck, Y. Ji, in Decision and Control, 1988., Proceedings of the 27th IEEE Conference On. Optimal quadratic control of jump linear systems with Gaussian noise in discrete-time, (1988), pp. 1989–19933. https://doi.org/10.1109/CDC.1988.194681.
M. H. A. Davis, R. B. Vinter, Stochastic modelling and control. Monographs on statistics and applied probability (Chapman and Hall, USA, 1985).
O. L. V. Costa, M. D. Fragoso, R. P. Marques, Discrete-time Markov jump linear systems. Applied probability (Springer, USA, 2005). https://books.google.com/books?id=4vyzaB6G3O0C.
I. Matei, N. C. Martins, J. S. Baras, in 2008 American Control Conference. Optimal state estimation for discrete-time markovian jump linear systems, in the presence of delayed mode observations, (2008), pp. 3560–3565. https://doi.org/10.1109/ACC.2008.4587045.
I. Matei, J. S. Baras, Optimal state estimation for discrete-time Markovian jump linear systems, in the presence of delayed output observations. IEEE Trans. Autom. Control. 56(9), 2235–2240 (2011). https://doi.org/10.1109/TAC.2011.2160027.
C. E. Seah, I. Hwang, Stochastic linear hybrid systems: modeling, estimation, and application in air traffic control. IEEE Trans. Control. Syst. Technol. 17(3), 563–575 (2009). https://doi.org/10.1109/TCST.2008.2001377.
W. Liu, C. E. Seah, I. Hwang, in Decision and Control, 2009 Held Jointly with the 2009 28th Chinese Control Conference. CDC/CCC 2009. Proceedings of the 48th IEEE Conference On. Estimation algorithm for stochastic linear hybrid systems with quadratic guard conditions, (2009), pp. 3946–3951. https://doi.org/10.1109/CDC.2009.5400909.
W. Zhang, B. Natarajan, in 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton). State estimation in stochastic hybrid systems with quadratic guard conditions, (2016), pp. 752–757. https://doi.org/10.1109/ALLERTON.2016.7852308.
M. W. Hofbaur, B. C. Williams, in Hybrid Systems: Computation and Control: 5th International Workshop, HSCC 2002 Stanford, CA, USA, March 25–27, 2002 Proceedings. Mode estimation of probabilistic hybrid systems (SpringerBerlin, 2002), pp. 253–266.
H. A. P. Blom, Y. Bar-Shalom, The interacting multiple model algorithm for systems with Markovian switching coefficients. IEEE Trans. Autom. Control. 33(8), 780–783 (1988). https://doi.org/10.1109/9.1299.
C. B. Chang, M. Athans, State estimation for discrete systems with switching parameters. IEEE Trans. Aerosp. Electron. Syst. AES-14(3), 418–425 (1978). https://doi.org/10.1109/TAES.1978.308603.
J. Tugnait, Adaptive estimation and identification for discrete systems with Markov jump parameters. IEEE Trans. Autom. Control. 27(5), 1054–1065 (1982). https://doi.org/10.1109/TAC.1982.1103061.
B. Sinopoli, L. Schenato, M. Franceschetti, K. Poolla, M. I. Jordan, S. S. Sastry, Kalman filtering with intermittent observations. IEEE Trans. Autom. Control. 49(9), 1453–1464 (2004). https://doi.org/10.1109/TAC.2004.834121.
X. Liu, A. Goldsmith, in Decision and Control, 2004. CDC. 43rd IEEE Conference On, vol. 4. Kalman filtering with partial observation losses, (2004), pp. 4180–41864. https://doi.org/10.1109/CDC.2004.1429408.
E. Rohr, D. Marelli, M. Fu, in 49th IEEE Conference on Decision and Control (CDC). Statistical properties of the error covariance in a Kalman filter with random measurement losses, (2010), pp. 5881–5886. https://doi.org/10.1109/CDC.2010.5717554.
S. Deshmukh, B. Natarajan, A. Pahwa, State estimation over a lossy network in spatially distributed cyber-physical systems. IEEE Trans. Signal Process. 62(15), 3911–3923 (2014). https://doi.org/10.1109/TSP.2014.2330810.
M. Moayedi, Y. C. Soh, Y. K. Foo, in 2009 American Control Conference. Optimal kalman filtering with random sensor delays, packet dropouts and missing measurements, (2009), pp. 3405–3410. https://doi.org/10.1109/ACC.2009.5160216.
B. Yan, H. Lev-Ari, A. M. Stankovic, Networked state estimation with delayed and irregularly-spaced time-stamped observations. IEEE Trans. Control Netw. Syst. PP(99), 1–1 (2017). https://doi.org/10.1109/TCNS.2017.2653422.
S. M. S. Alam, B. Natarajan, A. Pahwa, in 2015 IEEE Global Communications Conference (GLOBECOM). Agent based optimally weighted kalman consensus filter over a lossy network (IEEEUSA, 2015), pp. 1–6.
M. Nourian, A. S. Leong, S. Dey, D. E. Quevedo, An optimal transmission strategy for Kalman filtering over packet dropping links with imperfect acknowledgements. IEEE Trans. Control. Netw. Syst. 1(3), 259–271 (2014). https://doi.org/10.1109/TCNS.2014.2337975.
S. Dey, A. Chiuso, L. Schenato, Remote estimation with noisy measurements subject to packet loss and quantization noise. IEEE Trans. Control Netw. Syst. 1(3), 204–217 (2014). https://doi.org/10.1109/TCNS.2014.2337961.
P. D. Hanlon, P. S. Maybeck, Characterization of Kalman filter residuals in the presence of mismodeling. IEEE Trans. Aerosp. Electron. Syst. 36(1), 114–131 (2000). https://doi.org/10.1109/7.826316.
I. Hwang, H. Balakrishnan, C. Tomlin, in Decision and Control, 2003. Proceedings. 42nd IEEE Conference On, 5. Performance analysis of hybrid estimation algorithms, (2003), pp. 5353–53595. https://doi.org/10.1109/CDC.2003.1272488.
I. Hwang, H. Balakrishnan, C. Tomlin, in European Control Conference (ECC), 2003. Observability criteria and estimator design for stochastic linear hybrid systems (IEEEUSA, 2003), pp. 3317–3322.
C. E. Seah, I. Hwang, Algorithm for performance analysis of the IMM algorithm. IEEE Trans. Aerosp. Electron. Syst. 47(2), 1114–1124 (2011). https://doi.org/10.1109/TAES.2011.5751246.
I. Hwang, C. E. Seah, S. Lee, A study on stability of the interacting multiple model algorithm. IEEE Trans. Autom. Control. 62(2), 901–906 (2017). https://doi.org/10.1109/TAC.2016.2558156.
W. Zhang, B. Natarajan, in 2018 Annual American Control Conference (ACC). Quantifying the bias dynamics in a mode-based Kalman filter for stochastic hybrid systems, (2018), pp. 5849–5856. https://doi.org/10.23919/ACC.2018.8431697.
D. Liberzon, Switching in Systems and Control. Systems & Control: Foundations & Applications, (Birkha user Boston, 2003).
R. Weron, B. Kozłowska, J. Nowicka-Zagrajek, Modeling electricity loads in California: a continuous-time approach. Physica A: Statistical Mechanics and its Applications. 299(1), 344–350 (2001). https://doi.org/10.1016/S0378-4371(01)00315-6. Application of Physics in Economic Modelling.
R. Jungers, The joint spectral radius: theory and applications. Lecture Notes in Control and Information Sciences (Springer, Germany, 2009).
V. D. Blondel, J. N. Tsitsiklis, The boundedness of all products of a pair of matrices is undecidable. Syst. Control Lett. 41(2), 135–140 (2000). https://doi.org/10.1016/S0167-6911(00)00049-9.
O. Mason, R. Shorten, On common quadratic Lyapunov functions for stable discrete-time LTI systems. IMA J. Appl. Math. 69(3), 271 (2004). https://doi.org/10.1093/imamat/69.3.271.
D. Liberzon, J. P. Hespanha, A. S. Morse, Stability of switched systems: a lie-algebraic condition. Syst. Control Lett. 37(3), 117–122 (1999).
R. A. Decarlo, M. S. Branicky, S. Pettersson, B. Lennartson, Perspectives and results on the stability and stabilizability of hybrid systems. Proc. IEEE. 88(7), 1069–1082 (2000). https://doi.org/10.1109/5.871309.
F. Kittaneh, Spectral radius inequalities for Hilbert space operators. Proc. Am. Math. Soc. 134(2), 385–390 (2006).
S. Friedland, Convex spectral functions. Linear Multilinear Alg. 9(4), 299–316 (1981). https://doi.org/10.1080/03081088108817381.
H. Lin, P. J. Antsaklis, Stability and stabilizability of switched linear systems: a survey of recent results. IEEE Trans. Autom. Control. 54(2), 308–322 (2009). https://doi.org/10.1109/TAC.2008.2012009.
R. Shorten, K. S. Narendra, O. Mason, A result on common quadratic Lyapunov functions. IEEE Trans. Autom. Control. 48(1), 110–113 (2003).
R. Shorten, F. Wirth, O. Mason, K. Wulff, C. King, Stability criteria for switched and hybrid systems. SIAM Rev. 49(4), 545–592 (2007). https://doi.org/10.1137/05063516X.
G. Michaletzky, L. Gerencser, Bibo stability of linear switching systems. IEEE Trans. Autom. Control. 47(11), 1895–1898 (2002). https://doi.org/10.1109/TAC.2002.804470.
Acknowledgements
The authors would like to thank the reviewers for providing valuable feedback on the manuscript.
Funding
This research was supported by the National Science Foundation through the award no. CNS-1544705.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Author information
Authors and Affiliations
Contributions
Both authors contributed to the theoretical analysis and manuscript writing. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, W., Natarajan, B. On the statistical convergence of bias in mode-based Kalman filter for switched systems. EURASIP J. Adv. Signal Process. 2018, 71 (2018). https://doi.org/10.1186/s13634-018-0594-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-018-0594-0

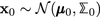 . The discrete state has a unique initial mode
. The discrete state has a unique initial mode 




