- Research Article
- Open access
- Published:
Marker-Based Human Motion Capture in Multiview Sequences
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 105476 (2010)
Abstract
This paper presents a low-cost real-time alternative to available commercial human motion capture systems. First, a set of distinguishable markers are placed on several human body landmarks, and the scene is captured by a number of calibrated and synchronized cameras. In order to establish a physical relation among markers, a human body model is defined. Markers are detected on all camera views and delivered as the input of an annealed particle filter scheme where every particle encodes an instance of the pose of the body model to be estimated. Likelihood between particles and input data is performed through the robust generalized symmetric epipolar distance and kinematic constrains are enforced in the propagation step towards avoiding impossible poses. Tests over the HumanEva annotated data set yield quantitative results showing the effectiveness of the proposed algorithm. Results over sequences involving fast and complex motions are also presented.
1. Introduction
Accurate retrieval of the configuration of an articulated structure from the information provided by multiple cameras is a field that found numerous applications in the recent years. The grown of computer graphics technology together with human motion capture (HMC) systems have been extensively used by the cinematographic and video games industry to generate virtual avatars [1]. Medicine also benefited from these advances in the field of orthopedics, locomotive pathologies assessment, or sports performance improvement [2]. In this field, despite markerless HMC systems have attained significant performance ratios in some scenarios [3], only HMC systems aided by markers placed on some body landmarks can produce high-accuracy results.
Depending on the type of employed markers, HMC systems are classified in two groups: nonoptical (inertial, magnetic, and mechanic) or optical systems (active and passive). Optical systems based on photogrammetric methods are more used than the nonoptical ones, usually requiring special suits embedding rigid skeletal-like structures [4], magnetic [5] or accelerometric devices [6] or multisensor fusion algorithms [7]. Instead, image-based or optical systems allow a relative freedom of movement and are less intrusive. A common issue of all optical and nonoptical systems is the fact that they are usually expensive and require a dedicated hardware. The most usual involve IR retro-reflective markers that reflect back light, that is, generated near the cameras lens [8]. Other optical systems triangulate positions by using active markers that emits a pulse modulated signal. This allows distinguishing among markers and to automatically label them [9].
This paper focuses on HMC systems with passive markers in a multicamera scenario. These systems first require an accurate reconstruction of the markers' 3D position from its 2D projections which is not a trivial problem. Matches need to be established between the detected markers in the different views, defining the multiple view correspondences through homographies or algebraic methods [10]. This process is prone to errors due to occlusions, detection noise, and the proximity between markers. A temporal tracking of the markers also needs to be performed, to identify the markers in each sequence frame, thus yielding a 3D trajectory for each marker. Although professional systems exist for this purpose, errors occur when crucial markers become occluded or when markers' trajectories are confused. Finally, most applications require the transformation of the markers localization and trajectories to the motion parameters of a kinematic skeleton model. Commercial tools that perform this transformation are generally semiautomatic, thus becoming a labor-intensive task.
Once the 3D marker positions are obtained, it is required to fit a selected human body model (HBM) to these data to obtain kinematically meaningful parameters to perform either an analysis (i.e., for gesture recognition) or a synthesis (i.e., for avatar animation). However, in most of the systems, the markers' 3D position estimation and the fitting steps are decoupled. One of the first attempts to use an anatomical human model to increase the robustness of a HMC system is presented in [11] were the algorithm computes a skeleton-and-marker model using a standardized set of motions and uses it to resolve the ambiguities during the 3D reconstruction process. Another approach using a HBM and data clustering is presented in [4]. Detection of 2D markers in separate images and its analysis using calibration information have been presented in [12] enforcing an HBM afterwards. A similar technique using a Kalman filter involving the HBM in the data association step was presented in [2].
In this paper, a low-cost real-time multicamera algorithm for marker-based human motion capture is presented. The proposed algorithm can work with any marker type detectable onto a set of 2D planes under perspective projection and it is robust to markers' occlusion and noisy detections. Since variables involved with the employed analysis HBM do not hold a linear relationship and the involved statistical distributions are non-Gaussian, we opted for a Monte Carlo approach to estimate the pose of the HBM at a given time instant. In our case, marker detection and HBM pose estimation are performed in the same analysis loop by means of an annealed particle filter [13]. Epipolar geometry is exploited in the particle likelihood evaluation by means of the symmetric epipolar distance [14] being robust to noisy marker detections and occlusions. Moreover, kinematic restrictions are applied in the particle propagation step towards avoiding impossible poses. Finally, effectiveness of the proposed algorithm is assessed by means of objective metrics defined in the framework of the HumanEva data set [3]. The presented algorithm is intended to work with any multicamera setup and regardless of the complexity of the selected human body model.
2. Monte Carlo-Based Human Motion Capture
2.1. Problem Formulation
The evolution of a physical articulated structure can be better captured with model-based tracking techniques [15]. In this process, the pose of an articulated HBM is sequentially estimated along time using video data from a number of cameras. Let  be the state vector to be estimated formed by the defining parameters of an articulated HBM, angles at every joint, and
be the state vector to be estimated formed by the defining parameters of an articulated HBM, angles at every joint, and  the state space describing all possible valid poses an HBM may adopt, where
the state space describing all possible valid poses an HBM may adopt, where  .
.
From a Bayesian perspective, the articulated motion estimation and tracking problem is to recursively estimate a certain degree of belief in the state vector  at time
at time  , given the data
, given the data  up to time
up to time  . Thus, it is required to calculate the posterior pdf
. Thus, it is required to calculate the posterior pdf . However, this pdf may be peaky and far from being convex, and hence cannot be computed analytically unless linear-Gaussian models are adopted. Even though Kalman filtering provides the optimal solution under certain assumptions, it tends to fail when the estimated probability density presents a multimodal distribution or the dimension of the state vector is high. Usually, this is the type of pdf s involved in HMC processes.
. However, this pdf may be peaky and far from being convex, and hence cannot be computed analytically unless linear-Gaussian models are adopted. Even though Kalman filtering provides the optimal solution under certain assumptions, it tends to fail when the estimated probability density presents a multimodal distribution or the dimension of the state vector is high. Usually, this is the type of pdf s involved in HMC processes.
2.2. Particle Filtering
Particle Filtering (PF) [16] algorithms are sequential Monte Carlo methods based on point mass (or "particle") representations of probability densities. These techniques are employed to tackle estimation and tracking problems where the pdf s of the involved variables do not hold Gaussianity uncertainty models, linear dynamics and exhibit multimodal distributions. In this case, PF expresses the belief about the system at time  by approximating the posterior probability distribution
by approximating the posterior probability distribution  ,
,  . This distribution is represented by a weighted particle set
. This distribution is represented by a weighted particle set , which can be interpreted as a sum of
, which can be interpreted as a sum of  Dirac functions centered on the
Dirac functions centered on the  with their associated real, nonnegative weights
with their associated real, nonnegative weights  :
:

In order to ensure convergence, weights must fulfill the normalization condition  . For this type of estimation and tracking problems, it is a common approach to employ a Sampling Importance Resampling-(SIR)-based strategy to drive particles along time [17]. This assumption leads to a recursive update of the weights as
. For this type of estimation and tracking problems, it is a common approach to employ a Sampling Importance Resampling-(SIR)-based strategy to drive particles along time [17]. This assumption leads to a recursive update of the weights as

SIR PF circumvents the particle degeneracy problem by resampling with replacement at every time step [16]. That is, to dismiss the particles with lower weights and proportionally replicate those with higher weights. In this case, weights are set to  , for all
, for all  , therefore
, therefore

Hence, the weights are proportional to the likelihood function that will be computed over the incoming data  .
.
The best state at time  ,
,  , is derived based on the discrete approximation of (1). The most common solution is the Monte Carlo approximation of the expectation
, is derived based on the discrete approximation of (1). The most common solution is the Monte Carlo approximation of the expectation

Usually, PF will be able to concentrate particles in the main mode of the likelihood function thus providing an estimation of the state space vector. However, multiple modes of similar size in the likelihood function might bias the estimation. In order to cope with such cases, the estimation is set to be the state vector associated to the maximum or the mean of all particle weights. Finally, a propagation model is adopted to add a drift to the state of the re-sampled particles in order to progressively sample the state space in the following iterations [16].
Another issue arising when applying PF techniques to computer vision problems is to derive a valid observation model  relating the input data
relating the input data  with the particle state
with the particle state  . Nevertheless, even if such likelihood model can be defined, its evaluation may be very computationally inefficient. Instead of that, a fitness function
. Nevertheless, even if such likelihood model can be defined, its evaluation may be very computationally inefficient. Instead of that, a fitness function  can be constructed according to the likelihood function, such that it provides a good approximation of
can be constructed according to the likelihood function, such that it provides a good approximation of  but is also relatively easy to calculate.
but is also relatively easy to calculate.
2.3. Annealing Strategy
PF is an appropriate technique to deal with problems where the posterior distribution is multimodal. This usually happens when state space dimensionality is high, like in HMC. To maintain a fair representation of  , a certain number of particles is required in order to find its global maxima instead of a local one. It has been proved in [18] that the amount of particles required by a standard PF algorithm to achieve a successful tracking follows an exponential law with the number of dimensions. Articulated motion tracking typically employs state spaces with dimension
, a certain number of particles is required in order to find its global maxima instead of a local one. It has been proved in [18] that the amount of particles required by a standard PF algorithm to achieve a successful tracking follows an exponential law with the number of dimensions. Articulated motion tracking typically employs state spaces with dimension  , thus standard PF turns out to be computationally unfeasible.
, thus standard PF turns out to be computationally unfeasible.
There exist several possible strategies to reduce the complexity of the problem based on refinements and variations of the seminal PF idea. Partitioned and hierarchical sampling [18, 19] are presented as highly efficient solutions to this problem. In the instance when there exists a tractable substructure between some variables of the state model, specific states can be marginalized out of the posterior, leading to the family of Rao-Blackwellized PF algorithms [20]. However, these techniques impose a linear hierarchy of sampling which may not be related to the true body structure assuming certain statistical independence among state variables. Finally, annealed PF [13] is one of the most general and robust approaches to estimation problems involving high-dimensional and multimodal state spaces. In this work, this technique will be extended to our marker-based scenario.
Likelihood functions  involved in HMC problems may contain several local maxima. Therefore, if using a single weighting function, a PF would require a large number of particles to properly sample the state space. By using annealing combined with PF, a series of weighting functions
involved in HMC problems may contain several local maxima. Therefore, if using a single weighting function, a PF would require a large number of particles to properly sample the state space. By using annealing combined with PF, a series of weighting functions  are constructed where
are constructed where  slightly differs from
slightly differs from  and represents a smoothed version of it. In our case,
and represents a smoothed version of it. In our case,  is designed to be a coarse smooth version of
is designed to be a coarse smooth version of  and, typically,
and, typically,  functions are constructed by using
functions are constructed by using

where  are the annealing scheduling parameters.
are the annealing scheduling parameters.
When a new measurement  is available an annealing iteration is performed. Every annealing run consists of
is available an annealing iteration is performed. Every annealing run consists of  steps or annealing layers where, in each of them, the appropriate weighting function is used and a set of pairs is constructed
steps or annealing layers where, in each of them, the appropriate weighting function is used and a set of pairs is constructed  . Starting with an initialized particle set
. Starting with an initialized particle set  , the annealing process for every layer
, the annealing process for every layer  can be summarized as the following.
can be summarized as the following.
-
(1)
Calculate the weights:
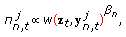 (6)
(6)enforcing the normalization condition
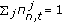 . The estimation of parameter
. The estimation of parameter 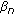 is based on the particle survival technique described in [13]. Once the weighted set is constructed, it will be used to draw the particles of the next layer.
is based on the particle survival technique described in [13]. Once the weighted set is constructed, it will be used to draw the particles of the next layer. -
(2)
Resampling: draw
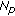 particles with replacement from the set
particles with replacement from the set  with distribution
with distribution 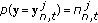 .
. -
(3)
Construct the particle set corresponding to layer
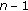 as
as (7)
(7)where
 stands for a truncated multivariate Gaussian distribution with mean
stands for a truncated multivariate Gaussian distribution with mean  and covariance matrix
and covariance matrix  that will be further described in Section 3.5. This process is repeated until reaching
that will be further described in Section 3.5. This process is repeated until reaching 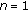 .
.Finally the estimated state
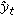 is computed as
is computed as (8)
(8)
The unweighted particle set for the next observation is defined as

where the covariance matrix  is set proportional to the maximum variation of the defining model parameters and
is set proportional to the maximum variation of the defining model parameters and  . Setting
. Setting  provided satisfactory results. A visual example of the annealed PF is depicted in Figure 1.
provided satisfactory results. A visual example of the annealed PF is depicted in Figure 1.
Annealed PF operation example. (a) The output of the employed marker detector where color boxes stand for correct (green), false (red), and missed (blue) detections. (b) The progressive fitting of particles driven by the annealing process and, (c) The final pose estimation  .(a) Input (b) Annealing PF (c) Result
.(a) Input (b) Annealing PF (c) Result
3. Filter Implementation
When implementing an annealed PF, several issues must be addressed: initialization, likelihood evaluation, particle propagation, and occlusion management. In the following section, we discuss the implementation of these two factors when employing a set of marker detections in multiple cameras as the input and an HBM as the tool to drive the physical relations among the variables of the state space (see Figure 2(a)).
Human body model and measurement examples. In (a), the HBM employed in this paper is parameterized as follows: 2 DOF in the neck, 3 DOF in the shoulders, 1 DOF in the elbows, 3 DOF in the hips, 3 in the lower torso and 1 DOF in the knee. Red dots mark the HBM landmarks that can be computed by applying forward kinematics. In (b), the output of the employed color based marker location detection algorithm. Colors describe the correct detections (green), the miss detections (blue) and the false positive detections (red). All this detections will conform the measurement set  .
.
3.1. Initialization
In the current scenario, it is supposed that the subject under study is tracked since the moment he/she enters the scene. A simple person tracking system is employed [21] to obtain a coarse estimation of person's position and velocity. Assuming that backward motions are unlikely, the velocity vector allows an initial estimation of the torso orientation. Finally, for the rest of limbs, a neutral and natural walking position is defined for the initialization of the HMC system.
In the case of a global miss of the tracked subject, the variance of the state space variables associated to every particle tend to be high in comparison of the variance obtained during a correct tracking operation. Therefore, the analysis of this variance allows detecting when the HMC system is out of track. In such case, the coarse tracking system is employed to start again the initialization loop described beforehand.
Although a beforehand selected HBM is employed to track any person, the size of the limbs must be adequate to the particular subject under study. For the majority of people, there is a strong quasilinear correlation between the height of a person and the length of the limbs [22] thus allowing a proper scaling of these magnitudes after automatically measuring the height directly from the input images as shown, for instance, in [14].
3.2. Measurement Generation
The input data  to the proposed tracking system will be the detection of the 2D projections of the set of distinguishable markers attached to the body of the performer onto the
to the proposed tracking system will be the detection of the 2D projections of the set of distinguishable markers attached to the body of the performer onto the  available images in contrast with markerless HMC systems relying on image features such as edges or silhouettes [13]. Let
available images in contrast with markerless HMC systems relying on image features such as edges or silhouettes [13]. Let  be the set of
be the set of  locations detected in the image captured in the
locations detected in the image captured in the  th view,
th view,  ,
,  . In order to generate
. In order to generate  , a generic marker detection algorithm
, a generic marker detection algorithm  is employed whose performance is assessed by the detection rate (
is employed whose performance is assessed by the detection rate ( ), the false positive rate (
), the false positive rate ( ), and the variance estimation error (
), and the variance estimation error ( ). This formulation of
). This formulation of  will allow performance comparisons of the tracking algorithm when using different marker detection algorithms and the assessment of occlusions.
will allow performance comparisons of the tracking algorithm when using different marker detection algorithms and the assessment of occlusions.
Markers are usually placed at the joints, the end of the limbs, the top of the head and the chest of the subject. The proposed method is general enough to be applied to any type of markers detectable onto a set of 2D planes under perspective projection. An example of the detections obtained by our color-based marker detection is shown in Figure 2(b).
3.3. Likelihood Evaluation
In order to evaluate the likelihood between the body pose represented by a given particle state  with reference to the input data
with reference to the input data  , a fitness function
, a fitness function  must be defined. The
must be defined. The  3D positions of the HBM landmarks corresponding to the pose described by the state vector
3D positions of the HBM landmarks corresponding to the pose described by the state vector  are computed through forward kinematics [12]. Let us denote these coordinates as the set
are computed through forward kinematics [12]. Let us denote these coordinates as the set  ,
,  . The fitness function relating the 3D locations set
. The fitness function relating the 3D locations set  with the 2D observations
with the 2D observations  should measure how well these 2D points fit as projections of the set
should measure how well these 2D points fit as projections of the set  . A similar problem was tackled by the authors in [14] in a Bayesian framework and the underlying idea is applied in this context.
. A similar problem was tackled by the authors in [14] in a Bayesian framework and the underlying idea is applied in this context.
For every element  , its projection onto every camera is computed as
, its projection onto every camera is computed as

where  is the projection matrix associated to the
is the projection matrix associated to the  th camera [10] and tilde denotes homogeneous coordinates. Then, the set
th camera [10] and tilde denotes homogeneous coordinates. Then, the set  containing the closest measurement in every camera view for every HBM landmark
containing the closest measurement in every camera view for every HBM landmark  is constructed as follows:
is constructed as follows:

However, not all the 3D points  may have a projection onto every view due to occlusions or a miss-detection of the marker detection algorithm. In order to detect such cases, a thresholding is applied to the elements
may have a projection onto every view due to occlusions or a miss-detection of the marker detection algorithm. In order to detect such cases, a thresholding is applied to the elements  dismissing those measurements above a threshold
dismissing those measurements above a threshold  . In this case,
. In this case,  using an empirically determined value of
using an empirically determined value of  pixels. At this point, it is required measure how likely are the set of 2D measurements
pixels. At this point, it is required measure how likely are the set of 2D measurements  to be projections of the 3D HBM landmark
to be projections of the 3D HBM landmark  . This can be done by means of the generalized symmetric epipolar distance
. This can be done by means of the generalized symmetric epipolar distance  [14].
[14].
Let  be the epipolar line generated by the point
be the epipolar line generated by the point  in a given view
in a given view  onto another view
onto another view  . Symmetric epipolar distance between two points
. Symmetric epipolar distance between two points  , in the two views
, in the two views  ,
, , is defined as
, is defined as

where  is defined as the Euclidean distance between the epipolar line
is defined as the Euclidean distance between the epipolar line  and the point
and the point  as depicted in Figure 3. The extension of the symmetric epipolar distance for
as depicted in Figure 3. The extension of the symmetric epipolar distance for  points (in
points (in  different views)
different views)  can be written in terms of the distance defined in (12) as [14]
can be written in terms of the distance defined in (12) as [14]

This distance produces low values when the 2D points are coherent, that is, when they are projections of the same 3D location. The score  associated to
associated to  , and therefore to
, and therefore to  , is defined as
, is defined as

and normalized such that  . In the case where the nonempty elements of
. In the case where the nonempty elements of  is below 2, the distance
is below 2, the distance  cannot be computed. Under these circumstances, we set
cannot be computed. Under these circumstances, we set  .
.
Assuming that the involved errors follow a Gaussian distribution [23], an accurate way to define the weighting function  is
is

3.4. Occlusion Management
Occlusions are a major problem in HMC systems and can be separated into two categories: auto-occlusions and occlusions generated by opaque elements in the scene. In both cases, when analyzed from a multi-view perspective, occlusions are reflected in a missing subset of detected markers into some views. Assuming that there are  markers attached to some HBM landmarks, the set
markers attached to some HBM landmarks, the set  would ideally contain the
would ideally contain the  2D projections of the markers that are not affected by the occlusions produced by the body itself onto the
2D projections of the markers that are not affected by the occlusions produced by the body itself onto the  th camera view. Moreover, there might be some miss-detections of these projection and a number of false measurements.
th camera view. Moreover, there might be some miss-detections of these projection and a number of false measurements.
Within the current analysis framework, occlusions and miss-detections can be assumed as an underperformance of the generic marker detection  thus regarded by the miss-detection rate
thus regarded by the miss-detection rate  . As previously noted, the amount of false positives is represented by the false positive rate
. As previously noted, the amount of false positives is represented by the false positive rate  and the error committed in the marker location estimation is assumed to have a Gaussian distribution with variance
and the error committed in the marker location estimation is assumed to have a Gaussian distribution with variance  . This formation will allow simulating an arbitrary degree of corruption of the input data, as will be shown in Section 4.
. This formation will allow simulating an arbitrary degree of corruption of the input data, as will be shown in Section 4.
Markers that are visible in, at least, three camera views can be correctly handled by the likelihood function. In the case of severe occlusions where there are only two camera views containing projections of a given marker, the distance  may become inaccurate. In such cases, the position of the occluded marker is estimated using information from both the correctly estimated 3D neighboring landmarks and applying temporal coherence.
may become inaccurate. In such cases, the position of the occluded marker is estimated using information from both the correctly estimated 3D neighboring landmarks and applying temporal coherence.
3.5. Propagation Model
Kinematic restrictions imposed by the angular limits at each joint of the HBM may produce a more robust tracking output. In this field, some methods employ large volumes of annotated data to accurately model the angular cross-dependencies among joints [24] or to learn dynamic models associated to a given action [25]. In our case, these angular constraints will be enforced in the propagation step of the APF scheme. Typically, the propagation step consists in adding a random component to the state vector of a particle as

That is, to generate samples from a multivariate Gaussian distribution centered at  with covariance matrix
with covariance matrix  . However, this may lead to poses out of the legal angular ranges of the HBM. In order to avoid such effect, some works [26] add a term into the likelihood function that penalizes particles that do not fulfill the angular constraints. The following alternative is proposed to take into account angular constrains and draw samples from a truncated Gaussian distribution [27], denoted as
. However, this may lead to poses out of the legal angular ranges of the HBM. In order to avoid such effect, some works [26] add a term into the likelihood function that penalizes particles that do not fulfill the angular constraints. The following alternative is proposed to take into account angular constrains and draw samples from a truncated Gaussian distribution [27], denoted as  and shown in Figure 4. In this way, particles are generated always within the allowed ranges thus avoiding the evaluation of particles that encode impossible poses and therefore increasing the performance of the sampling set.
and shown in Figure 4. In this way, particles are generated always within the allowed ranges thus avoiding the evaluation of particles that encode impossible poses and therefore increasing the performance of the sampling set.
Angular constraints enforcement by propagating particles within the allowed angular ranges  . In (a), samples are propagated following a truncated Gaussian distribution
. In (a), samples are propagated following a truncated Gaussian distribution  centered at
centered at  with covariance matrix
with covariance matrix  bounded between
bounded between  and
and  (green zone). (b) An example of particle propagation in the knee angle displaying how propagated particles never fall out the legal ranges (
(green zone). (b) An example of particle propagation in the knee angle displaying how propagated particles never fall out the legal ranges ( ).
).
4. Experiments and Results
4.1. Synthetic Data on HumanEva
In order to test the proposed algorithm, HumanEva data set [3] has been selected since it provides synchronized and calibrated data from both several cameras and a professional motion capture (MoCap) system to produce ground truth data. This data set contains a set of 5 actions performed by 3 different subjects captured by 4 fully calibrated cameras with a resolution of  pixels at 30 fps.
pixels at 30 fps.
HumanEva suggests two metrics, mean,  , and standard deviation of the estimation error,
, and standard deviation of the estimation error,  , towards providing quantitative and comparable results. In this paper, metrics proposed in [28] for 3D human pose tracking evaluation are also employed. Let
, towards providing quantitative and comparable results. In this paper, metrics proposed in [28] for 3D human pose tracking evaluation are also employed. Let  ,
,  , denote the
, denote the  landmark positions of the HBM (typically, the body joints and the end of the limbs) corresponding to the pose described by the state variable
landmark positions of the HBM (typically, the body joints and the end of the limbs) corresponding to the pose described by the state variable  computed using forward kinematics [12] at a given time
computed using forward kinematics [12] at a given time  . Assuming that landmark positions
. Assuming that landmark positions  associated to particle
associated to particle  are available, we can define a matched marker estimation
are available, we can define a matched marker estimation  with respect to the ground truth position
with respect to the ground truth position  as the one fulfilling
as the one fulfilling  . This stands for those estimations that fall
. This stands for those estimations that fall  -close to the ground truth position. Then, the Multiple Marker Tracking Accuracy (MMTA) is defined as the percentage of markers
-close to the ground truth position. Then, the Multiple Marker Tracking Accuracy (MMTA) is defined as the percentage of markers  fulfilling the
fulfilling the  condition, and the Multiple Marker Tracking Precision (MMTP) as the average of the metric error between
condition, and the Multiple Marker Tracking Precision (MMTP) as the average of the metric error between  and
and  , of all pairs fulfilling
, of all pairs fulfilling  . Finally, these scores are averaged for all frames in the sequence. Threshold
. Finally, these scores are averaged for all frames in the sequence. Threshold  , being an upper-bound of the maximum allowed error, is set to
, being an upper-bound of the maximum allowed error, is set to  in our experiments.
in our experiments.
As it has been presented in Section 3.2, the input measurements  of the proposed algorithm are a set of 2D detections,
of the proposed algorithm are a set of 2D detections,  , measured over
, measured over  cameras for every time instant
cameras for every time instant  . A synthetic data generation strategy has been devised where the 2D projection of the markers onto all camera views are computed from the 3D ground truth data, noted as
. A synthetic data generation strategy has been devised where the 2D projection of the markers onto all camera views are computed from the 3D ground truth data, noted as  . This process is exemplified in Figure 5 and defined as follows.
. This process is exemplified in Figure 5 and defined as follows.
-
(1)
Inverse kinematics are applied to
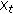 to estimate the pose of a HBM and body parts are fleshed out with super ellipsoids.
to estimate the pose of a HBM and body parts are fleshed out with super ellipsoids. -
(2)
Every 3D location in
 is projected onto every camera in order to generate the sets
is projected onto every camera in order to generate the sets 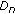 ,
, 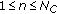 . The previously estimated fleshed HBM checks the visibility of markers onto a given camera view by modeling the possible auto-occlusions among body parts. At this point, the 2D locations contained in
. The previously estimated fleshed HBM checks the visibility of markers onto a given camera view by modeling the possible auto-occlusions among body parts. At this point, the 2D locations contained in  are the positions obtained by an ideal marker detection algorithm.
are the positions obtained by an ideal marker detection algorithm. -
(3)
The effect of the marker detection algorithm
 is simulated by generating a number of miss detections, false measurements and, finally, adding a Gaussian noise to all measurements, according to the statistics reflected by
is simulated by generating a number of miss detections, false measurements and, finally, adding a Gaussian noise to all measurements, according to the statistics reflected by  ,
, 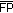 , and
, and  .
.
Synthetic data generation process. Since the reflective markers are not distinguishable in the original RGB image (a), the sets  are generated from the 3D locations provided by the MoCap system. First, for a given view
are generated from the 3D locations provided by the MoCap system. First, for a given view  , all 3D markers are projected onto the corresponding image (b), and those affected by body auto-occlusions are removed (c). Then, the marker detection algorithm
, all 3D markers are projected onto the corresponding image (b), and those affected by body auto-occlusions are removed (c). Then, the marker detection algorithm  is applied: some markers are missed due to the detection ratio (d), and a number of false measurements are generated (e). Finally, an amount of Gaussian noise with variance
is applied: some markers are missed due to the detection ratio (d), and a number of false measurements are generated (e). Finally, an amount of Gaussian noise with variance  is added simulating the position estimation error.
is added simulating the position estimation error.
In order to test the performance of the proposed tracking algorithm, two factors must be taken into account: the performance of the marker detection algorithm  (determined by the triplet
(determined by the triplet  ) and the algorithm design parameters, that is, the number of layers
) and the algorithm design parameters, that is, the number of layers  and the number of particles per layer
and the number of particles per layer  . A simulation has been conducted testing a large number of combinations between parameters of
. A simulation has been conducted testing a large number of combinations between parameters of  and the proposed APF algorithm. The results of this simulation are depicted in Figure 6 where the
and the proposed APF algorithm. The results of this simulation are depicted in Figure 6 where the  score is displayed as the more informative metric [28].
score is displayed as the more informative metric [28].
Quantitative results over the HumanEva data set where score MMTA is displayed in pseudocolor. In all plots, y-axis accounts for the number of layers L and x-axis for the number of particles per layer N
p
. In (a), assuming an ideal case where  and
and  , impact of the number of occlusions, regarded by
, impact of the number of occlusions, regarded by  in the overall performance. In (b), assuming a fixed occlusion level
in the overall performance. In (b), assuming a fixed occlusion level  , results for the cases
, results for the cases  and
and  mm.
mm.
When analyzing the impact of missing projections of markers, that is, occlusions, represented by  and shown in Figure 6(a), it can be seen that the algorithm is still robust producing accurate estimations even in the case of a large miss of data,
and shown in Figure 6(a), it can be seen that the algorithm is still robust producing accurate estimations even in the case of a large miss of data,  . Assuming a fixed and realistic amount of occlusions,
. Assuming a fixed and realistic amount of occlusions,  , we can explore the influence of the other distorting factors. Analyzing the results shown in Figure 6(b), it may be seen that the algorithm is robust against the number of false detections
, we can explore the influence of the other distorting factors. Analyzing the results shown in Figure 6(b), it may be seen that the algorithm is robust against the number of false detections  since it is very unlikely that false 2D measurements in different views keep a 3D coherence. In this case, the spacial redundancy is efficiently exploited to discard these measurements. On the other hand, the performance of the algorithm decreases as the 2D marker position estimation error increases,
since it is very unlikely that false 2D measurements in different views keep a 3D coherence. In this case, the spacial redundancy is efficiently exploited to discard these measurements. On the other hand, the performance of the algorithm decreases as the 2D marker position estimation error increases,  . Another evident fact to be emphasized is the overannealing effect. The performance of the algorithm is not monotonically increasing with the number of employed annealing layers. This happens when the particles concentrate too much around the peaks of the weighting function hence impoverishing the overall representation of the likelihood distribution. For this motion tracking problem, we found that the optimal configuration is
. Another evident fact to be emphasized is the overannealing effect. The performance of the algorithm is not monotonically increasing with the number of employed annealing layers. This happens when the particles concentrate too much around the peaks of the weighting function hence impoverishing the overall representation of the likelihood distribution. For this motion tracking problem, we found that the optimal configuration is  and
and  .
.
4.2. Real Data
The presented body tracking algorithm has been applied to capture motion figures from 4 different types of dances: salsa, belly dancing, and two Turkish folk dances. The analysis sequences were recorded with 6 fully calibrated cameras with a resolution of  pixels at 30 fps.
pixels at 30 fps.
Markers attached to the body of the dance performer were little yellow balls and a color-based detection algorithm  has been used to generate the sets
has been used to generate the sets  for every incoming multi-view frame. The original images are processed in the YCrCb color space which gives flexibility over intensity variations in the frames of a video as well as among the videos captured by the cameras from different views. In order to learn the chrominance information of the marker color, markers on the dancer are manually labeled in one frame for all camera views. It was assumed that the distributions of Cr and Cb channel intensity values belonging to marker regions are Gaussian. Thus, the mean can be computed over each marker region (a pixel neighborhood around the labeled point). Then, a threshold in the Mahalanobis sense is applied to all images in order to detect marker locations. An empirical analysis showed that the detector
for every incoming multi-view frame. The original images are processed in the YCrCb color space which gives flexibility over intensity variations in the frames of a video as well as among the videos captured by the cameras from different views. In order to learn the chrominance information of the marker color, markers on the dancer are manually labeled in one frame for all camera views. It was assumed that the distributions of Cr and Cb channel intensity values belonging to marker regions are Gaussian. Thus, the mean can be computed over each marker region (a pixel neighborhood around the labeled point). Then, a threshold in the Mahalanobis sense is applied to all images in order to detect marker locations. An empirical analysis showed that the detector  had the following performance triplet:
had the following performance triplet:  ,
,  , and
, and  mm.
mm.
In this particular scenario, the algorithm had to cope with very fast motion associated to some figures. Even though these harsh conditions, the results were satisfactory and visually accurate as shown in Figure 7. Check http://www.cristiancanton.org/ for some example videos.
4.3. Results Comparison
A number of algorithms in the literature have been evaluated using HumanEva-I and their results have been reported in Table 1. There are two main trends in pose estimation: methods based on a tracking formulation of the problem and methods based on statistical classification. The method presented in this paper falls into the first category where some comparisons can be made. Among the reported methods, we find the expectation-maximization (EM) kinematically constrained GMM method presented by Cheng and Trivedi [29] as the continuation of the techniques already presented by Mikič [35]. Addressing a complex problem such as human motion capture using EM is perhaps manageable in a benevolent scenario with well learnt constrains but, as suggested by Caillete and Howard [36] in the comparison of EM- and PF- based methods, Monte Carlo-based techniques clearly outperform those based in minimization algorithms. Other contributions reported over HumanEva-I are based on the seminal idea of PF. Husz and Wallance [26] included a particle propagation step relying on learnt information on the structure of the executed motion thus facing the already mentioned problem of lack of adaptivity to unseen motions. A very detailed dynamic model of the human kinematics is employed by Brubaker et al. [30]. Motion involving a more complex pattern such as boxing or gesturing may not cope well with these two methods.
 , as reported by the compared authors in their respective contributions.
, as reported by the compared authors in their respective contributions.The other family of human motion capture algorithms is based on learning and classification instead of tracking. Basically, these techniques examine the ground truth data and extract a number of features from them. Afterwards, when a new test frame is processed, these same features are extracted, and the best match between them and the already learnt ones is outputted. Results obtained with these techniques, specially those of Urtasun et al. [25] and Poppe [32], outperform the tracking-based ones. However, these techniques are constrained to track a beforehand selected action and their applicability to unknown motion patterns is limited. It is notable the technique presented by Münderman et al. [31] where a 3D reconstruction is performed before computing the features to be learnt.
To the authors knowledge, there is no evaluation of a marker-based HMC system using the HumanEva dataset. The obtained results are close to those presented by classification-based markerless methods and, although the employed input data is different, it allows qualitatively evaluating its performance. An advantage of using a marker-based method is its robustness to faulty inputs, its low complexity, and the possibility of real-time implementations.
4.4. Real-Time Considerations
Once the image measurements have been obtained, the fitting of an HBM to these data using the proposed algorithm is achieved in real time in a 3 GHz computer. Due to the low dimension of the input data ( ), the computation of the involved operations in both the likelihood and propagation steps require a low computational cost. Measurements, can be obtained using elementary image filtering techniques as shown in Section 4.2 usually computed directly on the camera (as done by [8]) or by the digitizing hardware.
), the computation of the involved operations in both the likelihood and propagation steps require a low computational cost. Measurements, can be obtained using elementary image filtering techniques as shown in Section 4.2 usually computed directly on the camera (as done by [8]) or by the digitizing hardware.
5. Conclusion
This paper presents a robust real-time low-cost approach to marker-based human motion capture using multiple cameras synchronized and calibrated. Progressive fitting of a human body model through the annealed particle filtering algorithm using a multi-view consistency likelihood function, the symmetric epipolar distance, and a kinematically constrained particle propagation model allow an accurate estimation of the body pose. Quantitative evaluation based on HumanEva dataset assessed the robustness of the algorithm when dealing faulty input data, even in very harsh conditions. Fast dance motion was also analyzed proving the adequateness of our technique to deal with a real scenario data.
References
Baran I, Popović J: Automatic rigging and animation of 3D characters. Proceedings of the ACM International Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '07), August 2007
Cerveri P, Pedotti A, Ferrigno G: Robust recovery of human motion from video using Kalman filters and virtual humans. Human Movement Science 2003, 22(3):377-404. 10.1016/S0167-9457(03)00004-6
Sigal L, Balan AO, Black MJ: HumanEva: synchronized video and motion capture dataset and baseline algorithm for evaluation of articulated human motion. International Journal of Computer Vision 2010, 87(1-2):4-27. 10.1007/s11263-009-0273-6
Kirk AG, O'Brien JF, Forsyth DA: Skeletal parameter estimation from optical motion capture data. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '05), June 2005 782-788.
Ascension http://www.ascension-tech.com/.
Moven-inertial motion capture http://www.moven.com/.
Roetenberg D: Inertial and magnetic sensing of human motion, Ph.D. dissertation. University of Twente, Twente, The Netherlands; 2006.
Vicon http://www.vicon.com/.
Raskar R, Nii H, Dedecker B, Hashimoto Y, Summet J, Moore D, Zhao Y, Westhues J, Dietz P, Barnwell J, Nayar S, Inami M, Bekaert P, Noland M, Branzoi V, Bruns E: Prakash: lighting aware motion capture using photosensing markers and multiplexed illuminators. ACM Transactions on Graphics 2007., 26(3):
Hartley R, Zisserman A: Multiple View Geometry in Computer Vision. C. U. Press; 2004.
Herda L, Fua P, Plänkers R, Boulic R, Thalmann D: Using skeleton-based tracking to increase the reliability of optical motion capture. Human Movement Science 2001, 20(3):313-341. 10.1016/S0167-9457(01)00050-1
Guerra-Filho G: Optical motion capture: theory and implementation. Journal of Theoretical and Applied Informatics 2005, 12(2):61-89.
Deutscher J, Reid I: Articulated body motion capture by stochastic search. International Journal of Computer Vision 2005, 61(2):185-205.
Canton-Ferrer C, Casas JR, Pardàs M: Towards a Bayesian approach to robust finding correspondences in multiple view geometry environments. Proceedings of the 4th International Workshop on Computer Graphics and Geometric Modelling, 2005, Lecture Notes on Computer Science 3515: 281-289.
Moeslund TB, Hilton A, Krüger V: A survey of advances in vision-based human motion capture and analysis. Computer Vision and Image Understanding 2006, 104(2-3):90-126. 10.1016/j.cviu.2006.08.002
Arulampalam MS, Maskell S, Gordon N, Clapp T: A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing 2002, 50(2):174-188. 10.1109/78.978374
Gordon NJ, Salmond DJ, Smith AFM: Novel approach to nonlinear/non-gaussian Bayesian state estimation. IEE Proceedings, Part F 1993, 140(2):107-113.
MacCormick J, Isard M: Partitioned sampling, articulated objects, and interface-quality hand tracking. Proceedings of the European Conference on Computer Vision, 2000 3-19.
Mitchelson J, Hilton A: Simultaneous pose estimation of multiple people using multiple-view cues with hierarchical sampling. Proceedings of the British Machine Vision Conference, 2003
Madapura J, Li B: 3D articulated human body tracking using KLD-Annealed Rao-Blackwellised Particle filter. Proceedings of IEEE International Conference onMultimedia and Expo (ICME '07), July 2007 1950-1953.
Canton-Ferrer C, Casas JR, Pardàs M, Sblendido R: Particle filtering and sparse sampling for multi-person 3D tracking. Proceedings of IEEE International Conference on Image Processing (ICIP '08), October 2008 2644-2647.
Dockstader SL, Berg MJ, Tekalp AM: Stochastic kinematic modeling and feature extraction for gait analysis. IEEE Transactions on Image Processing 2003, 12(8):962-976. 10.1109/TIP.2003.815259
Lichtenauer J, Reinders M, Hendriks E: Influence of the observation likelihood function on particle filtering performance in tracking applications. Proceedings of the 6th IEEE International Conference on Automatic Face and Gesture Recognition (FGR '04), May 2004 767-772.
Herda L, Urtasun R, Fua P: Hierarchical implicit surface joint limits for human body tracking. Computer Vision and Image Understanding 2005, 99(2):189-209. 10.1016/j.cviu.2005.01.005
Urtasun R, Fleet DJ, Fua P: 3D people tracking with Gaussian process dynamical models. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '06), June 2006 238-245.
Husz Z, Wallance A: Evaluation of a hierarchical partitioned particle filter with action primitives. Proceedings of the 2nd Workshop on Evaluation of Articulated Human Motion and Pose Estimation, 2007
Kotecha JH, Djuric PM: Gibbs sampling approach for generation of truncated multivariate Gaussian random variables. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '99), March 1999 1757-1760.
Canton-Ferrer C, Casas J, Pard`as M, Monte E: Towards a fair evaluation of 3D human pose estimation algorithms. Technical University of Catalonia; 2009.
Cheng S, Trivedi M: Articulated body pose estimation from voxel reconstructions using kinematically constrained Gaussian mixture models: algorithm and evaluation. Proceedings of the 2nd Workshop on Evaluation of Articulated Human Motion and Pose Estimation, 2007
Brubaker M, Fleet D, Hertzmann A: Physics-based human pose tracking. Proceedings of the Workshop on Evaluation of Articulated Human Motion and Pose Estimation, 2006
Münderman L, Corazza S, Andriacchi T: Markerless human motion capture through visual hull and articulated icp. Proceedings of the Workshop on Evaluation of Articulated Human Motion and Pose Estimation, 2006
Poppe R: Evaluating example-based pose estimation: experiments on the humaneva sets. Proceedings of the 2nd Workshop on Evaluation of Articulated Human Motion and Pose Estimation, 2007
Okada R, Soatto S: Relevant feature selection for human pose estimation and localization in cluttered images. Proceedings of the European Conference on Computer Vision, 2008
Canton-Ferrer C, Casas JR, Pardàs M: Voxel based annealed particle filtering for markerless 3D articulated motion capture. Proceedings of the 3rd IEEE Conference on 3DTV (3DTV-CON '09), May 2009
Mikič I: Human body model acquisition and tracking using multi-camera voxel data, Ph.D. dissertation. University of California, San Diego, Calif, USA; 2003.
Caillette F, Howard T: Real-time markerless human body tracking with multi-view 3-D voxel reconstruction. Proceedings of the British Machine Vision Conference, 2004 2: 597-606.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Canton-Ferrer, C., Casas, J.R. & Pardàs, M. Marker-Based Human Motion Capture in Multiview Sequences. EURASIP J. Adv. Signal Process. 2010, 105476 (2010). https://doi.org/10.1155/2010/105476
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/105476
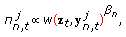
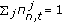 . The estimation of parameter
. The estimation of parameter 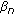 is based on the particle survival technique described in [
is based on the particle survival technique described in [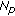 particles with replacement from the set
particles with replacement from the set  with distribution
with distribution 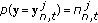 .
.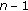 as
as
 stands for a truncated multivariate Gaussian distribution with mean
stands for a truncated multivariate Gaussian distribution with mean  and covariance matrix
and covariance matrix  that will be further described in Section 3.5. This process is repeated until reaching
that will be further described in Section 3.5. This process is repeated until reaching 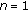 .
.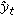 is computed as
is computed as



 .
.
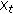 to estimate the pose of a HBM and body parts are fleshed out with super ellipsoids.
to estimate the pose of a HBM and body parts are fleshed out with super ellipsoids. is projected onto every camera in order to generate the sets
is projected onto every camera in order to generate the sets 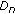 ,
, 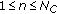 . The previously estimated fleshed HBM checks the visibility of markers onto a given camera view by modeling the possible auto-occlusions among body parts. At this point, the 2D locations contained in
. The previously estimated fleshed HBM checks the visibility of markers onto a given camera view by modeling the possible auto-occlusions among body parts. At this point, the 2D locations contained in  are the positions obtained by an ideal marker detection algorithm.
are the positions obtained by an ideal marker detection algorithm. is simulated by generating a number of miss detections, false measurements and, finally, adding a Gaussian noise to all measurements, according to the statistics reflected by
is simulated by generating a number of miss detections, false measurements and, finally, adding a Gaussian noise to all measurements, according to the statistics reflected by  ,
, 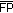 , and
, and  .
.

