- Research Article
- Open access
- Published:
Compressive Sampling of EEG Signals with Finite Rate of Innovation
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 183105 (2010)
Abstract
Analyses of electroencephalographic signals and subsequent diagnoses can only be done effectively on long term recordings that preserve the signals' morphologies. Currently, electroencephalographic signals are obtained at Nyquist rate or higher, thus introducing redundancies. Existing compression methods remove these redundancies, thereby achieving compression. We propose an alternative compression scheme based on a sampling theory developed for signals with a finite rate of innovation (FRI) which compresses electroencephalographic signals during acquisition. We model the signals as FRI signals and then sample them at their rate of innovation. The signals are thus effectively represented by a small set of Fourier coefficients corresponding to the signals' rate of innovation. Using the FRI theory, original signals can be reconstructed using this set of coefficients. Seventy-two hours of electroencephalographic recording are tested and results based on metrices used in compression literature and morphological similarities of electroencephalographic signals are presented. The proposed method achieves results comparable to that of wavelet compression methods, achieving low reconstruction errors while preserving the morphologiies of the signals. More importantly, it introduces a new framework to acquire electroencephalographic signals at their rate of innovation, thus entailing a less costly low-rate sampling device that does not waste precious computational resources.
1. Introduction
The electroencephalogram (EEG) is a recording of the brain's neural activities. Since its discovery by Berger [1], many research activities have focussed on how to automatically extract useful information about the brain's conditions based on the distinct characteristics of these electrical signals. Valuable information about the human brain conveyed by the EEG is used in various studies like the nervous system, sleep disorders, epilepsy, and dementia [2]. These applications require acquisition, storage, and automatic processing of EEG during an extended period of time. For example,  -hour monitoring of a multiple-channel EEG is needed for epilepsy patients. Traditionally, the EEG has been bandlimited to the frequency range between
-hour monitoring of a multiple-channel EEG is needed for epilepsy patients. Traditionally, the EEG has been bandlimited to the frequency range between  and
and  Hz; thus a minimum Nyquist sampling rate of
Hz; thus a minimum Nyquist sampling rate of  Hz is needed. At the quantization level of 16 bit/sample, a
Hz is needed. At the quantization level of 16 bit/sample, a  -channel EEG for a
-channel EEG for a  -hour period would amount to
-hour period would amount to  megabytes. Hence, to efficiently store and transmit a huge amount of data, effective compression techniques are desired. While lossy techniques yield higher compression, because of reliability considerations, lossy data compression techniques are not used as the morphology of the signals which are not always well retained. Excellent surveys of the performance of lossless and lossy EEG compression techniques can be found in [3] to [4]. Antoniol and Tonella presented and discussed several classical lossless EEG signal compression methods such as Huffman coding, predictive compression, and transform compression [3]. In [5], Memon et al. discussed lossless compression techniques ranging from simple dictionary searches to sophisticated context modeling. A long-term EEG compression method using features obtained from the signals' power spectral density was proposed in [6] while multi-channel EEG signals were compressed by exploiting the intercorrelation among the EEG channels through the Karhunen-Loeve transform in [7]. Nielsen et al. proposed a signal-dependent wavelet compression scheme that adapted optimal wavelets to biomedical signals for compression [8]. A near-lossless compression method described in [9] compressed EEG signals using neural network predictors followed by nonuniform quantization. More recently, a new compression method based on the construction process of the classified signature and envelop vector sets of the EEG signals [4].
megabytes. Hence, to efficiently store and transmit a huge amount of data, effective compression techniques are desired. While lossy techniques yield higher compression, because of reliability considerations, lossy data compression techniques are not used as the morphology of the signals which are not always well retained. Excellent surveys of the performance of lossless and lossy EEG compression techniques can be found in [3] to [4]. Antoniol and Tonella presented and discussed several classical lossless EEG signal compression methods such as Huffman coding, predictive compression, and transform compression [3]. In [5], Memon et al. discussed lossless compression techniques ranging from simple dictionary searches to sophisticated context modeling. A long-term EEG compression method using features obtained from the signals' power spectral density was proposed in [6] while multi-channel EEG signals were compressed by exploiting the intercorrelation among the EEG channels through the Karhunen-Loeve transform in [7]. Nielsen et al. proposed a signal-dependent wavelet compression scheme that adapted optimal wavelets to biomedical signals for compression [8]. A near-lossless compression method described in [9] compressed EEG signals using neural network predictors followed by nonuniform quantization. More recently, a new compression method based on the construction process of the classified signature and envelop vector sets of the EEG signals [4].
The techniques presented above operated on EEG signals obtained at or above Nyquist rate. This acquisition process leads to a collection of huge amounts of irrelevant data, only to be discarded during the compression stage of the signals. Furthermore, transients, which are common in EEG signals, are not bandlimited. Hence, Shannon's sampling theory cannot be applied to sampling EEG signals. Over the last few years, advancements in signal processing and data acquisition introduced a new sampling theory known as compressive sampling or compressed sensing [10]. Aviyente proposed a compressed sensing framework for EEG compression by exploiting the sparsity of EEG signals in a Gabor frame [11]. This method, however, does not operate on the analog EEG signals directly. Compressive sampling, on the other hand, asserts that its acquisition system directly translates analog signals into compressed digital form so that one can recover super-resolved signals from a few measurements [10]. Similarly, we propose to approach the problem of compressing EEG signals at source. In order to address the nonbandlimitedness of the EEG signals, our compression method will be based on the theory of sampling signals with finite rate of innovation (FRI) [12]. This theory has recently been investigated for a compression technique for electrocardiogram (ECG) signals [13] and neonatal EEG seizure signals [14] as well as for EEG seizure source localisation [15].
Our paper is organised as follows. In Section 2, a description of the EEG data, a review on sampling signals with finite rate of innovation, and an FRI model of EEG signals are presented. A scheme for compressively sampling EEG signals with finite rate of innovation will be described in Section 3. Results and discussions will be presented in Section 4 and finally, a conclusion will summarise our findings and provide directions for our future work.
2. EEG Data Description and the FRI Model
2.1. EEG Data Description
A total of  sets of normalised EEG signals comprising
sets of normalised EEG signals comprising  hours were used for the study. The data is further divided into
hours were used for the study. The data is further divided into  seconds epochs for processing. All
seconds epochs for processing. All  patients experienced similar seizure types at similar locations on the brain. From this dataset,
patients experienced similar seizure types at similar locations on the brain. From this dataset,  epochs of
epochs of  seconds duration were selected for establishing a finite rate of innovation model of EEG signals while the rest of the data were used to evaluate our compression scheme. The EEG data were acquired using a Neurofile NT digital video EEG system with
seconds duration were selected for establishing a finite rate of innovation model of EEG signals while the rest of the data were used to evaluate our compression scheme. The EEG data were acquired using a Neurofile NT digital video EEG system with  channels,
channels,  Hz sampling rate, and a
Hz sampling rate, and a  -bit analogue-to-digital converter. Notch or bandpass filters have not been applied. More details of the database can be found in [16]. In our experiments, these EEG signals are assumed to be the source signals. For each patient, there will be
-bit analogue-to-digital converter. Notch or bandpass filters have not been applied. More details of the database can be found in [16]. In our experiments, these EEG signals are assumed to be the source signals. For each patient, there will be  epochs and the epochs will be referenced as
epochs and the epochs will be referenced as  where
where  represents the patient number and
represents the patient number and  represents the epoch number.
represents the epoch number.
2.2. Review of Sampling Signals with Finite Rate of Innovation
Consider classes of parametric signals with a finite number of degrees of freedom per unit of time, which is defined as the rate of innovation (e.g., streams of Dirac pulses, nonuniform splines, and piecewise polynomials). It is shown in [12] that although these signals are not bandlimited, they can be sampled uniformly at (or above) the rate of innovation using an appropriate kernel, and then perfectly reconstructed by solving systems of linear equations.
2.2.1. Periodic Stream of Dirac Pulses
Consider a stream of  Dirac pulses periodized with period
Dirac pulses periodized with period  ,
,  where
where  and
and  for all
for all  . This signal has
. This signal has  degrees of freedom per period, thus the rate of innovation is
degrees of freedom per period, thus the rate of innovation is

By taking a continuous-time periodic sinc sampling kernel  with bandwidth
with bandwidth  greater than or equal to the rate of innovation
greater than or equal to the rate of innovation  given by (1), and sampling
given by (1), and sampling  at
at  uniform locations
uniform locations  =
=  where
where  =
=  and
and  then the samples defined by
then the samples defined by  =
=  sufficiently represent
sufficiently represent  [12].
[12].
2.2.2. Nonuniform Splines
A signal  is a nonuniform spline of degree
is a nonuniform spline of degree  with knots at
with knots at  if and only if its
if and only if its  th derivative is a stream of
th derivative is a stream of  weighted Dirac pulses
weighted Dirac pulses  [17]. Here, the rate of innovation is
[17]. Here, the rate of innovation is 
Consider a continuous-time periodic nonuniform linear spline  with period
with period  , containing
, containing  pieces of maximum degree
pieces of maximum degree  . By following the sampling method described in Section 2.2.1,
. By following the sampling method described in Section 2.2.1,  is uniquely defined by
is uniquely defined by  =
=  =
=  [12].
[12].
2.2.3. Noisy Case
In this section, we briefly present two types of noise signals that are added to the FRI signals. The first type of noise signal considered is the white noise, which is a zero-mean signal characterised by a flat power spectral density. The second type of noise signal is the  noise whose power spectral density is inversely proportional to its frequency [18]. Accordingly, we define
noise whose power spectral density is inversely proportional to its frequency [18]. Accordingly, we define

where  and
and  are the power spectral densities of white and
are the power spectral densities of white and  noise, respectively and
noise, respectively and  .
.
2.3. Spline-Based FRI Models with Additive Noise
In this section, an FRI model of EEG signals is validated and presented. In particular, we model the EEG signals as

where  is the nonuniform spline component, and
is the nonuniform spline component, and  is the noise component. We consider the cases of nonuniform linear spline, nonuniform quadratic spline, and lastly the nonuniform cubic spline (where
is the noise component. We consider the cases of nonuniform linear spline, nonuniform quadratic spline, and lastly the nonuniform cubic spline (where  respectively in Section 2.2.2) with additive white noise and
respectively in Section 2.2.2) with additive white noise and  noise. We also compare the models with the original signals based on the performance metrics described below and conclude with a suitable FRI model for EEG signals.
noise. We also compare the models with the original signals based on the performance metrics described below and conclude with a suitable FRI model for EEG signals.
2.3.1. Performance Metrics
The following evaluation metrics were employed to determine our method's performance [4].
The compression ratio ( ) is defined as a ratio between the number of bits required to represent the original signal and the compressed signal. First, we define a ratio
) is defined as a ratio between the number of bits required to represent the original signal and the compressed signal. First, we define a ratio

where  and
and  represent the numbers of bits required for the original and compressed signals, respectively.
represent the numbers of bits required for the original and compressed signals, respectively.
Thus we can define a  commonly used in the literature as
commonly used in the literature as

A metric that can be used to measure distortion is percent root difference ( ). This metric is commonly used for measuring the distortions in reconstructed biomedical signals such as Electrocardiographic (ECG) signals and EEG signals. For signals of length
). This metric is commonly used for measuring the distortions in reconstructed biomedical signals such as Electrocardiographic (ECG) signals and EEG signals. For signals of length  ,
,  can be defined as
can be defined as

where  and
and  are the sampled values of the original and reconstructed signals.
are the sampled values of the original and reconstructed signals.
Another distortion metric is the root mean square error ( ). In data compression, we are interested in finding an optimal approximation for minimizing this metric as defined by the following formula:
). In data compression, we are interested in finding an optimal approximation for minimizing this metric as defined by the following formula:

Since the similarity between the reconstructed and original signal is crucial from the clinical point of view, the cross correlation ( ) is used to evaluate the similarity between the original signal and its reconstruction.
) is used to evaluate the similarity between the original signal and its reconstruction.

where  and
and  are the mean values of the original and reconstructed signals, respectively.
are the mean values of the original and reconstructed signals, respectively.
In order to understand the local distortions between the original and the reconstructed signals, two metrics, the maximum error ( ) and the peak amplitude related error (
) and the peak amplitude related error ( ) [19], will be computed. The maximum error metric is defined as
) [19], will be computed. The maximum error metric is defined as

and it shows how large the error is between every sample of the original and reconstructed signals. This metric should ideally be small if both signals are similar. The  is defined as
is defined as

By plotting  , one will be able to understand the locations and magnitudes of the errors between the original and reconstructed signals.
, one will be able to understand the locations and magnitudes of the errors between the original and reconstructed signals.
2.3.2. Comparison of Models
As depicted in Figure 1, a comparison between the original EEG signal and its approximations shows that the nonuniform linear spline model gives the best approximation where a  of
of  , with an
, with an  of
of  , a
, a  of
of  and a
and a  of
of  are achieved. An evaluation of
are achieved. An evaluation of  sets of EEG signals in Table 1 shows that the nonuniform linear and cubic spline models best fitted the EEG signals. Since the results achieved with a linear spline model are very close to that of a cubic spline model, the nonuniform linear spline model is chosen as our EEG model to minimise computation costs.
sets of EEG signals in Table 1 shows that the nonuniform linear and cubic spline models best fitted the EEG signals. Since the results achieved with a linear spline model are very close to that of a cubic spline model, the nonuniform linear spline model is chosen as our EEG model to minimise computation costs.
 epochs of EEG signals.
epochs of EEG signals.Comparison of different spline models of EEG. (a) Original EEG signal; (b) Linear spline model, CC = 99.22%, RMSE = 0.0020, PRD = 13.07%, MAXERR = 0.0012; (c) Quadratic spline model, CC = 96.00%, RMSE = 0.0046, PRD = 29.65%, MAXERR =0.023; (d) Cubic spline model CC = 99.13%, RMSE = 0.0021, PRD = 13.65%, MAXERR = 0.0011.
Figure 2 illustrates the nonuniform linear spline model for different EEG signals whereby the approximations closely model the original signals with different  pieces of linear splines. As such, we conclude that with our data, different EEG signals can be modelled with
pieces of linear splines. As such, we conclude that with our data, different EEG signals can be modelled with  for each
for each  seconds EEG segment.
seconds EEG segment.
The nonuniform linear spline model makes up approximately  % of the EEG signal. We observed that the residue signal (EEG signal-nonuniform linear splines) resembled a
% of the EEG signal. We observed that the residue signal (EEG signal-nonuniform linear splines) resembled a  noise signal with a power spectral density
noise signal with a power spectral density  The range of this noise amplitude was found to be
The range of this noise amplitude was found to be  and
and  was estimated to be around
was estimated to be around  by computing the slope of a fitted line onto the log-log plot of
by computing the slope of a fitted line onto the log-log plot of  versus
versus  as shown in Figures 3(a) and 3(b) [20]. Thus, our EEG signals are modelled as nonuniform linear splines embedded in additive
as shown in Figures 3(a) and 3(b) [20]. Thus, our EEG signals are modelled as nonuniform linear splines embedded in additive  noise. In this way, the EEG signals have been cast as signals with finite rate of innovation embedded in noise and this provides a motivation to exploit the FRI framework for compressive sampling of EEG signals.
noise. In this way, the EEG signals have been cast as signals with finite rate of innovation embedded in noise and this provides a motivation to exploit the FRI framework for compressive sampling of EEG signals.
3. Compressive Sampling of EEG Signals with Finite Rate of Innovation
Since the EEG signals are modelled as an FRI signal  noise, we will employ methods developed in [12, 21] to acquire and reconstruct them. It is important that the rate of innovation of the EEG signals is known and in our case, it has to be estimated from the source signals. Let us assume that the number of pieces of linear splines needed to represent the EEG signals is given as shown in Table 2.
noise, we will employ methods developed in [12, 21] to acquire and reconstruct them. It is important that the rate of innovation of the EEG signals is known and in our case, it has to be estimated from the source signals. Let us assume that the number of pieces of linear splines needed to represent the EEG signals is given as shown in Table 2.
With these assumptions, we represent the EEG signals as  pieces of nonuniform linear splines embedded in
pieces of nonuniform linear splines embedded in  noise and the corresponding rate of innovation will be
noise and the corresponding rate of innovation will be  with
with  seconds.
seconds.
3.1. Our Method
Figure 4 shows our proposed EEG signal acquisition process with finite rate of innovation. Since the value of  is assumed to be known, the samples of the EEG signal are obtained based on the descriptions in Section 2.2.1. Corresponding to the representation for the EEG signals, a reconstruction method is presented in Figure 5.
is assumed to be known, the samples of the EEG signal are obtained based on the descriptions in Section 2.2.1. Corresponding to the representation for the EEG signals, a reconstruction method is presented in Figure 5.
In order to perform the Cadzow's noise reduction, a rectangular ( ) Toeplitz matrix
) Toeplitz matrix  is created from the spectral values of the source signal
is created from the spectral values of the source signal  in the form
in the form

We then perform a singular vector decomposition of the matrix  , and enforce rank
, and enforce rank  on
on  by choosing only
by choosing only  most significant singular values. This is iterated until the ratio of the largest singular value of the
most significant singular values. This is iterated until the ratio of the largest singular value of the  to that of the
to that of the  is smaller than a preset threshold. Thus the denoised DFT coefficients can be extracted from
is smaller than a preset threshold. Thus the denoised DFT coefficients can be extracted from  [21].
[21].
Since our EEG signals are modelled as nonuniform linear splines, we perform a differentiation operation twice on the denoised signals so as to reduce them into a stream of Dirac pulses. In order to find the locations and weights of the Dirac pulses, consider a filter  whose
whose  -transform has
-transform has  zeros at
zeros at  , that is,
, that is,  Since the CTFS of the differentiated EEG signal
Since the CTFS of the differentiated EEG signal  is a linear combination of
is a linear combination of  complex exponentials
complex exponentials  , it follows that
, it follows that  is an annihilating filter and satisfies the following condition:
is an annihilating filter and satisfies the following condition:

where

The coefficients of the annihilating filter are found solving (12) which is equivalent to the following Toeplitz linear system of equations:

Thus the locations  of the Dirac pulses are given by the roots of
of the Dirac pulses are given by the roots of  . Next, the weights
. Next, the weights  of the Dirac pulses are given by solving the Vandermonde system of equations given by
of the Dirac pulses are given by solving the Vandermonde system of equations given by

Lastly, the stream of Dirac pulses is integrated twice to obtain the reconstructed EEG signals which correspond to the nonuniform linear spline approximation of the EEG signals.
4. Results and Discussions
In this section, we will present our results based on the performance metrics in Section 2.3.1. Comparisons to wavelet based compression techniques using discrete wavelet transform with the Daubechies and Coiflets wavelets [8] will be included in our discussions. These wavelet transforms are performed with four detailed levels and one approximation. Both the wavelet coefficients and the FRI innovation parameters are coded using Huffman coding. We also compared our results to those found in [11] in terms of normalised mean square error ( ), which is the ratio of mean square error of the reconstructed signals to the range of amplitudes of the signals.
), which is the ratio of mean square error of the reconstructed signals to the range of amplitudes of the signals.
We applied our method on the  sets of EEG signals and the results of
sets of EEG signals and the results of  selected epochs are tabulated in Table 3.
selected epochs are tabulated in Table 3.
 ,
,  ,
,  and
and  .
.The  is selected as the primary evaluation metric and our results are generated with the best
is selected as the primary evaluation metric and our results are generated with the best  achievable for each EEG signal. As shown in Table 3, consistently high
achievable for each EEG signal. As shown in Table 3, consistently high  ranging from
ranging from  to
to  is achieved for our dataset. This implies that there is a great similarity in the morphology between the original and reconstructed EEG signals. This result is highly desirable because such diagnostic features are extremely important and must be preserved. Our method achieves a
is achieved for our dataset. This implies that there is a great similarity in the morphology between the original and reconstructed EEG signals. This result is highly desirable because such diagnostic features are extremely important and must be preserved. Our method achieves a  ranging from
ranging from  to
to  . This is due to the morphology of the EEG signals, where some signals need more linear splines to model them compared to the others. As
. This is due to the morphology of the EEG signals, where some signals need more linear splines to model them compared to the others. As  varies, the rate of innovation
varies, the rate of innovation  varies accordingly and leads to an increased or decreased number of spectral coefficients. Thus
varies accordingly and leads to an increased or decreased number of spectral coefficients. Thus  varies inversely as
varies inversely as  . Table 3 also tabulates the distortions arising from our method. We obtained low
. Table 3 also tabulates the distortions arising from our method. We obtained low  and
and  , implying that our method recovers signals with some distortion. Furthermore, a
, implying that our method recovers signals with some distortion. Furthermore, a  between
between  and
and  is obtained, suggesting that the distortions of the reconstructed signals are very small.
is obtained, suggesting that the distortions of the reconstructed signals are very small.
A typical plot of  and a histogram of the errors are shown in Figures 6 and 7. Errors between original samples of the signal and the corresponding reconstructed samples are amplified and shown in the
and a histogram of the errors are shown in Figures 6 and 7. Errors between original samples of the signal and the corresponding reconstructed samples are amplified and shown in the  plot. The values of
plot. The values of  are generally less than
are generally less than  of the original signal, although some
of the original signal, although some  values are larger than
values are larger than  of the original signal. By comparing Figure 8 to Figure 6, the
of the original signal. By comparing Figure 8 to Figure 6, the  is relatively high at
is relatively high at  and the
and the  value is
value is  . However, the differences between the original and reconstructed signals cannot be distinguished morphologically. Thus
. However, the differences between the original and reconstructed signals cannot be distinguished morphologically. Thus  alone cannot measure how well morphologies of the EEG signals are retained. The histogram of errors showed a concentration of errors in the range between
alone cannot measure how well morphologies of the EEG signals are retained. The histogram of errors showed a concentration of errors in the range between  to
to  , and some outliers in the larger error bins, thus contributing to distortions. Although the results are satisfactory, we observed that the distortions arise from the estimation of the innovation parameters. Let us make a comparison of the
, and some outliers in the larger error bins, thus contributing to distortions. Although the results are satisfactory, we observed that the distortions arise from the estimation of the innovation parameters. Let us make a comparison of the  obtained by sampling both the original EEG epochs and their nonuniform linear spline approximation (i.e., noise-free signals). If the estimation of the innovation parameters is accurate, the
obtained by sampling both the original EEG epochs and their nonuniform linear spline approximation (i.e., noise-free signals). If the estimation of the innovation parameters is accurate, the  obtained should be the same. As shown in Figure 9, the
obtained should be the same. As shown in Figure 9, the  obtained for the noise-free signal is higher than the noisy signal, due to wrong estimations of locations and weights.
obtained for the noise-free signal is higher than the noisy signal, due to wrong estimations of locations and weights.
A plot of PARE for the signals shown in Figure 8. Errors between original and reconstructed samples are depicted as spikes in this plot.
In addition, we present results for sampling three  -hour recordings. Figure 10 shows how the various metrics change in a continuous EEG recording of one patient. As illustrated in Figure 10(a), the number of coefficients
-hour recordings. Figure 10 shows how the various metrics change in a continuous EEG recording of one patient. As illustrated in Figure 10(a), the number of coefficients  varies between
varies between  and
and  , thus showing that for the same patient, the innovation parameters cannot be assumed to be constant. We also noted that although
, thus showing that for the same patient, the innovation parameters cannot be assumed to be constant. We also noted that although  varies in a large range,
varies in a large range,  is quite consistently lying in the range of
is quite consistently lying in the range of  to
to  as in Figure 10(b). Furthermore, the distortion in the EEG is kept very low, as depicted by Figure 10(c). Compression ratio for this recording ranges from about
as in Figure 10(b). Furthermore, the distortion in the EEG is kept very low, as depicted by Figure 10(c). Compression ratio for this recording ranges from about  to
to  , which varies faithfully with
, which varies faithfully with  . Table 4 tabulates the mean
. Table 4 tabulates the mean  and number of coefficients for each dataset. On the average, we achieved a
and number of coefficients for each dataset. On the average, we achieved a  of around
of around  with low
with low  and
and  errors of around
errors of around  ,
,  and
and  respectively. In addition, the
respectively. In addition, the  achieved is around
achieved is around  . Based on the observations of our experiments, a minimum
. Based on the observations of our experiments, a minimum  value of
value of  and a maximum
and a maximum  value of
value of  will maintain the morphologies of the reconstructed signals visually.
will maintain the morphologies of the reconstructed signals visually.
 EEG datasets.
EEG datasets.Figure 11 presents an example of the strength and uniqueness of our sampling scheme. The EEG signal's original sampling frequency is  Hz (Figure 11(a)). Our system estimated
Hz (Figure 11(a)). Our system estimated  to be
to be  and modelled the signal with
and modelled the signal with  samples of the original signal (Figure 11(b)), which has a
samples of the original signal (Figure 11(b)), which has a  of
of  . Effectively, we are sampling the original signal at
. Effectively, we are sampling the original signal at  Hz. We effectively reconstructed the
Hz. We effectively reconstructed the  Hz signal as shown in Figure 11(c) with
Hz signal as shown in Figure 11(c) with  =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  . As a comparison, we reconstructed the signal in Figure 11(b) with the traditional sinc interpolation method (Figure 11(d)) with
. As a comparison, we reconstructed the signal in Figure 11(b) with the traditional sinc interpolation method (Figure 11(d)) with  =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  . Clearly, we are able to represent EEG signals with a low number of samples and reconstruct them with high fidelity.
. Clearly, we are able to represent EEG signals with a low number of samples and reconstruct them with high fidelity.
Comparison of reconstruction of an EEG signal acquired by our method. (a) The original signal sampled at 256 Hz. (b) The EEG signal acquired by our method at 47.5 Hz with 2K = 474. (c) The reconstructed EEG signal at 256 Hz with our method CC = 97.08%, RMSE = 0.0099, PRD = 22.43%, MAXERR = 0.0016. (d) The reconstructed EEG signal using the traditional sinc interpolation method CC = 90.11%, RMSE = 0.0147, PRD = 48.30%, MAXERR = 0.428.
Figure 12 shows the relation between  and
and  with
with  respectively. The
respectively. The  is inversely proportional to the rate of innovation, as shown in the earlier discussion. In order to achieve a high
is inversely proportional to the rate of innovation, as shown in the earlier discussion. In order to achieve a high  has to be compromised. Similarly, as we increase
has to be compromised. Similarly, as we increase  , the error involved such as
, the error involved such as  and
and  will increase together, though not in a linear form. A comparison is made with traditional sinc interpolation and the performance of our method is superior since an interpolation process is unable to faithfully reconstruct signals acquired at a low-sampling rate into one of a higher sampling rate. Next we compared our results with that of compressing the EEG signals using wavelet compression methods. As illustrated, our method achieves comparable results in terms of
will increase together, though not in a linear form. A comparison is made with traditional sinc interpolation and the performance of our method is superior since an interpolation process is unable to faithfully reconstruct signals acquired at a low-sampling rate into one of a higher sampling rate. Next we compared our results with that of compressing the EEG signals using wavelet compression methods. As illustrated, our method achieves comparable results in terms of  and
and  although the
although the  achieved by wavelet methods is slightly better. Since
achieved by wavelet methods is slightly better. Since  only indicates how much error is incurred in the reconstruction without reference to the morphology of the signals, our results do not indicate that our reconstructed signals differ largely from the original signals morphologically. Furthermore, our method entails a less costly low-rate sampling device and does not waste precious computational resources collecting extra data only to discard them subsequently.
only indicates how much error is incurred in the reconstruction without reference to the morphology of the signals, our results do not indicate that our reconstructed signals differ largely from the original signals morphologically. Furthermore, our method entails a less costly low-rate sampling device and does not waste precious computational resources collecting extra data only to discard them subsequently.
Figure 13 illustrates a comparison between an original and a reconstructed EEG signal with the  coefficients, we reconstructed the signal and achieved
coefficients, we reconstructed the signal and achieved  =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  and
and  =
=  Furthermore, the
Furthermore, the  of the reconstructed signal is in the range of
of the reconstructed signal is in the range of  to
to  as opposed to
as opposed to  achieved by the method in [11]. A zoomed-in view in Figure 14 confirms that the morphology of the original signal is conserved in the reconstruction.
achieved by the method in [11]. A zoomed-in view in Figure 14 confirms that the morphology of the original signal is conserved in the reconstruction.
A zoom-in view of the comparison of original and reconstructed EEGs in Figure 13.
Lastly we will discuss about the computational costs of our scheme. With reference to Figure 5, the computational complexity can be estimated as follows.
-
(i)
Compute the DFT to obtain the Fourier series coefficients
 :
: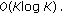
-
(ii)
Denoise:
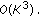
-
(iii)
Differentiate the denoised signal?:?
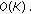
-
(iv)
Solve a Toeplitz system of equation of size
 by
by 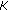 to get
to get 
-
(v)
Find the roots of
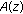 by factorization, to get
by factorization, to get 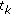 ?:?
?:?
-
(vi)
Solve a Vandermonde system of equation of size
 by
by 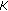 to get
to get 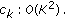
-
(vii)
Integrate the
 Dirac pulses-
Dirac pulses-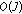
Hence effectively, the computational costs involved is  . For our dataset, the average time required to sample and reconstruct a
. For our dataset, the average time required to sample and reconstruct a  -second epoch is
-second epoch is  seconds on an Intel Core2 Duo 2.50 GHz system with
seconds on an Intel Core2 Duo 2.50 GHz system with  RAM. This computational time can be improved by employing fast algorithms on dedicated digital signal processors to achieve a realtime EEG signal acquisition and display.
RAM. This computational time can be improved by employing fast algorithms on dedicated digital signal processors to achieve a realtime EEG signal acquisition and display.
5. Conclusions
We proposed an approach to compress EEG signals at source based on the finite rate of innovation sampling theory. Unlike traditional compression methods which acquire many data samples and later discard redundant ones, our proposed method relies on acquiring a small set of data from the original signal based on the signal's rate of innovation and then reconstructing the signal with high resolution. Even though a small set of data is obtained, our method retains the morphologies of the EEG signals. It yielded promising results such as good cross correlation and low distortions at a low computational cost. In this way, we achieve computational savings which can be utilised in other more important signal processing stages. Moderate  ratios are obtained for some epochs, leading to a moderate compression ratio. Furthermore, it is observed that
ratios are obtained for some epochs, leading to a moderate compression ratio. Furthermore, it is observed that  changes depending on the state of the EEG, thus leading to a variable rate of innovation. Valuable information such as the occurrences of EEG abnormalities can be extracted through tracking the changes in the rate of innovation across the EEG. As such, the advantage of our compression method lies in the ability to compress EEG signals and track changes across EEG states concurrently. Although the accuracy of the estimated
changes depending on the state of the EEG, thus leading to a variable rate of innovation. Valuable information such as the occurrences of EEG abnormalities can be extracted through tracking the changes in the rate of innovation across the EEG. As such, the advantage of our compression method lies in the ability to compress EEG signals and track changes across EEG states concurrently. Although the accuracy of the estimated  affects the entire scheme, as discussed in [21], it can be estimated from the rank of a Toeplitz matrix. However, more research is needed to determine the correct duration of EEG signals to yield optimal
affects the entire scheme, as discussed in [21], it can be estimated from the rank of a Toeplitz matrix. However, more research is needed to determine the correct duration of EEG signals to yield optimal  values based on certain evaluation metrics such as
values based on certain evaluation metrics such as  or
or 
We will continue our work to minimise the local errors caused by outliers and to include adaptive rate of innovation to cater to the changing states of EEG signals. Finally we will investigate how EEG signals can be source compressed with finite rate of innovation in real time.
References
Berger H: Über das Elektrenkephalogramm des Menschen. Archiv für Psychiatrie und Nervenkrankheiten 1929, 87(1):527-570. 10.1007/BF01797193
Hirtz D, Thurman DJ, Gwinn-Hardy K, Mohamed M, Chaudhuri AR, Zalutsky R: How common are the "common" neurologic disorders? Neurology 2007, 68(5):326-337. 10.1212/01.wnl.0000252807.38124.a3
Antoniol G, Tonella P: EEG data compression techniques. IEEE Transactions on Biomedical Engineering 1997, 44(2):105-114. 10.1109/10.552239
Gürkan H, Guz U, Yarman BS: EEG signal compression based on classified signature and envelope vector sets. International Journal of Circuit Theory and Applications 2009, 37(2):351-363. 10.1002/cta.548
Memon N, Kong X, Cinkler J: Context-based lossless and near-lossless compression of EEG signals. IEEE Transactions on Information Technology in Biomedicine 1999, 3(3):231-238. 10.1109/4233.788586
Madan T, Agarwal R, Swamy MNS: Compression of long-term EEG using power spectral density. Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology (EMBS '04), September 2004 180-183.
Wongsawat Y, Oraintara S, Tanaka T, Rao KR: Lossless multi-channel EEG compression. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '06), May 2006, Island of Kos, Greece 1611-1614.
Nielsen M, Kamavuako EN, Andersen MM, Lucas M-F, Farina D: Optimal wavelets for biomedical signal compression. Medical and Biological Engineering and Computing 2006, 44(7):561-568. 10.1007/s11517-006-0062-0
Sriraam N: Neural network based near-lossless compression of EEG signals with non uniform quantization. Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS '07), August 2007, Lyon, France 3236-3240.
Baraniuk RG, Candes E, Nowak R, Vetterli M: Compressive sampling. IEEE Signal Processing Magazine 2008, 25(2):12-13.
Aviyente S: Compressed sensing framework for EEG compression. Proceedings of IEEE Workshop on Statistical Signal Processing, August 2007, Madison, Wis, USA 181-184.
Vetterli M, Marziliano P, Blu T: Sampling signals with finite rate of innovation. IEEE Transactions on Signal Processing 2002, 50(6):1417-1428. 10.1109/TSP.2002.1003065
Hao Y, Marziliano P, Vetterli M, Blu T: Compression of ECG as a signal with finite rate of innovation. Proceedings of the 27th Annual International Conference of the IEEE Engineering in Medicine and Biology (EMBS '05), September 2005, Shanghai, China 7: 7564-7567.
Poh K-K, Marziliano P: Compression of neonatal EEG seizure signals with finite rate of innovation. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), March-April 2008, Las Vegas, Nev, USA 433-436.
Kandaswamy D, Blu T, Van De Ville D: Analytic sensing: direct recovery of point sources from planar Cauchy boundary measurements. Wavelets XII, August 2007, San Diego, Calif, USA, Proceedings of SPIE 6701:
EEG time series Database https://epilepsy.uni-freiburg.de/freiburg-seizure-prediction-project/eeg-database
Unser M: Splines: a perfect fit for signal and image processing. IEEE Signal Processing Magazine 1999, 16(6):22-38. 10.1109/79.799930
Keshner MS:1/
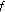 noise. Proceedings of the IEEE 1982, 70(3):212-218.
noise. Proceedings of the IEEE 1982, 70(3):212-218.Hadjileontiadis LJ: Biosignals and Compression Standards. Springer, Berlin, Germany; 2006.
McSharry PE, Malamud BD: Quantifying self-similarity in cardiac inter-beat interval time series. Computers in Cardiology 2005, 32: 459-462.
Blu T, Dragotti P-L, Vetterli M, Marziliano P, Coulot L: Sparse sampling of signal innovations: theory, algorithms, and performance bounds. IEEE Signal Processing Magazine 2008, 25(2):31-40.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Poh, KK., Marziliano, P. Compressive Sampling of EEG Signals with Finite Rate of Innovation. EURASIP J. Adv. Signal Process. 2010, 183105 (2010). https://doi.org/10.1155/2010/183105
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/183105














 :
: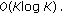
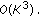
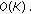
 by
by 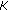 to get
to get 
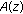 by factorization, to get
by factorization, to get 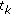 ?:?
?:?
 by
by 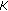 to get
to get 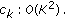
 Dirac pulses-
Dirac pulses-
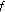 noise. Proceedings of the IEEE 1982, 70(3):212-218.
noise. Proceedings of the IEEE 1982, 70(3):212-218.