- Research Article
- Open access
- Published:
Missing Texture Reconstruction Method Based on Perceptually Optimized Algorithm
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 208976 (2010)
Abstract
This paper presents a simple and effective missing texture reconstruction method based on a perceptually optimized algorithm. The proposed method utilizes the structural similarity (SSIM) index as a new visual quality measure for reconstructing missing areas. Furthermore, in order to adaptively reconstruct target images containing several kinds of textures, the following two novel approaches are introduced into the SSIM-based reconstruction algorithm. First, the proposed method performs SSIM-based selection of the optimal known local textures to adaptively obtain subspaces for reconstructing missing textures. Secondly, missing texture reconstruction that maximizes the SSIM index in the known neighboring areas is performed. In this approach, the nonconvex maximization problem is reformulated as a quasi convex problem, and adaptive reconstruction of the missing textures based on the perceptually optimized algorithm becomes feasible. Experimental results show impressive improvements of the proposed method over previously reported reconstruction methods.
1. Introduction
Restoration of missing areas in digital images has been intensively studied since it can be applied to a number of fundamental applications such as restoration of corrupted old films, removal of unnecessary objects, and error concealment. Therefore, many methods have been proposed in order to realize these applications. Generally, they are broadly classified into two categories, structural and textural reconstruction approaches, and many papers on these approaches have been published. Attractive methods that perform simultaneous reconstruction of missing structures and textures in images have also been proposed [1, 2]. Most algorithms reported in the literature are based on structural inpainting techniques for accurate reconstruction of missing edges [3–5]. These techniques are effective for pure structure images. However, since general images also contain many textures, different methods work better in these areas. Thus, several methods have been proposed for accurate reconstruction of missing textures [6–12]. The remainder of this paper focuses on the texture reconstruction approach with discussion of its details.
Traditionally, missing texture reconstruction is realized as one of the applications of texture synthesis. Efros et al. firstly proposed a pioneered method for the texture synthesis [6, 7]. Their approach models textures by using the MRF (Markov random field) model and enables missing texture reconstruction by copying pixels of a target image itself, that is, nonparametric sampling in synthesis. Furthermore, Wei and Levoy proposed a fast algorithm for the searching step in the texture synthesis by utilizing multiresolution concepts [8]. Then many methods which perform the exemplar-based inpainting are mainly inspired by the nonparametric sampling in [6]. Drori et al. proposed a fragment-based algorithm for image completion which could preserve structures and textures [9]. Furthermore, the exemplar-based image inpainting method proposed by Criminisi et al. is a representative one based on the texture synthesis [10, 11]. This method adopts a patch-based greedy sampling scheme similar to the fragment-based completion, but it is simpler and faster. A good review of the exemplar-based inpainting methods based on [6] is shown in [12].
In the field of texture reconstruction, not only the methods based on the texture synthesis but also many methods, which estimate missing intensities by utilizing statistical features of known textures within a target image as training patterns, have been proposed. Generally, since the restoration of missing areas is an ill-posed problem, it is difficult to directly estimate the missing intensities. Thus, these methods perform approximation of textures within the target image in lower-dimensional subspaces and enable derivation of the inverse projection for the corruption. Amano and Sato proposed an effective PCA-based method for reconstructing missing textures using back projection for lost pixels and realized accurate reconstruction performance [13]. Furthermore, kernel methods have recently been developed and their achievements have been reported in a number of papers [14–16]. Subspaces constructed on the basis of kernel methods are also suitable for approximating nonlinear texture features in target images. Several missing texture reconstruction methods that utilize projection schemes onto nonlinear subspaces obtained by kernel PCA and CCA have been proposed [17, 18]. Furthermore, image reconstruction based on sparse representation approaches [19–21] have been intensively studied. By utilizing sparse representation, optimal signal atoms can be adaptively selected from a dictionary for representing target signals. This means that these methods can adaptively provide optimal subspaces for restoring missing areas. Several missing area reconstruction methods based on sparse representation have been proposed [21–23].
It should be noted that in conventional methods, reconstruction is mostly performed by minimizing errors of intensities, that is, the mean squared error (MSE), which is the most popular metric. However, it has been reported that MSE optimal algorithms do not necessarily produce images of high visual quality [24]. Thus, it may not be appropriate to utilize the MSE as a quality measure for reconstruction. Recent advances in full-reference image quality assessment (IQA) have resulted in the emergence of several powerful perceptual distortion measures that outperform the MSE and its variants. Criteria such as PQS [25], NQM [26], IFC [27], and VIF [28] are well known as perceptual distortion measures, and their performances have been evaluated in detail [29]. The structural similarity (SSIM) index [30] is utilized as a representative quality measure in many fields of image processing. Since its formulation is simple and easy to be analyzed, the SSIM index can be applied to not only image quality assessment but also design of linear equalizers [31]. Therefore, by using this quality measure, accurate reconstruction of missing textures can be expected.
In this paper, we present a simple and effective missing texture reconstruction method based on a perceptually optimized algorithm. The proposed method utilizes the SSIM index as a criterion for reconstructing missing areas in the target image. Specifically, we introduce the following two novel approaches into the SSIM-based algorithm and realize adaptive reconstruction of missing textures.
-
(1)
SSIM-based selection of the optimal known local textures for reconstructing target textures including missing areas.
-
(2)
Reconstruction of the target textures maximizing the SSIM index in the known neighboring areas.
The first approach provides optimal subspaces for the following SSIM-based reconstruction approach by using an algorithm similar to several matching pursuit algorithms [32, 33]. Furthermore, in the second approach, we introduce the computation scheme in [31] into the SSIM-based reconstruction algorithm, and its nonconvex maximization problem is reformulated as a quasi convex problem. Then the optimal solution based on the SSIM index can be computed, and accurate reconstruction of the missing textures is expected.
This paper is organized as follows. First, in Section 2, we briefly explain the SSIM index used as the quality measure in the proposed method. Next, the missing texture reconstruction method based on the perceptually optimized algorithm is proposed in Section 3. Experimental results that verify the performance of the proposed method are shown in Section 4. Finally, conclusions are given in Section 5.
2. SSIM Index
The SSIM index represents the similarity between two signal vectors  and
and  (
( ), and its specific definition is as follows:
), and its specific definition is as follows:

where the terms  and
and  , respectively, compare the mean and variance of the two signal vectors. Furthermore,
, respectively, compare the mean and variance of the two signal vectors. Furthermore,  measures their structural correlation. These three terms,
measures their structural correlation. These three terms,  ,
,  , and
, and  , are obtained as
, are obtained as

In the above equations,  and
and  are the means of
are the means of  and
and  ,
,  and
and  are the variances of
are the variances of  and
and  , and
, and  is the cross-covariance between
is the cross-covariance between  and
and  . The constants
. The constants  ,
,  and
and  are necessary for avoiding instability when the denominators are very close to zero. The parameters
are necessary for avoiding instability when the denominators are very close to zero. The parameters  ,
,  and
and  determine the relative importance of the three components in (1). As shown in [30], those parameters are set as
determine the relative importance of the three components in (1). As shown in [30], those parameters are set as  and
and  , and formulation of the SSIM is simplified as follows:
, and formulation of the SSIM is simplified as follows:

As shown in (1)–(3), the SSIM index is consistent with luminance and contrast masking and the correlation.
In [30, 34], the effectiveness of the SSIM index as a quality measure and its superiority to the MSE and its variants are presented in detail. Generally, the MSE cannot reflect perceptual distortions, and its value becomes higher for images altered with some distortions such as mean luminance shift, contrast stretch, spatial shift, spatial scaling, and rotation, yet negligible loss of subjective image quality. Furthermore, blurring severely deteriorates the image quality, but its MSE becomes lower than those of the above alternation. On the other hand, the SSIM index is defined by separately calculating the three similarities in terms of the luminance, variance, and structure, which are derived based on the HVS (human visual system) not accounted for by the MSE. Therefore, it becomes a better quality measure providing a solution to the above problem, and this is also confirmed in [34]. Then we can expect that the use of this similarity for the reconstruction of missing areas will provide successful results. The specific effectiveness of the SSIM index for the reconstruction is discussed in Section 4.
3. Adaptive Missing Texture Reconstruction Based on SSIM Index
In this section, we present an adaptive SSIM-based missing texture reconstruction method. In the proposed method, a patch  (
( pixels) including missing areas is clipped from the target image, and its missing textures are estimated from the other known areas. An overview of the proposed method is shown in Figure 1. For the following explanations, we denote two areas whose intensities are unknown and known within the target patch
pixels) including missing areas is clipped from the target image, and its missing textures are estimated from the other known areas. An overview of the proposed method is shown in Figure 1. For the following explanations, we denote two areas whose intensities are unknown and known within the target patch  as
as  and
and  , respectively. We also define vectors whose elements are intensities within
, respectively. We also define vectors whose elements are intensities within  and
and  as
as  and
and  , respectively, where
, respectively, where  is the number of pixels within the area
is the number of pixels within the area  .
.
In the target image, there are several kinds of textures, that is, there are many known patches whose textures are quite different from that of the target patch  . Such patches should not affect the reconstruction of the target patch
. Such patches should not affect the reconstruction of the target patch  . In order to reconstruct the missing textures within the target patch
. In order to reconstruct the missing textures within the target patch  from only the same kinds of textures, we have to select those textures from the known areas. Therefore, the proposed method first performs selection of the optimal known patches utilized for reconstruction of the target patch
from only the same kinds of textures, we have to select those textures from the known areas. Therefore, the proposed method first performs selection of the optimal known patches utilized for reconstruction of the target patch  based on the SSIM index. Furthermore, by using the selected patches, we derive the representation model optimized for the target patch
based on the SSIM index. Furthermore, by using the selected patches, we derive the representation model optimized for the target patch  in terms of the SSIM index to reconstruct the missing area
in terms of the SSIM index to reconstruct the missing area  . Then the proposed method can adaptively reconstruct the missing textures from only the same kinds of known textures based on the perceptually optimized scheme.
. Then the proposed method can adaptively reconstruct the missing textures from only the same kinds of known textures based on the perceptually optimized scheme.
In this section, we first show the SSIM-based algorithm for selecting the optimal known patches in Section 3.1. The reconstruction algorithm of the missing textures based on the SSIM index is shown in Section 3.2.
3.1. SSIM-Based Optimal Texture Selection Algorithm
In this subsection, we present the SSIM-based optimal texture selection algorithm. First, we clip known patches  (
( ) whose size is
) whose size is  pixels from the target image in the same interval. For the following explanation, two vectors that correspond to
pixels from the target image in the same interval. For the following explanation, two vectors that correspond to  and
and  of each patch
of each patch  are denoted as
are denoted as  (
( ) and
) and  (
( ), respectively. From the clipped patch, we select
), respectively. From the clipped patch, we select  patches that are optimal for reconstruction of the target patch
patches that are optimal for reconstruction of the target patch  . The order of the value
. The order of the value  is explained in Section 4. In the reconstruction algorithm shown in the following subsection, the target patch
is explained in Section 4. In the reconstruction algorithm shown in the following subsection, the target patch  is represented by a linear combination of the selected known patches in such a way that the SSIM index in the known area
is represented by a linear combination of the selected known patches in such a way that the SSIM index in the known area  becomes maximum. Therefore, we should select
becomes maximum. Therefore, we should select  known patches that provide the optimal linear combination. Note that the selection of such optimal
known patches that provide the optimal linear combination. Note that the selection of such optimal  known patches is an NP-hard problem. Thus, we adopt the simplest algorithm that selects the optimal known patches one by one, and it is similar to several matching pursuit algorithms [32, 33]. In the rest of this subsection, the details of the
known patches is an NP-hard problem. Thus, we adopt the simplest algorithm that selects the optimal known patches one by one, and it is similar to several matching pursuit algorithms [32, 33]. In the rest of this subsection, the details of the  th (
th ( ) optimal patch selection are shown.
) optimal patch selection are shown.
In the  th iteration, we first define the following vector:
th iteration, we first define the following vector:

where  is an
is an  matrix which contains
matrix which contains  vectors previously selected from
vectors previously selected from  (
( ) in
) in  iterations. Furthermore,
iterations. Furthermore,

is a coefficient vector for obtaining  . The proposed method estimates the optimal vector
. The proposed method estimates the optimal vector  of
of  (
( ) which provides the optimal representation performance based on the SSIM index. Then the best matched patch
) which provides the optimal representation performance based on the SSIM index. Then the best matched patch  , whose vector
, whose vector  approximating
approximating  has a higher value of the SSIM index than those of other patches, is selected.
has a higher value of the SSIM index than those of other patches, is selected.
In order to calculate  for each patch
for each patch  , we have to estimate the optimal coefficient vector
, we have to estimate the optimal coefficient vector  of
of  in (4) that satisfies
in (4) that satisfies

This means we have to solve the following equation:

where  is defined as follows:
is defined as follows:

In the above equation,  and
and  are the means of
are the means of  and
and  ,
,  and
and  are the variances of
are the variances of  and
and  , and
, and  is the cross covariance between
is the cross covariance between  and
and  . Furthermore, since
. Furthermore, since  is provided in (4), (8) is rewritten as follows:
is provided in (4), (8) is rewritten as follows:

where  is an
is an  vector, and
vector, and

The proposed method calculates the optimal vector  in (7) by simply applying the steepest ascend algorithm to
in (7) by simply applying the steepest ascend algorithm to  in (9). Note that we can calculate the optimal vector
in (9). Note that we can calculate the optimal vector  more accurately by using the algorithm shown in the following subsection. However, in order to reduce the computation time of the proposed method, we adopt the steepest ascend algorithm in this subsection. It is well known that the steepest ascend algorithm cannot necessarily provide the globally optimal solutions in (7), but this algorithm can save the computation time compared to the algorithm shown in the following subsection. The details are shown later. From the above reason, we utilize this scheme in the proposed method.
more accurately by using the algorithm shown in the following subsection. However, in order to reduce the computation time of the proposed method, we adopt the steepest ascend algorithm in this subsection. It is well known that the steepest ascend algorithm cannot necessarily provide the globally optimal solutions in (7), but this algorithm can save the computation time compared to the algorithm shown in the following subsection. The details are shown later. From the above reason, we utilize this scheme in the proposed method.
By iterating the above procedures  times, we can select the optimal
times, we can select the optimal  known patches based on the SSIM index and denote them as
known patches based on the SSIM index and denote them as  (
( ). Algorithm 1 shows the specific procedures of this selection algorithm. Then by utilizing the obtained known patches, the proposed method can adaptively provide the optimal subspace for the target patch
). Algorithm 1 shows the specific procedures of this selection algorithm. Then by utilizing the obtained known patches, the proposed method can adaptively provide the optimal subspace for the target patch  , and accurate reconstruction based on the SSIM index is also expected in the following subsection. For the following explanation, we denote two vectors obtained from
, and accurate reconstruction based on the SSIM index is also expected in the following subsection. For the following explanation, we denote two vectors obtained from  in the same way as
in the same way as  and
and  as
as  and
and  , respectively.
, respectively.
Algorithm 1: Specific procedures to select  optimal known patches
optimal known patches  (
( ) for the target patch
) for the target patch  based on the SSIM index.
based on the SSIM index.
-
(i)
Initialization is performed as follows:
 ,
, , and
, and 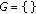 . Furthermore,
. Furthermore, 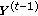 , and
, and 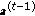 are, respectively, set to the empty matrix,and vector.
are, respectively, set to the empty matrix,and vector. -
(ii)
For each patch included in the set
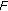 , the optimal value of the SSIM index maximizing (8) is calculated.
, the optimal value of the SSIM index maximizing (8) is calculated. -
(iii)
The best matched patch, whose maximized SSIM index is larger than those of the other patches in
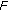 ,
,
is selected as  . Furthermore, this patch is removed from
. Furthermore, this patch is removed from  and added to
and added to  .
.
-
(iv)
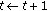 , and the matrix
, and the matrix  is constructed from the vectors of the patches belonging to
is constructed from the vectors of the patches belonging to  .
. -
(v)
The procedures (ii)–(iv) are repeated until
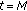 . If
. If 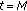 ,
,  outputs
outputs 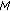 optimal known patches.
optimal known patches.
3.2. Texture Reconstruction Algorithm
In this subsection, we present the reconstruction algorithm of the missing area  in the target patch
in the target patch  based on the SSIM index. First, we approximate the known vector
based on the SSIM index. First, we approximate the known vector  of the target patch
of the target patch  by utilizing
by utilizing  of the patches
of the patches  selected in the previous subsection as follows:
selected in the previous subsection as follows:

where  is an
is an  matrix whose columns are
matrix whose columns are  (
( ), and
), and 
 is a coefficient vector for representing
is a coefficient vector for representing  . The proposed method estimates the optimal vector
. The proposed method estimates the optimal vector  as follows:
as follows:

In the above equation,  is defined as
is defined as

in the same way as (9), where

is an  vector whose elements are the means of
vector whose elements are the means of  (
( ) in
) in  .
.
It should be noted that the criterion  defined in (13) is a nonconvex function of
defined in (13) is a nonconvex function of  , and it is difficult to obtain its global optimal solution. Therefore, we introduce the calculation scheme utilized in [31] into the estimation of the optimal vector
, and it is difficult to obtain its global optimal solution. Therefore, we introduce the calculation scheme utilized in [31] into the estimation of the optimal vector  . Specifically, the above nonconvex problem is transformed into a quasiconvex formulation. First, we note that the first term in (13) is a function only of
. Specifically, the above nonconvex problem is transformed into a quasiconvex formulation. First, we note that the first term in (13) is a function only of 
 =
= . Thus, (13) can be rewritten as follows:
. Thus, (13) can be rewritten as follows:

where

Then we can simplify the optimization problem by constraining  . Specifically, the optimization problem can be simplified to find
. Specifically, the optimization problem can be simplified to find

Therefore, the overall problem is to find the highest SSIM index by searching over a range of  . Furthermore, since the optimization problem in (17) is still nonconvex, it is converted into a quasiconvex optimization problem as follows:
. Furthermore, since the optimization problem in (17) is still nonconvex, it is converted into a quasiconvex optimization problem as follows:

The first equivalence relationship holds since minimizing  is the same as finding the least upper bound of (17). The second equivalence relationship holds since the denominator in (17) is strictly positive, allowing us to multiply through and rearrange terms. Then
is the same as finding the least upper bound of (17). The second equivalence relationship holds since the denominator in (17) is strictly positive, allowing us to multiply through and rearrange terms. Then  becomes a true upper bound if the problem
becomes a true upper bound if the problem

has a non-negative optimal value, and the optimal vector  in (17) can be obtained. Specifically, the proposed method utilizes the following Lagrange multiplier approach:
in (17) can be obtained. Specifically, the proposed method utilizes the following Lagrange multiplier approach:

By solving for  and
and  , we can obtain
, we can obtain

where we denote them as  and
and  since they depend on
since they depend on  . Furthermore, in the above two equations,
. Furthermore, in the above two equations,  is a Moore-Penrose pseudoinverse matrix of
is a Moore-Penrose pseudoinverse matrix of  . Then the proposed method estimates the optimal value of
. Then the proposed method estimates the optimal value of  by using a standard bisection procedure, and the optimal vectors
by using a standard bisection procedure, and the optimal vectors  are calculated for several values of
are calculated for several values of  (
( ) to select
) to select  maximizing (13), where
maximizing (13), where  is a step size and
is a step size and  determines the search range of
determines the search range of  . Algorithm 2 shows the details on the estimation of
. Algorithm 2 shows the details on the estimation of  in the proposed method.
in the proposed method.
Algorithm 2: Specific procedures to search the optimal  in the proposed method.
in the proposed method.
-
(i)
An initial value of
 (say
(say 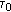 ) is determined between. zero to one. Furthermore,
) is determined between. zero to one. Furthermore, 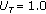
and
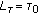 , where
, where 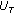 and
and 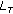 , respectively, represent the upper
, respectively, represent the upperlimit and the lower limit of
 . In this paper, we set
. In this paper, we set 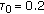
-
(ii)
The optimization problem in (19) is solved by using
 .
. -
(iii)
Two criteria
 and
and  are calculated as
are calculated as
 ,
,
 .
.
-
(iv)
According to the obtained criteria
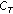 and
and 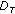 , the following steps are operated:
, the following steps are operated:
(a) If  and
and  , the final optimal solution of
, the final optimal solution of  is output, where
is output, where  .
.
(b) If  but
but  ,
,  and
and  .
.
(c) Otherwise,  and
and  .
.
-
(v)
The procedures (ii)–(iv) are iterated.
Note that the algorithm for calculating the optimal linear combination in this subsection provides better solutions than those in the previous subsection. However, this algorithm needs to perform  iterations to determine the value of
iterations to determine the value of  . Furthermore, it also needs the iteration to search the optimal value of
. Furthermore, it also needs the iteration to search the optimal value of  as shown in Algorithm 2. Then since it is confirmed that the algorithm shown in this subsection takes more computation time compared to the algorithm shown in the previous subsection, we perform the selection of the optimal
as shown in Algorithm 2. Then since it is confirmed that the algorithm shown in this subsection takes more computation time compared to the algorithm shown in the previous subsection, we perform the selection of the optimal  known patches
known patches  (
( ) as shown in the previous subsection.
) as shown in the previous subsection.
By utilizing the coefficient vector  , the estimation result
, the estimation result  of the unknown vector
of the unknown vector  whose elements are the intensities within
whose elements are the intensities within  is calculated as follows:
is calculated as follows:

where  is a matrix whose columns are
is a matrix whose columns are  (
( ). Finally, from the obtained result
). Finally, from the obtained result  , the proposed method outputs the estimated intensities in the missing area
, the proposed method outputs the estimated intensities in the missing area  .
.
As described above, we can reconstruct the missing texture in the target patch. The proposed method clips patches ( pixels) at the same interval from the upper-left of the target image in a rasterscanning order. If the clipped patches contain missing areas, we regard them as the target patches
pixels) at the same interval from the upper-left of the target image in a rasterscanning order. If the clipped patches contain missing areas, we regard them as the target patches  and reconstruct them by using the above approach. Note that each restored pixel has multiple estimation results if the clipping interval is smaller than the size of the patches. In this case, the proposed method regards the result maximizing (13) as the final one. The proposed method does not utilize the already obtained results for reconstructing other missing areas. Therefore, the performance of the proposed method does not depend on the order of the reconstruction, that is, the positions of the patches including missing areas do not influence the results.
and reconstruct them by using the above approach. Note that each restored pixel has multiple estimation results if the clipping interval is smaller than the size of the patches. In this case, the proposed method regards the result maximizing (13) as the final one. The proposed method does not utilize the already obtained results for reconstructing other missing areas. Therefore, the performance of the proposed method does not depend on the order of the reconstruction, that is, the positions of the patches including missing areas do not influence the results.
4. Experimental Results
The performance of the proposed method is shown in this section. Figure 2(a) is a test texture image ( pixels, 24-bit color levels), and from the flag image shown in Figure 2(b), a corrupted image, which includes text regions "Grand Canyon" as missing areas, is obtained as shown in Figure 2(c)(Note that positions of the missing areas are previously provided in this experiment.) Figure 2(d) shows the results of reconstruction by the proposed method. In this experiment, we set the parameters of the proposed method as follows:
pixels, 24-bit color levels), and from the flag image shown in Figure 2(b), a corrupted image, which includes text regions "Grand Canyon" as missing areas, is obtained as shown in Figure 2(c)(Note that positions of the missing areas are previously provided in this experiment.) Figure 2(d) shows the results of reconstruction by the proposed method. In this experiment, we set the parameters of the proposed method as follows:  ,
,  ,
,  ,
,  ,
,  ,
,  , where
, where  is the maximum value of intensities, and the clipping interval of patches is 10 and 8. The size of patches influences the reconstruction results. If the size of patches becomes smaller, the representation performance of their textures becomes better. However, these patches including missing areas must contain known intensities to select the optimal
is the maximum value of intensities, and the clipping interval of patches is 10 and 8. The size of patches influences the reconstruction results. If the size of patches becomes smaller, the representation performance of their textures becomes better. However, these patches including missing areas must contain known intensities to select the optimal  known patches in Section 3.1 and estimate the vector
known patches in Section 3.1 and estimate the vector  in Section 3.2. Thus, the size of patches should be determined in such a way that they necessarily contain several known intensities. In this experiment, we determine
in Section 3.2. Thus, the size of patches should be determined in such a way that they necessarily contain several known intensities. In this experiment, we determine  and
and  to satisfy the above condition. Furthermore, the clipping interval is set to about quarter size of
to satisfy the above condition. Furthermore, the clipping interval is set to about quarter size of  and
and  , that is, the horizontal and vertical intervals are, respectively, set to 10 and 8. Next,
, that is, the horizontal and vertical intervals are, respectively, set to 10 and 8. Next,  and
and  mean that the search range of
mean that the search range of  in the proposed method is from
in the proposed method is from  to
to  . From preliminary experiments,
. From preliminary experiments,  tends not to become smaller than
tends not to become smaller than  or larger than
or larger than  . Thus, we set the range of
. Thus, we set the range of  as shown above. The parameters
as shown above. The parameters  and
and  are determined in the same way as [30].
are determined in the same way as [30].
(a) Original image (480 × 359 pixels, 24-bit color levels). (b) Flag image whose white regions correspond to missing areas. (c) Corrupted image including text regions (8.9% loss), (d) Reconstructed image by the proposed method. (e) Reconstructed image by the method based on the random selection. (f) Reconstructed image by the method which utilizes the MSE instead of the SSIM index. (g) Reconstructed image by the conventional method [11]. (h) Reconstructed image by the conventional method [13]. (i) Reconstructed image by the conventional method [21].
For comparison, Figures 2(e)–2(i), respectively, show the results obtained by the method which selects  known patches randomly but reconstructs missing areas in the same way as Section 3.2, the method which utilizes the MSE instead of the SSIM index, the exemplar-based texture reconstruction method [11], the PCA-based texture reconstruction method [13], and the method based on sparse representation [21]. In order to verify the effectiveness of the selection algorithm shown in Section 3.1, we show the results in Figure 2(e). The method in [11] is one of the most influential works in the field of the exemplar-based texture reconstruction, and we utilize this method for the comparison of the proposed method as shown in Figure 2(g). Furthermore, since subspaces optimized on the basis of the MSE criterion are utilized for the reconstruction of missing textures, the other conventional methods shown in Figures 2(f), 2(h), and 2(i) are suitable for verifying the performance of the proposed method. Particularly, the methods in [13, 21] are, respectively, representative works using PCA and sparse representation.
known patches randomly but reconstructs missing areas in the same way as Section 3.2, the method which utilizes the MSE instead of the SSIM index, the exemplar-based texture reconstruction method [11], the PCA-based texture reconstruction method [13], and the method based on sparse representation [21]. In order to verify the effectiveness of the selection algorithm shown in Section 3.1, we show the results in Figure 2(e). The method in [11] is one of the most influential works in the field of the exemplar-based texture reconstruction, and we utilize this method for the comparison of the proposed method as shown in Figure 2(g). Furthermore, since subspaces optimized on the basis of the MSE criterion are utilized for the reconstruction of missing textures, the other conventional methods shown in Figures 2(f), 2(h), and 2(i) are suitable for verifying the performance of the proposed method. Particularly, the methods in [13, 21] are, respectively, representative works using PCA and sparse representation.
Note that the dimensions of the subspaces utilized in the proposed method and the conventional methods are set to the same value 40 ( ). In the proposed method, we have to set
). In the proposed method, we have to set  to a smaller value than the number of known pixels within the target patch
to a smaller value than the number of known pixels within the target patch  . Furthermore, this should be satisfied for all target patches including missing areas within the target image. Otherwise, the calculation of the optimal vector
. Furthermore, this should be satisfied for all target patches including missing areas within the target image. Otherwise, the calculation of the optimal vector  in (11) and (12) generally becomes an underdetermined problem. This means we have to set
in (11) and (12) generally becomes an underdetermined problem. This means we have to set  to a sufficiently small value in order to avoid the problem in (12), being an underdetermined problem. Generally, if
to a sufficiently small value in order to avoid the problem in (12), being an underdetermined problem. Generally, if  becomes larger than the number of the known pixels in
becomes larger than the number of the known pixels in  , some constraints must be introduced as regularization terms for avoiding the system instability. Furthermore, if there is no limitation of the cost function utilized for the reconstruction, some constraints must be also adopted. Several existing studies for inpainting using a linear combination of patches adopt some restrictions such as the sum of the linear coefficients being one [35], and so forth. On the other hand, our method sets the value of
, some constraints must be introduced as regularization terms for avoiding the system instability. Furthermore, if there is no limitation of the cost function utilized for the reconstruction, some constraints must be also adopted. Several existing studies for inpainting using a linear combination of patches adopt some restrictions such as the sum of the linear coefficients being one [35], and so forth. On the other hand, our method sets the value of  to a much smaller value than the number of known pixels within the target patch
to a much smaller value than the number of known pixels within the target patch  , and the maximum range of the SSIM index is limited to one. Thus, since the system is not instable in (12), we think that our method does not have to utilize other restrictions. Furthermore, it seems that the value of
, and the maximum range of the SSIM index is limited to one. Thus, since the system is not instable in (12), we think that our method does not have to utilize other restrictions. Furthermore, it seems that the value of  should be set to about one-tenth of the dimension of
should be set to about one-tenth of the dimension of  . This means we assume the percentages of the known pixels within the target patches
. This means we assume the percentages of the known pixels within the target patches  are larger than 10%. In the experiments, we set
are larger than 10%. In the experiments, we set  to 40, that is, a much smaller value than the above criterion to clearly show the difference of the reconstruction performance between the proposed method and the conventional methods.
to 40, that is, a much smaller value than the above criterion to clearly show the difference of the reconstruction performance between the proposed method and the conventional methods.
For better subjective evaluation, the enlarged portions around the upper left of the images are shown in Figure 3. It can be seen that the use of the proposed method has achieved noticeable improvements compared to the conventional methods. From the results in Figures 3(d) and 3(e), the effectiveness of the algorithm for selecting the optimal  known patches in Section 3.1 can be confirmed. Different experimental results are shown in Figures 4, 5, 6, and 7. Compared to the results obtained by the conventional methods, it can be seen that various kinds of textures are accurately restored by using the proposed method. Therefore, high performance of the proposed method was verified by the experiments.
known patches in Section 3.1 can be confirmed. Different experimental results are shown in Figures 4, 5, 6, and 7. Compared to the results obtained by the conventional methods, it can be seen that various kinds of textures are accurately restored by using the proposed method. Therefore, high performance of the proposed method was verified by the experiments.
(a) Zoomed portion of Figure 2(a). (b) Zoomed portion of Figure 2(b), (c) Zoomed portion of Figure 2(c), (d) Zoomed portion of Figure 2(d), (e) Zoomed portion of Figure 2(e), (f) Zoomed portion of Figure 2(f), (g) Zoomed portion of Figure 2(g), (h) Zoomed portion of Figure 2(h), (i) Zoomed portion of Figure 2(i).
(a) Original image (480 × 360 pixels, 24-bit color levels). (b) Flag image whose white regions correspond to missing areas. (c) Corrupted image including text regions (10.7% loss). (d) Reconstructed image by the proposed method. (e) Reconstructed image by the method based on the random selection. (f) Reconstructed image by the method which utilizes the MSE instead of the SSIM index. (g) Reconstructed image by the conventional method [11]. (h) Reconstructed image by the conventional method [13]. (i) Reconstructed image by the conventional method [21].
(a) Zoomed portion of Figure 4(a). (b) Zoomed portion of Figure 4(b). (c) Zoomed portion of Figure 4(c). (d) Zoomed portion of Figure 4(d). (e) Zoomed portion of Figure 4(e). (f) Zoomed portion of Figure 4(f). (g) Zoomed portion of Figure 4(g). (h) Zoomed portion of Figure 4(h). (i) Zoomed portion of Figure 4(i).
(a) Original image (480 × 360 pixels, 24-bit color levels). (b) Flag image whose white regions correspond to missing areas. (c) Corrupted image including text regions (11.9% loss). (d) Reconstructed image by the proposed method. (e) Reconstructed image by the method based on the random selection. (f) Reconstructed image by the method which utilizes the MSE instead of the SSIM index. (g) Reconstructed image by the conventional method [11]. (h) Reconstructed image by the conventional method [13]. (i) Reconstructed image by the conventional method [21].
(a) Zoomed portion of Figure 6(a). (b) Zoomed portion of Figure 6(b). (c) Zoomed portion of Figure 6(c). (d) Zoomed portion of Figure 6(d). (e) Zoomed portion of Figure 6(e). (f) Zoomed portion of Figure 6(f). (g) Zoomed portion of Figure 6(g). (h) Zoomed portion of Figure 6(h). (i) Zoomed portion of Figure 6(i).
In order to confirm the superiority of the SSIM index for evaluating visual qualities, we show the MSE and the SSIM index of the reconstruction results in Tables 1 and 2. It can be seen that our method has achieved improvement over the conventional methods in the SSIM index. Although the MSEs of the proposed method tend to become worse than those of the conventional methods, we can see that the MSE results cannot correctly reflect the visual quality in the subjective evaluation. On the other hand, the SSIM index can represent the visual quality more accurately. Therefore, we can conclude that the use of the SSIM index as a visual quality measure is appropriate for texture reconstruction.
In the conventional methods, the subspace estimation and texture reconstruction schemes are based on the MSE criterion. However, the MSE optimal algorithms do not necessarily produce images of high visual quality, and the reconstruction results may be degraded. Specifically, it is well known that most images contain more low-frequency components than high-frequency components. Thus, models using the subspaces based on the MSE can only represent such low-frequency components, and it becomes difficult to reconstruct the missing high-frequency components of the missing areas. This means the reconstruction results tend to be blurred. Then since the representation performance, that is, the reconstruction performance of each patch, becomes worse, the color discontinuities at the border of the missing areas and that of patches also occurs. On the other hand, the proposed method adopts the SSIM index for obtaining subspaces and reconstructing missing textures. The basic formulation of the SSIM index is obtained from the three terms  ,
,  , and
, and  as shown in (1). These terms respectively represent the mean similarity, the variance similarity, and the structural correlation. The first term
as shown in (1). These terms respectively represent the mean similarity, the variance similarity, and the structural correlation. The first term  and the third term
and the third term  compare the vector lengths and angles, and they separately provide those similarities. Note that the second term
compare the vector lengths and angles, and they separately provide those similarities. Note that the second term  compares the contrast of the two vectors, that is, it enables the comparison of the texture roughness. Therefore, this can be regarded as the term comparing how much high-frequency components the target textures contain. This is also pointed out in [34], and they confirmed that the SSIM index of blurred images which were perceptually degraded severely became lower. Then it seems that the proposed method can avoid the oversmoothness of the reconstruction results by utilizing the SSIM index including the above useful term. Since the SSIM index outperforms the MSE as a perceptual distortion measure, our method can provide the solution to the conventional problems and realize more accurate reconstruction.
compares the contrast of the two vectors, that is, it enables the comparison of the texture roughness. Therefore, this can be regarded as the term comparing how much high-frequency components the target textures contain. This is also pointed out in [34], and they confirmed that the SSIM index of blurred images which were perceptually degraded severely became lower. Then it seems that the proposed method can avoid the oversmoothness of the reconstruction results by utilizing the SSIM index including the above useful term. Since the SSIM index outperforms the MSE as a perceptual distortion measure, our method can provide the solution to the conventional problems and realize more accurate reconstruction.
Finally, we show the computation time of the proposed method. The experiments shown above were performed on a personal computer using Intel(R) Core(TM) i7 950 CPU 3.06 GHz with 8.0 Gbytes RAM. The proposed method was implemented by using Matlab. The average computation times to perform the algorithms shown in Sections 3.1 and 3.2 for each target patch are, respectively,  sec and
sec and  sec. Thus, from these results, we can see that the reduction of the computational cost in the optimal patch selection algorithm of the proposed method is necessary for practical use. This issue will be addressed in a future work.
sec. Thus, from these results, we can see that the reduction of the computational cost in the optimal patch selection algorithm of the proposed method is necessary for practical use. This issue will be addressed in a future work.
5. Conclusions
In this paper, we have presented an adaptive method for reconstructing missing textures based on the SSIM index. The proposed method adaptively obtains subspaces utilized for the reconstruction of missing textures by selecting the optimal known local textures based on the SSIM index. Furthermore, missing texture reconstruction maximizing the SSIM index can be realized by reformulating the nonconvex problem as a quasi convex problem. Then the proposed method enables adaptive texture reconstruction based on the perceptually optimized algorithm. Consequently, impressive improvement of the proposed method over previously reported methods was confirmed.
In the experiments, we manually determine the parameters of the proposed method. It is desirable that these parameters be adaptively determined from the target image. Thus, we need to complement this determination algorithm. Extension of the framework to texture reconstruction of other types of missing imagery data is also needed for various applications. Finally, we would like to study these ideas for interpolation in video data. These topics will be the subjects of subsequent reports.
References
Bertalmio M, Vese L, Sapiro G, Osher S: Simultaneous structure and texture image inpainting. IEEE Transactions on Image Processing 2003, 12(8):882-889. 10.1109/TIP.2003.815261
Rane SD, Sapiro G, Bertalmio M: Structure and texture filling-In of missing image blocks in wireless transmission and compression applications. IEEE Transactions on Image Processing 2003, 12(3):296-303. 10.1109/TIP.2002.804264
Ballester C, Bertalmio M, Caselles V, Sapiro G, Verdera J: Filling-in by joint interpolation of vector fields and gray levels. IEEE Transactions on Image Processing 2001, 10(8):1200-1211. 10.1109/83.935036
Chan TF, Shen J: Nontexture inpainting by curvature-driven diffusions. Journal of Visual Communication and Image Representation 2001, 12(4):436-449. 10.1006/jvci.2001.0487
Rareş A, Reinders MJT, Biemond J: Edge-based image restoration. IEEE Transactions on Image Processing 2005, 14(10):1454-1468.
Efros AA, Leung TK: Texture synthesis by non-parametric sampling. Proceedings of the 1999 7th IEEE International Conference on Computer Vision (ICCV'99), September 1999 1033-1038.
Efros AA, Freeman WT: Image quilting for texture synthesis and transfer. Proceedings of the Computer Graphics Annual Conference (SIGGRAPH '01), August 2001 341-346.
Wei L-Y, Levoy M: Fast texture synthesis using tree-structured vector quantization. In Proceedings of the ACM SIGGRAPH Conference on Computer Graphics (SIGGRAPH '00), 2000. Edited by: Akeley K. ACM Press /ACM SIGGRAPH /Addison Wesley Longman; 479-488.
Drori I, Cohen-Or D, Yeshurun H: Fragment-based image completion. In Proceedings of the ACM SIGGRAPH 2003 Papers (SIGGRAPH '03), 2003, New York, NY, USA. ACM Press; 303-312.
Criminisi A, Pérez P, Toyama K: Object removal by exemplar-based inpainting. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, June 2003 721-728.
Criminisi A, Pérez P, Toyama K: Region filling and object removal by exemplar-based image inpainting. IEEE Transactions on Image Processing 2004, 13(9):1200-1212. 10.1109/TIP.2004.833105
Fidaner IB: A survey on variational image inpainting texture synthesis and image completion. http://www.scribd.com/doc/3012627/A-Survey-on-Variational-Image-Inpainting-Texture-Synthesis-and-Image-Completion
Amano T, Sato Y: Image interpolation using BPLP method on the eigenspace. Systems and Computers in Japan 2007, 38(1):87-96. 10.1002/scj.10319
Schölkopf B, Mika S, Burges CJC, Knirsch P, Müller K-R, Rätsch G, Smola AJ: Input space versus feature space in kernel-based methods. IEEE Transactions on Neural Networks 1999, 10(5):1000-1017. 10.1109/72.788641
Mika S, Schölkoph B, Smola A, Müller K-R, Scholz M, Rätsch G: Kernel PCA and de-noising in feature spaces. Proceedings of the conference on Advances in Neural Information Processing Systems II, 1999 536-542.
Kim KI, Franz MO, Schölkopf B: Iterative kernel principal component analysis for image modeling. IEEE Transactions on Pattern Analysis and Machine Intelligence 2005, 27(9):1351-1366.
Ogawa T, Haseyama M: POCS-based texture reconstruction method using clustering scheme by kernel PCA. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 2007, 90(8):1519-1527.
Ogawa T, Haseyama M: Adaptive missing texture reconstruction method based on kernel canonical correlation analysis with a new clustering scheme. IEICE Transactions. Fundamentals 2009, 92(8):1950-1960.
Aharon M, Elad M, Bruckstein A: K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Signal Processing 2006, 54(11):4311-4322.
Elad M, Aharon M: Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image Processing 2006, 15(12):3736-3745.
Mairal J, Elad M, Sapiro G: Sparse representation for color image restoration. IEEE Transactions on Image Processing 2008, 17(1):53-69.
Wohlberg B: Inpainting with sparse linear combinations of exemplars. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '09), April 2009 689-692.
Shen B, Hu W, Zhang Y, Zhang Y-J: Image inpainting via sparse representation. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '09), April 2009 697-700.
Girod B: What's wrong with mean-squared error? In Digital Images and Human Vision. Edited by: Watson AB. MIT Press, Cambridge, Mass, USA; 1993:207-220.
Miyahara M, Kotani K, Algazi VR: Objective picture quality scale (PQS) for image coding. IEEE Transactions on Communications 1998, 46(9):1215-1226. 10.1109/26.718563
Damera-Venkata N, Kite TD, Geisler WS, Evans BL, Bovik AC: Image quality assessment based on a degradation model. IEEE Transactions on Image Processing 2000, 9(4):636-650. 10.1109/83.841940
Sheikh HR, Bovik AC, de Veciana G: An information fidelity criterion for image quality assessment using natural scene statistics. IEEE Transactions on Image Processing 2005, 14(12):2117-2128.
Sheikh HR, Bovik AC: Image information and visual quality. IEEE Transactions on Image Processing 2006, 15(2):430-444.
Sheikh HR, Sabir MF, Bovik AC: A statistical evaluation of recent full reference image quality assessment algorithms. IEEE Transactions on Image Processing 2006, 15(11):3440-3451.
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP: Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing 2004, 13(4):600-612. 10.1109/TIP.2003.819861
Channappayya SS, Bovik AC, Caramanis C, Heath RW Jr.: Design of linear equalizers optimized for the structural similarity index. IEEE Transactions on Image Processing 2008, 17(6):857-872.
Mallat SG, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993, 41(12):3397-3415. 10.1109/78.258082
Pati YC, Rezaiifar R, Krishnaprasad PS: Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. Proceedings of the 27th Asilomar Conference on Signals, Systems & Computers, November 1993 1: 40-44.
Wang Z, Bovik AC: Modern Image Quality Assessment. Morgan & Claypool, San Rafael, Calif, USA; 2006.
Arias P, Caselles V, Sapiro G: A variational framework for nonlocal image inpainting. Proceedings of the Energy Minimization Methods in Computer Vision and Pattern Recognition (EMMCVPR '09), 2009 345-358.
Acknowledgment
This work was partly supported by Grant-in-Aid for Scientific Research (B) 21300030, Japan Society for the Promotion of Science (JSPS).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ogawa, T., Haseyama, M. Missing Texture Reconstruction Method Based on Perceptually Optimized Algorithm. EURASIP J. Adv. Signal Process. 2010, 208976 (2010). https://doi.org/10.1155/2010/208976
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/208976

 ,
, , and
, and 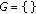 . Furthermore,
. Furthermore, 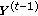 , and
, and 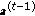 are, respectively, set to the empty matrix,and vector.
are, respectively, set to the empty matrix,and vector.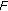 , the optimal value of the SSIM index maximizing (8) is calculated.
, the optimal value of the SSIM index maximizing (8) is calculated.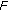 ,
,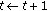 , and the matrix
, and the matrix  is constructed from the vectors of the patches belonging to
is constructed from the vectors of the patches belonging to  .
.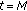 . If
. If 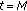 ,
,  outputs
outputs 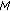 optimal known patches.
optimal known patches. (say
(say 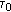 ) is determined between. zero to one. Furthermore,
) is determined between. zero to one. Furthermore, 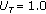
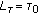 , where
, where 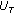 and
and 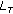 , respectively, represent the upper
, respectively, represent the upper . In this paper, we set
. In this paper, we set 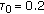
 .
. and
and  are calculated as
are calculated as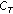 and
and 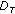 , the following steps are operated:
, the following steps are operated:




