- Research Article
- Open access
- Published:
An Efficient Two-Fold Marginalized Bayesian Filter for Multipath Estimation in Satellite Navigation Receivers
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 287215 (2010)
Abstract
Multipath is today still one of the most critical problems in satellite navigation, in particular in urban environments, where the received navigation signals can be affected by blockage, shadowing, and multipath reception. Latest multipath mitigation algorithms are based on the concept of sequential Bayesian estimation and improve the receiver performance by exploiting the temporal constraints of the channel dynamics. In this paper, we specifically address the problem of estimating and adjusting the number of multipath replicas that is considered by the receiver algorithm. An efficient implementation via a two-fold marginalized Bayesian filter is presented, in which a particle filter, grid-based filters, and Kalman filters are suitably combined in order to mitigate the multipath channel by efficiently estimating its time-variant parameters in a track-before-detect fashion. Results based on an experimentally derived set of channel data corresponding to a typical urban propagation environment are used to confirm the benefit of our novel approach.
1. Introduction
Within global navigation satellite systems (GNSS), such as the Global Positioning System (GPS) or the future European satellite navigation system Galileo, the user position is determined based upon the code division multiplex access (CDMA) navigation signals received from different satellites using the time-of-arrival method [1]. A major error source for positioning comes from multipath, the reception of additional signal replicas due to reflections caused by the receiver environment. The reception of multipath introduces a bias into the time-delay estimate of the delay-lock loop (DLL) of a conventional navigation receiver, which finally leads to a bias in the receiver's position estimate. Multipath is today still one of the most critical problems in GNSS, as the error occurs as a result of the local environment and can not be corrected through the use of correction data, which is provided by reference receiver stations or networks.
The advances in the development of signal processing techniques for multipath mitigation have led to a continual improvement of performance. Basically, two major approaches can be distinguished. Firstly, the class of techniques that actually mitigate the effect of multipath by modifications of the antenna pattern (either by means of hardware design or with signal processing techniques) or by aligning the more or less traditional receiver components (e.g., the early/late correlator). Secondly, the class of multipath estimation techniques, which treat multipath (in particular the delay of the paths) as something to be estimated from the received signal so that its effects can be trivially removed at a later processing stage. Most of the conventional mitigation techniques in some way align the discriminator/timing error detector of the DLL to the signal received in the multipath environment. Well-known examples of this category are, amongst others, the Narrow Correlator [2], the Strobe Correlator [3], the Gated Correlator [4], or the Pulse Aperture Correlator [5].
For the estimation techniques, static and dynamic approaches can be distinguished, according to the underlying assumption of the channel dynamics. Examples for static multipath estimation are those belonging to the family of maximum likelihood (ML) estimators, where the probably best-known technique is the multipath estimating delay-lock loop (MEDLL) [6]. In the ML approach, the signal parameters that maximize the probability of the received signal are determined. For this purpose, different maximization strategies exist, which basically characterize the different approaches. Most of these maximization algorithms are based on iterative techniques such as the Space-Alternating Generalized Expectation-Maximization algorithm (SAGE) [7, 8] and Newton-type methods. Newton-type methods have been considered with analytical [9] and numerical [10] expressions for the gradient and Hessian terms. Further ML algorithms have been reported in [11, 12].
During the last years, sequential estimation algorithms in the form of Bayesian filters [13–16] have gained some attention in the field of multipath mitigation. These algorithms exploit prior knowledge about the temporal channel statistics through the use of statistical channel models, which allows one to improve the multipath performance of the receiver. Bayesian filters for estimation of time-varying synchronization parameters in spread spectrum systems have already been suggested in the field of communications using the extended Kalman filter [17] as well as the sequential Monte Carlo approach [18, 19]. For navigation systems, an estimator based on sequential importance sampling (SIS) methods (particle filtering) was proposed in [20], which was shown to successfully mitigate multipath in a static channel scenario. An adaptation to dynamic multipath channels capable of coping with a time-variant number of multipath replicas was presented in [21]. To reduce the complexity of these approaches, it was proposed in [22] to employ reduced complexity methods for the computation of the likelihood function, which previously have been considered for ML estimation [23]. To improve the efficiency of the particle filter (PF) approach, a Rao-Blackwellized/marginalized filter was presented in [24], where the signal amplitudes are efficiently estimated via Kalman filters and where a novel proposal density for the particle filter based on a Gaussian approximation of the likelihood function was introduced. Furthermore, [24] includes a comprehensive analysis of the performance of various other Bayesian filters, and also the corresponding posterior Cramer-Rao bound (PCRB) is derived.
We believe that a key for successful application of the Bayesian approach in the future is to determine correctly the number of actually received replicas, which is unknown in practice. It is well known for the signal parameter estimation approaches that it is crucial to properly adjust the order of the employed signal model, since an improper number of degrees of freedom in the assumed model may lead to a heavy performance degradation. In previous work, however, often a known number of received replicas is assumed, and the problem of how to determine this number is not addressed [24]. To tackle this problem, we introduce in this paper a further structuring of the Bayesian approach by means of a two-fold marginalized Bayesian filter (TFMBF). The filter operates in line with filters that were presented previously, but is capable of simultaneously estimating all possible system models in terms of the number of received multipath replicas along with their respective probabilities. We achieve this by introducing an intermediate step of marginalization, which estimates the number of impinging replicas and their parameters in a track-before-detect (TBD) fashion [25, 26].
The paper is organized as follows: first, the Bayesian approach is reviewed, and the underlying signal and dynamic models are introduced. After that, we address the implementation of our two-fold marginalized filter. Subsequently, we present results based upon a set of experimentally derived realistic dynamic channel data, which corresponds to a typical satellite-to-user propagation channel in urban environments [27]. Finally, we conclude the paper by a discussion of our findings.
2. The Sequential Bayesian Approach
2.1. The Sequential Bayesian Framework
For the sequential Bayesian approach, the problem of multipath mitigation becomes one of sequential estimation of a hidden Markov process: the unknown channel parameters are estimated based on an evolving sequence of received noisy channel outputs  . Intuitively, this concept not only exploits the observations to estimate the hidden channel parameters but also exploits prior knowledge about the statistical dependencies between successive sets of channel parameters. The reader is referred to [13], which gives a derivation of the general framework for optimal estimation of temporally evolving parameters by means of inference via sequential Bayesian estimation. The entire history of observations up to the temporal index
. Intuitively, this concept not only exploits the observations to estimate the hidden channel parameters but also exploits prior knowledge about the statistical dependencies between successive sets of channel parameters. The reader is referred to [13], which gives a derivation of the general framework for optimal estimation of temporally evolving parameters by means of inference via sequential Bayesian estimation. The entire history of observations up to the temporal index  can be written as
can be written as

The goal is to determine the a posteriori probability density function (PDF) of every possible channel characterization given all channel observations:  , in which
, in which  represents the characterization of the hidden channel state. Once the a posteriori PDF is evaluated, either that channel configuration that maximizes it can be determined—the so called maximum a posteriori (MAP) estimate, or the expectation can be chosen—equivalent to the minimum mean square error (MMSE) estimate.
represents the characterization of the hidden channel state. Once the a posteriori PDF is evaluated, either that channel configuration that maximizes it can be determined—the so called maximum a posteriori (MAP) estimate, or the expectation can be chosen—equivalent to the minimum mean square error (MMSE) estimate.
In the so-called prediction step, the recursive sequential Bayesian estimation algorithm computes the a priori PDF  from the a posteriori PDF at time instant
from the a posteriori PDF at time instant  ,
,  via the Chapman-Kolmogorov equation
via the Chapman-Kolmogorov equation

with  being the state transition PDF of the Markov process. In the update step, the new a posteriori PDF for step
being the state transition PDF of the Markov process. In the update step, the new a posteriori PDF for step  is obtained via
is obtained via

The likelihood function  represents the probability of the measured channel output, conditioned on a certain configuration of channel parameters at the same time step
represents the probability of the measured channel output, conditioned on a certain configuration of channel parameters at the same time step  . To apply (2) and (3) correctly, two conditions need to be fulfilled.
. To apply (2) and (3) correctly, two conditions need to be fulfilled.
-
(1)
The noise affecting successive channel outputs is independent of the past noise values, so each channel observation depends only on the present channel state.
-
(2)
Future channel parameters, given the present state of the channel and all its past states, depend only on the present channel state and not on any past states.
2.2. Multipath Propagation and Receiver Requirements
The typical urban multipath environment [28] poses stringent requirements on the capabilities of a receiver that is based on a parametric channel estimator, which are partially contradicting.
-
(i)
High noise level: the power level of the received signal is usually more than 25?dB below the thermal noise, thus the algorithm has to be robust against false detection of line-of-sight (LOS) signals.
-
(ii)
Low bandwidth: since in particular those echoes which arrive within a chip period of the CDMA signal cause the most heavy errors, the signal bandwidth is relatively low with respect to the desired timing resolution.
-
(iii)
Multiple paths: multiple paths may impinge simultaneously at the receiver, so the algorithm must properly determine which of them is the actual LOS path.
-
(iv)
LOS blockage: the algorithm shall ensure that tracking of the LOS path is maintained also during periods where it is heavily attenuated.
-
(v)
Close-in echoes: tracking of closely spaced signals with the proper multiple path signal model may lead to increased mean square errors compared to the case when tracking is based on a single-path model [29].
-
(vi)
Track-before-detect: since it is difficult to declare distinct detections of multipath replicas due to the high noise and the low signal bandwidth, the algorithm will consider the echo detection in a probabilistic fashion. The track-before-detect approach [25] is suitable for this purpose, since for any echo both hypotheses (echo present/echo not present) are estimated simultaneously in a probabilistic sense.
These requirements are challenging, since weak signals need to be detected and tracked properly in a noisy environment, with echoes very close to the LOS signal.
3. Channel Model
3.1. Multipath Channel Signal Model
The complex valued baseband-equivalent received signal in a navigation receiver is assumed to be equal to

where  is the CDMA navigation signal,
is the CDMA navigation signal,  is the maximum number of considered multipath replicas reaching the receiver (to restrict the modeling complexity),
is the maximum number of considered multipath replicas reaching the receiver (to restrict the modeling complexity),  is a binary function that models the activity of the
is a binary function that models the activity of the  th path, and
th path, and  and
and  are their individual complex amplitudes and time delays, respectively. The signal is disturbed by additive white Gaussian noise
are their individual complex amplitudes and time delays, respectively. The signal is disturbed by additive white Gaussian noise  . The signal is sampled at times
. The signal is sampled at times  ,
,  and grouped in blocks of
and grouped in blocks of  samples together into vectors
samples together into vectors  , with the block index
, with the block index  ,
,  . The parameter functions
. The parameter functions  ,
,  and
and  are assumed to be constant and equal to
are assumed to be constant and equal to  ,
,  , and
, and  for the duration of an entire block. Furthermore, the vectors
for the duration of an entire block. Furthermore, the vectors  and
and  are used. The vector
are used. The vector  determines whether the
determines whether the  th path is active or not:
th path is active or not:  corresponds to an active path, and
corresponds to an active path, and  to a path that is currently not active. In the compact form, the samples of the delayed replicas
to a path that is currently not active. In the compact form, the samples of the delayed replicas  are stacked together as columns of the matrix
are stacked together as columns of the matrix  , and we may write
, and we may write

with  . In the following, we denote the signal hypothesis by the concise notation
. In the following, we denote the signal hypothesis by the concise notation  . Thus, we may write according to (5) the associated likelihood function for observation block
. Thus, we may write according to (5) the associated likelihood function for observation block 

where  refers to the variance of the elements within the noise vector
refers to the variance of the elements within the noise vector  . The purpose of the likelihood function is to quantify the conditional probability of the received signal conditioned on the unknown signal (specifically the channel parameters
. The purpose of the likelihood function is to quantify the conditional probability of the received signal conditioned on the unknown signal (specifically the channel parameters  ,
,  , and
, and  ).
).
3.2. Markovian Channel Process Model
To exploit the advantages of sequential estimation for the task of multipath mitigation/estimation, the actual channel characteristics have to be described such that these are captured by  . In other words, the model must be a first-order Markov model, and all transition probabilities must be known. The channel state model used here is motivated by channel modeling work for multipath prone environments such as the urban satellite navigation channel [28, 30]. In fact, the process of constructing a channel model in order to characterize the channel for signal level simulations and receiver evaluation comes close to our task of building a first-order Markov process for sequential estimation. Here, the channel is approximated as follows.
. In other words, the model must be a first-order Markov model, and all transition probabilities must be known. The channel state model used here is motivated by channel modeling work for multipath prone environments such as the urban satellite navigation channel [28, 30]. In fact, the process of constructing a channel model in order to characterize the channel for signal level simulations and receiver evaluation comes close to our task of building a first-order Markov process for sequential estimation. Here, the channel is approximated as follows.
-
(i)
The channel is totally characterized by a LOS path (index
 ) and at most
) and at most  echoes.
echoes. -
(ii)
Each path has complex amplitude
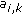 and delay
and delay  , where echoes are constrained to have delay
, where echoes are constrained to have delay 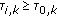 ,
,  , to reflect that multipath replicas are physically constrained to arrive later at the receiver than the LOS path.
, to reflect that multipath replicas are physically constrained to arrive later at the receiver than the LOS path. -
(iii)
The delay of each path follows the process
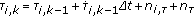 (7)
(7)with noise
 ,
, 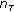 , where
, where 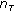 is the same value for all indices
is the same value for all indices  .
. -
(iv)
Each parameter
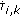 that specifies the rate of the change of the path delay follows its own process
that specifies the rate of the change of the path delay follows its own process (8)
(8)with noise
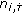 ,
, 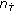 , in which
, in which  has the same value for all indices
has the same value for all indices  .
. -
(v)
Each echo is either "on" or "off", as defined by the channel parameter
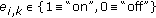 , where
, where 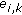 ,
,  follows a simple two-state Markov process with a-symmetric crossover and same-state probabilities
follows a simple two-state Markov process with a-symmetric crossover and same-state probabilities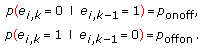 (9)
(9) -
(vi)
The LOS component is always present, and consequently
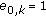 for all
for all  .
. -
(vii)
Newly appearing echoes (
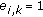 with
with 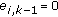 ) are initialized with
) are initialized with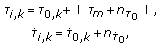 (10)
(10)with noise
 ,
, 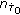 and the characteristic constant
and the characteristic constant 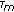 (cf. [20]).
(cf. [20]). -
(viii)
Blockage and shadowing of the LOS signal is considered through variations of the LOS amplitude
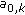 .
. -
(ix)
Following [30], the complex amplitudes
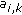 depend on the previous amplitudes
depend on the previous amplitudes 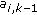 through
through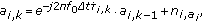 (11)
(11)with complex noise
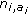 and the carrier frequency
and the carrier frequency  . Thus, the rate of change in the delay affects the evolution of the complex amplitude in a statistical manner in order to consider the physical relationships between phase, Doppler-frequency, and time delay adequately.
. Thus, the rate of change in the delay affects the evolution of the complex amplitude in a statistical manner in order to consider the physical relationships between phase, Doppler-frequency, and time delay adequately.
The model implicitly incorporates nine i.i.d. noise sources: Gaussian  ,
,  ,
,  ,
,  ,
,  ,
,  , and complex Gaussian
, and complex Gaussian  , as well as the noise process driving the state changes for
, as well as the noise process driving the state changes for  . These sources provide the randomness of the model. The noise sources
. These sources provide the randomness of the model. The noise sources  and
and  are included to model the impact of the receiver clock on the individual delays and delay rates, since they are actually affected simultaneously by the same random process. Finally,
are included to model the impact of the receiver clock on the individual delays and delay rates, since they are actually affected simultaneously by the same random process. Finally,  is the time between instants
is the time between instants  and
and  . It is assumed that all model parameters (i.e.,
. It is assumed that all model parameters (i.e.,  , noise variances, and the "on"/"off" Markov model) are independent of
, noise variances, and the "on"/"off" Markov model) are independent of  . Note that the model implicitly represents the number of actually impinging paths through the time variant parameter
. Note that the model implicitly represents the number of actually impinging paths through the time variant parameter

Using  , the hidden channel state vector
, the hidden channel state vector  is thus represented as
is thus represented as

4. Estimator Implementation
Various algorithms are known which implement the Bayesian recursion (2) and (3), including the Kalman filter, the grid-based filter, and the family of particle filtering algorithms [13]. Certain restrictions are imposed on the use of these algorithms. The objective here is to estimate the channel parameters (13) via the likelihood function (6) and the channel process model defined in Section 3.2, which makes the estimation complicated: the amplitude parameters  are continuous, and the measurement depends linearly on them like the activity parameters
are continuous, and the measurement depends linearly on them like the activity parameters  , which are discrete and thus follow a discrete evolution. In contrast the observations depend nonlinearly on the continuous delays
, which are discrete and thus follow a discrete evolution. In contrast the observations depend nonlinearly on the continuous delays  , which are also nonlinear with respect to their dynamics. A straightforward way would be to implement the estimation algorithm completely with a particle filter, which is the most general method with respect to system nonlinearities, but depending on the considered number of paths
, which are also nonlinear with respect to their dynamics. A straightforward way would be to implement the estimation algorithm completely with a particle filter, which is the most general method with respect to system nonlinearities, but depending on the considered number of paths  the state space in such a filter becomes large, and it becomes difficult to cover the entire space with a reasonable number of particles. To consider the nonlinearities while keeping the state space to be covered by the particles as small as possible, it has been proposed to reduce the computational complexity of the filter by means of marginalization over the linear state variables [16], a technique also known as Rao-Blackwellization [15]. In a marginalized filter, particles are still used to estimate the nonlinear states, while for each of the particles, the linear states can be estimated analytically. Our marginalized estimator factorizes the a posteriori density via the chain rule two-fold according to
the state space in such a filter becomes large, and it becomes difficult to cover the entire space with a reasonable number of particles. To consider the nonlinearities while keeping the state space to be covered by the particles as small as possible, it has been proposed to reduce the computational complexity of the filter by means of marginalization over the linear state variables [16], a technique also known as Rao-Blackwellization [15]. In a marginalized filter, particles are still used to estimate the nonlinear states, while for each of the particles, the linear states can be estimated analytically. Our marginalized estimator factorizes the a posteriori density via the chain rule two-fold according to

A Kalman filter is used to estimate the amplitudes  analytically conditional on the parameters
analytically conditional on the parameters  ,
,  . The discrete path activity parameters are in turn estimated conditionally on the delays
. The discrete path activity parameters are in turn estimated conditionally on the delays  and the delay rates
and the delay rates  using a grid-based method [13], which is appropriate to optimally estimate a discrete state space. Finally, the delays
using a grid-based method [13], which is appropriate to optimally estimate a discrete state space. Finally, the delays  and the delay rates
and the delay rates  are the only remaining parameters that are estimated by the particle filtering algorithm. It is straightforward to show that (14) indeed corresponds to three Bayesian filters, in which the update step (3) can be expressed as
are the only remaining parameters that are estimated by the particle filtering algorithm. It is straightforward to show that (14) indeed corresponds to three Bayesian filters, in which the update step (3) can be expressed as





The structure of the two-fold marginalization is illustrated in Figure 1, which reveals that the complexity of our filter is heavily dependent on the choice of  . However, our results that are presented in Section 5 will show that with a practically reasonable choice of
. However, our results that are presented in Section 5 will show that with a practically reasonable choice of  , the complexity remains still moderate.
, the complexity remains still moderate.
Structure of the two-fold marginalized filter, which infers the a posteriori PDF of the channel parameters from the blockwise processed received signal. Each particle (black dots) of the central particle filter (PF) carries a grid-based filter (GBF) in which there are several Kalman filters (KF) according to the combination of active paths. The number of complex amplitudes to be tracked per KF (as indicated by the numbers in the boxes) ranges from 1 to  .
.
4.1. Estimation of Amplitudes
The implementation of the conditional amplitude filter follows from (16). The conditional a posteriori PDF with respect to the complex amplitudes is thus given by

in which  corresponds to the likelihood function given in (6). Recalling the structure of the measurement model (5), the observed signal
corresponds to the likelihood function given in (6). Recalling the structure of the measurement model (5), the observed signal  is disturbed by white Gaussian noise and depends linearly on the amplitudes
is disturbed by white Gaussian noise and depends linearly on the amplitudes  . According to (11)), the amplitude dynamics are linear conditioned on the delay rates. Hence, (20) can be estimated with a Kalman filter and the a priori PDF for the amplitudes is given by the Gaussian density
. According to (11)), the amplitude dynamics are linear conditioned on the delay rates. Hence, (20) can be estimated with a Kalman filter and the a priori PDF for the amplitudes is given by the Gaussian density

Its mean  and its covariance matrix
and its covariance matrix  are obtained in the prediction step from the previous time instant
are obtained in the prediction step from the previous time instant  through the framework of the Kalman filter equations
through the framework of the Kalman filter equations


The matrices  and
and  follow directly from the state transition model (11)) and are computed using
follow directly from the state transition model (11)) and are computed using

The notation  above indicates that dimension and values of the respective matrices and vectors correspond to the active paths as given by
above indicates that dimension and values of the respective matrices and vectors correspond to the active paths as given by  . We assume in our implementation that (21) is still a circular symmetric complex normal PDF [31], which is enforced by the approximation via (23).
. We assume in our implementation that (21) is still a circular symmetric complex normal PDF [31], which is enforced by the approximation via (23).
The a posteriori PDF of the amplitude filter becomes

with mean and covariance given by

with  and the Kalman gain
and the Kalman gain

The value of  follows directly from (6).
follows directly from (6).
4.2. Estimation of Path Activity
The estimation of the path activity  follows (17), and thus the a posteriori PDF with respect to the path activity is given by
follows (17), and thus the a posteriori PDF with respect to the path activity is given by

The activity state space is finite and discrete and can thus be estimated optimally using a grid-based filter [13]. In this case, the prediction (2) simplifies to the evaluation of the sum

The transition density with respect to the activity states is given by (9) and depends, therefore, on the realization of the path transition  , and it can be shown that
, and it can be shown that

where  is the number of paths switching from "off" to "on",
is the number of paths switching from "off" to "on",  is the number of paths switching from "on" to "off",
is the number of paths switching from "on" to "off",  is the number of paths remaining "off", and
is the number of paths remaining "off", and  is the number of paths remaining "on" during the transition from
is the number of paths remaining "on" during the transition from  to
to  . Note that there are
. Note that there are  discrete states and
discrete states and  transitions to be covered by the grid-based filter. The marginal likelihood value used in the update step is given by the integral
transitions to be covered by the grid-based filter. The marginal likelihood value used in the update step is given by the integral

The first term is independent of  (6), and the second follows from (21). This yields the Gaussian distribution
(6), and the second follows from (21). This yields the Gaussian distribution

A proof for (32) can be found in [32].
4.3. Estimation of Path Delays
Due to the nonlinearity in the system model, the remaining parts of the state vector, namely, the delays and the delay rates, are to be estimated by a particle filter. Particle filters belong to the family of sequential Monte Carlo (SMC) filters [13], which solve the Bayesian filtering equations based on the principle of importance sampling and thus inherently implement only a suboptimal approximation of the optimal Bayesian solution. According to (18), the marginalized a posteriori density with respect to the path delays and delay rates is

Here, a simple sampling importance resampling particle filter (SIR-PF) according to [14] is used to implement the marginalized delay and delay rate estimator. In the SIR-PF algorithm, the a posteriori density at step  is represented as a sum, and is specified by a set of
is represented as a sum, and is specified by a set of  particles
particles

where each particle with index μ has a state  and has a weight
and has a weight  . Due to the marginalization, each particle carries in addition a grid-based filter, in which for each of the discrete states a Kalman filter is associated to the particle, resulting thus in
. Due to the marginalization, each particle carries in addition a grid-based filter, in which for each of the discrete states a Kalman filter is associated to the particle, resulting thus in  Kalman filters per particle (see Figure 1).
Kalman filters per particle (see Figure 1).
The key step of the particle filter algorithm is the calculation of the weight

with the so-called proposal density  . In the SIR-PF, the recent measurement
. In the SIR-PF, the recent measurement  is not taken into account by the proposal density. This choice is appropriate here, since we operate our filter in an environment that is characterized by high measurement noise, such that the likelihood function is rather flat and the dynamics of the particles are more dominant with respect to the shape of the optimal proposal density. However, other choices have been suggested in the literature, for example, a Gaussian approximation strategy [24], which may be applied as well to the particle filter employed here. The characterization of the channel process enters in the algorithm when at each time instant
is not taken into account by the proposal density. This choice is appropriate here, since we operate our filter in an environment that is characterized by high measurement noise, such that the likelihood function is rather flat and the dynamics of the particles are more dominant with respect to the shape of the optimal proposal density. However, other choices have been suggested in the literature, for example, a Gaussian approximation strategy [24], which may be applied as well to the particle filter employed here. The characterization of the channel process enters in the algorithm when at each time instant  the state of each particle
the state of each particle  is drawn randomly from the SIR-PF's proposal distribution; that is, from
is drawn randomly from the SIR-PF's proposal distribution; that is, from  , which corresponds to drawing values for
, which corresponds to drawing values for  ,
,  ,
,  ,
,  ,
,  and
and  . As a consequence, in (35),
. As a consequence, in (35),  and
and  cancel out, and the computation of the new weight
cancel out, and the computation of the new weight  simplifies to the evaluation of the product of the previous weight and the marginalized likelihood function:
simplifies to the evaluation of the product of the previous weight and the marginalized likelihood function:  . The marginal likelihood value is given by summing up the marginal likelihoods over all path activity hypotheses using (32) and (29)
. The marginal likelihood value is given by summing up the marginal likelihoods over all path activity hypotheses using (32) and (29)

The particle filter approach allows us to enforce the nonlinear constraint  ,
,  in an easy way: when drawing new realizations of
in an easy way: when drawing new realizations of  according to our proposal density via (7), we reinitialize
according to our proposal density via (7), we reinitialize  and
and  according to (10) in case
according to (10) in case  . In our implementation of the particle filter, we apply resampling at every time instant. To tackle this potential bottleneck, advanced resampling strategies may be applied [33, 34].
. In our implementation of the particle filter, we apply resampling at every time instant. To tackle this potential bottleneck, advanced resampling strategies may be applied [33, 34].
5. Algorithm Assessment
5.1. Scenario
To validate our algorithm, we build on the concept of the stored channel: a channel profile is recorded during a measurement campaign, and the stored profile is fed back into the receiver simulation. Though the statistical significance of such an assessment is limited, it is the most realistic approach, since the employed channel corresponds to a real world scenario. In Figure 2, the recorded channel profile from [28] which we use is illustrated. It has a total duration of 350 seconds and corresponds to a scenario, where a satellite at 10 degrees elevation transmits to a pedestrian user moving within an urban environment. The profile clearly motivates the pursued algorithmic approach. Discrete echoes due to reflectors such as house fronts are clearly visible. Thereby, each echo experiences a typical life-cycle: the reflectors cause echo traces that persist, approach, and depart along with the occasionally shadowed LOS path. Dominant channel properties are the long correlation times in the multipath echoes and their clearly observable binding to the user dynamics and the surrounding environment. The overall power variation in the channel is depicted in Figure 3. As navigation signal, we assume a GPS C/A code signal, which is a CDMA signal with a code length of 1023 (Gold code) and a chip rate of 1.023 MChips/s, such that a single chip corresponds to a signal travel time of approximately 300 meters and the duration of an entire codeword is a millisecond. The carrier frequency of the transmitted signal is the GPS L1 center frequency  MHz and the receiver's assumed reception bandwidth is
MHz and the receiver's assumed reception bandwidth is  MHz. Our TFMBF computes (15) at a rate of 100 Hz corresponding to
MHz. Our TFMBF computes (15) at a rate of 100 Hz corresponding to  ms and unless stated otherwise, we employ 50 particles.
ms and unless stated otherwise, we employ 50 particles.
5.2. Model Matching
It is important to point out that a sequential estimator is only as good as its state transition model matches the real-world situation. The state model needs to capture all relevant hidden states with memory and needs to correctly model their dependencies, while adhering to the first order Markov condition. Furthermore, any memory of the measurement noise affecting the likelihood function must be explicitly contained as additional states of the model, so that the measurement noise is i.i.d. Adapting the model parameters to a real channel environment is a challenging task for current and future work, since the tuning of the parameters has to take into account the potential model mismatch. The result of an adaption by empirical means, which has been the basis of the present simulations, is given in Table 1.
5.3. Results
The results of the assessment are illustrated in Figure 4 in terms of the cumulative density function (CDF) of the LOS estimation error when processing the entire channel scenario that is shown in Figure 2. Note that all results have been converted from signal delays to the equivalent pseudorange measures by means of the speed of light  and that the statistics are obtained from single Monte Carlo trials on the 350 second scenario, respectively. Due to LOS blockage and shadowing, large errors can occur occasionally for the conventional DLL receiver, which in our case employs a standard combination of a second-order DLL with narrow correlator spacing (0.1 Chips) [2] and a loop bandwidth of
and that the statistics are obtained from single Monte Carlo trials on the 350 second scenario, respectively. Due to LOS blockage and shadowing, large errors can occur occasionally for the conventional DLL receiver, which in our case employs a standard combination of a second-order DLL with narrow correlator spacing (0.1 Chips) [2] and a loop bandwidth of  Hz and a second-order phase locked loop (PLL) with a loop bandwidth of
Hz and a second-order phase locked loop (PLL) with a loop bandwidth of  Hz. Due to frequent cycle slips in this demanding scenario, the PLL output is neither used to aid the DLL nor to smooth its delay estimates [1]. It can be seen clearly that the use of the sequential estimation algorithm enhances the performance significantly, even if only a single LOS path (
Hz. Due to frequent cycle slips in this demanding scenario, the PLL output is neither used to aid the DLL nor to smooth its delay estimates [1]. It can be seen clearly that the use of the sequential estimation algorithm enhances the performance significantly, even if only a single LOS path ( ) is considered by the estimation algorithm. This is due to the dynamic model that underlies the recursive estimation procedure and which prohibits the LOS estimate of having errors that become effectively as large as those of the conventional DLL receiver. Furthermore, our approach exploits the phase information that is provided by the received signal (for all
) is considered by the estimation algorithm. This is due to the dynamic model that underlies the recursive estimation procedure and which prohibits the LOS estimate of having errors that become effectively as large as those of the conventional DLL receiver. Furthermore, our approach exploits the phase information that is provided by the received signal (for all  ) and is thus superior to the plain DLL. Since the comparison with the DLL is not quite fair with respect to the use of carrier information and dynamic constraints, the reader is referred to the case of
) and is thus superior to the plain DLL. Since the comparison with the DLL is not quite fair with respect to the use of carrier information and dynamic constraints, the reader is referred to the case of  as a reference implementation, from which one could derive the actual benefit of the multipath activity modeling, which is implemented for
as a reference implementation, from which one could derive the actual benefit of the multipath activity modeling, which is implemented for  . For these actual mitigation algorithms, which are capable of detecting and tracking multipath and which thus are able to remove the estimation bias due to multipath, it can be observed that the estimation performance tends to saturate quickly for
. For these actual mitigation algorithms, which are capable of detecting and tracking multipath and which thus are able to remove the estimation bias due to multipath, it can be observed that the estimation performance tends to saturate quickly for  . Thus, the additional complexity that is needed by considering more simultaneous paths may not be justified, given the amount of performance gain. Furthermore, the rapid performance saturation for
. Thus, the additional complexity that is needed by considering more simultaneous paths may not be justified, given the amount of performance gain. Furthermore, the rapid performance saturation for  shows that the presence of more than a single relevant multipath component tends to happen only rarely, and if so, that the simultaneous tracking of two or more multipath replicas leads only to a small amount of performance improvement in the average error statistics.
shows that the presence of more than a single relevant multipath component tends to happen only rarely, and if so, that the simultaneous tracking of two or more multipath replicas leads only to a small amount of performance improvement in the average error statistics.
Cumulative normalized histogram of the LOS delay estimation error of the Bayesian approach in comparison with a conventional narrow correlator DLL. Already without considering multipath, the advanced approach is significantly superior. Considering more simultaneously echoes (via  ) leads to a further improved performance, which tends to saturate rapidly for more than one additional path.
) leads to a further improved performance, which tends to saturate rapidly for more than one additional path.
5.4. Complexity
As illustrated in Figure 1, the complexity of the filter depends crucially on the number of considered paths  . The dimension of the particle filter is given by the maximum number of required multipath replicas. For the LOS path and each replicas delay and delay rate are to be estimated. Thus, the state dimension to be covered by the particle filter is
. The dimension of the particle filter is given by the maximum number of required multipath replicas. For the LOS path and each replicas delay and delay rate are to be estimated. Thus, the state dimension to be covered by the particle filter is  . Each particle needs to carry a grid-based filter to estimate the path activities. Their respective state dimension is
. Each particle needs to carry a grid-based filter to estimate the path activities. Their respective state dimension is  , because the LOS path is assumed to be always active. The number of Kalman filters totals
, because the LOS path is assumed to be always active. The number of Kalman filters totals  , since each activity hypothesis is required to carry its own Kalman filter. The dimension of the Kalman filters thus depends on the number of active paths and is in the range of
, since each activity hypothesis is required to carry its own Kalman filter. The dimension of the Kalman filters thus depends on the number of active paths and is in the range of  . In the overall implementation, there are
. In the overall implementation, there are  Kalman filters with a state dimension of
Kalman filters with a state dimension of  , where
, where  corresponds to the number of active echo paths. For a given
corresponds to the number of active echo paths. For a given  , the worst case state dimension of the Kalman filters is thus
, the worst case state dimension of the Kalman filters is thus  . Table 2 summarizes these values for
. Table 2 summarizes these values for  . Experience with our simulations confirm that increasing
. Experience with our simulations confirm that increasing  from 2 to 3 roughly doubles computation time. For a more detailed complexity analysis of marginalized particle filters, the reader is referred to [35].
from 2 to 3 roughly doubles computation time. For a more detailed complexity analysis of marginalized particle filters, the reader is referred to [35].
 .
.In Figure 5, the average performance of the TFMBF is shown as a function of the employed number of particles  and the parameter
and the parameter  . In contrast to previous work, the novel two-fold filter structure allows us to reduce the number of required particles significantly (cf. [22] ≈ 20.000, [24] ≈ 2.000). We are able to cover the state-space more efficiently by the particles' hypotheses, since each particle is able to exploit the carrier phase information via (11): since the complex amplitude can be measured quite precisely, we are able to infer the delay rates accurately as well. Precise delay rates in turn allow a proper prediction of the particles' delays (7), so that in the end much fewer particles are needed to represent the a posteriori density, as the delay spread of the particles during the importance sampling is kept much smaller, since delay hypotheses, which do not match the delay rates are not generated during the importance sampling. Thus, many particles, which would be deleted during the resampling anyway and thus are a waste of computational resources, are not even generated using our approach.
. In contrast to previous work, the novel two-fold filter structure allows us to reduce the number of required particles significantly (cf. [22] ≈ 20.000, [24] ≈ 2.000). We are able to cover the state-space more efficiently by the particles' hypotheses, since each particle is able to exploit the carrier phase information via (11): since the complex amplitude can be measured quite precisely, we are able to infer the delay rates accurately as well. Precise delay rates in turn allow a proper prediction of the particles' delays (7), so that in the end much fewer particles are needed to represent the a posteriori density, as the delay spread of the particles during the importance sampling is kept much smaller, since delay hypotheses, which do not match the delay rates are not generated during the importance sampling. Thus, many particles, which would be deleted during the resampling anyway and thus are a waste of computational resources, are not even generated using our approach.
5.5. Filter Behavior
To illustrate the operation of the sequential estimation algorithm its MMSE estimates of the LOS and multipath delays are depicted in Figures 6 and 7, which correspond to two typical scenarios a navigation receiver has to cope with in urban environments. The scenario illustrated in Figure 6 represents a situation where a partially shadowed LOS component is superimposed by a strong multipath signal. The scenario shown in Figure 7 corresponds to a situation where several simultaneous echoes arrive at the receiver. The evolution of these echoes shows the typical behavior that can be observed in urban environments, including echoes that are approaching and other echoes that are departing due to the movement of the receiver towards or away from the reflector. Both scenarios reveal the general benefit of the sequential estimation approach compared to the conventional DLL. On the one hand, the explicit consideration of the multipath replicas in the signal model at the receiver allows us to mitigate the multipath errors successfully; on the other hand, the exploitation of the constrained dynamic model yields smoother and more realistic estimates, which do not follow the abrupt changes in the channel such as the DLL does occasionally; for example, in Figure 6, during the period from 275 s to 295 s, which are quite unlikely given the limited dynamics of the pedestrian. In particular this period shows the major drawback of the conventional DLL: though the DLL implements a low-pass characteristic and thus limits the dynamics, it is not able to take into account a real probabilistic and physical model of the receiver dynamics and thus tends to immediately track the strongest path while neglecting any weaker earlier paths, which are much more likely to be the actual LOS path due to the recent channel history and the limited user dynamics.
In the illustrated scenario, there is a partially shadowed LOS path (red) that is superimposed by a heavy multipath component. During some periods with weak LOS, the DLL receiver (green) tracks the multipath signal instead of the true LOS, which leads to high errors in the order of 100 meters. The TFMBF's LOS estimate (dark blue) is still slightly biased if the multipath replicas are not taken into account by the estimator ( , (a)). Nevertheless, the magnitude of the errors is much smaller than the DLL errors, since the dynamic model of the estimator prevents fast variations of the LOS estimate and also because phase information is being used implicitly. Once the number of considered replicas is sufficient to take into account multipath signals (
, (a)). Nevertheless, the magnitude of the errors is much smaller than the DLL errors, since the dynamic model of the estimator prevents fast variations of the LOS estimate and also because phase information is being used implicitly. Once the number of considered replicas is sufficient to take into account multipath signals ( , (b, c, d)), the estimation algorithm detects and properly tracks the additional replicas (light blue), and thus successfully mitigates the multipath errors. (a)
, (b, c, d)), the estimation algorithm detects and properly tracks the additional replicas (light blue), and thus successfully mitigates the multipath errors. (a) , (b)
, (b)  , (c)
, (c)  , (d)
, (d) 
In this scenario, the channel estimation algorithm has to cope with a LOS path (red) that is superimposed by several simultaneous multipath replicas. The DLL receiver (green) shows the typical multipath errors, whose magnitude varies due to the fading processes of the path amplitudes. If the multipath replicas are not taken into account by the estimator ( , (a)), the LOS estimate (dark blue) shows still significant errors, but their magnitude is smaller than the DLL errors, since the dynamic model used in the estimator helps to constrain variation of the LOS estimate. With
, (a)), the LOS estimate (dark blue) shows still significant errors, but their magnitude is smaller than the DLL errors, since the dynamic model used in the estimator helps to constrain variation of the LOS estimate. With  (b) the number of considered paths is too small to track all replicas and thus the multipath delay estimates (light blue) tend to jump between the respective multipath signals. Once the number of considered replicas is sufficient to take into account all present signals (
(b) the number of considered paths is too small to track all replicas and thus the multipath delay estimates (light blue) tend to jump between the respective multipath signals. Once the number of considered replicas is sufficient to take into account all present signals ( , (c, d)), the estimation algorithm detects and tracks the channel, except for the period between 40 s and 80 s. During this interval, a proper resolution of the actual LOS does not seem feasible any more, due to the presence of an echo which is born with almost zero delay w.r.t. the LOS path which itself is strongly attenuated, hence its history does not allow to separate it suitably from the LOS component.
, (c, d)), the estimation algorithm detects and tracks the channel, except for the period between 40 s and 80 s. During this interval, a proper resolution of the actual LOS does not seem feasible any more, due to the presence of an echo which is born with almost zero delay w.r.t. the LOS path which itself is strongly attenuated, hence its history does not allow to separate it suitably from the LOS component.
6. Conclusions
In this paper, we have introduced a novel two-fold marginalized Bayesian filter for multipath mitigation in satellite navigation receivers. Our approach allows us to exploit the constrained channel dynamics within a typical satellite-to-user propagation scenario in an urban environment. We have proposed an efficient implementation of the filter by applying the concept of marginalization, where we proposed to estimate impinging multipath replicas in a typical track-before-detect approach. Our approach is able to adapt to the channel dynamics and favors implicitly the most likely channel configuration for a given sequence of channel observations. This has been shown to be of particular benefit in case the LOS path is shadowed or blocked, since unlike other approaches, the presented filter does not synchronize on powerful replicas during such periods. We have shown that our approach requires a significantly reduced number of particles compared to previous work, which is achieved as a result of the implicit use of phase information. Our results for a real urban environment show that our approach is practically viable and confirm its benefits. They also provide insights on how many simultaneous multipath replicas a future Bayesian navigation receiver should consider. Our findings reveal that the LOS tracking performance of our Bayesian filter tends to saturate rapidly when increasing of the number of simultaneously detectable multipath replicas.
References
Kaplan ED (Ed): Understanding GPS: Principles and Applications. Artech-House, Boston, Mass, USA; 1996.
van Dierendonck A, Fenton P, Ford T: Theory and performance of narrow correlator spacing in a GPS receiver. Proceedings of the ION National Technical Meeting, 1992, San Diego, Calif, USA
Garin L, van Diggelen F, Rousseau J: Strobe and Edge correlator multipath mitigation for code. Proceedings of the 9th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS '96), 1996, Kansas City, Mo, USA 657-664.
MacGraw G, Brasch M: GNSS multipath mitigation using gated and high resolution correlator concepts. Proceedings of the ION National Technical Meeting, 1999, San Diego, Calif, USA
Jones J, Fenton P, Smith B: Theory and performance of the Pulse Aperture Correlator. In NovAtel Technical Report. NovAtel, Calgary, Canada; 2004.
van Nee D, Siereveld J, Fenton P, Townsend B: The multipath estimating delay lock loop: approaching theoretical accuracy limits. Proceedings of the IEEE Position Location and Navigation Symposium (PLANS '94), 1994, Las Vegas, Nev, USA 246-251.
Fessler JA, Hero AO: Space-alternating generalized expectation-maximization algorithm. IEEE Transactions on Signal Processing 1994, 42(10):2664-2677. 10.1109/78.324732
Antreich F, Esbri-Rodriguez O, Nossek J, Utschick W: Estimation of synchronization parameters using SAGE in a GNSS receiver. Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS '05), 2005, Long Beach, Calif, USA 2124-2131.
Selva J: An efficient Newton-type method for the computation of ML estimators in a uniform linear array. IEEE Transactions on Signal Processing 2005, 53(6):2036-2045.
Sahmoudi M, Amin M: Fast iterative maximum-likelihood algorithm (FIMLA) for multipath mitigation in next generation of GNSS receivers. Proceedings of the 40th Asilomar Conference on Signals, Systems and Computers (ACSSC '06), October 2006, Pacific Grove, Calif, USA 579-584.
Fenton P, Jones J: The theory and performance of NovAtel Inc.s Vision Correlator. Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS '05),, September 2005, Long Beach, Calif, USA 2178-2186.
Weill L: Achieving theoretical bounds for receiver-based multipath mitigation using Galileo OS signals. Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS '06), September 2006, Fort Worth, Tex, USA 1035-1047.
Arulampalam MS, Maskell S, Gordon N, Clapp T: A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing 2002, 50(2):174-188. 10.1109/78.978374
Doucet A, de Freitas N, Gordon N (Eds): Sequential Monte Carlo Methods in Practice. Springer, New York, NY, USA; 2001.
Doucet A, de Freitas N, Murphy K, Russell S: Rao-Blackwellised particle filtering for dynamic Bayesian networks. Proceedings of the 16th Annual Conference on Uncertainty in Artificial Intelligence (UAI '00), 2000, San Francisco, Calif, USA 176-183.
Schön T, Gustafsson F, Nordlund P-J: Marginalized particle filters for mixed linear/nonlinear state-space models. IEEE Transactions on Signal Processing 2005, 53(7):2279-2289.
Iltis RA: Joint estimation of PN code delay and multipath using the extended Kalman filter. IEEE Transactions on Communications 1990, 38(10):1677-1685. 10.1109/26.61437
Punskaya E, Doucet A, Fitzgerald WJ: Particle filtering for joint symbol and code delay estimation in DS spread spectrum systems in multipath environment. EURASIP Journal on Applied Signal Processing 2004, 2004(15):2306-2314. 10.1155/S1110865704408063
Bertozzi T, Le Ruyet D, Panazio C, Vu Thien H: Channel tracking using particle filtering in unresolvable multipath environments. EURASIP Journal on Applied Signal Processing 2004, 2004(15):2328-2338. 10.1155/S1110865704409019
Closas P, Fernandez-Prades C, Fernandez-Rubio J: Bayesian DLL for multipath mitigation in navigation systems using particle filters. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing 2006 (ICASSP '06), May 2006, Toulouse, France
Lentmaier M, Krach B, Robertson P, Thiasiriphet T: Dynamic multipath estimation by sequential Monte Carlo methods. Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS '07), September 2007, Fort Worth, Tex, USA
Lentmaier M, Krach B, Robertson P: Bayesian time delay estimation of GNSS signals in dynamic multipath environments. International Journal of Navigation and Observation 2008, 2008:-11.
Selva J: Complexity reduction in the parametric estimation of superimposed signal replicas. Signal Processing 2004, 84(12):2325-2343. 10.1016/j.sigpro.2004.07.026
Closas P, Fernández-Prades C, Fernández-Rubio JA: A Bayesian approach to multipath mitigation in GNSS receivers. IEEE Journal on Selected Topics in Signal Processing 2009, 3(4):695-706.
Salmond DJ, Birch H: A particle filter for track-before-detect. Proceedings of the American Control Conference, June 2001, Arlington, Va, USA 5: 3755-3760.
Särkkä S, Vehtari A, Lampinen J: Rao-Blackwellized particle filter for multiple target tracking. Information Fusion 2007, 8(1):2-15. 10.1016/j.inffus.2005.09.009
Steingass A, Lehner A: Land mobile satellite navigation—characteristics of the multipath channel. Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS '03), September 2003, Portland, Ore, USA
Steingass A, Lehner A: Measuring the navigation multipath channel—a statistical analysis. Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS '04), September 2004, Long Beach, Calif, USA 1157-1164.
Stoica P, Nehorai A: MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(5):720-741. 10.1109/29.17564
Lehner A, Steingass A: A novel channel model for land mobile satellite navigation. Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS '05), September 2005, Fort Worth, Tex, USA
Picinbono B: Second-order complex random vectors and normal distributions. IEEE Transactions on Signal Processing 1996, 44(10):2637-2640. 10.1109/78.539051
Schön T: On computational methods for nonlinear estimation. In Licentiate Thesis. Department of Electrical Engineering, Linköping University, Linköping, Sweden; October 2003.
Bolić M, Djurić PM, Hong S: Resampling algorithms and architectures for distributed particle filters. IEEE Transactions on Signal Processing 2005, 53(7):2442-2450.
Míguez J: Analysis of parallelizable resampling algorithms for particle filtering. Signal Processing 2007, 87(12):3155-3174. 10.1016/j.sigpro.2007.06.011
Karlsson R, Schön T, Gustafsson F: Complexity analysis of the marginalized particle filter. IEEE Transactions on Signal Processing 2005, 53(11):4408-4411.
Acknowledgments
The authors would kindly thank the anonymous reviewers for their most valuable suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Krach, B., Robertson, P. & Weigel, R. An Efficient Two-Fold Marginalized Bayesian Filter for Multipath Estimation in Satellite Navigation Receivers. EURASIP J. Adv. Signal Process. 2010, 287215 (2010). https://doi.org/10.1155/2010/287215
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/287215
 ) and at most
) and at most  echoes.
echoes.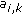 and delay
and delay  , where echoes are constrained to have delay
, where echoes are constrained to have delay 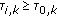 ,
,  , to reflect that multipath replicas are physically constrained to arrive later at the receiver than the LOS path.
, to reflect that multipath replicas are physically constrained to arrive later at the receiver than the LOS path.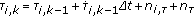
 ,
, 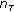 , where
, where 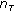 is the same value for all indices
is the same value for all indices  .
.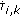 that specifies the rate of the change of the path delay follows its own process
that specifies the rate of the change of the path delay follows its own process
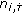 ,
, 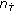 , in which
, in which  has the same value for all indices
has the same value for all indices  .
.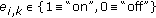 , where
, where 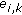 ,
,  follows a simple two-state Markov process with a-symmetric crossover and same-state probabilities
follows a simple two-state Markov process with a-symmetric crossover and same-state probabilities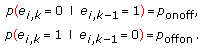
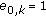 for all
for all  .
.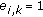 with
with 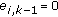 ) are initialized with
) are initialized with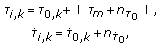
 ,
, 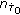 and the characteristic constant
and the characteristic constant 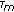 (cf. [
(cf. [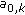 .
.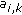 depend on the previous amplitudes
depend on the previous amplitudes 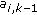 through
through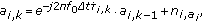
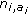 and the carrier frequency
and the carrier frequency  . Thus, the rate of change in the delay affects the evolution of the complex amplitude in a statistical manner in order to consider the physical relationships between phase, Doppler-frequency, and time delay adequately.
. Thus, the rate of change in the delay affects the evolution of the complex amplitude in a statistical manner in order to consider the physical relationships between phase, Doppler-frequency, and time delay adequately.

 . The boxes highlight the channel sections that are shown subsequently in Figures
. The boxes highlight the channel sections that are shown subsequently in Figures 
 during the scenario.
during the scenario.


 and the number of considered paths
and the number of considered paths  . Only few particles (
. Only few particles ( ) are needed to attain convergence.
) are needed to attain convergence.
